An Alternative Treatment Effect Measure for Time-to-Event Oncology Randomized Trials
Simple Summary
Abstract
1. Introduction
2. Definition of Univariate Martingale Residuals
3. Randomization Testing with UMRs
4. Simulation Study
4.1. Examples
- Hazard Functions
- For : ,
- For : .
- Hazard Ratio
- Scenario 1
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): .
- Median survival: for A, for B.
- Log-rank test: , .
- Cox PH model: with 95% CI , .
- Scenario 2
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): .
- Median survival: for A, for B.
- Log-rank test: , .
- Cox PH model: with 95% CI , .
- Scenario 3
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): .
- Median survival: not estimable for either group due to heavy censoring.
- Log-rank test: , .
- Cox PH model: with 95% CI , .
- Scenario 4
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): .
- Median survival: not estimable for A, for B.
- Log-rank test: , .
- Cox PH model: with 95% CI , .
4.2. Power Comparison
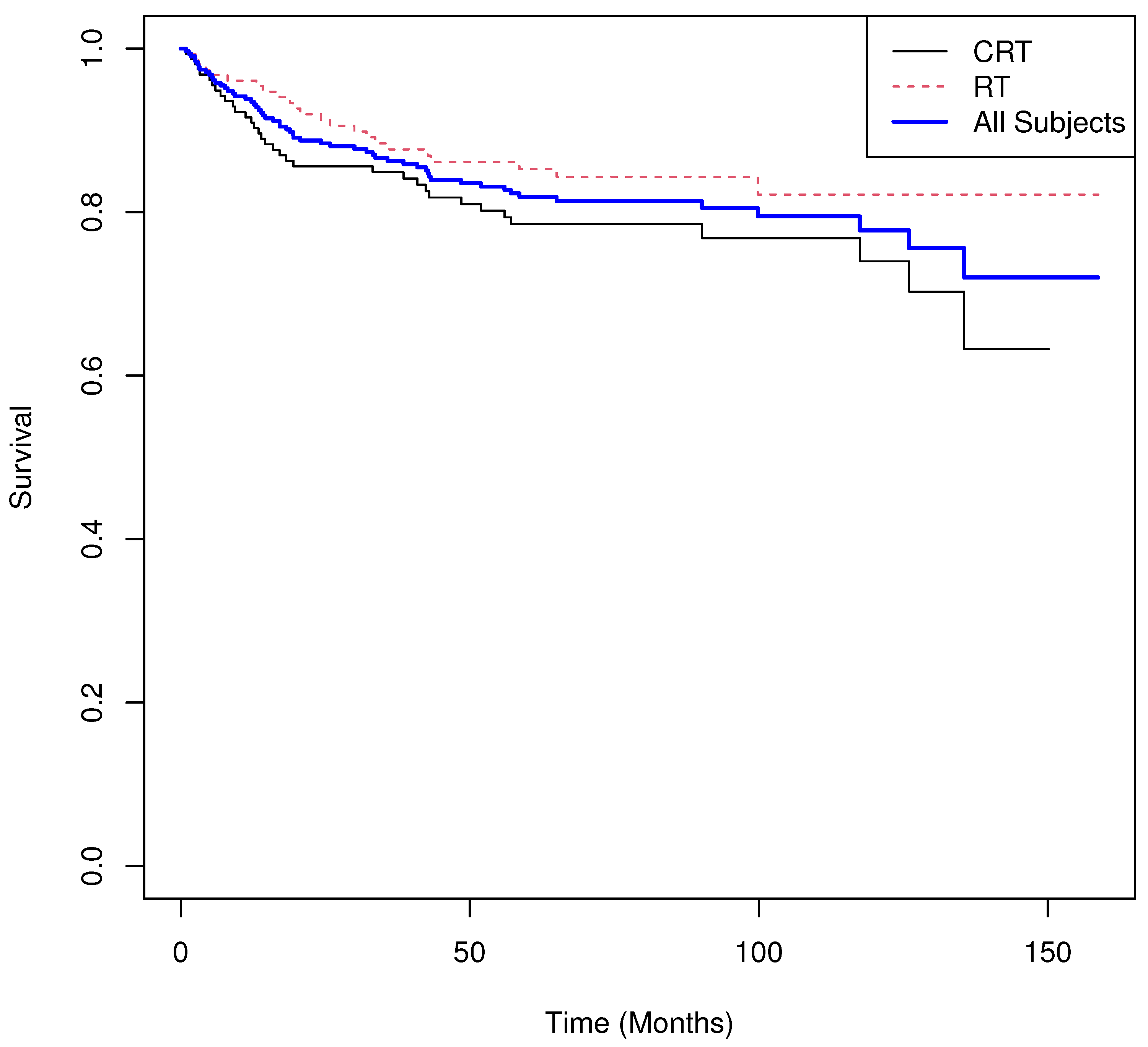
5. Real World Examples
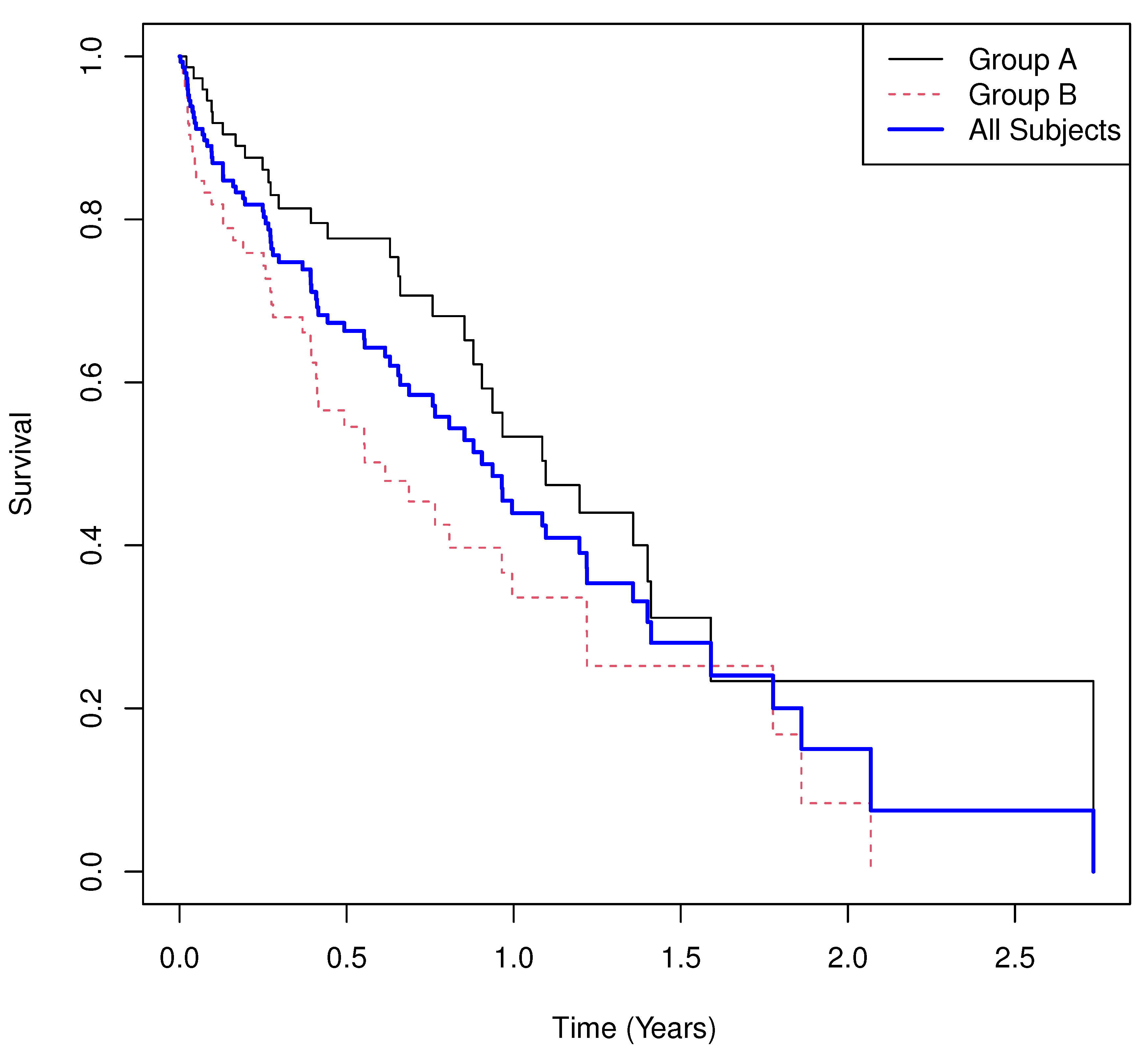
5.1. Example 1
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): two-sided .
- Median survival: for , for .
- Log-rank test: , .
- Cox PH model: with 95% CI , .
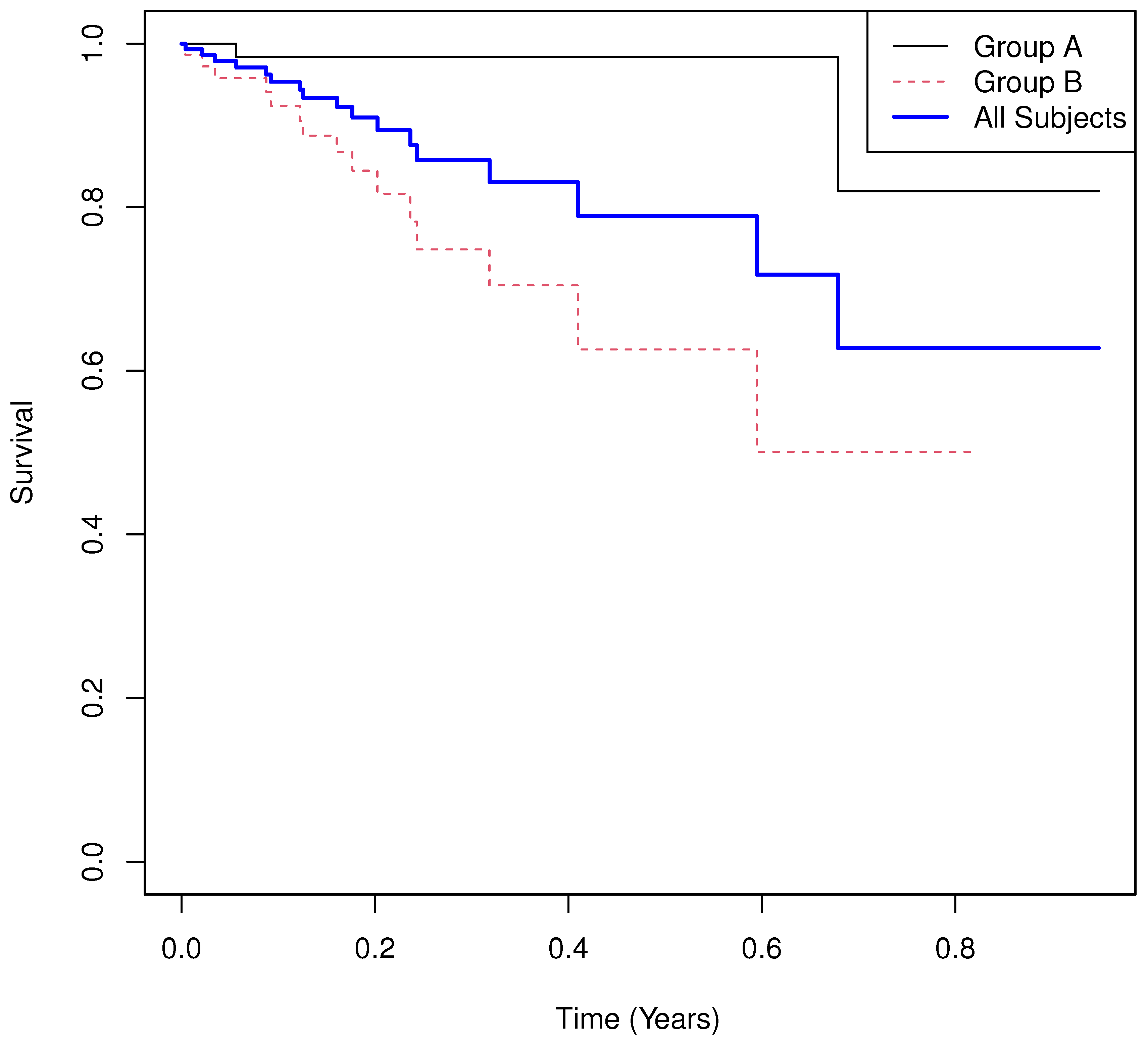
5.2. Example 2
- Results.
- Group means of martingale residuals: , .
- Randomization test (UMR difference): two-sided .
- Median survival: for , for .
- Log-rank test: , .
- Cox PH model: with 95% CI , .
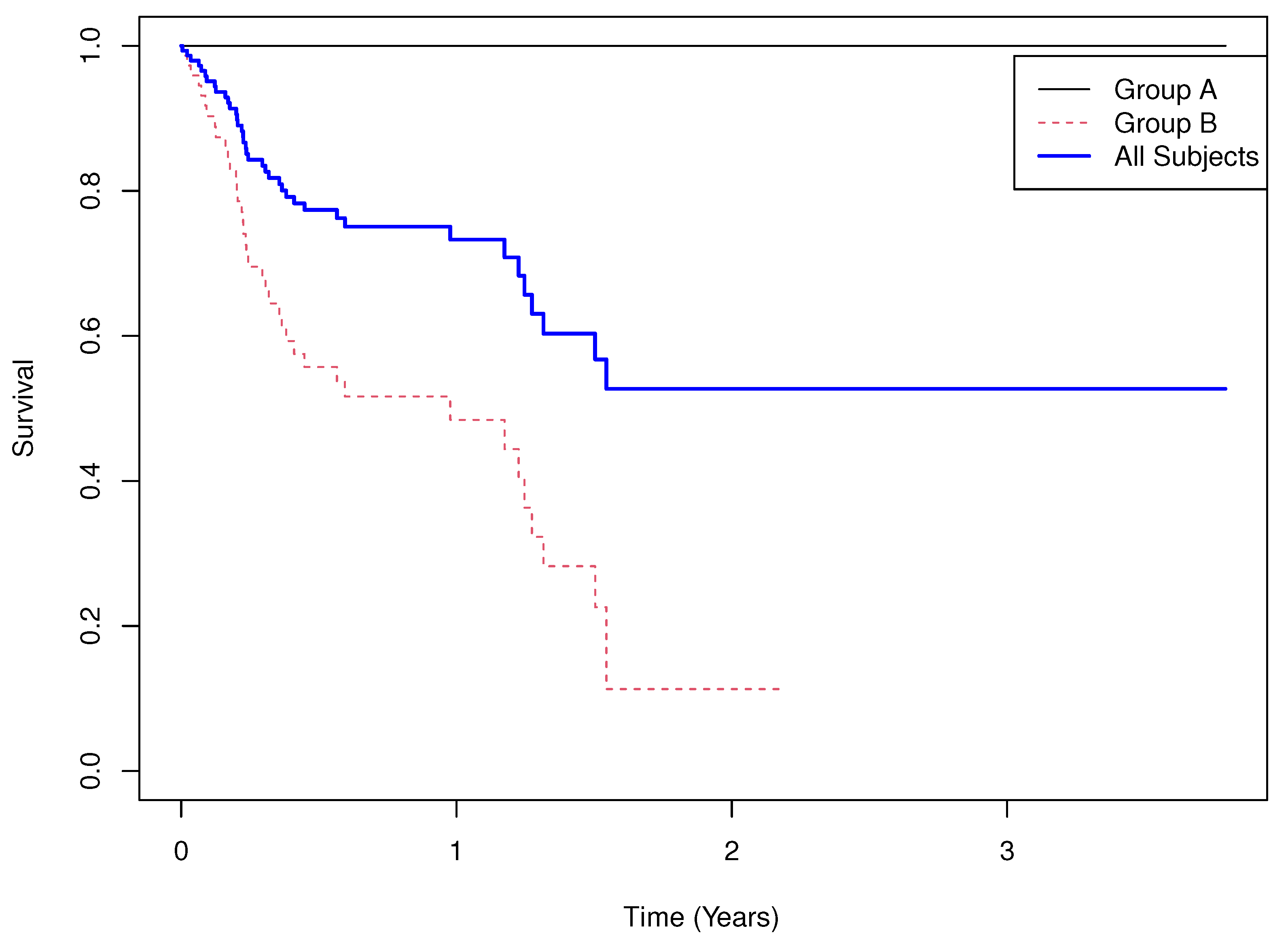
5.3. Example 3
- Results.
- Group means of martingale residuals: , .
- Randomization test (mean difference): two-sided .
- Median survival: not estimable for either group.
- Log-rank test: , .
- Cox PH model: with 95% CI , .
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barry, D.A. Statistical Methods in the Pharmaceutical Industry; Marcel Dekker, Inc.: New York, NY, USA, 1990. [Google Scholar]
- Peduzzi, P.; Concato, J.; Feinstein, A.R.; Holford, T.R. Importance of events per independent variable in proportional hazards regression analysis. II. Accuracy and precision of regression estimates. J. Clin. Epidemiol. 1995, 48, 1503–1510. [Google Scholar] [CrossRef]
- Lin, N.X.; Logan, S.; Henley, W.E. Bias and Sensitivity Analysis When Estimating Treatment Effects from the Cox Model with Omitted Covariates. Biometrics 2013, 69, 850–860. [Google Scholar] [CrossRef]
- Shao, Y.; Ye, Z.; Zhang, Z. Exact test and exact confidence interval for the Cox model. Stat. Med. 2024, epub ahead of print. [Google Scholar] [CrossRef] [PubMed]
- Campone, M.; De Laurentiis, M.; Jhaveri, K.; Hu, X.; Ladoire, S.; Patsouris, A.; Zamagni, C.; Cui, J.; Cazzaniga, M.; Cil, T.; et al. Vepdegestrant, a PROTAC Estrogen Receptor Degrader, in Advanced Breast Cancer. N. Engl. J. Med. 2025, epub ahead of print. [Google Scholar] [CrossRef]
- Turner, N.C.; Im, S.-A.; Saura, C.; Juric, D.; Loibl, S.; Kalinsky, K.; Schmid, P.; Loi, S.; Sunpaweravong, P.; Musolino, A.; et al. Inavolisib-Based Therapy in PIK3CA-Mutated Advanced Breast Cancer. N. Engl. J. Med. 2024, 391, 1584–1596. [Google Scholar] [CrossRef] [PubMed]
- Janjigian, Y.Y.; Al-Batran, S.E.; Wainberg, Z.A.; Muro, K.; Molena, D.; Van Cutsem, E.; Hyung, W.J.; Wyrwicz, L.; Oh, D.Y.; Omori, T.; et al. Perioperative Durvalumab in Gastric and Gastroesophageal Junction Cancer. N. Engl. J. Med. 2025, epub ahead of print. [Google Scholar] [CrossRef]
- Wu, Y.L.; Dziadziuszko, R.; Ahn, J.S.; Barlesi, F.; Nishio, M.; Lee, D.H.; Lee, J.S.; Zhong, W.; Horinouchi, H.; Mao, W.; et al. Alectinib in Resected ALK-Positive Non–Small-Cell Lung Cancer. N. Engl. J. Med. 2024, 390, 1265–1276. [Google Scholar] [CrossRef] [PubMed]
- Hoeppner, J.; Brunner, T.; Schmoor, C.; Bronsert, P.; Kulemann, B.; Claus, R.; Utzolino, S.; Izbicki, J.R.; Gockel, I.; Gerdes, B.; et al. Perioperative Chemotherapy or Preoperative Chemoradiotherapy in Esophageal Cancer. N. Engl. J. Med. 2025, 392, 323–335. [Google Scholar] [CrossRef]
- Zhou, C.; Solomon, B.; Loong, H.H.; Park, K.; Perol, M.; Arriola, E.; Novello, S.; Han, B.; Zhou, J.; Ardizzoni, A.; et al. First-Line Selpercatinib or Chemotherapy and Pembrolizumab in RET Fusion–Positive NSCLC. N. Engl. J. Med. 2024, 389, 1839–1850. [Google Scholar] [CrossRef]
- Herrera, A.F.; LeBlanc, M.; Castellino, S.M.; Li, H.; Rutherford, S.C.; Evens, A.M.; Davison, K.; Punnett, A.; Parsons, S.K.; Ahmed, S.; et al. Nivolumab plus AVD in Advanced-Stage Classic Hodgkin’s Lymphoma. N. Engl. J. Med. 2024, 391, 1379–1389. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Spigel, D.R.; Cho, B.C.; Laktionov, K.K.; Fang, J.; Chen, Y.; Zenke, Y.; Lee, K.H.; Wang, Q.; Navarro, A.; et al. Durvalumab after Chemoradiotherapy in Limited-Stage Small-Cell Lung Cancer. N. Engl. J. Med. 2024, 391, 1313–1327. [Google Scholar] [CrossRef]
- Munir, T.; Cairns, D.A.; Bloor, A.; Allsup, D.; Cwynarski, K.; Pettitt, A.; Paneesha, S.; Fox, C.P.; Eyre, T.A.; Forconi, F.; et al. Chronic Lymphocytic Leukemia Therapy Guided by Measurable Residual Disease. N. Engl. J. Med. 2024, 390, 326–337. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Tang, K.J.; Cho, B.C.; Liu, B.; Paz-Ares, L.; Cheng, S.; Kitazono, S.; Thiagarajan, M.; Goldman, J.W.; Sabari, J.K.; et al. Amivantamab plus Chemotherapy in NSCLC with EGFR Exon 20 Insertions. N. Engl. J. Med. 2024, 389, 2039–2051. [Google Scholar] [CrossRef] [PubMed]
- Eskander, R.N.; Sill, M.W.; Beffa, L.; Moore, R.G.; Hope, J.M.; Musa, F.B.; Mannel, R.; Shahin, M.S.; Cantuaria, G.H.; Girda, E.; et al. Pembrolizumab plus Chemotherapy in Advanced Endometrial Cancer. N. Engl. J. Med. 2023, 388, 2159–2170. [Google Scholar] [CrossRef] [PubMed]
- Powles, T.; Valderrama, B.P.; Gupta, S.; Bedke, J.; Kikuchi, E.; Hoffman-Censits, J.; Iyer, G.; Vulsteke, C.; Park, S.H.; Shin, S.J.; et al. Enfortumab Vedotin and Pembrolizumab in Untreated Advanced Urothelial Cancer. N. Engl. J. Med. 2024, 390, 875–888. [Google Scholar] [CrossRef]
- Fakih, M.G.; Salvatore, L.; Esaki, T.; Modest, D.P.; Lopez-Bravo, D.P.; Taieb, J.; Karamouzis, M.V.; Ruiz-Garcia, E.; Kim, T.W.; Kuboki, Y.; et al. Sotorasib plus Panitumumab in Refractory Colorectal Cancer with Mutated KRAS G12C. N. Engl. J. Med. 2023, 389, 2125–2139. [Google Scholar] [CrossRef]
- Powles, T.; Catto, J.W.F.; Galsky, M.D.; Al-Ahmadie, H.; Meeks, J.J.; Nishiyama, H.; Vu, T.Q.; Antonuzzo, L.; Wiechno, P.; Atduev, V.; et al. Perioperative Durvalumab with Neoadjuvant Chemotherapy in Operable Bladder Cancer. N. Engl. J. Med. 2024, 391, 1773–1786. [Google Scholar] [CrossRef]
- Jhaveri, K.L.; Im, S.A.; Saura, C.; Loibl, S.; Kalinsky, K.; Schmid, P.; Loi, S.; Thanopoulou, E.; Shankar, N.; Jin, Y.; et al. Overall Survival with Inavolisib in PIK3CA-Mutated Advanced Breast Cancer. N. Engl. J. Med. 2025, epub ahead of print. [Google Scholar] [CrossRef]
- Fizazi, K.; Piulats, J.M.; Reaume, M.N.; Ostler, P.; McDermott, R.; Gingerich, J.R.; Pintus, E.; Sridhar, S.S.; Bambury, R.M.; Emmenegger, U.; et al. Rucaparib or Physician’s Choice in Metastatic Prostate Cancer. N. Engl. J. Med. 2023, 388, 719–732. [Google Scholar] [CrossRef]
- Wakelee, H.; Liberman, M.; Kato, T.; Tsuboi, M.; Lee, S.-H.; Gao, S.; Chen, K.-N.; Dooms, C.; Majem, M.; Eigendorff, E.; et al. Perioperative Pembrolizumab for Early-Stage Non-Small-Cell Lung Cancer. N. Engl. J. Med. 2023, 389, 491–503. [Google Scholar] [CrossRef]
- Mirza, M.R.; Chase, D.M.; Slomovitz, B.M.; Christensen, R.D.; Novak, Z.; Black, D.; Gilbert, L.; Sharma, S.; Valabrega, G.; Landrum, L.M.; et al. Dostarlimab for Primary Advanced or Recurrent Endometrial Cancer. N. Engl. J. Med. 2023, 388, 2145–2158. [Google Scholar] [CrossRef]
- Cho, B.C.; Lu, S.; Felip, E.; Spira, A.I.; Girard, N.; Lee, J.S.; Lee, S.H.; Ostapenko, Y.; Danchaivijitr, P.; Liu, B. Amivantamab plus Lazertinib in Previously Untreated EGFR-Mutated Advanced NSCLC. N. Engl. J. Med. 2024, 391, 1486–1498. [Google Scholar] [CrossRef] [PubMed]
- Slamon, D.; Lipatov, O.; Nowecki, Z.; McAndrew, N.; Kukielka-Budny, B.; Stroyakovskiy, D.; Yardley, D.A.; Huang, C.S.; Fasching, P.A.; Crown, J. Ribociclib plus Endocrine Therapy in Early Breast Cancer. N. Engl. J. Med. 2024, 390, 1080–1091. [Google Scholar] [CrossRef]
- Hadoux, J.; Elisei, R.; Brose, M.S.; Hoff, A.O.; Robinson, B.G.; Gao, M.; Jarzab, B.; Isaev, P.; Kopeckova, K.; Wadsley, J.; et al. Phase 3 Trial of Selpercatinib in Advanced RET-Mutant Medullary Thyroid Cancer. N. Engl. J. Med. 2023, 389, 1851–1861. [Google Scholar] [CrossRef]
- Schrag, D.; Shi, Q.; Weiser, M.R.; Gollub, M.J.; Saltz, L.B.; Musher, B.L.; Goldberg, J.; Al Baghdadi, T.; Goodman, K.A.; McWilliams, R.R.; et al. Preoperative Treatment of Locally Advanced Rectal Cancer. N. Engl. J. Med. 2023, 389, 322–334. [Google Scholar] [CrossRef]
- Turner, N.C.; Oliveira, M.; Howell, S.J.; Dalenc, F.; Cortes, J.; Moreno, H.L.G.; Hu, X.; Jhaveri, K.; Krivorotko, P.; Loibl, S.; et al. Capivasertib in Hormone Receptor-Positive Advanced Breast Cancer. N. Engl. J. Med. 2023, 388, 2058–2070. [Google Scholar] [CrossRef] [PubMed]
- Plante, M.; Kwon, J.S.; Ferguson, S.; Samouëlian, V.; Ferron, G.; Maulard, A.; de Kroon, C.; Van Driel, W.; Tidy, J.; Williamson, K. Simple versus Radical Hysterectomy in Women with Low-Risk Cervical Cancer. N. Engl. J. Med. 2024, 390, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Moore, K.N.; Angelergues, A.; Konecny, G.E.; Garcia, Y.; Banerjee, S.; Lorusso, D.; Lee, J.-Y.; Moroney, J.W.; Colombo, N.; Roszak, A.; et al. Mirvetuximab Soravtansine in FRalpha-Positive, Platinum-Resistant Ovarian Cancer. N. Engl. J. Med. 2023, 389, 2162–2174. [Google Scholar] [CrossRef]
- Courneya, K.S.; Vardy, J.L.; O’cAllaghan, C.J.; Gill, S.; Friedenreich, C.M.; Wong, R.K.; Dhillon, H.M.; Coyle, V.; Chua, N.S.; Jonker, D.J.; et al. Structured Exercise after Adjuvant Chemotherapy for Colon Cancer. N. Engl. J. Med. 2025, epub ahead of print. [Google Scholar] [CrossRef]
- Cascone, T.; Awad, M.M.; Spicer, J.D.; He, J.; Lu, S.; Sepesi, B.; Tanaka, F.; Taube, J.M.; Cornelissen, R.; Havel, L. Perioperative Nivolumab in Resectable Lung Cancer. N. Engl. J. Med. 2024, 390, 1756–1769. [Google Scholar] [CrossRef]
- Shitara, K.; Van Cutsem, E.; Gümüş, M.; Lonardi, S.; de la Fouchardière, C.; Coutzac, C.; Dekervel, J.; Hochhauser, D.; Shen, L.; Mansoor, W. Trastuzumab Deruxtecan or Ramucirumab plus Paclitaxel in Gastric Cancer. N. Engl. J. Med. 2025, epub ahead of print. [Google Scholar] [CrossRef]
- Prager, G.W.; Taieb, J.; Fakih, M.; Ciardiello, F.; Van Cutsem, E.; Elez, E.; Cruz, F.M.; Wyrwicz, L.; Stroyakovskiy, D.; Pápai, Z.; et al. Trifluridine-Tipiracil and Bevacizumab in Refractory Metastatic Colorectal Cancer. N. Engl. J. Med. 2023, 388, 1657–1667. [Google Scholar] [CrossRef] [PubMed]
- Kunkler, I.H.; Williams, L.J.; Jack, W.J.; Cameron, D.A.; Dixon, J.M. Breast-Conserving Surgery with or without Irradiation in Early Breast Cancer. N. Engl. J. Med. 2023, 388, 585–594. [Google Scholar] [CrossRef]
- Hutson, A.; Yu, H. Strategies to Boost Statistical Efficiency in Randomized Oncology Trials with Primary Time-to-Event Endpoints. Stat. Methods Med. Res. 2025, 34, 1534–1552. [Google Scholar] [CrossRef] [PubMed]
- Kempthorne, O. The Randomization Theory of Experimental Inference. J. Am. Stat. Assoc. 1955, 50, 946–967. [Google Scholar] [PubMed]
- Cox, D.R.; Oakes, D. Analysis of Survival Data; Chapman and Hall/CRC: New York, NY, USA, 1984. [Google Scholar]
- Therneau, M.T.; Grambsch, P.M.; Fleming, T.R. Martingale-Based Residuals for Survival Models. Biometrika 1990, 77, 147–160. [Google Scholar] [CrossRef]
- Rosenbaum, P.R. Covariance Adjustment in Randomized Experiments and Observational Studies. Stat. Sci. 2002, 17, 286–327. [Google Scholar] [CrossRef]
- Sweeney, C.J.; Chen, Y.-H.; Carducci, M.; Liu, G.; Jarrard, D.F.; Eisenberger, M.; Wong, Y.-N.; Hahn, N.; Kohli, M.; Cooney, M.M.; et al. Chemohormonal therapy in metastatic hormone-sensitive prostate cancer. N. Engl. J. Med. 2015, 373, 737–746. [Google Scholar] [CrossRef]
- Salgia, R.; Stille, J.R.; Weaver, R.W.; McCleod, M.; Hamid, O.; Polzer, J.; Roberson, S.; Flynt, A.; Spigel, D.R. A randomized phase II study of LY2510924 and carboplatin/etoposide versus carboplatin/etoposide in extensive-disease small cell lung cancer. Lung Cancer 2017, 105, 7–13. [Google Scholar] [CrossRef]
- Ryu, S.Y.; Deng, W.; Albuquerque, K.; Koh, W.J.; Mayadev, J.; Heugel, A.; Kim, B.J.; Kim, D.Y.; Cho, C.H.; Kim, J.W.; et al. Randomized Phase III Trial of Adjuvant Radiation Versus Chemoradiation in Intermediate-Risk, Early-Stage Cervical Cancer Following Radical Hysterectomy and Lymphadenectomy: Results from NRG Oncology/GOG-263/KGOG 1008. Ann. Oncol. 2025, in press. [Google Scholar] [CrossRef]



| Permutation | Logrank | |||
|---|---|---|---|---|
| 0.5 | 0.5 | 0.5 | 0.055 | 0.058 |
| 1.0 | 0.5 | 0.5 | 0.441 | 0.449 |
| 1.5 | 0.5 | 0.5 | 0.827 | 0.827 |
| 2.0 | 0.5 | 0.5 | 0.949 | 0.952 |
| 0.5 | 1.0 | 0.5 | 0.344 | 0.369 |
| 1.0 | 1.0 | 0.5 | 0.148 | 0.148 |
| 1.5 | 1.0 | 0.5 | 0.615 | 0.621 |
| 2.0 | 1.0 | 0.5 | 0.895 | 0.900 |
| 0.5 | 1.5 | 0.5 | 0.614 | 0.654 |
| 1.0 | 1.5 | 0.5 | 0.052 | 0.053 |
| 1.5 | 1.5 | 0.5 | 0.412 | 0.420 |
| 2.0 | 1.5 | 0.5 | 0.796 | 0.800 |
| 0.5 | 0.5 | 1.0 | 0.888 | 0.888 |
| 1.0 | 0.5 | 1.0 | 0.048 | 0.049 |
| 1.5 | 0.5 | 1.0 | 0.340 | 0.345 |
| 2.0 | 0.5 | 1.0 | 0.680 | 0.692 |
| 0.5 | 1.0 | 1.0 | 0.958 | 0.959 |
| 1.0 | 1.0 | 1.0 | 0.060 | 0.063 |
| 1.5 | 1.0 | 1.0 | 0.443 | 0.443 |
| 2.0 | 1.0 | 1.0 | 0.882 | 0.884 |
| 0.5 | 1.5 | 1.0 | 0.982 | 0.982 |
| 1.0 | 1.5 | 1.0 | 0.048 | 0.047 |
| 1.5 | 1.5 | 1.0 | 0.567 | 0.566 |
| 2.0 | 1.5 | 1.0 | 0.934 | 0.941 |
| Permutation | Logrank | |||
|---|---|---|---|---|
| 0.5 | 0.5 | 1.5 | 0.996 | 0.996 |
| 1.0 | 0.5 | 1.5 | 0.215 | 0.221 |
| 1.5 | 0.5 | 1.5 | 0.100 | 0.102 |
| 2.0 | 0.5 | 1.5 | 0.352 | 0.355 |
| 0.5 | 1.0 | 1.5 | 0.999 | 0.999 |
| 1.0 | 1.0 | 1.5 | 0.111 | 0.109 |
| 1.5 | 1.0 | 1.5 | 0.278 | 0.277 |
| 2.0 | 1.0 | 1.5 | 0.749 | 0.749 |
| 0.5 | 1.5 | 1.5 | 0.997 | 0.997 |
| 1.0 | 1.5 | 1.5 | 0.054 | 0.057 |
| 1.5 | 1.5 | 1.5 | 0.472 | 0.484 |
| 2.0 | 1.5 | 1.5 | 0.931 | 0.936 |
| 0.5 | 0.5 | 2.0 | 1.000 | 1.000 |
| 1.0 | 0.5 | 2.0 | 0.526 | 0.526 |
| 1.5 | 0.5 | 2.0 | 0.042 | 0.047 |
| 2.0 | 0.5 | 2.0 | 0.209 | 0.215 |
| 0.5 | 1.0 | 2.0 | 1.000 | 1.000 |
| 1.0 | 1.0 | 2.0 | 0.237 | 0.241 |
| 1.5 | 1.0 | 2.0 | 0.176 | 0.181 |
| 2.0 | 1.0 | 2.0 | 0.658 | 0.665 |
| 0.5 | 1.5 | 2.0 | 1.000 | 1.000 |
| 1.0 | 1.5 | 2.0 | 0.108 | 0.110 |
| 1.5 | 1.5 | 2.0 | 0.401 | 0.412 |
| 2.0 | 1.5 | 2.0 | 0.887 | 0.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutson, A.D.; Yu, H. An Alternative Treatment Effect Measure for Time-to-Event Oncology Randomized Trials. Cancers 2025, 17, 3750. https://doi.org/10.3390/cancers17233750
Hutson AD, Yu H. An Alternative Treatment Effect Measure for Time-to-Event Oncology Randomized Trials. Cancers. 2025; 17(23):3750. https://doi.org/10.3390/cancers17233750
Chicago/Turabian StyleHutson, Alan D., and Han Yu. 2025. "An Alternative Treatment Effect Measure for Time-to-Event Oncology Randomized Trials" Cancers 17, no. 23: 3750. https://doi.org/10.3390/cancers17233750
APA StyleHutson, A. D., & Yu, H. (2025). An Alternative Treatment Effect Measure for Time-to-Event Oncology Randomized Trials. Cancers, 17(23), 3750. https://doi.org/10.3390/cancers17233750






