Reducing Bias in the Evaluation of Robotic Surgery for Lung Cancer Through Machine Learning
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Database and Inclusion
2.2. Patient Characteristics
2.3. Modeling and Propensity Score Estimation
- Logistic Regression (LR): A classical statistical model for propensity score estimation, based on a logistic function that models the probability of belonging to a treatment group according to covariates [8].
- Random Forest (RF): A supervised learning algorithm based on an ensemble of decision trees. Each tree is trained on a subsample of the data, and the final prediction is obtained through majority voting. RF is robust to nonlinear interactions and highly correlated variables [5]. To mitigate the risk of overfitting (i.e., when a model learns the training data excessively well but fails to generalize to unseen data) and to prevent data leakage (the inadvertent use of future or test set information during training), we implemented a rigorous methodological framework. The Random Forest algorithm, which aggregates multiple decision trees built from random subsamples of the dataset, is widely recognized for its robustness in handling correlated variables and complex interactions. Model hyperparameters (including the number of trees, tree depth, and the minimum number of patients per terminal node) were optimized through a systematic grid search embedded within a 5-fold cross-validation procedure. In this approach, the dataset was partitioned into five subsets of comparable size: in each iteration, four subsets were used for training and one for validation, with roles rotated to ensure that all data contributed to both training and validation. Final performance metrics were derived exclusively from an independent test set, which was set aside at the outset and never used during model training or parameter tuning. This strategy ensures that the reported results reflect genuine generalizability rather than methodological artifacts.
- Gradient Boosting Machine (GBM): A supervised learning method that progressively improves model performance by minimizing a loss function. Each new tree corrects the errors of previous trees, allowing for higher predictive accuracy [6]. The Gradient Boosting Machine (GBM) is a supervised statistical learning method that combines multiple weak learners (decision trees) to predict a clinical outcome. Each successive tree is built to correct the errors of the previous one, thereby progressively improving predictive accuracy.
- Learning rate: regulates the contribution of each new tree; excessively high values may lead to model instability, while overly low values may slow down learning.
- n_estimators: total number of trees constructed; larger values allow the model to capture more complex relationships, but increase the risk of overfitting.
- max_depth: maximum depth of the trees; this parameter constrains individual tree complexity to prevent the model from fitting only the idiosyncrasies of the training sample.
- subsample: proportion of the data used at each iteration; this introduces randomness that is beneficial in reducing the risk of overfitting.
- XGBoost (XGB): An optimized variant of GBM that incorporates regularization to prevent overfitting and improve computational efficiency. This algorithm is well known for its high performance and fast learning capabilities [7]. XGBoost (Extreme Gradient Boosting) is an optimized implementation of the Gradient Boosting Machine (GBM). It is widely recognized for its high predictive performance and computational efficiency. The algorithm incorporates regularization mechanisms to reduce the risk of overfitting, i.e., excessive adaptation to the training data.
- learning_rate: controls the contribution of each new tree; lower values lead to a more gradual and stable learning process.
- n_estimators: total number of trees constructed; directly influences the complexity and accuracy of the model.
- max_depth: maximum depth of the trees; constrains tree complexity to avoid oversensitivity to sample-specific patterns.
- alpha and lambda: regularization parameters (penalties) that regulate model complexity and mitigate overfitting.
- subsample and colsample_bytree: proportions of data and variables used at each iteration, introducing beneficial randomness that enhances robustness.
2.4. Bias Reduction Strategy
- Propensity score weighting assigns a weight to each observation to balance the distribution of covariates between treatment groups, thereby minimizing initial imbalances [19].
- Propensity score matching: Matches patients who underwent robot-assisted surgery with thoracotomy patients who have similar characteristics, reducing potential confounding sources [20].
3. Results
3.1. Patient and Hospital Characteristics by Surgical Approach
3.2. Model Performance Evaluation
3.3. Effect of Robotic Surgery on 90-Day Mortality
4. Discussion
4.1. Key Findings
4.2. Comparison with Existing Literature
4.3. Bias Reduction and Model Performance
4.4. Impact of Robot-Assisted Surgery on 90-Day Mortality
4.5. Limitations
4.6. Strength
4.7. Unanswered Questions and Future Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | Area Under the Curve |
| AI | artificial intelligence |
| BMI | body mass index |
| CCI | Charlson Comorbidity Index |
| CI | confidence interval |
| FEV1 | forced expiratory volume in one second |
| CCAM | French Common Classification of Medical Procedures |
| PMSI | French national hospital database |
| GBM | Gradient Boosting Machine |
| ICD-10 | International Classification of Diseases |
| LR | logistic regression |
| LC | lung cancer |
| ML | machine learning |
| OR | odds ratio |
| RF | random forest |
| RAS | Robot-assisted surgery |
| SMD | Standardized Mean Differences |
| VATS | video-assisted thoracic surgery |
| WHO | World Health Organization |
| XGB | XGBoost |
References
- Reddy, K.; Gharde, P.; Tayade, H.; Patil, M.; Reddy, L.S.; Surya, D. Advancements in Robotic Surgery: A Comprehensive Overview of Current Utilizations and Upcoming Frontiers. Cureus 2023, 15, e50415. [Google Scholar] [CrossRef]
- Madelaine, L.; Baste, J.M.; Trousse, D.; Vidal, R.; Durand, M.; Pagès, P.B. Impact of robotic access on outcomes after lung cancer surgery in France: Analysis from the Epithor database. JTCVS Open 2023, 14, 523–537. [Google Scholar] [CrossRef]
- Bernard, A. Observational studies to evaluate robotic-assisted lung cancer surgery? Rev. Mal. Respir. 2024, 41, 562–570. [Google Scholar] [CrossRef]
- Austin, P.C. The performance of different propensity score methods for estimating marginal hazard ratios. Stat. Med. 2013, 32, 2837–2849. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- World Health Organization (WHO). ICD-10: International Statistical Classification of Diseases and Related Health Problems; 10th Revision (ICD-10); WHO: Geneva, Switzerland, 1994.
- Iezzoni, L.I. Assessing quality using administrative data. Ann. Intern. Med. 1997, 127 Pt 2, 666–674. [Google Scholar] [CrossRef]
- Bernard, A.; Cottenet, J.; Pagès, P.B.; Quantin, C. Mortality and failure-to-rescue major complication trends after lung cancer surgery between 2005 and 2020: A nationwide population-based study. BMJ Open 2023, 13, e075463. [Google Scholar] [CrossRef]
- Bernard, A.; Cottenet, J.; Quantin, C. Is the Validity of Logistic Regression Models Developed with a National Hospital Database Inferior to Models Developed from Clinical Databases to Analyze Surgical Lung Cancers? Cancers 2024, 16, 734. [Google Scholar] [CrossRef]
- Charlson, M.; Szatrowski, T.P.; Peterson, J.; Gold, J. Validation of a combined comorbidity index. J. Clin. Epidemiol. 1994, 47, 1245–1251. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Normand, S.L.T.; Landrum, M.B.; Guadagnoli, E.; Ayanian, J.Z.; Ryan, T.J.; Cleary, P.D.; McNeil, B.J. Validating recommendations for coronary angiography following acute myocardial infarction in the elderly: A matched analysis using propensity scores. J. Clin. Epidemiol. 2001, 54, 387–398. [Google Scholar] [CrossRef]
- Austin, P.C.; Stuart, E.A. Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat. Med. 2015, 34, 3661–3679. [Google Scholar] [CrossRef]
- Stuart, E.A. Matching methods for causal inference: A review and a look forward. Stat. Sci. Rev. J. Inst. Math. Stat. 2010, 25, 1–21. [Google Scholar] [CrossRef]
- Yu, K.H.; Kohane, I.S. Framing the challenges of artificial intelligence in medicine. BMJ Qual. Saf. 2019, 28, 238–241. [Google Scholar] [CrossRef]
- Deeny, S.R.; Steventon, A. Making sense of the shadows: Priorities for creating a learning healthcare system based on routinely collected data. BMJ Qual. Saf. 2015, 24, 505–515. [Google Scholar] [CrossRef]
- Lee, B.K.; Lessler, J.; Stuart, E.A. Improving propensity score weighting using machine learning. Stat. Med. 2010, 29, 337–346. [Google Scholar] [CrossRef]
- Lourenço, L.; Weber, L.; Garcia, L.; Ramos, V.; Souza, J. Machine Learning Algorithms to Estimate Propensity Scores in Health Policy Evaluation: A Scoping Review. Int. J. Environ. Res. Public Health 2024, 21, 1484. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, H.; Fang, Z.; Li, F. Primary tumor surgery improves survival of cancer patients with synchronous solitary bone metastasis: A large population-based study. Ann. Transl. Med. 2021, 9, 31. [Google Scholar] [CrossRef]
- Mansur, A.; Saleem, Z.; Potter, A.L.; Mathey-Andrews, C.; Senthil, P.; Yang, C.F.J. Primary clear cell adenocarcinoma of the lung: A national analysis. J. Thorac. Dis. 2023, 15, 4248–4261. [Google Scholar] [CrossRef]
- Hage Chehade, A.; Abdallah, N.; Marion, J.M.; Oueidat, M.; Chauvet, P. Lung and colon cancer classification using medical imaging: A feature engineering approach. Phys. Eng. Sci. Med. 2022, 45, 729–746. [Google Scholar] [CrossRef]
- Yang, Y.H.; Park, S.Y.; Kim, H.E.; Park, B.J.; Lee, C.Y.; Lee, J.G.; Kim, D.J.; Paik, H.C. Effects of mediastinal lymph node dissection in colorectal cancer-related pulmonary metastasectomy. Thorac. Cancer 2021, 12, 3248–3254. [Google Scholar] [CrossRef]
- Williams, N.R.; Macbeth, F.; Treasure, T. Colorectal cancer-related pulmonary metastasectomy: Factors affecting survival time. Thorac. Cancer 2022, 13, 517–518. [Google Scholar] [CrossRef]
- O’Sullivan, K.E.; Kreaden, U.S.; Hebert, A.E.; Eaton, D.; Redmond, K.C. A systematic review and meta-analysis of robotic versus open and video-assisted thoracoscopic surgery approaches for lobectomy. Interact. Cardiovasc. Thorac. Surg. 2019, 28, 526–534. [Google Scholar] [CrossRef]

| Model | AUC ROC | Accuracy | Brier Score |
|---|---|---|---|
| Random Forest (RF) | 0.9987 | 0.9838 | 0.0121 |
| Logistic Regression (LR) | 0.9162 | 0.8744 | 0.0870 |
| Gradient Boosting Machine (GBM) | 0.9954 | 0.9814 | 0.0165 |
| XGBoost (XGB) | 0.9984 | 0.9867 | 0.0119 |
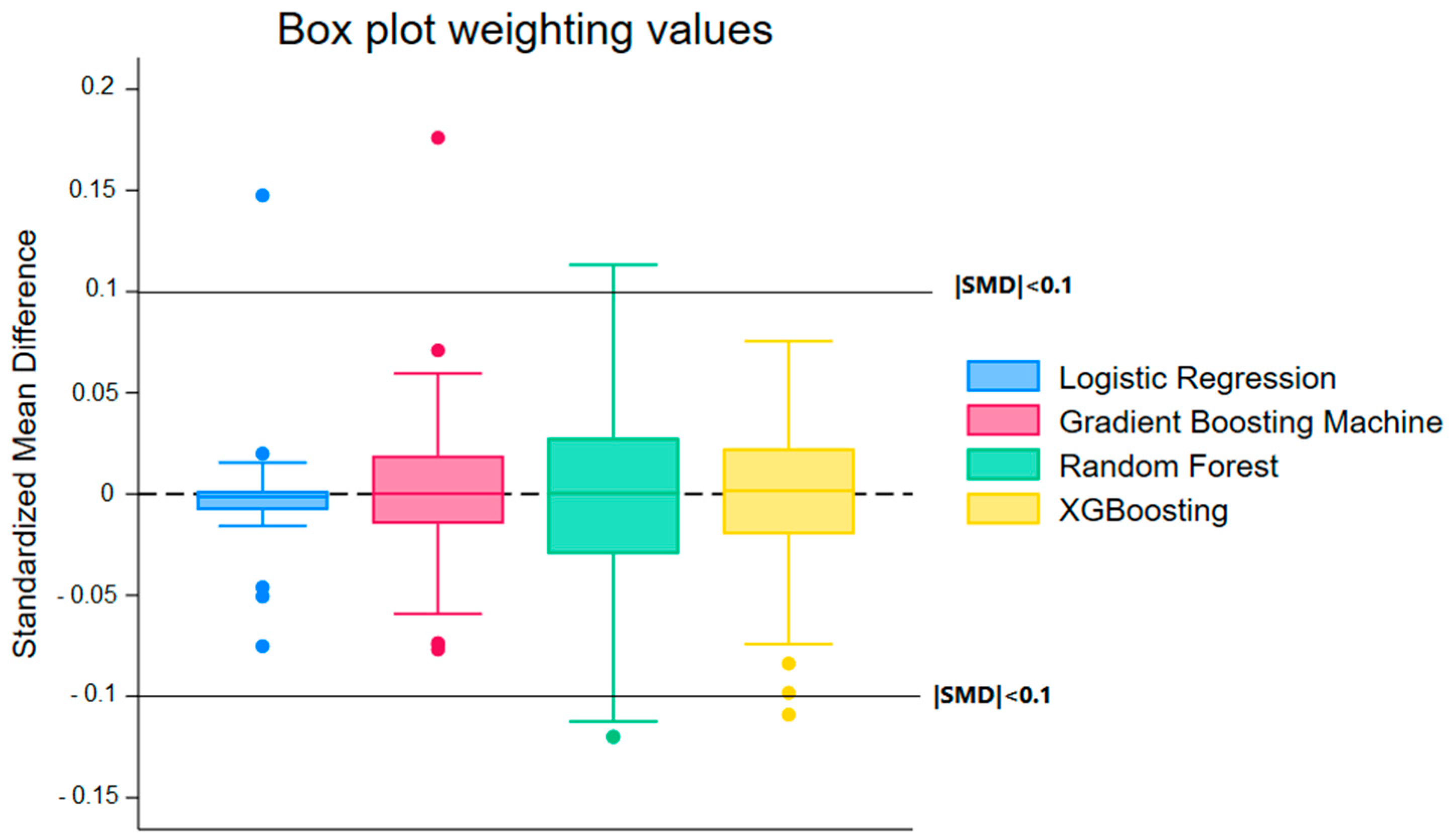
| Model | Median (Weighting) | Min (Weighting) | Max (Weighting) | Median (Matching) | Min (Matching) | Max (Matching) |
|---|---|---|---|---|---|---|
| Random Forest (RF) | 0.0004 | −0.12 | 0.1132 | −0.0112 | −0.1837 | 0.2592 |
| Logistic Regression (LR) | −0.0014 | −0.0752 | 0.1475 | −0.0005 | −0.1149 | 0.1434 |
| Gradient Boosting Machine (GBM) | 0.0002 | −0.0769 | 0.176 | −0.0019 | −0.1896 | 0.204 |
| XGBoost (XGB) | 0.0016 | −0.1091 | 0.0756 | 0.0005 | −0.1562 | 0.2009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernard, A.; Cottenet, J.; Tubert-Bitter, P.; Quantin, C. Reducing Bias in the Evaluation of Robotic Surgery for Lung Cancer Through Machine Learning. Cancers 2025, 17, 3347. https://doi.org/10.3390/cancers17203347
Bernard A, Cottenet J, Tubert-Bitter P, Quantin C. Reducing Bias in the Evaluation of Robotic Surgery for Lung Cancer Through Machine Learning. Cancers. 2025; 17(20):3347. https://doi.org/10.3390/cancers17203347
Chicago/Turabian StyleBernard, Alain, Jonathan Cottenet, Pascale Tubert-Bitter, and Catherine Quantin. 2025. "Reducing Bias in the Evaluation of Robotic Surgery for Lung Cancer Through Machine Learning" Cancers 17, no. 20: 3347. https://doi.org/10.3390/cancers17203347
APA StyleBernard, A., Cottenet, J., Tubert-Bitter, P., & Quantin, C. (2025). Reducing Bias in the Evaluation of Robotic Surgery for Lung Cancer Through Machine Learning. Cancers, 17(20), 3347. https://doi.org/10.3390/cancers17203347







