Specific Absorption Rate Optimization in Microwave Cancer Hyperthermia via Local Power Synthesis Algorithm
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Heating Mechanism in Hyperthermia
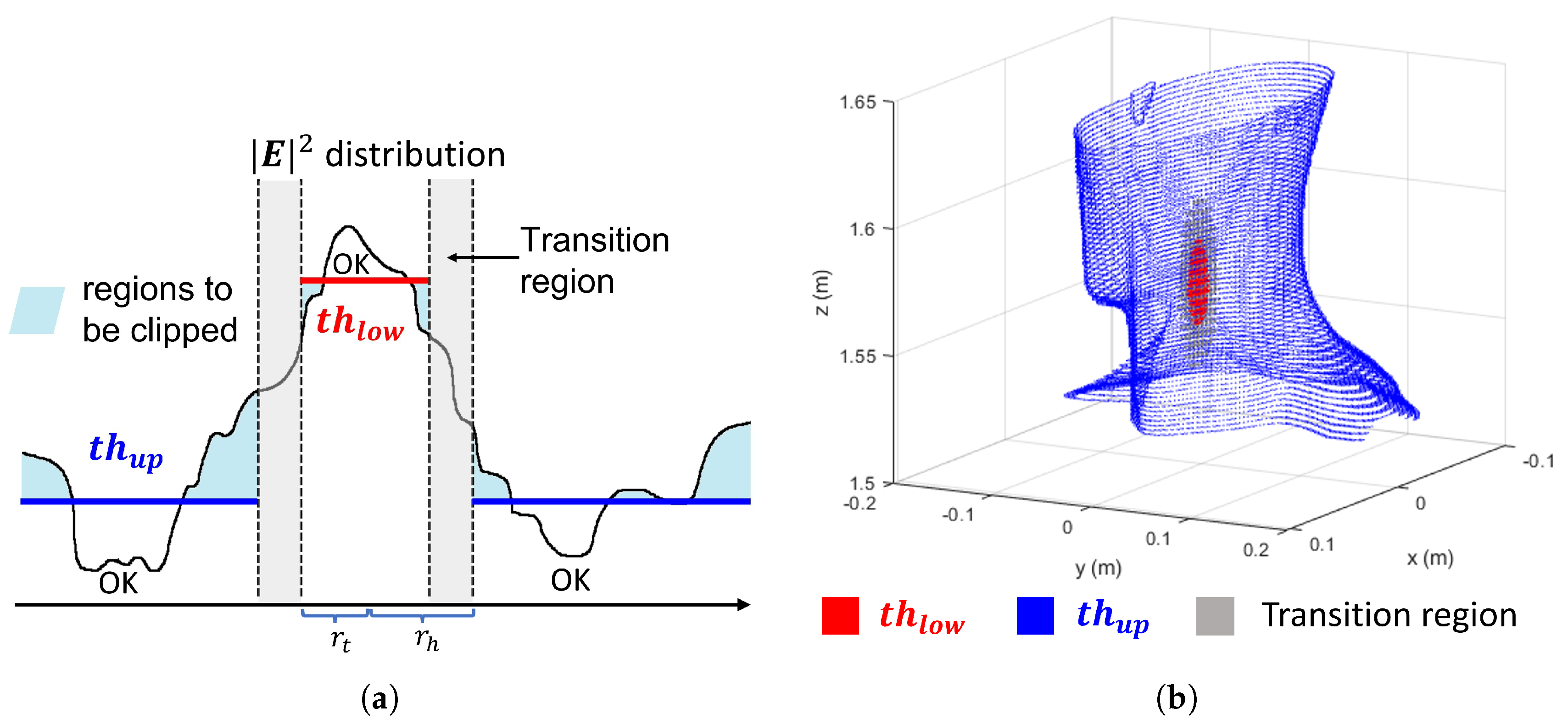
2.2. Optimization Approach
| Algorithm 1 APA Optimization Algorithm |
|
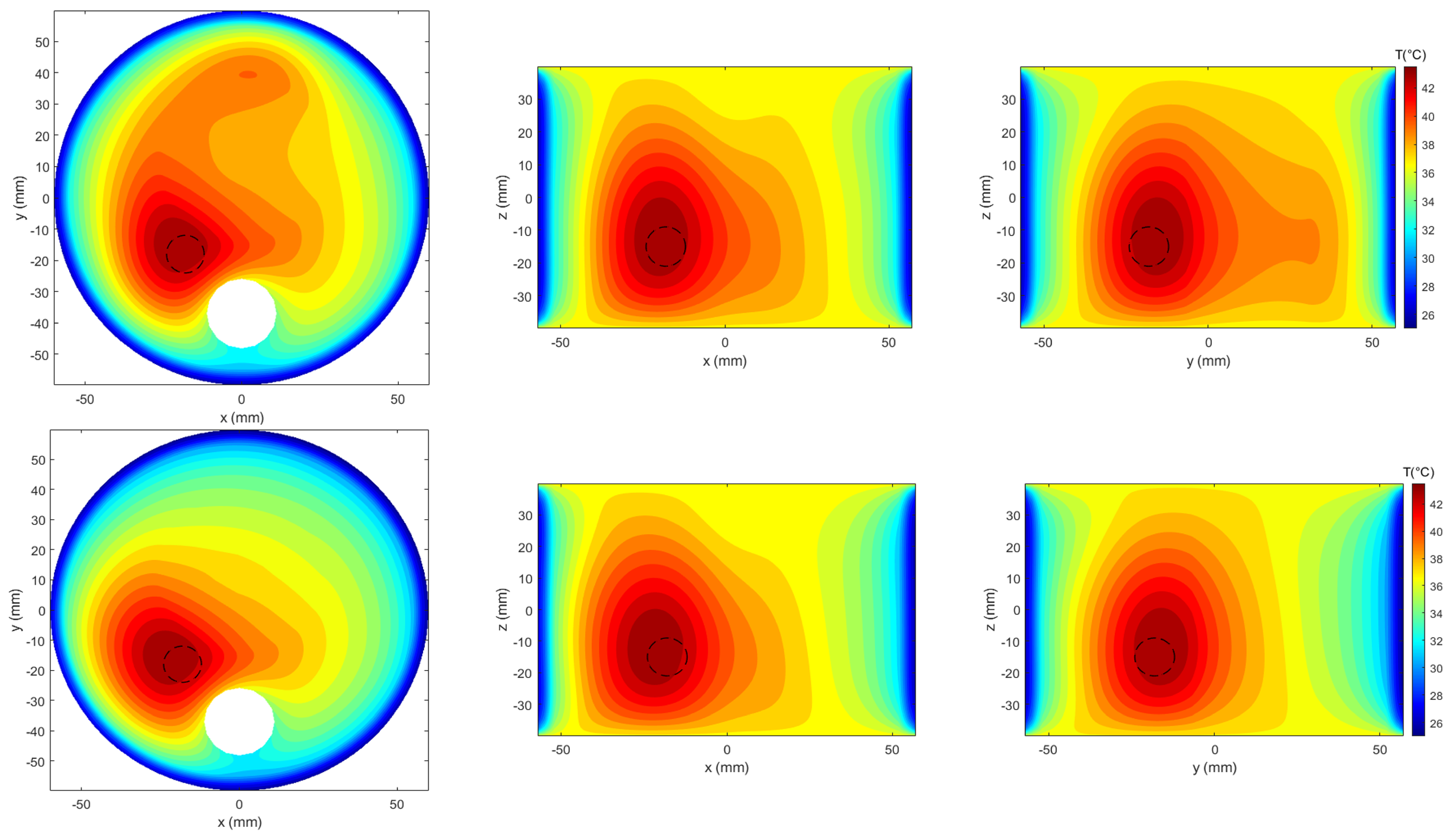
3. Results
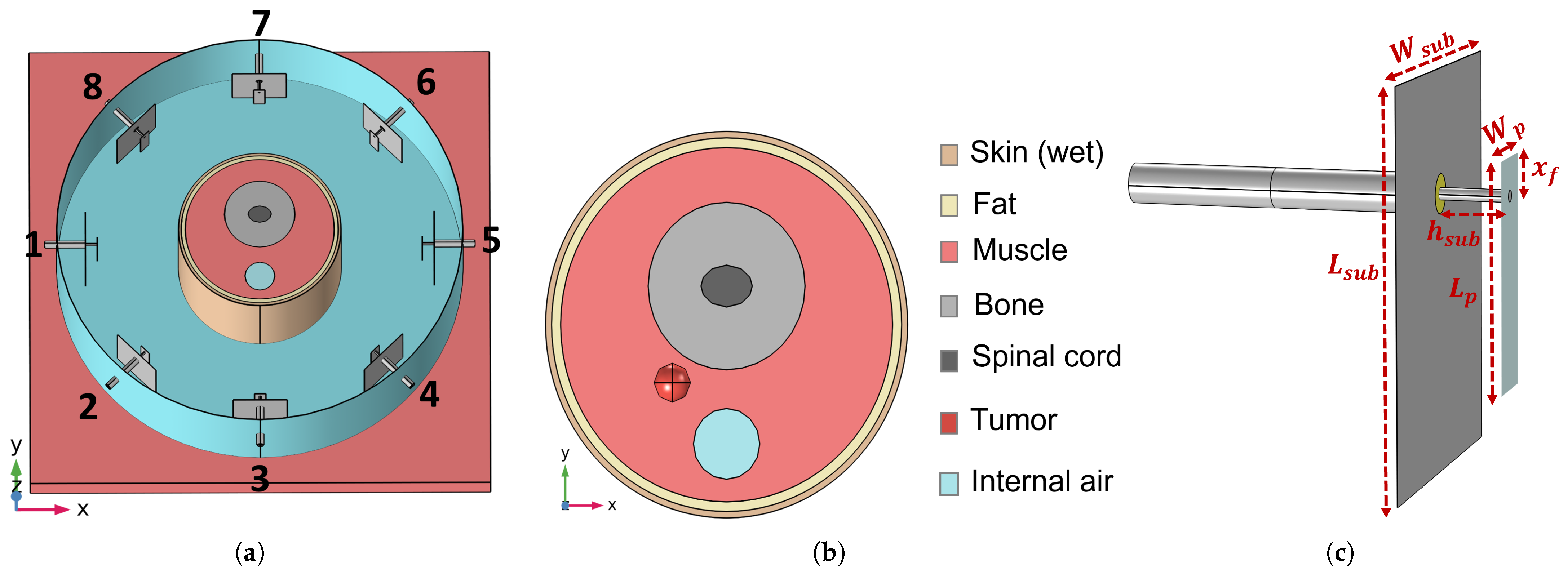
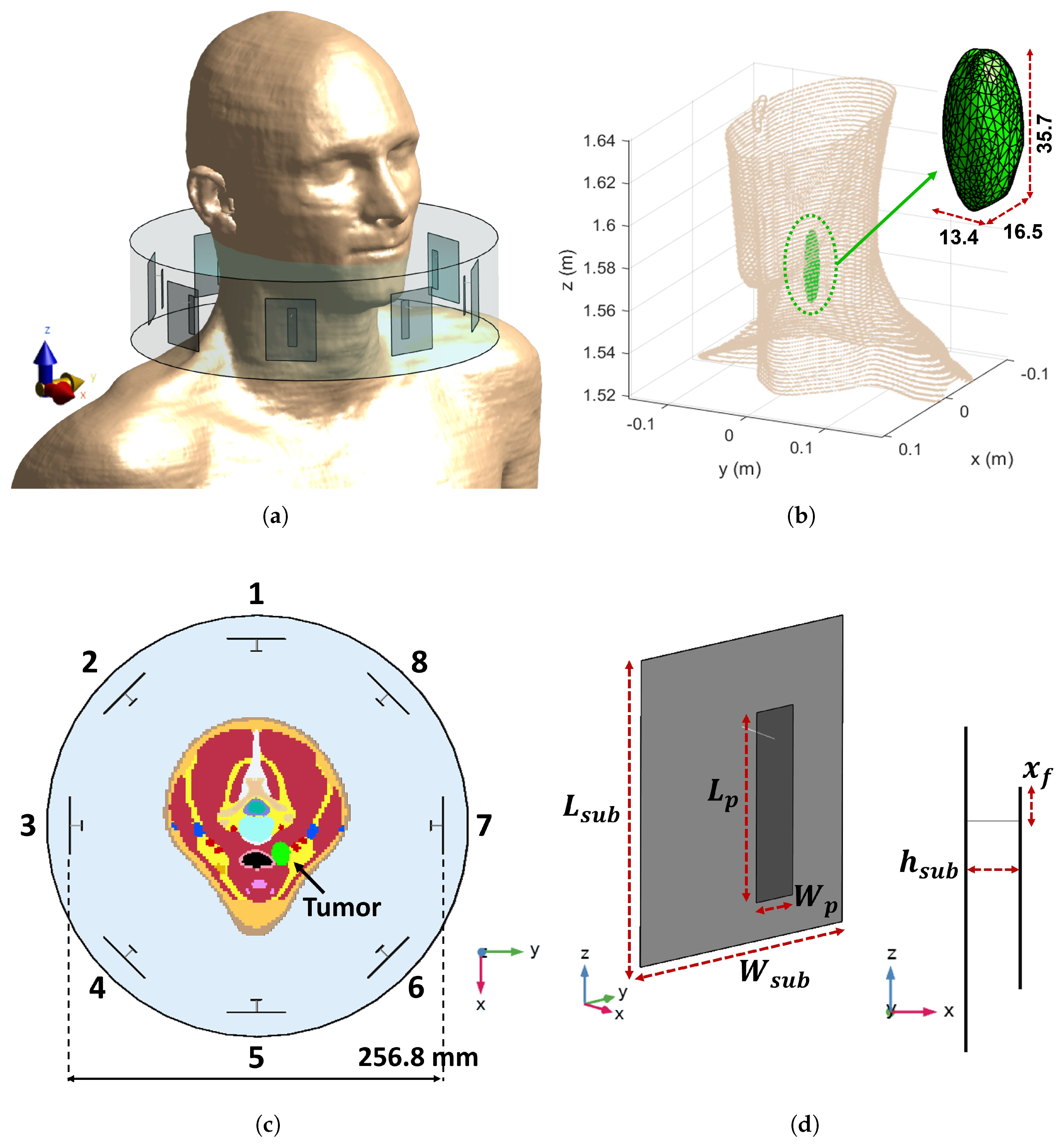
3.1. Reference Testbed
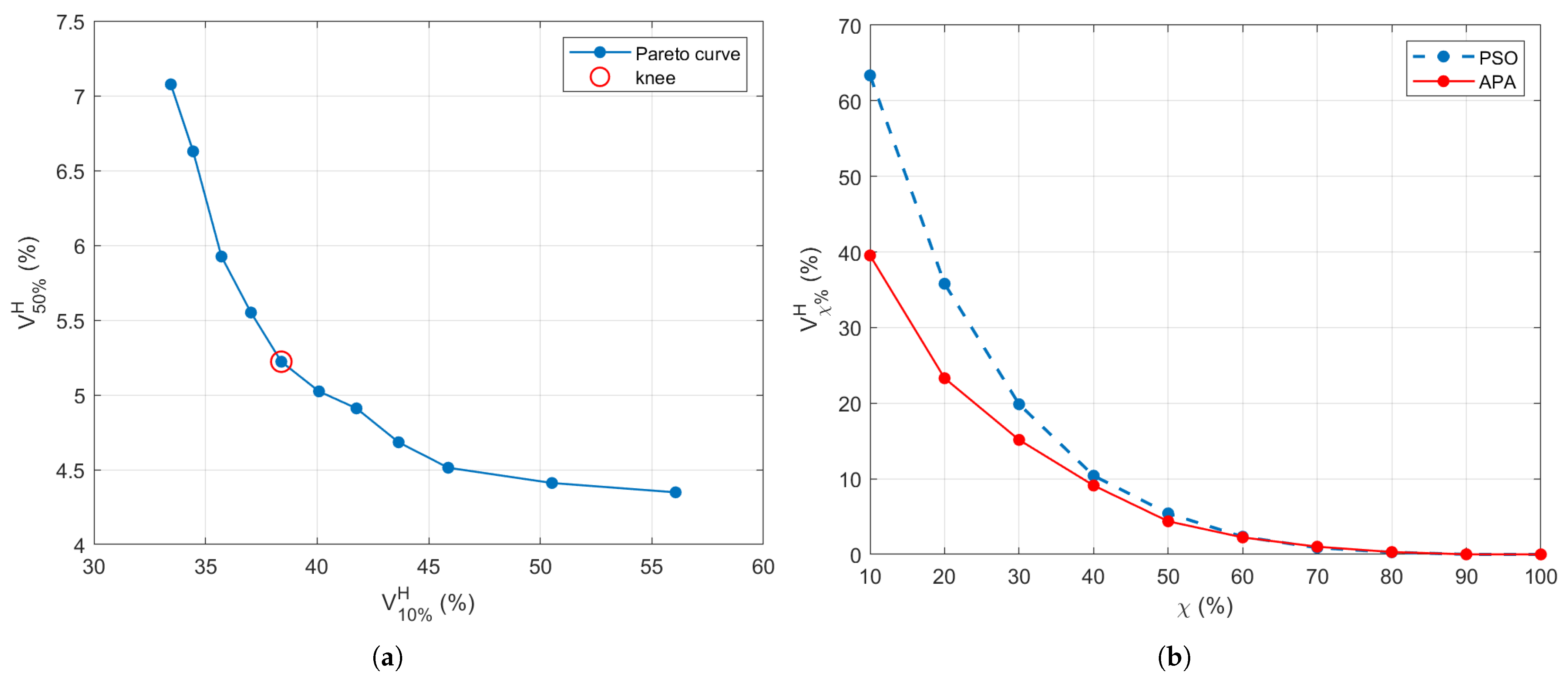
3.2. Power Levels Search
| Algorithm 2 Adaptive Threshold Search for APA Optimization |
|
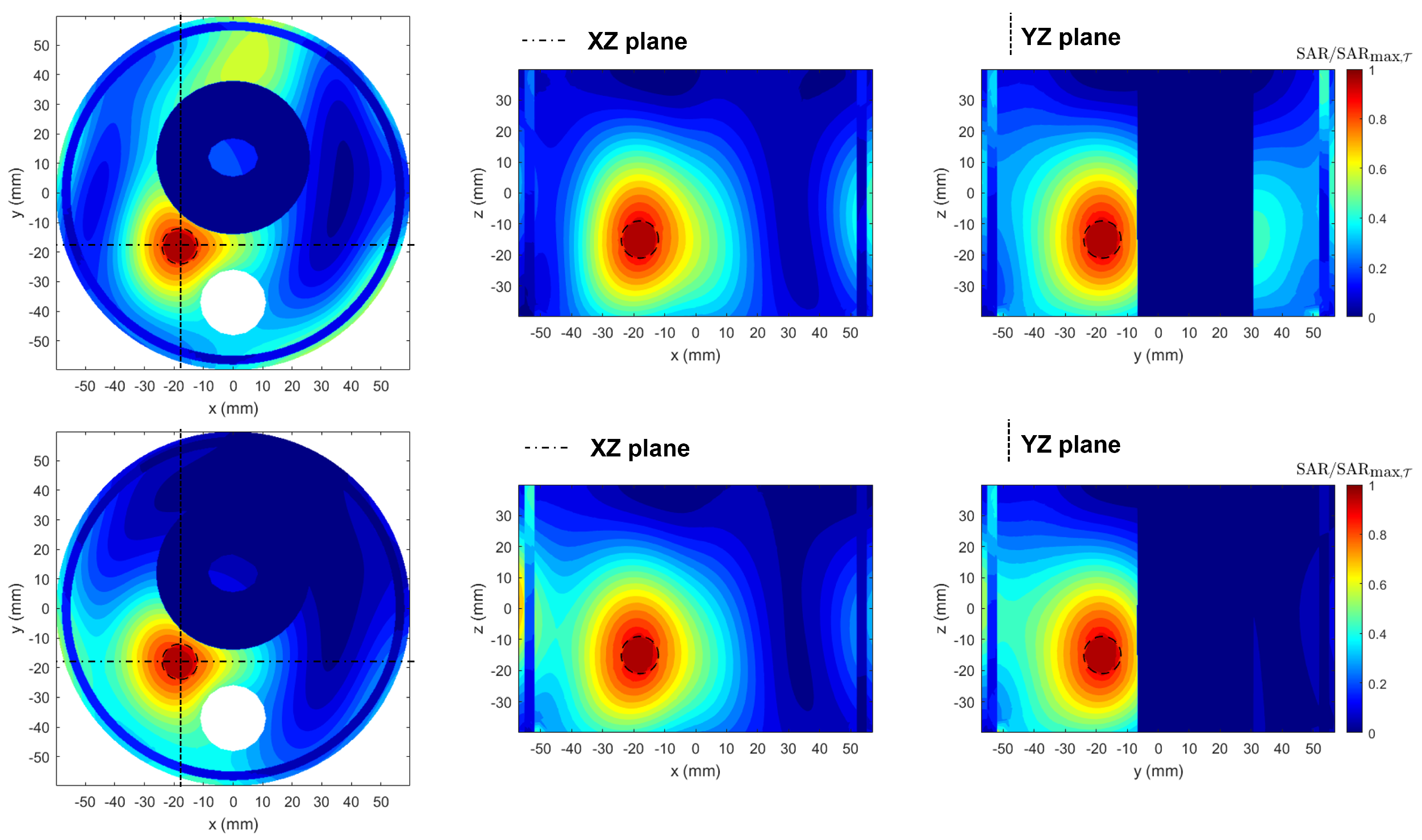
3.3. SoA Comparison
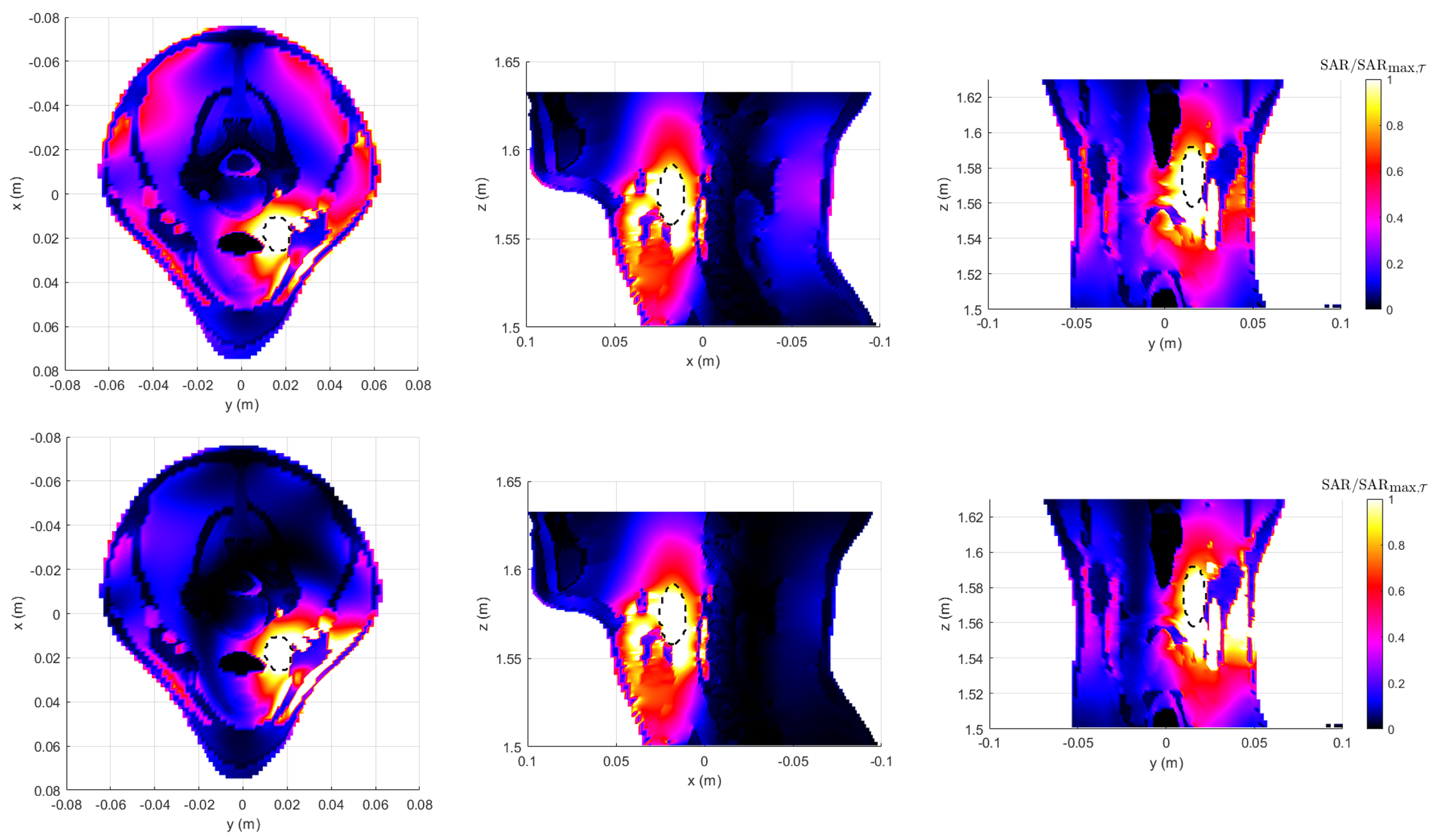
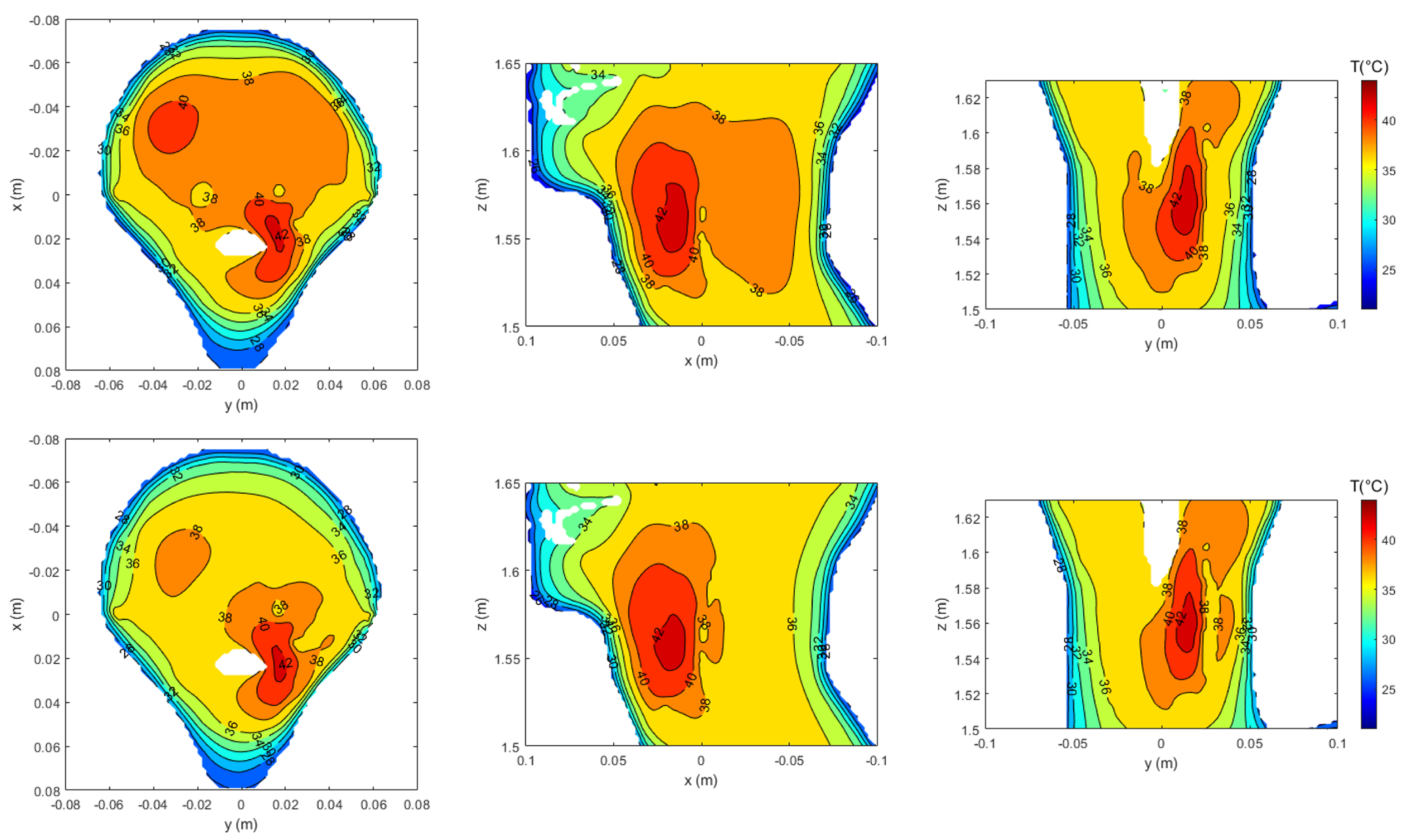
3.4. Realistic Testbed
4. Discussion and Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Datta, N.R.; Ordóñez, S.G.; Gaipl, U.S.; Paulides, M.M.; Crezee, H.; Gellermann, J.; Marder, D.; Puric, E.; Bodis, S. Local hyperthermia combined with radiotherapy and-/or chemotherapy: Recent advances and promises for the future. Cancer Treat. Rev. 2015, 41, 742–753. [Google Scholar] [CrossRef]
- Paulides, M.M.; Rodrigues, D.B.; Bellizzi, G.G.; Sumser, K.; Curto, S.; Neufeld, E.; Montanaro, H.; Kok, H.P.; Trefna, H.D. ESHO benchmarks for computational modeling and optimization in hyperthermia therapy. Int. J. Hyperth. 2021, 38, 1425–1442. [Google Scholar] [CrossRef]
- Sneed, P.K.; Stauffer, P.R.; McDermott, M.W.; Diederich, C.J.; Lamborn, K.R.; Prados, M.D.; Chang, S.; Weaver, K.A.; Spry, L.; Malec, M.K.; et al. Survival benefit of hyperthermia in a prospective randomized trial of brachytherapy boost ± hyperthermia for glioblastoma multiforme. Int. J. Radiat. Oncol. Biol. Phys. 1998, 40, 287–295. [Google Scholar] [CrossRef]
- Roemer, R.B. Engineering Aspects of Hyperthermia Therapy. Annu. Rev. Biomed. Eng. 1999, 1, 347–376. [Google Scholar] [CrossRef]
- van der Zee, J.; González, D.; van Rhoon, G.C.; van Dijk, J.D.; van Putten, W.L.; Hart, A.A. Comparison of radiotherapy alone with radiotherapy plus hyperthermia in locally advanced pelvic tumours: A prospective, randomised, multicentre trial. Lancet 2000, 355, 1119–1125. [Google Scholar] [CrossRef]
- Lepock, J.R. Cellular effects of hyperthermia: Relevance to the minimum dose for thermal damage. Int. J. Hyperth. 2003, 19, 252–266. [Google Scholar] [CrossRef] [PubMed]
- Issels, R.D. High-risk soft tissue sarcoma: Clinical trial and hyperthermia combined chemotherapy. Int. J. Hyperth. 2006, 22, 235–239. [Google Scholar] [CrossRef]
- Vernon, C.C.; Hand, J.W.; Field, S.B.; Machin, D.; Whaley, J.B.; Zee, J.v.d.; van Putten, W.L.J.; van Rhoon, G.C.; van Dijk, J.D.P.; González, D.G.; et al. Radiotherapy with or without hyperthermia in the treatment of superficial localized breast cancer: Results from five randomized controlled trials. Int. J. Radiat. Oncol. Biol. Phys. 1996, 35, 731–744. [Google Scholar] [CrossRef] [PubMed]
- Bakker, A.; van der Zee, J.; van Tienhoven, G.; Kok, H.P.; Rasch, C.R.N.; Crezee, H. Temperature and thermal dose during radiotherapy and hyperthermia for recurrent breast cancer are related to clinical outcome and thermal toxicity: A systematic review. Int. J. Hyperth. 2019, 36, 1024–1039. [Google Scholar] [CrossRef]
- Overgaard, J.; Gonzalez Gonzalez, D.; Hulshof, M.C.C.M.; Arcangeli, G.; Dahl, O.; Mella, O.; Bentzen, S.M. Randomised trial of hyperthermia as adjuvant to radiotherapy for recurrent or metastatic malignant melanoma. Lancet 1995, 345, 540–543. [Google Scholar] [CrossRef] [PubMed]
- Paulides, M.; Dobsicek Trefna, H.; Curto, S.; Rodrigues, D. Recent technological advancements in radiofrequency- andmicrowave-mediated hyperthermia for enhancing drug delivery. Adv. Drug Deliv. Rev. 2020, 163–164, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; Cressman, E.N.K.; Ceelen, W.; Brace, C.L.; Ivkov, R.; Grüll, H.; ter Haar, G.; Wust, P.; Crezee, J. Heating technology for malignant tumors: A review. Int. J. Hyperth. 2020, 37, 711–741. [Google Scholar] [CrossRef]
- Wust, P.; Rau, B.; Gellerman, J.; Pegios, W.; Löffel, J.; Riess, H.; Felix, R.; Schlag, P.M. Radiochemotherapy and hyperthermia in the treatment of rectal cancer. Recent Results Cancer Res 1998, 146, 175–191. [Google Scholar] [CrossRef] [PubMed]
- Thrall, D.E.; LaRue, S.M.; Yu, D.; Samulski, T.; Sanders, L.; Case, B.; Rosner, G.; Azuma, C.; Poulson, J.; Pruitt, A.F.; et al. Thermal Dose is Related to Duration of Local Control in Canine Sarcomas Undergoing Thermoradiotherapy. Clin. Cancer Res. 2005, 11, 5206–5214. [Google Scholar] [CrossRef]
- Franckena, M.; Fatehi, D.; de Bruijne, M.; Canters, R.A.M.; van Norden, Y.; Mens, J.W.; van Rhoon, G.C.; van der Zee, J. Hyperthermia dose-effect relationship in 420 patients with cervical cancer treated with combined radiotherapy and hyperthermia. Eur. J. Cancer 2009, 45, 1969–1978. [Google Scholar] [CrossRef]
- Bruggmoser, G.; Bauchowitz, S.; Canters, R.; Crezee, H.; Ehmann, M.; Gellermann, J.; Lamprecht, U.; Lomax, N.; Messmer, M.B.; Ott, O.; et al. Quality assurance for clinical studies in regional deep hyperthermia. Strahlenther. Onkol. 2011, 187, 605–610. [Google Scholar] [CrossRef]
- Kok, H.P.; Wust, P.; Stauffer, P.R.; Bardati, F.; van Rhoon, G.C.; Crezee, J. Current state of the art of regional hyperthermia treatment planning: A review. Radiat. Oncol. 2015, 10, 196. [Google Scholar] [CrossRef]
- Nikita, K.; Maratos, N.; Uzunoglu, N. Optimal steady-state temperature distribution for a phased array hyperthermia system. IEEE Trans. Bio Eng. 1993, 40, 1299–1306. [Google Scholar] [CrossRef]
- Das, S.K.; Clegg, S.T.; Samulski, T.V. Computational techniques for fast hyperthermia temperature optimization. Med. Phys. 1999, 26, 319–328. [Google Scholar] [CrossRef]
- Bardati, F.; Borrani, A.; Gerardino, A.; Lovisolo, G. SAR optimization in a phased array radiofrequency hyperthermia system. IEEE Trans. Bio Eng. 1995, 42, 1201–1207. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; van Haaren, P.M.; van de Kamer, J.B.; Wiersma, J.; van Dijk, J.D.; Crezee, J. High-resolution temperature-based optimization for hyperthermia treatment planning. Phys. Med. Biol. 2005, 50, 3127–3141. [Google Scholar] [CrossRef]
- Trefná, H.D.; Vrba, J.; Persson, M. Time-reversal focusing in microwave hyperthermia for deep-seated tumors. Phys. Med. Biol. 2010, 55, 2167–2185. [Google Scholar] [CrossRef]
- Rijnen, Z.; Bakker, J.F.; Canters, R.A.M.; Togni, P.; Verduijn, G.M.; Levendag, P.C.; Van Rhoon, G.C.; Paulides, M.M. Clinical integration of software tool VEDO for adaptive and quantitative application of phased array hyperthermia in the head and neck. Int. J. Hyperth. 2013, 29, 181–193. [Google Scholar] [CrossRef] [PubMed]
- Iero, D.A.M.; Crocco, L.; Isernia, T. Thermal and Microwave Constrained Focusing for Patient-Specific Breast Cancer Hyperthermia: A Robustness Assessment. IEEE Trans. Antennas Propag. 2014, 62, 814–821. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Drizdal, T.; van Rhoon, G.C.; Crocco, L.; Isernia, T.; Paulides, M.M. The potential of constrained SAR focusing for hyperthermia treatment planning: Analysis for the head & neck region. Phys. Med. Biol. 2018, 64, 015013. [Google Scholar] [CrossRef]
- Firuzalizadeh, M.; Gaffoglio, R.; Giordanengo, G.; Righero, M.; Zucchi, M.; Musacchio Adorisio, G.; Bellone, A.; Vallan, A.; Perrone, G.; Vecchi, G. Joint Optimization of Antenna System Matching and Specific Absorption Rate Focusing in Microwave Hyperthermia Cancer Treatment. Cancers 2025, 17, 386. [Google Scholar] [CrossRef] [PubMed]
- Gaffoglio, R.; Righero, M.; Giordanengo, G.; Zucchi, M.; Vecchi, G. Fast Optimization of Temperature Focusing in Hyperthermia Treatment of Sub-Superficial Tumors. IEEE J. Electromagn. RF Microw. Med. Biol. 2021, 5, 286–293. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4. [Google Scholar]
- Liontas, C.A.; Knott, P. An Alternating Projections Algorithm for optimizing electromagnetic fields in regional hyperthermia. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Liontas, C.A. Alternating Projections of Auxiliary Vector Fields for Electric Field Optimization in Temperature-guided Hyperthermia. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Bucci, O.M.; D’Elia, G.; Mazzarella, G.; Panariello, G. Antenna pattern synthesis: A new general approach. Proc. IEEE 1994, 82, 358–371. [Google Scholar] [CrossRef]
- Araque Quijano, J.L.; Vecchi, G. Alternating Adaptive Projections in Antenna Synthesis. IEEE Trans. Antennas Propag. 2010, 58, 727–737. [Google Scholar] [CrossRef]
- Polk, C.; Postow, E. Handbook of Biological Effects of Electromagnetic Fields, Third Edition—2 Volume Set; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Kampinga, H.H. Cell biological effects of hyperthermia alone or combined with radiation or drugs: A short introduction to newcomers in the field. Int. J. Hyperth. 2006, 22, 191–196. [Google Scholar] [CrossRef]
- Vander Vorst, A.; Rosen, A. RF/Microwave Interaction with Biological Tissues; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Volume 91. [Google Scholar] [CrossRef]
- Debye, P.J.W. Polar Molecules; The Chemical Catalog Company, Inc.: New York, NY, USA, 1929. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef]
- Hasgall, P.; Neufeld, E.; Gosselin, M.C.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues; IT’IS Foundation: Zurich, Switzerland, 2018. [Google Scholar]
- Verhaart, R.F.; Verduijn, G.M.; Fortunati, V.; Rijnen, Z.; van Walsum, T.; Veenland, J.F.; Paulides, M.M. Accurate 3D temperature dosimetry during hyperthermia therapy by combining invasive measurements and patient-specific simulations. Int. J. Hyperth. 2015, 31, 686–692. [Google Scholar] [CrossRef] [PubMed]
- Joines, W.T.; Zhang, Y.; Li, C.; Jirtle, R.L. The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz. Med. Phys. 1994, 21, 547–550. [Google Scholar] [CrossRef]
- Lazebnik, M.; Popovic, D.; McCartney, L.; Watkins, C.B.; Lindstrom, M.J.; Harter, J.; Sewall, S.; Ogilvie, T.; Magliocco, A.; Breslin, T.M.; et al. A large-scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries. Phys. Med. Biol. 2007, 52, 6093–6115. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Ltd: New York, NY, USA, 1999. [Google Scholar]
- IEC/IEEE 62704-1:2017; IEC/IEEE International Standard—Determining the Peak Spatial-Average Specific Absorption Rate (SAR) in the Human Body from Wireless Communications Devices, 30 MHz to 6 GHz—Part 1: General Requirements for Using the Finite-Difference Time-Domain (FDTD) Method for SAR Calculations. IEC: Geneva, Switzerland, 2017. [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Kok, H.P.; van den Berg, C.A.T.; Bel, A.; Crezee, J. Fast thermal simulations and temperature optimization for hyperthermia treatment planning, including realistic 3D vessel networks. Med. Phys. 2013, 40, 103303. [Google Scholar] [CrossRef]
- Paulides, M.M.; Bakker, J.F.; Chavannes, N.; van Rhoon, G.C. A Patch Antenna Design for Application in a Phased-Array Head and Neck Hyperthermia Applicator. IEEE Trans. Biomed. Eng. 2007, 54, 2057–2063. [Google Scholar] [CrossRef]
- Paulides, M.M.; Bakker, J.F.; Neufeld, E.; van der Zee, J.; Jansen, P.P.; Levendag, P.C.; van Rhoon, G.C. The HYPERcollar: A novel applicator for hyperthermia in the head and neck. Int. J. Hyperth. 2007, 23, 567–576. [Google Scholar] [CrossRef]
- Rijnen, Z.; Togni, P.; Roskam, R.; van de Geer, S.G.; Goossens, R.H.; Paulides, M.M. Quality and comfort in head and neck hyperthermia: A redesign according to clinical experience and simulation studies. Int. J. Hyperth. 2015, 31, 823–830. [Google Scholar] [CrossRef][Green Version]
- Canters, R.A.; Franckena, M.; Paulides, M.M.; van Rhoon, G.C. Patient positioning in deep hyperthermia: Influences of inaccuracies, signal correction possibilities and optimization potential. Phys. Med. Biol. 2009, 54, 3923–3936. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics. Version 6.1. 2023. Available online: http://www.comsol.it/ (accessed on 20 December 2024).
- Yosandha, F.P.; Adi, K.; Widodo, C.E. Calculation of Lung Cancer Volume of Target Based on Thorax Computed Tomography Images using Active Contour Segmentation Method for Treatment Planning System. J. Phys. Conf. Ser. 2017, 855, 012063. [Google Scholar] [CrossRef]
- Gaffoglio, R.; Giordanengo, G.; Righero, M.; Zucchi, M.; Firuzalizadeh, M.; Musacchio Adorisio, G.; Bellone, A.; Vallan, A.; Perrone, G.; Vecchi, G. Real-time 3D temperature reconstruction in microwave cancer hyperthermia from scarce temperature measurements. Nat. Commun. 2025, 16, 4824. [Google Scholar] [CrossRef] [PubMed]
- Sim4Life. Version 6.2.1.4972. 2021. Available online: https://zmt.swiss/sim4life/ (accessed on 6 March 2023).
- Duke_34y_m_v3.1.1b01_posable. ViP. 2016. Available online: https://itis.swiss/virtual-population (accessed on 8 October 2024). [CrossRef]

| n | APA Optimization | PSO Optimization | ||
|---|---|---|---|---|
| Amplitude (V) | Phase (°) | Amplitude (V) | Phase (°) | |
| 1 | 4.68 | 45.3 | 3.591 | 318.0 |
| 2 | 5.06 | 29.4 | 2.270 | 288.3 |
| 3 | 3.37 | 33.2 | 3.053 | 298.3 |
| 4 | 3.77 | 76.1 | 3.568 | 349.6 |
| 5 | 3.15 | 124.4 | 4.686 | 57.5 |
| 6 | 1.05 | 120.6 | 2.680 | 359.9 |
| 7 | 1.08 | 128.4 | 2.912 | 326.2 |
| 8 | 3.84 | 92.4 | 4.719 | 0.0 |
| APA Optimization | PSO Optimization | |
|---|---|---|
| Num. iterations | 1001 | 266 |
| Total time (s) | 128 | 140 |
| (final) | 0.8089 | 0.7998 |
| Method | T90 (°) | T50 (°) | T10 (°) |
|---|---|---|---|
| PSO | 42.62 | 43.14 | 43.48 |
| APA | 42.55 | 43.14 | 43.51 |
| APA (finer mesh) | 42.63 | 43.13 | 43.46 |
| Method | T90 (°) | T50 (°) | T10 (°) |
|---|---|---|---|
| PSO | 41.08 | 41.94 | 42.63 |
| APA | 41.05 | 41.83 | 42.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Firuzalizadeh, M.; Gaffoglio, R.; Giordanengo, G.; Righero, M.; Vecchi, G. Specific Absorption Rate Optimization in Microwave Cancer Hyperthermia via Local Power Synthesis Algorithm. Cancers 2025, 17, 2813. https://doi.org/10.3390/cancers17172813
Firuzalizadeh M, Gaffoglio R, Giordanengo G, Righero M, Vecchi G. Specific Absorption Rate Optimization in Microwave Cancer Hyperthermia via Local Power Synthesis Algorithm. Cancers. 2025; 17(17):2813. https://doi.org/10.3390/cancers17172813
Chicago/Turabian StyleFiruzalizadeh, Maryam, Rossella Gaffoglio, Giorgio Giordanengo, Marco Righero, and Giuseppe Vecchi. 2025. "Specific Absorption Rate Optimization in Microwave Cancer Hyperthermia via Local Power Synthesis Algorithm" Cancers 17, no. 17: 2813. https://doi.org/10.3390/cancers17172813
APA StyleFiruzalizadeh, M., Gaffoglio, R., Giordanengo, G., Righero, M., & Vecchi, G. (2025). Specific Absorption Rate Optimization in Microwave Cancer Hyperthermia via Local Power Synthesis Algorithm. Cancers, 17(17), 2813. https://doi.org/10.3390/cancers17172813





