2.1. Trial Examples
A large number of basket trials are conducted in an exploratory phase II setting. The primary endpoint is typically tumor response. If the drug is deemed promising in some cancer (sub)types, it would warrant further investigation in a confirmatory study or conditional marketing approval.
We review three such trials. The first trial was aimed at assessing the efficacy of imatinib in patients with one of 10 different subtypes of advanced sarcoma [
7]. These included angiosarcoma, Ewing sarcoma, fibrosarcoma, leiomyosarcoma, liposarcoma, malignant fibrous histiocytoma (MFH), osteosarcoma, malignant peripheral-nerve sheath tumor (MPNST), rhabdomyosarcoma, and synovial sarcoma. The primary endpoint was tumor response, defined as complete response (CR) or partial response (PR) at 2 months, or stable disease, CR or PR at 4 months. The trial was designed based on a Bayesian hierarchical model [
10].
Table 1 summarizes the patient responses by sarcoma subtype. A total of 179 patients were available for analysis. By comparing the response rates to a reference rate of 30%, the authors concluded that imatinib was not an active agent in advanced sarcoma in these subtypes.
The second trial was conducted to study vemurafenib in BRAF V600 mutation-positive non-melanoma cancers. The study included the following cancer cohorts that received vemurafenib monotherapy: non-small-cell lung cancer (NSCLC), cholangiocarcinoma (CCA), Erdheim–Chester disease or Langerhans’ cell histiocytosis (ECD/LCH), anaplastic thyroid cancer, breast cancer, ovarian cancer, multiple myeloma, colorectal cancer (CRC-V), and all others. An additional cohort of patients with colorectal cancer received vemurafenib combined with cetuximab (CRC-VC). The primary endpoint was tumor response at week 8, as assessed by the site investigators according to the Response Evaluation Criteria in Solid Tumors [
29], or the criteria of the International Myeloma Working Group [
30]. The trial was designed using Simon’s two-stage method [
31,
32], separately for each cohort. Due to insufficient accrual, patients in the breast cancer, multiple myeloma, and ovarian cancer cohorts were eventually included in the all-others cohort.
Table 2 summarizes the patient responses by cohort (not including the all-others cohort). A total of 84 patients were available for analysis. By comparing the response rates to a reference rate of 15%, the authors concluded that BRAF V600 appeared to be a targetable oncogene in some, but not all, non-melanoma cancers. Specifically, preliminary vemurafenib activity was observed in NSCLC and in ECD/LCH.
The data from the imatinib and vemurafenib trials have since then been reanalyzed multiple times [
12,
16,
21].
A third example is the recent pivotal study of larotrectinib [
9]. A family of genes called NTRK1, NTRK2, and NTRK3 encode a protein called tropomyosin receptor kinases (TRK). Mutation in NTRK genes results in TRK fusion proteins that lead to tissue-independent oncogenic transformation [
33,
34,
35]. TRK fusion proteins are found in more than 20 different tumor types. As a result, a phase II basket trial was conducted to evaluate the therapeutic effect of larotrectinib, a TRK inhibitor, in 55 patients diagnosed with 12 different cancer types. The overall response rate was 75% based on central assessment with a 95% confidence interval of (61%, 85%). Larotrectinib was well tolerated in both adult and child populations. Based on the efficacy and safety data, the drug has been approved for treating NTRK gene fusion-positive tumors in adult and pediatric patients across cancer types. Statistical analysis pooled all the patients enrolled in the trial regardless of their tumor types. Therefore, the baskets were not differentiated in the statistical inference of drug effects. This is a special case where the biomarker, NTRK gene fusion, is highly specific and causal to a small fraction of cancers, regardless of their tissue types. In general, a targeted therapy may work in some cancer types or subtypes, which requires more sophisticated statistical design and analysis.
2.3. Prior Specification and Exchangeability
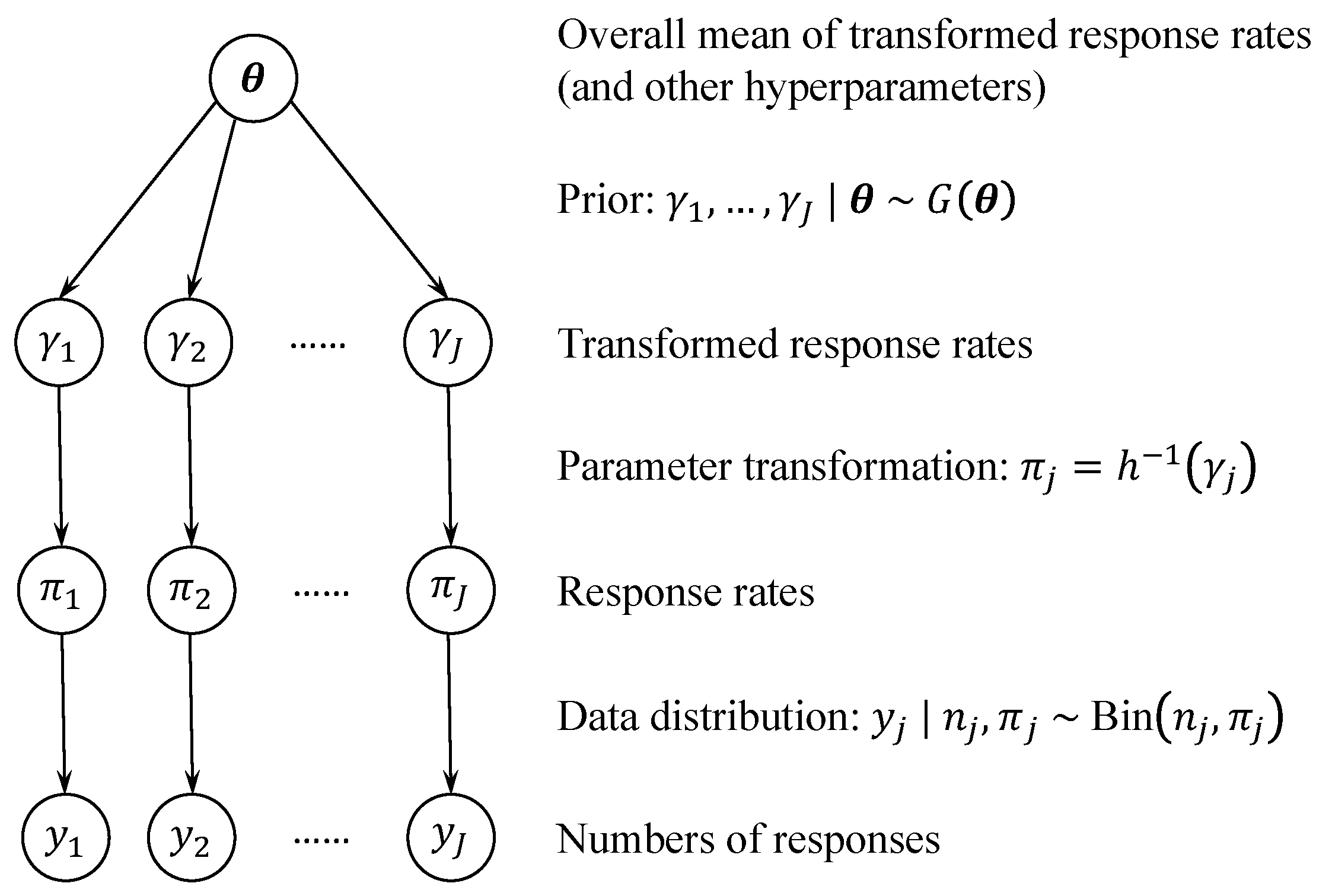
Most existing methods start by transforming
into a real value using, for example, a logit transformation. We denote the transformation and the real-valued parameter as
Note that each basket
j is indexed by a different parameter
. Then, the
s are modeled as a random sample from a common population distribution
G,
where
denotes the vector of hyperparameters that parameterize
G.
Figure 1 displays a graphical representation of the hierarchical model given by Equations (
1) and (
3). More discussions on the choices of
h and
are deferred to
Section 2.3 and
Section 2.4. Importantly,
is unknown and is estimated based on data from all baskets. As a result, the posterior of
is informed by both the responses within basket
j, through the likelihood (
1), and those in other baskets, through the prior (
3).
Figure 2 illustrates the effect of information borrowing through an analysis of the imatinib data in
Table 1. The point estimates of
for individual baskets are shrunk towards the overall response rate. Additionally, the interval estimates of
have shorter lengths under borrowing compared to those under stratified analysis. More details of the analysis can be found in the caption of
Figure 2.
Suppose a prior
is placed on
. Implicit in model (
3) is the (marginal) prior dependence among the
s. Note that
In fact, it can be shown that the
s are positively correlated a priori [
36], which enables information borrowing across baskets. Furthermore, model (
3) implies an assumption of prior exchangeability among the
s. Mathematically, a sequence of random variables is called
exchangeable if their joint distribution is invariant to permutations. From Equation (
4), the joint density
is invariant to permutations of the indexes
. The assumption of prior exchangeability is reasonable when no information is available before the trial to claim that the treatment is more likely to be efficacious in certain baskets than others [
37]. We note that modeling the
s as independent draws from a common distribution is a stronger assumption than finite exchangeability: the former implies the latter, but not vice versa.
If there is prior knowledge to distinguish some
s from others, one may incorporate an expanded notion of exchangeability in the prior construction. For example, historical clinical trials may suggest that the baskets can be divided into several subgroups. Each subgroup consists of baskets with similar historical success rates. Then, one may specify a separate prior model for the
s within each subgroup. While the parameters within the same subgroup are exchangeable, those across different subgroups are not. This is known as partial exchangeability. For another example, patient responses are often associated with basket-level and patient-level covariates. If these covariates are available, they may be used to construct a regression model with an underlying assumption of conditional exchangeability. For the rest of this paper, we will restrict our attention to the exchangeable model given by Equation (
3), which is employed by most existing methods.
2.4. What Information to Borrow?
The transformation reflects what information is borrowed across baskets. A straightforward choice is to directly borrow the response rates by assuming , where is a distribution on the unit interval, e.g., a beta distribution. In this case, is the identity transformation, and the underlying assumption is that the treatment has similar response rates across baskets. A variation in this choice is to consider a logit transformation, . This can simplify posterior computation by allowing to be a distribution over the real line, e.g., a normal distribution.
An alternative choice of
h incorporates an adjustment for the reference rate
. Typically, the reference rate for each basket is determined based on how well the cancer (sub)type responds to the standard of care. If there are substantial differences in the reference rates across baskets, it may be implausible to assume that the
s are similar. This is because baskets with lower (or higher) reference rates are also more likely to respond poorly (or positively) to the new treatment. To account for the differential reference rates, it may be more appropriate to model the response rate increments from the reference rates. For example, Berry et al. [
11] considered borrowing the increments of the logit response rates,
.
Lastly, a different strategy is to borrow information at the hypothesis level by letting
. See, e.g., Zhou and Ji [
21]. Here,
(or 0) represents
is true (or false), indicating that the treatment is efficacious (or inefficacious) in basket
j. The prior
for
s can be a Bernoulli distribution. Borrowing across
s reflects the assumption that if the treatment is promising, it is likely to be efficacious across multiple baskets simultaneously. This is a more general assumption than assuming the response rates are similar. For example,
and
may be quite different, but as long as they are larger than
and
, respectively, the treatment is efficacious in both baskets
j and
. An additional complexity of this approach is that
h is a many-to-one transformation, and the value of
cannot be uniquely determined by
through
. Instead, one needs to construct a prior for
conditional on the value of
. For example,
can be a beta distribution truncated to the interval
, and
can be a beta distribution truncated to the interval
. The prior
establishes the connection between
and
in
Figure 1.
2.5. How Is Information Borrowed?
The choice of the prior
determines how information is borrowed across baskets. To illustrate ideas, suppose
is real-valued, e.g.,
. A natural choice of
is then a normal distribution,
where the hyperparameter vector
. The mean parameter
represents a transformed version of the overall response rate of the treatment across all baskets. The basket-specific
s are shrunk toward the common
. The variance parameter
controls the degree of borrowing, with smaller values implying stronger shrinkage effects. At one extreme, when
, all
values must be equal. At the other extreme, when
approaches infinity, the shrinkage effects become negligible. The estimation of
plays a crucial role in the statistical analysis. On the ond hand, overestimating
may lead to inadequate borrowing, diminishing the benefits of shrinkage estimation. On the other hand, underestimating
may result in excessive borrowing, leading to inflated type I error rates and potential failures in drug development (more on this point in
Section 2.6). Yet, due to the typically limited number of baskets in a basket trial, accurate estimation of
is a challenging task.
Taking a full Bayesian approach, a hyperprior is assigned to
. A computationally convenient choice is the inverse-gamma prior,
. See, e.g., Thall et al. [
10] and Berry et al. [
11]. It is commonly thought that small values of
and
produce a noninformative prior for
. However, Gelman [
36] showed that even with small values of
and
, the
prior could still be quite informative and might lead to underestimation of
. Instead, the author advocated the use of a half-
t prior as a less informative choice for the hierarchical standard deviation parameter,
-
tν(
A), with small
and large
A. Here,
is the number of degrees of freedom, and
A is the scale parameter. Special cases of the half-
t prior include the half-Cauchy (when
) and half-normal (when
) priors. The half-
t prior was used by Neuenschwander et al. [
12] and Zhou and Ji [
21].
Alternatively, Chu and Yuan [
14] proposed an empirical Bayesian approach to specify the value of
based on a measure of homogeneity among the baskets. The relationship between
and the homogeneity measure is determined through a simulation-based calibration procedure.
To further reduce the risk of excessive borrowing, the normal distribution prior in Equation (
5) may be replaced by a distribution with heavier tails, e.g., a
t-distribution. Such a prior accommodates occasional extreme parameters. In a basket trial, the response rates in a few baskets may be quite different from the others. A heavy-tailed prior still shrinks these extreme response rates toward the overall mean but avoids pulling them too much [
37].
2.5.1. Mixture Models
In some basket trials, patient responses across baskets exhibit a clustering structure. For example, in the vemurafenib trial (
Table 2), the ECD/LCH and NSCLC cohorts have similar proportions of responses, suggesting they can be clustered together. The same applies to the CRC-V and CRC-VC cohorts. To exploit such a clustering structure, a multimodal mixture prior can be placed on
[
12,
15,
18,
21]. For example, consider
to be a mixture of normal distributions,
In this case, the hyperparameter vector
with
,
, and
. Here,
K is the number of mixture components, and
,
, and
are the weight, mean, and variance of mixture component
k, respectively. The weights satisfy
.
To facilitate interpretation, observe that the mixture prior in Equation (
6) is equivalent to the following hierarchical prior,
In other words, each basket can be thought of as belonging to one of
K latent subgroups. The indicator
denotes the subgroup membership for basket
j, and
represents the prevalence of subgroup
k. Conditional on the subgroup memberships, information borrowing only occurs within each subgroup. Therefore, compared to the simple normal prior, the normal mixture prior allows for more judicious information borrowing. Specifically, in the presence of substantial heterogeneity among baskets, the normal mixture prior usually leads to less borrowing, reducing the risk of type I error rate inflation. Note that the subgroup memberships are unknown a priori, and all baskets share the same prior probability of belonging to any given subgroup. As a result, prior exchangeability of the
s still holds under model (
6) or (
7). This differs from the situation where prior knowledge exists to distinguish some baskets from others, thereby breaking the prior exchangeability assumption as discussed in
Section 2.3.
The estimation of
and
follows a similar logic as in the simple normal prior case. The number and weights of mixture components,
K and
, may be prespecified or estimated from the data. Standard prior choices include a symmetric Dirichlet distribution prior for
conditional on
K, and a zero-truncated Poisson distribution prior for
K [
38]. Since the dimensions of
,
, and
depend on
K, posterior computation under this approach typically requires trans-dimensional Markov chain Monte Carlo [
39]. To avoid such computational complexity, an alternative strategy is to fit multiple models with different values of
K and select the most appropriate
K based on a model selection criterion such as the deviance information criterion [
15,
40]. From a nonparametric Bayesian modeling perspective, one may set
to allow for flexibility. By further letting
and
,
becomes a Dirichlet process mixture model [
21,
41].
2.5.2. Bayesian Model Averaging
When it is reasonable to assume that the treatment has the same (transformed) response rate across multiple baskets, Bayesian model averaging can be utilized to facilitate information borrowing [
16,
22]. Let
denote a partition of the
J baskets into subsets. For example, when
baskets, the possible partitions include
,
,
,
, and
. Each partition constrains different subsets of the (transformed) basket-specific response rates to be equal. For example, under partition
,
must be equal to
, but there is no constraint on
. To perform Bayesian inference, one may specify a prior for the distinct values of the (transformed) response rates conditional on the partition, as well as an additional prior for the partition itself.
Conditional on a given partition, information is pooled among baskets belonging to the same subset, while no information is borrowed between baskets in different subsets. The (marginal) posterior distribution of
is a weighted average of its posteriors under different partitions,
which represents a compromise between complete pooling and stratified analysis. The weights in this average correspond to the posterior probabilities of the partitions.
2.6. Operating Characteristics
The likelihood (
1) and prior (
3) on
(or a transformation of
) allow one to compute the posterior distribution of
. In most cases, the posterior is not analytically available, and Monte Carlo methods are used to approximate the posterior [
42,
43]. For the hypothesis test in Equation (
2), a commonly used criterion to reject the null hypothesis
is when the posterior probability
, where
is a prespecified threshold that may differ across baskets.
It is common practice to evaluate the operating characteristics of a Bayesian procedure under the frequentist paradigm, as it provides insights into the procedure’s long-run average behavior in repeated practical use [
44]. In the context of basket trials, such evaluations are useful for understanding the practical implications of different prior choices for
s. Often, a set of scenarios is considered in which the true response rates are specified for the baskets, hypothetical response data are generated under each scenario, and relevant operating characteristics are recorded over repeated simulations.
Table 3 provides an illustration of some possible response rate scenarios with four baskets and a reference rate of 20% for every basket. The scenarios encompass different combinations of promising and nonpromising baskets. The treatment response rates may also vary across the promising (or nonpromising) baskets. In
Table 3, Scenario 1 is a global null scenario in which the treatment is inefficacious in all baskets, Scenario 2 is a global alternative scenario in which the treatment is efficacious in all baskets, and Scenarios 3–6 are mixed scenarios in which the treatment is efficacious in some but not all baskets.
The type I error rate and power are the most pertinent operating characteristics for basket trials [
45]. A type I error refers to the incorrect rejection of a true null hypothesis, which, for basket trials, means to select a nonpromising basket for further investigation in a large-scale phase III study. The
basket-specific type I error rate refers to the probability of committing a type I error in a specific basket, whereas the
family wise type I error rate (FWER) is the probability of committing a type I error in any of the baskets. Using computer simulations, these error rates can be approximated by the relative frequencies of making the corresponding errors in a large number of simulated trials. When the null hypothesis is false, the correct action is to reject the null and select a truly promising basket for further investigation. The
basket-specific power refers to the probability of correctly selecting a promising basket. The
family wise power (FWP) is defined in a few different ways. For example, the
disjunctive power (FWP-D) is the probability of correctly selecting any promising baskets, while the
conjunctive power (FWP-C) is the probability of correctly selecting all promising baskets [
46]. For a quick summary of the statistical concepts pertaining to type I error rate and power, refer to
Table 4.
In exploratory basket trials, strict type I error rate control is not enforced by the regulators and is often at the discretion of the sponsors. While a more lenient type I error rate is linked to increased power, it implies a higher chance of selecting a nonpromising basket for further development, increasing the cost associated with a drug development program that will ultimately fail. On the other hand, a more stringent type I error rate is associated with reduced power, which leads to an increased chance of missing a truly promising basket. Sponsors should carefully navigate the tradeoff between risk and benefit, determining appropriate decision criteria under limited sample size that align with their specific needs and objectives.
We illustrate the impact of information borrowing on the type I error rate and power through a simulation study based on the six scenarios in
Table 3. Under each scenario, 1000 sets of hypothetical response data are generated with sample size of 20 patients for every basket. Suppose that the borrowing occurs at the logit response rate level with an adjustment for the reference rate, i.e., we let
. Three prior choices are considered for the
s that lead to different degrees of borrowing:
Here, Half-
represents a half-normal distribution with scale parameter
A, which belongs to the half-
t prior family discussed by Gelman [
36]. Priors I, II and III correspond to no, moderate and strong borrowing, respectively.
Recall that the null hypothesis associated with basket
j,
, is rejected when
. These posterior probability thresholds are typically chosen to achieve certain desirable type I error rate. Since multiple hypotheses are tested simultaneously, it may be desirable to incorporate a notion of FWER control, which limits the chance of falsely selecting any nonpromising baskets for further investigation [
46]. The first type of FWER control, called
weak control, requires that the FWER is controlled when all of the
J null hypotheses are simultaneously true. For the six scenarios considered in
Table 3, weak control of the FWER requires that the FWER is controlled under Scenario 1, the global null scenario. Suppose for simplicity the same posterior probability threshold is used across all baskets. To achieve a FWER of 5% under Scenario 1, the threshold values are
,
and
under Priors I, II and III, respectively. The second type of FWER control, called
strong control, is more stringent. It requires the control of the FWER regardless of which and how many null hypotheses are true. For the scenarios considered, strong control of the FWER requires that the FWER is controlled under all six scenarios including the mixed scenarios. Note that this does not guarantee FWER control beyond these six scenarios, but we restrict our attention to the six scenarios for simplicity. To achieve a FWER of below 5% under all six scenarios, the required threshold values under Priors I, II and III are
,
and
, respectively.
Table 5 shows the simulation results with weak FWER control. From
Table 5, information borrowing is beneficial when the treatment response rates are homogeneous across baskets. For example, in Scenario 2, borrowing leads to substantially increased basket-specific and family wise power. In this case, the stronger the borrowing, the larger the increase in power. When the response rates are heterogeneous, the performance of borrowing does not always compare favorably with that of no borrowing. For example, in Scenario 3, borrowing results in inflated type I error rate. In Scenario 6, strong borrowing results in lower power compared to no borrowing.
Table 6 reports the simulation results with strong FWER control. The issue of inflated type I error rate due to borrowing is mitigated by increasing the posterior probability thresholds. In the global alternative scenario, although less substantial, borrowing still leads to increased power. In the mixed scenarios, however, borrowing (especially strong borrowing) usually results in lower power compared to no borrowing.
In summary, in terms of operating characteristics, borrowing is beneficial when the response rates are homogeneous but may be unfavorable when the response rates are heterogeneous. For this reason, there has been some controversy about the usefulness of information borrowing in basket trials [
47]. Our opinion is that borrowing is still useful. First, in the Bayesian framework, a prior serves as an expression of belief regarding which parameter values are deemed more plausible. When the prior is designed to encourage information borrowing, it implies a belief that the response rates are more likely to be homogeneous across baskets. Consequently, the performance in scenarios with homogeneous response rates should be given greater weight compared to that in scenarios with heterogeneous response rates. Second,
Table 5 shows that under weak FWER control, moderate borrowing leads to considerable gain in power in the global alternative scenario without compromising much of the type I error rate and power in the mixed scenarios. In fact, with more sophisticated Bayesian modeling and judicious information borrowing, many recent methods achieve even more improvements in power while maintaining type I error rates at reasonable levels, even in the mixed scenarios [
12,
14,
21]. To this end, we recommend setting up the statistical analysis to borrow information across baskets where the treatment is expected to exhibit similar behavior based on the drug mechanism. If there is uncertainty about the homogeneity of the true response rates, it is recommended to borrow information in a judicious manner.
2.7. Interim Analysis
Patient enrollment in clinical trials typically occurs sequentially. Therefore, when designing a clinical trial, it may be desirable to incorporate provisions for interim analyses of accumulating data, allowing for the possibility of early termination of the trial [
48]. Oftentimes, basket trial designs include interim monitoring for futility [
11,
14,
16]. At the
rth interim analysis, if
patient accrual in basket
j is halted, as the treatment is deemed inefficacious in this basket. Here,
is a prespecified threshold (e.g., 0.05), and
may be chosen based on both the reference rate
and a prespecified target response rate
(e.g.,
). Alternatively, the futility stopping rule can be based on the posterior predictive probability of success [
48,
49]. Early stopping rules have an impact on the operating characteristics of a design. For example, futility stopping rules reduce the expected number of patients enrolled and type I error rate, which can help avoid devoting too much resources to nonpromising baskets. However, they also result in a decrease in the power of finding the promising baskets.
Interim analyses can also be used to serve the purpose of adjusting the extent of information borrowing as the trial progresses. In Cunanan et al. [
50], the authors proposed to assess the homogeneity of treatment effects across baskets in an interim analysis via Fisher’s exact test [
51]. If homogeneity is not rejected, data across all baskets are pooled into one group in the final analysis, whereas otherwise each basket is analyzed individually. The critical value of the Fisher’s exact test statistic is a tuning parameter and is prespecified. As another example, Liu et al. [
13] proposed to evaluate response rate heterogeneity in an interim analysis using Cochran’s Q test [
52]. If homogeneity is not rejected, a Bayesian hierarchical mixture model is used to borrow information across baskets in the final analysis. Otherwise, each basket is investigated independently.