A Deep Learning-Based Framework for Highly Accelerated Prostate MR Dispersion Imaging
Abstract
Simple Summary
Abstract
1. Introduction
- 1.
- The fMRDI model resembles intravascular dispersion with a simple linear combination of slow and fast AIFs, which is easier to optimize and requires less computation.
- 2.
- The dispersion parameter in our fMRDI model can be used to differentiate csPCa from normal tissue and improve the overall performance of csPCa identification (Section 3.2).
- 3.
- The two-stage estimation framework is fast, accurate, flexible, and more robust against noise and initializations. It does not restrict the form of the AIF or the sampling interval. It operates significantly faster than NLLS and achieves more accurate fitting results.
2. Methods and Materials
2.1. From Tofts Model to Fast MRDI Model
2.1.1. The Tofts Model
2.1.2. MRDI and mMRDI: Dispersion-Applied AIFs
2.1.3. fMRDI: Fast MRDI Model
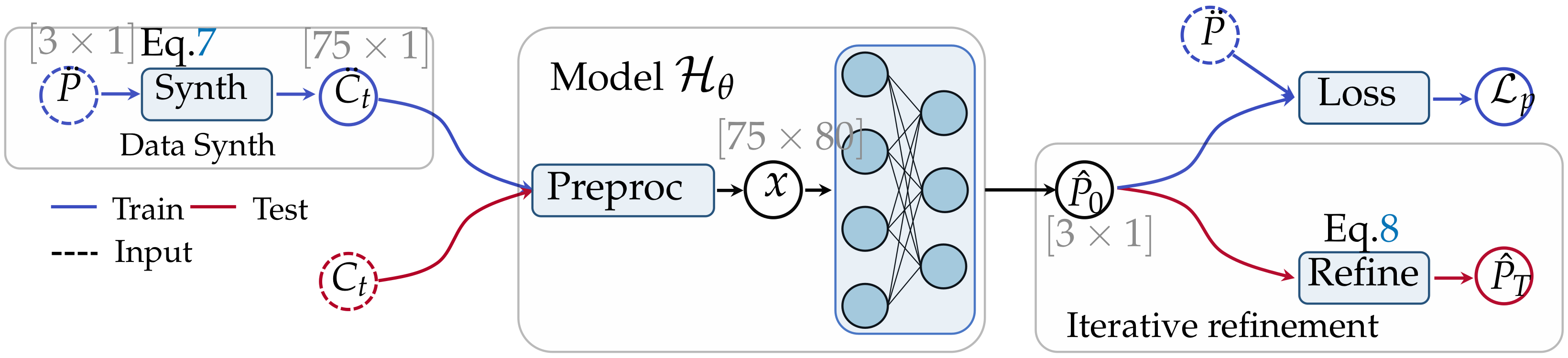
2.2. Overall Workflows
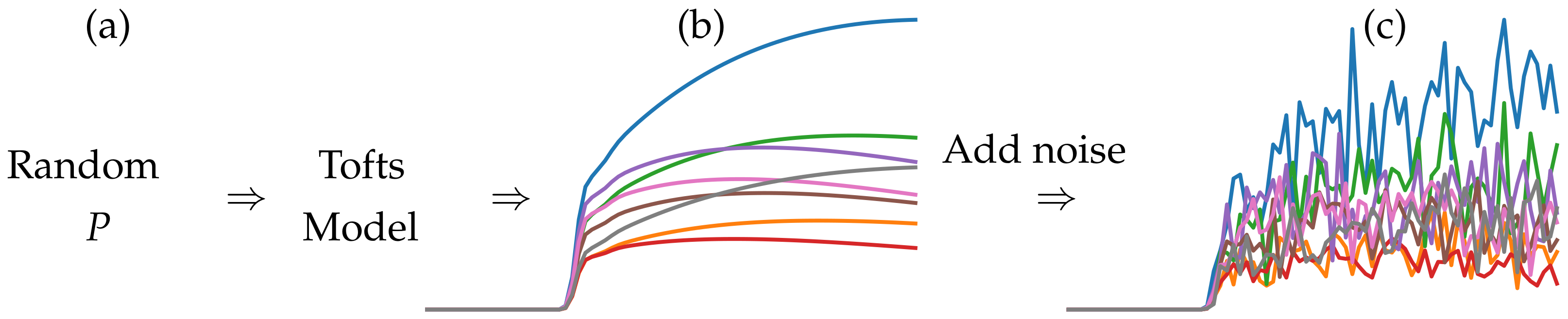
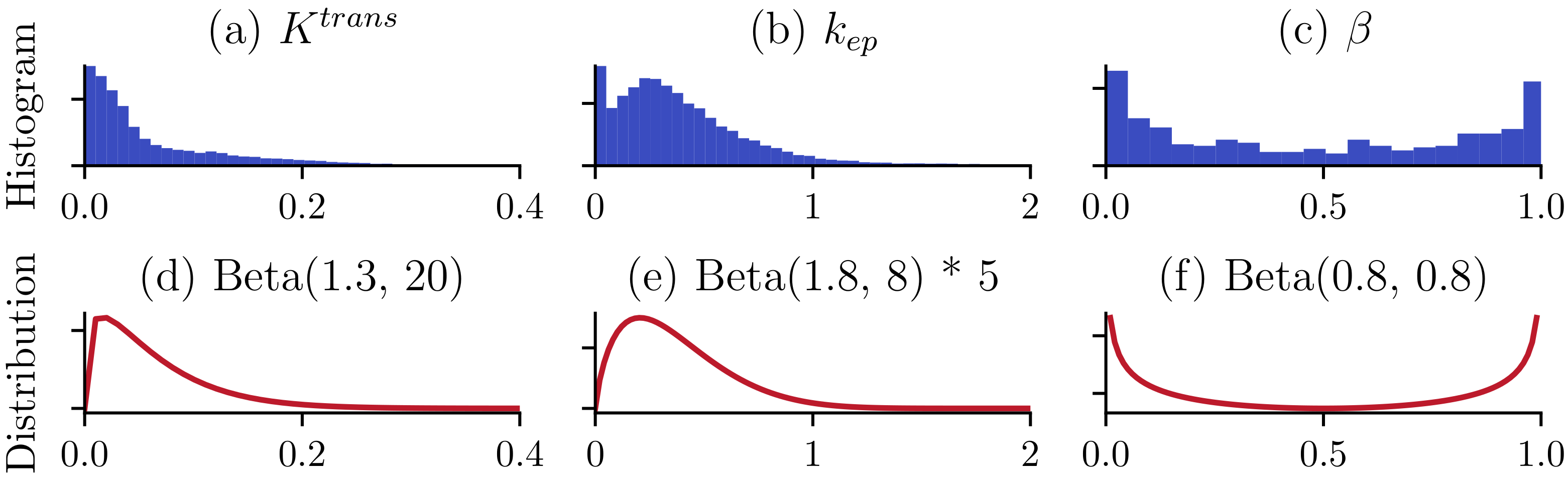
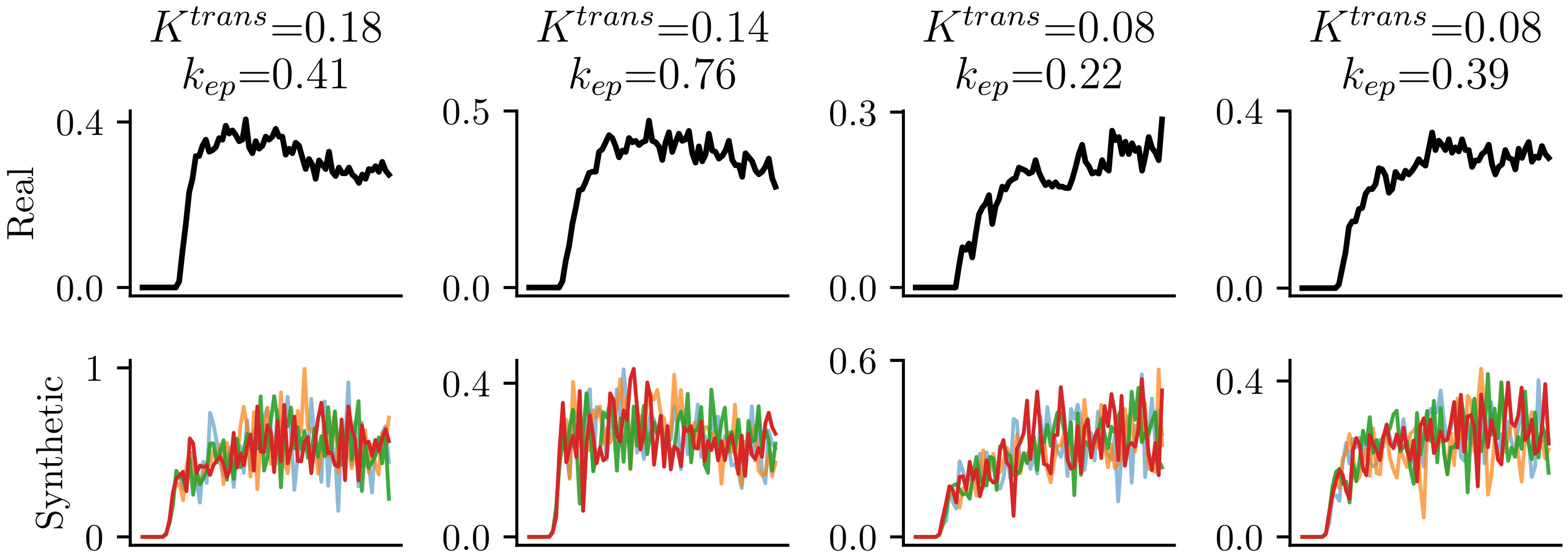
2.3. Training Data Synthesis
- 1.
- Sample random PK parameters , and from designated distributions.
- 2.
- Synthesize smooth time series using the fMRDI formulated in Equation (5).
- 3.
- Add Gaussian noise to the smooth time series to close the gap between synthetical and real data.
2.4. Model Training Workflow
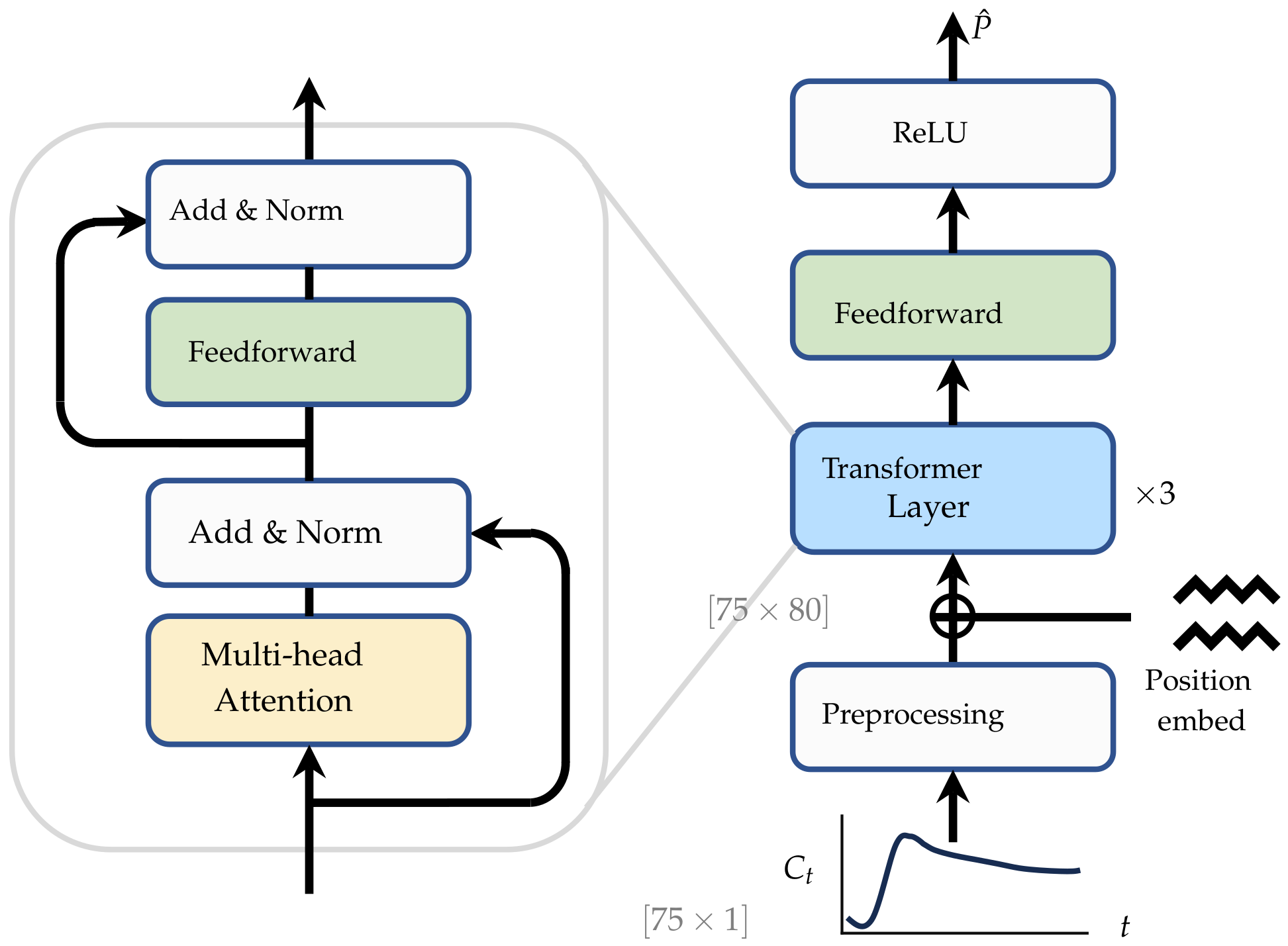
2.4.1. Model Architecture
2.4.2. Preprocessing for Robust Neural Networks
- 1.
- To enhance the model’s robustness against the noise and capture information at various scales.
- 2.
- To increase the data dimension and project the one-dimensional time series into high-dimensional space.
- 3.
- To normalize the time series data into a fixed range with zero mean and constant variance.
2.4.3. Model Training
2.5. Model Inference Workflow
2.5.1. From MRI Signal to CA Concentration
2.5.2. Initial Coarse Estimation
2.5.3. Coarse-to-Fine via Iterative Fitting
2.6. Study Population and DCE-MRI Data
3. Experiments and Results
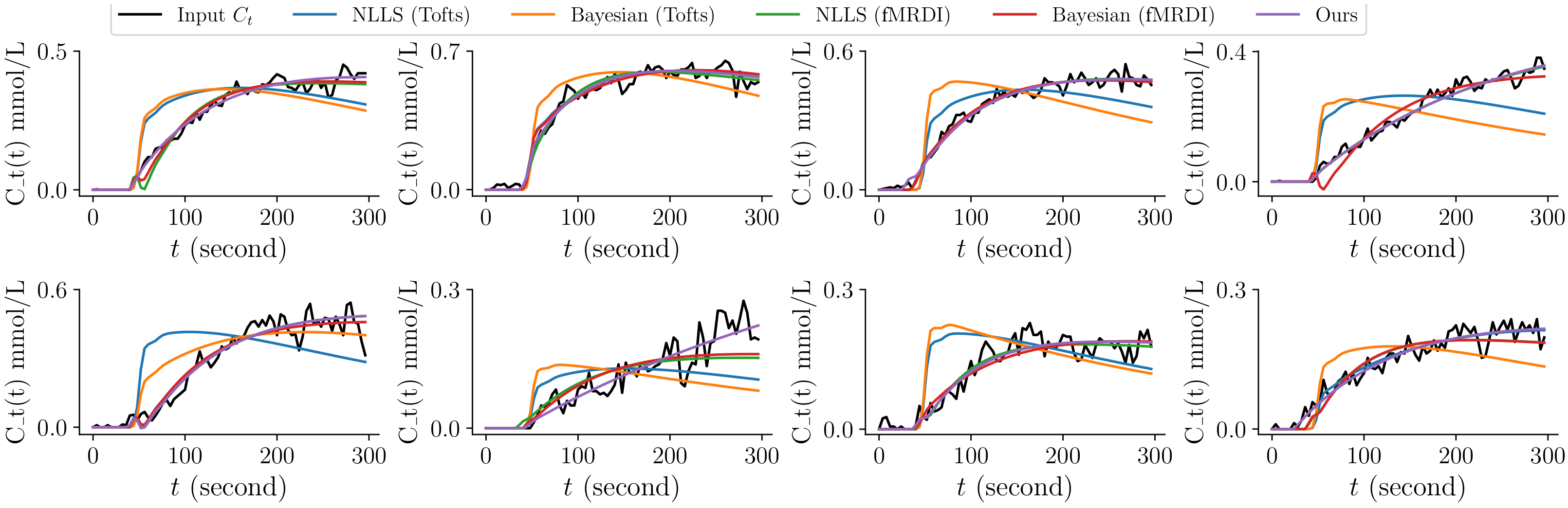
3.1. Running Time and Quality of Fitting
3.1.1. Running Time and Fitting Errors
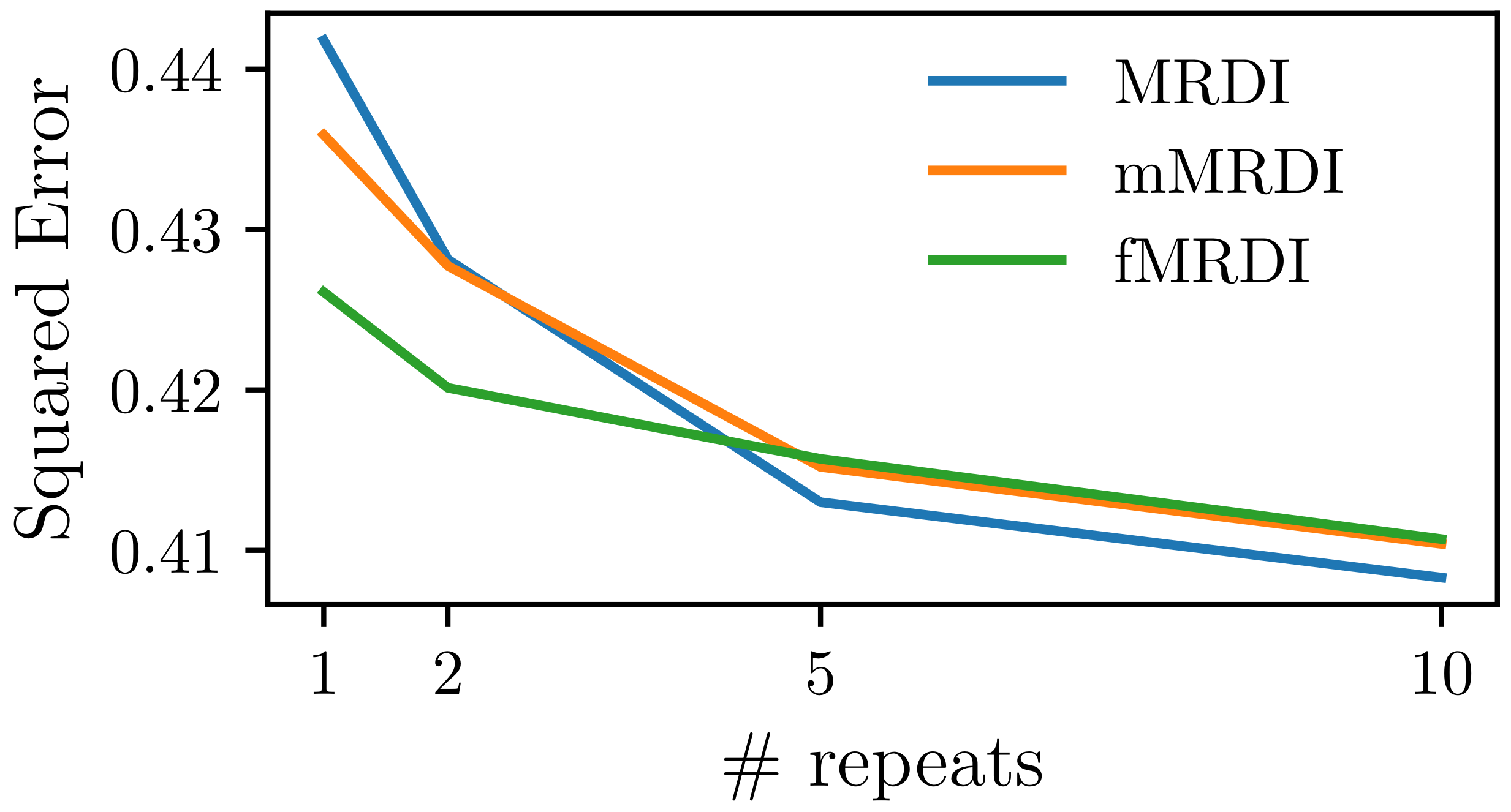
3.1.2. Compared with MRDI and mMRDI
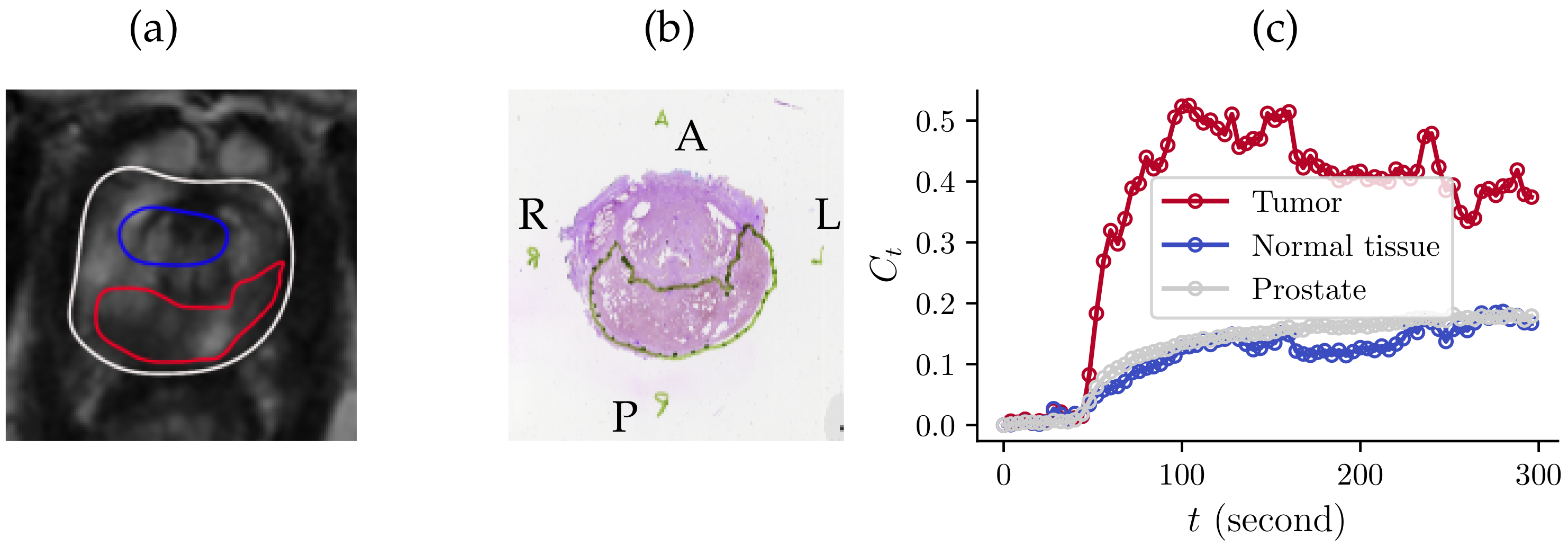
3.2. csPCa Lesions with
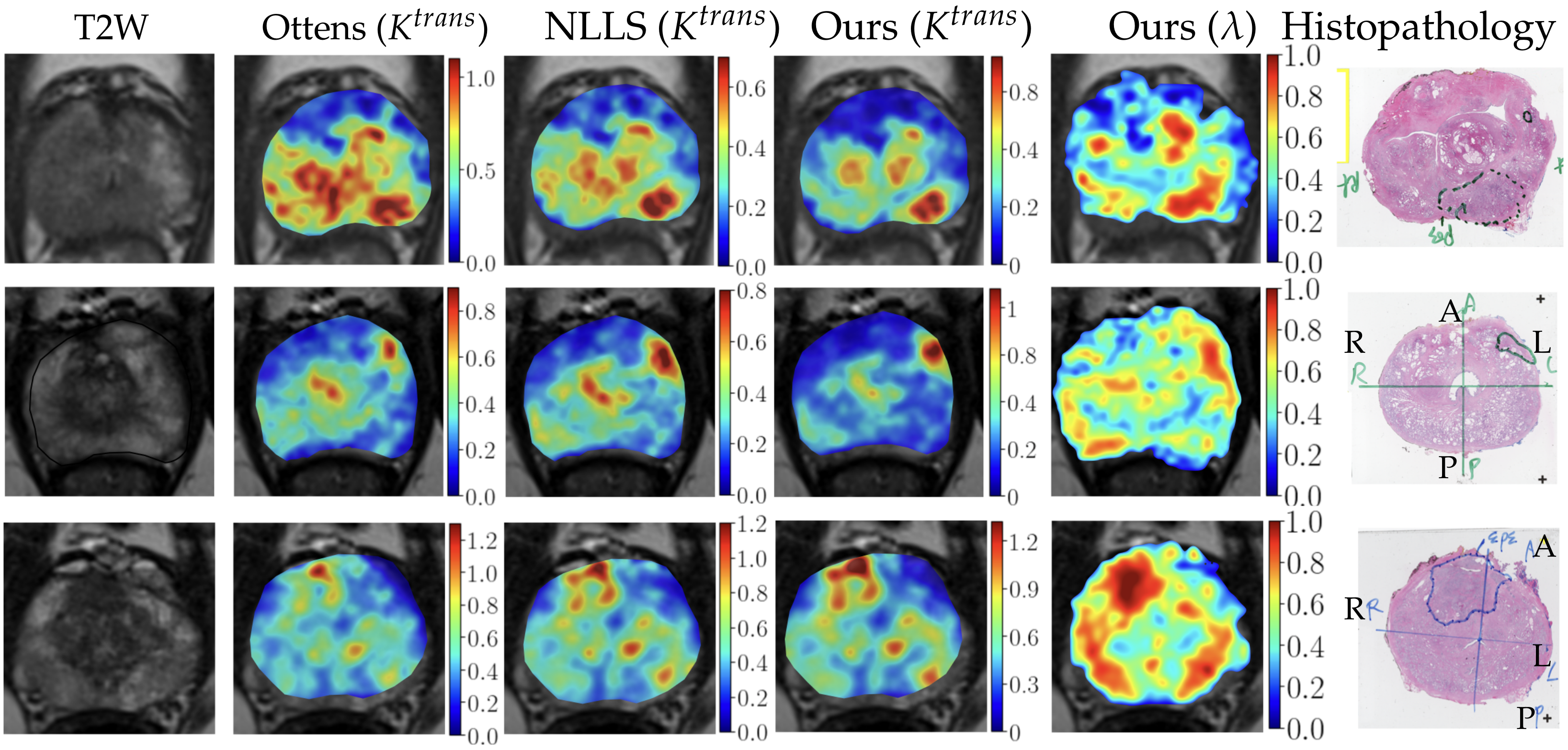
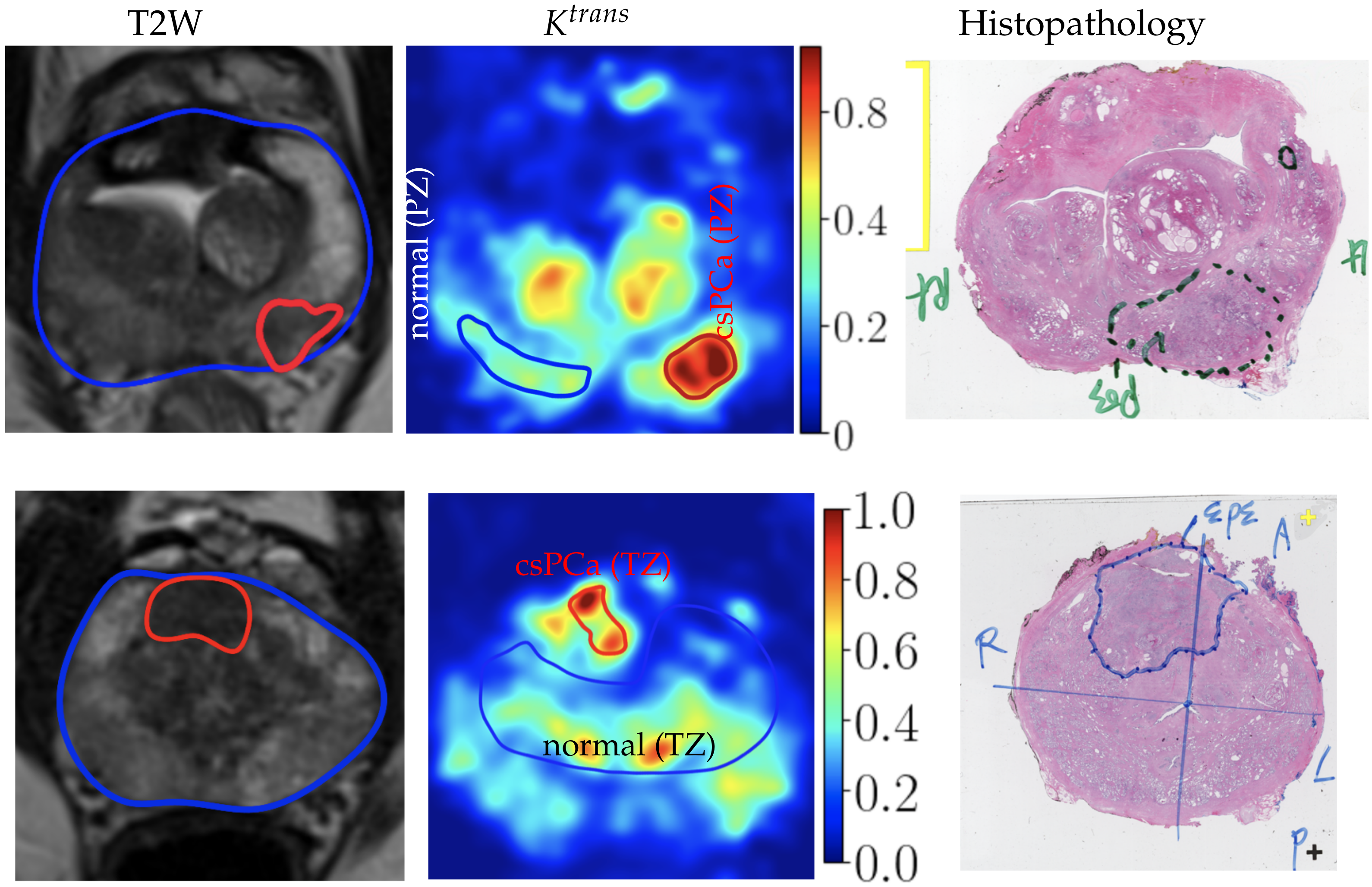
3.2.1. Qualitative Visualization of Maps
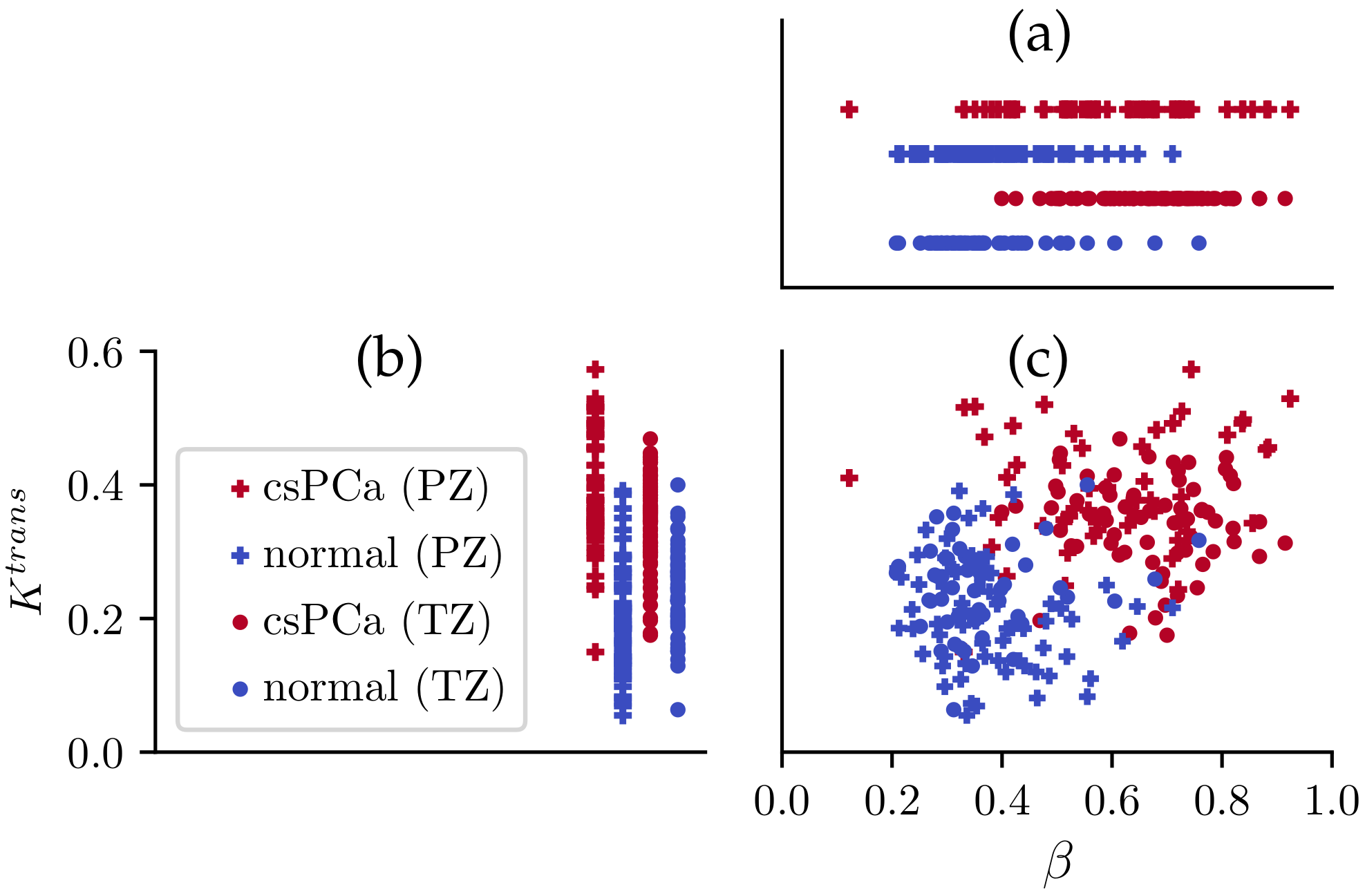
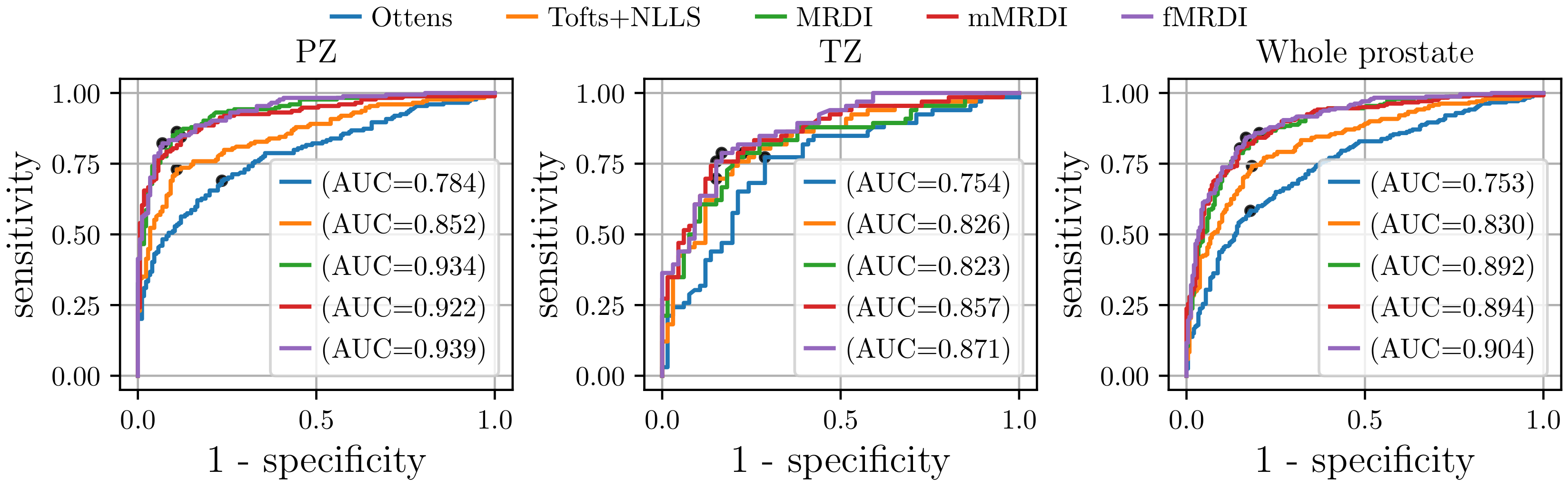
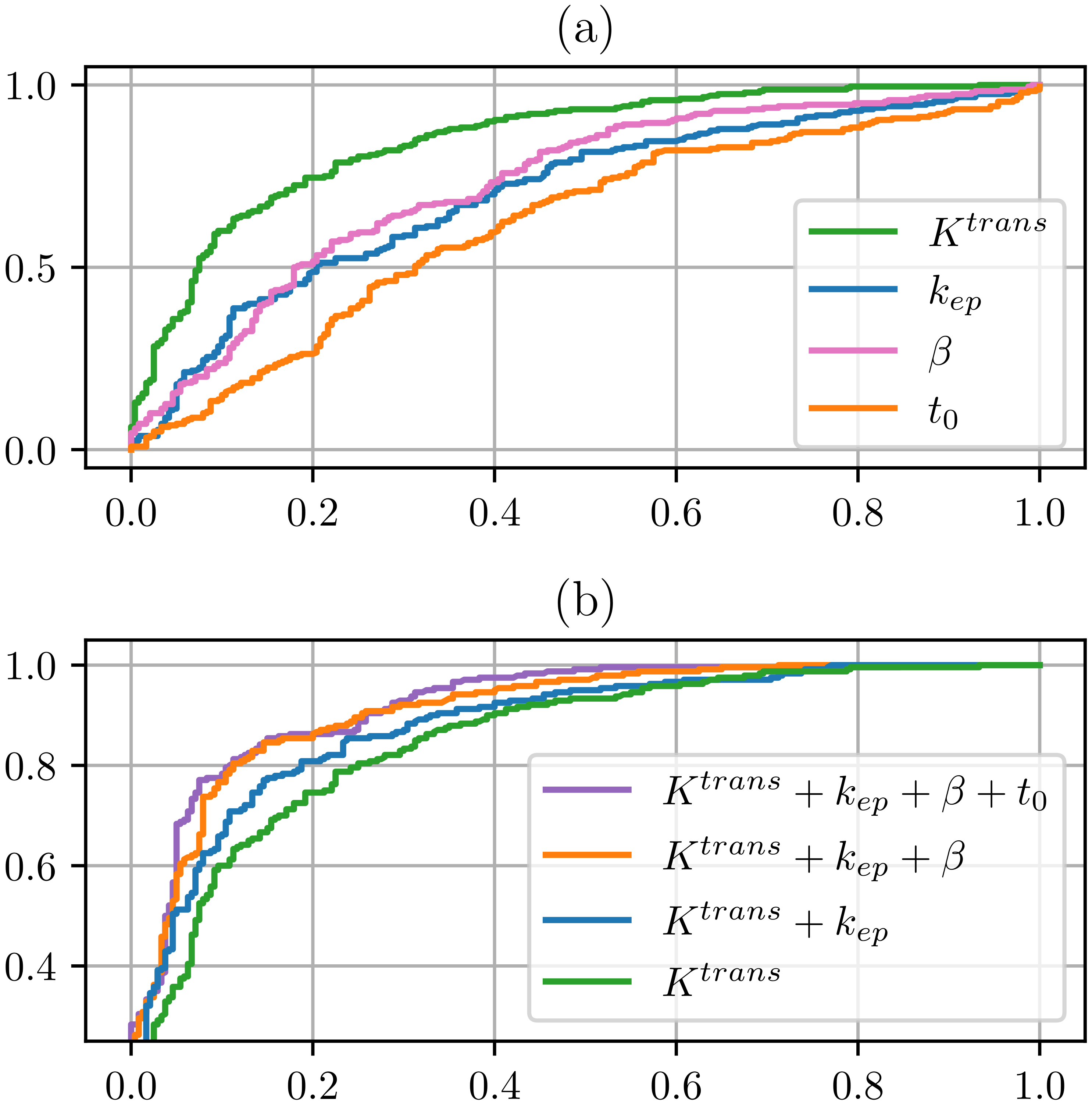
3.2.2. Quantitative Comparison of Tissue Contrast
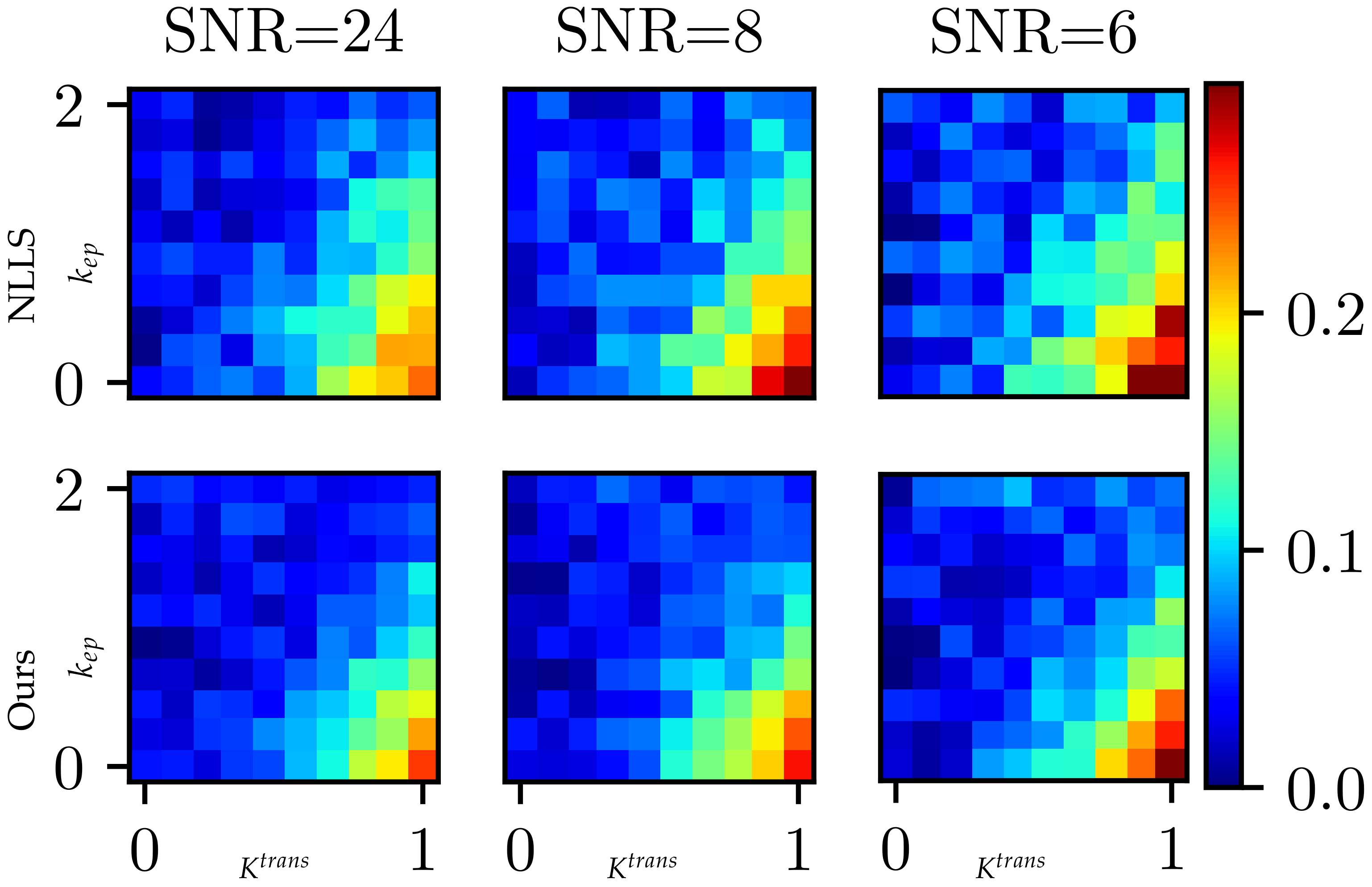
3.3. Validation with Digital Reference Objects
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carmeliet, P.; Jain, R.K. Angiogenesis in cancer and other diseases. Nature 2000, 407, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Russo, G.; Mischi, M.; Scheepens, W.; De la Rosette, J.J.; Wijkstra, H. Angiogenesis in prostate cancer: Onset, progression and imaging. BJU Int. 2012, 110, E794–E808. [Google Scholar] [CrossRef] [PubMed]
- Folkman, J. Tumor angiogenesis. Adv. Cancer Res. 1985, 43, 175–203. [Google Scholar] [PubMed]
- Weidner, N. Tumoural vascularity as a prognostic factor in cancer patients: The evidence continues to grow. J. Pathol. 1998, 184, 119–122. [Google Scholar] [CrossRef]
- Weidner, N.; Carroll, P.; Flax, J.; Blumenfeld, W.; Folkman, J. Tumor angiogenesis correlates with metastasis in invasive prostate carcinoma. Am. J. Pathol. 1993, 143, 401. [Google Scholar]
- Brawer, M.K. Quantitative microvessel density: A staging and prognostic marker for human prostatic carcinoma. Cancer Interdiscip. Int. J. Am. Cancer Soc. 1996, 78, 345–349. [Google Scholar] [CrossRef]
- Rosenkrantz, A.B.; Oto, A.; Turkbey, B.; Westphalen, A.C. Prostate imaging reporting and data system (PI-RADS), version 2: A critical look. Am. J. Roentgenol. 2016, 206, 1179–1183. [Google Scholar] [CrossRef]
- Turco, S.; Lavini, C.; Heijmink, S.; Barentsz, J.; Wijkstra, H.; Mischi, M. Evaluation of dispersion MRI for improved prostate cancer diagnosis in a multicenter study. Am. J. Roentgenol. 2018, 211, W242–W251. [Google Scholar] [CrossRef]
- Fedorov, A.; Fluckiger, J.; Ayers, G.D.; Li, X.; Gupta, S.N.; Tempany, C.; Mulkern, R.; Yankeelov, T.E.; Fennessy, F.M. A comparison of two methods for estimating DCE-MRI parameters via individual and cohort based AIFs in prostate cancer: A step towards practical implementation. Magn. Reson. Imaging 2014, 32, 321–329. [Google Scholar] [CrossRef]
- Tofts, P.S.; Brix, G.; Buckley, D.L.; Evelhoch, J.L.; Henderson, E.; Knopp, M.V.; Larsson, H.B.; Lee, T.Y.; Mayr, N.A.; Parker, G.J.; et al. Estimating kinetic parameters from dynamic contrast-enhanced T1-weighted MRI of a diffusable tracer: Standardized quantities and symbols. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 1999, 10, 223–232. [Google Scholar] [CrossRef]
- Jackson, A.; Buckley, D.L.; Parker, G.J. Dynamic Contrast-Enhanced Magnetic Resonance Imaging in Oncology; Springer: Berlin/Heidelberg, Germany, 2005; Volume 12. [Google Scholar]
- Folkman, J. The role of angiogenesis in tumor growth. Semin. Cancer Biol. 1992, 3, 65–71. [Google Scholar] [PubMed]
- Parker, G.; Tanner, S.; Leach, M. Pitfalls in the measurement of tissue permeability over short time-scales using a low temporal resolution blood input function. In Proceedings of the 4th Annual Meeting of International Society of Magnetic Resonance in Medicine, New York, NY, USA, 27 April–3 May 1996; Volume 1582. [Google Scholar]
- Orton, M.R.; d’Arcy, J.A.; Walker-Samuel, S.; Hawkes, D.J.; Atkinson, D.; Collins, D.J.; Leach, M.O. Computationally efficient vascular input function models for quantitative kinetic modelling using DCE-MRI. Phys. Med. Biol. 2008, 53, 1225. [Google Scholar] [CrossRef]
- Fluckiger, J.U.; Schabel, M.C.; DiBella, E.V. Toward local arterial input functions in dynamic contrast-enhanced MRI. J. Magn. Reson. Imaging 2010, 32, 924–934. [Google Scholar] [CrossRef]
- Huang, W.; Chen, Y.; Fedorov, A.; Li, X.; Jajamovich, G.H.; Malyarenko, D.I.; Aryal, M.P.; LaViolette, P.S.; Oborski, M.J.; O’Sullivan, F.; et al. The impact of arterial input function determination variations on prostate dynamic contrast-enhanced magnetic resonance imaging pharmacokinetic modeling: A multicenter data analysis challenge, part II. Tomography 2019, 5, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Weinmann, H.J.; Laniado, M.; Mützel, W. Pharmacokinetics of GdDTPA/dimeglumine after intravenous injection into healthy volunteers. Physiol. Chem. Phys. Med. NMR 1984, 16, 167–172. [Google Scholar]
- Parker, G.J.; Roberts, C.; Macdonald, A.; Buonaccorsi, G.A.; Cheung, S.; Buckley, D.L.; Jackson, A.; Watson, Y.; Davies, K.; Jayson, G.C. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2006, 56, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- Henderson, E.; Rutt, B.K.; Lee, T.Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magn. Reson. Imaging 1998, 16, 1057–1073. [Google Scholar] [CrossRef]
- Fritz-Hansen, T.; Rostrup, E.; Larsson, H.B.; Søndergaard, L.; Ring, P.; Henriksen, O. Measurement of the arterial concentration of Gd-DTPA using MRI: A step toward quantitative perfusion imaging. Magn. Reson. Med. 1996, 36, 225–231. [Google Scholar] [CrossRef]
- Lewis, D.; Zhu, X.; Coope, D.J.; Zhao, S.; King, A.T.; Cootes, T.; Jackson, A.; Li, K.L. Surrogate vascular input function measurements from the superior sagittal sinus are repeatable and provide tissue-validated kinetic parameters in brain DCE-MRI. Sci. Rep. 2022, 12, 8737. [Google Scholar] [CrossRef]
- Miyazaki, K.; Jerome, N.P.; Collins, D.J.; Orton, M.R.; d’Arcy, J.A.; Wallace, T.; Moreno, L.; Pearson, A.D.; Marshall, L.V.; Carceller, F.; et al. Demonstration of the reproducibility of free-breathing diffusion-weighted MRI and dynamic contrast enhanced MRI in children with solid tumours: A pilot study. Eur. Radiol. 2015, 25, 2641–2650. [Google Scholar] [CrossRef][Green Version]
- Rata, M.; Collins, D.J.; Darcy, J.; Messiou, C.; Tunariu, N.; Desouza, N.; Young, H.; Leach, M.O.; Orton, M.R. Assessment of repeatability and treatment response in early phase clinical trials using DCE-MRI: Comparison of parametric analysis using MR-and CT-derived arterial input functions. Eur. Radiol. 2016, 26, 1991–1998. [Google Scholar] [CrossRef]
- Kuenen, M.; Saidov, T.; Wijkstra, H.; Mischi, M. Contrast-ultrasound dispersion imaging for prostate cancer localization by improved spatiotemporal similarity analysis. Ultrasound Med. Biol. 2013, 39, 1631–1641. [Google Scholar] [CrossRef]
- Sung, K. Modified MR dispersion imaging in prostate dynamic contrast-enhanced MRI. J. Magn. Reson. Imaging 2019, 50, 1307–1317. [Google Scholar] [CrossRef]
- Mischi, M.; Turco, S.; Lavini, C.; Kompatsiari, K.; de la Rosette, J.J.; Breeuwer, M.; Wijkstra, H. Magnetic resonance dispersion imaging for localization of angiogenesis and cancer growth. Investig. Radiol. 2014, 49, 561–569. [Google Scholar] [CrossRef] [PubMed]
- Sourbron, S.; Buckley, D.L. Tracer kinetic modelling in MRI: Estimating perfusion and capillary permeability. Phys. Med. Biol. 2011, 57, R1. [Google Scholar] [CrossRef] [PubMed]
- Jager, A.; Oddens, J.R.; Postema, A.W.; Miclea, R.L.; Schoots, I.G.; Nooijen, P.G.; van der Linden, H.; Barentsz, J.O.; Heijmink, S.W.; Wijkstra, H.; et al. Is There an Added Value of Quantitative DCE-MRI by Magnetic Resonance Dispersion Imaging for Prostate Cancer Diagnosis? Cancers 2024, 16, 2431. [Google Scholar] [CrossRef] [PubMed]
- Kuenen, M.P.; Mischi, M.; Wijkstra, H. Contrast-ultrasound diffusion imaging for localization of prostate cancer. IEEE Trans. Med. Imaging 2011, 30, 1493–1502. [Google Scholar] [CrossRef]
- Yankeelov, T.E.; Gore, J.C. Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples. Curr. Med. Imaging 2007, 3, 91–107. [Google Scholar] [CrossRef]
- Hsu, Y.H.H.; Ferl, G.Z.; Ng, C.M. GPU-accelerated nonparametric kinetic analysis of DCE-MRI data from glioblastoma patients treated with bevacizumab. Magn. Reson. Imaging 2013, 31, 618–623. [Google Scholar] [CrossRef]
- Vajuvalli, N.N.; Nayak, K.N.; Geethanath, S. Accelerated pharmacokinetic map determination for dynamic contrast enhanced MRI using frequency-domain based Tofts model. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Chicago, IL, USA, 26–30 August 2014; pp. 2404–2407. [Google Scholar]
- Murase, K. Efficient method for calculating kinetic parameters using T1-weighted dynamic contrast-enhanced magnetic resonance imaging. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2004, 51, 858–862. [Google Scholar] [CrossRef]
- Kelm, B.M.; Menze, B.H.; Nix, O.; Zechmann, C.M.; Hamprecht, F.A. Estimating kinetic parameter maps from dynamic contrast-enhanced MRI using spatial prior knowledge. IEEE Trans. Med. Imaging 2009, 28, 1534–1547. [Google Scholar] [CrossRef]
- Dikaios, N.; Arridge, S.; Hamy, V.; Punwani, S.; Atkinson, D. Direct parametric reconstruction from undersampled (k, t)-space data in dynamic contrast enhanced MRI. Med. Image Anal. 2014, 18, 989–1001. [Google Scholar] [CrossRef] [PubMed]
- You, D.; Aryal, M.; Samuels, S.E.; Eisbruch, A.; Cao, Y. Temporal feature extraction from DCE-MRI to identify poorly perfused subvolumes of tumors related to outcomes of radiation therapy in head and neck cancer. Tomography 2016, 2, 341–352. [Google Scholar] [CrossRef] [PubMed]
- Bliesener, Y.; Acharya, J.; Nayak, K.S. Efficient DCE-MRI parameter and uncertainty estimation using a neural network. IEEE Trans. Med. Imaging 2019, 39, 1712–1723. [Google Scholar] [CrossRef] [PubMed]
- Ottens, T.; Barbieri, S.; Orton, M.R.; Klaassen, R.; van Laarhoven, H.W.; Crezee, H.; Nederveen, A.J.; Zhen, X.; Gurney-Champion, O.J. Deep learning DCE-MRI parameter estimation: Application in pancreatic cancer. Med. Image Anal. 2022, 80, 102512. [Google Scholar] [CrossRef] [PubMed]
- Witowski, J.; Heacock, L.; Reig, B.; Kang, S.K.; Lewin, A.; Pysarenko, K.; Patel, S.; Samreen, N.; Rudnicki, W.; Łuczyńska, E.; et al. Improving breast cancer diagnostics with deep learning for MRI. Sci. Transl. Med. 2022, 14, eabo4802. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Futterer, J.J.; Engelbrecht, M.R.; Huisman, H.J.; Jager, G.J.; Hulsbergen-van De Kaa, C.A.; Witjes, J.A.; Barentsz, J.O. Staging prostate cancer with dynamic contrast-enhanced endorectal MR imaging prior to radical prostatectomy: Experienced versus less experienced readers. Radiology 2005, 237, 541–549. [Google Scholar] [CrossRef]
- Klaassen, R.; Gurney-Champion, O.J.; Wilmink, J.W.; Besselink, M.G.; Engelbrecht, M.R.; Stoker, J.; Nederveen, A.J.; van Laarhoven, H.W. Repeatability and correlations of dynamic contrast enhanced and T2* MRI in patients with advanced pancreatic ductal adenocarcinoma. Magn. Reson. Imaging 2018, 50, 1–9. [Google Scholar] [CrossRef]
- Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ulas, C.; Das, D.; Thrippleton, M.J.; Valdes Hernandez, M.d.C.; Armitage, P.A.; Makin, S.D.; Wardlaw, J.M.; Menze, B.H. Convolutional neural networks for direct inference of pharmacokinetic parameters: Application to stroke dynamic contrast-enhanced MRI. Front. Neurol. 2019, 9, 1147. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Adelson, E.H.; Anderson, C.H.; Bergen, J.R.; Burt, P.J.; Ogden, J.M. Pyramid methods in image processing. RCA Eng. 1984, 29, 33–41. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2012; Volume 25. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Wang, H.Z.; Riederer, S.J.; Lee, J.N. Optimizing the precision in T1 relaxation estimation using limited flip angles. Magn. Reson. Med. 1987, 5, 399–416. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Chatterjee, A.; Yousuf, A.; Antic, T.; Eggener, S.; Karczmar, G.S.; Oto, A. Comparison of T2-weighted imaging, DWI, and dynamic contrast-enhanced MRI for calculation of prostate cancer index lesion volume: Correlation with whole-mount pathology. Am. J. Roentgenol. 2019, 212, 351–356. [Google Scholar] [CrossRef] [PubMed]


| NN + Parker AIF | |
| +WS AIF | |
| +Pyramid | |
| +Sinusoidal | |
| +Refine |
| Fitting Method | Ottens | NLLS | NN + NLLS Refine | ||||
|---|---|---|---|---|---|---|---|
| PK Model | Tofts + Exp | Tofts + Parker | MRDI | fMRDI | Tofts + Parker | MRDI | fMRDI |
| Error | 0.6723 ±2.2209 | 0.6184 ±1.9867 | 0.4272 ±1.6618 | 0.4261 ±1.5687 | 0.5917 ±2.1221 | 0.4175 ±1.5212 | 0.4114 ±1.5181 |
| Iterations | N/A | 200 | 300 | 200 | 20 | 50 | 30 |
| Time (per-patient) | 109 s | 480 s | 644 s | 480 s | 71 s | 115 s | 176 s |
| Method | Ottens [38] | NLLS+Tofts+Parker | MRDI | fMRDI (Ours) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone | PZ | TZ | PZ+TZ | PZ | TZ | PZ+TZ | PZ | TZ | PZ+TZ | PZ | TZ | PZ+TZ |
| AUC | 0.784 | 0.754 | 0.753 | 0.852 | 0.826 | 0.830 | 0.934 | 0.823 | 0.892 | 0.939 | 0.871 | 0.904 |
| 1 - specificity | 0.236 | 0.288 | 0.179 | 0.109 | 0.152 | 0.183 | 0.109 | 0.227 | 0.204 | 0.069 | 0.167 | 0.167 |
| Sensitivity | 0.690 | 0.773 | 0.583 | 0.730 | 0.697 | 0.742 | 0.862 | 0.788 | 0.858 | 0.822 | 0.788 | 0.842 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Pang, K.; Hung, A.L.; Zheng, H.; Yan, R.; Sung, K. A Deep Learning-Based Framework for Highly Accelerated Prostate MR Dispersion Imaging. Cancers 2024, 16, 2983. https://doi.org/10.3390/cancers16172983
Zhao K, Pang K, Hung AL, Zheng H, Yan R, Sung K. A Deep Learning-Based Framework for Highly Accelerated Prostate MR Dispersion Imaging. Cancers. 2024; 16(17):2983. https://doi.org/10.3390/cancers16172983
Chicago/Turabian StyleZhao, Kai, Kaifeng Pang, Alex LingYu Hung, Haoxin Zheng, Ran Yan, and Kyunghyun Sung. 2024. "A Deep Learning-Based Framework for Highly Accelerated Prostate MR Dispersion Imaging" Cancers 16, no. 17: 2983. https://doi.org/10.3390/cancers16172983
APA StyleZhao, K., Pang, K., Hung, A. L., Zheng, H., Yan, R., & Sung, K. (2024). A Deep Learning-Based Framework for Highly Accelerated Prostate MR Dispersion Imaging. Cancers, 16(17), 2983. https://doi.org/10.3390/cancers16172983









