A Systematic Review of LET-Guided Treatment Plan Optimisation in Proton Therapy: Identifying the Current State and Future Needs
Abstract
Simple Summary
Abstract
1. Introduction
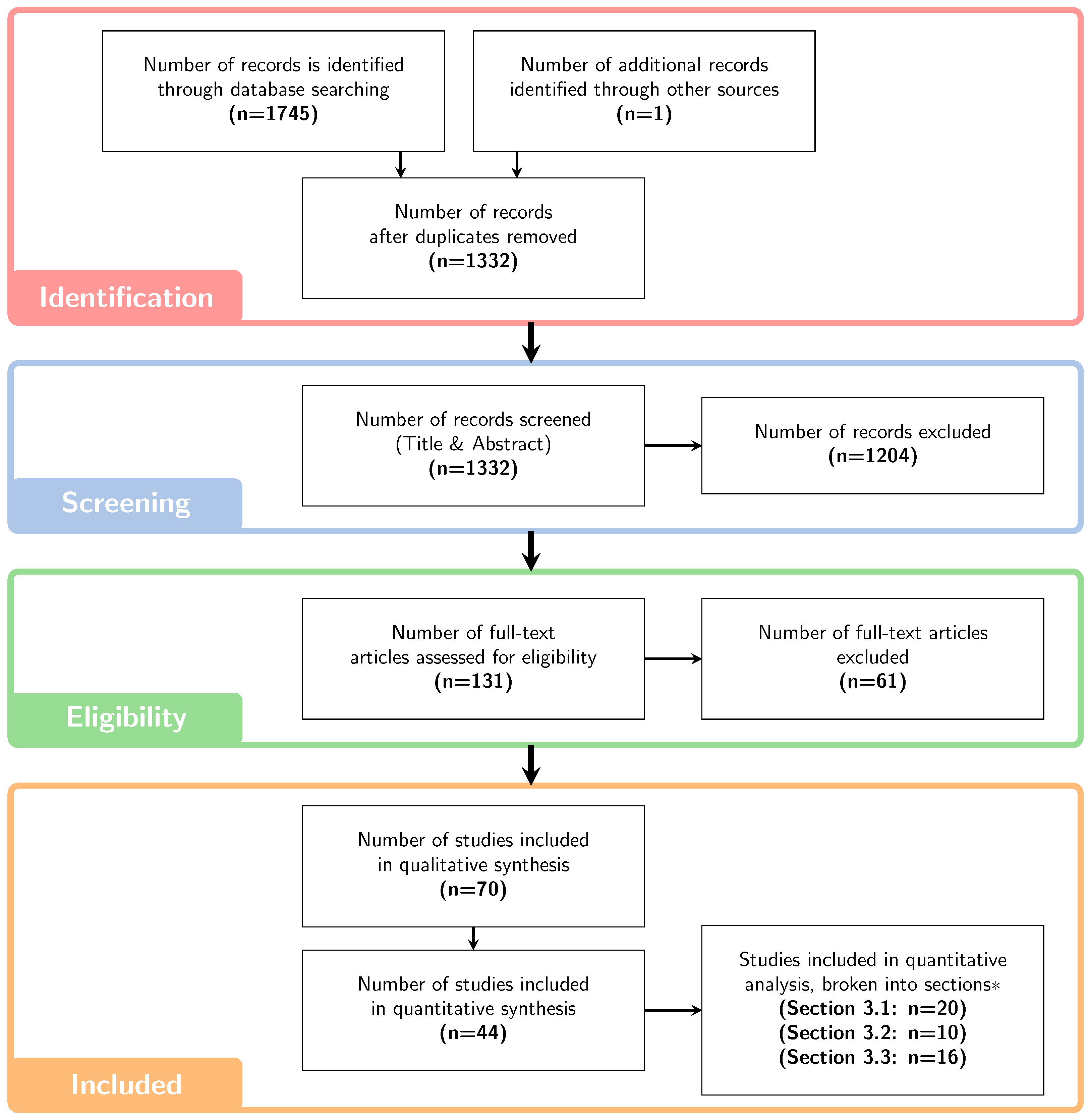
2. Materials and Methods
3. Results and Discussion
3.1. Clinical Data and Evidence
| Study | Patient Details | Treatment Details | Clinical Endpoint | Follow-Up/ Diagnosis (Months) | Key Findings (p-Value) |
|---|---|---|---|---|---|
Roberts et al. [58]  | 30 Brain (Paediatric) | PBS, ≥50.4 GyRBE | Brain image changes | Median 21 (2–35) | Stronger correlation with BD than with physical prescription dose |
Harrabi et al. [38]  | 110 LGG (Adult) | NR, Median 54 GyRBE | CEBL lesions | 39 | Increased incidence of asymptomatic radiation-induced brain injuries with an increased LET. |
Bahn et al. [41]  | 110 LGG (Adult and Paediatric, AE = 23) | PBS, 45–60 GyRBE | CEBL (total of 67 across all patients) | Median 38 (1–91) | Independent correlation between CEBLs and dose, LET and distance to ventricular system. LET ranges from 3.56 to 8.18 keV/m within CEBL regions. |
Eulitz et al. [45]  | 42 LGG (Adult) | PBS with chemotherapy, 54–60 GyRBE | RIBI (64 in 21 patients) | 24 | Spatial correlation with RIBI and elevated LET, dose and periventrivular radiosensitivity. |
Peeler et al. [39]  | 34 Ependymoma (Paediatric) | PS, 54 GyRBE | MR Image Changes | NR | Significant correlation between CEBLs and track-averaged LET (>2.5 keV/m) in CTV (p = 0.02). Insignificant change for LET (p = 0.06), D (p = 0.49) and D (p = 0.77) in CTV. |
Oden et al. [17]  | 3 Intracranial | PBS, 50.4–54 GyRBE (28–30 FX), 2 opposed beams | Brain toxicity, Blindness | 5–10 (toxicity), 9 (blindness) | Elevated LET of 4–6 keV/m with high dose occurred inside toxicity volumes. |
Bertolet et al. [40]  | 26 Medulloblastoma (Adult) | PBS, 1.8 GyRBE(30–34 FX) | Brain image changes | 17 (2–61) | 11 patients showed elevated LET in image change regions of equivalent dose. These patients had shallower targets, used fewer beams and smaller angles. |
Bolsi et al. [43]  | 16 Craniopharyngioma (Paediatric, AE = 2) | PBS, 54 GyRBE | RICV | 14, 24 (for AE patients) | LET and LET increased significantly (p = 0.02) for RICV patients. |
Engeseth et al. [44]  | 15 Base of Skull (Adult) | NR, 75.6–79.2 GyRBE | Brain image changes | 19 (9–33) | LET and D increased in image change regions (3.61 keV/m and 63.5 GyRBE). TD is 63.6 GyRBE and 2 keV/m or 50.1 GyRBE and 5 keV/m, respectively. |
Yang et al. [53]  | 55 Prostate(Paediatric, AE = 9) | PBS, 75.6–79.2 GyRBE (42–44 FX) | Rectal Bleeding | NR | Significant increase in both V (67.8 GyRBE, 2.86 keV/m) (p = 0.007) and V (72.2 GyRBE, 0 keV/m) (p = 0.01) in the rectum for group that experienced rectal bleeding. * |
Fossum et al. [59]  | 11 H&N | PBS, 60–70 GyRBE | Dermatitis, dry mouth, dysgeusia, fatigue, mucosal infection, oral mucositis, oral and skin pain, pharyngolaryngeal pain, salivary duct inflammation, trismus, weight loss | Immediately post-treatment (3, 6 and 12 mo thereafter) | BD hotspot correlated exactly with AE for 2 patients, correlations strong for AEs in oropharynx and oral cavity, correlations were not as strong in the brain and mandible. |
Wang et al. [49]  | 203 Breast (Adult, AE = 13) | PBS and PS, 50.4 (32–59.4) GyRBE | Low-grade rib fractures | NR | Increase in BD in fracture regions by 56.4 Gy. |
Giantsoudi et al. [52]  | 111 Medulloblastoma (Paediatric) | PS, NR, Distal track-end in brainstem | CNS Injury | 50.4 | Increase in LET for symptomatic AE but no clear correlation. |
Indelicato et al. [51]  | 73 Ependymoma, 68 Craniopharyngioma, 66 LGG (Paediatric) | NR, 54–59.4 Gy | Brainstem Injury | 24 | Hypothesised a correlation of high LET with endothelial damage. |
Yang et al. [47]  | 113 H&N (Adult, AE = 20) | PBS, 1.8–2.1 GyRBE (25–35 FX) | Ulceration, Hemorrhage, Osteoradionecrosis, Mucositis | 18, 24, 35 | Correlation of Osteoradionecrosis and Mucositis (out-field). No correlation of ulceration and mucositis (in-field). |
Sethi et al. [48]  | 109 Medulloblastoma (Paediatric) | PS, Median 54 GyRBE | Recurrence | 38.8 (1.4–119.2) | No correlation with LET. |
Skaarup et al. [56]  | 6 Brain (Paediatric) | PS, 36–59.4 GyRBE | Brain image changes | 12 post-treatment, 3 thereafter | No strong correlation of image changes with LET as a function of time post-treatment (Due to no significant image changes observed on follow-up scans and small sample size). |
Garbacz et al. [42]  | 45 Base of Skull (Adult) | NR, 70–74 GyRBE | CEBL | 3 post-treatment, 6 thereafter | No clear correlation between CEBL and high LET. |
Niemierko et al. [46]  | 179 H&N, Brain and Base of Skull (Adult) | PS, ≥59.4 GyRBE | Brain Necrosis | NR | No correlation between LET adjusted for dose and brain necrosis. |
Wagenaar et al. [50]  | 100 H&N | PBS, 70 GyRBE | Xerostomia, Tube Feeding, Dysphagia | NR | No correlation between LET nor D and NTCP for any endpoint due to inter-patient variability. |
3.2. LET Optimisation via Delivery Technique
3.2.1. Beam Field Configuration and Spot Size
3.2.2. Beam Multiplicity and Spot-Scanning Proton Arc Therapy
3.2.3. Beam Weighting and Shifting
| Study (Intervention) | Patient Details | Treatment Details | Key Findings (p-Value) | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Cases | Adjacent or Overlapping OARs | Delivery | Prescription [GyRBE] (Target) | |||
| Henjum et al. [63] (Beam Configuration + LETOpt) | 1 | Brain | Brainstem, L optic nerve Rectum, Bladder | PBS, 2 fields (cranial, lateral) ( 34), MFO | 54, 30 FX (PTV) | LETOpt resulted in dose sparing of the brainstem and optic nerve, but with little change to LET. | |
| 1 | Prostate | PBS, 2-bilateral coplanar fields, MFO | 67.5, 25 FX (PTV) | LETOpt had little effect on OAR sparing to the rectum and bladder as the fields were directly opposed. | |||
| 1 | H&N | R parotid gland, L pterygoid | 3 coplanar fields (50, 30), MFO | 50.4, 28 FX (PTV) | LETOpt has little effect on the dose and LET distribution. | ||
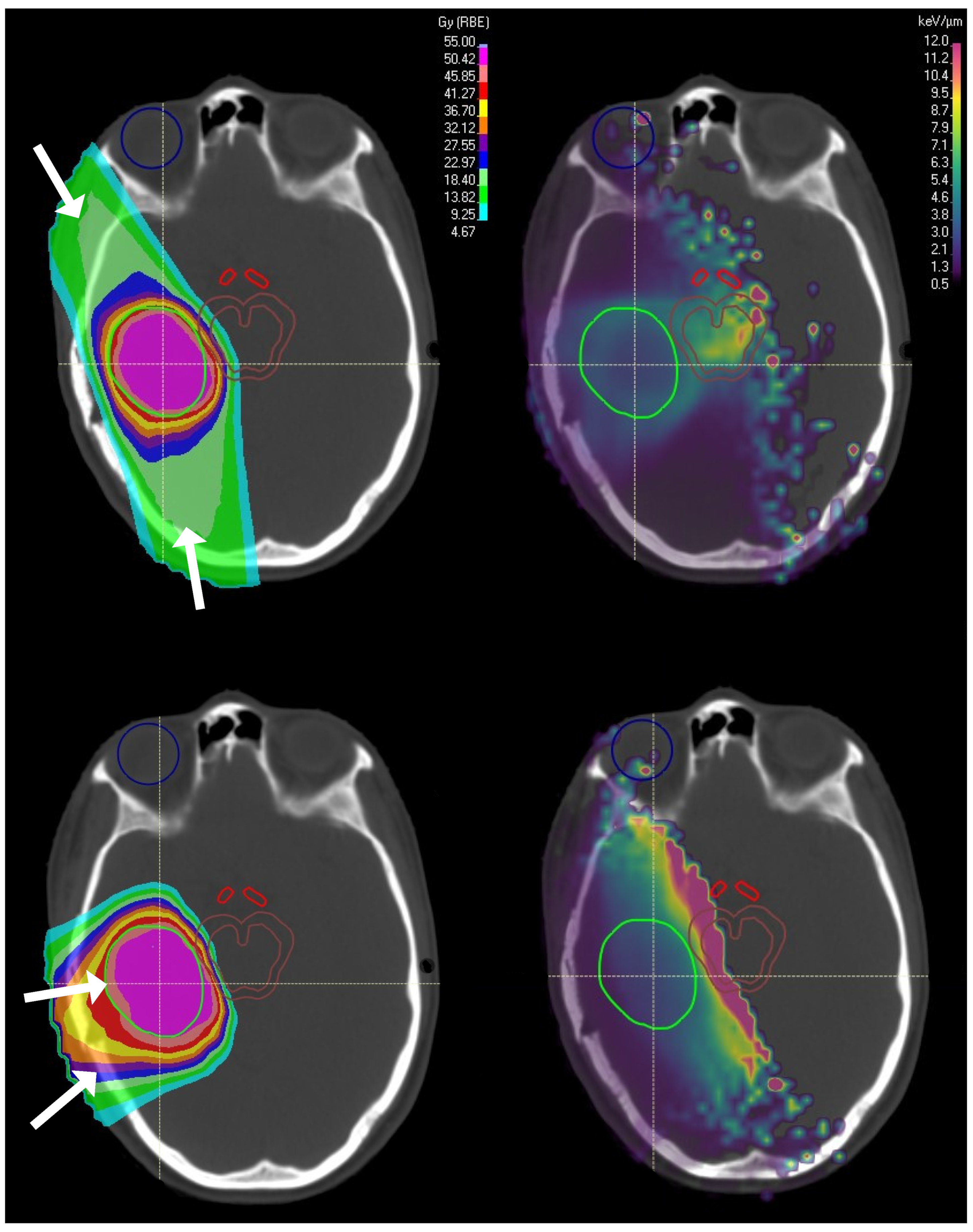
| Fjæra et al. [64] (Beam Configuration) | 1 | Brain (Paediatric) | Brainstem | PBS, 3 fields (2 lateral, 1 posterior non-coplanar), target shifted to overlap, abut and separate from the brainstem | 59.4, 33 FX (PTV) | Addition of a third (vertex) field lowered LET, whilst smaller angles between the 2 lateral fields increased LET. No significant LET change when increasing spot size. Shifting the PTV away from the brainstem decreased LET to the brainstem but increased D. | |
| Faught et al. [10] (Beam Configuration) | 1, 4 | Water phantom, Brain (Paediatric) | Brainstem | PBS, two fields at 60, 90, 120 and 180 | NR | Inside the target RO margins and use of range shifter had the biggest impact (0.6 keV/m for both cases). LET increased by 4.3 keV/m on the outer target boundary as beam angles decreased from 180→60. Lower effect for spot size and SFO vs. MFO. | |
| Giantsoudi et al. [70] (Distal-end Shifting) | 6 | Ependymoma | Brainstem | PS, 2–3 fields, large/small beam angles, shift DE past brainstem, DE occurs distal to the target and inside brainstem | NR | Brainstem: From to for both 2 and 3 fields, D increased (p < 0.01, <0.01), D decreased (p = 0.04, 0.02) (<1 GyRBE) and LET decreased (p < 0.01, =0.01). Brainstem-CTV overlap: No statistically significant change (p > 0.05) in D for from 3 to 2 fields. Significant decrease (p = 0.04) in D and LET (of only 0.1 keV/m). | |
| Study (Intervention) | Patient Details | Treatment Details | Key Findings (p-Value) | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Cases | Adjacent or Overlapping OARs | Delivery | Prescription [GyRBE] (Target) | |||
| Li et al. [65] (SPArcT + 2-stepLETOpt) | 1 | Liver | Normal liver tissue | IMPT 2 fields vs. SPArcT | 75, 25 FX (CTV) | CTV: From 2 field IMPT→SPArcT both with LETOpt, dose conformality similar and LET increased from 2.4 to 4.9 keV/m. Normal liver tissue: From 2 field IMPT→SPArcT with LETOpt, the low dose bath is larger but D decreased by 1.5 GyRBE. | |
| 1 | Prostate | Rectum | IMPT 2–8 fields vs. SPArcT | 78, 39 FX (CTV) | CTV: From 2 field IMPT→SPArcT, similar dose coverage, LET increased from 4.38 to 5.06 keV/m. D to the bladder and rectum increased. | ||
| 1 | Brain | Brainstem, Chiasm, L and R optic nerve | IMPT 3 fields vs. SPArcT | 54, 30 FX (CTV) | CTV: 3 field IMPT→SPArcT both with LETOpt saw similar dose coverage and LET increased from 3.13 to 4.03 keV/m. OAR: Smaller D for brainstem and chiasm but higher for optic nerve. LET decreased from 2.74 to 2.14 keV/m, 3.45–2.43 keV/m, 4.09–2.96 keV/m and 3.22–2.66 keV/m for the brainstem, chiasm, L and R optic nerve, respectively. | ||
| Bertolet et al. [68] (SPArcT) | 1 | Water Phantom (Cylinder) | N/A | Compared SPArcT to 2–3 field IMPT (coplanar or noncoplanar) | 2, 1 FX (N/A) | From 3 field IMPT→SPArcT, LET and LET increased in the target. In the brainstem LET decreases by % for SPArcT vs. 2 beam IMPT but D increases. | |
| 3 | Brain | Brainstem (All), R optic nerve (1), L hippocampus (1) | 26, 30 FX (PTV) | CTV: In all cases D and D did not change but LET, LET and LET nearly doubled. Brainstem: D halved for patient 1 but did not change for the others. D increased slightly for patients 2 and 3 and did not change for 1. D increased significantly for all patients. | |||
| Toussaint et al. [61] (SPArcT) | 4 | Craniopharyngioma (Paediatric) | Brainstem, Temporal Lobes | PBS, 3–36 fields (coplanar, sagittal) | 54, 30 FX (NR) | Dose and LET conformality improved as beam multiplicity increased. Volume that received >3.5 keV/m decreased but at expense of increased volume receiving <3.5 keV/m. Low isodose volume increased with beam multiplicity. | |
| Study (Intervention) | Patient Details | Treatment Details | Key Findings (p-Value) | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Cases | Adjacent or Overlapping OARs | Delivery | Prescription [GyRBE] (Target) | |||
| Fager et al. [71] (LET painting) | 8 | Prostate | Rectum, Bladder | PBS, 2–7 beams, target was split so all beams stopped at its centre (STP) vs. full target plan (FTP) | 79.2, 44 FX | CTV: LET 2.5 keV/m (FTP), increased by 1.5 (p = 0.008), 1.8 (p = 0.016) and 2.1 keV/m (p = 0.031) for 2STP, 4STP and 7STP, respectively. Non-OAR normal tissue: LET 2.8 keV/m (FTP), decreased by 0.1 (p = 0.125), 0.5 (p = 0.016) and 0.5 keV/m (p = 0.031) for 2STP, 4STP and 7STP, respectively. Rectum: LET 2.9 keV/m for FTP, increased by 1.5 keV/m (p = 0.008) for 2STP and decreased by 0.1 keV/m for 4STP and 7STP (p = 0.81, 0.84), respectively. Bladder: LET 3.2 keV/m for FTP, increased by 0.5, 0.0 and 0.2 keV/m for 2STP, 4STP and 7STP, respectively. D decreased by 5.3, 4.4 and 4.4 GyRBE for 2STP, 4STP and 7STP, respectively. | |
| Guan et al. [8] (LET-Painting) | 1 | Water Phantom | N/A | PBS, 2 laterally opposed fields, with flat SOBPs (Case A) and decreased spot weighting in SOBPs toward the distal-edge (Case B) | NR | Case A: LET inside the target 5.6–5.7 keV/m on the target edge and 2.6 keV/m in the centre. LET outside the target <1 keV/m. Case B: LET inside the target is 4.3–4.4 keV/m on the distal edges and 3.8 keV/m in the centre. Outside the target, LET is <1 keV/m. | |
| Malinen et al. [72] (LET-Painting) | 1 | Tumour Model with hypoxic regions | N/A | NR, no field information, compared dose painting (DP), LET painting (LP) and DP+LP to reference plans (no DP or LP) | NR, up to 16 FX | LET range 1–11 keV/m. Therapeutic ratio for DP = 1.43, LP = 1.09 and DP + LP = 1.45 | |
3.2.4. LET Painting
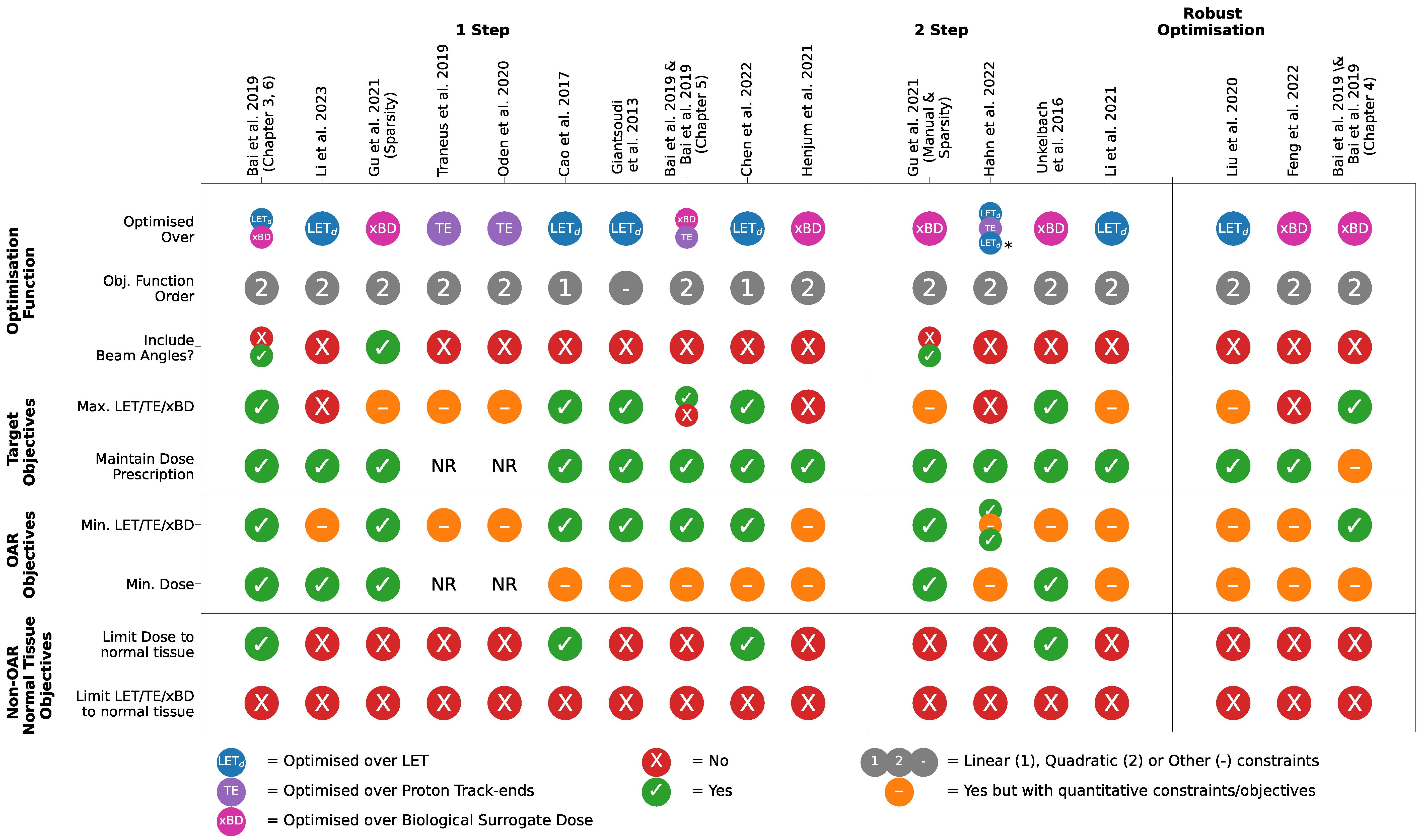
3.3. Objective Function-Based LET Optimisation
3.3.1. Selection of Constraints, Objectives and Algorithms
3.3.2. Managing the Dose–LET Trade-Off
3.3.3. 1-Step versus 2-Step Optimisations
3.3.4. Optimising over Beam Weights and Angles
3.3.5. Track-End Objectives as a LET Surrogate
| Study (Intervention) | Patient Details | Treatment Details | Key Findings (p-Value) | ||||
|---|---|---|---|---|---|---|---|
| Sample Size | Cases | Adjacent or Overlapping OARs | Delivery | Prescription [GyRBE] (Target) | |||
| Bai et al. [31] (1-step) (Ch. 3) | 5 | Glioblastoma, Anaplastic Astrocytoma, Ependymoma | Brainstem, Optical Chiasm (CTV) | PBS, 3–4 coplanar and non-coplanar fields | 54–59.2, 30–32 FX (CTV) | CTV: D remained unchanged from DoseOpt to LETOpt. D increased for all cases by <1 GyRBE. LET increased by up to 0.47 keV/m for all but 1 case. Brainstem: D increased in all cases up to 2.89 GyRBE from DoseOpt→LETOpt. D either increased or remained the same. LET and LET reduced significantly for all cases. | |
| Li et al. [77] (1-step) | 1 | Lung | Heart | PBS, 3 coplanar fields | 54, 30 FX (CTV) | From QN→ICR methods ± LETOpt: 1 cm CTV Boundary: D decreased by <1 GyRBE, LET decreased by 0.5 keV/m (for ICR more than QN) and BD decreased by <1 Gy. Heart: Insignificant decrease in D. Decreases of <0.5 keV/m and <1 Gy in LET and BD, respectively. Computation time: 3-fold decrease from QN→ICR ± LETOpt. | |
| 1 | H&N | L parotid gland | PBS, 2 coplanar fields | 63.6, 33 FX (CTV) | 1 cm CTV Boundary: Same as lung case except LET decreased by 0.6 and 0.5 keV/m for ICR and QN, respectively. L parotid gland: BD decreased by Gy for ICR vs. <1 Gy for QN. Computation time: 9 fold decrease from QN→ICR ± LETOpt. | ||
| 1 | Abdominal | Bowel | PBS, 2 coplanar fields | 50, 25 FX (CTV) | 1 cm CTV Boundary: Similar trend to lung case. Bowel: Same trend as lung case. | ||
| 1 | Brain | Brainstem | PBS, 2 coplanar fields | 54, 30 FX (CTV) | 1 cm CTV Boundary: Same as lung case except LET decreased by 0.57 and 0.59 keV/m for QN and ICR, respectively. Brainstem: D increased by 1.5 and 0.5 GyRBE for ICR and QN, respectively. LET decreased by <0.5 keV/m for both cases. BD increased by 1.5 Gy and decreased by 1.2 Gy for QN and ICR, respectively. Computation time: 6 and 2-fold decrease from QN→ICR ± LETOpt, respectively. | ||
| Chen et al. [79] (1-step) | 10 | Prostate | Rectum | PBS, 2, 4, 6 and 8 coplanar fields | 78, 39 FX (NR) | CTV: LET and LET increased significantly by 53–63% (p < 0.05) and 63–70% (p < 0.05), respectively. | |
| Giantsoudi et al. [20] (1-step) | 2 | Pancreas | NR | PBS, NR | 25, 5 FX | LET variation over base plans in Pareto-space for small vs. large spot size for patients 1 and 2. PTV: Smaller variation (7.9, 14.3% vs. 1.2, 5.1%) Liver: Same trend as PTV with 61.3, 38.1% vs. 11.7, 13.9%. | |
| 5 | H&N | Brainstem (PTV) | PBS, NR | 50.4-59.4, 28–33 FX | Similar trend in PTV to pancreatic patients except LET variation in brainstem up to 222% for small spot size. | ||
| Cao et al. [78] (1-step) | 5 | Brain (Glioblastoma, Anaplastic Astrocytoma, Ependymoma) | Brainstem, Chiasm (CTV) | PBS, 2–3 noncoplanar beams | 48–54, 28–30 FX (GTV) | GTV: Negligible changes in D and D, increases in LET and LET by keV/m for 3/5 cases and increases of 2–3 keV/m for the rest. Brainstem: No change to D and D, LET decreased by up to 2.5 keV/m in 3 cases with no change to the rest, LET decreased by up to 1.5 keV/m in 2/5 cases. Chiasm: No change in D and D, large decrease in LET and LET for 1/5 cases. | |
| Gu et al. [32] (1- and 2-step) | 3 | Base of Skull | Chiasm, Optic Nerve (PTV) | PBS, 2–4 non-coplanar beams (selected from 600 candidate beams) | 56–74, NR (CTV) | PTV: D, D, BD, BD unchanged with LETOpt±angle selection. BD increased for all LETOpt plans. In-field OARs: BD, BD decreased the most for LETOpt with angle selection. D and D also decreased by up to 3 GyRBE with LETOpt+angle selection. Out-field OARs: Smaller decreases in BD, BD were observed compared to in-field OARs. Larger decreases in D, D compared to in-field OARs. 1 vs. 2-step: Dosimetrically equivalent, BD and BD lowered more for 1-step than 2-step. | |
| 3 | H&N | NR | 54–63, NR (CTV) | PTV: Same as Base of Skull OARs: Same as Base of Skull except D increased by 7–8 GyRBE for 1 patient. | |||
| Bai et al. [34] &Bai et al. [31] (Ch. 6) (1-step) | 2 | Brain | Brainstem | PBS, 3–4 coplanar or noncoplanar (out of 36 candidates) | 54, 30 FX (CTV) | CTV: From DoseOpt→LETOpt ± angle selection, D did not change and D increased by ≤0.4 GyRBE. BD and BD increased by 2 and 3 Gy, respectively. Brainstem: D and D increased by <0.5 GyRBE. BD mostly unchanged for 1 case and decreased by 3 Gy for the other. BD decreased for both cases. Beam Angle Selection: 2 of the 3 fields differed by 30 with LETOpt. | |
| 2 | H&N | NR | PBS, 3 coplanar or noncoplanar (out of 36 candidates) | 60 GyRBE, 30 FX (NR) | CTV: From DoseOpt→LETOpt ± angle selection, with no change in D, D, BD and BD. OARs: Small decreases of D, D, BD and BD within 1 GyRBE and 1 Gy. Changes were not as significant as brain patients. | ||
| Traneus et al. [62] (1-step) | 3 | H&N | Pituitary Gland (PTV) | PBS, 3 coplanar | 56–70, 35 FX (PTV) | CTV: D, D unchanged, decreases of ≤0.7 keV/m and ≤0.5 keV/m in LET and LET, respectively. Pituitary Gland: D unchanged, D decrease <0.5 GyRBE. Decreases of ≤0.5 and 1–3 keV/m in LET and LET. | |
| 3 | Intracranial | Brainstem, Chiasm (PTV) | PBS, 2 coplanar or noncoplanar | 54, 30 FX (PTV) | CTV: D and D unchanged. Increase of 1–2 and 0.5 keV/m for LET and LET, respectively. Brain-CTV: D, D unchanged. Change of <0.2 and <0.6 keV/m in LET and LET. OARs: D, D increase and decrease of <0.8 GyRBE in chiasm and brainstem, respectively. LET decreased by 1–3.4 keV/m and LET decreased by 1–3 keV/m in both the brainstem and chiasm. | ||
| Oden et al. [17] (1-step) | 3 | Intracranial | Brainstem, Chiasm, Optic Nerves (PTV) | PBS, 2–3 coplanar or noncoplanar | 50.4–54, 28–30 FX (PTV) | From DoseOpt→TEOpt with 2 or 3 beams (voxels >5% of prescription only): CTV: D, D and LET equivalent. LET increased by 0.7 keV/m for 3 beam TEOpt and differs <0.2 keV/m for 2 beam TEOpt. Brain-CTV: D, LET unchanged for 2 and 3 beams. LET increased by 0.8 and decreased by 2.5 GyRBE for 2 and 3 beam plans, respectively. OARs: LET, LET and D decreased in all cases but decrease was larger for 3 beam plans. D decreased more for 3 beam plans in 2/3 cases. | |
| Henjum et al. [63] (1-step) | - | - | - | - | - | See Table 2 | |
| Li et al. [65] (2-step) | - | - | - | - | - | See Table 3 | |
| Unkelbach et al. [30] (2-step) | 5 (1,2,2) | Brain (Meningioma, Ependymoma, Base of Skull Chordoma) | Brainstem, Chiasm, Pituitary Gland | PBS, 2–6 coplanar (1 beam noncoplanar for 1 patient) , spot size 2.2–5.6 mm | 50, NR (PTV) | PTV: All dose, BD±LETOpt unchanged. Brainstem: BD, BD and BD decreased by 25–50% for all patients. | |
| Hahn et al. [60] (2-step) | 10 | Intracranial | Brainstem, Chiasm, Optic Nerve | PBS, 2–3 coplanar and noncoplanar | 54, 30 FX (Primary CTV) | For TEOpt, LETOpt, DDOpt vs. DoseOpt - CTV: For all plans, equivalent dose, LET and LET. D to normal brain tissue increased by <3%. OARs: LET, LET decreased significantly (p < 0.05, <1 keV/m) in brainstem and chiasm. Insignificant change (p > 0.05) in D and D. | |
| Bai et al. [33] and Bai et al. [31] (Ch. 4) (RO) | 1 | Prostate | Rectum, Bladder | PBS, 2 directly opposed coplanar beams | 54, 30 FX (CTV) | From PTV-based→Dose-based RO→LETRO - CTV: D, D, BD, BD robustness increases from PTV-based→RO but only BD, BD robustness increased with LETRO. Rectum: D, BD, BD robustness increased from PTV-based→RO but unchanged with LETRO. Bladder: Same trend as rectum. | |
| 1 | Brain | Brainstem | PBS, 3 coplanar or noncoplanar | 78, 39 FX (CTV) | CTV: Same trend as prostate patient. Brainstem: Similar robustness in D from PTV-based→RO→LETRO. Robustness of D, BD, BD increases from PTV-based→RO but unchanged with LETRO. | ||
| 1 | H&N | NR | PBS, 3 coplanar or noncoplanar | 66, 33 FX (CTV) | CTV: Same trend as prostate and brain patient. OARs: Similar trend as brainstem in brain patient for larynx and the parotid glands. | ||
| Liu et al. [80](RO) | 14 | H&N | Brainstem | PBS, 3 coplanar or noncoplanar | 41.4–70, 20–35 FX (NR) | CTV: LET increased by <0.5 keV/m, dose coverage improved up to 1.8% of the prescription dose with LETRO (where dose homogeneity = D − D) Brainstem: D decreased for 8 and increased for 6 patients by 5% of prescribed dose. LET decreased 0–7 keV/m. | |
| Feng et al. [35] (RO) | 10 | Base of Skull | Temporal Lobes, necrosis occurred just outside CTV | PBS, 2–6 coplanar or noncoplanar | 60–70, 30–35 FX (NR) | CTV + 3cm Margin: Insignificant change in D, D, D, V, BD and BD (p = 0.508, 0.285, 0.241, 0.314, 0.445, 0.056). Significant decrease in BD, BD, V, V and V (p = 0.017, 0.022, 0.009, 0.025, 0.021). | |
3.3.6. LET-Based Robust Optimisation
3.4. Clinical Deployment of LET Optimisation
- Patients with critical structures immediately proximal to the clinical target are ideal candidates and will see the most LET reduction in OARs.
- Plans that often involve asymmetric beam arrangements, such as intracranial or H&N patients, should be considered at-risk due to a higher presence of LET hotspots, and thus are good candidates for LET optimisation. Whereas plans that involve directly opposed fields, such as prostate patients, should be considered lower risk. Further, modalities that do not involve LET hotspots, such as proton FLASH radiotherapy using transmission proton beams, need not be considered for LET optimisation.
- Clinical data are needed to properly quantify OAR-specific LET-constraints to enable LET-volume plan evaluations in conjunction with dose.
- Clinically achievable LET distributions are dependent on patient anatomy or the nature of the clinical target, which should also be considered in patient selection. For instance, a non-uniform or complex-shaped tumour may benefit from additional beams to increase the degrees of freedom, e.g., SPArcT.
- LET optimisation via delivery technique approaches are conceptually simpler than inverse planning and does not involve long computation times. Further systematic study of the effect that different treatment techniques have on the LET distribution will provide further insight into using this approach to its full extent.
- Using additional beams leads to a reduction in the overall LET distribution; however, this is at the expense of a higher volume of normal tissue receiving a low-dose bath. A more comprehensive understanding of the effects of low dose exposure to normal tissue compared to high LET will prove useful.
- Inverse planning approaches require long computation times but ensure a mathematically optimal plan, compared to optimising via the delivery technique. Thus, clinics would need adequate computing facilities to regularly perform LET optimisations.
- A 1-step inverse planning LET optimisation will give a more optimal plan than the 2-step method as the trade-off between dose and LET is managed simultaneously.
- The 2-step method will allow patients to be selected for LET optimisation based on their dose-optimised plan, once patient-selection protocols have been established, thus avoiding the need for computation of the LET distribution for every patient.
- If LET optimisation is implemented in RO, steps should be taken to ensure the objectives do not directly complete through careful selection of objective priority weights.
- Beam angle selection should be made with consideration given to LET. As including beam angle as an optimisable parameter in Equation (2) would increase the computation time required, a manual beam selection will still yield some improvement.
- Using BD or dose thresholds in place of LET alone can manage the dose–LET trade-off, ensuring that computation time is not wasted on clinically irrelevant voxels.
3.5. Limitations and Bias
3.5.1. In the Published Data
3.5.2. This Review
4. Conclusions
- Clinical studies with earlier and more frequent follow-ups may prove more informative than retrospective studies because the correlation between an adverse effect and LET diminishes as the endpoint progresses to a later stage. This will provide (1) a better understanding of which patient cohorts would benefit from LET optimisation and those who will not to inform future patient selection protocol and (2) the ability to quantify LET-based constraints for future implementation.
- Two major approaches to LET optimisation can be performed—via the delivery technique or a LET-based extension of the conventional dose objective function.
- Beam angles and multiplicity of a treatment plan have a strong influence on the LET distribution, whilst target size, shape and location can strongly influence the achievable LET range within. This knowledge can also be used to advise patient selection for LET optimisation.
- Dosimetrically, there is no clear stand-out between the methods proposed so far, but in most cases, the objectives of each study were met with varying success.
- Diversity between studies with respect to optimisation objectives, patient/case characteristics and reported metrics makes meta-analysis unfeasible with the current state of the literature. This would require more consistent future data reporting and would further validate or invalidate the key findings of this review.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Adverse Effect |
| BD | Biological Surrogate Dose |
| CEBL | Contrast-Enhancing Brain Lesions |
| CNS | Central Nervous System |
| CTV | Clinical Target Volume |
| DE | Distal Track-End |
| FX | Fractions |
| GTV | Gross Target Volume |
| H&N | Head and Neck |
| ICR | Iterative Convex Relaxation |
| IMPT | Intensity-Modulated Proton Therapy |
| LET | Linear Energy Transfer |
| LETRO | LET-guided Robust Optimisation |
| LGG | Low-Grade Glioma |
| MFO | Multi-field Optimisation |
| MR | Magnetic Resonance |
| NTCP | Normal-Tissue Complication Probability |
| OAR | Organ-at-risk |
| PS | Passively Scattered |
| PBS | Pencil Beam Scanning |
| PBT | Proton Beam Therapy |
| PTV | Planning Target Volume |
| QN | Quasi-Newton |
| RBE | Relative Biological Effectiveness |
| RIBI | Radiation-Induced Brain Injury |
| RICV | Radiation-Induced Cerebral Vasculopathies |
| RO | Robust Optimisation |
| RT | Radiotherapy |
| SFO | Single-field Optimisation |
| SPArcT | Spot-scanning Proton Arc Therapy |
Appendix A
Appendix A.1
| Search Term | Hits | |
|---|---|---|
| MEDLINE | ||
| 1 | exp Heavy Ion Radiotherapy/ | 6308 |
| 2 | Protons/ and (therap* or radiotherap*).ti,ab,kf. | 2687 |
| 3 | Radiotherapy/ and (proton* or hadron* or ion* or carbon).ti,ab,kf. | 2687 |
| 4 | ((proton* or hadron* or ion* or carbon) adj3 (therap* or radiotherap*)).ti,ab,kf. | 13,591 |
| 5 | or/1-4 | 17,496 |
| 6 | Relative Biological Effectiveness/ | 4638 |
| 7 | linear energy transfer/ | 2874 |
| 8 | ((let or linear energy transfer or rbe or biologic* or radiobiolog*) adj5 (optimi* or reoptimi* or weight* or vari* or robust)).ti,ab,kf. | 59,866 |
| 9 | or/6-8 | 66,020 |
| 10 | 5 and 9 | 1258 |
| 11 | limit 10 to yr="2000 -Current" | 1185 |
| Scopus | ||
| 1 | TITLE-ABS-KEY(((proton* OR hadron* OR ion* OR carbon) W/2 (therap* OR radiotherap*)) | 23,386 |
| 2 | AND ( ( let OR “linear energy transfer” OR rbe OR biolog* OR radiobiolog* ) W/4 ( optimi* OR reoptimi* OR weight* OR variab* OR robust* ) ) ) | 29,618 |
| 3 | #1 AND #2 | 465 |
| 4 | #3 AND limit to 2000-current | 460 |
Appendix A.2
| Inclusion | Exclusion |
|---|---|
| LET optimisation performed with LET directly or via the biological surrogate dose | Optimisation with RBE models dependent on tissue-specific parameters (e.g., ) |
| OR LET-sparing methods | |
| OR LET clinical endpoint correlation studies | |
| Proton Therapy | Heavy Ion Therapy (e.g., Carbon ions and heavier) |
Appendix B
| Metric | Definition |
|---|---|
| LET/BD/D | The mean dose/LET/biological dose imparted in a structure |
| LET/BD/D | The minimum physical dose/LET/biological dose imparted in a non-zero CT voxel of a specified volume |
| LET/BD/D | The maximum physical dose/LET/biological dose imparted in a non-zero CT voxel of a specified volume |
| LET/BD/D | The physical dose/LET/biological dose that covers x% of the structure |
| LET/BD/D | The physical dose/LET/biological dose that overs x cc of the structure |
| V | Percentage volume of a structure covered by at least x Gy |
References
- Particle Therapy Facilities in Clinical Operation. Available online: https://ptcog.site/index.php/facilities-in-operation-public (accessed on 16 April 2023).
- Zhang, X. A Review of the Robust Optimization Process and Advances with Monte Carlo in the Proton Therapy Management of Head and Neck Tumors. Int. J. Part. Ther. 2021, 8, 14–24. [Google Scholar] [CrossRef] [PubMed]
- Molitoris, J.; Diwanji, T.; Snider, J.; Mossahebi, S.; Samanta, S.; Badiyan, S.; Simone, C.; Mohindra, P. Advances in the use of motion management and image guidance in radiation therapy treatment for lung cancer. J. Thorac. Dis. 2018, 10, S2437–S2450. [Google Scholar] [CrossRef] [PubMed]
- Thomas, D.J. ICRU report 85: Fundamental quantities and units for ionizing radiation. Radiat. Prot. Dosim. 2012, 150, 550–552. [Google Scholar] [CrossRef]
- Paganetti, H.; Blakely, E.; Carabe, A.; Carlson, D.; Das, I.; Dong, L.; Grosshans, D.; Held, K.; Mohan, R.; Moiseenko, V.; et al. Report of the AAPM TG-256 on the relative biological effectiveness of proton beams in radiation therapy. Med. Phys. 2019, 46, e53–e78. [Google Scholar] [CrossRef]
- Bettega, D.; Calzolari, P.; Chauvel, P.; Courdi, A.; Herault, J.; Iborra, N.; Marchesini, R.; Massariello, P.; Poli, G.L.; Tallone, L. Radiobiological studies on the 65 MeV therapeutic proton beam at Nice using human tumour cells. Int. J. Radiat. Biol. 2000, 76, 1297–1303. [Google Scholar] [CrossRef]
- Guan, F.; Bronk, L.; Titt, U.; Lin, S.; Mirkovic, D.; Kerr, M.; Zhu, X.; Dinh, J.; Sobieski, M.; Stephan, C.; et al. Spatial mapping of the Biologic Effectiveness of scanned particle beams: Towards biologically optimized particle therapy. Sci. Rep. 2015, 5, 9850. [Google Scholar] [CrossRef] [PubMed]
- Guan, F.; Geng, C.; Ma, D.; Bronk, L.; Kerr, M.; Li, Y.; Gates, D.; Kroger, B.; Sahoo, N.; Titt, U.; et al. RBE Model-Based Biological Dose Optimization for Proton Radiobiology Studies. Int. J. Part. Ther. 2018, 5, 160–171. [Google Scholar] [CrossRef]
- Grassberger, C.; Trofimov, A.; Lomax, A.; Paganetti, H. Variations in linear energy transfer within clinical proton therapy fields and the potential for biological treatment planning. Int. J. Radiat. Oncol. Biol. Phys. 2011, 80, 1559–1566. [Google Scholar] [CrossRef]
- Faught, A.M.; Wilson, L.J.; Gargone, M.; Pirlepesov, F.; Moskvin, V.P.; Hua, C.H. Treatment-planning approaches to intensity modulated proton therapy and the impact on dose-weighted linear energy transfer. J. Appl. Clin. Med. Phys. 2022, 24, e13782. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, D.; Bradley, J.A.; Mailhot Vega, R.B.; Zhang, Y.; Indelicato, D.J.; Mendenhall, N.; Liang, X. Incorporation of the LETd-weighted biological dose in the evaluation of breast intensity-modulated proton therapy plans. Acta Oncol. 2021, 60, 252–259. [Google Scholar] [CrossRef]
- Paganetti, H. Relative Biological Effectiveness (RBE) values for Proton Beam Therapy. Variations as a function of Biological Endpoint, Dose and Linear Energy Transfer. Phys. Med. Biol. 2014, 59, R419. [Google Scholar] [PubMed]
- Underwood, T.; McMahon, S. Proton relative biological effectiveness (RBE): A multi-scale problem. Br. J. Radiol. 2018, 92, 20180004. [Google Scholar] [CrossRef] [PubMed]
- Rørvik, E.; Fjæra, L.; Dahle, T.; Dale, J.; Engeseth, G.M.; Stokkevåg, C.; Thörnqvist, S.; Ytre-Hauge, K. Exploration and application of phenomenological RBE models for proton therapy. Phys. Med. Biol. 2018, 63, 185013. [Google Scholar] [CrossRef]
- McNamara, A.; Willers, H.; Paganetti, H. Modelling variable proton relative biological effectiveness for treatment planning. Br. J. Radiol. 2019, 93, 20190334. [Google Scholar] [CrossRef]
- Oden, J.; Eriksson, K.; Toma-Dasu, I. Inclusion of a variable RBE into proton and photon plan comparison for various fractionation schedules in prostate radiation therapy. Med. Phys. 2017, 44, 810–822. [Google Scholar] [CrossRef]
- Oden, J.; Toma-Dasu, I.; Witt Nystrom, P.; Traneus, E.; Dasu, A. Spatial correlation of linear energy transfer and relative biological effectiveness with suspected treatment-related toxicities following proton therapy for intracranial tumors. Med. Phys. 2020, 47, 342–351. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.J.; Paganetti, H.; Prise, K.M. LET-weighted doses effectively reduce biological variability in proton radiotherapy planning. Phys. Med. Biol. 2018, 63, 225009. [Google Scholar] [CrossRef]
- Deng, W.; Yang, Y.; Liu, C.; Bues, M.; Mohan, R.; Wong, W.; Foote, R.; Patel, S.; Liu, W. A critical review of LET-based intensity- modulated proton therapy plan evaluation and optimization for head and neck cancer management. Int. J. Part. Ther. 2021, 8, 36–49. [Google Scholar] [CrossRef]
- Giantsoudi, D.; Grassberger, C.; Craft, D.; Niemierko, A.; Trofimov, A.; Paganetti, H. Linear energy transfer-guided optimization in intensity modulated proton therapy: Feasibility study and clinical potential. Int. J. Radiat. Oncol. Biol. Phys. 2013, 87, 216–222. [Google Scholar] [CrossRef]
- Sørensen, B.S.; Overgaard, J.; Bassler, N. In vitro RBE-LET dependence for multiple particle types. Acta Oncol. 2011, 50, 757–762. [Google Scholar] [CrossRef]
- An, S.; Pak, S.i.; Jeong, S.; Min, S.; Kim, T.; Shin, D.; Lim, Y.; Jeong, H.; Kim, H.S.; Lee, S. Measurement of Proton Beam Dose-Averaged Linear Energy Transfer Using a Radiochromic Film. Prog. Med. Phys. 2022, 33, 80–87. [Google Scholar] [CrossRef]
- Kalholm, F.; Grzanka, L.; Traneus, E.; Bassler, N. A Systematic Review on the Usage of Averaged LET in Radiation Biology for Particle Therapy. Radiother. Oncol. 2021, 161, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, 105906. [Google Scholar] [CrossRef]
- Grosshagauer, S.; Fossati, P.; Schafasand, M.; Carlino, A.; Poljanc, K.; Radakovits, T.; Stock, M.; Hug, E.; Georg, P.; Pelak, M.; et al. Organs at risk dose constraints in carbon ion radiotherapy at MedAustron: Translations between LEM and MKM RBE models and preliminary clinical results. Radiother. Oncol. 2022, 175, 73–78. [Google Scholar] [CrossRef] [PubMed]
- Yonekura, Y.; Tsujii, H.; Hopewell, J.; Lopez, P.O.; Cosset, J.M.; Paganetti, H.; Montelius, A.; Schardt, D.; Jones, B.; Nakamura, T. ICRP Publication 127: Radiological Protection in Ion Beam Radiotherapy. Ann. ICRU 2014, 43, 5–113. [Google Scholar] [CrossRef] [PubMed]
- Underwood, T.S.; McNamara, A.L.; Appelt, A.; Haviland, J.S.; Sørensen, B.S.; Troost, E.G. A systematic review of clinical studies on variable proton Relative Biological Effectiveness (RBE). Radiother. Oncol. 2022, 175, 79–92. [Google Scholar] [CrossRef]
- Smith, E.; Winterhalter, C.; Underwood, T.; Aitkenhead, A.; Richardson, J.; Merchant, M.; Kirkby, N.; Mackay, R. A Monte Carlo study of different LET definitions and calculation parameters for proton beam therapy. Biomed. Phys. Eng. Express 2021, 8, 015024. [Google Scholar] [CrossRef]
- Hahn, C.; Ödén, J.; Dasu, A.; Vestergaard, A.; Jensen, M.F.; Sokol, O.; Pardi, C.; Bourhaleb, F.; Leite, A.; de Marzi, L.; et al. Towards harmonizing clinical linear energy transfer (LET) reporting in proton radiotherapy: A European multi-centric study. Acta Oncol. 2022, 61, 206–214. [Google Scholar] [CrossRef]
- Unkelbach, J.; Botas, P.; Giantsoudi, D.; Gorissen, B.L.; Paganetti, H. Reoptimization of Intensity Modulated Proton Therapy Plans Based on Linear Energy Transfer. Int. J. Radiat. Oncol. Biol. Phys. 2016, 96, 1097–1106. [Google Scholar] [CrossRef]
- Bai, X. Linear Energy Transfer (LET)-Guided Optimization Incorporating Biological Effectiveness for Intensity-Modulated Proton Therapy. Ph.D. Thesis, University of Houston, Houston, TX, USA, 2019. [Google Scholar]
- Gu, W.; Ruan, D.; Zou, W.; Dong, L.; Sheng, K. Linear energy transfer weighted beam orientation optimization for intensity-modulated proton therapy. Med. Phys. 2021, 48, 57–70. [Google Scholar] [CrossRef]
- Bai, X.; Lim, G.; Grosshans, D.; Mohan, R.; Cao, W. Robust optimization to reduce the impact of biological effect variation from physical uncertainties in intensity-modulated proton therapy. Phys. Med. Biol. 2019, 64, 025004. [Google Scholar] [CrossRef] [PubMed]
- Bai, X.; Lim, G.; Grosshans, D.; Mohan, R.; Cao, W. A biological effect-guided optimization approach using beam distal-edge avoidance for intensity-modulated proton therapy. Med. Phys. 2020, 47, 3816–3825. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Shan, J.; Anderson, J.D.; Wong, W.W.; Schild, S.E.; Foote, R.L.; Patrick, C.L.; Tinnon, K.B.; Fatyga, M.; Bues, M.; et al. Per-voxel constraints to minimize hot spots in linear energy transfer-guided robust optimization for base of skull head and neck cancer patients in IMPT. Med. Phys. 2022, 49, 632–647. [Google Scholar] [CrossRef] [PubMed]
- ClinicalTrials.gov. Identifier: NCT03750513. LET Optimized IMPT in Treating Pediatric Patients with Ependymoma; ClinicalTrials.gov: Bethesda, MD, USA, 2018.
- ClinicalTrials.gov. Identifier: NCT03690921. LET-IMPT and Standard Chemotherapy in Treating Patients with Newly Diagnosed Stage I-III Anal Canal Squamous Cell Cancer; ClinicalTrials.gov: Bethesda, MD, USA, 2018.
- Harrabi, S.B.; von Nettelbladt, B.; Gudden, C.; Adeberg, S.; Seidensaal, K.; Bauer, J.; Bahn, E.; Mairani, A.; Alber, M.; Haberer, T.; et al. Radiation induced contrast enhancement after proton beam therapy in patients with low grade glioma—How safe are protons? Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2022, 167, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Peeler, C.R.; Mirkovic, D.; Titt, U.; Blanchard, P.; Gunther, J.R.; Mahajan, A.; Mohan, R.; Grosshans, D.R. Clinical evidence of variable proton biological effectiveness in pediatric patients treated for ependymoma. Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2016, 121, 395–401. [Google Scholar] [CrossRef]
- Bertolet, A.; Abolfath, R.; Carlson, D.J.; Lustig, R.A.; Hill-Kayser, C.; Alonso-Basanta, M.; Carabe, A. Correlation of LET with MRI Changes in Brain and Potential Implications for Normal Tissue Complication Probability for Patients with Meningioma Treated with Pencil Beam Scanning Proton Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2022, 112, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Bahn, E.; Bauer, J.; Harrabi, S.; Herfarth, K.; Debus, J.; Alber, M. Late Contrast Enhancing Brain Lesions in Proton-Treated Patients with Low-Grade Glioma: Clinical Evidence for Increased Periventricular Sensitivity and Variable RBE. Int. J. Radiat. Oncol. Biol. Phys. 2020, 107, 571–578. [Google Scholar] [CrossRef] [PubMed]
- Garbacz, M.; Cordoni, F.G.; Durante, M.; Gajewski, J.; Kisielewicz, K.; Krah, N.; Kopec, R.; Olko, P.; Patera, V.; Rinaldi, I.; et al. Study of relationship between dose, LET and the risk of brain necrosis after proton therapy for skull base tumors. Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2021, 163, 143–149. [Google Scholar] [CrossRef]
- Bolsi, A.; Placidi, L.; Pica, A.; Ahlhelm, F.J.; Walser, M.; Lomax, A.J.; Weber, D.C. Pencil beam scanning proton therapy for the treatment of craniopharyngioma complicated with radiation-induced cerebral vasculopathies: A dosimetric and linear energy transfer (LET) evaluation. Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2020, 149, 197–204. [Google Scholar] [CrossRef]
- Engeseth, G.M.; He, R.; Mirkovic, D.; Yepes, P.; Mohamed, A.S.R.; Stieb, S.; Fuller, C.D.; Wu, R.; Zhang, X.; Hysing, L.B.; et al. Mixed Effect Modeling of Dose and Linear Energy Transfer Correlations with Brain Image Changes after Intensity Modulated Proton Therapy for Skull Base Head and Neck Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2021, 111, 684–692. [Google Scholar] [CrossRef]
- Eulitz, J.; Troost, E.G.C.; Klunder, L.; Raschke, F.; Hahn, C.; Schulz, E.; Seidlitz, A.; Thiem, J.; Karpowitz, C.; Hahlbohm, P.; et al. Increased relative biological effectiveness and periventricular radiosensitivity in proton therapy of glioma patients. Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2022, 178, 109422. [Google Scholar] [CrossRef] [PubMed]
- Niemierko, A.; Schuemann, J.; Niyazi, M.; Giantsoudi, D.; Maquilan, G.; Shih, H.A.; Paganetti, H. Brain Necrosis in Adult Patients After Proton Therapy: Is There Evidence for Dependency on Linear Energy Transfer? Int. J. Radiat. Oncol. Biol. Phys. 2021, 109, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Patel, S.H.; Bridhikitti, J.; Wong, W.W.; Halyard, M.Y.; McGee, L.A.; Rwigema, J.C.M.; Schild, S.E.; Vora, S.A.; Liu, T.; et al. Exploratory study of seed spots analysis to characterize dose and linear-energy-transfer effect in adverse event initialization of pencil-beam-scanning proton therapy. Med. Phys. 2022, 49, 6237–6252. [Google Scholar] [CrossRef] [PubMed]
- Sethi, R.; Giantsoudi, D.; Raiford, M.; Malhi, I.; Niemierko, A.; Rapalino, O.; Caruso, P.; Yock, T.I.; Tarbell, N.J.; Paganetti, H. Patterns of failure following proton therapy in medulloblastoma: LET distributions and RBE associations for relapses. Int. J. Radiat. Oncol. Biol. Phys. 2014, 90, S720. [Google Scholar] [CrossRef]
- Wang, C.C.; McNamara, A.L.; Shin, J.; Schuemann, J.; Grassberger, C.; Taghian, A.G.; Jimenez, R.B.; MacDonald, S.M.; Paganetti, H. End-of-Range Radiobiological Effect on Rib Fractures in Patients Receiving Proton Therapy for Breast Cancer. Int. J. Radiat. Oncol. 2020, 107, 449–454. [Google Scholar] [CrossRef]
- Wagenaar, D.; Schuit, E.; van der Schaaf, A.; Langendijk, J.A.; Both, S. Can the mean linear energy transfer of organs be directly related to patient toxicities for current head and neck cancer intensity-modulated proton therapy practice? Radiother. Oncol. J. Eur. Soc. Ther. Radiol. Oncol. 2021, 165, 159–165. [Google Scholar] [CrossRef]
- Indelicato, D.; Flampouri, S.; Rotondo, R.; Bradley, J.; Morris, C.; Aldana, P.; Sandler, E.; Mendenhall, N. Incidence and dosimetric parameters of pediatric brainstem toxicity following proton therapy. Acta Oncol. 2014, 53, 1298–1304. [Google Scholar] [CrossRef]
- Giantsoudi, D.; Sethi, R.V.; Yeap, B.Y.; Eaton, B.R.; Ebb, D.H.; Caruso, P.A.; Rapalino, O.; Chen, Y.L.E.; Adams, J.A.; Yock, T.I.; et al. Incidence of CNS Injury for a Cohort of 111 Patients Treated with Proton Therapy for Medulloblastoma: LET and RBE Associations for Areas of Injury. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 287–296. [Google Scholar] [CrossRef]
- Yang, Y.; Vargas, C.E.; Bhangoo, R.S.; Wong, W.W.; Schild, S.E.; Daniels, T.B.; Keole, S.R.; Rwigema, J.C.M.; Glass, J.L.; Shen, J.; et al. Exploratory Investigation of Dose-Linear Energy Transfer (LET) Volume Histogram (DLVH) for Adverse Events Study in Intensity Modulated Proton Therapy (IMPT). Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 1189–1199. [Google Scholar] [CrossRef]
- Giantsoudi, D.; Adams, J.; MacDonald, S.; Paganetti, H. Can differences in linear energy transfer and thus relative biological effectiveness compromise the dosimetric advantage of intensity-modulated proton therapy as compared to passively scattered proton therapy? Acta Oncol. 2018, 57, 1259–1264. [Google Scholar] [CrossRef]
- Inaniwa, T.; Kanematsu, N.; Noda, K.; Kamada, T. Treatment planning of intensity modulated composite particle therapy with dose and linear energy transfer optimization. Phys. Med. Biol. 2017, 62, 5180–5197. [Google Scholar] [CrossRef]
- Skaarup, M.; Lundemann, M.J.; Darkner, S.; Jørgensen, M.; Marner, L.; Mirkovic, D.; Grosshans, D.; Peeler, C.; Mohan, R.; Vogelius, I.R.; et al. A framework for voxel-based assessment of biological effect after proton radiotherapy in pediatric brain cancer patients using multi-modal imaging. Med. Phys. 2021, 48, 4110–4121. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Q.; Chen, P.; Jain, V.; Reilly, R.M.; Wong, C.S. Early Radiation-Induced Endothelial Cell Loss and Blood-Spinal Cord Barrier Breakdown in the Rat Spinal Cord. Radiat. Res. 2004, 161, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Roberts, K.W.; Wan Chan Tseung, H.S.; Eckel, L.J.; Harmsen, W.S.; Beltran, C.; Laack, N.N. Biologic Dose and Imaging Changes in Pediatric Brain Tumor Patients Receiving Spot Scanning Proton Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2019, 105, 664–673. [Google Scholar] [CrossRef] [PubMed]
- Fossum, C.; Beltran, C.; Whitaker, T.; Ma, D.; Foote, R. Biological Model for Predicting Toxicity in Head and Neck Cancer Patients Receiving Proton Therapy. Int. J. Part. Ther. 2017, 4, 18–25. [Google Scholar] [CrossRef]
- Hahn, C.; Heuchel, L.; Oden, J.; Traneus, E.; Wulff, J.; Plaude, S.; Timmermann, B.; Baumer, C.; Luhr, A. Comparing biological effectiveness guided plan optimization strategies for cranial proton therapy: Potential and challenges. Radiat. Oncol. 2022, 17, 169. [Google Scholar] [CrossRef] [PubMed]
- Toussaint, L.; Indelicato, D.J.; Holgersen, K.S.; Petersen, J.B.B.; Stokkevag, C.H.; Lassen-Ramshad, Y.; Casares-Magaz, O.; Vestergaard, A.; Muren, L.P. Towards proton arc therapy: Physical and biologically equivalent doses with increasing number of beams in pediatric brain irradiation. Acta Oncol. 2019, 58, 1451–1456. [Google Scholar] [CrossRef] [PubMed]
- Traneus, E.; Oden, J. Introducing Proton Track-End Objectives in Intensity Modulated Proton Therapy Optimization to Reduce Linear Energy Transfer and Relative Biological Effectiveness in Critical Structures. Int. J. Radiat. Oncol. Biol. Phys. 2019, 103, 747–757. [Google Scholar] [CrossRef]
- Henjum, H.; Dahle, T.J.; Fjaera, L.F.; Rorvik, E.; Pilskog, S.; Stokkevag, C.H.; Mairani, A.; Ytre-Hauge, K.S. The Organ Sparing Potential of Different Biological Optimization Strategies in Proton Therapy. Adv. Radiat. Oncol. 2021, 6, 100776. [Google Scholar] [CrossRef]
- Fjæra, L.F.; Li, Z.; Ytre-Hauge, K.S.; Muren, L.P.; Indelicato, D.J.; Lassen-Ramshad, Y.; Engeseth, G.M.; Brydoy, M.; Mairani, A.; Flampouri, S.; et al. Linear energy transfer distributions in the brainstem depending on tumour location in intensity-modulated proton therapy of paediatric cancer. Acta Oncol. 2017, 56, 763–768. [Google Scholar] [CrossRef]
- Li, X.; Ding, X.; Zheng, W.; Liu, G.; Janssens, G.; Souris, K.; Barragan-Montero, A.M.; Yan, D.; Stevens, C.; Kabolizadeh, P. Linear Energy Transfer Incorporated Spot-Scanning Proton Arc Therapy Optimization: A Feasibility Study. Front. Oncol. 2021, 11, 698537. [Google Scholar] [CrossRef] [PubMed]
- Shang, H.; Pu, Y.; Chen, Z.; Wang, X.; Yuan, C.; Jin, X.; Liu, C. Impact of Multiple Beams on Plan Quality, Linear Energy Transfer Distribution, and Plan Robustness of Intensity Modulated Proton Therapy for Lung Cancer. ACS Sens. 2021, 6, 408–417. [Google Scholar] [CrossRef] [PubMed]
- Carabe-Fernandez, A.; Bertolet-Reina, A.; Karagounis, I.V.; Huynh, K.; Dale, R.G. Is there a role for arcing techniques in proton therapy? Br. J. Radiol. 2019, 93, 20190469. [Google Scholar] [CrossRef]
- Bertolet, A.; Carabe, A. Proton monoenergetic arc therapy (PMAT) to enhance LETd within the target. Phys. Med. Biol. 2020, 65, 165006. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, G.; Janssens, G.; De Wilde, O.; Bossier, V.; Lerot, X.; Pouppez, A.; Yan, D.; Stevens, C.; Kabolizadeh, P.; et al. The first prototype of spot-scanning proton arc treatment delivery. Radiother. Oncol. 2019, 137, 130–136. [Google Scholar] [CrossRef]
- Giantsoudi, D.; Adams, J.; MacDonald, S.M.; Paganetti, H. Proton Treatment Techniques for Posterior Fossa Tumors: Consequences for Linear Energy Transfer and Dose-Volume Parameters for the Brainstem and Organs at Risk. Int. J. Radiat. Oncol. Biol. Phys. 2017, 97, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Fager, M.; Toma-Dasu, I.; Kirk, M.; Dolney, D.; Diffenderfer, E.S.; Vapiwala, N.; Carabe, A. Linear energy transfer painting with proton therapy: A means of reducing radiation doses with equivalent clinical effectiveness. Int. J. Radiat. Oncol. Biol. Phys. 2015, 91, 1057–1064. [Google Scholar] [CrossRef]
- Malinen, E.; Sovik, A. Dose or ‘LET’ painting—What is optimal in particle therapy of hypoxic tumors? Acta Oncol. 2015, 54, 1614–1622. [Google Scholar] [CrossRef]
- Zeng, C.; Giantsoudi, D.; Grassberger, C.; Goldberg, S.; Niemierko, A.; Paganetti, H.; Efstathiou, J.A.; Trofimov, A. Maximizing the biological effect of proton dose delivered with scanned beams via inhomogeneous daily dose distributions. Med. Phys. 2013, 40, 051708. [Google Scholar] [CrossRef]
- Bassler, N.; Jäkel, O.; Søndergaard, C.S.; Petersen, J.B. Dose-and LET-painting with particle therapy. Acta Oncol. 2010, 49, 1170–1176. [Google Scholar] [CrossRef]
- Koong, A.C.; Mehta, V.K.; Le, Q.T.; Fisher, G.A.; Terris, D.J.; Brown, J.; Bastidas, A.J.; Vierra, M. Pancreatic tumors show high levels of hypoxia. Int. J. Radiat. Oncol. 2000, 48, 919–922. [Google Scholar] [CrossRef] [PubMed]
- Zarepisheh, M.; Hong, L.; Zhou, Y.; Huang, Q.; Yang, J.; Jhanwar, G.; Pham, H.D.; Dursun, P.; Zhang, P.; Hunt, M.A.; et al. Automated and Clinically Optimal Treatment Planning for Cancer Radiotherapy. INFORMS J. Appl. Anal. 2022, 52, 69–89. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Lin, Y.; Li, H.; Rotondo, R.; Gao, H. An iterative convex relaxation method for proton LET optimization. Phys. Med. Biol. 2023, 68, 055002. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Khabazian, A.; Yepes, P.P.; Lim, G.; Poenisch, F.; Grosshans, D.R.; Mohan, R. Linear energy transfer incorporated intensity modulated proton therapy optimization. Phys. Med. Biol. 2017, 63, 015013. [Google Scholar] [CrossRef]
- Chen, M.; Cao, W.; Yepes, P.; Guan, F.; Poenisch, F.; Xu, C.; Chen, J.; Li, Y.; Vazquez, I.; Yang, M.; et al. Impact of dose calculation accuracy on inverse linear energy transfer optimization for intensity-modulated proton therapy. Precis. Radiat. Oncol. 2022, 7, 36–44. [Google Scholar] [CrossRef]
- Liu, C.; Patel, S.H.; Shan, J.; Schild, S.E.; Vargas, C.E.; Wong, W.W.; Ding, X.; Bues, M.; Liu, W. Robust Optimization for Intensity Modulated Proton Therapy to Redistribute High Linear Energy Transfer from Nearby Critical Organs to Tumors in Head and Neck Cancer. Int. J. Radiat. Oncol. Biol. Phys. 2020, 107, 181–193. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Vaniqui, A.; Vaassen, F.; Di Perri, D.; Eekers, D.; Compter, I.; Rinaldi, I.; van Elmpt, W.; Unipan, M. Linear Energy Transfer and Relative Biological Effectiveness Investigation of Various Structures for a Cohort of Proton Patients with Brain Tumors. Adv. Radiat. Oncol. 2023, 8, 101128. [Google Scholar] [CrossRef]
- Hahn, C.; Eulitz, J.; Peters, N.; Wohlfahrt, P.; Enghardt, W.; Richter, C.; Luhr, A. Impact of range uncertainty on clinical distributions of linear energy transfer and biological effectiveness in proton therapy. Med. Phys. 2020, 47, 6151–6162. [Google Scholar] [CrossRef]
- Rana, S.; Traneus, E.; Jackson, M.; Tran, L.; Rosenfeld, A.B. Quantitative analysis of dose-averaged linear energy transfer (LETd ) robustness in pencil beam scanning proton lung plans. Med. Phys. 2022, 49, 3444–3456. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McIntyre, M.; Wilson, P.; Gorayski, P.; Bezak, E. A Systematic Review of LET-Guided Treatment Plan Optimisation in Proton Therapy: Identifying the Current State and Future Needs. Cancers 2023, 15, 4268. https://doi.org/10.3390/cancers15174268
McIntyre M, Wilson P, Gorayski P, Bezak E. A Systematic Review of LET-Guided Treatment Plan Optimisation in Proton Therapy: Identifying the Current State and Future Needs. Cancers. 2023; 15(17):4268. https://doi.org/10.3390/cancers15174268
Chicago/Turabian StyleMcIntyre, Melissa, Puthenparampil Wilson, Peter Gorayski, and Eva Bezak. 2023. "A Systematic Review of LET-Guided Treatment Plan Optimisation in Proton Therapy: Identifying the Current State and Future Needs" Cancers 15, no. 17: 4268. https://doi.org/10.3390/cancers15174268
APA StyleMcIntyre, M., Wilson, P., Gorayski, P., & Bezak, E. (2023). A Systematic Review of LET-Guided Treatment Plan Optimisation in Proton Therapy: Identifying the Current State and Future Needs. Cancers, 15(17), 4268. https://doi.org/10.3390/cancers15174268






