Brain Re-Irradiation Robustly Accounting for Previously Delivered Dose
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Cases
2.2. Treatment Planning Strategy and Cumulative Dose Evaluation
2.3. Image Registration
2.4. STRIDeR Planning Pathway
- (Deformable) image registration with organ-specific quality assessment;
- Mapping of origRT dose distribution to reRT dataset;
- Radiobiological optimisation in EQD2, voxel-by-voxel, using origRT dose as background dose;
- Dose summation in EQD2 for plan evaluation;
- Pathway options include number of fractions, α/β per OAR and recovery per OAR.
2.5. Manual Planning Pathway
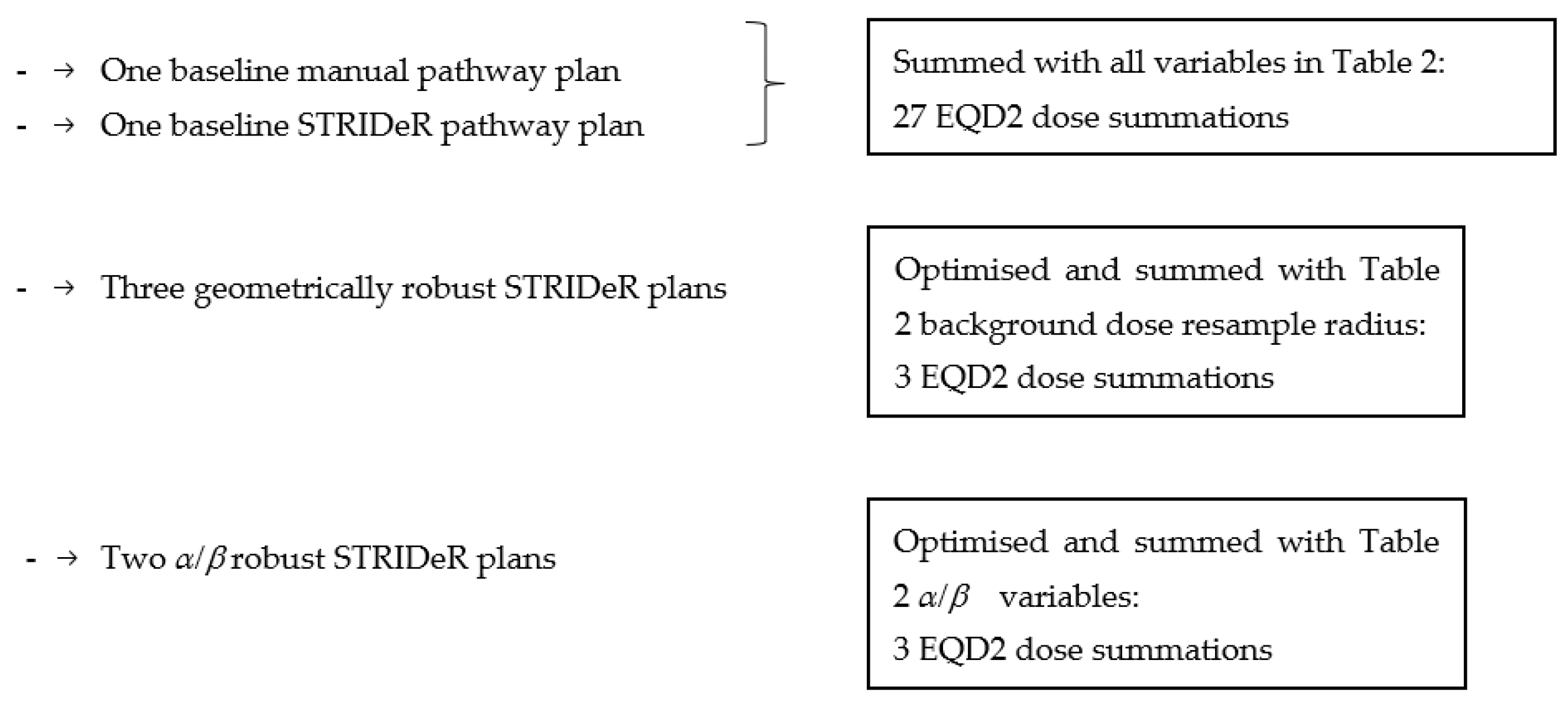
2.6. Robustness Evaluation (Re-Summed Plans)
2.7. Robust Optimisation
2.8. Data Analysis
3. Results
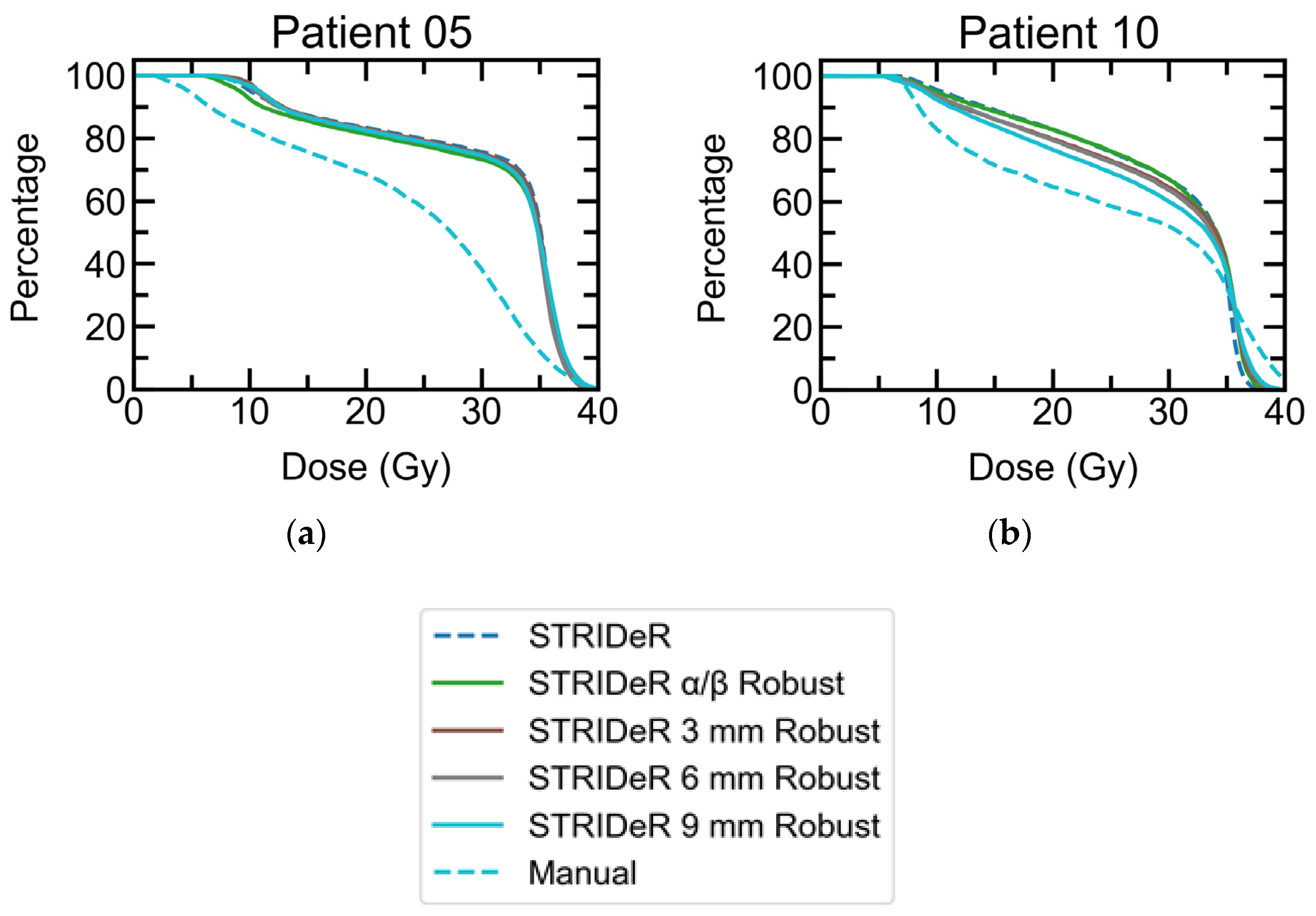
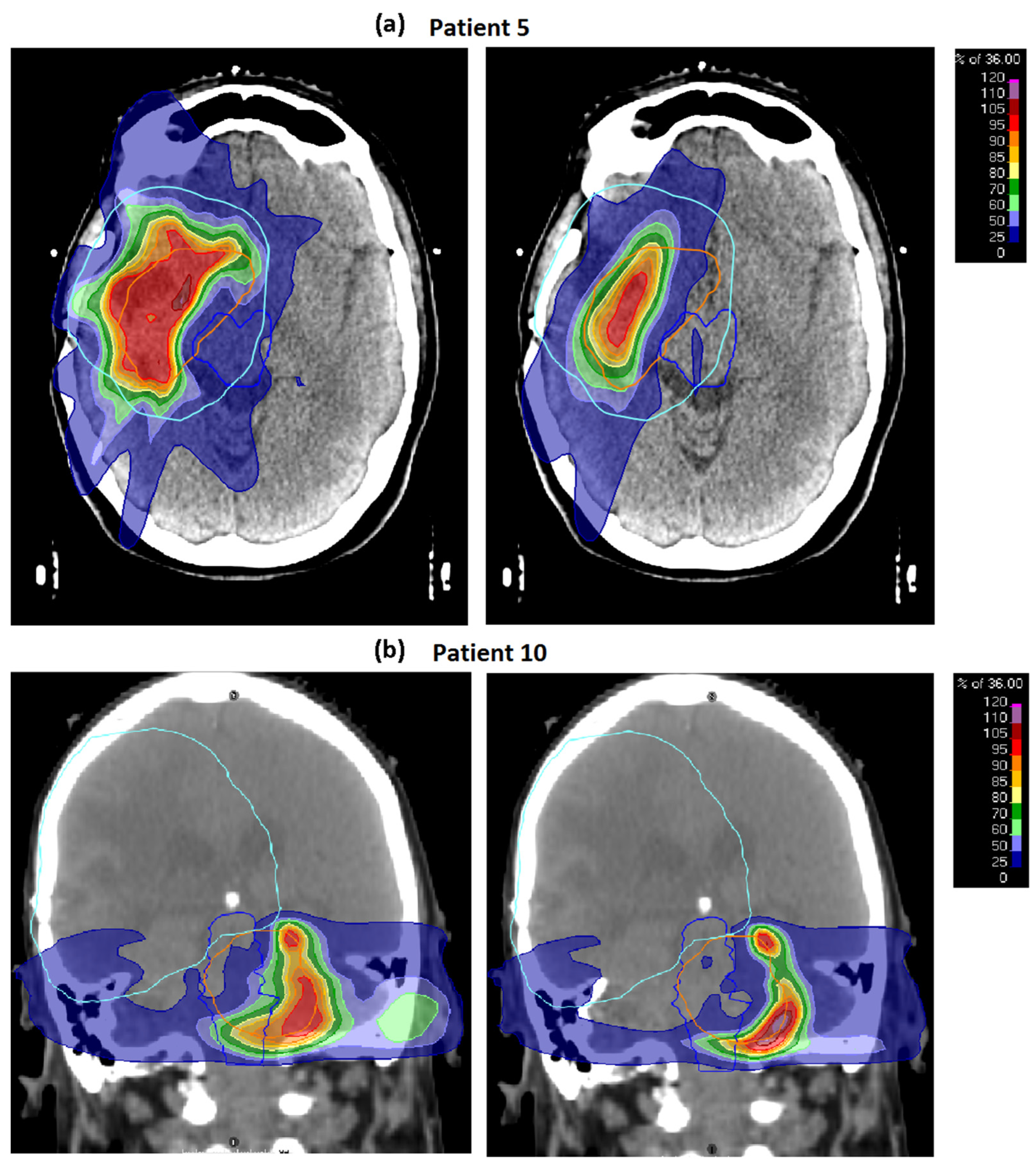
3.1. Baseline Plans
3.2. Robustness
3.2.1. Geometric Robustness
3.2.2. Fractionation Sensitivity
3.2.3. LQ Model Robustness
3.3. Weighting Factor
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Murray, L.J.; Lilley, J.; Hawkins, M.A.; Henry, A.M.; Dickinson, P.; Sebag-Montefiore, D. Pelvic re-irradiation using stereotactic ablative radiotherapy (SABR): A systematic review. Radiother. Oncol. 2017, 125, 213–222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barney, C.; Shukla, G.; Bhamidipati, D.; Palmer, J.D. Re-irradiation for recurrent glioblastoma multiforme. Chin. Clin. Oncol. 2017, 6, 36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slevin, F.; Aitken, K.; Alongi, F.; Arcangeli, S.; Chadwick, E.; Chang, A.R.; Cheung, P.; Crane, C.; Guckenberger, M.; Jereczek-Fossa, B.A.; et al. An international Delphi consensus for pelvic stereotactic ablative radiotherapy re-irradiation. Radiother. Oncol. 2021, 164, 104–114. [Google Scholar] [CrossRef] [PubMed]
- Rulach, R.; Ball, D.; Chua, K.L.; Dahele, M.; De Ruysscher, D.; Franks, K.; Gomez, D.; Guckenberg, M.; Hanna, G.G.; Louie, A.V.; et al. An international expert survey on the indications and practice of radical thoracic reirradiation for non-small cell lung cancer. Adv. Radiat. Oncol. 2021, 6, 100653. [Google Scholar] [CrossRef] [PubMed]
- Jereczek-Fossa, B.A.; Marvaso, G.; Zaffaroni, M.; Gugliandolo, S.G.; Zerini, D.; Corso, F.; Gandini, S.; Along, F.; Bossi, A.; Cornford, P.; et al. Salvage stereotactic body radiotherapy (SBRT) for intraprostatic relapse after prostate cancer radiotherapy: An ESTRO ACROP Delphi consensus. Cancer Treat. Rev. 2021, 98, 102206. [Google Scholar] [CrossRef] [PubMed]
- Ng, W.T.; Soong, Y.L.; Ahn, Y.C.; AlHussain, H.; Choi, H.C.; Corry, J.; Gregoire, V.; Harrington, K.J.; Hu, C.S.; Jensen, K.; et al. International recommendations on re-irradiation by intensity-modulated radiotherapy for locally recurrent nasopharyngeal carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 682–695. [Google Scholar] [CrossRef]
- Richter, A.; Weick, S.; Krieger, T.; Exner, F.; Kellner, S.; Polat, B.; Flentje, M. Evaluation of a software module for adaptive treatment planning and re-irradiation. Radiat. Oncol. 2017, 12, 205. [Google Scholar] [CrossRef] [Green Version]
- Andratschke, N.; Willmann, J.; Appelt, A.L.; Alyamani, N.; Balermpas, P.; Baumert, B.G.; Hurkmans, C.; Høyer, M.; Langendijk, J.A.; Kaidar-Person, O.; et al. European society for radiotherapy and oncology and european organisation for research and treatment of cancer consensus on re-irradiation: Definition, reporting, and clinical decision making. Lancet Oncol. 2022, 23, e469–e478. [Google Scholar] [CrossRef]
- Price, R.A.; Jin, L.; Meyer, J.; Chen, L.; Lin, T.; Eldib, A.; Chen, X.; Liu, J.; Veltchev, I.; Wang, L.; et al. Practical clinical implementation of the special physics consultation process in the re-irradiation environment. Adv. Radiat. Oncol. 2021, 6, 100594. [Google Scholar] [CrossRef]
- McVicar, N.; Thomas, S.; Liu, M.; Carolan, H.; Bergman, A. Re-irradiation volumetric modulated arc therapy optimization based on cumulative biologically effective dose objectives. J. Appl. Clin. Med. Phys. 2018, 19, 341–345. [Google Scholar] [CrossRef]
- Nix, M.; Gregory, S.; Aldred, M.; Aspin, L.; Lilley, J.; Al-Qaisieh, B.; Uzan, J.; Svensson, S.; Dickinson, P.; Appelt, A.L.; et al. Dose summation and image registration strategies for radiobiologically and anatomically corrected dose accumulation in pelvic re-irradiation. Acta Oncol. 2022, 61, 64–72. [Google Scholar] [CrossRef]
- Murray, L.; Gregory, S.; Nix, M.; Aldred, M.; Aspin, L.; Uzan, J.; Lilley, J.; Al-Qaisieh, B.; Appelt, A. PV-0427 improving cumulative dose evaluation for re-irradiation: First results from the STRIDeR project. Radiother. Oncol. 2019, 133, S223–S224. [Google Scholar] [CrossRef]
- Murray, L.; Thompson, C.; Pagett, C.; Lilley, J.; Al-Qaisieh, B.; Svensson, S.; Eriksson, K.; Nix, M.; Aldred, M.; Aspin, L.; et al. Treatment plan optimisation for reirradiation. Radiother. Oncol. 2023, 182, 109545. [Google Scholar] [CrossRef]
- Rigaud, B.; Simon, A.; Castelli, J.; Lafond, C.; Acosta, O.; Haigron, P.; Cazoulat, G.; de Crevoisier, R. Deformable image registration for radiation therapy: Principle, methods, applications and evaluation. Acta Oncol. 2019, 58, 1225–1237. [Google Scholar] [CrossRef] [PubMed]
- Speckter, H.; Santana, J.; Miches, I.; Hernandez, G.; Bido, J.; Rivera, D.; Suazo, L.; Valenzuela, S.; Garcia, J.; Stoeter, P. Assessment of the alpha/beta ratio of the optic pathway to adjust hypofractionated stereotactic radiosurgery regimens for perioptic lesions. J. Radiat. Oncol. 2019, 8, 279–289. [Google Scholar] [CrossRef]
- Nieder, C.; Milas, L.; Ang, K.K. Tissue tolerance to reirradiation. Semin. Radiat. Oncol. 2000, 10, 200–209. [Google Scholar] [CrossRef]
- Guerrero, M.; Carlone, M. Mechanistic formulation of a lineal-quadratic-linear (LQL) model: Split-dose experiments and exponentially decaying sources. Med. Phys. 2010, 37, 4173–4181. [Google Scholar] [CrossRef]
- Guerrero, M.; Li, X.A. Extending the linear–quadratic model for large fraction doses pertinent to stereotactic radiotherapy. Phys. Med. Biol. 2004, 49, 4825–4835. [Google Scholar] [CrossRef]
- Pagett, C.J.H.; Lilley, J.; Lindsay, R.; Short, S.; Murray, L. Optimising tumour coverage and organ at risk sparing for hypofractionated re-irradiation in glioblastoma. Phys. Imaging Radiat. Oncol. 2022, 21, 84–89. [Google Scholar] [CrossRef]
- Mayer, R.; Sminia, P. Reirradiation tolerance of the human brain. Int. J. Radiat. Oncol. Biol. Phys. 2008, 70, 1350–1360. [Google Scholar] [CrossRef]
- Lee, J.; Dean, C.; Patel, R.; Webster, G.; Eaton, D.J. Multi-center evaluation of dose conformity in stereotactic body radiotherapy. Phys. Imaging Radiat. Oncol. 2019, 11, 41–46. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weistrand, O.; Svensson, S. The ANACONDA algorithm for deformable image registration in radiotherapy. Med. Phys. 2015, 42, 40–53. [Google Scholar] [CrossRef]
- Emami, B. Tolerance of normal tissue to therapeutic radiation. Rep. Radiother. Oncol. 2013, 1, 35–38. [Google Scholar]
- Joiner, M.; van der Kogel, A. Basic Clinical Radiobiology, 5th ed.; CRC Press: Boca Raton, FL, USA, 2019; p. 360. [Google Scholar]
- Brock, K.K.; Mutic, S.; McNutt, T.R.; Li, H.; Kessler, M.L. Use of image registration and fusion algorithms and techniques in radiotherapy: Report of the AAPM radiation therapy committee task group no. 132. Med. Phys. 2017, 44, e43–e76. [Google Scholar] [CrossRef] [Green Version]
- Boman, E.; Kapanen, M.; Pickup, L.; Lahtela, S.L. Importance of deformable image registration and biological dose summation in planning of radiotherapy retreatments. Med. Dosim. 2017, 42, 296–303. [Google Scholar] [CrossRef]
- Kumar, K.; Gulal, O.; Franich, R.D.; Kron, T.; Yeo, A.U. A validation framework to assess performance of commercial deformable image registration in lung radiotherapy. Phys. Med. 2021, 87, 106–114. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Shi, C.; Long, T.; Xu, X.G. The impact of robustness of deformable image registration on contour propagation and dose accumulation for head and neck adaptive radiotherapy. J. Appl. Clin. Med. Phys. 2018, 19, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Kuo, L.; Hu, Y.C.; Ballangrud, A.; Mechalakos, J.; Deasy, J.; Zhang, P.; Cervino, L. Estimating cumulative radiation dose to organs at risk for glioblastoma multiforme cases via a radiotherapy dose accumulation routine. Int. J. Radiat. Oncol. Biol. Phys. 2021, 111, S54–S55. [Google Scholar] [CrossRef]
| Structure | Metric | Cumulative Constraint EQD2 |
|---|---|---|
| Brainstem PRV | D0.1cc (Gy) | 51.3 |
| Dmean (Gy) | 48.5 | |
| Orbit | D0.1cc (Gy) | 39.4 |
| Optic Chiasm PRV | D0.1cc (Gy) | 51.3 |
| Optic Nerves PRV | D0.1cc (Gy) | 51.3 |
| re-RT PTV | D95% (Gy) | |
| D98% (Gy) | ||
| Dmean (Gy) | ||
| PxDose Spillage [21] | =Vol(100%)/PTV V100% | |
| Modified gradient index [21] | =Vol(50%)/PTV V100% |
| Values | ||||
|---|---|---|---|---|
| Robustness Test | Variable | Min | Mid | Max |
| Geometric | Sampling Radius, r (mm) | 3 | 6 | 9 |
| Fraction Sensitivity | α/β (Gy) | 1 | 2 | 5 |
| LQL | δ | 0 | 0.1 | 0.2 |
| Structure | Metric | STRIDeR Pathway Median (IQR) | Manual Pathway Median (IQR) | In-Patient Difference | Wilcoxon Signed Rank | ||
|---|---|---|---|---|---|---|---|
| DIR Doses | DIR-RIR Doses | DIR Doses | DIR-RIR Doses | Strider-Manual Median (IQR) | p-Value | ||
| Brainstem PRV3 | D0.1cc (Gy) | 44.5 (36.0−49.3) | 0.0 (−0.9–0.3) | 44.1 (34.1–47.4) | 0.0 (−0.7–0.1) | 0.7 (0.0–2.4) | 0.05 |
| Dmean (Gy) | 16.2 (9.5–33.0) | 0.0 (−0.2–0.4) | 16.7 (9.4–31.1) | 0.0 (−0.1–0.4) | 0.1 (0.0–0.6) | 0.08 | |
| Left Eye | D0.1cc (Gy) | 3.0 (1.8–5.7) | 0.0 (0.0–0.0) | 2.6 (1.8–5.4) | 0.0 (0.0–0.0) | 0.1 (0.0–0.2) | 0.14 |
| Right Eye | D0.1cc (Gy) | 5.2 (1.7–15.5) | 0.0 (−0.3–0.0) | 5.4 (1.7–11.7) | 0.0 (−0.3–0.0) | 0.0 (0.0–0.3) | 0.08 |
| Optic Chiasm PRV3 | D0.1cc (Gy) | 39.4 (17.9–45.5) | 0.0 (−0.2–0.3) | 39.4 (17.9–44.9) | 0.0 (−0.2–0.1) | 0.0 (−0.2–0.1) | 0.62 |
| Left Optic Nerve PRV3 | D0.1cc (Gy) | 27.4 (3.4–38.3) | 0.1 (0.0–0.2) | 27.4 (3.3–37.8) | 0.1 (0.0–0.1) | 0.0 (−0.1–0.1) | 0.46 |
| Right Optic Nerve PRV3 | D0.1cc (Gy) | 19.2 (7.2–40.7) | 0.0 (−0.1–0.0) | 19.7 (5.7–40.6) | 0.0 (0.0–0.0) | 0.0 (0.0–0.1) | 0.28 |
| Brain-PTV | Dmean (Gy) | 24.0 (22.7–25.5) | 0.0 (−0.1–0.1) | 24.1 (22.6–25.7) | 0.0 (−0.1–0.1) | 0.0 (−0.1–0.2) | 0.46 |
| D10% (Gy) | 51.2 (48.4–55.0) | −0.1 (−0.3−0.1) | 50.5 (48.1–52.4) | −0.1 (−0.4−0.1) | 0.0 (−0.2–0.2) | 0.42 | |
| PTV PTV PTV | D95% (Gy) | 34.9 (34.6–34.9) | NA | 34.9 (34.2–34.9) | NA | 0.1 (0.0–0.4) | 0.12 |
| D98% (Gy) | 34.5 (33.2–34.6) | NA | 34.4 (32.0–34.5) | NA | 0.1 (0.0–0.9) | 0.01 | |
| Dmean (Gy) | 35.5 (35.5–35.5) | NA | 35.5 (35.5–35.5) | NA | 0.0 (0.0–0.1) | 0.12 | |
| PxDose Spillage [21] | Vol(100%)/VPTV(100%) | 1.11 (1.07–1.15) | NA | 1.09 (1.06–1.11) | NA | 0.0 (0.0–0.0) | 0.22 |
| Modified gradient index [21] | Vol(50%)/Vol(PTV) | 3.5 (3.2–4.8) | NA | 3.6 (3.3–5.1) | NA | −0.1 (−0.2–0.0) | 0.88 |
| Plan Type | Test Parameters | Number of Clinical Goal Failures | Total Dose Exceeding Constraints (Gy) | |||
|---|---|---|---|---|---|---|
| Brain Stem | Optic Nerves | Optic Chiasm | Eyes | |||
| Baseline Plans | ||||||
| Manual pathway | α/β = 2 Gy Sample Radius = 0 mm | 0 | 0 | 1 | 0 | 0.2 |
| STRIDeR | α/β = 2 Gy Sample Radius = 0 mm | 1 | 0 | 0 | 0 | 0.1 |
| Geometric Robustness Test | ||||||
| Manual (re-summation) | Sample Radius = 3 mm | 0 | 0 | 1 | 0 | 1.5 |
| Sample Radius = 6 mm | 0 | 0 | 1 | 0 | 2.3 | |
| Sample Radius = 9 mm | 3 | 0 | 1 | 1 | 8.9 | |
| STRIDeR (re-summation) | Sample Radius = 3 mm | 2 | 0 | 1 | 0 | 2.6 |
| Sample Radius = 6 mm | 2 | 0 | 1 | 0 | 5.6 | |
| Sample Radius = 9 mm | 4 | 0 | 1 | 2 | 21.6 | |
| STRIDeR robust (optimisation **) | Sample Radius = 3 mm | 0 | 0 | 0 | 0 | 0.0 |
| Sample Radius = 6 mm | 1 | 0 | 0 | 0 | 0.3 | |
| Sample Radius = 9 mm | 2 | 0 | 0 | 0 | 3.9 | |
| LQ Model Robustness Test | ||||||
| Manual (re-summation) | α/β = 1 Gy | 0 | 0 | 1 | 0 | 0.9 |
| α/β = 5 Gy | 1 | 1 | 1 | 0 | 5.7 | |
| δ = 0.1 (LQL model) | 0 | 1 | 1 | 0 | 2.7 | |
| δ = 0.2 (LQL model) | 1 | 0 | 1 | 0 | 2.9 | |
| STRIDeR (re-summation) | α/β = 1 Gy | 1 | 0 | 0 | 0 | 0.9 |
| α/β = 5 Gy | 2 | 1 | 0 | 0 | 3.3 | |
| δ = 0.1 (LQL model) | 1 | 0 | 0 | 0 | 0.4 | |
| δ = 0.2 (LQL model) | 1 | 1 | 0 | 0 | 0.8 | |
| STRIDeR robust (optimisation **) | α/β = 1 Gy | 0 | 0 | 0 | 0 | 0.0 |
| α/β = 2 Gy | 0 | 0 | 0 | 0 | 0.0 | |
| α/β = 5 Gy | 1 | 0 | 0 | 0 | 0.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thompson, C.; Pagett, C.; Lilley, J.; Svensson, S.; Eriksson, K.; Bokrantz, R.; Ödén, J.; Nix, M.; Murray, L.; Appelt, A. Brain Re-Irradiation Robustly Accounting for Previously Delivered Dose. Cancers 2023, 15, 3831. https://doi.org/10.3390/cancers15153831
Thompson C, Pagett C, Lilley J, Svensson S, Eriksson K, Bokrantz R, Ödén J, Nix M, Murray L, Appelt A. Brain Re-Irradiation Robustly Accounting for Previously Delivered Dose. Cancers. 2023; 15(15):3831. https://doi.org/10.3390/cancers15153831
Chicago/Turabian StyleThompson, Christopher, Christopher Pagett, John Lilley, Stina Svensson, Kjell Eriksson, Rasmus Bokrantz, Jakob Ödén, Michael Nix, Louise Murray, and Ane Appelt. 2023. "Brain Re-Irradiation Robustly Accounting for Previously Delivered Dose" Cancers 15, no. 15: 3831. https://doi.org/10.3390/cancers15153831
APA StyleThompson, C., Pagett, C., Lilley, J., Svensson, S., Eriksson, K., Bokrantz, R., Ödén, J., Nix, M., Murray, L., & Appelt, A. (2023). Brain Re-Irradiation Robustly Accounting for Previously Delivered Dose. Cancers, 15(15), 3831. https://doi.org/10.3390/cancers15153831





