Dosiomics-Based Prediction of Radiation-Induced Valvulopathy after Childhood Cancer
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Population and Identification of VHD Events
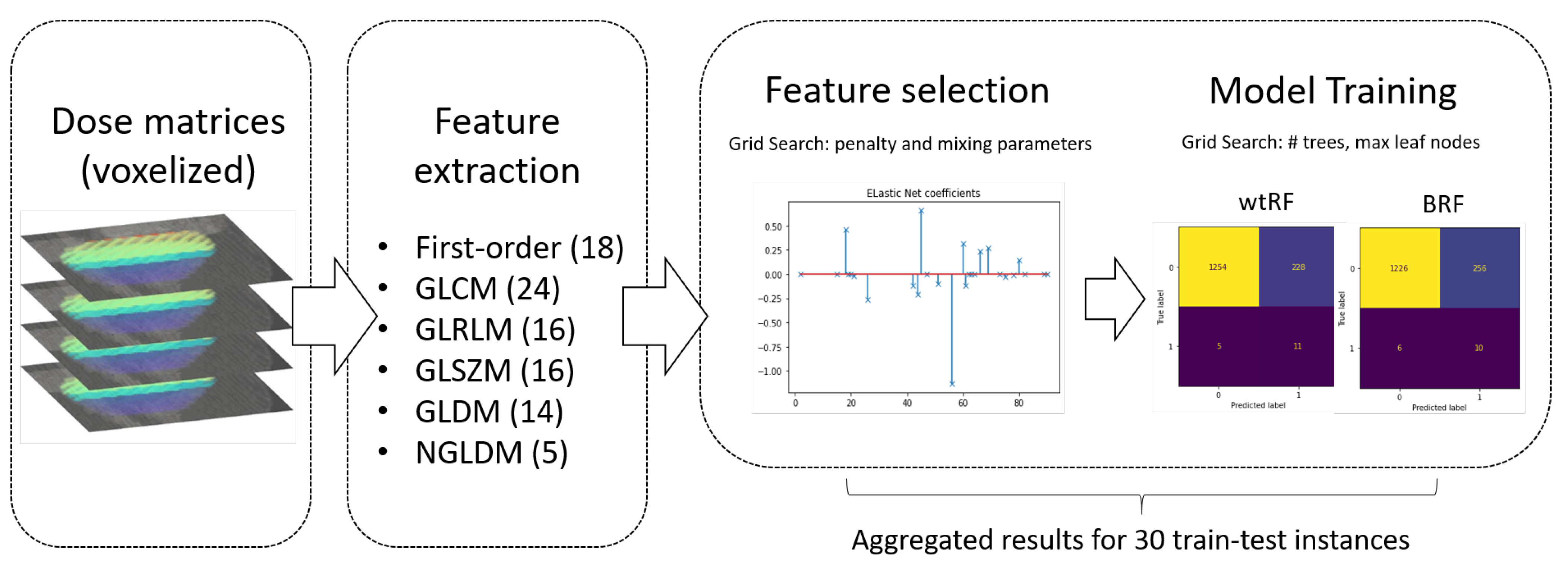
2.2. Voxelised Dosimetric Data: Dosimetry Factors and Dosiomics Features
- Eighteen first-order statistics of the heart dose;
- Twenty-four Gray Level Co-occurrence Matrix (GLCM) features;
- Sixteen Gray Level Run Length Matrix (GLRLM) features;
- Sixteen Gray Level Size Zone Matrix (GLSZM) features;
- Fourteen Gray Level Dependence Matrix (GLDM) features;
- Five Neighboring Gray Tone Difference Matrix (NGLDM) features.
2.3. Imbalanced Classification and Feature Selection
2.4. Modeling Workflow
2.5. Dosiomics Signature
2.6. Model Evaluation
2.7. Cohort Partition Based on Heart Dose Heterogeneity
3. Results
3.1. Descriptive Analysis
3.2. Dosiomics versus Mean Heart Dose
3.3. Models Adjusted on Clinical Variables
3.4. Sensitivity Analysis According to the Type of First Childhood Cancer
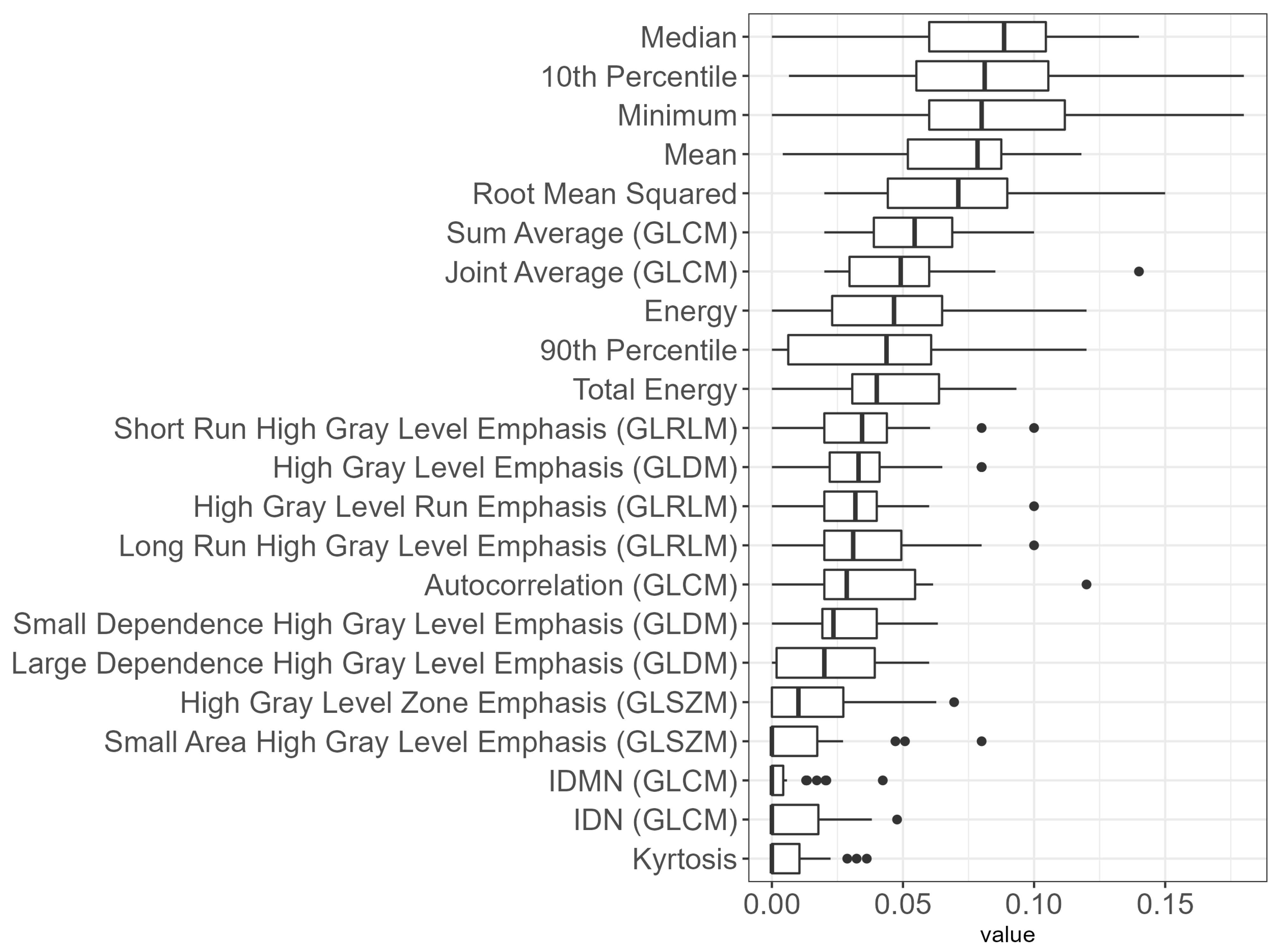
3.5. Dosiomics Signature
- First order statistics: Tenth percentile, ninetieth percentile, energy, kurtosis, mean heart dose, median heart dose, minimum heart dose, root mean squared, total energy;
- GLCM: Autocorrelation, IDMN, IDN, joint average, sum average;
- GLDM: High gray level emphasis, large dependence high gray level emphasis, small dependence high gray level emphasis;
- GLRLM: High gray level run emphasis, long run high gray level emphasis, short run high gray level emphasis;
- GLSZM: Gigh gray level zone emphasis, small area high gray level emphasis.
4. Discussion
4.1. The Role of Heterogeneity of the Heart Dose in Late Valvular Heart Disease
4.2. Model Choice and Performance
4.3. The Dosiomics Signature
4.4. Limitations
4.5. Perspectives
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VHD | Valvular Heart Disease |
| CC | Childhood Cancer |
| FCCSS | French Childhood Cancer Survivors Study |
| wtRF | weighted Random Forest |
| BRF | Balanced Random Forest |
| MHD | Mean Heart Dose |
Appendix A
| Feature Class | First-Order Statistics | Gray Level Co-Occurrence Matrix (GLCM) | Gray Level Run Length Matrix (GLRLM) | Gray Level Size Zone Matrix (GLSZM) | Gray Level Dependence Matrix (GLDM) | Neighbouring Gray Tone Difference Matrix (NGLDM) |
|---|---|---|---|---|---|---|
| Number of features | 18 | 24 | 16 | 16 | 14 | 5 |
| mean heart dose (MHD) | autocorrelation | gray level non-uniformity | gray level non-uniformity | dependence entropy | busyness | |
| median | cluster prominence | non-uniformity normalized | gray level non-uniformity normalized | dependence non-uniformity | coarseness | |
| minimum | cluster shade | gray level variance | gray level variance | dependence non-uniformity normalized | complexity | |
| maximum | cluster tendency | high gray level run emphasis | high gray level zone emphasis | dependence variance | contrast | |
| variance | contrast | long run emphasis | large area emphasis | gray level non-uniformity | strength | |
| skewness | correlation | long run high gray level emphasis | large area high gray level emphasis | gray level variance | ||
| kurtosis | difference average | long run low gray level emphasis | large area low gray level emphasis | high gray level emphasis | ||
| entropy | difference entropy | low gray level run emphasis | low gray level zone emphasis | large dependence emphasis | ||
| uniformity | difference variance | run entropy | size zone non-uniformity | large dependence high gray level emphasis | ||
| 10th percentile | Inverse Difference (ID) | run length non-uniformity | size zone non-uniformity normalized | large dependence low gray level emphasis | ||
| 90th percentile | Inverse Difference Moment (IDM) | run length non-uniformity normalized | small area emphasis | low gray level emphasis | ||
| energy | Inverse Difference Moment Normalized (IDMN) | run percentage | small area high gray level emphasis | small dependence emphasis | ||
| total energy | Inverse Difference Normalized (IDN) | run variance | small area low gray level emphasis | small dependence high gray level emphasis | ||
| range | Informational Measure of Correlation 1 (IMC1) | short run emphasis | zone entropy | small dependence low gray level emphasis | ||
| interquartile range | Informational Measure of Correlation 2 (IMC2) | short run high gray level emphasis | zone 6 percentage | |||
| mean absolute deviation | inverse variance | short run low gray level emphasis | zone variance | |||
| robust mean absolute deviation | joint average | |||||
| root mean squared | joint energy | |||||
| joint entropy | ||||||
| Maximal Correlation Coefficient (MCC) | ||||||
| maximum probability | ||||||
| sum average | ||||||
| sum entropy | ||||||
| sum squares |
| Heart Radiation Measure | Balanced Accuracy | AUC ROC | Sensitivity (Recall) | Specificity | |||
|---|---|---|---|---|---|---|---|
| FCCSS | wtRF | Mean heart dose | 0.75 ± 0.041 | 0.8 ± 0.044 | 0.62 ± 0.091 | 0.89 ± 0.027 | |
| Dosiomics features | 0.74 ± 0.039 | 0.77 ± 0.051 | 0.6 ± 0.077 | 0.88 ± 0.012 | |||
| p-values | 0.208 | 0.028 | 0.403 | 0.141 | |||
| BRF | Mean heart dose | 0.76 ± 0.045 | 0.8 ± 0.054 | 0.68 ± 0.097 | 0.84 ± 0.029 | ||
| Dosiomics features | 0.74 ± 0.04 | 0.78 ± 0.054 | 0.65 ± 0.073 | 0.82 ± 0.023 | 4 | ||
| p-values | 0.057 | 0.126 | 0.169 | 0.092 | |||
| Uniformity < 1 | wtRF | Mean heart dose | 0.81 ± 0.054 | 0.87 ± 0.048 | 0.74 ± 0.108 | 0.87 ± 0.028 | |
| Dosiomics features | 0.78 ± 0.063 | 0.86 ± 0.057 | 0.73 ± 0.134 | 0.83 ± 0.028 | |||
| p-value | 0.117 | 0.594 | 0.666 | <0.001 | |||
| BRF | Mean heart dose | 0.82 ± 0.053 | 0.88 ± 0.046 | 0.82 ± 0.106 | 0.82 ± 0.023 | ||
| Dosiomics features | 0.8 ± 0.062 | 0.86 ± 0.057 | 0.8 ± 0.123 | 0.8 ± 0.019 | 8 | ||
| p-values | 0.171 | 0.219 | 0.526 | <0.001 | |||
| Uniformity | wtRF | Mean heart dose | 0.76 ± 0.077 | 0.85 ± 0.052 | 0.69 ± 0.155 | 0.83 ± 0.025 | |
| Dosiomics features | 0.77 ± 0.061 | 0.85 ± 0.057 | 0.71 ± 0.145 | 0.83 ± 0.031 | |||
| p-values | 0.718 | 0.086 | 0.811 | 0.482 | |||
| BRF | Mean heart dose | 0.77 ± 0.059 | 0.84 ± 0.057 | 0.76 ± 0.123 | 0.78 ± 0.026 | ||
| Dosiomics features | 0.78 ± 0.049 | 0.86 ± 0.05 | 0.76 ± 0.113 | 0.8 ± 0.032 | 12 | ||
| p-values | 0.779 | 0.183 | 0.673 | 0.482 |
| Heart Radiation Measure | Balanced Accuracy | AUC ROC | Sensitivity (Recall) | Specificity | |||
|---|---|---|---|---|---|---|---|
| Non Adjusted models | wtRF | Mean heart dose | 0.78 ± 0.09 | 0.82 ± 0.071 | 0.7 ± 0.199 | 0.86 ± 0.033 | |
| Dosiomics features | 0.75 ± 0.08 | 0.83 ± 0.053 | 0.66 ± 0.182 | 0.85 ± 0.028 | |||
| p-values | 0.527 | 0.751 | 0.628 | 0.588 | |||
| BRF | Mean heart dose | 0.78 ± 0.086 | 0.83 ± 0.062 | 0.73 ± 0.2 | 0.82 ± 0.035 | ||
| Dosiomics features | 0.76 ± 0.072 | 0.83 ± 0.065 | 0.71 ± 0.166 | 0.81 ± 0.029 | 4 | ||
| p-values | 0.712 | 0.870 | 0.801 | 0.705 | |||
| Adjusted models | wtRF | Mean heart dose | 0.79 ± 0.086 | 0.87 ± 0.059 | 0.71 ± 0.187 | 0.87 ± 0.033 | |
| Dosiomics features | 0.76 ± 0.088 | 0.83 ± 0.059 | 0.67 ± 0.192 | 0.84 ± 0.028 | |||
| p-values | 0.406 | 0.155 | 0.627 | 0.088 | |||
| BRF | Mean heart dose | 0.8 ± 0.056 | 0.87 ± 0.059 | 0.76 ± 0.12 | 0.84 ± 0.016 | ||
| Dosiomics features | 0.78 ± 0.062 | 0.85 ± 0.064 | 0.73 ± 0.142 | 0.82 ± 0.027 | 8 | ||
| p-values | 0.394 | 0.544 | 0.723 | 0.022 |
References
- INSERM. 5-Year Overall Survival Rates of Childhood Cancer in Mainland France over 2000–2014, by Diagnostic and Age Groups-RNCE; INSERM: Pairs, France, 2022. [Google Scholar]
- Society, A.C. Key Statistics for Childhood Cancers; American Cancer Society: Atlanta, GA, USA, 2023. [Google Scholar]
- SIOP Europe. Mission and Vision. 2022. Available online: https://siope.eu/about-siope/mission-and-vision/ (accessed on 28 February 2023).
- Shen, C.J.; Terezakis, S.A. The Evolving Role of Radiotherapy for Pediatric Cancers with Advancements in Molecular Tumor Characterization and Targeted Therapies. Front. Oncol. 2021, 11, 679701. [Google Scholar] [CrossRef] [PubMed]
- Jairam, V.; Roberts, K.B.; Yu, J.B. Historical Trends in the use of radiation for pediatric cancers: 1973–2008. Int. J. Radiat. Oncol. Biol. Phys. 2013, 85, e151–e155. [Google Scholar] [CrossRef] [PubMed]
- Lautenschlaeger, S.; Iancu, G.; Flatten, V.; Baumann, K.; Thiemer, M.; Dumke, C.; Zink, K.; Hauswald, H.; Vordermark, D.; Mauz-Körholz, C.; et al. Advantage of proton-radiotherapy for pediatric patients and adolescents with Hodgkin’s disease. Radiat. Oncol. 2019, 14, 157. [Google Scholar] [CrossRef] [PubMed]
- Baues, C.; Marnitz, S.; Engert, A.; Baus, W.; Jablonska, K.; Fogliata, A.; Vásquez-Torres, A.; Scorsetti, M.; Cozzi, L. Proton versus photon deep inspiration breath hold technique in patients with hodgkin lymphoma and mediastinal radiation. Radiat. Oncol. 2018, 13, 122. [Google Scholar] [CrossRef]
- Butler, E.; Ludwig, K.; Pacenta, H.L.; Klesse, L.J.; Watt, T.C.; Laetsch, T.W. Recent progress in the treatment of cancer in children. CA Cancer J. Clin. 2021, 71, 315–332. [Google Scholar] [CrossRef]
- Güntürkün, F.; Akbilgic, O.; Davis, R.L.; Armstrong, G.T.; Howell, R.M.; Jefferies, J.L.; Ness, K.K.; Karabayir, I.; Lucas, J.T., Jr.; Srivastava, D.K.; et al. Artificial intelligence-assisted prediction of late-onset cardiomyopathy among childhood cancer survivors. JCO Clin. Cancer Inform. 2021, 5, 459–468. [Google Scholar] [CrossRef]
- Isaksson, L.J.; Pepa, M.; Zaffaroni, M.; Marvaso, G.; Alterio, D.; Volpe, S.; Corrao, G.; Augugliaro, M.; Starzyńska, A.; Leonardi, M.C.; et al. Machine learning-based models for prediction of toxicity outcomes in radiotherapy. Front. Oncol. 2020, 10, 790. [Google Scholar] [CrossRef]
- Landier, W.; Skinner, R.; Wallace, W.H.; Hjorth, L.; Mulder, R.L.; Wong, F.L.; Yasui, Y.; Bhakta, N.; Constine, L.S.; Bhatia, S.; et al. Surveillance for Late Effects in Childhood Cancer Survivors. J. Clin. Oncol. 2018, 36, 2216–2222. [Google Scholar] [CrossRef]
- Haddy, N.; Diallo, S.; El-Fayech, C.; Schwartz, B.; Pein, F.; Hawkins, M.; Veres, C.; Oberlin, O.; Guibout, C.; Pacquement, H.; et al. Cardiac Diseases Following Childhood Cancer Treatment: Cohort Study. Circulation 2016, 133, 31–38. [Google Scholar] [CrossRef]
- Mulrooney, D.A.; Hyun, G.; Ness, K.K.; Ehrhardt, M.J.; Yasui, Y.; Duprez, D.; Howell, R.M.; Leisenring, W.M.; Constine, L.S.; Tonorezos, E.; et al. Major cardiac events for adult survivors of childhood cancer diagnosed between 1970 and 1999: Report from the Childhood Cancer Survivor Study cohort. BMJ 2020, 368, l6794. [Google Scholar] [CrossRef]
- Leerink, J.M.; de Baat, E.C.; Feijen, E.A.; Bellersen, L.; van Dalen, E.C.; Grotenhuis, H.B.; Kapusta, L.; Kok, W.E.; Loonen, J.; van der Pal, H.J.; et al. Cardiac Disease in Childhood Cancer Survivors. JACC Cardio Oncol. 2020, 2, 363–378. [Google Scholar] [CrossRef] [PubMed]
- Hau, E.M.; Caccia, J.N.; Kasteler, R.; Spycher, B.; Suter, T.; Ammann, R.A.; von der Weid, N.X.; Kuehni, C.E. Cardiovascular disease after childhood acute lymphoblastic leukaemia: A cohort study. Swiss Med. Wkly. 2019, 149, w20012. [Google Scholar] [CrossRef] [PubMed]
- Cutter, D.J.; Schaapveld, M.; Darby, S.C.; Hauptmann, M.; van Nimwegen, F.A.; Krol, A.D.G.; Janus, C.P.M.; van Leeuwen, F.E.; Aleman, B.M.P. Risk for Valvular Heart Disease after Treatment for Hodgkin Lymphoma. JNCI J. Natl. Cancer Inst. 2015, 107, djv008. [Google Scholar] [CrossRef] [PubMed]
- Cella, L.; Oh, J.H.; Deasy, J.O.; Palma, G.; Liuzzi, R.; D’avino, V.; Conson, M.; Picardi, M.; Salvatore, M.; Pacelli, R. Predicting radiation-induced valvular heart damage. Acta Oncol. 2015, 54, 1796–1804. [Google Scholar] [CrossRef]
- Chounta, S.; Lemler, S.; Haddy, N.; Fresneau, B.; Mansouri, I.; Bentriou, M.; Demoor-Goldschmidt, C.; Diallo, I.; Souchard Msc, V.; Do Thi, D.; et al. The risk of valvular heart disease in the french childhood cancer survivors’ study: Contribution of dose-volume histogram parameters. Radiother. Oncol. 2023, 180, 109479. [Google Scholar] [CrossRef]
- Cella, L.; Liuzzi, R.; Conson, M.; Torre, G.; Caterino, M.; De Rosa, N.; Picardi, M.; Camera, L.; Solla, R.; Farella, A.; et al. Dosimetric predictors of asymptomatic heart valvular dysfunction following mediastinal irradiation for Hodgkin’s lymphoma. Radiother. Oncol. 2011, 101, 316–321. [Google Scholar] [CrossRef]
- Gujral, D.M.; Lloyd, G.; Bhattacharyya, S. Radiation-induced valvular heart disease. Heart 2016, 102, 269–276. [Google Scholar] [CrossRef]
- Schellong, G.; Riepenhausen, M.; Bruch, C.; Kotthoff, S.; Vogt, J.; Bölling, T.; Dieckmann, K.; Pötter, R.; Heinecke, A.; Brämswig, J.; et al. Late valvular and other cardiac diseases after different doses of mediastinal radiotherapy for hodgkin disease in children and adolescents: Report from the longitudinal GPOH follow-up project of the German-Austrian DAL-HD studies. Pediatr. Blood Cancer 2010, 55, 1145–1152. [Google Scholar] [CrossRef]
- van der Pal, H.J.; van Dijk, I.W.; Geskus, R.B.; Kok, W.E.; Koolen, M.; Sieswerda, E.; Oldenburger, F.; Koning, C.C.; van Leeuwen, F.E.; Caron, H.N.; et al. Valvular abnormalities detected by echocardiography in 5-year survivors of childhood cancer: A long-term follow-up study. Int. J. Radiat. Oncol. Biol. Phys. 2015, 91, 213–222. [Google Scholar] [CrossRef]
- Bates, J.E.; Howell, R.M.; Liu, Q.; Yasui, Y.; Mulrooney, D.A.; Dhakal, S.; Smith, S.A.; Leisenring, W.M.; Indelicato, D.J.; Gibson, T.M.; et al. Therapy-Related Cardiac Risk in Childhood Cancer Survivors: An Analysis of the Childhood Cancer Survivor Study. J. Clin. Oncol. 2019, 37, 1090–1101. [Google Scholar] [CrossRef]
- Galper, S.L.; Yu, J.B.; Mauch, P.M.; Strasser, J.F.; Silver, B.; LaCasce, A.; Marcus, K.J.; Stevenson, M.A.; Chen, M.H.; Ng, A.K. Clinically significant cardiac disease in patients with Hodgkin lymphoma treated with mediastinal irradiation. Blood 2011, 117, 412–418. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Bates, J.E.; Liu, Q.; Smith, S.A.; Oeffinger, K.C.; Chow, E.J.; Gupta, A.C.; Owens, C.A.; Constine, L.S.; Hoppe, B.S.; et al. Radiation therapy related cardiac disease risk in childhood cancer survivors: Updated dosimetry analysis from the Childhood Cancer Survivor Study. Radiother. Oncol. 2021, 163, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.S.; OuYang, P.Y.; Guo, J.G.; Cai, J.J.; Zhang, J.; Peng, Q.H.; He, Y.; Zhang, B.Y.; Liu, Z.Q.; Hu, X.F.; et al. Dosiomics Risk Model for Predicting Radiation Induced Temporal Lobe Injury and Guiding Individual Intensity Modulated Radiation Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2022, 115, S0360301622036057. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Yan, H.; Tian, Y.; Chen, X.; Yan, L.; Zhang, T.; Zhou, Z.; Wang, L.; Dai, J. Dosiomics: Extracting 3D Spatial Features from Dose Distribution to Predict Incidence of Radiation Pneumonitis. Front. Oncol. 2019, 9, 269. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; Li, Y.; Qi, M.; Lu, X.; Jia, Q.; Guo, F.; Dai, Z.; Liu, Y.; Chen, C.; Zhou, L.; et al. Dosiomics improves prediction of locoregional recurrence for intensity modulated radiotherapy treated head and neck cancer cases. Oral Oncol. 2020, 104, 104625. [Google Scholar] [CrossRef]
- Ren, W.; Liang, B.; Sun, C.; Wu, R.; Men, K.; Xu, Y.; Han, F.; Yi, J.; Qu, Y.; Dai, J. Dosiomics-based prediction of radiation-induced hypothyroidism in nasopharyngeal carcinoma patients. Phys. Medica 2021, 89, 219–225. [Google Scholar] [CrossRef]
- Murakami, Y.; Soyano, T.; Kozuka, T.; Ushijima, M.; Koizumi, Y.; Miyauchi, H.; Kaneko, M.; Nakano, M.; Kamima, T.; Hashimoto, T.; et al. Dose-Based Radiomic Analysis (Dosiomics) for Intensity Modulated Radiation Therapy in Patients with Prostate Cancer: Correlation Between Planned Dose Distribution and Biochemical Failure. Int. J. Radiat. Oncol. 2022, 112, 247–259. [Google Scholar] [CrossRef]
- ICCC. Third Edition (ICD-O-3), Main Classification Table-SEER Recodes. 2022. Available online: https://seer.cancer.gov/iccc/iccc3.html (accessed on 28 February 2023).
- Mansouri, I.; Allodji, R.S.; Hill, C.; El-Fayech, C.; Pein, F.; Diallo, S.; Schwartz, B.; Vu-Bezin, G.; Veres, C.; Souchard, V.; et al. The role of irradiated heart and left ventricular volumes in heart failure occurrence after childhood cancer. Eur. J. Heart Fail. 2019, 21, 509–518. [Google Scholar] [CrossRef]
- Allodji, R.S.; Haddy, N.; Vu-Bezin, G.; Dumas, A.; Fresneau, B.; Mansouri, I.; Demoor-Goldschmidt, C.; El-Fayech, C.; Pacquement, H.; Munzer, M.; et al. Risk of subsequent colorectal cancers after a solid tumor in childhood: Effects of radiation therapy and chemotherapy. Pediatr. Blood Cancer 2019, 66, e27495. [Google Scholar] [CrossRef]
- Journy, N.M.Y.; Zrafi, W.S.; Bolle, S.; Fresneau, B.; Alapetite, C.; Allodji, R.S.; Berchery, D.; Haddy, N.; Kobayashi, I.; Labbé, M.; et al. Risk Factors of Subsequent Central Nervous System Tumors after Childhood and Adolescent Cancers: Findings from the French Childhood Cancer Survivor Study. Cancer Epidemiol. Biomark. Prev. 2021, 30, 133–141. [Google Scholar] [CrossRef]
- Accueil CépiDc. 2022. Available online: https://www.cepidc.inserm.fr/ (accessed on 28 February 2023).
- Système National D’information Inter-Régimes de l’Assurance Maladie; Caisse Nationale De L’assurance Maladie Des Travailleurs Salaries: Paris, France, 2022; Available online: https://www.snds.gouv.fr/SNDS/Open-Data (accessed on 28 February 2023).
- Common Terminology Criteria for Adverse Events (CTCAE); U.S. Department of Health and Human Services: Washington, DC, USA; National Institutes of Health, National Cancer Institute: Bethesda, MD, USA, 2009; p. 196.
- Taylor, N.; Absolom, K.; Michel, G.; Urquhart, T.; Gerrard, M.; Jenkins, A.; Lee, V.; Vora, A.; Eiser, C. Comparison of self-reported late effects with medical records among survivors of childhood cancer. Eur. J. Cancer 2010, 46, 1069–1078. [Google Scholar] [CrossRef] [PubMed]
- Veres, C.; Allodji, R.S.; Llanas, D.; Vu Bezin, J.; Chavaudra, J.; Mège, J.P.; Lefkopoulos, D.; Quiniou, E.; Deutsh, E.; de Vathaire, F.; et al. Retrospective Reconstructions of Active Bone Marrow Dose-Volume Histograms. Int. J. Radiat. Oncol. 2014, 90, 1216–1224. [Google Scholar] [CrossRef] [PubMed]
- Diallo, I.; Lamon, A.; Shamsaldin, A.; Grimaud, E.; de Vathaire, F.; Chavaudra, J. Estimation of the radiation dose delivered to any point outside the target volume per patient treated with external beam radiotherapy. Radiother. Oncol. 1996, 38, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, A.; Vallières, M.; Abdalah, M.A.; Aerts, H.J.W.L.; Andrearczyk, V.; Apte, A.; Ashrafinia, S.; Bakas, S.; Beukinga, R.J.; Boellaard, R.; et al. The image biomarker standardization initiative: Standardized quantitative radiomics for high-throughput image-based phenotyping. Radiology 2020, 295, 328–338. [Google Scholar] [CrossRef]
- van Griethuysen, J.J.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.; Fillion-Robin, J.C.; Pieper, S.; Aerts, H.J. Computational Radiomics System to Decode the Radiographic Phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L2 theory. Z. Für Wahrscheinlichkeitstheorie Verwandte Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; Technical Report 666; Department of Statistics: Berkley, CA, USA, 2004. [Google Scholar]
- Shan, G. Monte Carlo cross-validation for a study with binary outcome and limited sample size. BMC Med. Inform. Decis. Mak. 2022, 22, 270. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Dkengne Sielenou, P.; Viallon-Galinier, L.; Hagenmuller, P.; Naveau, P.; Morin, S.; Dumont, M.; Verfaillie, D.; Eckert, N. Combining random forests and class-balancing to discriminate between three classes of avalanche activity in the French Alps. Cold Reg. Sci. Technol. 2021, 187, 103276. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference 2010 (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; Available online: https://conference.scipy.org/proceedings/scipy2010/mckinney.html (accessed on 28 February 2023).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Waskom, M.L. seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Patil, S.; Pingle, S.R.; Shalaby, K.; Kim, A.S. Mediastinal irradiation and valvular heart disease. Cardio-Oncol. 2022, 8, 7. [Google Scholar] [CrossRef]
- Menezes, K.M.; Wang, H.; Hada, M.; Saganti, P.B. Radiation matters of the heart: A mini review. Front. Cardiovasc. Med. 2018, 5, 83. [Google Scholar] [CrossRef]
- Placidi, L.; Gioscio, E.; Garibaldi, C.; Rancati, T.; Fanizzi, A.; Maestri, D.; Massafra, R.; Menghi, E.; Mirandola, A.; Reggiori, G.; et al. A multicentre evaluation of dosiomics features reproducibility, stability and sensitivity. Cancers 2021, 13, 3835. [Google Scholar] [CrossRef]
- Vũ Bezin, J.; Allodji, R.S.; Mège, J.P.; Beldjoudi, G.; Saunier, F.; Chavaudra, J.; Deutsch, E.; de Vathaire, F.; Bernier, V.; Carrie, C.; et al. A review of uncertainties in radiotherapy dose reconstruction and their impacts on dose-response relationships. J. Radiol. Prot. 2017, 37, R1–R18. [Google Scholar] [CrossRef]
- Alabdoaburas, M. Etude DosiméTrique et ModéLisation des Composantes de la Dose à Distance Pour les Faisceaux D’éLectrons en RadiothéRapie Externe. Ph.D. Thesis, Université Paris-Saclay (ComUE), Paris, France, 2017. [Google Scholar]
- Appelt, A.L.; Elhaminia, B.; Gooya, A.; Gilbert, A.; Nix, M. Deep learning for radiotherapy outcome prediction using dose data—A review. Clin. Oncol. R Coll. Radiol. 2022, 34, e87–e96. [Google Scholar] [CrossRef]
- DICOM-NEMA. DICOM in Radiotherapy—dicom.nema.org. 2023. Available online: https://dicom.nema.org/dicom/geninfo/brochure/rtaapm.htm (accessed on 24 April 2023).
- Dumane, V.A.; Saksornchai, K.; Zhou, Y.; Hong, L.; Powell, S.; Ho, A.Y. Reduction in low-dose to normal tissue with the addition of deep inspiration breath hold (DIBH) to volumetric modulated arc therapy (VMAT) in breast cancer patients with implant reconstruction receiving regional nodal irradiation. Radiat. Oncol. 2018, 13, 187. [Google Scholar] [CrossRef]
- Gomarteli, K.; Fleckenstein, J.; Meyer, M.; Henzler, T.; Kirschner, S.; Kraenzlin, B.; Brockmann, M.A.; Welzel, G.; Glatting, G.; Wenz, F.; et al. Focus on the low-dose bath: No increased cancer risk after mediastinal VMAT versus AP/PA irradiation in a tumor-prone rat model. Int. J. Radiat. Oncol. Biol. Phys. 2017, 99, S76–S77. [Google Scholar] [CrossRef]
- COG Homepage—childrensoncologygroup.org. Available online: https://childrensoncologygroup.org/ (accessed on 16 May 2023).
- Lyon, A.R.; López-Fernández, T.; Couch, L.S.; Asteggiano, R.; Aznar, M.C.; Bergler-Klein, J.; Boriani, G.; Cardinale, D.; Cordoba, R.; Cosyns, B.; et al. 2022 ESC guidelines on cardio-oncology developed in collaboration with the European hematology association (EHA), the European society for therapeutic radiology and oncology (ESTRO) and the international cardio-oncology society (IC-OS). Eur. Heart J. Cardiovasc. Imaging 2022, 23, e333–e465. [Google Scholar] [CrossRef] [PubMed]
- Novo, G.; Santoro, C.; Manno, G.; Di Lisi, D.; Esposito, R.; Mandoli, G.E.; Evola, V.; Pastore, M.C.; Sperlongano, S.; D’Andrea, A.; et al. Usefulness of stress echocardiography in the management of patients treated with anticancer drugs. J. Am. Soc. Echocardiogr. 2021, 34, 107–116. [Google Scholar] [CrossRef] [PubMed]
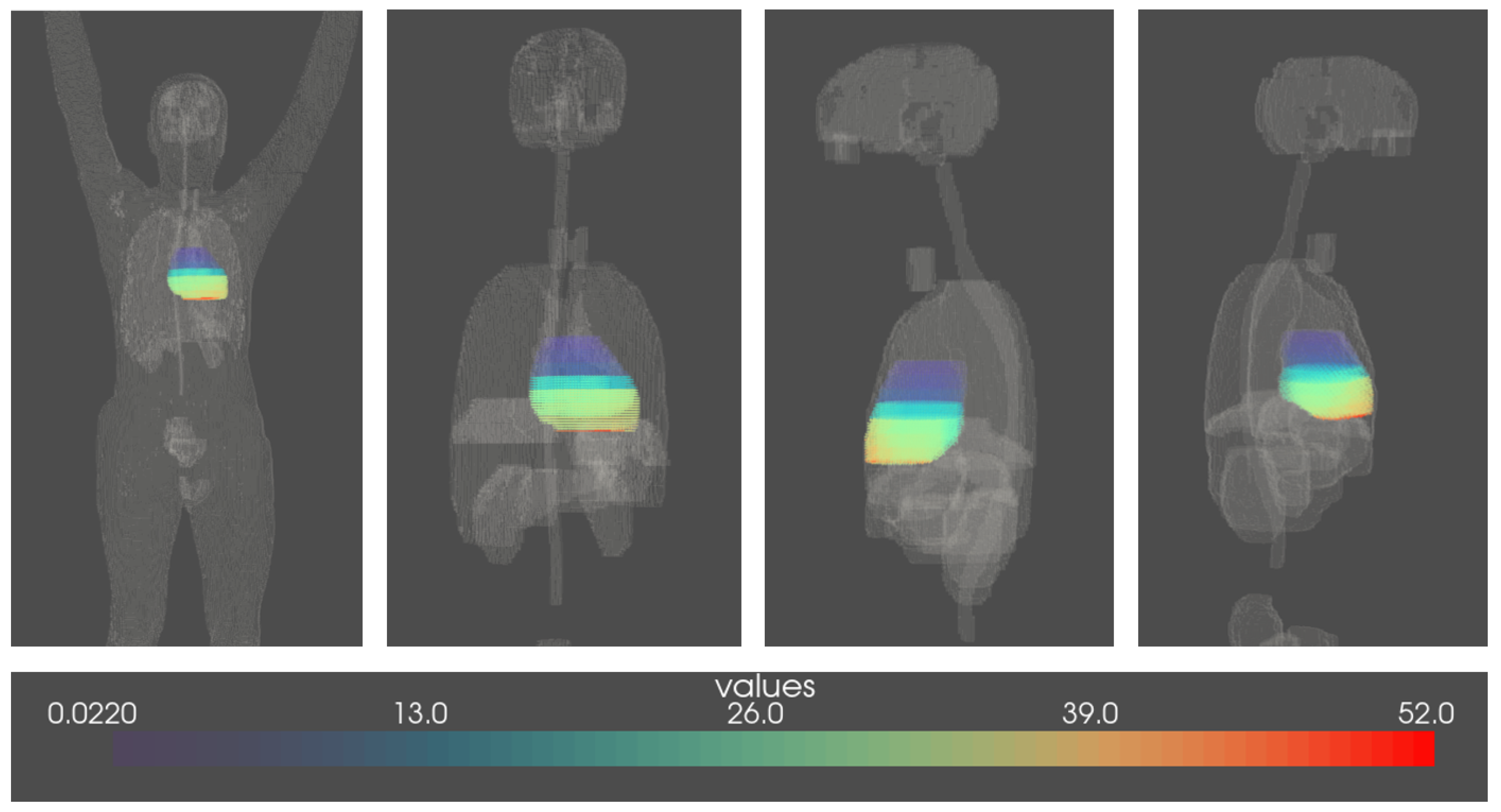
| FCCSS 1 | No RT 2 | Uniformity = 1 | Uniformity in [0.1, 1) | Uniformity < 0.1 | |
|---|---|---|---|---|---|
| Total | 7488 | 3586 | 346 | 1593 | 1963 |
| VHD 3 | 81 (1.08%) | 18 (0.5%) | 2 (0.58%) | 4 (0.25%) | 57 (2.9%) |
| Age at CC 4 diagnosis | 6.62 [0–20.61] | 6.18 [0–20.41] | 6.01 [0–18.41] | 7.08 [0–20.28] | 7.17 [020.61] |
| Year at CC diagnosis | 1984 [1946–2000] | 1988 [1949–2000] | 1983 [1951–2000] | 1982 [1946–2000] | 1980 [1948–2000] |
| Attained age | 37.76 [5.39–79.83] | 35.79 [5.392–76.37] | 39.37 [7.27–79.83] | 38.94 [6.16–78.65] | 40.12 [6.66–77.82] |
| Biological Sex | |||||
| Male | 3384 (45.19%) | 1622 (45.23%) | 146 (42.2%) | 701 (44.01%) | 915 (46.61%) |
| Female | 4104 (54.81%) | 1964 (54.77%) | 200 (57.8%) | 892 (55.99%) | 1048 (53.39%) |
| Chemotherapy | |||||
| No | 1828 (24.41%) | 957 (26.69%) | 109 (31.5%) | 480 (30.13%) | 282 (14.37%) |
| Yes | 5660 (75.59%) | 2629 (73.31%) | 237 (68.5%) | 1113 (69.87%) | 1681 (85.63%) |
| Mean dose to the heart | 6.82 [0–61.20] | 0 [0–0] | 0.02 [0–0.25] | 0.98 [0–37.65] | 12.76 [0–61.20] |
| Median dose to the heart | 6.75 [0–67.54] | 0 [0–0] | 0.02 [0–0.25] | 0.88 [0–37.66] | 12.69 [0–67.54] |
| Maximum dose to the heart | 13.68 [0–109.43] | 0 [0–0] | 0.04 [0–0.26] | 2.18 [0.1–60.28] | 25.424 [1.326–109.43] |
| Heart dose uniformity | 0.27 [0.003–1] | 1 [1–1] | 1 [1–1] | 0.4 [0.1–1) | 0.036 [0.003–0.1] |
| FCCSS 1 | No RT 2 | Uniformity = 1 | Uniformity in [0.1, 1) | Uniformity < 0.1 | |
|---|---|---|---|---|---|
| Total | 7488 | 3586 (48%) | 346 (5%) | 1593 (21%) | 1963 (26%) |
| VHD 3 | 81 | 18 (22%) | 2 (2%) | 4 (5%) | 57 (70%) |
| Type of CC 4: | |||||
| Hodgkin lymphoma | 471 | 27 (6%) | 5 (1%) | 45 (10%) | 394 (84%) |
| Other lymphomas and reticuloendothelial neoplasms | 788 | 540 (69%) | 16 (2%) | 158 (20%) | 74 (9%) |
| CNS and miscellaneous intracranial and intraspinal neoplasms | 1124 | 160 (14%) | 17 (2%) | 552 (49%) | 395 (35%) |
| Neuroblastoma and other peripheral nervous cell tumors | 1028 | 646 (63%) | 12 (1%) | 144 (14%) | 226 (22%) |
| Retinoblastoma | 519 | 310 (60%) | 114 (22%) | 91 (18%) | 4 (1%) |
| Renal tumors | 1136 | 503 (44%) | 0 (0%) | 102 (9%) | 531 (47%) |
| Hepatic tumors | 79 | 62 (78%) | 0 (0%) | 5 (6%) | 12 (15%) |
| Malignant bone tumors | 679 | 392 (58%) | 64 (9%) | 124 (18%) | 99 (15%) |
| Soft tissue and other extraosseous sarcomas | 846 | 387 (46%) | 99 (12%) | 261 (31%) | 99 (12%) |
| Germ cell tumors, trophoblastic tumors, and neoplasms of gonads | 469 | 332 (71%) | 6 (1%) | 65 (14%) | 66 (14%) |
| Other | 349 | 227 (65%) | 13 (4%) | 46 (13%) | 63 (18%) |
| Heart Radiation Measure | Balanced Accuracy | AUC ROC | Sensitivity (Recall) | Specificity | |||
|---|---|---|---|---|---|---|---|
| FCCSS | wtRF | Mean heart dose | 0.74 ± 0.04 | 0.77 ± 0.051 | 0.57 ± 0.083 | 0.90 ± 0.019 | |
| Dosiomics features | 0.74 ± 0.038 | 0.77 ± 0.047 | 0.59 ± 0.075 | 0.88 ± 0.015 | |||
| p-values | 0.792 | 0.883 | 0.319 | 0.001 | |||
| BRF | Mean heart dose | 0.73 ± 0.04 | 0.76 ± 0.046 | 0.61 ± 0.088 | 0.84 ± 0.034 | ||
| Dosiomics features | 0.74 ± 0.039 | 0.77 ± 0.051 | 0.62 ± 0.074 | 0.86 ± 0.018 | 4 | ||
| p-values | 0.234 | 0.358 | 0.627 | 0.044 | |||
| Uniformity < 1 | wtRF | Mean heart dose | 0.78 ± 0.057 | 0.85 ± 0.059 | 0.72 ± 0.127 | 0.84 ± 0.029 | |
| Dosiomics features | 0.78 ± 0.057 | 0.86 ± 0.059 | 0.73 ± 0.126 | 0.83 ± 0.031 | |||
| p-values | 0.981 | 0.483 | 0.617 | 0.057 | |||
| BRF | Mean heart dose | 0.74 ± 0.054 | 0.83 ± 0.057 | 0.73 ± 0.113 | 0.76 ± 0.043 | ||
| Dosiomics features | 0.79 ± 0.056 | 0.86 ± 0.057 | 0.78 ± 0.113 | 0.79 ± 0.021 | 8 | ||
| p-values | 0.004 | 0.046 | 0.08 | <0.001 | |||
| Uniformity < 0.1 | wtRF | Mean heart dose | 0.76 ± 0.068 | 0.81 ± 0.069 | 0.71 ± 0.146 | 0.79 ± 0.031 | |
| Dosiomics features | 0.76 ± 0.062 | 0.82 ± 0.073 | 0.69 ± 0.13 | 0.82 ± 0.026 | |||
| p-values | 0.909 | 0.773 | 0.4 | 0.001 | |||
| BRF | Mean heart dose | 0.72 ± 0.076 | 0.79 ± 0.064 | 0.72 ± 0.151 | 0.73 ± 0.052 | ||
| Dosiomics features | 0.75 ± 0.056 | 0.8 ± 0.071 | 0.74 ± 0.126 | 0.77 ± 0.028 | 12 | ||
| p-values | 0.162 | 0.437 | 0.701 | 0.002 |
| FCCSS | Uniformity < 1 | Uniformity < 0.1 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Features | wtRF | BRF | Average [min–max] | wtRF | BRF | Average [min–max] | wtRF | BRF | Average [min–max] |
| First Order Statistics: | |||||||||
| 10th percentile | ✔ | ✔ | 1.78 [0–49.23] | ✔ | ✔ | 3.75 [0–49.23] | ✔ | ✔ | 6.18 [0–49.23] |
| 90th percentile | ✔ | ✔ | 5.37 [0–89.78] | 11.31 [0–89.78] | 19.36 [1.01–89.78] | ||||
| energy | ✔ | ✔ | 3.7 × 106 [0–2.1 × 108] | ✔ | ✔ | 7.9 × 106 [2.49–2.1 × 108] | ✔ | ✔ | 14 × 106 [8.4 × 103–2.1 × 108] |
| kyrtosis | ✔ | 3.49 [0–1753.9] | 7.14 [1.1–1753.9] | 6.03 [1.1–115.99] | |||||
| mean heart dose | ✔ | ✔ | 3.55 [0–61.09] | ✔ | ✔ | 7.48 [0–61.09] | ✔ | ✔ | 12.75 [0.64–61.09] |
| median heart dose | ✔ | ✔ | 3.51 [0–67.91] | ✔ | ✔ | 7.4 [0–67.91] | ✔ | ✔ | 12.68 [0.44–67.91] |
| minimum heart dose | ✔ | ✔ | 0.88 [0–38.24] | ✔ | ✔ | 1.85 [0–38.24] | 2.88 [0–38.24] | ||
| root mean squared | ✔ | ✔ | 3.98 [0–64.33] | ✔ | ✔ | 8.37 [0.01–64.33] | ✔ | ✔ | 14.27 [0.7–64.33] |
| total energy | ✔ | ✔ | 3 × 107 [0–1.7 × 109] | ✔ | ✔ | 6.3 × 107 [19.89–1.7 × 109] | ✔ | ✔ | 11 × 107 [6.7 × 104–1.7 × 109] |
| GLCM: | |||||||||
| autocorrelation | ✔ | ✔ | 0.58 × 104 [1–3.1 × 105] | ✔ | ✔ | 1.2 × 104 [1–3.1 × 105] | ✔ | ✔ | 2.1 × 104 [41–3.1 × 105] |
| IDMN | ✔ | 1 [0.86–1] | ✔ | 0.99 [0.86–1] | 0.99 [0.86–1] | ||||
| IDN | ✔ | 0.99 [0.83–1] | ✔ | 0.98 [0.83–1] | ✔ | ✔ | 0.98 [0.83–1] | ||
| joint average | ✔ | ✔ | 27.72 [1–512.79] | ✔ | ✔ | 57.27 [1–512.79] | ✔ | ✔ | 99.75 [5.38–512.79] |
| sum average | ✔ | ✔ | 54.97 [1–104] | ✔ | ✔ | 114.54 [2–104] | ✔ | ✔ | 199.49 [10.76–104] |
| GLDM: | |||||||||
| high gray level emphasis | ✔ | ✔ | 0.59 × 104 [1–3.1 × 105] | ✔ | ✔ | 1.2 × 104 [1–3.1 × 105] | ✔ | ✔ | 2.2 × 104 [42–3.1 × 105] |
| large dependence high gray level emphasis | ✔ | ✔ | 0.89 × 106 [1–7.9 × 107] | 1.8 × 106 [593–7.9 × 107] | 3.3 × 106 [4.2 × 103–7.9 × 107] | ||||
| small dependence high gray level emphasis | ✔ | ✔ | 325.95 [0–39,643.4] | ✔ | ✔ | 685.36 [0–39,643.4] | ✔ | ✔ | 1239.17 [0.18–39,643.4] |
| GLRLM: | |||||||||
| high gray level run emphasis | ✔ | ✔ | 6120.11 [1–321,807.62] | ✔ | ✔ | 12,886.24 [1–321,807.62] | ✔ | ✔ | 23,021.99 [45.97–321,807.62] |
| long run high gray level emphasis | ✔ | ✔ | 55,488.09 [1–9,755,180.03] | ✔ | ✔ | 116,805.48 [77.31–9,755,180.03] | ✔ | ✔ | 205,185.69 [514.48–9,755,180.03] |
| short run high gray level emphasis | ✔ | ✔ | 4118.5 [0.05–247,740.25] | ✔ | ✔ | 8671.47 [0.07–247,740.25] | ✔ | ✔ | 15,560.49 [14.08–247,740.25] |
| GLSZM: | |||||||||
| high gray level zone emphasis | ✔ | ✔ | 6717.88 [1–347,651.5] | 14,144.98 [1.2–347,651.5] | 24,962.32 [50.85–347,651.5] | ||||
| small area high gray level emphasis | ✔ | ✔ | 1206.64 [0–99,793.65] | 2539.85 [0–99,793.65] | 4533 [0.09–99,793.65] | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chounta, S.; Allodji, R.; Vakalopoulou, M.; Bentriou, M.; Do, D.T.; De Vathaire, F.; Diallo, I.; Fresneau, B.; Charrier, T.; Zossou, V.; et al. Dosiomics-Based Prediction of Radiation-Induced Valvulopathy after Childhood Cancer. Cancers 2023, 15, 3107. https://doi.org/10.3390/cancers15123107
Chounta S, Allodji R, Vakalopoulou M, Bentriou M, Do DT, De Vathaire F, Diallo I, Fresneau B, Charrier T, Zossou V, et al. Dosiomics-Based Prediction of Radiation-Induced Valvulopathy after Childhood Cancer. Cancers. 2023; 15(12):3107. https://doi.org/10.3390/cancers15123107
Chicago/Turabian StyleChounta, Stefania, Rodrigue Allodji, Maria Vakalopoulou, Mahmoud Bentriou, Duyen Thi Do, Florent De Vathaire, Ibrahima Diallo, Brice Fresneau, Thibaud Charrier, Vincent Zossou, and et al. 2023. "Dosiomics-Based Prediction of Radiation-Induced Valvulopathy after Childhood Cancer" Cancers 15, no. 12: 3107. https://doi.org/10.3390/cancers15123107
APA StyleChounta, S., Allodji, R., Vakalopoulou, M., Bentriou, M., Do, D. T., De Vathaire, F., Diallo, I., Fresneau, B., Charrier, T., Zossou, V., Christodoulidis, S., Lemler, S., & Letort Le Chevalier, V. (2023). Dosiomics-Based Prediction of Radiation-Induced Valvulopathy after Childhood Cancer. Cancers, 15(12), 3107. https://doi.org/10.3390/cancers15123107






