Utility of Continuous Disease Subtyping Systems for Improved Evaluation of Etiologic Heterogeneity
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
3. Results
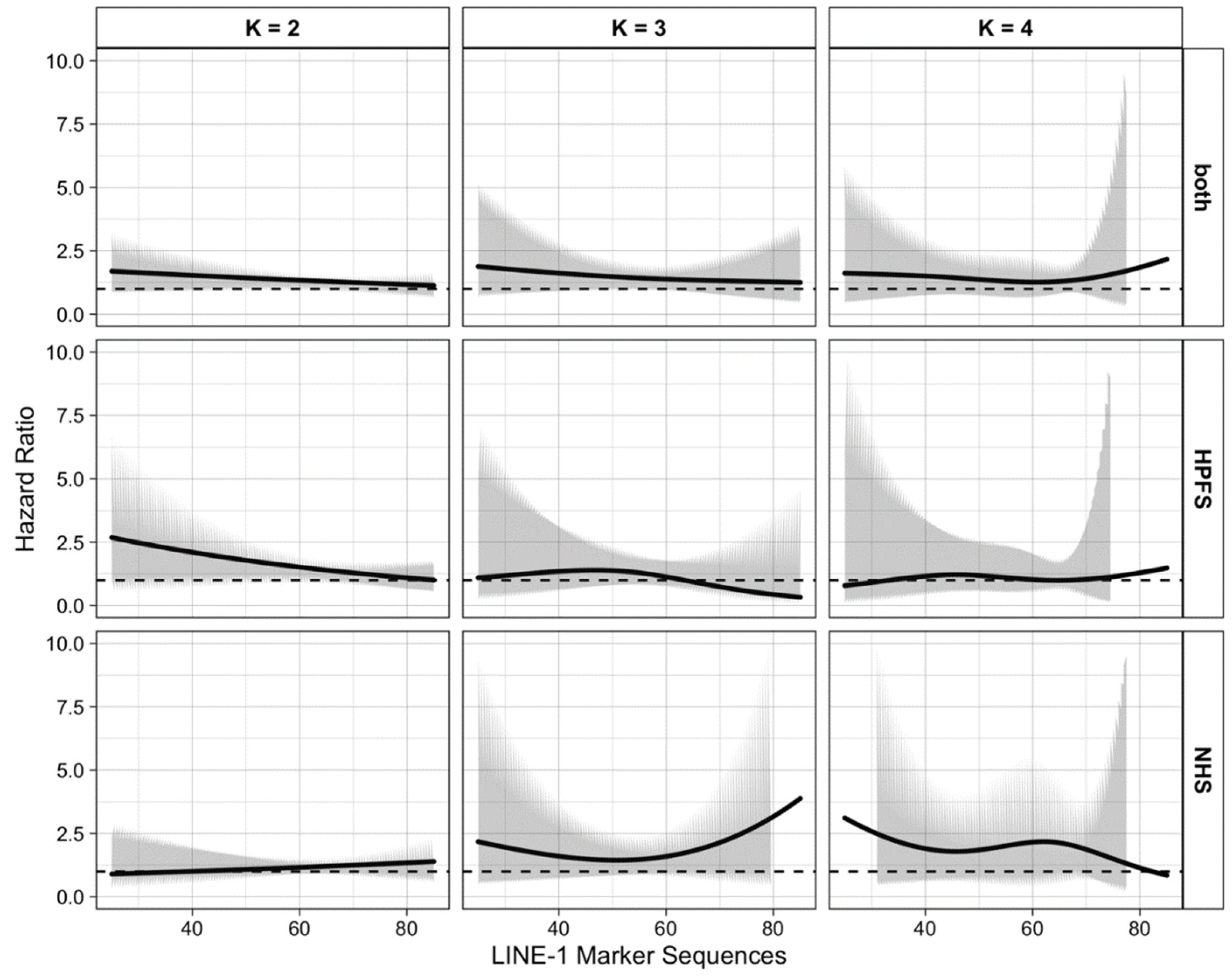
3.1. Simulation Study
3.2. Results of Illustrative Example
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| HPFS | Health Professionals Follow-up Study |
| HR | hazard ratio |
| LINE-1 | long interspersed nucleotide element-1 |
| NHS | Nurses’ Health Study |
References
- Begg, C.B. A strategy for distinguishing optimal cancer subtypes. Int. J. Cancer 2011, 129, 931–937. [Google Scholar] [CrossRef] [PubMed]
- Begg, C.B.; Zabor, E.C. Detecting and exploiting etiologic heterogeneity in epidemiologic studies. Am. J. Epidemiol. 2012, 176, 512–518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Begg, C.B.; Zabor, E.C.; Bernstein, J.L.; Bernstein, L.; Press, M.F.; Seshan, V.E. A conceptual and methodological framework for investigating etiologic heterogeneity. Stat. Med. 2013, 32, 5039–5052. [Google Scholar] [CrossRef] [PubMed]
- Richiardi, L.; Barone-Adesi, F.; Pearce, N. Cancer subtypes in aetiological research. Eur. J. Epidemiol. 2017, 32, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Ogino, S.; Chan, A.T.; Fuchs, C.S.; Giovannucci, E. Molecular pathological epidemiology of colorectal neoplasia: An emerging transdisciplinary and interdisciplinary field. Gut 2011, 60, 397–411. [Google Scholar] [CrossRef]
- Ogino, S.; Nishihara, R.; VanderWeele, T.J.; Wang, M.; Nishi, A.; Lochhead, P.; Qian, Z.R.; Zhang, X.; Wu, K.; Nan, H. The role of molecular pathological epidemiology in the study of neoplastic and non-neoplastic diseases in the era of precision medicine. Epidemiology 2016, 27, 602. [Google Scholar] [CrossRef]
- Ogino, S.; Nowak, J.A.; Hamada, T.; Milner, D.A., Jr.; Nishihara, R. Insights into pathogenic interactions among environment, host, and tumor at the crossroads of molecular pathology and epidemiology. Annu. Rev. Pathol. Mech. Dis. 2019, 14, 83–103. [Google Scholar] [CrossRef]
- Holm, J.; Eriksson, L.; Ploner, A.; Eriksson, M.; Rantalainen, M.; Li, J.; Hall, P.; Czene, K. Assessment of breast cancer risk factors reveals subtype heterogeneity. Cancer Res. 2017, 77, 3708–3717. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Spiegelman, D.; Kuchiba, A.; Lochhead, P.; Kim, S.; Chan, A.T.; Poole, E.M.; Tamimi, R.; Tworoger, S.S.; Giovannucci, E. Statistical methods for studying disease subtype heterogeneity. Stat. Med. 2016, 35, 782–800. [Google Scholar] [CrossRef]
- Schernhammer, E.S.; Giovannucci, E.; Kawasaki, T.; Rosner, B.; Fuchs, C.S.; Ogino, S. Dietary folate, alcohol and B vitamins in relation to LINE-1 hypomethylation in colon cancer. Gut 2010, 59, 794–799. [Google Scholar] [CrossRef] [Green Version]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Prentice, R.L.; Kalbfleisch, J.D.; Peterson, A.V., Jr.; Flournoy, N.; Farewell, V.T.; Breslow, N.E. The analysis of failure times in the presence of competing risks. Biometrics 1978, 34, 541–554. [Google Scholar] [CrossRef] [PubMed]
- Cox, D.R. Partial likelihood. Biometrika 1975, 62, 269–276. [Google Scholar] [CrossRef]
- Chatterjee, N.; Sinha, S.; Diver, W.R.; Feigelson, H.S. Analysis of cohort studies with multivariate and partially observed disease classification data. Biometrika 2010, 97, 683–698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Durrleman, S.; Simon, R. Flexible regression models with cubic splines. Stat. Med. 1989, 8, 551–561. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Irahara, N.; Nosho, K.; Baba, Y.; Shima, K.; Lindeman, N.I.; Hazra, A.; Schernhammer, E.S.; Hunter, D.J.; Fuchs, C.S.; Ogino, S. Precision of pyrosequencing assay to measure LINE-1 methylation in colon cancer, normal colonic mucosa, and peripheral blood cells. J. Mol. Diagn. 2010, 12, 177–183. [Google Scholar] [CrossRef]
- Bao, Y.; Bertoia, M.L.; Lenart, E.B.; Stampfer, M.J.; Willett, W.C.; Speizer, F.E.; Chavarro, J.E. Origin, Methods, and Evolution of the Three Nurses’ Health Studies. Am. J. Public Health 2016, 106, 1573–1581. [Google Scholar] [CrossRef]
- Ugai, T.; Vayrynen, J.P.; Haruki, K.; Akimoto, N.; Lau, M.C.; Zhong, R.; Kishikawa, J.; Vayrynen, S.A.; Zhao, M.; Fujiyoshi, K.; et al. Smoking and Incidence of Colorectal Cancer Subclassified by Tumor-Associated Macrophage Infiltrates. J. Natl. Cancer Inst. 2022, 114, 68–77. [Google Scholar] [CrossRef]
- Nishihara, R.; Wu, K.; Lochhead, P.; Morikawa, T.; Liao, X.; Qian, Z.R.; Inamura, K.; Kim, S.A.; Kuchiba, A.; Yamauchi, M.; et al. Long-term colorectal-cancer incidence and mortality after lower endoscopy. N. Engl. J. Med. 2013, 369, 1095–1105. [Google Scholar] [CrossRef] [Green Version]
- Ugai, T.; Haruki, K.; Vayrynen, J.P.; Borowsky, J.; Fujiyoshi, K.; Lau, M.C.; Akimoto, N.; Zhong, R.; Kishikawa, J.; Arima, K.; et al. Coffee Intake of Colorectal Cancer Patients and Prognosis According to Histopathologic Lymphocytic Reaction and T-Cell Infiltrates. Mayo Clin. Proc. 2022, 97, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Baba, Y.; Huttenhower, C.; Nosho, K.; Tanaka, N.; Shima, K.; Hazra, A.; Schernhammer, E.S.; Hunter, D.J.; Giovannucci, E.L.; Fuchs, C.S.; et al. Epigenomic diversity of colorectal cancer indicated by LINE-1 methylation in a database of 869 tumors. Mol. Cancer 2010, 9, 125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Estecio, M.R.; Gharibyan, V.; Shen, L.; Ibrahim, A.E.; Doshi, K.; He, R.; Jelinek, J.; Yang, A.S.; Yan, P.S.; Huang, T.H.; et al. LINE-1 hypomethylation in cancer is highly variable and inversely correlated with microsatellite instability. PLoS ONE 2007, 2, e399. [Google Scholar] [CrossRef] [PubMed]
- Havel, J.J.; Chowell, D.; Chan, T.A. The evolving landscape of biomarkers for checkpoint inhibitor immunotherapy. Nat. Rev. Cancer 2019, 19, 133–150. [Google Scholar] [CrossRef] [PubMed]
- Paucek, R.D.; Baltimore, D.; Li, G. The Cellular Immunotherapy Revolution: Arming the Immune System for Precision Therapy. Trends Immunol. 2019, 40, 292–309. [Google Scholar] [CrossRef]
- Grizzi, F.; Basso, G.; Borroni, E.M.; Cavalleri, T.; Bianchi, P.; Stifter, S.; Chiriva-Internati, M.; Malesci, A.; Laghi, L. Evolving notions on immune response in colorectal cancer and their implications for biomarker development. Inflamm. Res. 2018, 67, 375–389. [Google Scholar] [CrossRef]
- Kather, J.N.; Halama, N. Harnessing the innate immune system and local immunological microenvironment to treat colorectal cancer. Br. J. Cancer 2019, 120, 871–882. [Google Scholar] [CrossRef] [Green Version]
- Ogino, S.; Giannakis, M. Immunoscore for (colorectal) cancer precision medicine. Lancet 2018, 391, 2084–2086. [Google Scholar] [CrossRef]
- Ogino, S.; Nowak, J.A.; Hamada, T.; Phipps, A.I.; Peters, U.; Milner, D.A., Jr.; Giovannucci, E.L.; Nishihara, R.; Giannakis, M.; Garrett, W.S.; et al. Integrative analysis of exogenous, endogenous, tumour and immune factors for precision medicine. Gut 2018, 67, 1168–1180. [Google Scholar] [CrossRef]
- Le, D.T.; Hubbard-Lucey, V.M.; Morse, M.A.; Heery, C.R.; Dwyer, A.; Marsilje, T.H.; Brodsky, A.N.; Chan, E.; Deming, D.A.; Diaz, L.A., Jr.; et al. A Blueprint to Advance Colorectal Cancer Immunotherapies. Cancer Immunol. Res. 2017, 5, 942–949. [Google Scholar] [CrossRef] [Green Version]
- Kather, J.N.; Halama, N.; Jaeger, D. Genomics and emerging biomarkers for immunotherapy of colorectal cancer. Semin. Cancer Biol. 2018, 52, 189–197. [Google Scholar] [CrossRef] [PubMed]
- Pages, F.; Galon, J.; Dieu-Nosjean, M.C.; Tartour, E.; Sautes-Fridman, C.; Fridman, W.H. Immune infiltration in human tumors: A prognostic factor that should not be ignored. Oncogene 2010, 29, 1093–1102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamada, T.; Nowak, J.A.; Milner, D.A., Jr.; Song, M.; Ogino, S. Integration of microbiology, molecular pathology, and epidemiology: A new paradigm to explore the pathogenesis of microbiome-driven neoplasms. J. Pathol. 2019, 247, 615–628. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mima, K.; Kosumi, K.; Baba, Y.; Hamada, T.; Baba, H.; Ogino, S. The microbiome, genetics, and gastrointestinal neoplasms: The evolving field of molecular pathological epidemiology to analyze the tumor-immune-microbiome interaction. Hum. Genet. 2021, 140, 725–746. [Google Scholar] [CrossRef]
- Mima, K.; Nishihara, R.; Qian, Z.R.; Cao, Y.; Sukawa, Y.; Nowak, J.A.; Yang, J.; Dou, R.; Masugi, Y.; Song, M.; et al. Fusobacterium nucleatum in colorectal carcinoma tissue and patient prognosis. Gut 2016, 65, 1973–1980. [Google Scholar] [CrossRef] [Green Version]
- Mima, K.; Cao, Y.; Chan, A.T.; Qian, Z.R.; Nowak, J.A.; Masugi, Y.; Shi, Y.; Song, M.; da Silva, A.; Gu, M.; et al. Fusobacterium nucleatum in Colorectal Carcinoma Tissue According to Tumor Location. Clin. Transl. Gastroenterol. 2016, 7, e200. [Google Scholar] [CrossRef]
- Mehta, R.S.; Nishihara, R.; Cao, Y.; Song, M.; Mima, K.; Qian, Z.R.; Nowak, J.A.; Kosumi, K.; Hamada, T.; Masugi, Y.; et al. Association of Dietary Patterns With Risk of Colorectal Cancer Subtypes Classified by Fusobacterium nucleatum in Tumor Tissue. JAMA Oncol. 2017, 3, 921–927. [Google Scholar] [CrossRef] [Green Version]
- Borowsky, J.; Haruki, K.; Lau, M.C.; Dias Costa, A.; Vayrynen, J.P.; Ugai, T.; Arima, K.; da Silva, A.; Felt, K.D.; Zhao, M.; et al. Association of Fusobacterium nucleatum with Specific T-cell Subsets in the Colorectal Carcinoma Microenvironment. Clin. Cancer Res. 2021, 27, 2816–2826. [Google Scholar] [CrossRef]
- Lin, D.; Fleming, T.R. Proceedings of the First Seattle Symposium in Biostatistics: Survival Analysis: Survival Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 123. [Google Scholar]
- Verweij, P.J.; Van Houwelingen, H.C. Cross-validation in survival analysis. Stat. Med. 1993, 12, 2305–2314. [Google Scholar] [CrossRef]
- Fujiyoshi, K.; Bruford, E.A.; Mroz, P.; Sims, C.L.; O’Leary, T.J.; Lo, A.W.I.; Chen, N.; Patel, N.R.; Patel, K.P.; Seliger, B.; et al. Opinion: Standardizing gene product nomenclature—A call to action. Proc. Natl. Acad. Sci. USA 2021, 118, e2025207118. [Google Scholar] [CrossRef]
| Knots | Model Assessment | NHS | HPFS | Combined |
|---|---|---|---|---|
| K = 2 | p-value | |||
| Overall | 0.19 | <0.001 | <0.001 | |
| Heterogeneity | - | <0.001 | <0.001 | |
| BIC | 11,634 | 7784 | 20,436 | |
| AIC | 11,586 | 7739 | 20,386 | |
| K = 3 | p-value | |||
| Overall | 0.12 | <0.001 | <0.001 | |
| Heterogeneity | - | <0.001 | <0.001 | |
| Nonlinearity | - | <0.001 | 0.54 | |
| BIC | 11,660 | 7804 | 20,464 | |
| AIC | 11,588 | 7736 | 20,389 | |
| K = 4 | p-value | |||
| Overall | 0.17 | <0.001 | 0.002 | |
| Heterogeneity | - | <0.001 | <0.001 | |
| Nonlinearity | - | <0.001 | 0.56 | |
| BIC | 11,686 | 7830 | 20,492 | |
| AIC | 11,589 | 7741 | 20,393 | |
| Cohort | LINE-1 Methylation Level | Hazard Ratio with 95% Confidence Interval | |||||
|---|---|---|---|---|---|---|---|
| Linear Function | Restricted Cubic Spline | Restricted Cubic Spline | |||||
| Combined | 30 | 1.64 | (0.95, 2.82) | 1.79 | (0.76, 4.21) | 1.59 | (0.55, 4.61) |
| 40 | 1.53 | (1.03, 2.28) | 1.62 | (0.91, 2.87) | 1.51 | (0.76, 3.01) | |
| 50 | 1.43 | (1.10, 1.86) | 1.48 | (1.03, 2.13) | 1.37 | (0.78, 2.40) | |
| 60 | 1.34 | (1.14, 1.58) | 1.38 | (1.00, 1.92) | 1.27 | (0.72, 2.22) | |
| 70 | 1.25 | (1.05, 1.50) | 1.32 | (0.77, 2.26) | 1.40 | (0.74, 2.64) | |
| 80 | 1.17 | (0.87, 1.57) | 1.28 | (0.53, 3.05) | 1.85 | (0.18, 18.5) | |
| HPFS | 30 | 2.47 | (1.12, 5.48) | 1.18 | (0.32, 4.32) | 0.91 | (0.17, 4.87) |
| 40 | 2.10 | (1.18, 3.75) | 1.35 | (0.57, 3.16) | 1.16 | (0.40, 3.31) | |
| 50 | 1.78 | (1.22, 2.61) | 1.38 | (0.82, 2.32) | 1.18 | (0.54, 2.59) | |
| 60 | 1.52 | (1.19, 1.93) | 1.13 | (0.72, 1.77) | 1.02 | (0.52, 2.00) | |
| 70 | 1.29 | (0.98, 1.70) | 0.74 | (0.35, 1.56) | 1.03 | (0.33, 3.22) | |
| 80 | 1.09 | (0.7, 1.710) | 0.43 | (0.13, 1.50) | 1.29 | (0.03, 63.8) | |
| NHS | 30 | 0.94 | (0.41, 2.15) | 1.95 | (0.56, 6.82) | 2.58 | (0.61, 10.9) |
| 40 | 1.01 | (0.54, 1.86) | 1.60 | (0.69, 3.73) | 1.90 | (0.74, 4.91) | |
| 50 | 1.08 | (0.72, 1.63) | 1.45 | (0.84, 2.50) | 1.85 | (0.82, 4.17) | |
| 60 | 1.16 | (0.90, 1.49) | 1.59 | (0.98, 2.58) | 2.16 | (0.86, 5.43) | |
| 70 | 1.25 | (0.97, 1.61) | 2.14 | (1.00, 4.57) | 1.87 | (0.91, 3.86) | |
| 80 | 1.34 | (0.89, 2.03) | 3.17 | (0.94, 10.7) | 1.14 | (0.08, 15.6) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Ugai, T.; Xu, L.; Zucker, D.; Ogino, S.; Wang, M. Utility of Continuous Disease Subtyping Systems for Improved Evaluation of Etiologic Heterogeneity. Cancers 2022, 14, 1811. https://doi.org/10.3390/cancers14071811
Li R, Ugai T, Xu L, Zucker D, Ogino S, Wang M. Utility of Continuous Disease Subtyping Systems for Improved Evaluation of Etiologic Heterogeneity. Cancers. 2022; 14(7):1811. https://doi.org/10.3390/cancers14071811
Chicago/Turabian StyleLi, Ruitong, Tomotaka Ugai, Lantian Xu, David Zucker, Shuji Ogino, and Molin Wang. 2022. "Utility of Continuous Disease Subtyping Systems for Improved Evaluation of Etiologic Heterogeneity" Cancers 14, no. 7: 1811. https://doi.org/10.3390/cancers14071811
APA StyleLi, R., Ugai, T., Xu, L., Zucker, D., Ogino, S., & Wang, M. (2022). Utility of Continuous Disease Subtyping Systems for Improved Evaluation of Etiologic Heterogeneity. Cancers, 14(7), 1811. https://doi.org/10.3390/cancers14071811







