Converging Proton Minibeams with Magnetic Fields for Optimized Radiation Therapy: A Proof of Concept
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Monte Carlo Simulations
2.2. Simulation Geometry and Configurations
2.3. Magnetic Field Optimization
2.4. SOBP Optimization
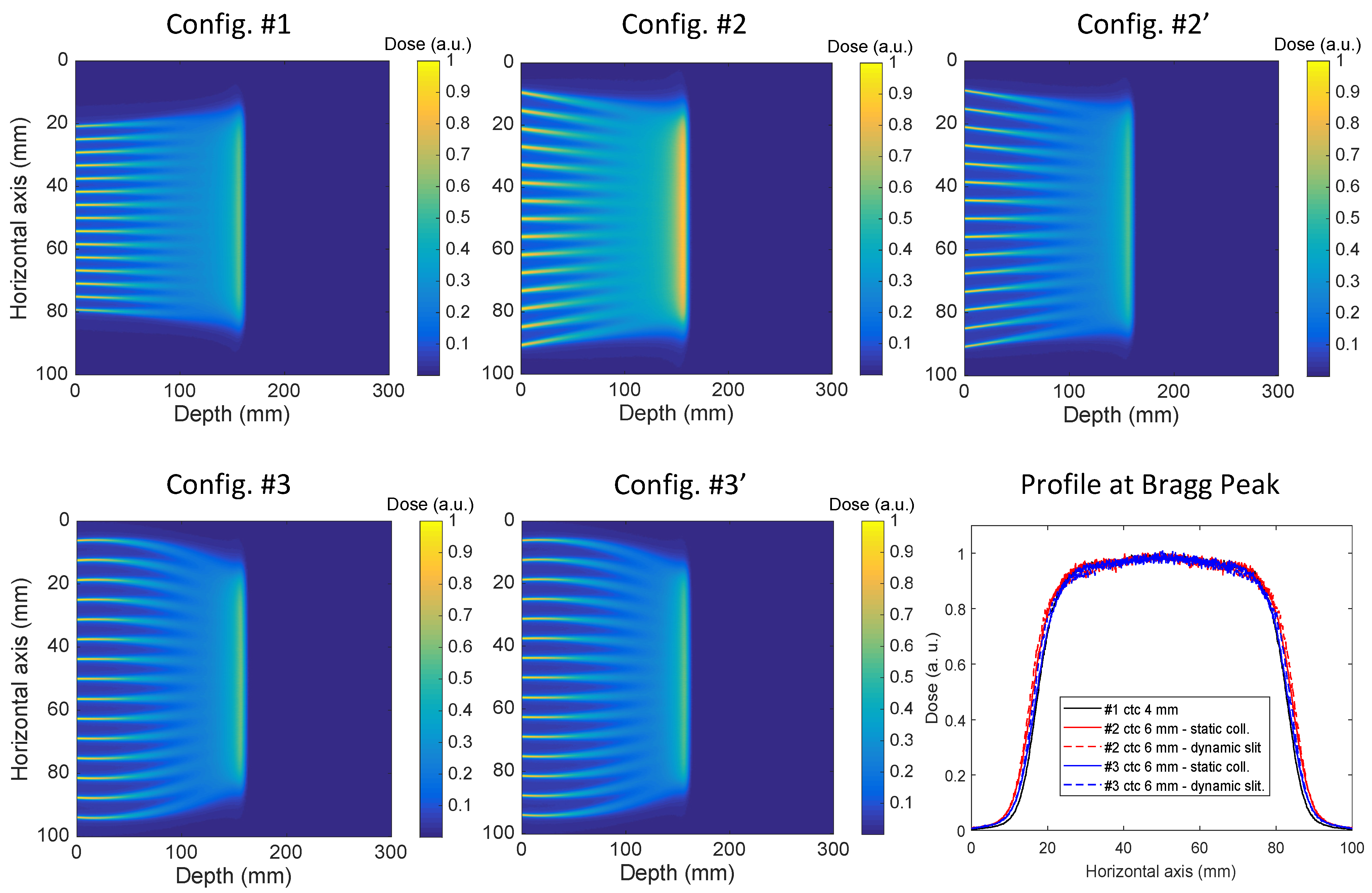
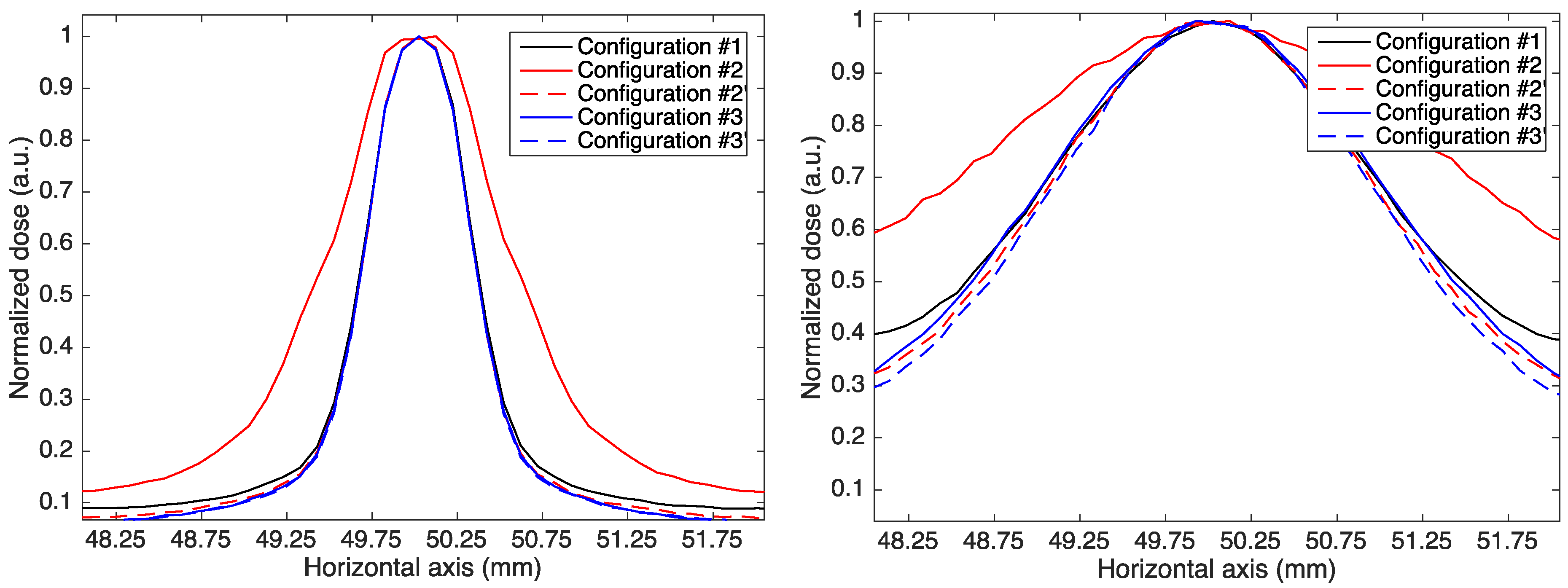
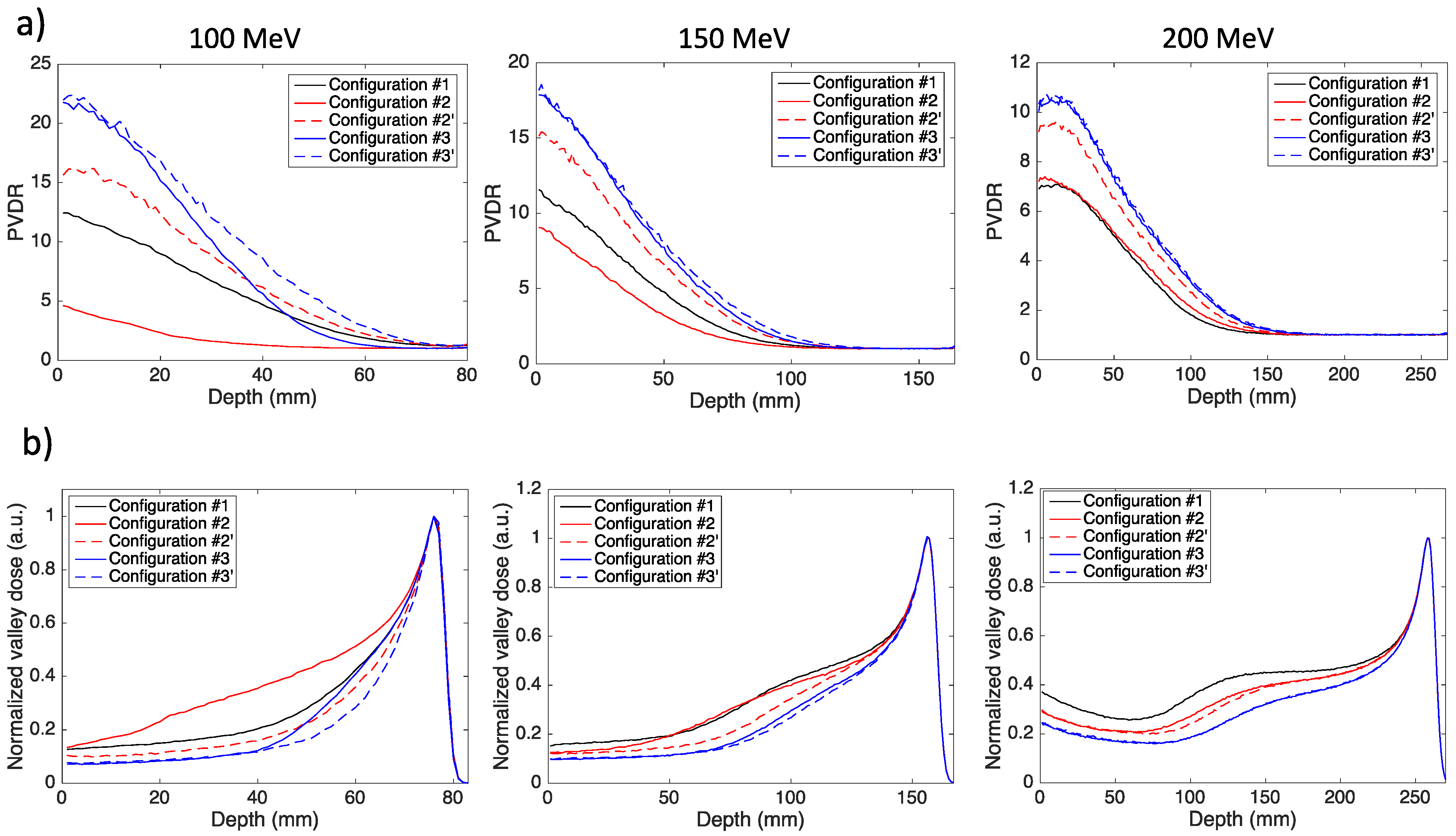
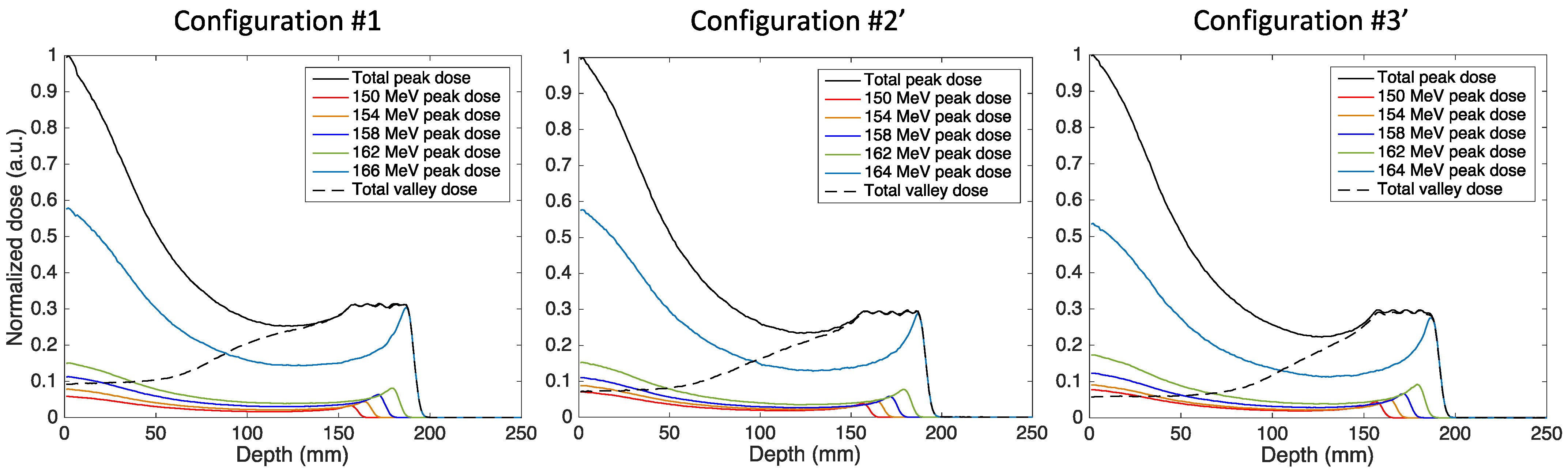
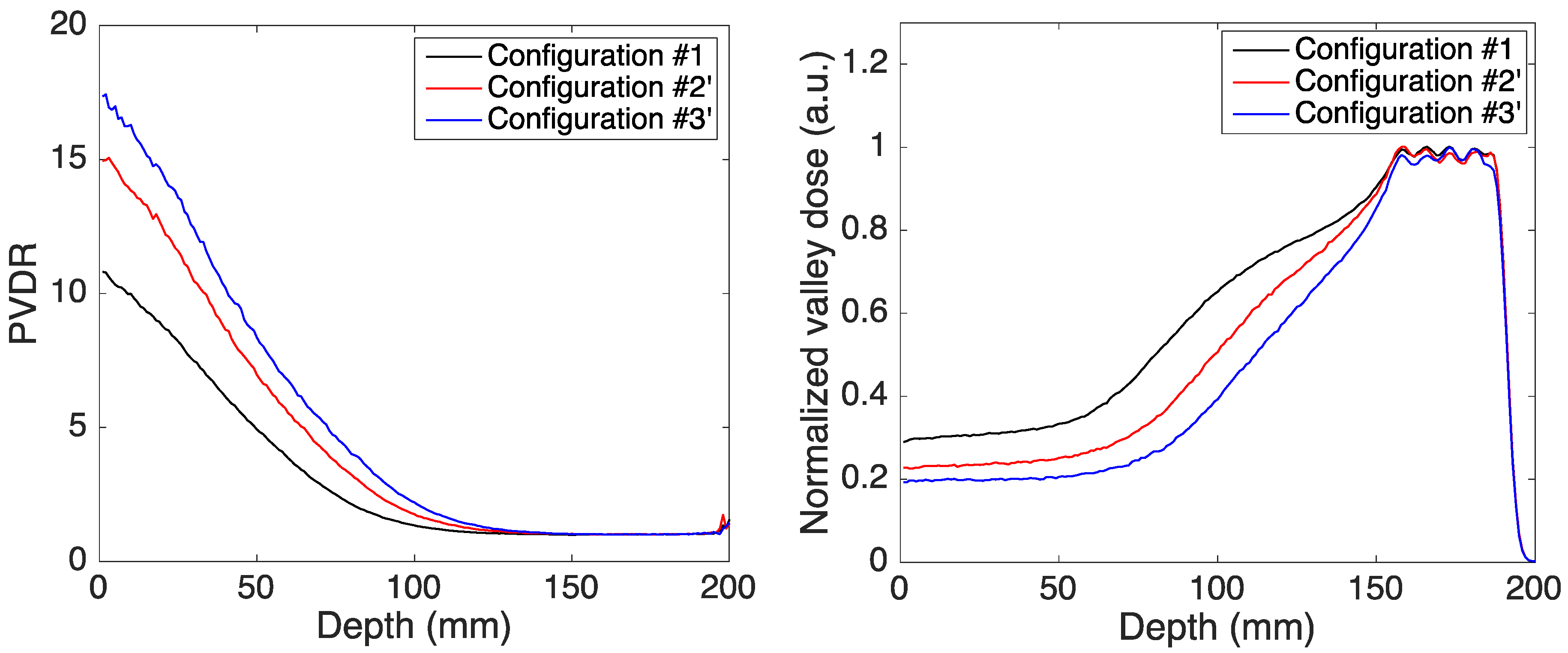
3. Results
3.1. Monoenergetic Beams
3.2. Spread-Out Bragg Peak
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tian, X.; Liu, K.; Hou, Y.; Cheng, J.; Zhang, J. The Evolution of Proton Beam Therapy: Current and Future Status (Review). Mol. Clin. Oncol. 2017, 8, 15–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Marzi, L.; Nauraye, C.; Lansonneur, P.; Pouzoulet, F.; Patriarca, A.; Schneider, T.; Guardiola, C.; Mammar, H.; Dendale, R.; Prezado, Y. Spatial Fractionation of the Dose in Proton Therapy: Proton Minibeam Radiation Therapy. Cancer/Radiothérapie 2019, 23, 677–681. [Google Scholar] [CrossRef]
- Wilson, J.D.; Hammond, E.M.; Higgins, G.S.; Petersson, K. Ultra-High Dose Rate (FLASH) Radiotherapy: Silver Bullet or Fool’s Gold? Front. Oncol. 2020, 9, 1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barkova, A.M.; Kholin, V.V. Theoretical calculation of the spatial distribution of a Co 60 gamma radiation dose field under a grid. Med. Radiol. 1971, 16, 64–70. [Google Scholar]
- Mohiuddin, M.; Curtis, D.L.; Grizos, W.T.; Komarnicky, L. Palliative Treatment of Advanced Cancer Using Multiple Nonconfluent Pencil Beam Radiation: A Pilot Study. Cancer 1990, 66, 114–118. [Google Scholar] [CrossRef]
- Slatkin, D.N.; Spanne, P.; Dilmanian, F.A.; Sandborg, M. Microbeam Radiation Therapy. Med. Phys. 1992, 19, 1395–1400. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Khan, M.K.; Wu, X.; Simone, C.B.; Fan, J.; Gressen, E.; Zhang, X.; Limoli, C.L.; Bahig, H.; Tubin, S.; et al. Spatially Fractionated Radiation Therapy: History, Present and the Future. Clin. Transl. Radiat. Oncol. 2020, 20, 30–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prezado, Y.; Fois, G.R. Proton-Minibeam Radiation Therapy: A Proof of Concept: Proton-Minibeam Radiation Therapy: A Proof of Concept. Med. Phys. 2013, 40, 031712. [Google Scholar] [CrossRef]
- Martínez-Rovira, I.; Fois, G.; Prezado, Y. Dosimetric Evaluation of New Approaches in GRID Therapy Using Nonconventional Radiation Sources: Dosimetric Evaluation of New Approaches in GRID Therapy. Med. Phys. 2015, 42, 685–693. [Google Scholar] [CrossRef] [PubMed]
- Peucelle, C.; Nauraye, C.; Patriarca, A.; Hierso, E.; Fournier-Bidoz, N.; Martínez-Rovira, I.; Prezado, Y. Proton Minibeam Radiation Therapy: Experimental Dosimetry Evaluation: Proton Minibeam Radiation Therapy: Experimental Evaluation. Med. Phys. 2015, 42, 7108–7113. [Google Scholar] [CrossRef]
- De Marzi, L.; Patriarca, A.; Nauraye, C.; Hierso, E.; Dendale, R.; Guardiola, C.; Prezado, Y. Implementation of Planar Proton Minibeam Radiation Therapy Using a Pencil Beam Scanning System: A Proof of Concept Study. Med. Phys. 2018, 45, 5305–5316. [Google Scholar] [CrossRef]
- Girst, S.; Greubel, C.; Reindl, J.; Siebenwirth, C.; Zlobinskaya, O.; Walsh, D.W.M.; Ilicic, K.; Aichler, M.; Walch, A.; Wilkens, J.J.; et al. Proton Minibeam Radiation Therapy Reduces Side Effects in an In Vivo Mouse Ear Model. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 234–241. [Google Scholar] [CrossRef] [Green Version]
- Prezado, Y.; Jouvion, G.; Hardy, D.; Patriarca, A.; Nauraye, C.; Bergs, J.; González, W.; Guardiola, C.; Juchaux, M.; Labiod, D.; et al. Proton Minibeam Radiation Therapy Spares Normal Rat Brain: Long-Term Clinical, Radiological and Histopathological Analysis. Sci. Rep. 2017, 7, 14403. [Google Scholar] [CrossRef] [PubMed]
- Lamirault, C.; Doyère, V.; Juchaux, M.; Pouzoulet, F.; Labiod, D.; Dendale, R.; Patriarca, A.; Nauraye, C.; Le Dudal, M.; Jouvion, G.; et al. Short and Long-Term Evaluation of the Impact of Proton Minibeam Radiation Therapy on Motor, Emotional and Cognitive Functions. Sci. Rep. 2020, 10, 13511. [Google Scholar] [CrossRef] [PubMed]
- Lamirault, C.; Brisebard, E.; Patriarca, A.; Juchaux, M.; Crepin, D.; Labiod, D.; Pouzoulet, F.; Sebrie, C.; Jourdain, L.; Le Dudal, M.; et al. Spatially Modulated Proton Minibeams Results in the Same Increase of Lifespan as a Uniform Target Dose Coverage in F98-Glioma-Bearing Rats. Radiat. Res. 2020, 194, 715–723. [Google Scholar] [CrossRef] [PubMed]
- Prezado, Y.; Jouvion, G.; Patriarca, A.; Nauraye, C.; Guardiola, C.; Juchaux, M.; Lamirault, C.; Labiod, D.; Jourdain, L.; Sebrie, C.; et al. Proton Minibeam Radiation Therapy Widens the Therapeutic Index for High-Grade Gliomas. Sci. Rep. 2018, 8, 16479. [Google Scholar] [CrossRef] [PubMed]
- Prezado, Y.; Jouvion, G.; Guardiola, C.; Gonzalez, W.; Juchaux, M.; Bergs, J.; Nauraye, C.; Labiod, D.; De Marzi, L.; Pouzoulet, F.; et al. Tumor Control in RG2 Glioma-Bearing Rats: A Comparison Between Proton Minibeam Therapy and Standard Proton Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2019, 104, 266–271. [Google Scholar] [CrossRef]
- Lansonneur, P.; Mammar, H.; Nauraye, C.; Patriarca, A.; Hierso, E.; Dendale, R.; Prezado, Y.; De Marzi, L. First Proton Minibeam Radiation Therapy Treatment Plan Evaluation. Sci. Rep. 2020, 10, 7025. [Google Scholar] [CrossRef] [PubMed]
- Kurz, C.; Buizza, G.; Landry, G.; Kamp, F.; Rabe, M.; Paganelli, C.; Baroni, G.; Reiner, M.; Keall, P.J.; van den Berg, C.A.T.; et al. Medical Physics Challenges in Clinical MR-Guided Radiotherapy. Radiat. Oncol. 2020, 15, 93. [Google Scholar] [CrossRef] [PubMed]
- Schellhammer, S.M.; Hoffmann, A.L. Prediction and Compensation of Magnetic Beam Deflection in MR-Integrated Proton Therapy: A Method Optimized Regarding Accuracy, Versatility and Speed. Phys. Med. Biol. 2017, 62, 1548–1564. [Google Scholar] [CrossRef]
- Schellhammer, S.M.; Gantz, S.; Lühr, A.; Oborn, B.M.; Bussmann, M.; Hoffmann, A.L. Technical Note: Experimental Verification of Magnetic Field-induced Beam Deflection and Bragg Peak Displacement for MR-integrated Proton Therapy. Med. Phys. 2018, 45, 3429–3434. [Google Scholar] [CrossRef]
- Padilla-Cabal, F.; Georg, D.; Fuchs, H. A Pencil Beam Algorithm for Magnetic Resonance Image-Guided Proton Therapy. Med. Phys. 2018, 45, 2195–2204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Padilla-Cabal, F.; Alejandro Fragoso, J.; Franz Resch, A.; Georg, D.; Fuchs, H. Benchmarking a GATE/Geant4 Monte Carlo Model for Proton Beams in Magnetic Fields. Med. Phys. 2020, 47, 223–233. [Google Scholar] [CrossRef] [Green Version]
- Wolf, R.; Bortfeld, T. An Analytical Solution to Proton Bragg Peak Deflection in a Magnetic Field. Phys. Med. Biol. 2012, 57, N329–N337. [Google Scholar] [CrossRef]
- Moteabbed, M.; Schuemann, J.; Paganetti, H. Dosimetric Feasibility of Real-Time MRI-Guided Proton Therapy: Dosimetric Feasibility of Real-Time MRI-Guided Proton Therapy. Med. Phys. 2014, 41, 111713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kurz, C.; Landry, G.; Resch, A.F.; Dedes, G.; Kamp, F.; Ganswindt, U.; Belka, C.; Raaymakers, B.W.; Parodi, K. A Monte-Carlo Study to Assess the Effect of 1.5 T Magnetic Fields on the Overall Robustness of Pencil-Beam Scanning Proton Radiotherapy Plans for Prostate Cancer. Phys. Med. Biol. 2017, 62, 8470–8482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kokurewicz, K.; Brunetti, E.; Curcio, A.; Gamba, D.; Garolfi, L.; Gilardi, A.; Senes, E.; Sjobak, K.N.; Farabolini, W.; Corsini, R.; et al. An Experimental Study of Focused Very High Energy Electron Beams for Radiotherapy. Commun. Phys. 2021, 4, 33. [Google Scholar] [CrossRef]
- Schneider, T.; De Marzi, L.; Patriarca, A.; Prezado, Y. Advancing Proton Minibeam Radiation Therapy: Magnetically Focussed Proton Minibeams at a Clinical Centre. Sci. Rep. 2020, 10, 1384. [Google Scholar] [CrossRef]
- Schneider, T.; Patriarca, A.; Degiovanni, A.; Gallas, M.; Prezado, Y. Conceptual Design of a Novel Nozzle Combined with a Clinical Proton Linac for Magnetically Focussed Minibeams. Cancers 2021, 13, 4657. [Google Scholar] [CrossRef]
- Perl, J.; Shin, J.; Schümann, J.; Faddegon, B.; Paganetti, H. TOPAS: An Innovative Proton Monte Carlo Platform for Research and Clinical Applications: TOPAS: An Innovative Proton Monte Carlo Platform. Med. Phys. 2012, 39, 6818–6837. [Google Scholar] [CrossRef] [PubMed]
- De Marzi, L.; Da Fonseca, A.; Moignier, C.; Patriarca, A.; Goudjil, F.; Mazal, A.; Buvat, I.; Hérault, J. Experimental Characterisation of a Proton Kernel Model for Pencil Beam Scanning Techniques. Phys. Medica 2019, 64, 195–203. [Google Scholar] [CrossRef]
- Peterson, S.W.; Polf, J.; Bues, M.; Ciangaru, G.; Archambault, L.; Beddar, S.; Smith, A. Experimental Validation of a Monte Carlo Proton Therapy Nozzle Model Incorporating Magnetically Steered Protons. Phys. Med. Biol. 2009, 54, 3217–3229. [Google Scholar] [CrossRef]
- Sotiropoulos, M.; Prezado, Y. A Scanning Dynamic Collimator for Spot-Scanning Proton Minibeam Production. Sci. Rep. 2021, 11, 18321. [Google Scholar] [CrossRef]
- McCall, J. Genetic Algorithms for Modelling and Optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Smyth, L.M.L.; Senthi, S.; Crosbie, J.C.; Rogers, P.A.W. The Normal Tissue Effects of Microbeam Radiotherapy: What Do We Know, and What Do We Need to Know to Plan a Human Clinical Trial? Int. J. Radiat. Biol. 2016, 92, 302–311. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.; Eley, J.; Schmid, T.E.; Combs, S.E.; Dendale, R.; Prezado, Y. Spatially Fractionated Proton Minibeams. BJR 2019, 92, 20180466. [Google Scholar] [CrossRef]
- Rivera, J.N.; Kierski, T.M.; Kasoji, S.K.; Abrantes, A.S.; Dayton, P.A.; Chang, S.X. Conventional Dose Rate Spatially-Fractionated Radiation Therapy (SFRT) Treatment Response and Its Association with Dosimetric Parameters—A Preclinical Study in a Fisher 344 Rat Model. PLoS ONE 2020, 6, e0229053. [Google Scholar] [CrossRef]
- Raaymakers, B.W.; Lagendijk, J.J.W.; Overweg, J.; Kok, J.G.M.; Raaijmakers, A.J.E.; Kerkhof, E.M.; van der Put, R.W.; Meijsing, I.; Crijns, S.P.M.; Benedosso, F.; et al. Integrating a 1.5 T MRI Scanner with a 6 MV Accelerator: Proof of Concept. Phys. Med. Biol. 2009, 54, N229–N237. [Google Scholar] [CrossRef] [PubMed]
- Lagendijk, J.J.W.; Raaymakers, B.W.; van Vulpen, M. The Magnetic Resonance Imaging–Linac System. Semin. Radiat. Oncol. 2014, 24, 207–209. [Google Scholar] [CrossRef]
- Oborn, B.M.; Dowdell, S.; Metcalfe, P.E.; Crozier, S.; Mohan, R.; Keall, P.J. Proton Beam Deflection in MRI Fields: Implications for MRI-Guided Proton Therapy: Beam Delivery in MRI-Guided Proton Beam Therapy. Med. Phys. 2015, 42, 2113–2124. [Google Scholar] [CrossRef] [PubMed]
- Tahmasebi Birgani, M.J.; Chegeni, N.; Zabihzadeh, M.; Tahmasbi, M. Analytical Investigation of Magnetic Field Effects on Proton Lateral Deflection and Penetrating Depth in the Water Phantom: A Relativistic Approach. Electron. Physician 2017, 9, 5932–5939. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Magnetic Field | Slit Off-Axis Distance (mm) | 100 MeV Beam | 150 MeV Beam | 200 MeV Beam |
|---|---|---|---|---|
| Configuration #2 | 6 | 0.5 T | 0.37 T | 0.279 T |
| 12 | 1 T | 0.74 T | 0.558 T | |
| 18 | 1.5 T | 1.105 T | 0.837 T | |
| 24 | 2 T | 1.475 T | 1.116 T | |
| 30 | 2.5 T | 1.84 T | 1.395 T | |
| 36 | 2.99 T | 2.21 T | 1.674 T | |
| 42 | 3.48 T | 2.575 T | 1.953 T | |
| Configuration #3 | 6 | 0.883 T | 0.274 T | 0.121 T |
| 12 | 1.766 T | 0.548 T | 0.243 T | |
| 18 | 2.649 T | 0.822 T | 0.364 T | |
| 24 | 3.532 T | 1.096 T | 0.486 T | |
| 30 | 4.415 T | 1.37 T | 0.607 T | |
| 36 | 5.298 T | 1.644 T | 0.728 T | |
| 42 | 6.181 T | 1.918 T | 0.85 T |
| Depth in Phantom | Configuration #1 | Configuration #2′ | Configuration #3′ | |
|---|---|---|---|---|
| 100 MeV | Phantom entrance | 12.5 ± 0.1 | 15.6 ± 0.1 | 22.3 ± 0.2 |
| 3.8 cm | 5.07 ± 0.05 | 6.35 ± 0.06 | 9.18 ± 0.09 | |
| 7.5 cm (BP) | 1.22 ± 0.01 | 1.26 ± 0.01 | 1.30 ± 0.01 | |
| 150 MeV | Phantom entrance | 11.6 ± 0.1 | 15.1 ± 0.1 | 18.2 ± 0.2 |
| 3.8 cm | 6.42 ± 0.06 | 8.59 ± 0.09 | 10.4 ± 0.1 | |
| 7.5 cm | 2.20 ± 0.02 | 3.10 ± 0.03 | 4.09 ± 0.04 | |
| 12.5 cm | 1.03 ± 0.01 | 1.07 ± 0.01 | 1.12 ± 0.01 | |
| 200 MeV | Phantom entrance | 6.98 ± 0.07 | 9.22 ± 0.09 | 10.3 ± 0.1 |
| 3.8 cm | 5.91 ± 0.06 | 7.77 ± 0.08 | 8.71 ± 0.09 | |
| 7.5 cm | 3.24 ± 0.03 | 4.45 ± 0.04 | 5.21 ± 0.05 | |
| 12.5 cm | 1.21 ± 0.01 | 1.58 ± 0.02 | 1.89 ± 0.02 | |
| 15 cm | 1.05 ± 0.01 | 1.14 ± 0.01 | 1.27 ± 0.01 |
| Weights wi | 150 MeV | 154 MeV | 158 MeV | 162 MeV | 166 MeV |
|---|---|---|---|---|---|
| Configuration #1 | 0.104 | 0.140 | 0.202 | 0.263 | 1 |
| Configuration #2′ | 0.141 | 0.171 | 0.210 | 0.275 | 1 |
| Configuration #3′ | 0.167 | 0.190 | 0.248 | 0.338 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavallone, M.; Prezado, Y.; De Marzi, L. Converging Proton Minibeams with Magnetic Fields for Optimized Radiation Therapy: A Proof of Concept. Cancers 2022, 14, 26. https://doi.org/10.3390/cancers14010026
Cavallone M, Prezado Y, De Marzi L. Converging Proton Minibeams with Magnetic Fields for Optimized Radiation Therapy: A Proof of Concept. Cancers. 2022; 14(1):26. https://doi.org/10.3390/cancers14010026
Chicago/Turabian StyleCavallone, Marco, Yolanda Prezado, and Ludovic De Marzi. 2022. "Converging Proton Minibeams with Magnetic Fields for Optimized Radiation Therapy: A Proof of Concept" Cancers 14, no. 1: 26. https://doi.org/10.3390/cancers14010026
APA StyleCavallone, M., Prezado, Y., & De Marzi, L. (2022). Converging Proton Minibeams with Magnetic Fields for Optimized Radiation Therapy: A Proof of Concept. Cancers, 14(1), 26. https://doi.org/10.3390/cancers14010026







