Random Forest Modelling of High-Dimensional Mixed-Type Data for Breast Cancer Classification
Abstract
Simple Summary
Abstract
1. Introduction
2. Results
2.1. Implementation of Permutation-Based Random Forest Classification
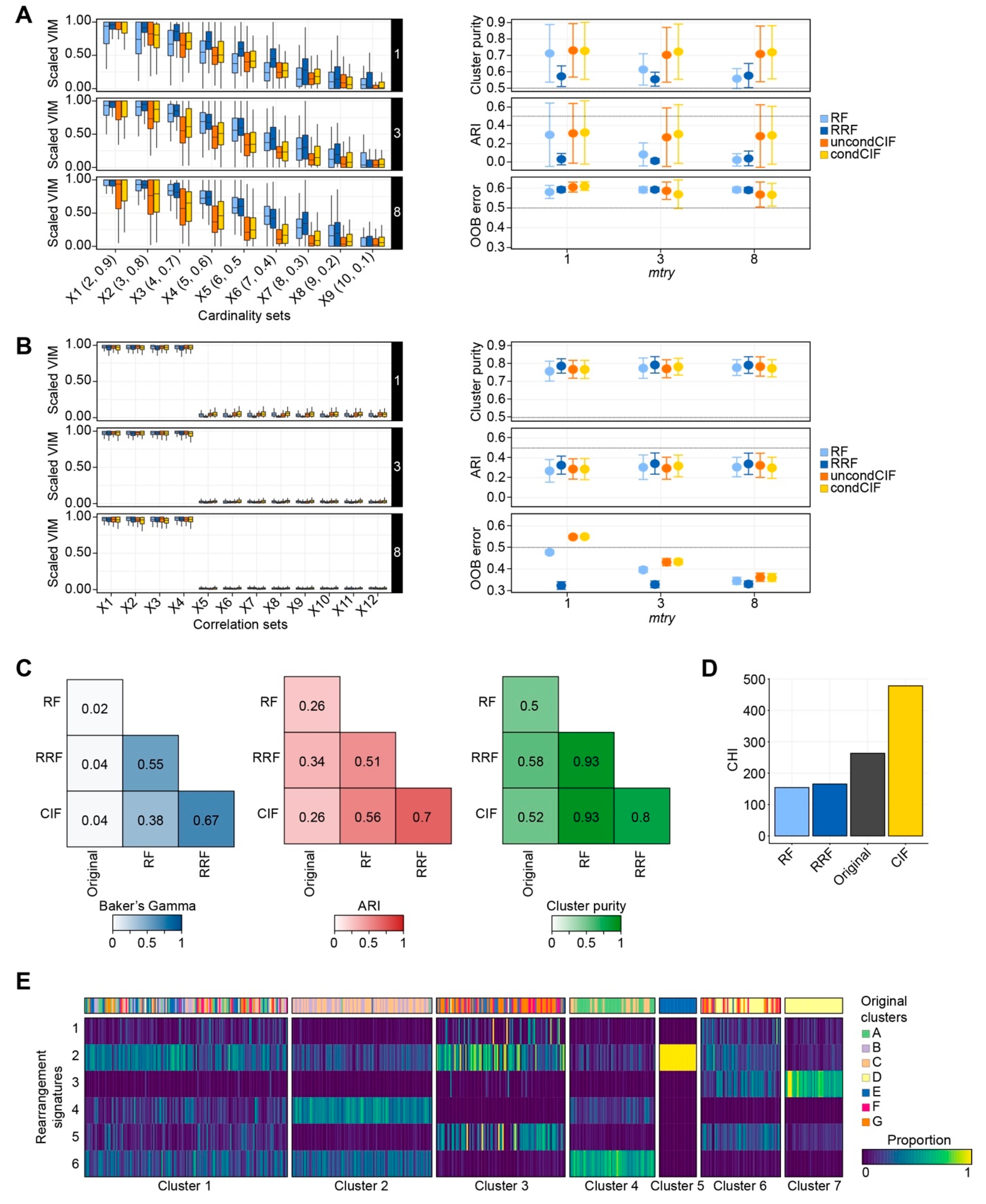
2.1.1. Cardinality in Simulation Studies
2.1.2. Correlation Bias in Simulation Studies
2.1.3. Performance Evaluation Using Real-World Datasets
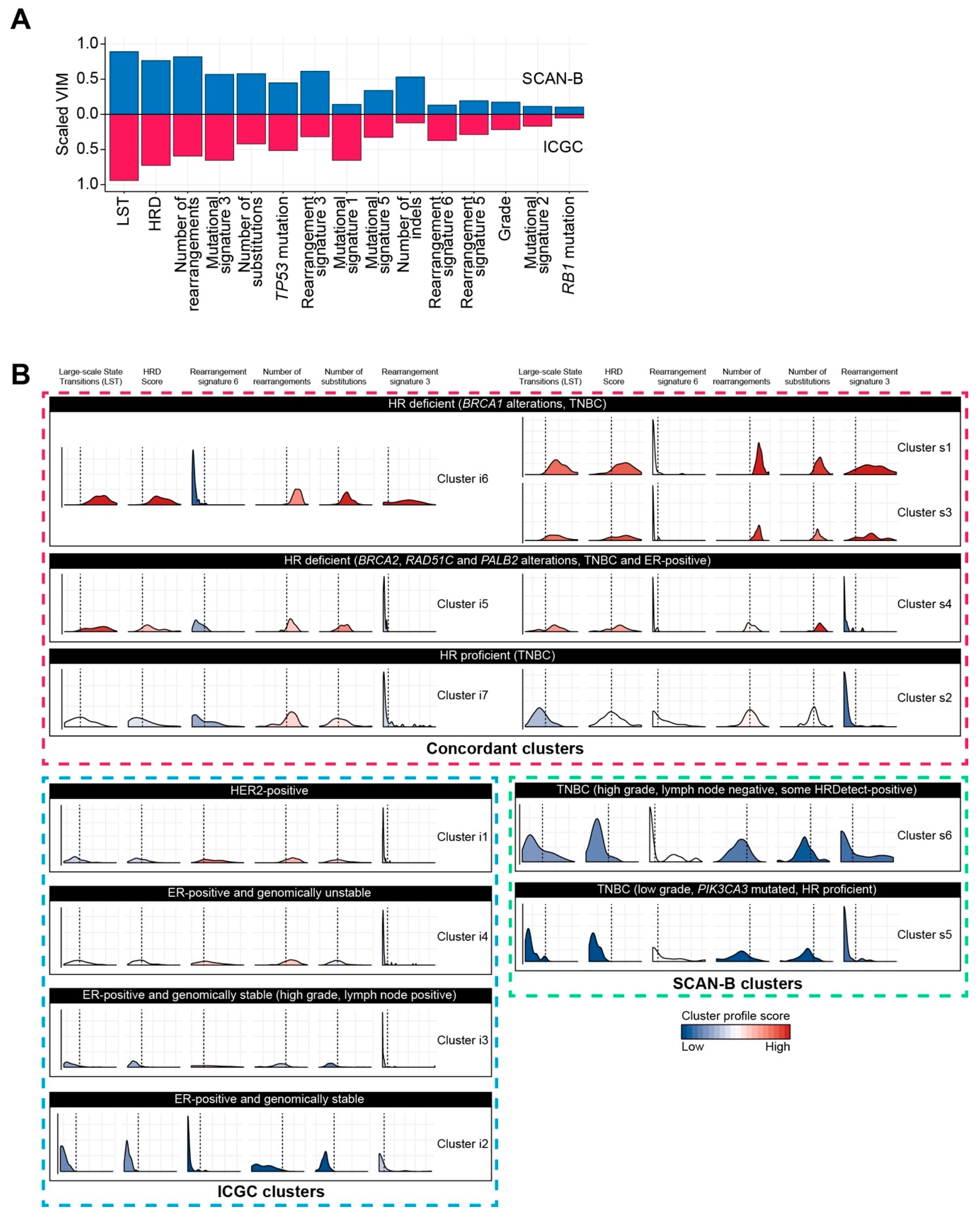
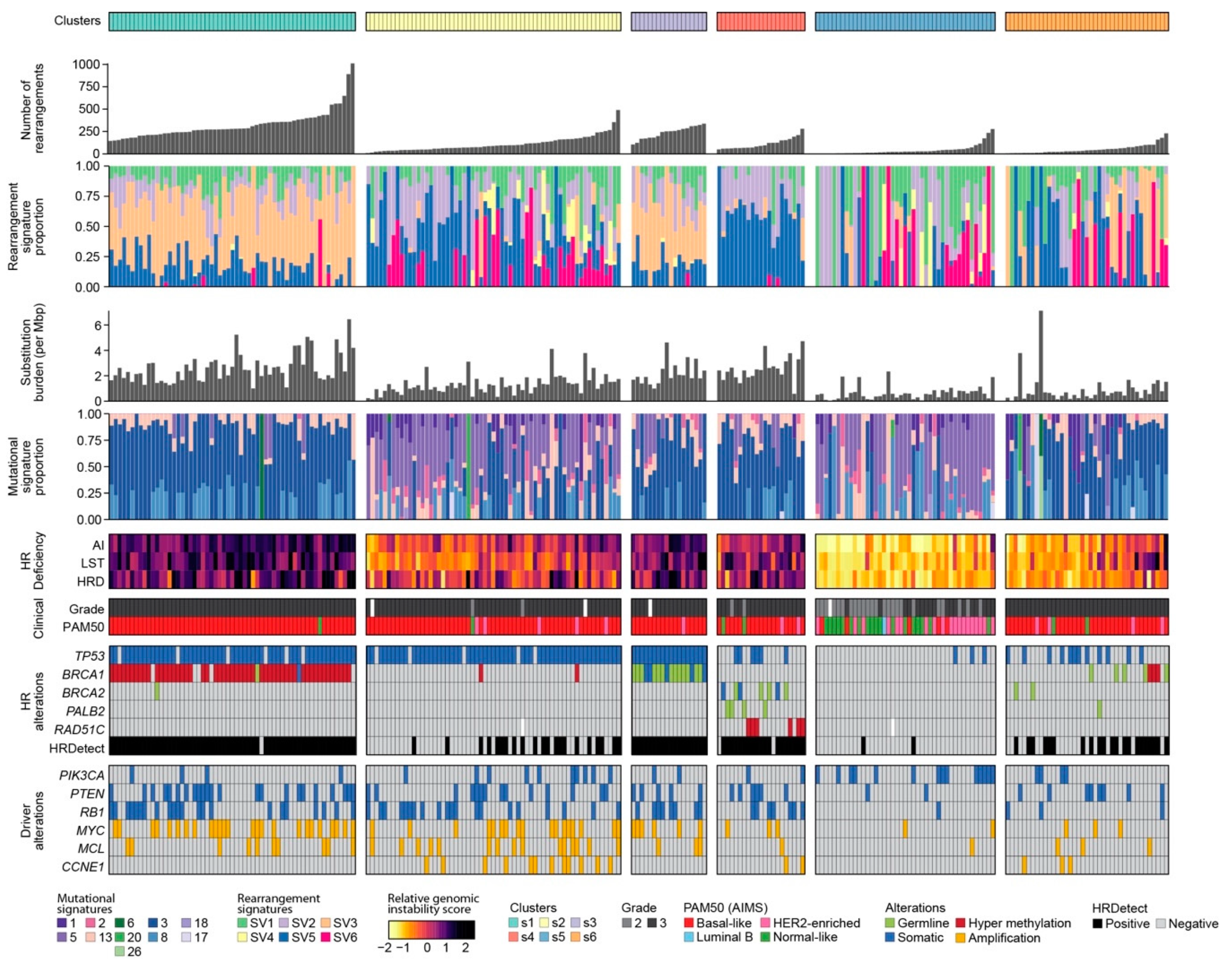
2.2. Classification of Breast Cancers Based on Rearrangement Signatures
2.2.1. Classification of Breast Cancers by Mixed-Type High-Dimensional Data
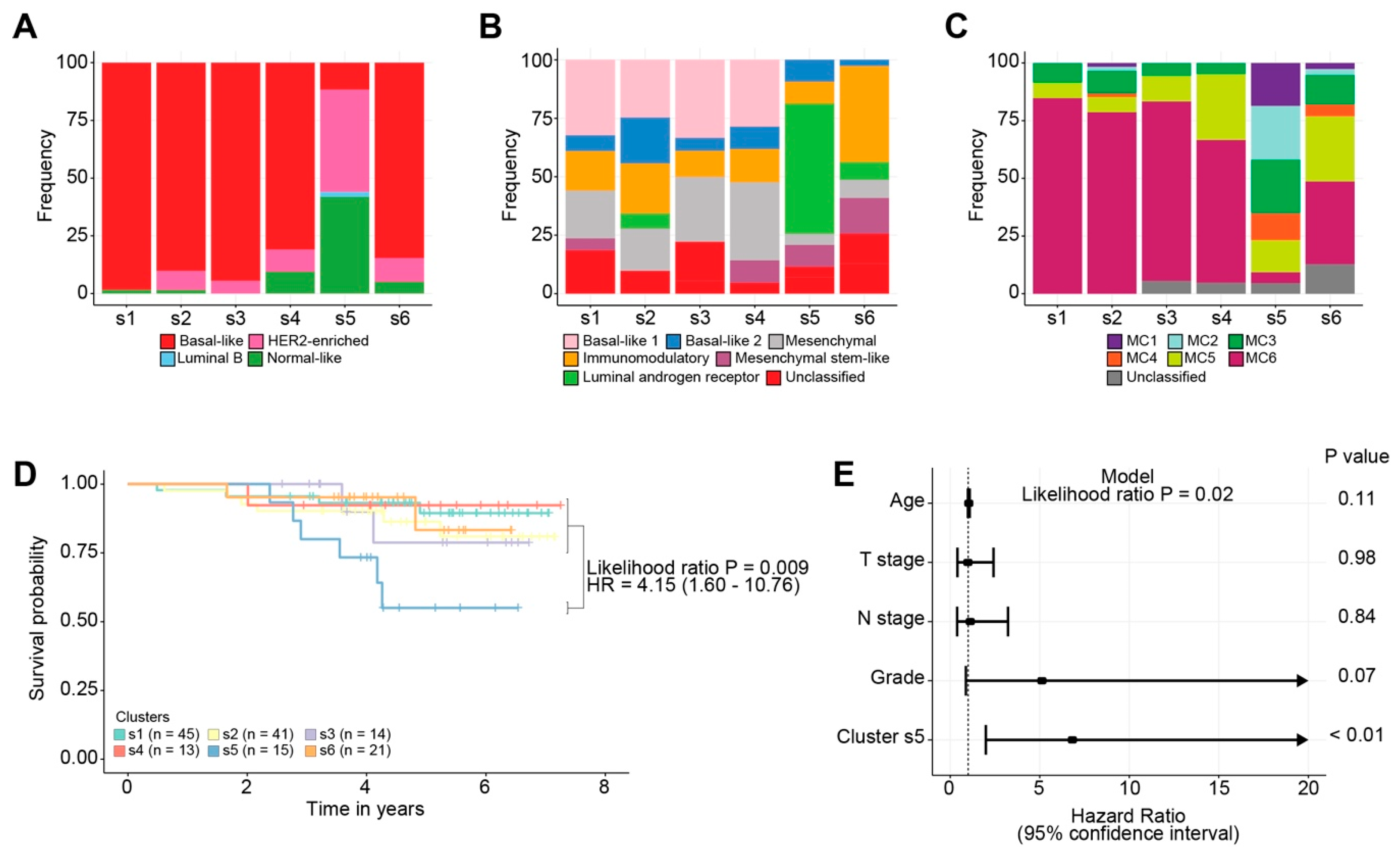
2.2.2. Association of Breast Cancer Classification and Clinical Outcome
3. Discussion
4. Materials and Methods
4.1. Permutation-Based Forest Clustering Algorithm
4.2. Evaluation Metrics
4.3. Datasets
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef] [PubMed]
- Nik-Zainal, S.; Davies, H.; Staaf, J.; Ramakrishna, M.; Glodzik, D.; Zou, X.; Martincorena, I.; Alexandrov, L.B.; Martin, S.; Wedge, D.C.; et al. Landscape of somatic mutations in 560 breast cancer whole-genome sequences. Nature 2016, 534, 47–54. [Google Scholar] [CrossRef]
- Parker, J.S.; Mullins, M.; Cheang, M.C.; Leung, S.; Voduc, D.; Vickery, T.; Davies, S.; Fauron, C.; He, X.; Hu, Z.; et al. Supervised risk predictor of breast cancer based on intrinsic subtypes. J. Clin. Oncol. 2009, 27, 1160–1167. [Google Scholar] [CrossRef] [PubMed]
- Sorlie, T.; Perou, C.M.; Tibshirani, R.; Aas, T.; Geisler, S.; Johnsen, H.; Hastie, T.; Eisen, M.B.; van de Rijn, M.; Jeffrey, S.S.; et al. Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proc. Natl. Acad. Sci. USA 2001, 98, 10869–10874. [Google Scholar] [CrossRef] [PubMed]
- Perou, C.M.; Sorlie, T.; Eisen, M.B.; van de Rijn, M.; Jeffrey, S.S.; Rees, C.A.; Pollack, J.R.; Ross, D.T.; Johnsen, H.; Akslen, L.A.; et al. Molecular portraits of human breast tumours. Nature 2000, 406, 747–752. [Google Scholar] [CrossRef]
- Sestak, I.; Cuzick, J.; Dowsett, M.; Lopez-Knowles, E.; Filipits, M.; Dubsky, P.; Cowens, J.W.; Ferree, S.; Schaper, C.; Fesl, C.; et al. Prediction of late distant recurrence after 5 years of endocrine treatment: A combined analysis of patients from the Austrian breast and colorectal cancer study group 8 and arimidex, tamoxifen alone or in combination randomized trials using the PAM50 risk of recurrence score. J. Clin. Oncol. 2015, 33, 916–922. [Google Scholar] [CrossRef]
- Staaf, J.; Glodzik, D.; Bosch, A.; Vallon-Christersson, J.; Reutersward, C.; Hakkinen, J.; Degasperi, A.; Amarante, T.D.; Saal, L.H.; Hegardt, C.; et al. Whole-genome sequencing of triple-negative breast cancers in a population-based clinical study. Nat. Med. 2019, 25, 1526–1533. [Google Scholar] [CrossRef]
- Davies, H.; Glodzik, D.; Morganella, S.; Yates, L.R.; Staaf, J.; Zou, X.; Ramakrishna, M.; Martin, S.; Boyault, S.; Sieuwerts, A.M.; et al. HRDetect is a predictor of BRCA1 and BRCA2 deficiency based on mutational signatures. Nat. Med. 2017, 23, 517–525. [Google Scholar] [CrossRef]
- Willis, N.A.; Frock, R.L.; Menghi, F.; Duffey, E.E.; Panday, A.; Camacho, V.; Hasty, E.P.; Liu, E.T.; Alt, F.W.; Scully, R. Mechanism of tandem duplication formation in BRCA1-mutant cells. Nature 2017, 551, 590–595. [Google Scholar] [CrossRef]
- Popova, T.; Manie, E.; Rieunier, G.; Caux-Moncoutier, V.; Tirapo, C.; Dubois, T.; Delattre, O.; Sigal-Zafrani, B.; Bollet, M.; Longy, M.; et al. Ploidy and large-scale genomic instability consistently identify basal-like breast carcinomas with BRCA1/2 inactivation. Cancer Res. 2012, 72, 5454–5462. [Google Scholar] [CrossRef] [PubMed]
- Birkbak, N.J.; Wang, Z.C.; Kim, J.Y.; Eklund, A.C.; Li, Q.; Tian, R.; Bowman-Colin, C.; Li, Y.; Greene-Colozzi, A.; Iglehart, J.D.; et al. Telomeric allelic imbalance indicates defective DNA repair and sensitivity to DNA-damaging agents. Cancer Discov. 2012, 2, 366–375. [Google Scholar] [CrossRef]
- Abkevich, V.; Timms, K.M.; Hennessy, B.T.; Potter, J.; Carey, M.S.; Meyer, L.A.; Smith-McCune, K.; Broaddus, R.; Lu, K.H.; Chen, J.; et al. Patterns of genomic loss of heterozygosity predict homologous recombination repair defects in epithelial ovarian cancer. Br. J. Cancer 2012, 107, 1776–1782. [Google Scholar] [CrossRef]
- Telli, M.L.; Timms, K.M.; Reid, J.; Hennessy, B.; Mills, G.B.; Jensen, K.C.; Szallasi, Z.; Barry, W.T.; Winer, E.P.; Tung, N.M.; et al. Homologous Recombination Deficiency (HRD) Score Predicts Response to Platinum-Containing Neoadjuvant Chemotherapy in Patients with Triple-Negative Breast Cancer. Clin. Cancer Res. 2016, 22, 3764–3773. [Google Scholar] [CrossRef] [PubMed]
- Menghi, F.; Inaki, K.; Woo, X.; Kumar, P.A.; Grzeda, K.R.; Malhotra, A.; Yadav, V.; Kim, H.; Marquez, E.J.; Ucar, D.; et al. The tandem duplicator phenotype as a distinct genomic configuration in cancer. Proc. Natl. Acad. Sci. USA 2016, 113, E2373–E2382. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, B.D.; Bauer, J.A.; Chen, X.; Sanders, M.E.; Chakravarthy, A.B.; Shyr, Y.; Pietenpol, J.A. Identification of human triple-negative breast cancer subtypes and preclinical models for selection of targeted therapies. J. Clin. Investig. 2011, 121, 2750–2767. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, B.D.; Jovanovic, B.; Chen, X.; Estrada, M.V.; Johnson, K.N.; Shyr, Y.; Moses, H.L.; Sanders, M.E.; Pietenpol, J.A. Refinement of Triple-Negative Breast Cancer Molecular Subtypes: Implications for Neoadjuvant Chemotherapy Selection. PLoS ONE 2016, 11, e0157368. [Google Scholar] [CrossRef] [PubMed]
- Quist, J.; Mirza, H.; Cheang, M.C.U.; Telli, M.L.; O’Shaughnessy, J.A.; Lord, C.J.; Tutt, A.N.J.; Grigoriadis, A. A Four-gene Decision Tree Signature Classification of Triple-negative Breast Cancer: Implications for Targeted Therapeutics. Mol. Cancer Ther. 2019, 18, 204–212. [Google Scholar] [CrossRef]
- Ali, H.R.; Rueda, O.M.; Chin, S.F.; Curtis, C.; Dunning, M.J.; Aparicio, S.A.; Caldas, C. Genome-driven integrated classification of breast cancer validated in over 7500 samples. Genome Biol. 2014, 15, 431. [Google Scholar] [CrossRef]
- Lord, C.J.; Ashworth, A. PARP inhibitors: Synthetic lethality in the clinic. Science 2017, 355, 1152–1158. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ceriani, L.; Verme, P. The origins of the Gini index: Extracts from VariabilitA e MutabilitA (1912) by Corrado Gini. J. Econ. Inequal. 2012, 10, 1–23. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Toth, R.; Schiffmann, H.; Hube-Magg, C.; Buscheck, F.; Hoflmayer, D.; Weidemann, S.; Lebok, P.; Fraune, C.; Minner, S.; Schlomm, T.; et al. Random forest-based modelling to detect biomarkers for prostate cancer progression. Clin. Epigenetics 2019, 11, 148. [Google Scholar] [CrossRef]
- Bownes, R.J.; Turnbull, A.K.; Martinez-Perez, C.; Cameron, D.A.; Sims, A.H.; Oikonomidou, O. On-treatment biomarkers can improve prediction of response to neoadjuvant chemotherapy in breast cancer. Breast Cancer Res. 2019, 21, 73. [Google Scholar] [CrossRef]
- Rahman, R.; Matlock, K.; Ghosh, S.; Pal, R. Heterogeneity Aware Random Forest for Drug Sensitivity Prediction. Sci. Rep. 2017, 7, 11347. [Google Scholar] [CrossRef]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H. Machine Learning methods for Quantitative Radiomic Biomarkers. Sci. Rep. 2015, 5, 13087. [Google Scholar] [CrossRef] [PubMed]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased Recursive Partitioning: A Conditional Inference Framework. J. Computational Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G. Feature Selection via Regularized Trees. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012. [Google Scholar] [CrossRef]
- Shi, T.; Horvath, S. Unsupervised Learning with Random Forest Predictors. J. Comput. Graph. Stat. 2006, 15, 118–138. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; 2018; Available online: https://www.R-project.org/ (accessed on 27 February 2021)R Foundation for Statistical Computing.
- Nicodemus, K.K.; Malley, J.D.; Strobl, C.; Ziegler, A. The behaviour of random forest permutation-based variable importance measures under predictor correlation. BMC Bioinform. 2010, 11, 110. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 1 January 2019).
- Gong, Y.; Ji, P.; Yang, Y.S.; Xie, S.; Yu, T.J.; Xiao, Y.; Jin, M.L.; Ma, D.; Guo, L.W.; Pei, Y.C.; et al. Metabolic-Pathway-Based Subtyping of Triple-Negative Breast Cancer Reveals Potential Therapeutic Targets. Cell Metab. 2021, 33, 51–64.e59. [Google Scholar] [CrossRef]
- Tsherniak, A.; Vazquez, F.; Montgomery, P.G.; Weir, B.A.; Kryukov, G.; Cowley, G.S.; Gill, S.; Harrington, W.F.; Pantel, S.; Krill-Burger, J.M.; et al. Defining a Cancer Dependency Map. Cell 2017, 170, 564–576.e516. [Google Scholar] [CrossRef] [PubMed]
- Nasejje, J.B.; Mwambi, H.; Dheda, K.; Lesosky, M. A comparison of the conditional inference survival forest model to random survival forests based on a simulation study as well as on two applications with time-to-event data. BMC Med. Res. Methodol. 2017, 17, 115. [Google Scholar] [CrossRef]
- Du, M.; Haag, D.G.; Lynch, J.W.; Mittinty, M.N. Comparison of the Tree-Based Machine Learning Algorithms to Cox Regression in Predicting the Survival of Oral and Pharyngeal Cancers: Analyses Based on SEER Database. Cancers 2020, 12, 2802. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, L.B.; Nik-Zainal, S.; Wedge, D.C.; Aparicio, S.A.; Behjati, S.; Biankin, A.V.; Bignell, G.R.; Bolli, N.; Borg, A.; Borresen-Dale, A.L.; et al. Signatures of mutational processes in human cancer. Nature 2013, 500, 415–421. [Google Scholar] [CrossRef]
- Helleday, T.; Eshtad, S.; Nik-Zainal, S. Mechanisms underlying mutational signatures in human cancers. Nat. Rev. Genet. 2014, 15, 585–598. [Google Scholar] [CrossRef]
- Fribbens, C.; Garcia Murillas, I.; Beaney, M.; Hrebien, S.; O’Leary, B.; Kilburn, L.; Howarth, K.; Epstein, M.; Green, E.; Rosenfeld, N.; et al. Tracking evolution of aromatase inhibitor resistance with circulating tumour DNA analysis in metastatic breast cancer. Ann. Oncol. 2018, 29, 145–153. [Google Scholar] [CrossRef]
- Andre, F.; Ciruelos, E.; Rubovszky, G.; Campone, M.; Loibl, S.; Rugo, H.S.; Iwata, H.; Conte, P.; Mayer, I.A.; Kaufman, B.; et al. Alpelisib for PIK3CA-Mutated, Hormone Receptor-Positive Advanced Breast Cancer. N. Engl. J. Med. 2019, 380, 1929–1940. [Google Scholar] [CrossRef] [PubMed]
- Tung, N.; Arun, B.; Hacker, M.R.; Hofstatter, E.; Toppmeyer, D.L.; Isakoff, S.J.; Borges, V.; Legare, R.D.; Isaacs, C.; Wolff, A.C.; et al. TBCRC 031: Randomized Phase II Study of Neoadjuvant Cisplatin Versus Doxorubicin-Cyclophosphamide in Germline BRCA Carriers With HER2-Negative Breast Cancer (the INFORM trial). J. Clin. Oncol. 2020, 38, 1539–1548. [Google Scholar] [CrossRef]
- Wilkerson, M.D.; Hayes, D.N. ConsensusClusterPlus: A class discovery tool with confidence assessments and item tracking. Bioinformatics 2010, 26, 1572–1573. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Uriarte, R.; Alvarez de Andres, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.M.; Embrechts, M. On the Use of the Adjusted Rand Index as a Metric for Evaluating Supervised Classification. In Proceedings of the 19th International Conference on Artificial Neural Networks: Part II, Limassol, Cyprus, 14–17 September 2009; pp. 175–184. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schuetze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Baker, F.B. Stability of two hierarchical grouping techniques Case I: Sensitivity to data errors. J. Am. Stat. Assoc. 1974, 69, 440–445. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quist, J.; Taylor, L.; Staaf, J.; Grigoriadis, A. Random Forest Modelling of High-Dimensional Mixed-Type Data for Breast Cancer Classification. Cancers 2021, 13, 991. https://doi.org/10.3390/cancers13050991
Quist J, Taylor L, Staaf J, Grigoriadis A. Random Forest Modelling of High-Dimensional Mixed-Type Data for Breast Cancer Classification. Cancers. 2021; 13(5):991. https://doi.org/10.3390/cancers13050991
Chicago/Turabian StyleQuist, Jelmar, Lawson Taylor, Johan Staaf, and Anita Grigoriadis. 2021. "Random Forest Modelling of High-Dimensional Mixed-Type Data for Breast Cancer Classification" Cancers 13, no. 5: 991. https://doi.org/10.3390/cancers13050991
APA StyleQuist, J., Taylor, L., Staaf, J., & Grigoriadis, A. (2021). Random Forest Modelling of High-Dimensional Mixed-Type Data for Breast Cancer Classification. Cancers, 13(5), 991. https://doi.org/10.3390/cancers13050991





