A Geant4-DNA Evaluation of Radiation-Induced DNA Damage on a Human Fibroblast
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
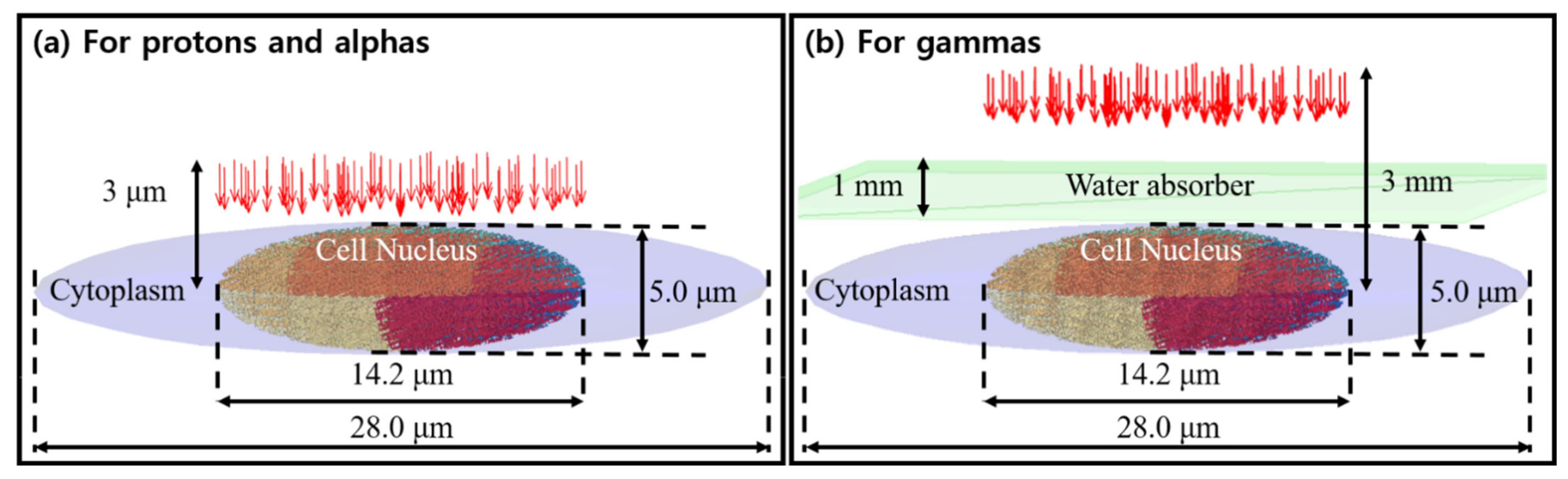
2.1. DNA Geometry
2.2. DNA Damage and Scoring
2.3. Simulation Configuration for Validation Study Using a Simplified Human Fibroblast Cell
2.4. Cell Repair Model
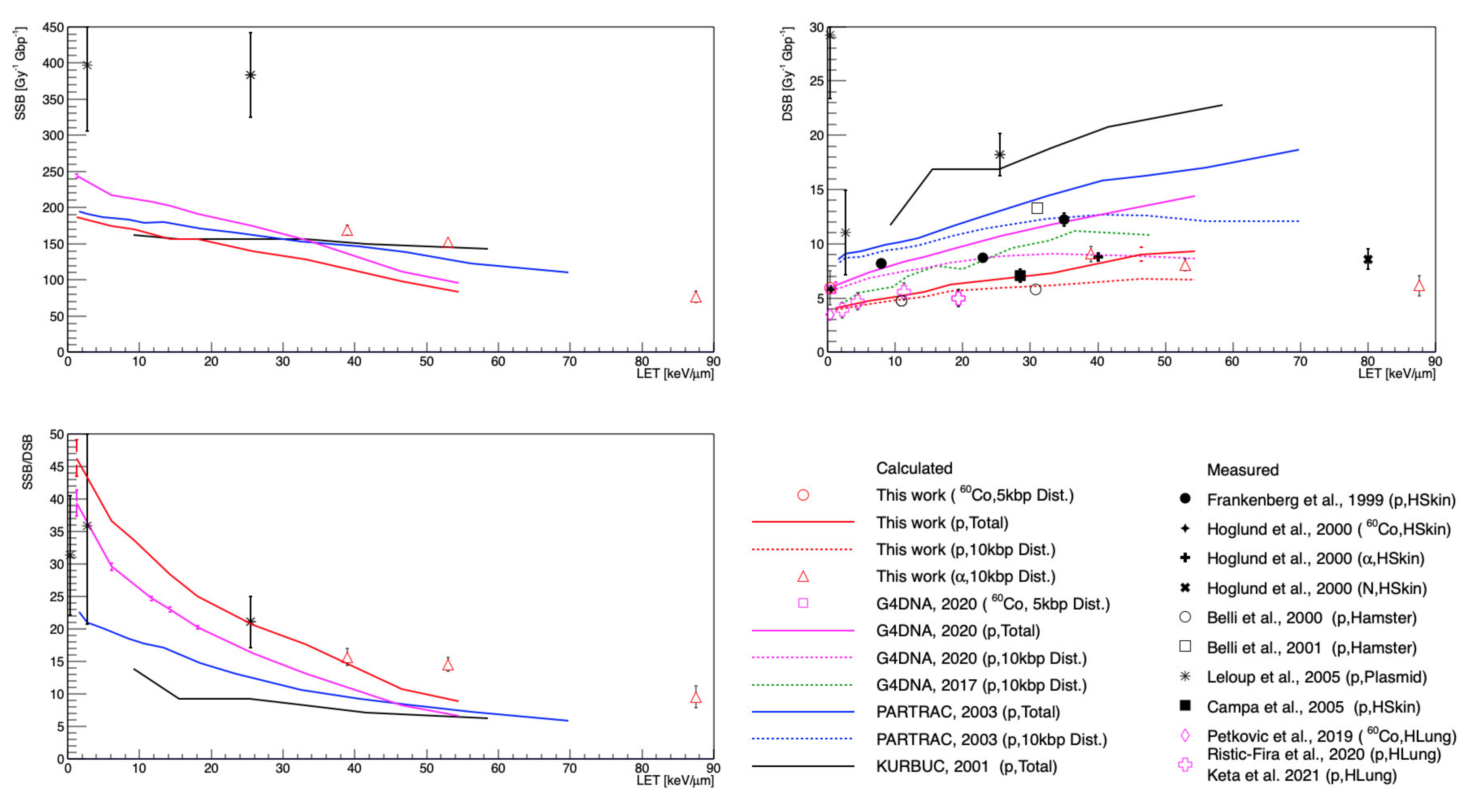
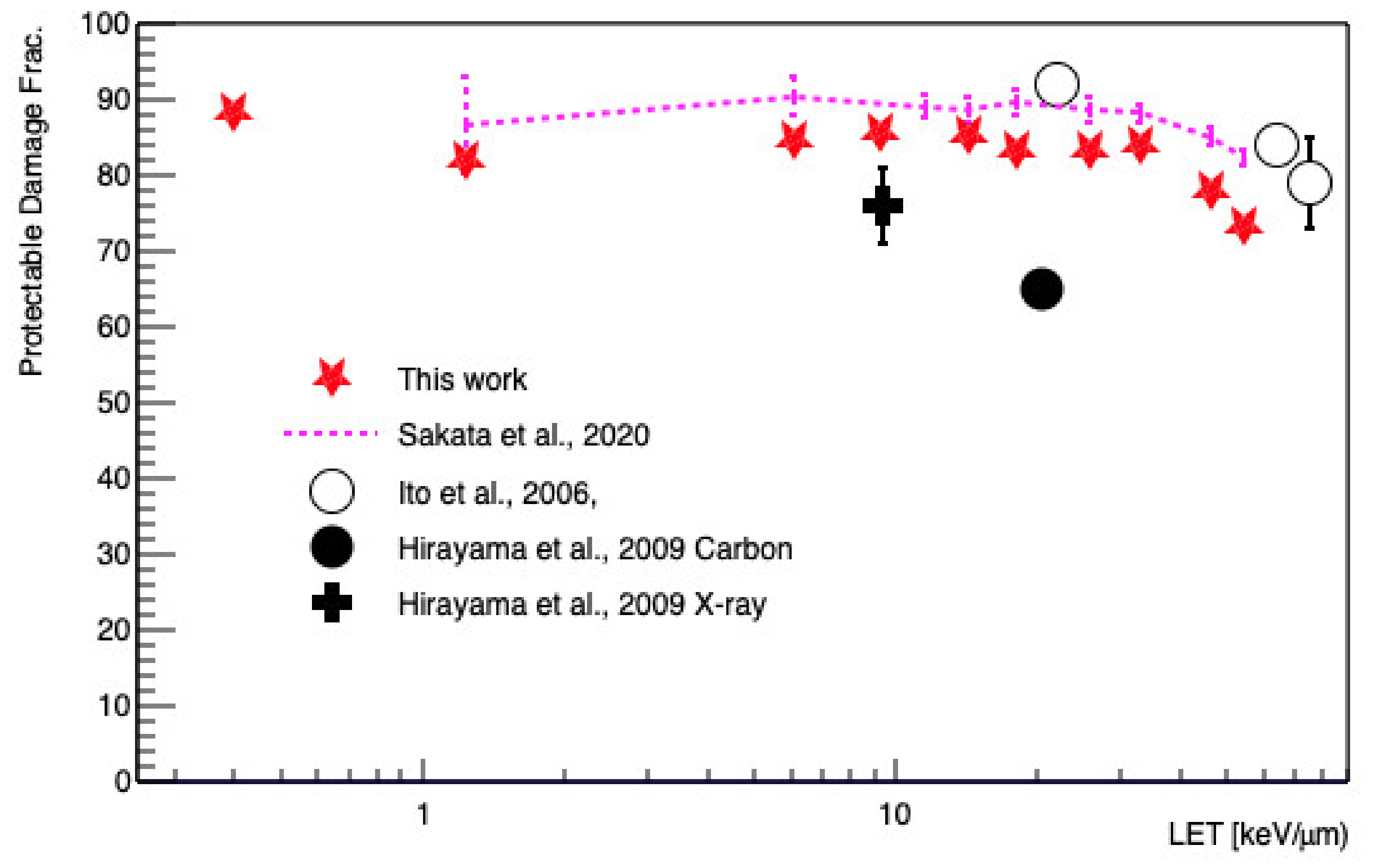
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nikjoo, H.; Emfietzoglou, D.; Liamsuwan, T.; Taleei, R.; Liljequist, D.; Uehara, S. Radiation track, DNA damage and response—A review. Rep. Prog. Phys. 2016, 79, 116601. [Google Scholar] [CrossRef]
- Keta, O.; Petkovic, V.D.; Cirrone, P.; Petringa, G.; Cuttone, G.; Sakata, D.; Shin, W.G.; Incerti, S.; Petrovic, I.; Ristić Fira, A. DNA double-strand breaks in cancer cells as a function of proton linear energy transfer and its variation in time. Int. J. Radiat. Biol. 2021, 97, 1229–1240. [Google Scholar] [CrossRef]
- Dingfelder, M. Track-structure simulations for charged particles. Health Phys. 2012, 103, 590–595. [Google Scholar] [CrossRef] [PubMed]
- Friedland, W.; Dingfelder, M.; Kundrat, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. 2011, 711, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Incerti, S.; Baldacchino, G.; Bernal, M.; Capra, R.; Champion, C.; Francis, Z.; Guèye, P.; Mantero, A.; Mascialino, B.; Moretto, P. The Geant4-DNA project. Int. J. Model. Simul. Sci. Comput. 2010, 1, 157–178. [Google Scholar] [CrossRef]
- Incerti, S.; Ivanchenko, A.; Karamitros, M.; Mantero, A.; Moretto, P.; Tran, H.; Mascialino, B.; Champion, C.; Ivanchenko, V.; Bernal, M. Comparison of GEANT4 very low energy cross section models with experimental data in water. Med. Phys. 2010, 37, 4692–4708. [Google Scholar] [CrossRef]
- Bernal, M.A.; Bordage, M.C.; Brown, J.M.C.; Davidkova, M.; Delage, E.; El Bitar, Z.; Enger, S.A.; Francis, Z.; Guatelli, S.; Ivanchenko, V.N.; et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys. Med. 2015, 31, 861–874. [Google Scholar] [CrossRef]
- Incerti, S.; Kyriakou, I.; Bernal, M.; Bordage, M.C.; Francis, Z.; Guatelli, S.; Ivanchenko, V.; Karamitros, M.; Lampe, N.; Lee, S.B.; et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med. Phys. 2018, 45, e722–e739. [Google Scholar] [CrossRef]
- McNamara, A.; Geng, C.; Turner, R.; Mendez, J.R.; Perl, J.; Held, K.; Faddegon, B.; Paganetti, H.; Schuemann, J. Validation of the radiobiology toolkit TOPAS-nBio in simple DNA geometries. Phys. Med. 2017, 33, 207–215. [Google Scholar] [CrossRef]
- Plante, I.; Ponomarev, A.; Patel, Z.; Slaba, T.; Hada, M. RITCARD: Radiation-Induced Tracks, Chromosome Aberrations, Repair and Damage. Radiat. Res. 2019, 192, 282–298. [Google Scholar] [CrossRef] [PubMed]
- Lampe, N. The Long Term Impact of Ionising Radiation on Living Systems. Ph.D. Thesis, Université Clermont Auvergne, Clermont, France, 2017. [Google Scholar]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.; Kyriakou, I.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA part 1: A parameter study in a simplified geometry. Phys. Med. 2018, 48, 135–145. [Google Scholar] [CrossRef]
- Lampe, N.; Karamitros, M.; Breton, V.; Brown, J.M.C.; Sakata, D.; Sarramia, D.; Incerti, S. Mechanistic DNA damage simulations in Geant4-DNA Part 2: Electron and proton damage in a bacterial cell. Phys. Med. 2018, 48, 146–155. [Google Scholar] [CrossRef]
- Sakata, D.; Lampe, N.; Karamitros, M.; Kyriakou, I.; Belov, O.; Bernal, M.A.; Bolst, D.; Bordage, M.C.; Breton, V.; Brown, J.M.C.; et al. Evaluation of early radiation DNA damage in a fractal cell nucleus model using Geant4-DNA. Phys. Med. 2019, 62, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Sakata, D.; Belov, O.; Bordage, M.C.; Emfietzoglou, D.; Guatelli, S.; Inaniwa, T.; Ivanchenko, V.; Karamitros, M.; Kyriakou, I.; Lampe, N.; et al. Fully integrated Monte Carlo simulation for evaluating radiation induced DNA damage and subsequent repair using Geant4-DNA. Sci. Rep. 2020, 10, 20788. [Google Scholar] [CrossRef]
- Meylan, S.; Incerti, S.; Karamitros, M.; Tang, N.; Bueno, M.; Clairand, I.; Villagrasa, C. Simulation of early DNA damage after the irradiation of a fibroblast cell nucleus using Geant4-DNA. Sci. Rep. 2017, 7, 11923. [Google Scholar] [CrossRef] [PubMed]
- Shin, W.G.; Bordage, M.C.; Emfietzoglou, D.; Kyriakou, I.; Sakata, D.; Min, C.H.; Lee, S.B.; Guatelli, S.; Incerti, S. Development of a new Geant4-DNA electron elastic scattering model for liquid-phase water using the ELSEPA code. J. Appl. Phys. 2018, 124, 224901. [Google Scholar] [CrossRef]
- Shin, W.-G.; Ramos-Mendez, J.; Tran, N.H.; Okada, S.; Perrot, Y.; Villagrasa, C.; Incerti, S. Geant4-DNA simulation of the pre-chemical stage of water radiolysis and its impact on initial radiochemical yields. Phys. Med. 2021, 88, 86–90. [Google Scholar] [CrossRef]
- Shin, W.G.; Ramos-Mendez, J.; Faddegon, B.; Tran, H.N.; Villagrasa, C.; Perrot, Y.; Okada, S.; Karamitros, M.; Emfietzoglou, D.; Kyriakou, I.; et al. Evaluation of the influence of physical and chemical parameters on water radiolysis simulations under MeV electron irradiation using Geant4-DNA. J. Appl. Phys. 2019, 126, 114301. [Google Scholar] [CrossRef]
- Ramos-Mendez, J.; Shin, W.G.; Dominguez-Kondo, J.N.; Incerti, S.; Tran, H.N.; Villagrasa, C.; Perrot, Y.; Stepan, V.; Karamitros, M.; Okada, S.; et al. Independent reaction times method in Geant4-DNA: Implementation and performance. Med. Phys. 2020, 47, 5919–5930. [Google Scholar] [CrossRef]
- Hilbert, D. Über die stetige Abbildung einer Linie auf ein Flächenstück. In Dritter Band: Analysis·Grundlagen der Mathematik Physik Verschiedenes; Springer: Berlin/Heidelberg, Germany, 1935; pp. 1–2. [Google Scholar]
- Nikjoo, H.; O’Neill, P.; Goodhead, D.T.; Terrissol, M. Computational modelling of low-energy electron-induced DNA damage by early physical and chemical events. Int. J. Radiat. Biol. 1997, 71, 467–483. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Paretzke, H.G.; Dingfelder, M. Simulation of DNA Damage after Proton Irradiation. Radiat. Res. 2003, 159, 401–410. [Google Scholar] [CrossRef]
- Prise, K.M.; Folkard, M.; Michael, B.D.; Vojnovic, B.; Brocklehurst, B.; Hopkirk, A.; Munro, I.H. Critical energies for SSB and DSB induction in plasmid DNA by low-energy photons: Action spectra for strand-break induction in plasmid DNA irradiated in vacuum. Int. J. Radiat. Biol. 2000, 76, 881–890. [Google Scholar] [CrossRef] [PubMed]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 2000, 287, 1658–1660. [Google Scholar]
- Ljungman, M.; Nyberg, S.; Nygren, J.; Eriksson, M.; Ahnström, G. DNA-bound proteins contribute much more than soluble intracellular compounds to the intrinsic protection against radiation-induced DNA strand breaks in human cells. Radiat. Res. 1991, 127, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Daly, M.J. Death by protein damage in irradiated cells. DNA Repair 2012, 11, 12–21. [Google Scholar] [CrossRef]
- Karamitros, M.; Brown, J.M.C.; Lampe, N.; Sakata, D.; Tran, H.N.; Shin, W.G.; Ramos-Mendez, J.; Guatelli, S.; Incerti, S.; LaVerne, J.A. Implementing the independent reaction time method in Geant4 for radiation chemistry simulations. Arxiv 2020, arXiv:2006.14225. [Google Scholar]
- Tran, H.N.; Ramos-Mendez, J.; Shin, W.G.; Perrot, Y.; Faddegon, B.; Okada, S.; Karamitros, M.; Davidkova, M.; Stepan, V.; Incerti, S.; et al. Assessment of DNA damage with an adapted independent reaction time approach implemented in Geant4-DNA for the simulation of diffusion-controlled reactions between radio-induced reactive species and a chromatin fiber. Med. Phys. 2021, 48, 890–901. [Google Scholar] [CrossRef]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (⋅OH/⋅O− in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef]
- Meesungnoen, J.; Jay-Gerin, J.-P.; Filali-Mouhim, A.; Mankhetkorn, S. Low-energy electron penetration range in liquid water. Radiat. Res. 2002, 158, 657–660. [Google Scholar] [CrossRef]
- Shin, W.G. Development and Application of the Geant4-DNA Toolkit for the Simulation of Radiobiological Effects at the Sub-Cellular Scale. Ph.D. Thesis, Bordeaux and Yonsei University, Bordeaux, France, 2021. [Google Scholar]
- Finkel, R.; Friedman, J.; Bentley, J. An algorithm for finding best matches in logarithmic expected time. ACM T. Math. Softw. 1977, 3, 200–226. [Google Scholar]
- Mitsui, Y.; Schneider, E.L. Relationship between cell replication and volume in senescent human diploid fibroblasts. Mech. Ageing Dev. 1976, 5, 45–46. [Google Scholar] [CrossRef]
- Lamond, A.I.; Sleeman, J.E. Nuclear substructure and dynamics. Curr. Biol. 2003, 13, R825–R828. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Suzuki, S.; Yamanashi, T.; Tazawa, S.; Kurosawa, O.; Washizu, M. Quantitative analysis of DNA orientation in stationary AC electric fields using fluorescence anisotropy. IEEE T. Ind. Appl. 1998, 34, 75–83. [Google Scholar] [CrossRef]
- Zhong, S.; Ghosh, S.K.; Jost, D. How epigenome drives chromatin folding and dynamics, insights from efficient coarse-grained models of chromosomes. PLoS Comput. Biol. 2018, 14, e1006159. [Google Scholar] [CrossRef]
- Asaithamby, A.; Uematsu, N.; Chatterjee, A.; Story, M.D.; Burma, S.; Chen, D.J. Repair of HZE-particle-induced DNA double-strand breaks in normal human fibroblasts. Radiat. Res. 2008, 169, 437–446. [Google Scholar] [CrossRef]
- ICRU. Key Data for Ionizing-Radiation Dosimetry: Measurement Standards and Applications; The International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 2014. [Google Scholar]
- Frankenberg, D.; Brede, H.J.; Schrewe, U.J.; Steinmetz, C.; Frankenberg-Schwager, M.; Kasten, G.; Pralle, E. Induction of DNA double-strand breaks by 1H and 4He ions in primary human skin fibroblasts in the LET range of 8 to 124 keV/μm. Radiat. Res. 1999, 151, 540–549. [Google Scholar] [CrossRef]
- Hoglund, E.; Blomquist, E.; Carlsson, J.; Stenerlow, B. DNA damage induced by radiation of different linear energy transfer: Initial fragmentation. Int. J. Radiat. Biol. 2000, 76, 539–547. [Google Scholar] [CrossRef]
- Belli, M.; Cherubini, R.; Dalla Vecchia, M.; Dini, V.; Moschini, G.; Signoretti, C.; Simone, G.; Tabocchini, M.A.; Tiveron, P. DNA DSB induction and rejoining in V79 cells irradiated with light ions: A constant field gel electrophoresis study. Int. J. Radiat. Biol. 2000, 76, 1095–1104. [Google Scholar] [CrossRef]
- Belli, M.; Cherubini, R.; Vecchia, D.; Dini, V.; Esposito, G.; Moschini, G.; Sapora, O.; Signoretti, C.; Simone, G.; Sorrentino, E.; et al. DNA fragmentation in mammalian cells exposed to various light ions. Adv. Space Res. 2001, 27, 393–399. [Google Scholar] [CrossRef]
- Leloup, C.; Garty, G.; Assaf, G.; Cristovao, A.; Breskin, A.; Chechik, R.; Shchemelinin, S.; Paz-Elizur, T.; Livneh, Z.; Schulte, R.W.; et al. Evaluation of lesion clustering in irradiated plasmid DNA. Int. J. Radiat. Biol. 2005, 81, 41–54. [Google Scholar] [CrossRef] [PubMed]
- Campa, A.; Ballarini, F.; Belli, M.; Cherubini, R.; Dini, V.; Esposito, G.; Friedland, W.; Gerardi, S.; Molinelli, S.; Ottolenghi, A.; et al. DNA DSB induced in human cells by charged particles and gamma rays: Experimental results and theoretical approaches. Int. J. Radiat. Biol. 2005, 81, 841–854. [Google Scholar] [CrossRef]
- Kryndushkin, D.S.; Alexandrov, I.M.; Ter-Avanesyan, M.D.; Kushnirov, V.V. Yeast [PSI+] Prion Aggregates Are Formed by Small Sup35 Polymers Fragmented by Hsp104. J. Biol. Chem. 2003, 278, 49636–49643. [Google Scholar] [CrossRef] [PubMed]
- Iliakis, G.E.; Cicilioni, O.; Metzger, L. Measurement of DNA Double-strand Breaks in CHO Cells at Various Stages of the Cell Cycle Using Pulsed Field Gel Electrophoresis: Calibration by Means of125I Decay. Int. J. Radiat. Biol. 2009, 59, 343–357. [Google Scholar] [CrossRef] [PubMed]
- Olive, P.L. Detection of DNA damage in individual cells by analysis of histone H2AX phosphorylation. Methods Cell Biol. 2004, 75, 355–373. [Google Scholar] [PubMed]
- Rothkamm, K.; Barnard, S.; Moquet, J.; Ellender, M.; Rana, Z.; Burdak-Rothkamm, S. DNA damage foci: Meaning and significance. Environ. Mol. Mutagen. 2015, 56, 491–504. [Google Scholar] [CrossRef]
- Redon, C.E.; Dickey, J.S.; Bonner, W.M.; Sedelnikova, O.A. Gamma-H2AX as a biomarker of DNA damage induced by ionizing radiation in human peripheral blood lymphocytes and artificial skin. Adv. Space Res. 2009, 43, 1171–1178. [Google Scholar] [CrossRef]
- Löbrich, M.; Shibata, A.; Beucher, A.; Fisher, A.; Ensminger, M.; Goodarzi, A.A.; Barton, O.; Jeggo, P.A. γH2AX foci analysis for monitoring DNA double-strand break repair: Strengths, limitations and optimization. Cell Cycle 2010, 9, 662–669. [Google Scholar] [CrossRef]
- Petkovic, V.D.; Keta, O.D.; Vidosavljevic, M.Z.; Incerti, S.; Ristic Fira, A.M.; Petrovic, I.M. Biological outcomes of gamma-radiation induced DNA damages in breast and lung cancer cells pretreated with free radical scavengers. Int. J. Radiat. Biol. 2019, 95, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Ristić Fira, A.; Keta, O.; Petkovic, V.D.; Cammarata, F.; Petringa, G.; Cirrone, G.A.; Cuttone, G.; Incerti, S.; Petrovic, I. DNA damage assessment of human breast and lung carcinoma cells irradiated with protons and carbon ions. J. Radiat. Res. Appl. Sci. 2020, 13, 672–687. [Google Scholar] [CrossRef]
- Nikitaki, Z.; Nikolov, V.; Mavragani, I.V.; Plante, I.; Emfietzoglou, D.; Iliakis, G.; Georgakilas, A.G. Non-DSB clustered DNA lesions. Does theory colocalize with the experiment? Radiat. Phys. Chem. 2016, 128, 26–35. [Google Scholar] [CrossRef]
- Nikitaki, Z.; Nikolov, V.; Mavragani, I.V.; Mladenov, E.; Mangelis, A.; Laskaratou, D.A.; Fragkoulis, G.I.; Hellweg, C.E.; Martin, O.A.; Emfietzoglou, D. Measurement of complex DNA damage induction and repair in human cellular systems after exposure to ionizing radiations of varying linear energy transfer (LET). Free Radical Res. 2016, 50, S64–S78. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; O’Neill, P.; Wilson, W.E.; Goodhead, D.T. Computational approach for determining the spectrum of DNA damage induced by ionizing radiation. Radiat. Res. 2001, 156, 577–583. [Google Scholar] [CrossRef]
- Ito, A.; Nakano, H.; Kusano, Y.; Hirayama, R.; Furusawa, Y.; Murayama, C.; Mori, T.; Katsumura, Y.; Shinohara, K. Contribution of indirect action to radiation-induced mammalian cell inactivation: Dependence on photon energy and heavy-ion LET. Radiat. Res. 2006, 165, 703–712. [Google Scholar] [CrossRef] [PubMed]
- Hirayama, R.; Ito, A.; Tomita, M.; Tsukada, T.; Yatagai, F.; Noguchi, M.; Matsumoto, Y.; Kase, Y.; Ando, K.; Okayasu, R.; et al. Contributions of direct and indirect actions in cell killing by high-LET radiations. Radiat. Res. 2009, 171, 212–218. [Google Scholar] [CrossRef]
- Lea, D.E. Actions of Radiations on Living Cells, 2nd ed.; Cambridge University Press: Cambridge, UK, 1955. [Google Scholar]
- Negritto, M.C. Reparing double-strand DNA breaks. Nat. Educ. 2010, 3, 26. [Google Scholar]
- Frankenberg-Schwager, M. Review of repair kinetics for DNA damage induced in eukaryotic cells in vitro by ionizing radiation. Radiother. Oncol. 1989, 14, 307–320. [Google Scholar] [CrossRef]
- Belov, O.V.; Krasavin, E.A.; Lyashko, M.S.; Batmunkh, M.; Sweilam, N.H. A quantitative model of the major pathways for radiation-induced DNA double-strand break repair. J. Theor. Biol. 2015, 366, 115–130. [Google Scholar] [CrossRef]
- Heyer, W.D.; Ehmsen, K.T.; Liu, J. Regulation of homologous recombination in eukaryotes. Annu. Rev. Genet. 2010, 44, 113–139. [Google Scholar] [CrossRef]
- Decottignies, A. Alternative end-joining mechanisms: A historical perspective. Front. Genet. 2013, 4, 48. [Google Scholar] [CrossRef]
- Valentin, J. Relative biological effectiveness (RBE), quality factor (Q), and radiation weighting factor (wR). Ann. ICRP 2016, 92, 1–121. [Google Scholar] [CrossRef]
- Hall, E.J.; Giaccia, A.J. Radiobiology for the Radiologist, 8th ed.; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2018. [Google Scholar]
- Zhu, H.; McNamara, A.L.; Ramos-Mendez, J.; McMahon, S.J.; Henthorn, N.T.; Faddegon, B.; Held, K.D.; Perl, J.; Li, J.; Paganetti, H.; et al. A parameter sensitivity study for simulating DNA damage after proton irradiation using TOPAS-nBio. Phys. Med. Biol. 2020, 65, 085015. [Google Scholar] [CrossRef]
- Pinto, M.; Newman, H.C.; Prise, K.M.; Michael, B.D. Quantification of DNA damage by PFGE: Development of an analytical approach to correct for the background distribution. Int. J. Radiat. Biol. 2000, 76, 741–748. [Google Scholar] [CrossRef] [PubMed]
- Newman, H.C.; Prise, K.M.; Michael, B.D. The role of higher-order chromatin structure in the yield and distribution of DNA double-strand breaks in cells irradiated with X-rays or alpha-particles. Int. J. Radiat. Biol. 2000, 76, 1085–1093. [Google Scholar] [CrossRef] [PubMed]
- Tang, N.; Bueno, M.; Meylan, S.; Perrot, Y.; Tran, H.N.; Freneau, A.; Dos Santos, M.; Vaurijoux, A.; Gruel, G.; Bernal, M.A.; et al. Assessment of radio-induced damage in endothelial cells irradiated with 40 kVp, 220 kVp, and 4 MV X-rays by means of micro and nanodosimetric calculations. Int. J. Mol. Sci. 2019, 20, 6204. [Google Scholar] [CrossRef]
- Kyriakou, I.; Incerti, S.; Francis, Z. Technical Note: Improvements in Geant4 energy-loss model and the effect on low-energy electron transport in liquid water. Med. Phys. 2015, 42, 3870–3876. [Google Scholar] [CrossRef] [PubMed]
- Kyriakou, I.; Šefl, M.; Nourry, V.; Incerti, S. The impact of new Geant4-DNA cross section models on electron track structure simulations in liquid water. J. Appl. Phys. 2016, 119, 194902. [Google Scholar] [CrossRef]



| Damage Parameters | Values [15] |
|---|---|
| Rdirect | 3.5 Å |
| Elower | 5 eV |
| Ehigher | 37.5 eV |
| POH | 40.5% |
| dkill | 9 nm |
| Tchem | 5 ns |
| dtmax | 0.5 ns |
| Reference | Cell Line | Description | Damage Measurement |
|---|---|---|---|
| Frankenberg et al. (1999) [40] | - | Human fibroblasts | PFGE |
| Hoglund et al. (2000) [41] | GM5758 | Human fibroblasts | PFGE |
| Belli et al. (2000) [42] | V79 | Chinese hamster cells | CFGE |
| Belli et al. (2001) [43] | PFGE | ||
| Leloup et al. (2005) [44] | XL2-Blue MRF | Plasmid DNA of bacteria | PFGE |
| Campa et al. (2005) [45] | AG1522 | Human fibroblasts | PFGE |
| Petkovic et al. (2019) [52] | HTB177 | Non-small lung cancer cells | γ-H2AX |
| Ristic-Fira et al. (2020) [53] Keta et al. (2021) [2] |
| Energy (MeV) | ICRU-90 LET in Water [39] (keV/μm) | Total Number of Particles | Run Splitting | Simulation Time per Run (CPU Hours) |
|---|---|---|---|---|
| Gamma Rays | ||||
| 137Cs | 0.8 (a) | 25,000,000 (b) | 25 | 47.43 |
| 60Co | 0.4 (a) | 5,000,000 | 10 | 56.69 |
| Protons | ||||
| 0.30 | 54.41 | 3000 | 30 | 146.90 |
| 0.40 | 46.48 | 3000 | 30 | 101.76 |
| 0.70 | 33.14 | 3000 | 30 | 44.60 |
| 1.00 | 25.77 | 3600 (c) | 36 | 27.78 |
| 1.67 | 18.12 | 3000 | 30 | 15.46 |
| 2.34 | 14.31 | 8000 | 20 | 100.63 |
| 4.00 | 9.33 | 10,000 | 1 | 435.54 |
| 7.00 | 6.11 | 10,000 | 1 | 654.87 |
| 50.00 | 1.24 | 10,000 | 1 | 25.67 |
| Alphas | ||||
| 5.00 | 87.54 | 100 | 10 | 29.67 |
| 10.00 | 52.94 | 100 | 10 | 21.51 |
| 15.00 | 38.96 | 100 | 10 | 12.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, W.-G.; Sakata, D.; Lampe, N.; Belov, O.; Tran, N.H.; Petrovic, I.; Ristic-Fira, A.; Dordevic, M.; Bernal, M.A.; Bordage, M.-C.; et al. A Geant4-DNA Evaluation of Radiation-Induced DNA Damage on a Human Fibroblast. Cancers 2021, 13, 4940. https://doi.org/10.3390/cancers13194940
Shin W-G, Sakata D, Lampe N, Belov O, Tran NH, Petrovic I, Ristic-Fira A, Dordevic M, Bernal MA, Bordage M-C, et al. A Geant4-DNA Evaluation of Radiation-Induced DNA Damage on a Human Fibroblast. Cancers. 2021; 13(19):4940. https://doi.org/10.3390/cancers13194940
Chicago/Turabian StyleShin, Wook-Geun, Dousatsu Sakata, Nathanael Lampe, Oleg Belov, Ngoc Hoang Tran, Ivan Petrovic, Aleksandra Ristic-Fira, Milos Dordevic, Mario A. Bernal, Marie-Claude Bordage, and et al. 2021. "A Geant4-DNA Evaluation of Radiation-Induced DNA Damage on a Human Fibroblast" Cancers 13, no. 19: 4940. https://doi.org/10.3390/cancers13194940
APA StyleShin, W.-G., Sakata, D., Lampe, N., Belov, O., Tran, N. H., Petrovic, I., Ristic-Fira, A., Dordevic, M., Bernal, M. A., Bordage, M.-C., Francis, Z., Kyriakou, I., Perrot, Y., Sasaki, T., Villagrasa, C., Guatelli, S., Breton, V., Emfietzoglou, D., & Incerti, S. (2021). A Geant4-DNA Evaluation of Radiation-Induced DNA Damage on a Human Fibroblast. Cancers, 13(19), 4940. https://doi.org/10.3390/cancers13194940







