Discovering Digital Tumor Signatures—Using Latent Code Representations to Manipulate and Classify Liver Lesions
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data and Preprocessing
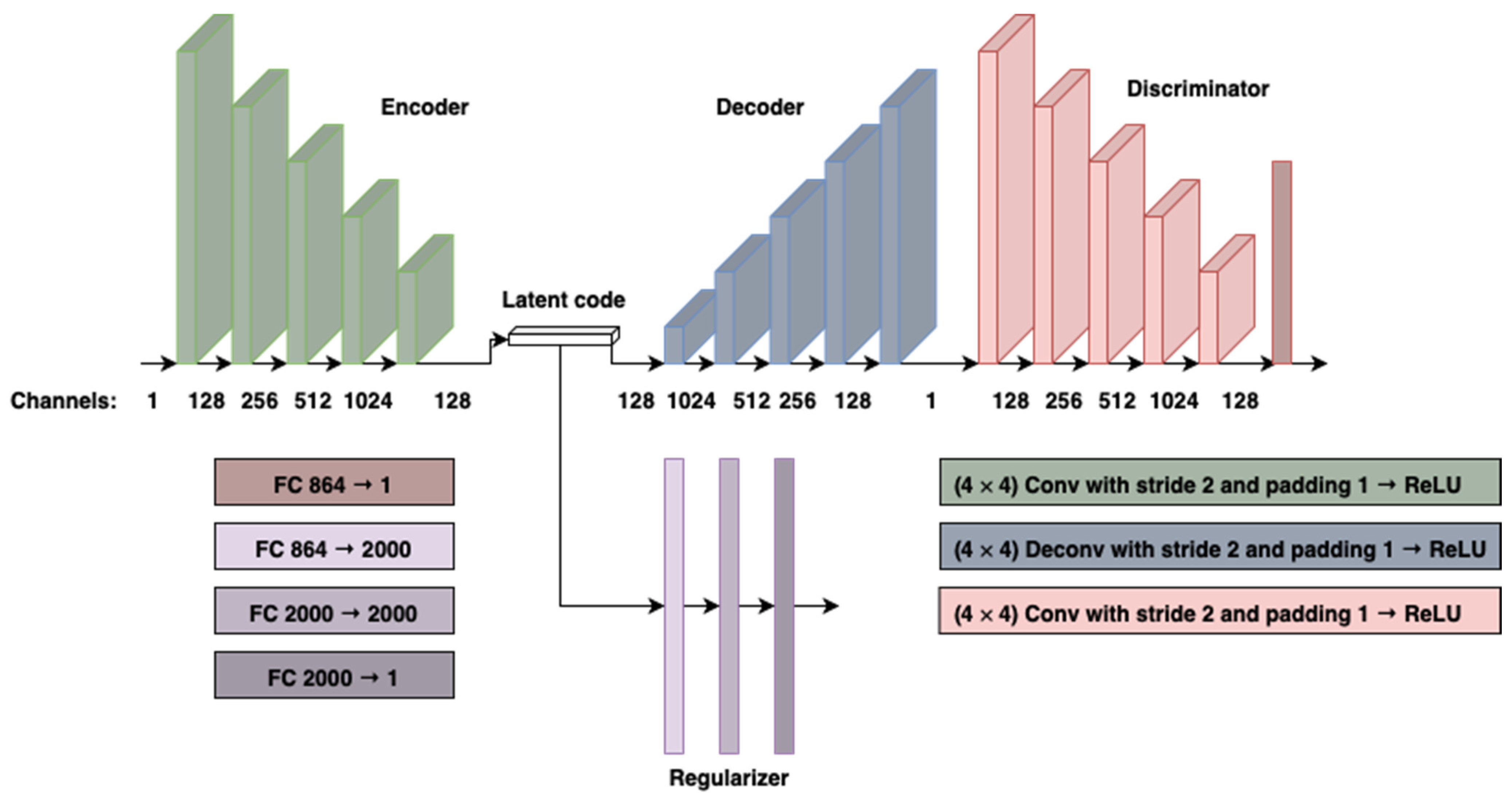
2.2. Model Architecture and Training
2.3. Evaluation of Synthetic Images
2.4. Latent Code Lesion Classification
3. Results
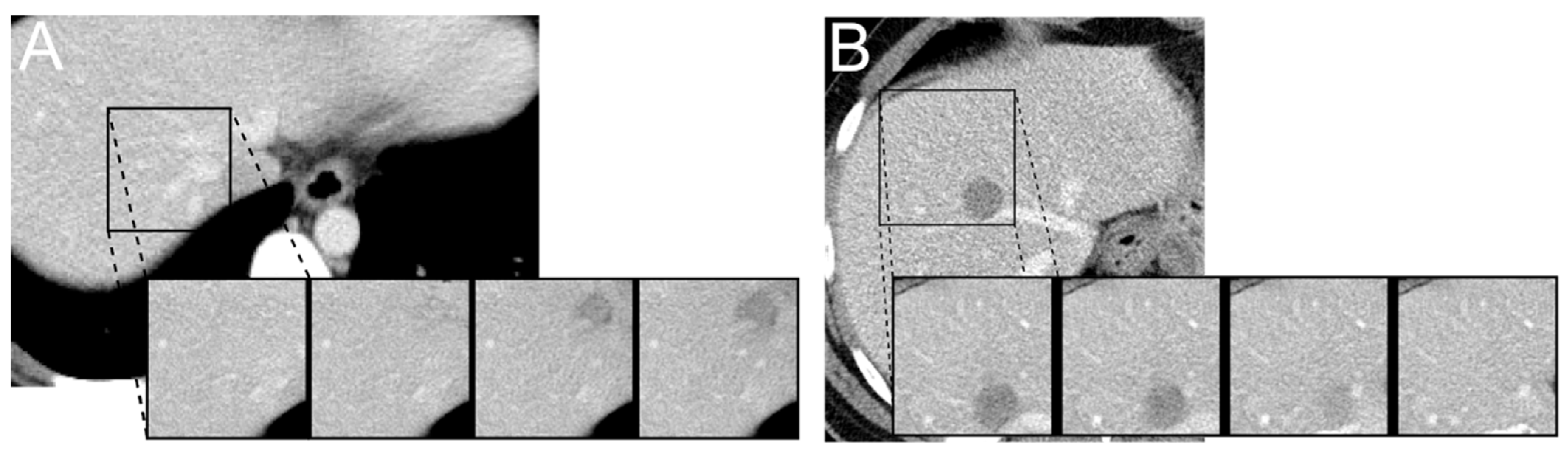
3.1. Latent Code Manipulation
3.2. Evaluation of Synthetic Images
3.3. Latent Code Lesion Classification
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A—Statistical Analysis
Appendix B—Classifier Parameters
References
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. arXiv 2018, arXiv:1611.07004. [Google Scholar]
- Wolterink, J.M.; Dinkla, A.M.; Savenije, M.H.F.; Seevinck, P.R.; van den Berg, C.A.T.; Isgum, I. Deep MR to CT Synthesis Using Unpaired Data. arXiv 2017, arXiv:1708.01155. [Google Scholar]
- Liu, F.; Jang, H.; Kijowski, R.; Bradshaw, T.; McMillan, A.B. Deep Learning MR Imaging–Based Attenuation Correction for PET/MR Imaging. Radiology 2017, 286, 676–684. [Google Scholar] [CrossRef]
- Armanious, K.; Jiang, C.; Abdulatif, S.; Küstner, T.; Gatidis, S.; Yang, B. Unsupervised medical image translation using cycle-MedGAN. In Proceedings of the 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 2–6 September 2019; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Choi, H.; Lee, D.S. Generation of Structural MR Images from Amyloid PET: Application to MR-Less Quantification. J. Nucl. Med. 2018, 59, 1111–1117. [Google Scholar] [CrossRef] [Green Version]
- Han, C.; Kitamura, Y.; Kudo, A.; Ichinose, A.; Rundo, L.; Furukawa, Y.; Umemoto, K.; Li, Y.; Nakayama, H. Synthesizing diverse lung nodules wherever massively: 3D multi-conditional GAN-based CT image augmentation for object detection. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; pp. 729–737. [Google Scholar]
- Mirsky, Y.; Mahler, T.; Shelef, I.; Elovici, Y. CT-GAN: Malicious Tampering of 3D Medical Imagery Using Deep Learning. arXiv 2019, arXiv:1901.03597. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. arXiv 2014, arXiv:1401.4082. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Baur, C.; Wiestler, B.; Albarqouni, S.; Navab, N. Deep Autoencoding Models for Unsupervised Anomaly Segmentation in Brain MR Images. arXiv 2019, 11383, 161–169. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Konukoglu, E. Unsupervised Detection of Lesions in Brain MRI Using Constrained Adversarial Auto-Encoders. arXiv 2018, arXiv:1806.04972. [Google Scholar]
- Zimmerer, D.; Kohl, S.A.A.; Petersen, J.; Isensee, F.; Maier-Hein, K.H. Context-Encoding Variational Autoencoder for Unsupervised Anomaly Detection. arXiv 2018, arXiv:1812.05941. [Google Scholar]
- Rezende, D.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Bach, F., Blei, D., Eds.; PMLR: Lille, France, 2015; Volume 37, pp. 1530–1538. [Google Scholar]
- Huszár, F. Variational Inference Using Implicit Distributions. arXiv 2017, arXiv:1702.08235. [Google Scholar]
- Karaletsos, T. Adversarial Message Passing for Graphical Models. arXiv 2016, arXiv:1612.05048. [Google Scholar]
- Makhzani, A. Implicit Autoencoders. arXiv 2019, arXiv:1805.09804. [Google Scholar]
- Mescheder, L.; Nowozin, S.; Geiger, A. Adversarial variational Bayes: Unifying variational autoencoders and generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; PMLR: Sydney, Australia, 2017; Volume 70, pp. 2391–2400. [Google Scholar]
- Mohamed, S.; Lakshminarayanan, B. Learning in Implicit Generative Models. arXiv 2016, arXiv:1610.03483. [Google Scholar]
- Tran, D.; Ranganath, R.; Blei, D.M. Hierarchical implicit models and likelihood-free variational inference. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5529–5539. [Google Scholar]
- Hahn, H.K. Radiomics & Deep Learning: Quo vadis? Forum 2020, 35, 117–124. [Google Scholar] [CrossRef]
- Hosny, A.; Parmar, C.; Coroller, T.P.; Grossmann, P.; Zeleznik, R.; Kumar, A.; Bussink, J.; Gillies, R.J.; Mak, R.H.; Aerts, H.J.W.L. Deep Learning for Lung Cancer Prognostication: A Retrospective Multi-Cohort Radiomics Study. PLoS Med. 2018, 15, e1002711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobayashi, K.; Miyake, M.; Takahashi, M.; Hamamoto, R. Observing Deep Radiomics for the Classification of Glioma Grades. Sci. Rep. 2021, 11, 10942. [Google Scholar] [CrossRef]
- Bilic, P.; Christ, P.F.; Vorontsov, E.; Chlebus, G.; Chen, H.; Dou, Q.; Fu, C.-W.; Han, X.; Heng, P.-A.; Hesser, J.; et al. The Liver Tumor Segmentation Benchmark (LiTS). arXiv 2019, arXiv:1901.04056. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th international conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 1096–1103. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar]
- Gletsos, M.; Mougiakakou, S.G.; Matsopoulos, G.K.; Nikita, K.S.; Nikita, A.S.; Kelekis, D. A Computer-Aided Diagnostic System to Characterize CT Focal Liver Lesions: Design and Optimization of a Neural Network Classifier. IEEE Trans. Inf. Technol. Biomed. 2003, 7, 153–162. [Google Scholar] [CrossRef]
- Adcock, A.; Rubin, D.; Carlsson, G. Classification of Hepatic Lesions Using the Matching Metric. Comput. Vis. Image Underst. 2014, 121, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-C.; Chen, H.-H.; Chang, Y.-C.; Yang, M.-Y.; Lo, C.-M.; Ko, W.-C.; Lee, Y.-F.; Liu, K.-L.; Chang, R.-F. Computer-Aided Diagnosis of Liver Tumors on Computed Tomography Images. Comput. Methods Programs Biomed. 2017, 145, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Mougiakakou, S.G.; Valavanis, I.K.; Nikita, A.; Nikita, K.S. Differential Diagnosis of CT Focal Liver Lesions Using Texture Features, Feature Selection and Ensemble Driven Classifiers. Artif. Intell. Med. 2007, 41, 25–37. [Google Scholar] [CrossRef]
- Diamant, I.; Klang, E.; Amitai, M.; Konen, E.; Goldberger, J.; Greenspan, H. Task-Driven Dictionary Learning Based on Mutual Information for Medical Image Classification. IEEE Trans. Biomed. Eng. 2017, 64, 1380–1392. [Google Scholar] [CrossRef] [PubMed]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-Based Synthetic Medical Image Augmentation for Increased CNN Performance in Liver Lesion Classification. Neurocomputing 2018, 321, 321–331. [Google Scholar] [CrossRef] [Green Version]
- Sorrenson, P.; Rother, C.; Köthe, U. Disentanglement by Nonlinear ICA with General Incompressible-Flow Networks (GIN). arXiv 2020, arXiv:2001.04872. [Google Scholar]
- Chen, J.; Milot, L.; Cheung, H.M.C.; Martel, A.L. Unsupervised clustering of quantitative imaging phenotypes using autoencoder and gaussian mixture model. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2019. Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI, Shenzhen, China, 13–17 October 2019; Shen, D., Liu, T., Peters, T.M., Staib, L.H., Essert, C., Zhou, S., Yap, P.-T., Khan, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 575–582. [Google Scholar]
- Song, J.; Wang, L.; Ng, N.N.; Zhao, M.; Shi, J.; Wu, N.; Li, W.; Liu, Z.; Yeom, K.W.; Tian, J. Development and Validation of a Machine Learning Model to Explore Tyrosine Kinase Inhibitor Response in Patients With Stage IV EGFR Variant–Positive Non–Small Cell Lung Cancer. JAMA Netw. Open 2020, 3, e2030442. [Google Scholar] [CrossRef]
- Donahue, J.; Simonyan, K. Large scale adversarial representation learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]


| Rater | Accuracy Experiment | Times s (std) Experiment 1 | Accuracy Experiment 2 | Times s (std) Experiment 2 |
|---|---|---|---|---|
| 1 | 0.65 | 8.05 (4.71) | 0.425 | 5.03 (2.9) |
| 2 | 0.625 | 14.34 (13.53) | 0.575 | 7.84 (5.84) |
| 3 | 0.575 | 7.62 (13.99) | 0.6 | 4.01 (3.67) |
| 4 | 0.6 | 9.86 (6.65) | 0.6 | 6.21 (4.5) |
| 5 | 0.725 | 72.3 (216.61) | 0.65 | 15.29 (9.48) |
| Ensemble | 0.7 | - | 0.65 | - |
| Classifier | All Data | Normal | ||||||
|---|---|---|---|---|---|---|---|---|
| ACC | SE | SP | AUC | ACC | SE | SP | AUC | |
| Linear SVM | 0.95 (0.02) | 0.94 (0.04) | 0.97 (0.01) | 0.96 (0.02) | 0.97 (0.02) | 0.95 (0.03) | 0.99 (0.02) | 0.97 (0.02) |
| Random Forest | 0.87 (0.04) | 0.93 (0.04) | 0.80 (0.06) | 0.86 (0.04) | 0.91 (0.04) | 0.92 (0.06) | 0.89 (0.04) | 0.90 (0.04) |
| MLP | 0.95 (0.03) | 0.93 (0.05) | 0.98 (0.03) | 0.95 (0.02) | 0.96 (0.02) | 0.93 (0.04) | 0.99 (0.02) | 0.96 (0.02) |
| Naive Bayes | 0.84 (0.05) | 0.92 (0.05) | 0.76 (0.09) | 0.84 (0.05) | 0.88 (0.04) | 0.91 (0.06) | 0.84 (0.06) | 0.88 (0.04) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleesiek, J.; Kersjes, B.; Ueltzhöffer, K.; Murray, J.M.; Rother, C.; Köthe, U.; Schlemmer, H.-P. Discovering Digital Tumor Signatures—Using Latent Code Representations to Manipulate and Classify Liver Lesions. Cancers 2021, 13, 3108. https://doi.org/10.3390/cancers13133108
Kleesiek J, Kersjes B, Ueltzhöffer K, Murray JM, Rother C, Köthe U, Schlemmer H-P. Discovering Digital Tumor Signatures—Using Latent Code Representations to Manipulate and Classify Liver Lesions. Cancers. 2021; 13(13):3108. https://doi.org/10.3390/cancers13133108
Chicago/Turabian StyleKleesiek, Jens, Benedikt Kersjes, Kai Ueltzhöffer, Jacob M. Murray, Carsten Rother, Ullrich Köthe, and Heinz-Peter Schlemmer. 2021. "Discovering Digital Tumor Signatures—Using Latent Code Representations to Manipulate and Classify Liver Lesions" Cancers 13, no. 13: 3108. https://doi.org/10.3390/cancers13133108
APA StyleKleesiek, J., Kersjes, B., Ueltzhöffer, K., Murray, J. M., Rother, C., Köthe, U., & Schlemmer, H.-P. (2021). Discovering Digital Tumor Signatures—Using Latent Code Representations to Manipulate and Classify Liver Lesions. Cancers, 13(13), 3108. https://doi.org/10.3390/cancers13133108







