An Improved, Assay Platform Agnostic, Absolute Single Sample Breast Cancer Subtype Classifier
Abstract
Simple Summary
Abstract
1. Introduction
2. Results
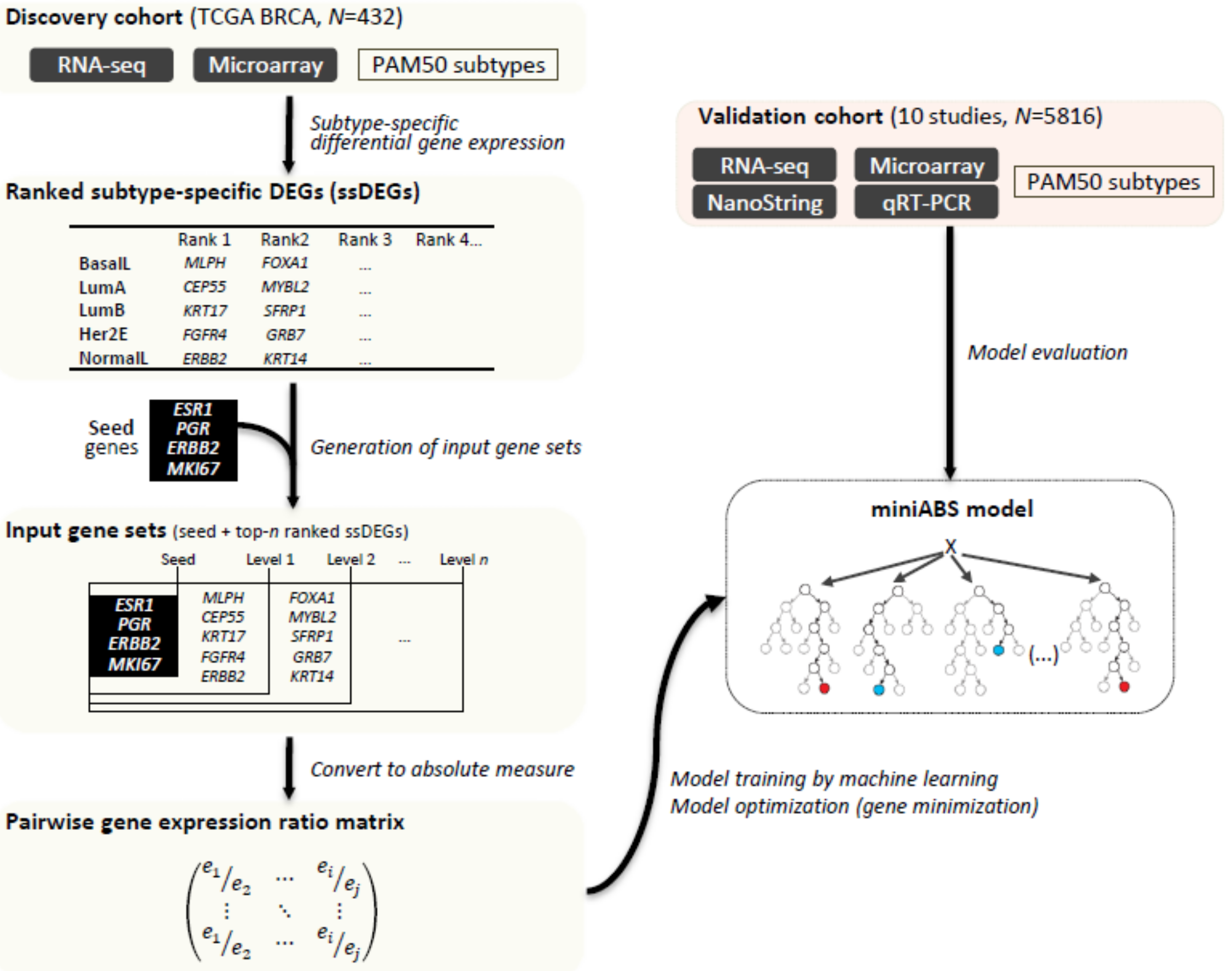
2.1. Overview of MiniABS
2.2. Training and Optimization of the Classifiers
2.3. Biological Relevance of the PGERs
2.4. Validation on Independent Datasets
3. Discussion
4. Materials and Methods
4.1. Method Overview
4.2. Training Dataset
4.3. Feature Selection and Input Data (PGER Matrix) Preparation
4.4. Training and Optimization of the Classifier
4.5. Independent Validation and Processing
4.6. Performance Assessment with and without Normal-Like
4.7. Modeling with Seed Genes, ssDEGs, and Intrinsic Gene Set
4.8. Feature Analysis
4.9. Statistical Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Clarke, M. Meta-analyses of adjuvant therapies for women with early breast cancer: The Early Breast Cancer Trialists’ Collaborative Group overview. Ann. Oncol. 2006, 17 (Suppl. 10), x59–x62. [Google Scholar] [CrossRef]
- Perou, C.M.; Sorlie, T.; Eisen, M.B.; van de Rijn, M.; Jeffrey, S.S.; Rees, C.A.; Pollack, J.R.; Ross, D.T.; Johnsen, H.; Akslen, L.A.; et al. Molecular portraits of human breast tumours. Nature 2000, 406, 747–752. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.S.; Mullins, M.; Cheang, M.C.; Leung, S.; Voduc, D.; Vickery, T.; Davies, S.; Fauron, C.; He, X.; Hu, Z.; et al. Supervised risk predictor of breast cancer based on intrinsic subtypes. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2009, 27, 1160–1167. [Google Scholar] [CrossRef] [PubMed]
- Paquet, E.R.; Hallett, M.T. Absolute assignment of breast cancer intrinsic molecular subtype. J. Natl. Cancer Inst. 2015, 107, 357. [Google Scholar] [CrossRef] [PubMed]
- Patil, P.; Bachant-Winner, P.O.; Haibe-Kains, B.; Leek, J.T. Test set bias affects reproducibility of gene signatures. Bioinformatics 2015, 31, 2318–2323. [Google Scholar] [CrossRef] [PubMed]
- Goldhirsch, A.; Winer, E.P.; Coates, A.S.; Gelber, R.D.; Piccart-Gebhart, M.; Thurlimann, B.; Senn, H.J.; Panel, M. Personalizing the treatment of women with early breast cancer: Highlights of the St Gallen International Expert Consensus on the Primary Therapy of Early Breast Cancer 2013. Ann. Oncol. 2013, 24, 2206–2223. [Google Scholar] [CrossRef] [PubMed]
- Curigliano, G.; Burstein, H.J.; Winer, E.P.; Gnant, M.; Dubsky, P.; Loibl, S.; Colleoni, M.; Regan, M.M.; Piccart-Gebhart, M.; Senn, H.J.; et al. De-escalating and escalating treatments for early-stage breast cancer: The St. Gallen International Expert Consensus Conference on the Primary Therapy of Early Breast Cancer 2017. Ann. Oncol. 2017, 28, 1700–1712. [Google Scholar] [CrossRef] [PubMed]
- Bastien, R.R.; Rodriguez-Lescure, A.; Ebbert, M.T.; Prat, A.; Munarriz, B.; Rowe, L.; Miller, P.; Ruiz-Borrego, M.; Anderson, D.; Lyons, B.; et al. PAM50 breast cancer subtyping by RT-qPCR and concordance with standard clinical molecular markers. BMC Med. Genom. 2012, 5, 44. [Google Scholar] [CrossRef] [PubMed]
- Wallden, B.; Storhoff, J.; Nielsen, T.; Dowidar, N.; Schaper, C.; Ferree, S.; Liu, S.; Leung, S.; Geiss, G.; Snider, J.; et al. Development and verification of the PAM50-based Prosigna breast cancer gene signature assay. BMC Med. Genom. 2015, 8, 54. [Google Scholar] [CrossRef] [PubMed]
- Sparano, J.A.; Gray, R.J.; Makower, D.F.; Pritchard, K.I.; Albain, K.S.; Hayes, D.F.; Geyer, C.E., Jr.; Dees, E.C.; Perez, E.A.; Olson, J.A., Jr.; et al. Prospective Validation of a 21-Gene Expression Assay in Breast Cancer. N. Engl. J. Med. 2015, 373, 2005–2014. [Google Scholar] [CrossRef] [PubMed]
- Sparano, J.A.; Gray, R.J.; Makower, D.F.; Albain, K.S.; Saphner, T.J.; Badve, S.S.; Wagner, L.I.; Kaklamani, V.G.; Keane, M.M.; Gomez, H.L.; et al. Clinical Outcomes in Early Breast Cancer With a High 21-Gene Recurrence Score of 26 to 100 Assigned to Adjuvant Chemotherapy Plus Endocrine Therapy: A Secondary Analysis of the TAILORx Randomized Clinical Trial. JAMA Oncol. 2020, 6, 367–374. [Google Scholar] [CrossRef]
- Gluz, O.; Nitz, U.A.; Christgen, M.; Kates, R.E.; Shak, S.; Clemens, M.; Kraemer, S.; Aktas, B.; Kuemmel, S.; Reimer, T.; et al. West German Study Group Phase III PlanB Trial: First Prospective Outcome Data for the 21-Gene Recurrence Score Assay and Concordance of Prognostic Markers by Central and Local Pathology Assessment. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2016, 34, 2341–2349. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, F.; van’t Veer, L.J.; Bogaerts, J.; Slaets, L.; Viale, G.; Delaloge, S.; Pierga, J.Y.; Brain, E.; Causeret, S.; DeLorenzi, M.; et al. 70-Gene Signature as an Aid to Treatment Decisions in Early-Stage Breast Cancer. N. Engl. J. Med. 2016, 375, 717–729. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, T.; Wallden, B.; Schaper, C.; Ferree, S.; Liu, S.; Gao, D.; Barry, G.; Dowidar, N.; Maysuria, M.; Storhoff, J. Analytical validation of the PAM50-based Prosigna Breast Cancer Prognostic Gene Signature Assay and nCounter Analysis System using formalin-fixed paraffin-embedded breast tumor specimens. BMC Cancer 2014, 14, 177. [Google Scholar] [CrossRef]
- Cardoso, F.; Kyriakides, S.; Ohno, S.; Penault-Llorca, F.; Poortmans, P.; Rubio, I.T.; Zackrisson, S.; Senkus, E. Early breast cancer: ESMO Clinical Practice Guidelines for diagnosis, treatment and follow-updagger. Ann. Oncol. 2019, 30, 1194–1220. [Google Scholar] [CrossRef] [PubMed]
- Ohnstad, H.O.; Borgen, E.; Falk, R.S.; Lien, T.G.; Aaserud, M.; Sveli, M.A.T.; Kyte, J.A.; Kristensen, V.N.; Geitvik, G.A.; Schlichting, E.; et al. Prognostic value of PAM50 and risk of recurrence score in patients with early-stage breast cancer with long-term follow-up. Breast Cancer Res. BCR 2017, 19, 120. [Google Scholar] [CrossRef]
- Bartlett, J.M.; Bayani, J.; Marshall, A.; Dunn, J.A.; Campbell, A.; Cunningham, C.; Sobol, M.S.; Hall, P.S.; Poole, C.J.; Cameron, D.A.; et al. Comparing Breast Cancer Multiparameter Tests in the OPTIMA Prelim Trial: No Test Is More Equal Than the Others. J. Natl. Cancer Inst. 2016, 108. [Google Scholar] [CrossRef]
- Brueffer, C. Clinical Value of RNA Sequencing–Based Classifiers for Prediction of the Five Conventional Breast Cancer Biomarkers: A Report From the Population-Based Multicenter Sweden Cancerome Analysis Network—Breast Initiative. JCO Precis. Oncol. 2018. [Google Scholar] [CrossRef]
- Cheang, M.C.; Chia, S.K.; Voduc, D.; Gao, D.; Leung, S.; Snider, J.; Watson, M.; Davies, S.; Bernard, P.S.; Parker, J.S.; et al. Ki67 index, HER2 status, and prognosis of patients with luminal B breast cancer. J. Natl. Cancer Inst. 2009, 101, 736–750. [Google Scholar] [CrossRef]
- Sinha, D.; Nag, P.; Nanayakkara, D.; Duijf, P.H.G.; Burgess, A.; Raninga, P.; Smits, V.A.J.; Bain, A.L.; Subramanian, G.; Wall, M.; et al. Cep55 overexpression promotes genomic instability and tumorigenesis in mice. Commun. Biol. 2020, 3, 593. [Google Scholar] [CrossRef]
- Madsen, M.J.; Knight, S.; Sweeney, C.; Factor, R.; Salama, M.; Stijleman, I.J.; Rajamanickam, V.; Welm, B.E.; Arunachalam, S.; Jones, B.; et al. Reparameterization of PAM50 Expression Identifies Novel Breast Tumor Dimensions and Leads to Discovery of a Genome-Wide Significant Breast Cancer Locus at 12q15. Cancer Epidemiol. Biomark. Prev. 2018, 27, 644–652. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.H.; Man, H.T.; Zhao, X.D.; Dong, N.; Ma, S.L. Estrogen receptor-positive breast cancer molecular signatures and therapeutic potentials (Review). Biomed. Rep. 2014, 2, 41–52. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Cancer Genome Atlas Network. Comprehensive molecular portraits of human breast tumours. Nature 2012, 490, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Saal, L.H.; Vallon-Christersson, J.; Hakkinen, J.; Hegardt, C.; Grabau, D.; Winter, C.; Brueffer, C.; Tang, M.H.; Reutersward, C.; Schulz, R.; et al. The Sweden Cancerome Analysis Network—Breast (SCAN-B) Initiative: A large-scale multicenter infrastructure towards implementation of breast cancer genomic analyses in the clinical routine. Genome Med. 2015, 7, 20. [Google Scholar] [CrossRef] [PubMed]
- Hatzis, C.; Pusztai, L.; Valero, V.; Booser, D.J.; Esserman, L.; Lluch, A.; Vidaurre, T.; Holmes, F.; Souchon, E.; Wang, H.; et al. A genomic predictor of response and survival following taxane-anthracycline chemotherapy for invasive breast cancer. JAMA 2011, 305, 1873–1881. [Google Scholar] [CrossRef] [PubMed]
- Horak, C.E.; Pusztai, L.; Xing, G.; Trifan, O.C.; Saura, C.; Tseng, L.M.; Chan, S.; Welcher, R.; Liu, D. Biomarker analysis of neoadjuvant doxorubicin/cyclophosphamide followed by ixabepilone or Paclitaxel in early-stage breast cancer. Clin. Cancer Res. Off. J. Am. Assoc. Cancer Res. 2013, 19, 1587–1595. [Google Scholar] [CrossRef]
- Anders, C.; Deal, A.M.; Abramson, V.; Liu, M.C.; Storniolo, A.M.; Carpenter, J.T.; Puhalla, S.; Nanda, R.; Melhem-Bertrandt, A.; Lin, N.U.; et al. TBCRC 018: Phase II study of iniparib in combination with irinotecan to treat progressive triple negative breast cancer brain metastases. Breast Cancer Res. Treat. 2014, 146, 557–566. [Google Scholar] [CrossRef]
- Prat, A.; Lluch, A.; Albanell, J.; Barry, W.T.; Fan, C.; Chacon, J.I.; Parker, J.S.; Calvo, L.; Plazaola, A.; Arcusa, A.; et al. Predicting response and survival in chemotherapy-treated triple-negative breast cancer. Br. J. Cancer 2014, 111, 1532–1541. [Google Scholar] [CrossRef]
- Cejalvo, J.M.; Martinez de Duenas, E.; Galvan, P.; Garcia-Recio, S.; Burgues Gasion, O.; Pare, L.; Antolin, S.; Martinello, R.; Blancas, I.; Adamo, B.; et al. Intrinsic Subtypes and Gene Expression Profiles in Primary and Metastatic Breast Cancer. Cancer Res. 2017, 77, 2213–2221. [Google Scholar] [CrossRef]
- Priedigkeit, N.; Hartmaier, R.J.; Chen, Y.; Vareslija, D.; Basudan, A.; Watters, R.J.; Thomas, R.; Leone, J.P.; Lucas, P.C.; Bhargava, R.; et al. Intrinsic Subtype Switching and Acquired ERBB2/HER2 Amplifications and Mutations in Breast Cancer Brain Metastases. JAMA Oncol. 2017, 3, 666–671. [Google Scholar] [CrossRef] [PubMed]
- Edgar, R.; Domrachev, M.; Lash, A.E. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002, 30, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Gautier, L. Affy—Analysis of Affymetrix GeneChip data at the probe level. Bioinformatics 2004, 20, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Prat, A.; Fan, C.; Fernandez, A.; Hoadley, K.A.; Martinello, R.; Vidal, M.; Viladot, M.; Pineda, E.; Arance, A.; Munoz, M.; et al. Response and survival of breast cancer intrinsic subtypes following multi-agent neoadjuvant chemotherapy. BMC Med. 2015, 13, 303. [Google Scholar] [CrossRef]
- Gendoo, D.M.; Ratanasirigulchai, N.; Schroder, M.S.; Pare, L.; Parker, J.S.; Prat, A.; Haibe-Kains, B. Genefu: An R/Bioconductor package for computation of gene expression-based signatures in breast cancer. Bioinformatics 2016, 32, 1097–1099. [Google Scholar] [CrossRef]
- Sontrop, H.M.J.; Reinders, M.J.T.; Moerland, P.D. Breast cancer subtype predictors revisited: From consensus to concordance? BMC Med. Genom. 2016, 9, 26. [Google Scholar] [CrossRef]
- Prat, A.; Perou, C.M. Deconstructing the molecular portraits of breast cancer. Mol. Oncol. 2011, 5, 5–23. [Google Scholar] [CrossRef]
- Culhane, A.C.; Schroder, M.S.; Sultana, R.; Picard, S.C.; Martinelli, E.N.; Kelly, C.; Haibe-Kains, B.; Kapushesky, M.; St Pierre, A.A.; Flahive, W.; et al. GeneSigDB: A manually curated database and resource for analysis of gene expression signatures. Nucleic Acids Res. 2012, 40, D1060–D1066. [Google Scholar] [CrossRef]



| Rank | Basal-Like ssDEGs | Her2E ssDEGs | LumA ssDEGs | LumB ssDEGs | Normal-Like ssDEGs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbol | p-Value | FDR | Symbol | p-Value | FDR | Symbol | p-Value | FDR | Symbol | p-Value | FDR | Symbol | p-Value | FDR | |
| 1 | MLPH | 4.0 × 10−41 | 8.2 × 10−37 | FGFR4 | 4.6 × 10−19 | 4.3 × 10−15 | CEP55 | 2.4 × 10−50 | 1.2 × 10−46 | KRT17 | 2.0 × 10−20 | 6.8 × 10−17 | ERBB2 | 5.4 × 10−3 | 2.4 × 10−1 |
| 2 | FOXA1 | 9.6 × 10−40 | 6.6 × 10−36 | GRB7 | 5.6 × 10−16 | 7.7 × 10−13 | MYBL2 | 7.0 × 10−49 | 2.4 × 10−45 | SFRP1 | 7.7 × 10−20 | 1.6 × 10−16 | KRT14 | 2.3 × 10−3 | 2.4 × 10−1 |
| 3 | FOXC1 | 1.0 × 10−38 | 3.4 × 10−35 | ERBB2 | 1.4 × 10−15 | 1.6 × 10−12 | MELK | 3.8 × 10−47 | 5.2 × 10−44 | KRT14 | 5.7 × 10−18 | 4.3 × 10−15 | KRT5 | 3.0 × 10−3 | 2.4 × 10−1 |
| 4 | ESR1 | 1.0 × 10−35 | 6.5 × 10−33 | BCL2 | 5.2 × 10−14 | 2.8 × 10−11 | KIF2C | 7.5 × 10−47 | 9.6 × 10−44 | KRT5 | 1.6 × 10−17 | 8.7 × 10−15 | MIA | 3.2 × 10−3 | 2.4 × 10−1 |
| 5 | NAT1 | 1.4 × 10−35 | 8.1 × 10−33 | ESR1 | 3.6 × 10−12 | 9.5 × 10−10 | ANLN | 1.2 × 10−46 | 1.5 × 10−43 | EGFR | 1.1 × 10−16 | 5.0 × 10−14 | SFRP1 | 4.9 × 10−3 | 2.5 × 10−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, M.-k.; Paik, S.; Kim, S. An Improved, Assay Platform Agnostic, Absolute Single Sample Breast Cancer Subtype Classifier. Cancers 2020, 12, 3506. https://doi.org/10.3390/cancers12123506
Seo M-k, Paik S, Kim S. An Improved, Assay Platform Agnostic, Absolute Single Sample Breast Cancer Subtype Classifier. Cancers. 2020; 12(12):3506. https://doi.org/10.3390/cancers12123506
Chicago/Turabian StyleSeo, Mi-kyoung, Soonmyung Paik, and Sangwoo Kim. 2020. "An Improved, Assay Platform Agnostic, Absolute Single Sample Breast Cancer Subtype Classifier" Cancers 12, no. 12: 3506. https://doi.org/10.3390/cancers12123506
APA StyleSeo, M.-k., Paik, S., & Kim, S. (2020). An Improved, Assay Platform Agnostic, Absolute Single Sample Breast Cancer Subtype Classifier. Cancers, 12(12), 3506. https://doi.org/10.3390/cancers12123506





