Population-Based Brain Tumor Survival Analysis via Spatial- and Temporal-Smoothing
Abstract
:1. Introduction
2. Materials and Method
2.1. Materials
2.2. Methods
2.2.1. Computation
- when ,where is a matrix, with diagonal elements equal to , and off-diagonal elements equal to 0;
- when ,where has diagonal elements and off-diagonal elements 0;
- when ,where has diagonal elements and off-diagonal elements 0.
2.2.2. Simulation
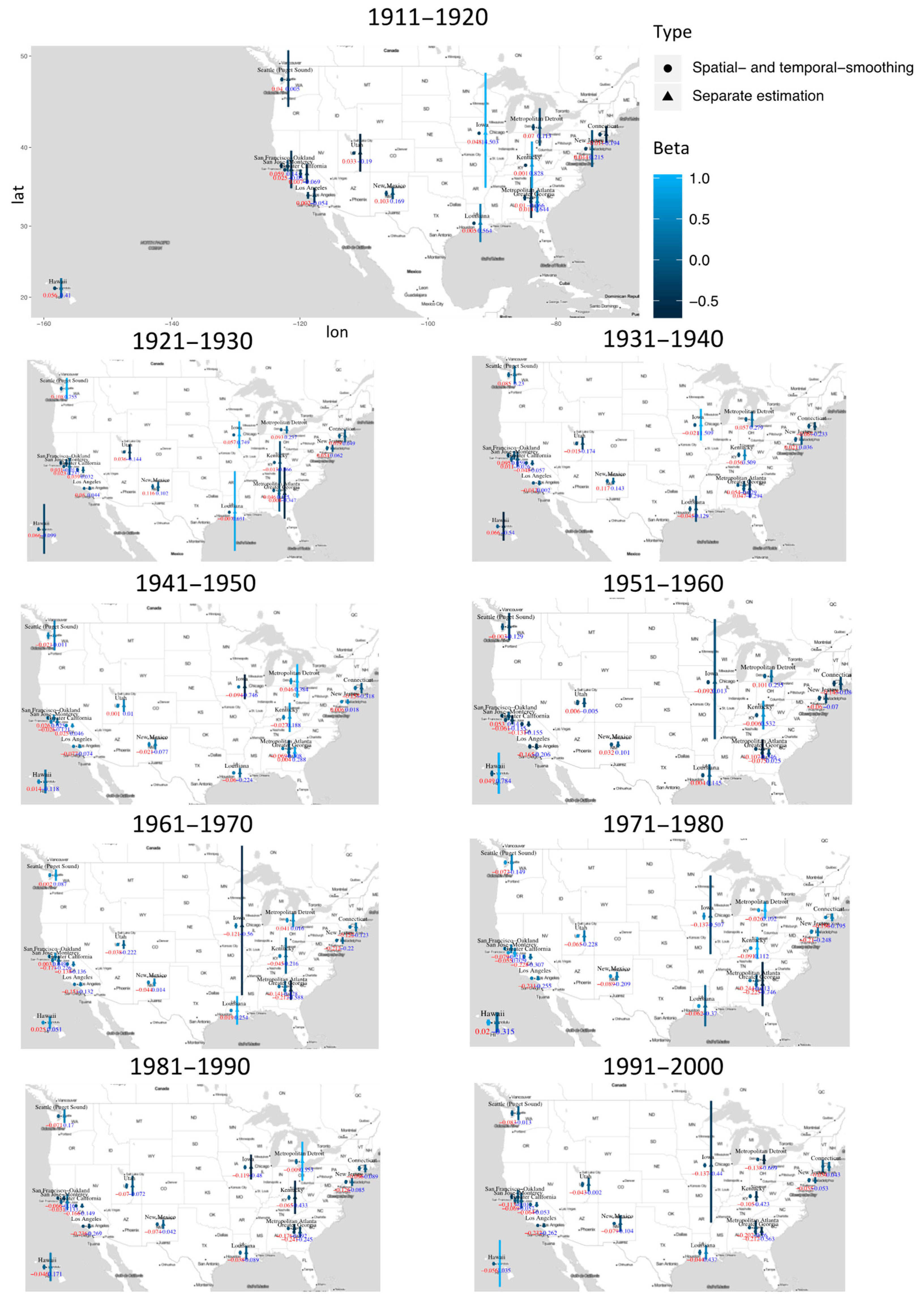
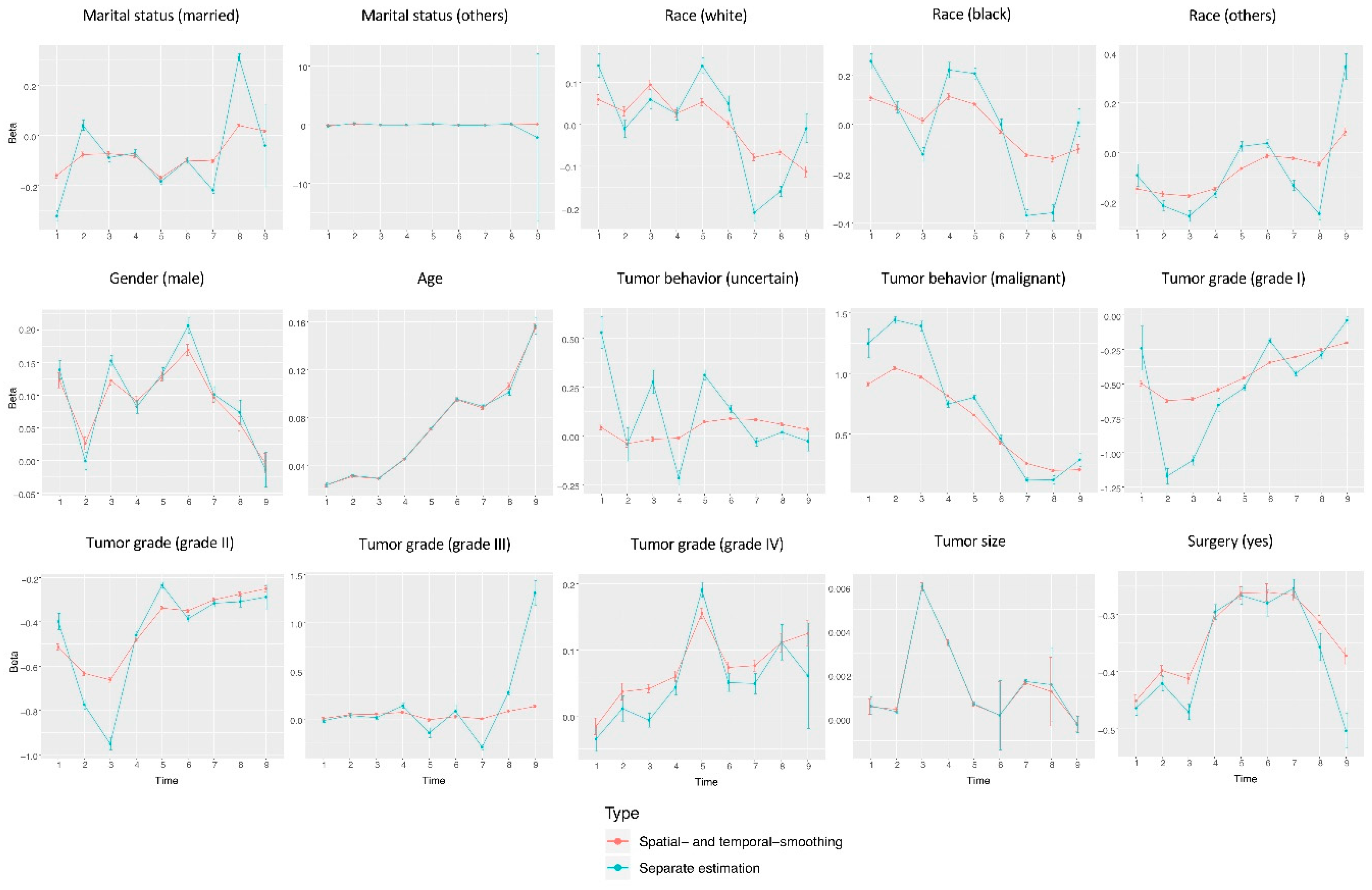
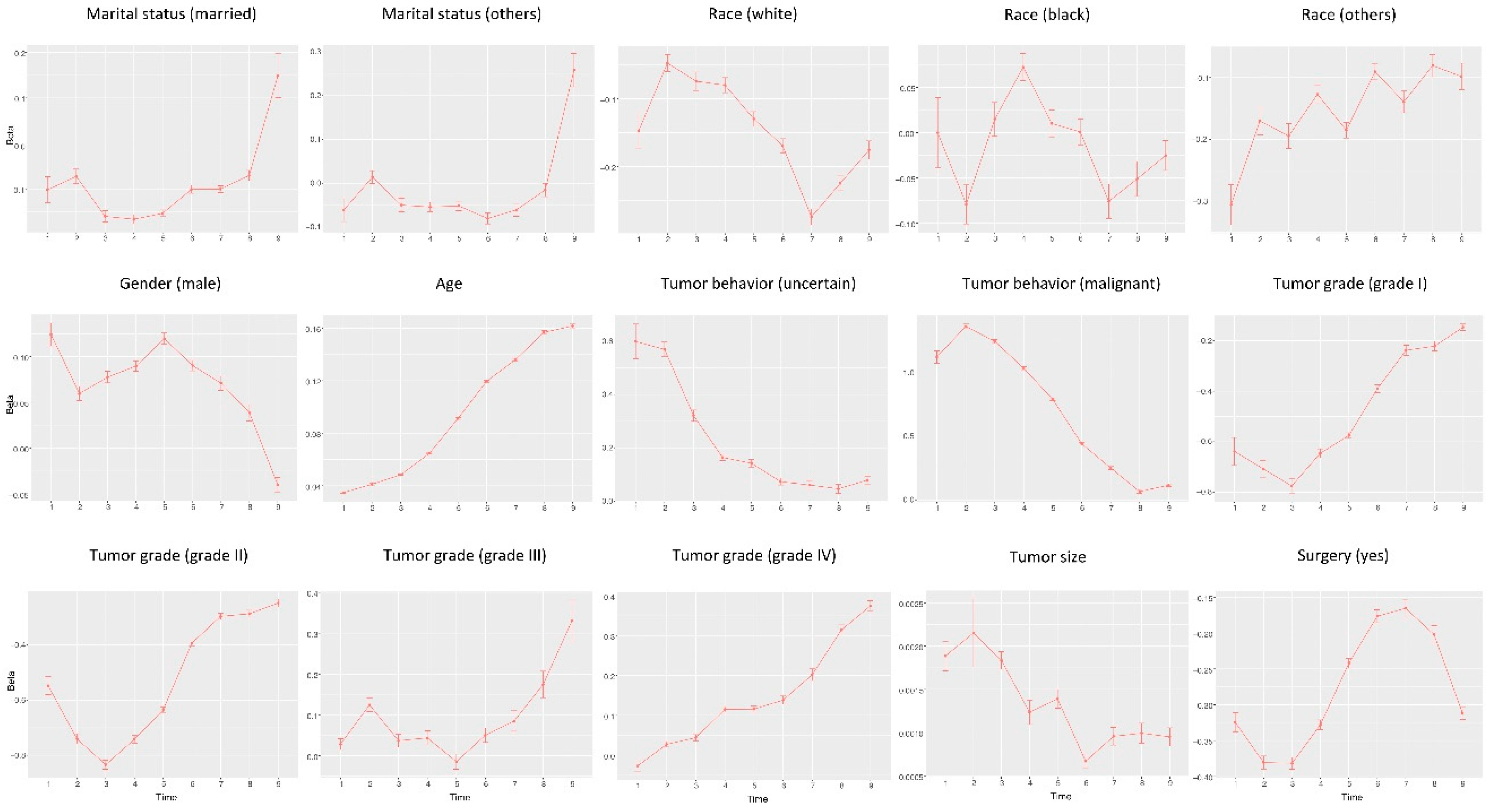
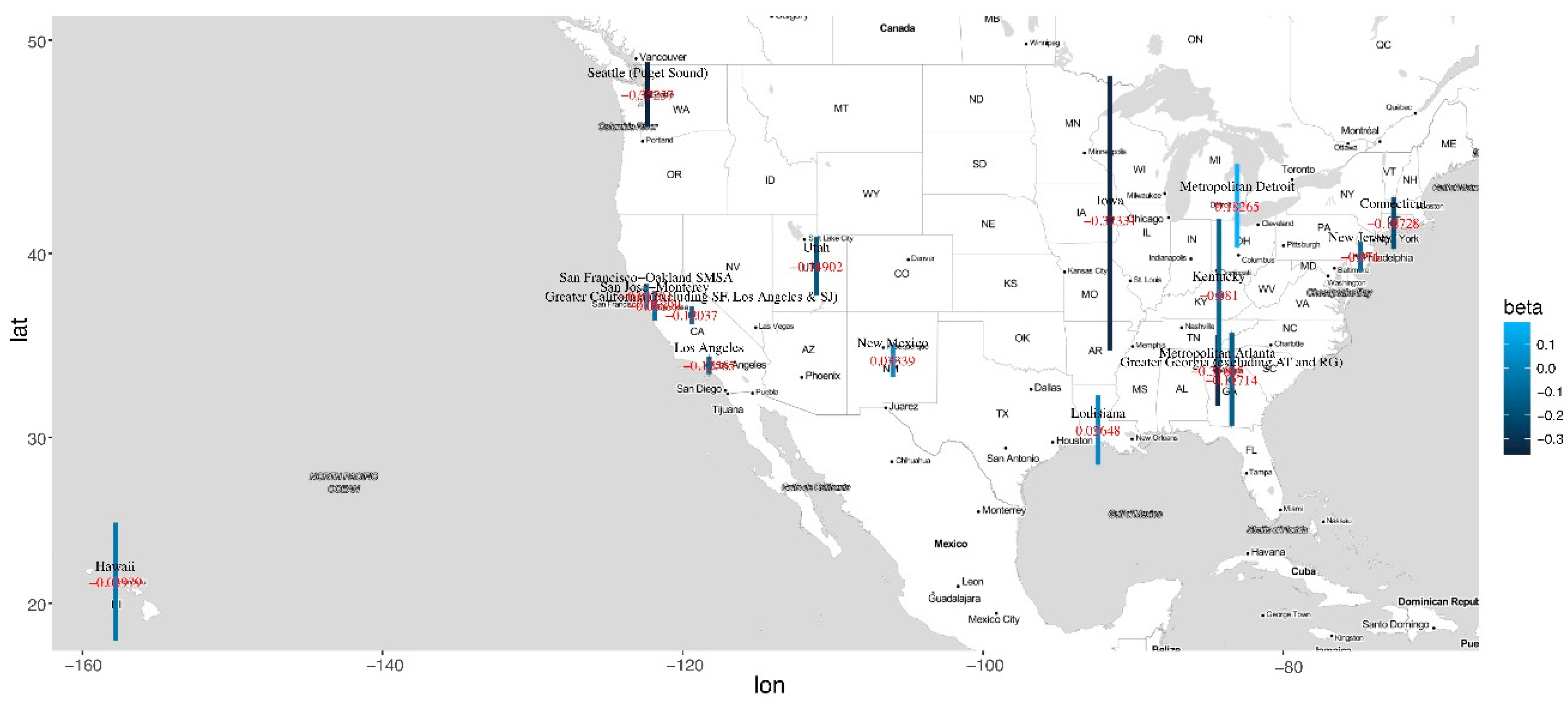
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kotake, K.; Asano, M.; Ozawa, H.; Kobayashi, H.; Sugihara, K. Gender differences in colorectal cancer survival in Japan. Int. J. Clin. Oncol. 2016, 21, 194–203. [Google Scholar] [CrossRef]
- Murphy, C.T.; Galloway, T.J.; Handorf, E.A.; Egleston, B.L.; Wang, L.S.; Mehra, R.; Flieder, D.B.; Ridge, J.A. Survival impact of increasing time to treatment initiation for patients with head and neck cancer in the United States. J. Clin. Oncol. 2016, 34, 169. [Google Scholar] [CrossRef]
- Bertelsen, C.A.; Neuenschwander, A.U.; Jansen, J.E.; Wilhelmsen, M.; Kirkegaard-Klitbo, A.; Tenma, J.R.; Bols, B.; Ingeholm, P.; Rasmussen, L.A.; Jepsen, L.V. Disease-free survival after complete mesocolic excision compared with conventional colon cancer surgery: a retrospective, population-based study. Lancet Oncol. 2015, 16, 161–168. [Google Scholar] [CrossRef]
- Tsikitis, V.L.; Wertheim, B.C.; Guerrero, M.A. Trends of incidence and survival of gastrointestinal neuroendocrine tumors in the United States: a seer analysis. J. Cancer 2012, 3, 292. [Google Scholar] [CrossRef]
- Calverley, P.M.; Anderson, J.A.; Celli, B.; Ferguson, G.T.; Jenkins, C.; Jones, P.W.; Yates, J.C.; Vestbo, J. Salmeterol and fluticasone propionate and survival in chronic obstructive pulmonary disease. N. Engl. J. Med. 2007, 356, 775–789. [Google Scholar] [CrossRef]
- Surawicz, T.S.; Davis, F.; Freels, S.; Laws, E.R.; Menck, H.R. Brain tumor survival: results from the National Cancer Data Base. J. Neuro Oncol. 1998, 40, 151–169. [Google Scholar] [CrossRef] [PubMed]
- Kamoun, W.S.; Ley, C.D.; Farrar, C.T.; Duyverman, A.M.; Lahdenranta, J.; Lacorre, D.A.; Batchelor, T.T.; di Tomaso, E.; Duda, D.G.; Munn, L.L. Edema control by cediranib, a vascular endothelial growth factor receptor–targeted kinase inhibitor, prolongs survival despite persistent brain tumor growth in mice. J. Clin. Oncol. 2009, 27, 2542. [Google Scholar] [CrossRef] [PubMed]
- Carey, L.A.; Perou, C.M.; Livasy, C.A.; Dressler, L.G.; Cowan, D.; Conway, K.; Karaca, G.; Troester, M.A.; Tse, C.K.; Edmiston, S. Race, breast cancer subtypes, and survival in the Carolina Breast Cancer Study. JAMA 2006, 295, 2492–2502. [Google Scholar] [CrossRef]
- O’Connell, J.B.; Maggard, M.A.; Ko, C.Y. Colon cancer survival rates with the new American Joint Committee on Cancer sixth edition staging. J. Natl. Cancer Inst. 2004, 96, 1420–1425. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.G.; Freels, S.; Grutsch, J.; Barlas, S.; Brem, S. Survival rates in patients with primary malignant brain tumors stratified by patient age and tumor histological type: an analysis based on Surveillance, Epidemiology, and End Results (SEER) data, 1973–1991. J. Neurosurg. 1998, 88, 1–10. [Google Scholar] [CrossRef]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Kosary, C.; Trimble, E.L. Treatment and survival for women with fallopian tube carcinoma: a population-based study. Gynecol. Oncol. 2002, 86, 190–191. [Google Scholar] [CrossRef] [PubMed]
- Clarke, C.A.; Glaser, S.L.; Dorfman, R.F.; Mann, R.; DiGiuseppe, J.A.; Prehn, A.W.; Ambinder, R.F. Epstein–Barr virus and survival after Hodgkin disease in a population-based series of women. Cancer Interdiscip. Int. J. Am. Cancer Soc. 2001, 91, 1579–1587. [Google Scholar] [CrossRef]
- Larsen, M.; Mose, H.; Gislum, M.; Skriver, M.V.; Jepsen, P.; Nørgård, B.; Sørensen, H.T. Survival after colorectal cancer in patients with Crohn’s disease: a nationwide population-based Danish follow-up study. Am. J. Gastroenterol. 2007, 102, 163. [Google Scholar] [CrossRef] [PubMed]
- Gnerlich, J.; Jeffe, D.B.; Deshpande, A.D.; Beers, C.; Zander, C.; Margenthaler, J.A. Surgical removal of the primary tumor increases overall survival in patients with metastatic breast cancer: analysis of the 1988–2003 SEER data. Ann. Surg. Oncol. 2007, 14, 2187–2194. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, W. Overview of non-insulin-dependent diabetes mellitus (NIDDM) in different population groups. Diabet. Med. 1996, 13, 7–10. [Google Scholar] [CrossRef]
- Poortinga, W. The prevalence and clustering of four major lifestyle risk factors in an English adult population. Prev. Med. 2007, 44, 124–128. [Google Scholar] [CrossRef]
- Pienta, K.J.; Demers, R.; Hoff, M.; Kau, T.Y.; Montie, J.E.; Severson, R.K. Effect of age and race on the survival of men with prostate cancer in the Metropolitan Detroit tricounty area, 1973 to 1987. Urology 1995, 45, 93–101. [Google Scholar] [CrossRef]
- Jukich, P.J.; McCarthy, B.J.; Surawicz, T.S.; Freels, S.; Davis, F.G. Trends in incidence of primary brain tumors in the United States, 1985-1994. Neuro-oncology 2001, 3, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Miranda-Filho, A.; Piñeros, M.; Soerjomataram, I.; Deltour, I.; Bray, F. Cancers of the brain and CNS: global patterns and trends in incidence. Neuro-oncology 2016, 19, 270–280. [Google Scholar] [CrossRef]
- Ferlay, J.; Soerjomataram, I.; Dikshit, R.; Eser, S.; Mathers, C.; Rebelo, M.; Parkin, D.M.; Forman, D.; Bray, F. Cancer incidence and mortality worldwide: sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer 2015, 136, E359–E386. [Google Scholar] [CrossRef]
- Chien, L.-N.; Gittleman, H.; Ostrom, Q.T.; Hung, K.-S.; Sloan, A.E.; Hsieh, Y.-C.; Kruchko, C.; Rogers, L.R.; Wang, Y.-F.G.; Chiou, H.-Y. Comparative brain and central nervous system tumor incidence and survival between the United States and Taiwan based on population-based registry. Front. Public Health 2016, 4, 151. [Google Scholar] [CrossRef] [PubMed]
- Bondy, M.L.; Scheurer, M.E.; Malmer, B.; Barnholtz-Sloan, J.S.; Davis, F.G.; Il’Yasova, D.; Kruchko, C.; McCarthy, B.J.; Rajaraman, P.; Schwartzbaum, J.A. Brain tumor epidemiology: consensus from the Brain Tumor Epidemiology Consortium. Cancer 2008, 113, 1953–1968. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-H.; Jung, K.-W.; Yoo, H.; Park, S.; Lee, S.H. Epidemiology of primary brain and central nervous system tumors in Korea. J. Korean Neurosurg. Soc. 2010, 48, 145. [Google Scholar] [CrossRef] [PubMed]
- Abrahams, H.; Gielissen, M.; Schmits, I.; Verhagen, C.; Rovers, M.; Knoop, H. Risk factors, prevalence, and course of severe fatigue after breast cancer treatment: a meta-analysis involving 12 327 breast cancer survivors. Ann. Oncol. 2016, 27, 965–974. [Google Scholar] [CrossRef] [PubMed]
- McGirt, M.J.; Chaichana, K.L.; Gathinji, M.; Attenello, F.J.; Than, K.; Olivi, A.; Weingart, J.D.; Brem, H.; redo Quiñones-Hinojosa, A. Independent association of extent of resection with survival in patients with malignant brain astrocytoma. J. Neurosurg. 2009, 110, 156–162. [Google Scholar] [CrossRef] [Green Version]
- Efron, B. Nonparametric estimates of standard error: the jackknife, the bootstrap and other methods. Biometrika 1981, 68, 589–599. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Li, H.; Zhang, C.-H. The sparse Laplacian shrinkage estimator for high-dimensional regression. Ann. Stat. 2011, 39, 2021. [Google Scholar] [CrossRef]
- Land, S.R.; Friedman, J.H. Variable Fusion: A New Adaptive Signal Regression Method; Technical Report 656; Department of Statistics, Carnegie Mellon University: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Pan, W.; Xie, B.; Shen, X. Incorporating predictor network in penalized regression with application to microarray data. Biometrics 2010, 66, 474–484. [Google Scholar] [CrossRef]
- Daye, Z.J.; Jeng, X.J. Shrinkage and model selection with correlated variables via weighted fusion. Comput. Stat. Data Anal. 2009, 53, 1284–1298. [Google Scholar] [CrossRef]
- Villano, J.; Koshy, M.; Shaikh, H.; Dolecek, T.; McCarthy, B. Age, gender, and racial differences in incidence and survival in primary CNS lymphoma. Br. J. Cancer 2011, 105, 1414. [Google Scholar] [CrossRef] [PubMed]
- Bindal, A.K.; Bindal, R.K.; Hess, K.R.; Shiu, A.; Hassenbusch, S.J.; Shi, W.M.; Sawaya, R. Surgery versus radiosurgery in the treatment of brain metastasis. J. Neurosurg. 1996, 84, 748–754. [Google Scholar] [CrossRef] [PubMed]
- Barnholtz-Sloan, J.S.; Sloan, A.E.; Schwartz, A.G. Racial differences in survival after diagnosis with primary malignant brain tumor. Cancer Interdiscip. Int. J. Am. Cancer Soc. 2003, 98, 603–609. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Xue, Y.; Ma, S. Population-Based Brain Tumor Survival Analysis via Spatial- and Temporal-Smoothing. Cancers 2019, 11, 1732. https://doi.org/10.3390/cancers11111732
Ma C, Xue Y, Ma S. Population-Based Brain Tumor Survival Analysis via Spatial- and Temporal-Smoothing. Cancers. 2019; 11(11):1732. https://doi.org/10.3390/cancers11111732
Chicago/Turabian StyleMa, Chenjin, Yuan Xue, and Shuangge Ma. 2019. "Population-Based Brain Tumor Survival Analysis via Spatial- and Temporal-Smoothing" Cancers 11, no. 11: 1732. https://doi.org/10.3390/cancers11111732
APA StyleMa, C., Xue, Y., & Ma, S. (2019). Population-Based Brain Tumor Survival Analysis via Spatial- and Temporal-Smoothing. Cancers, 11(11), 1732. https://doi.org/10.3390/cancers11111732




