Application of Generalized Finite Difference Method for Nonlinear Analysis of the Electrothermal Micro-Actuator
Abstract
1. Introduction
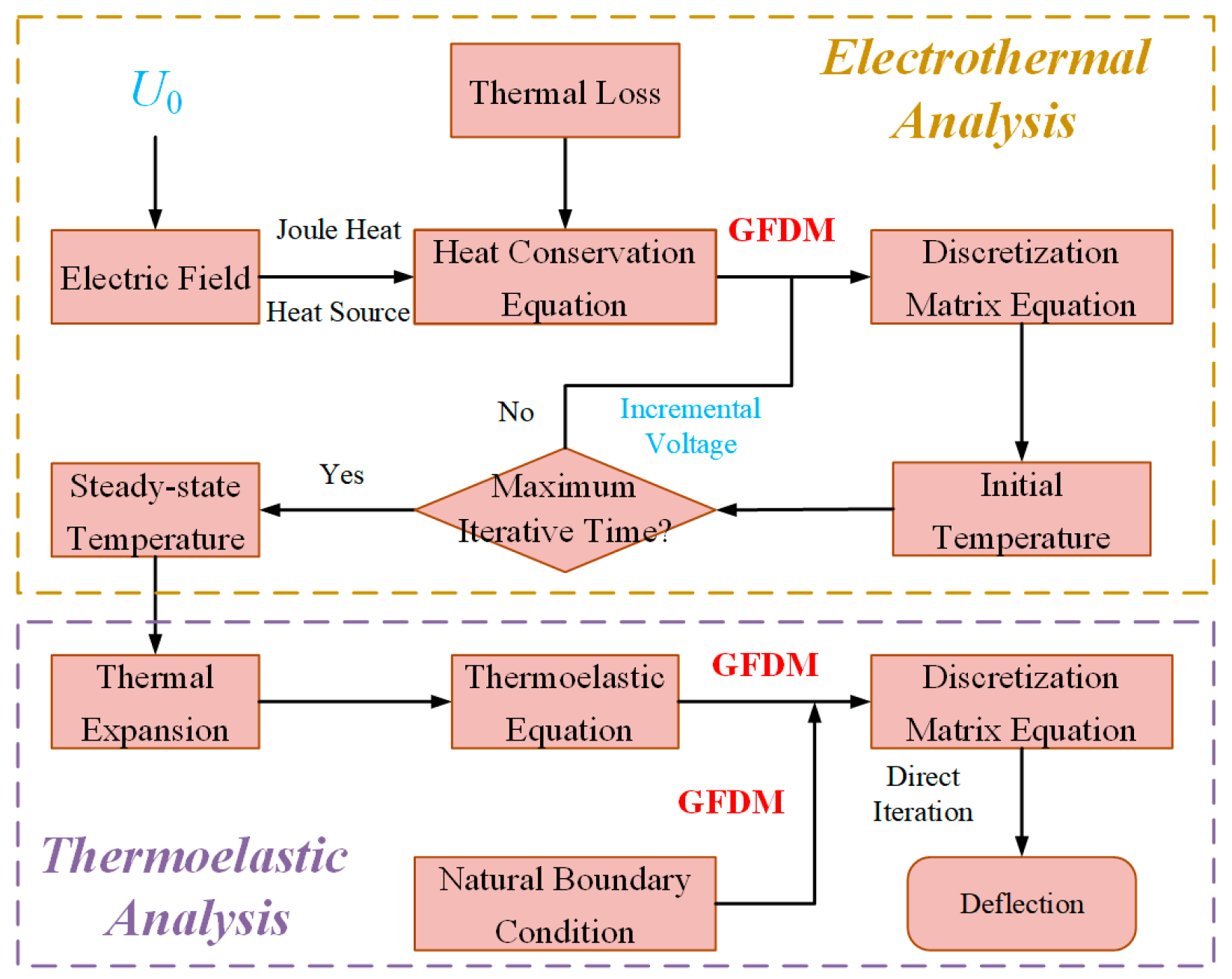
2. Generalized Finite Difference Method
3. Electrothermal Analysis
- (i)
- Initialize the material parameters based on the initial condition and then determine the total stiffness matrix K and the inverse matrix K−1. The initial voltage U1 is so that P1 can be calculated. According to these metrics, the temperature at the first iterative step T1 is obtained using Equation (22).
- (ii)
- Update the material parameters according to the temperature from the previous iterative step. The applied voltage Un should also be renewed as nU2/NU at the nth iterative step. After that, the matrixes , , and vector are obtained. Thus, the transition temperature Tt can be calculated by Equation (23) to avoid the computational error accumulation.
- (iii)
- Predict and revise the transition temperature by
- (iv)
- Re-update the material parameters using the Tθ. Further, the matrixes , , and vector can be renewed again. Finally, the temperature Tn is obtained at the nth iterative step by
- (v)
- Termination condition judgment: If the maximum number of iterations is reached or other termination conditions are satisfied, the iteration is stopped. Otherwise, go back to step (ii).
4. Thermomechanical Analysis
- Case I: If the point (xI, yI) is the interior node of the computational domain, Equation (26) is adopted to obtain KI and pI. The matrix KI is with the 2 × (2Nl + 2).andwhere and are the first derivative of the x-direction and y-direction thermal strain at the point (xI, yI) versus x, respectively. Based on the temperature distribution, their value can be calculated via finite difference. and can both be regarded as 0 in light of the 1D model established in the electrothermal analysis.
- Case II: If the point (xI, yI) is at the natural boundary, Equation (27) is adopted to obtain KI and pI.andwhere nIx and nIy are components of the normal vector in the x and y-direction at the point (xI, yI).
- Case III: Otherwise, the point (xI, yI) is at the Dirichlet boundary. Matrix KI and pI, based on the Equation (28), are derived as follows:andwhere other elements in matrix KI are 0. Finally, the Equations (32)–(39) need to be assembled into the total matrix equation similar to (22). In this total matrix equation, K and P are with N × N and N × 1, respectively. For the element , I is the global index of the point (xI, yI) and j is the local index of the point (xj, yj). J is the global index of the j. Thus, the element should be placed in the (2I − 1)th row and (2J − 1)th column of the total stiffness matrix K. The element is in the (2I)th row and (2J − 1)th column. The and are, respectively, located in the (2I − 1)th and (2I)th row of the P. The direct iteration method can be used to solve the total matrix equation from this analysis.
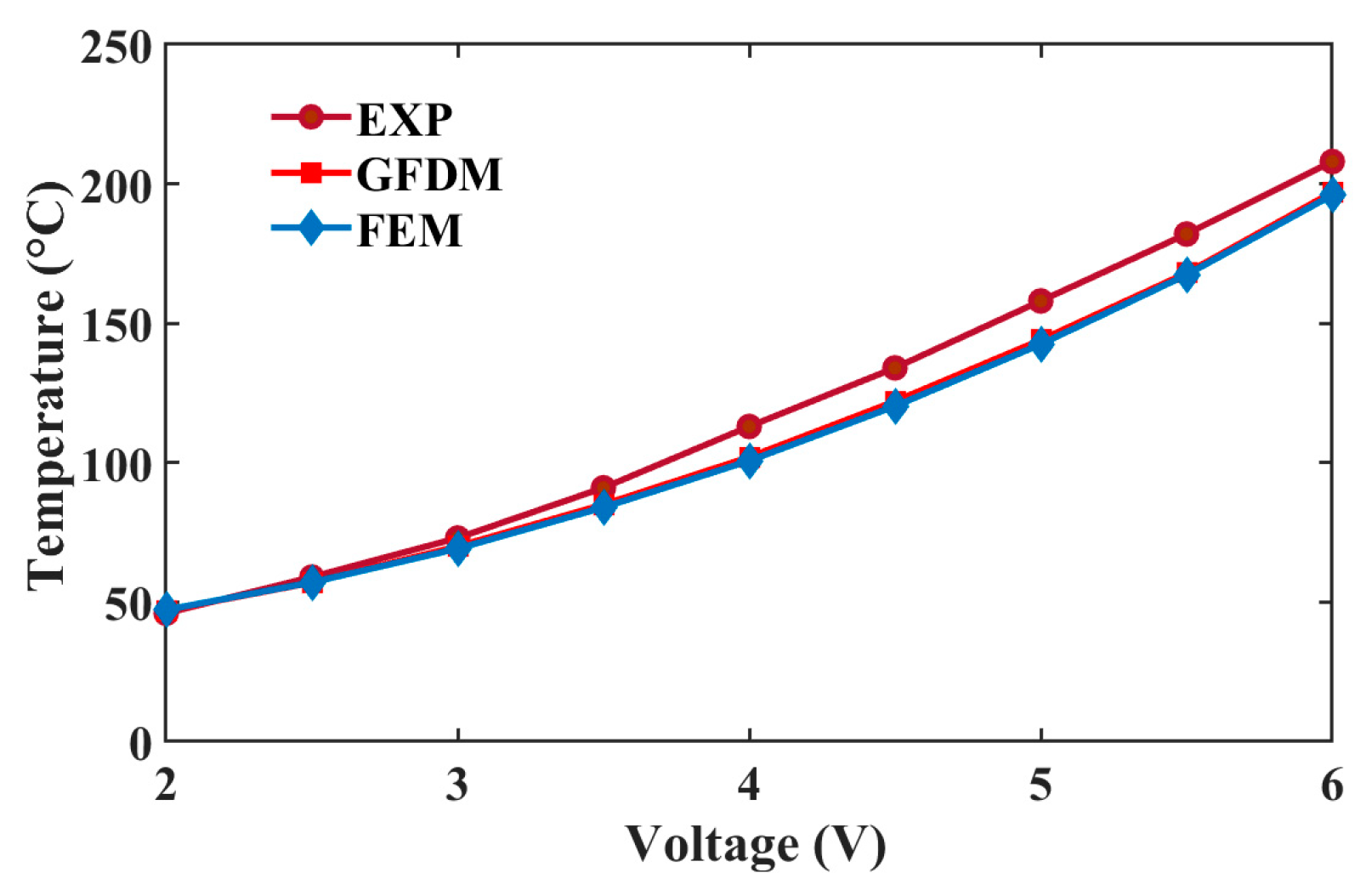
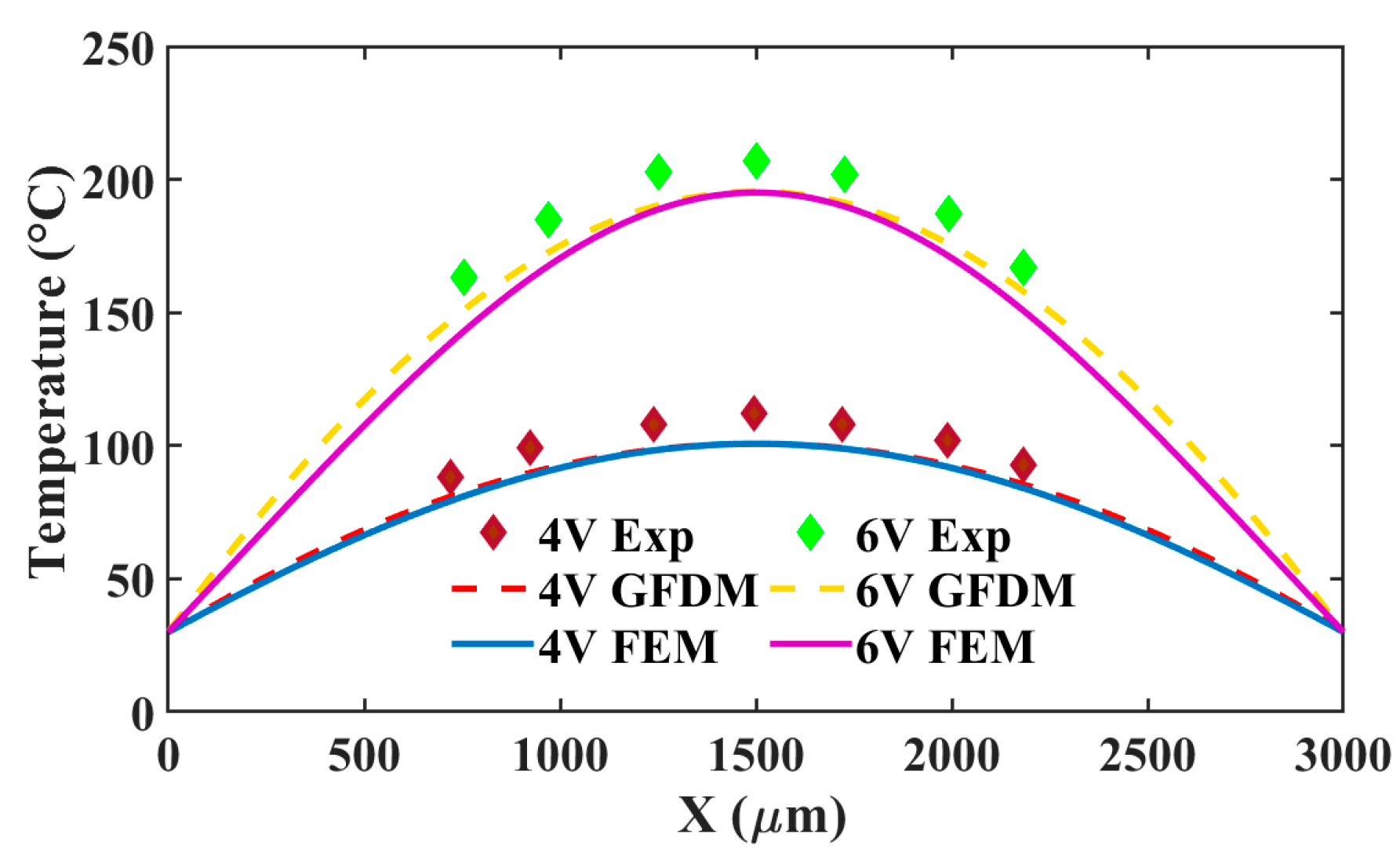
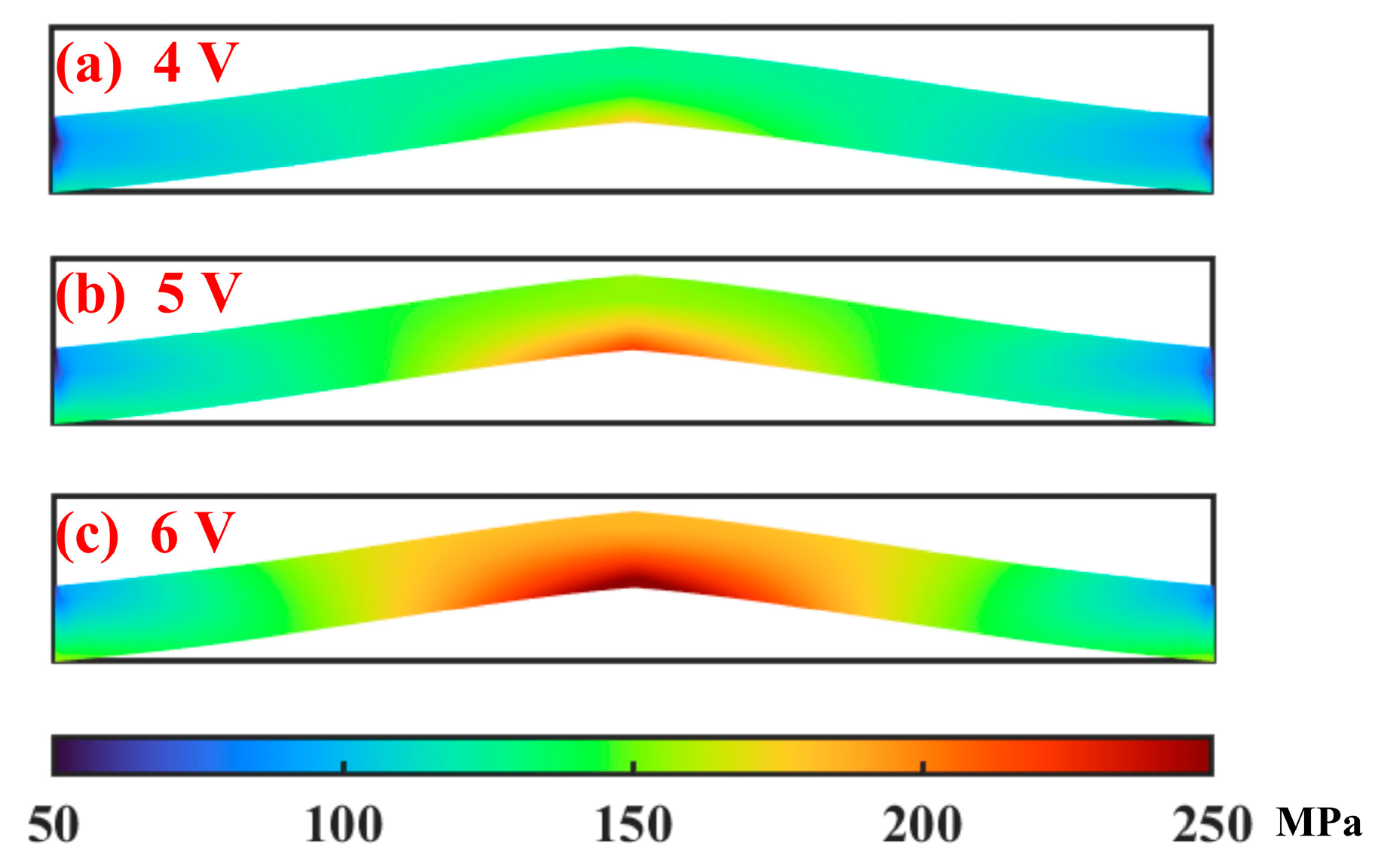
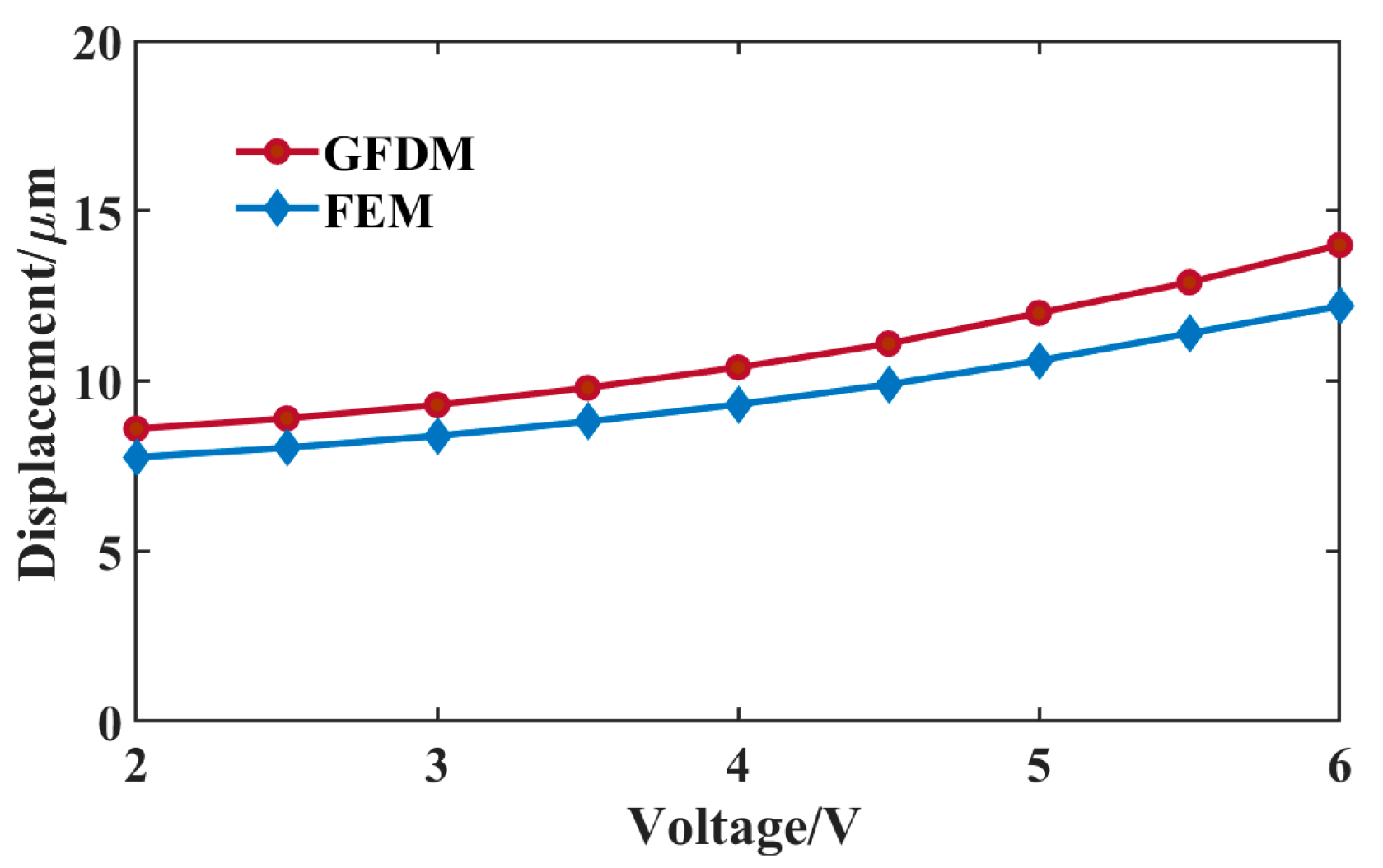
5. Numerical Results and Discussions
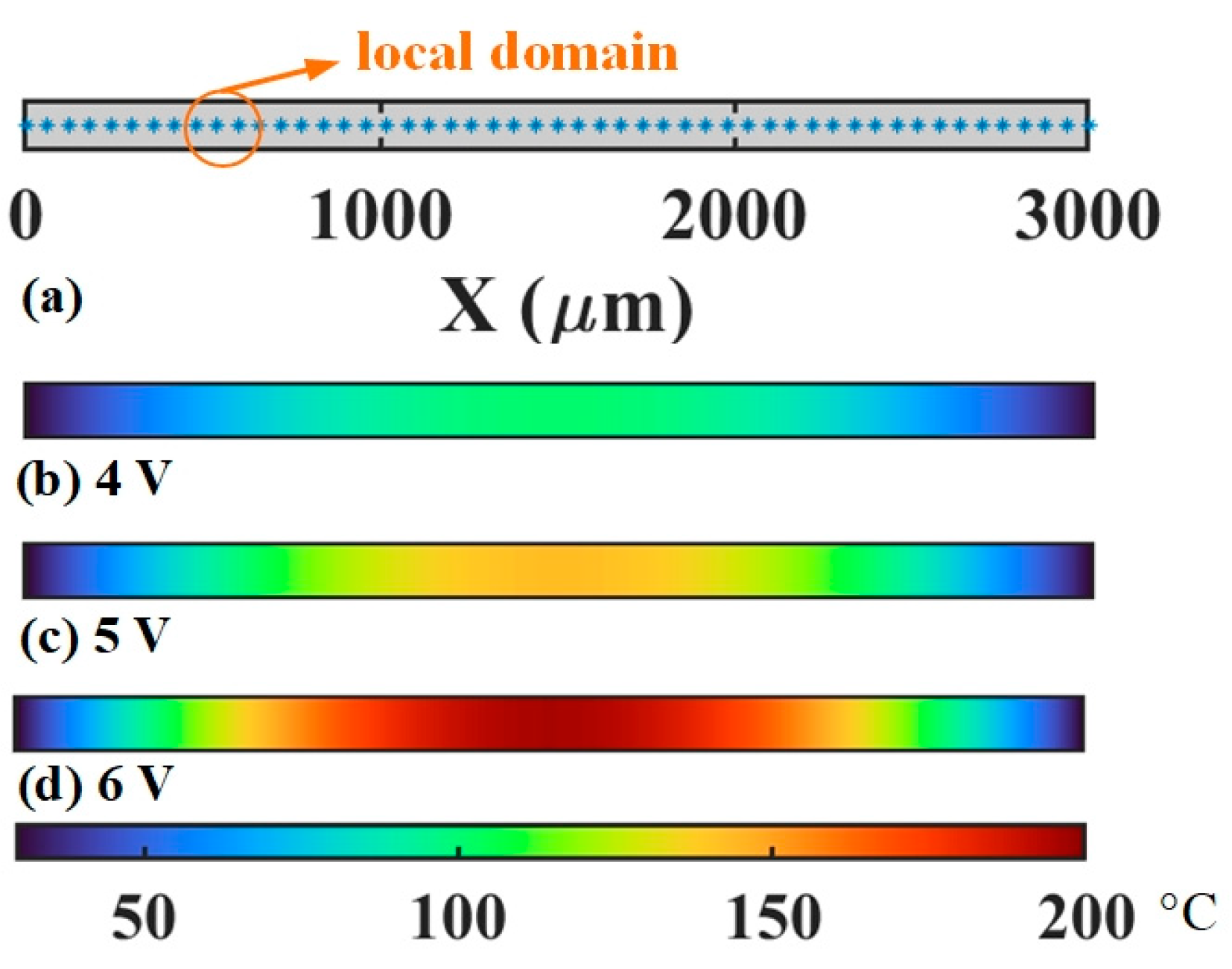
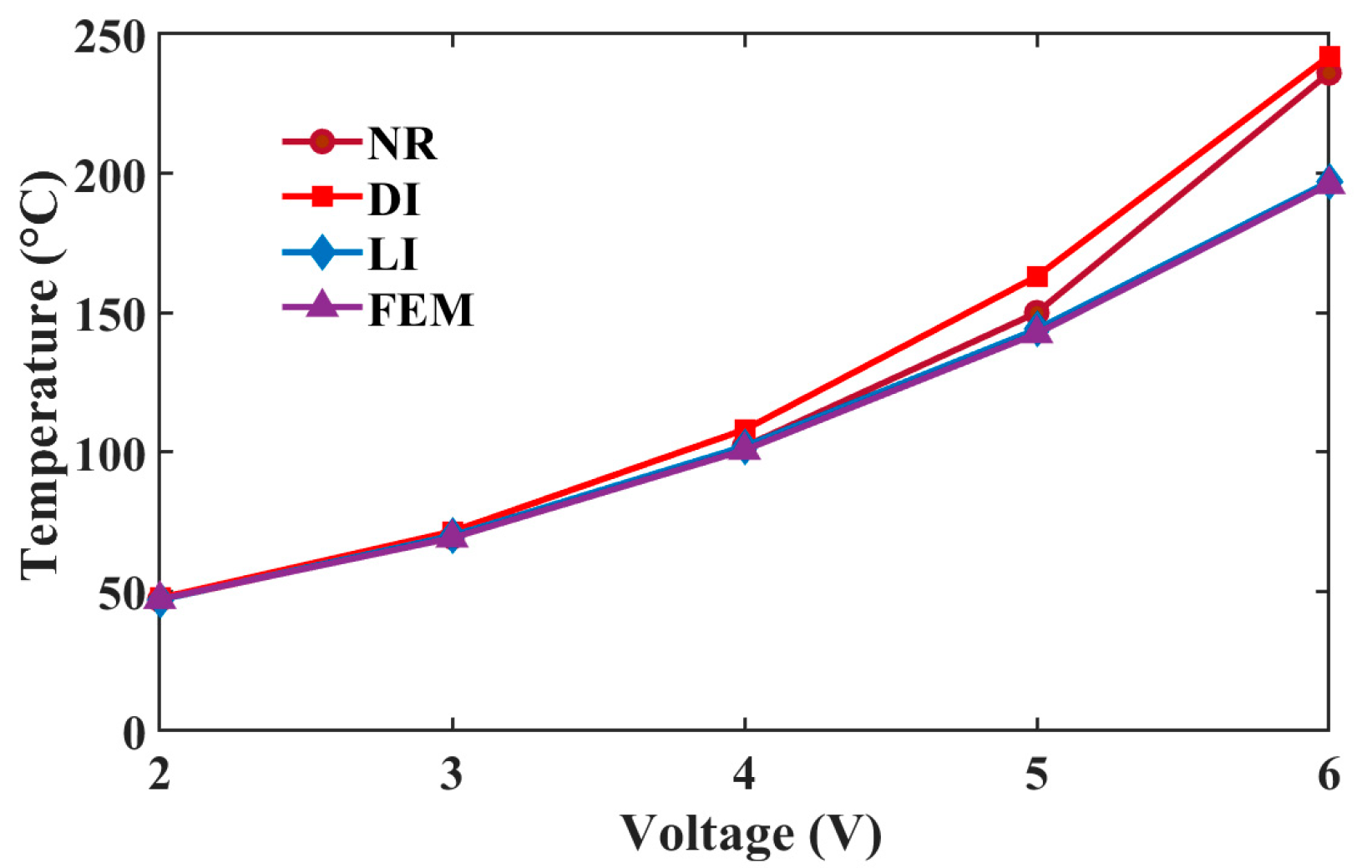
5.1. Thermal Prediction
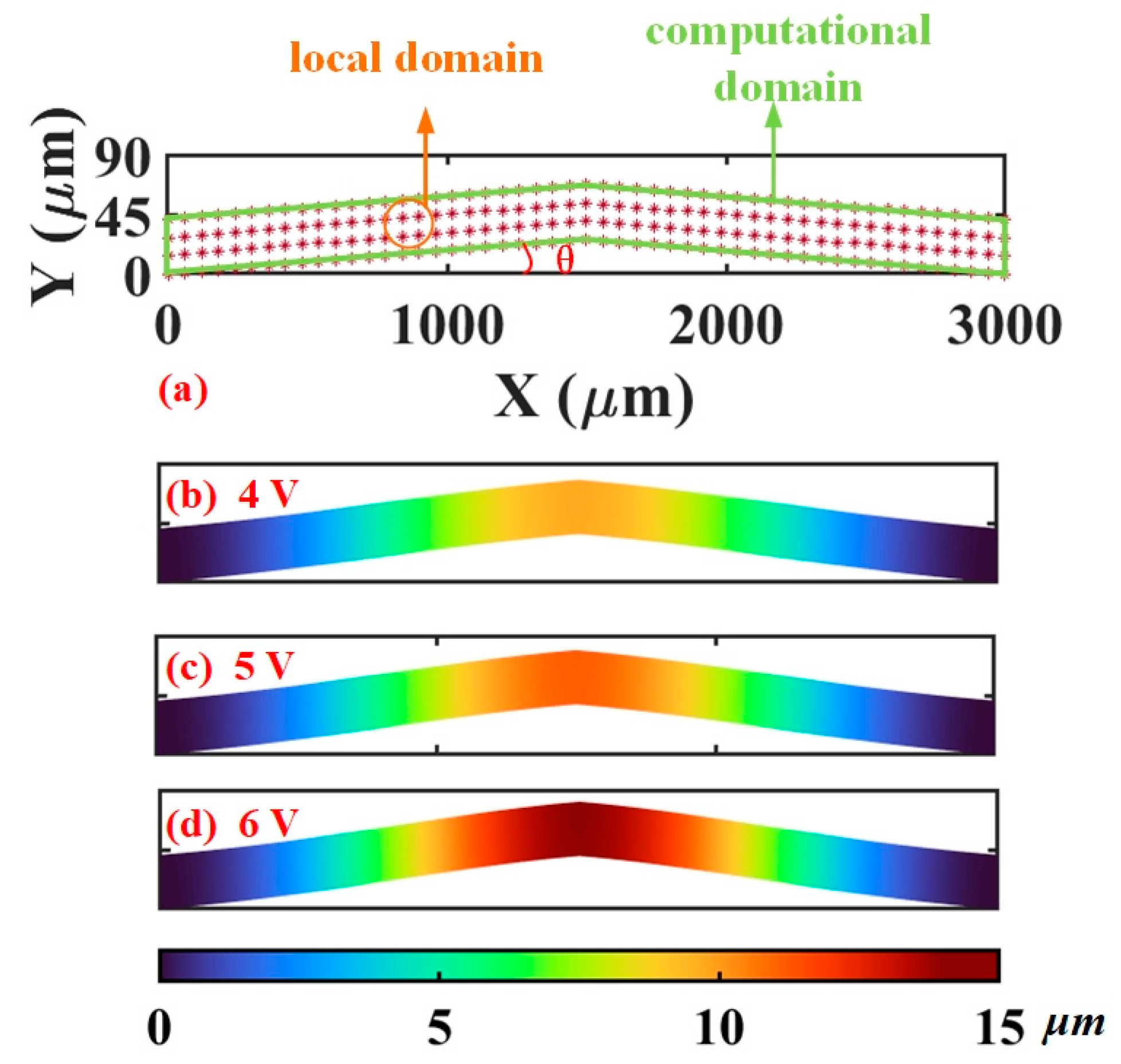
5.2. Mechanical Prediction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, L.; Ogura, I.; Ashida, K.; Yabuno, H. Mechanism of mechanical nanolithography using self-excitation microcantilever. Nonlinear Dyn. 2024, 112, 5811–5824. [Google Scholar] [CrossRef]
- Jalili, H.; Salarieh, H.; Vossoughi, G. Study of a piezo-electric actuated vibratory micro-robot in stick-slip mode and investigating the design parameters. Nonlinear Dyn. 2017, 89, 1927–1948. [Google Scholar] [CrossRef]
- Gao, X.; Deng, J.; Zhang, S.; Li, J.; Liu, Y. A compact 2-dof micro/nano manipulator using single miniature piezoelectric tube actuator. IEEE Trans. Ind. Electron. 2022, 69, 3928–3937. [Google Scholar] [CrossRef]
- Kong, X.; Cao, Y.; Zhu, H.; Nie, W.; Xi, Z. A self-latching MEMS optical interrupter with status monitoring for laser initiation system. IEEE Trans. Electron Devices 2023, 70, 2473–2480. [Google Scholar] [CrossRef]
- Dai, J.; Feng, C.; Xie, J.; Gao, M.; Zhen, T. Design and control of an analog optical switch based on the coupling of an electrothermal actuator and a mass–spring system. IEEE/ASME Trans. Mechatron. 2023, 28, 2517–2528. [Google Scholar] [CrossRef]
- Ghanbari, M.; Rezazadeh, G.; Moloudpour-Tolkani, V.; Sheikhlou, M. Dynamic analysis of a novel wide-tunable microbeam resonator with a sliding free-of-charge electrode. Nonlinear Dyn. 2023, 111, 8039–8060. [Google Scholar] [CrossRef]
- Benedetti, K.C.B.; Gonçalves, P.B. Nonlinear response of an imperfect microcantilever static and dynamically actuated considering uncertainties and noise. Nonlinear Dyn. 2022, 107, 1725–1754. [Google Scholar] [CrossRef]
- Ma, M.; Ekinci, K.L. Electrothermal actuation of NEMS resonators: Modeling and experimental validation. J. Appl. Phys. 2023, 134, 074302. [Google Scholar] [CrossRef]
- Yunas, J.; Mulyanti, B.; Hamidah, I.; Said, M.M.; Pawinanto, R.E.; Ali, W.A.F.W.; Subandi, A.; Hamzah, A.A.; Latif, R.; Majlis, B.Y. Polymer-based MEMS electromagnetic actuator for biomedical application: A review. Polymers 2020, 12, 1184. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Krzysztof Kamil, U.R. On the snap-through buckling analysis of electrostatic shallow arch micro-actuator via meshless galerkin decomposition technique. Eng. Anal. Bound. Elem. 2022, 134, 388–397. [Google Scholar] [CrossRef]
- Khorasani, V.S.; Żur, K.K.; Kim, J.; Reddy, J. On the dynamics and stability of size-dependent symmetric FGM plates with electro-elastic coupling using meshless local Petrov-Galerkin method. Compos. Struct. 2022, 298, 115993. [Google Scholar] [CrossRef]
- Chen, H.; Sun, X.; Chen, M.; Kong, X. Dynamic response of a MEMS electrothremal actuator by the local radial point interpolation method. Nonlinear Dyn. 2025, 1–11. [Google Scholar] [CrossRef]
- Nguyen, B.H.H.; Torri, G.B.; Rochus, V. Physics-informed neural networks with data-driven in modeling and characterizing piezoelectric micro-bender. J. Micromech. Microeng. 2024, 34, 115004. [Google Scholar] [CrossRef]
- Xia, H.; Gu, Y. The generalized finite difference method for electroelastic analysis of 2D piezoelectric structures. Eng. Anal. Bound. Elem. 2021, 124, 82–86. [Google Scholar] [CrossRef]
- Shao, Y.; Duan, Q.; Chen, R. Adaptive meshfree method for fourth-order phase-field model of fracture using consistent integration schemes. Comput. Mater. Sci. 2024, 233, 112743. [Google Scholar] [CrossRef]
- Demkowicz, L.F.; Gopalakrishnan, J. An overview of the discontinuous Petrov Galerkin method. In Proceedings of the Recent Developments in Discontinuous Galerkin Finite Element Methods for Partial Differential Equations: 2012 John H Barrett Memorial Lectures, Knoxville, TN, USA, 9–11 May 2012; pp. 149–180. [Google Scholar]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Guo, R.; Sui, F.; Yue, W.; Wang, Z.; Pala, S.; Li, K.; Xu, R.; Lin, L. Deep learning for non-parameterized MEMS structural design. Microsyst. Nanoeng. 2022, 8, 91. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, R.; Yang, K.; Yu, G.; Chen, Y. Application of generalized finite difference method for elastoplastic torsion analysis of prismatic bars. Eng. Anal. Bound. Elem. 2023, 146, 939–950. [Google Scholar] [CrossRef]
- Sun, W.; Qu, W.; Gu, Y.; Zhao, S. Meshless generalized finite difference method for two-and three-dimensional transient elastodynamic analysis. Eng. Anal. Bound. Elem. 2023, 152, 645–654. [Google Scholar] [CrossRef]
- Zhao, Q.; Fan, C.-M.; Wang, F.; Qu, W. Topology optimization of steady-state heat conduction structures using meshless generalized finite difference method. Eng. Anal. Bound. Elem. 2020, 119, 13–24. [Google Scholar] [CrossRef]
- Ju, B.; Yu, B.; Zhou, Z. A generalized finite difference method for 2D dynamic crack analysis. Results Appl. Math. 2024, 21, 100418. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.-J.; Wang, J.; Xi, Z.-W. Analysis of the dynamic behavior of a V-shaped electrothermal microactuator. J. Micromech. Microeng. 2020, 30, 085005. [Google Scholar] [CrossRef]
- Zhu, H.; Cao, Y.; Ma, W.; Kong, X.; Lei, S.; Lu, H.; Nie, W.; Xi, Z. Dynamic modeling of a mems electro-thermal actuator considering micro-scale heat transfer with end effectors. J. Microelectromech. 2024, 33, 217–226. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, H.; Chen, H.; Zhu, H.; Nie, W.; Xi, Z. Dynamic thermal characterization of MEMS electrothermal actuators in air. IEEE Sens. J. 2021, 21, 15979–15986. [Google Scholar] [CrossRef]
- Kong, X.; Cao, Y.; Zhu, H.; Wang, H.; Lu, J.; Xu, X.; Nie, W.; Xi, Z. Experimental and numerical study of MEMS electrothermal actuators: Comparing dynamic behavior and heat transfer process in vacuum and non-vacuum environments. Vacuum 2024, 227, 113409. [Google Scholar] [CrossRef]
- Asgari, M.; Kouchakzadeh, M.A. An equivalent von Mises stress and corresponding equivalent plastic strain for elastic–plastic ordinary peridynamics. Meccanica 2019, 54, 1001–1014. [Google Scholar] [CrossRef]
| N | 11 | 101 | 501 | 1001 |
| Max temperature (°C) | 189.1 | 195.3 | 195.2 | 195.2 |
| CPU time (s) | 0.04 | 0.39 | 2.64 | 8.29 |
| NU | 10 | 50 | 100 | 1001 |
| Max temperature (°C) | 216.1 | 197.8 | 195.3 | 195.1 |
| CPU time (s) | 0.06 | 0.22 | 0.39 | 1.64 |
| N | 201 | 505 | 1206 | 2406 |
| Max displacement (μm) | 11.4 | 13.9 | 14.0 | 14.0 |
| CPU time (s) | 0.05 | 0.06 | 0.17 | 0.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Kong, X.; Sun, X.; Chen, M.; Yuan, H. Application of Generalized Finite Difference Method for Nonlinear Analysis of the Electrothermal Micro-Actuator. Micromachines 2025, 16, 325. https://doi.org/10.3390/mi16030325
Chen H, Kong X, Sun X, Chen M, Yuan H. Application of Generalized Finite Difference Method for Nonlinear Analysis of the Electrothermal Micro-Actuator. Micromachines. 2025; 16(3):325. https://doi.org/10.3390/mi16030325
Chicago/Turabian StyleChen, Hao, Xiaoyu Kong, Xiangdong Sun, Mengxu Chen, and Haiyang Yuan. 2025. "Application of Generalized Finite Difference Method for Nonlinear Analysis of the Electrothermal Micro-Actuator" Micromachines 16, no. 3: 325. https://doi.org/10.3390/mi16030325
APA StyleChen, H., Kong, X., Sun, X., Chen, M., & Yuan, H. (2025). Application of Generalized Finite Difference Method for Nonlinear Analysis of the Electrothermal Micro-Actuator. Micromachines, 16(3), 325. https://doi.org/10.3390/mi16030325






