Electromagnetically Induced Transparency (EIT) Like Transmission Based on 3 × 3 Cascaded Multimode Interference Resonators
Abstract
1. Introduction
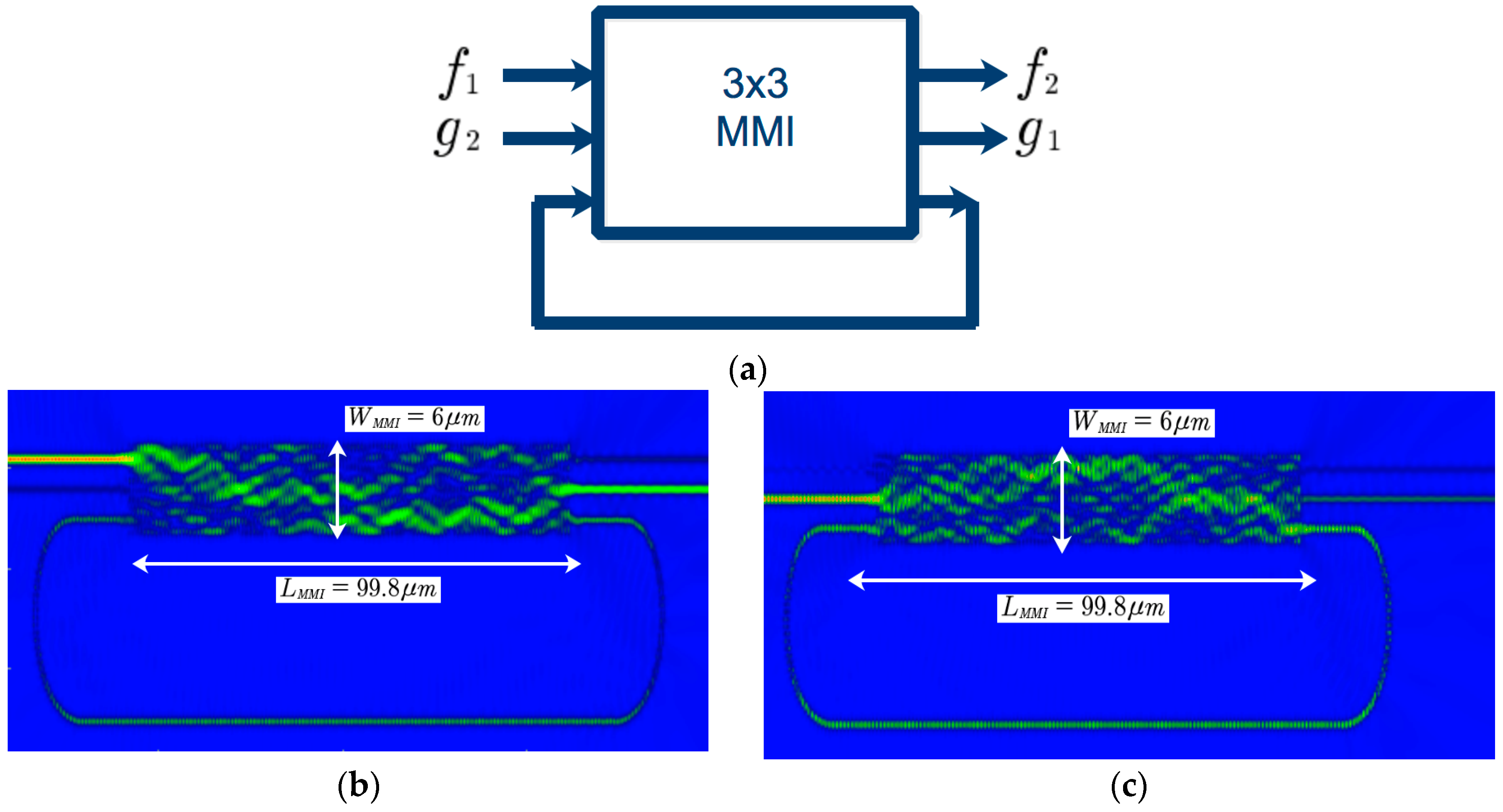
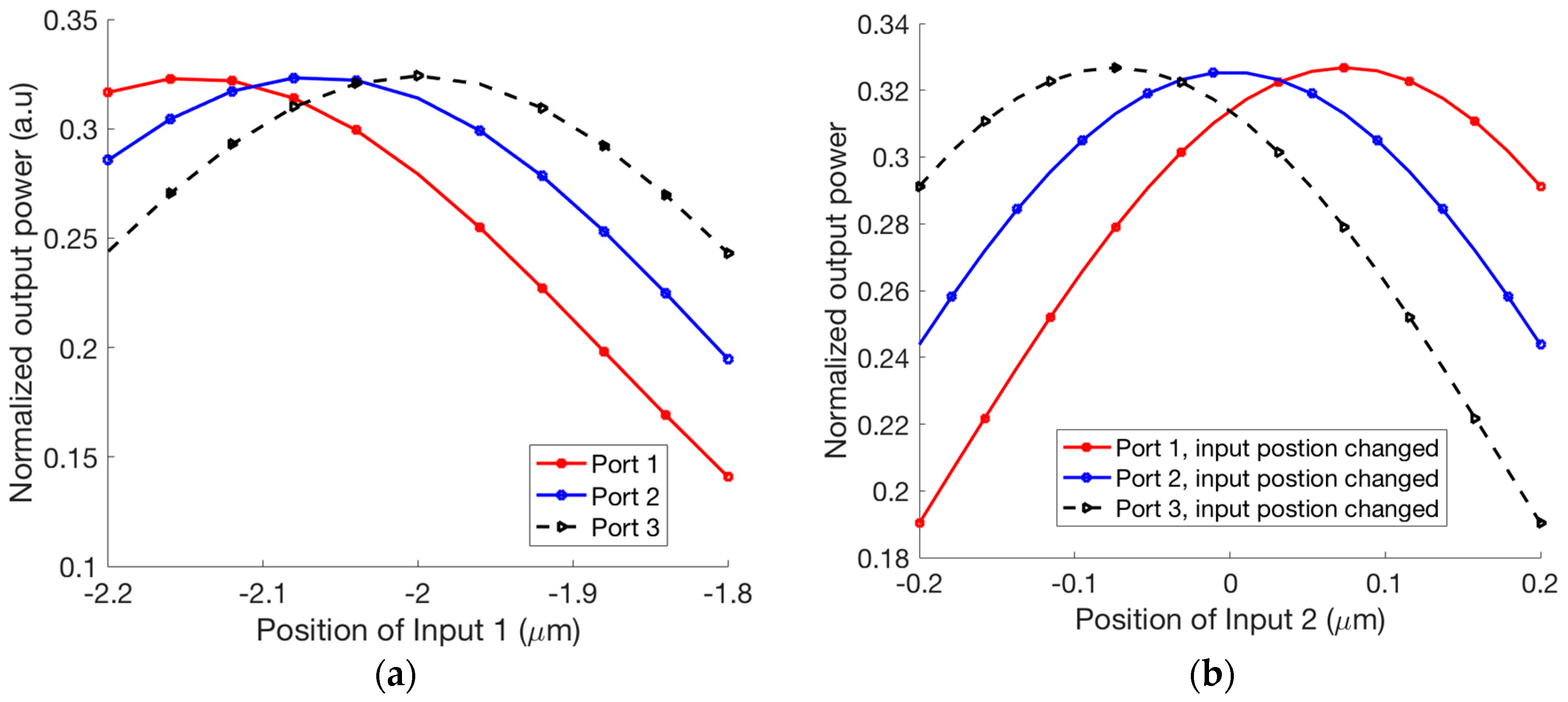
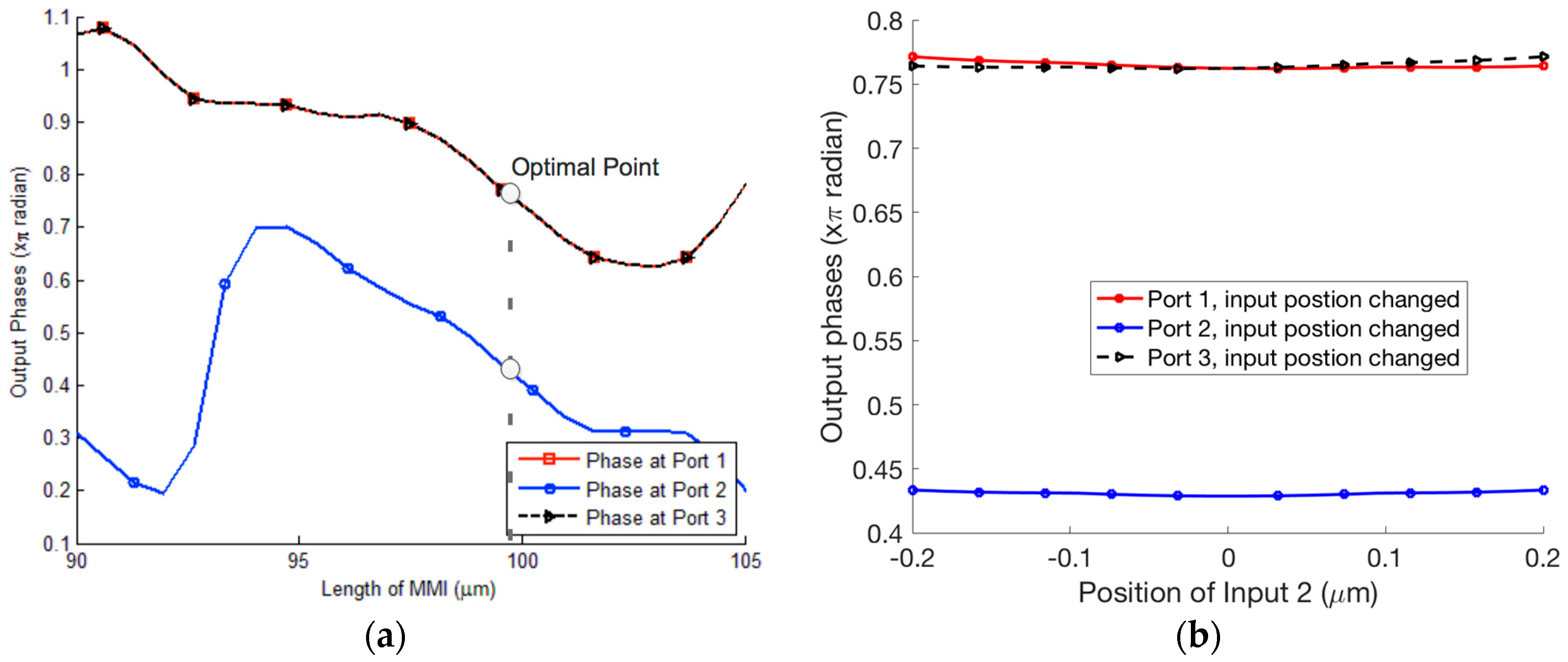
2. Single Fano Resonance Unit (FRU)
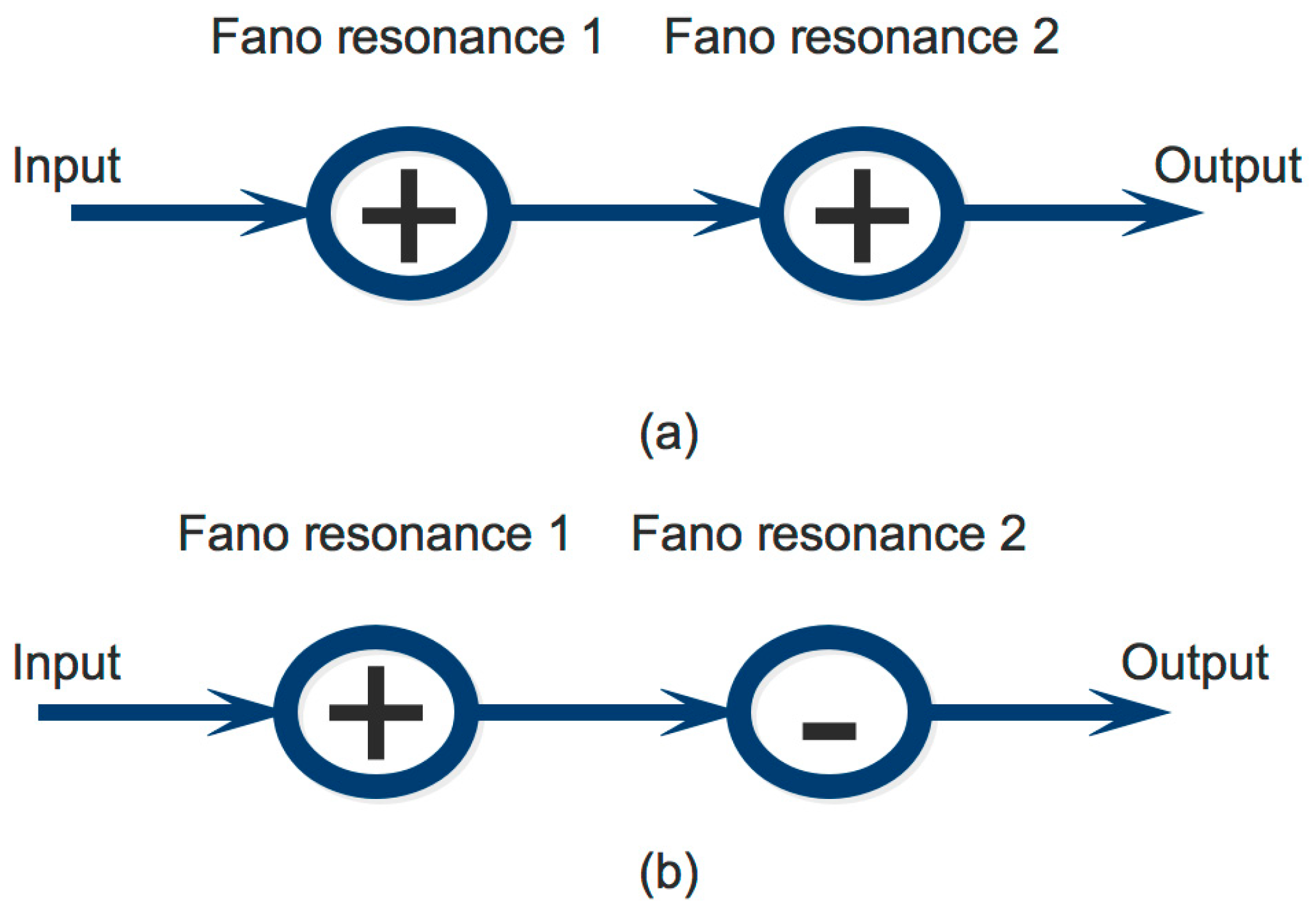
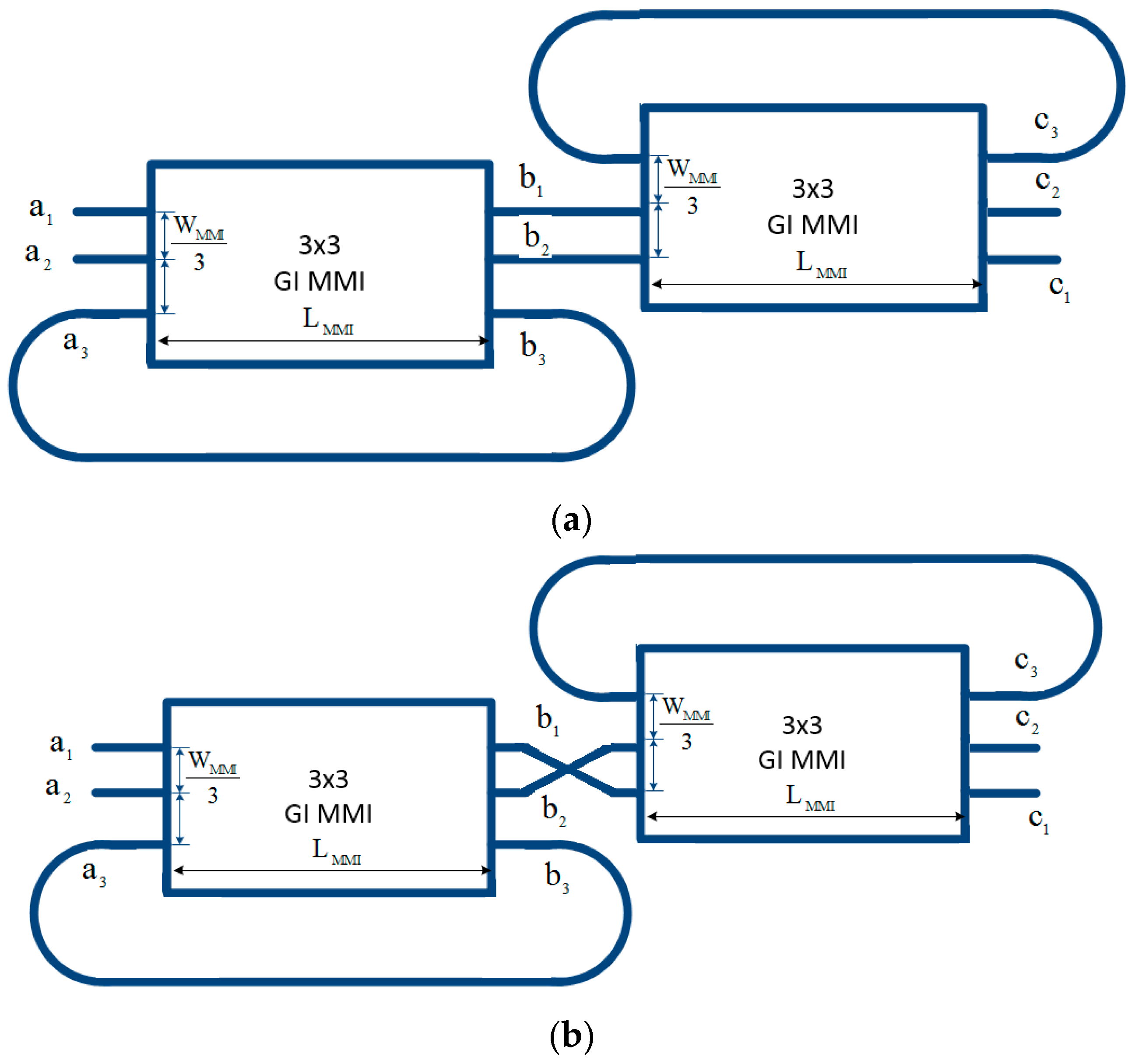
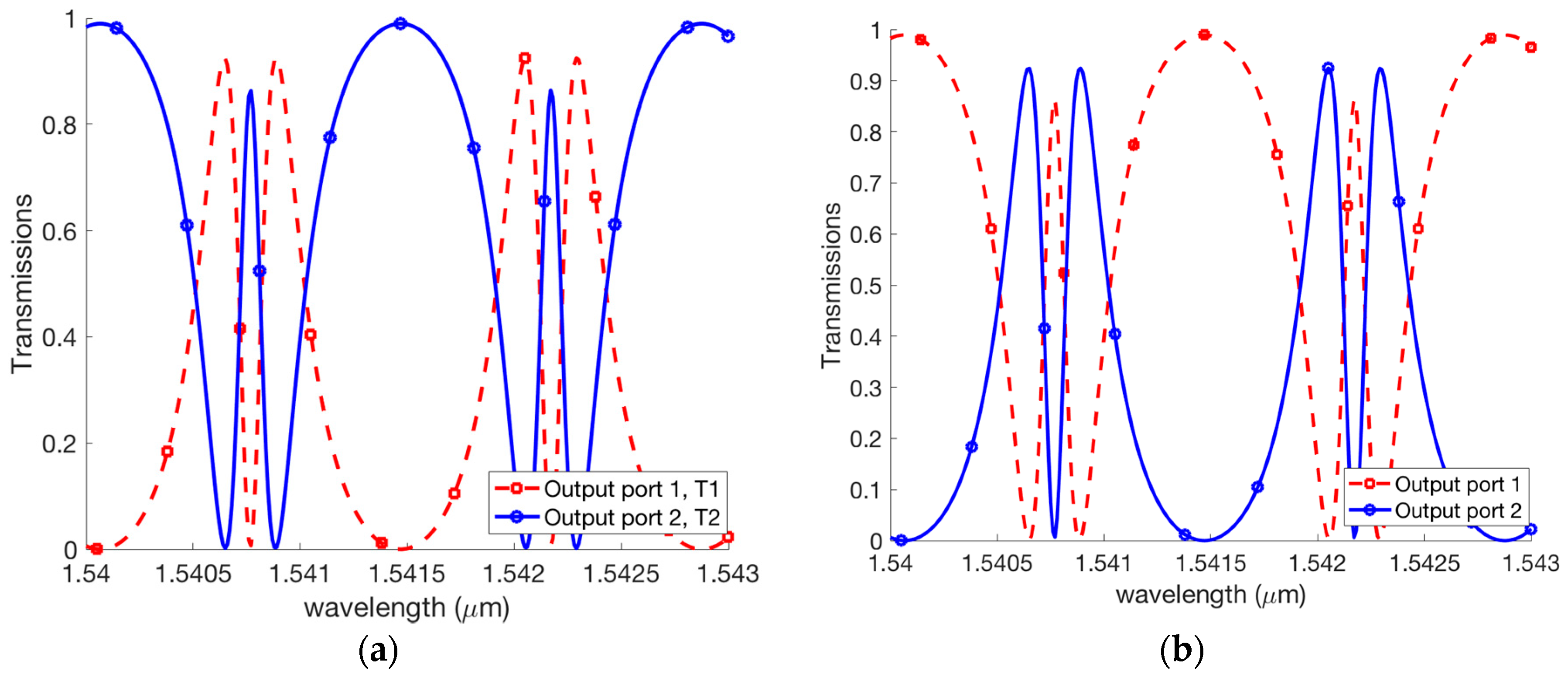
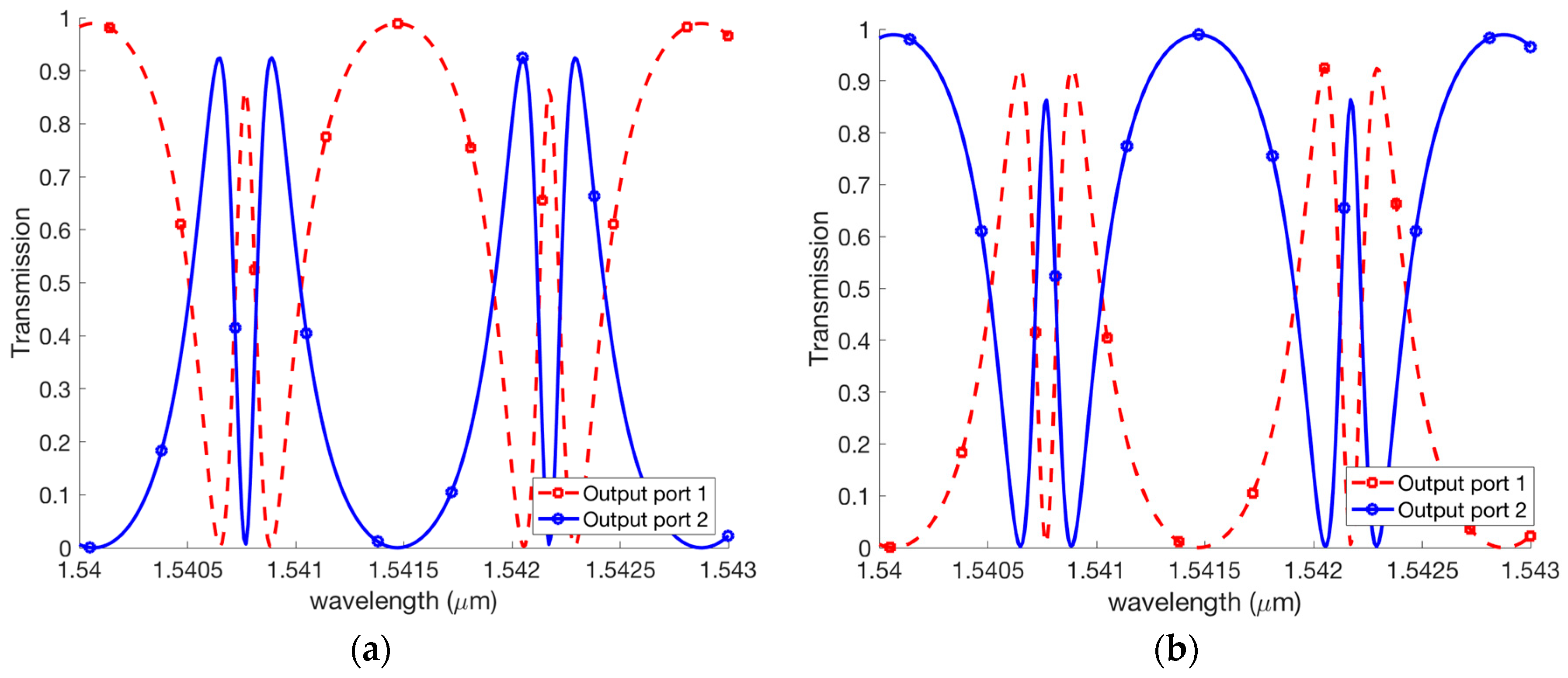
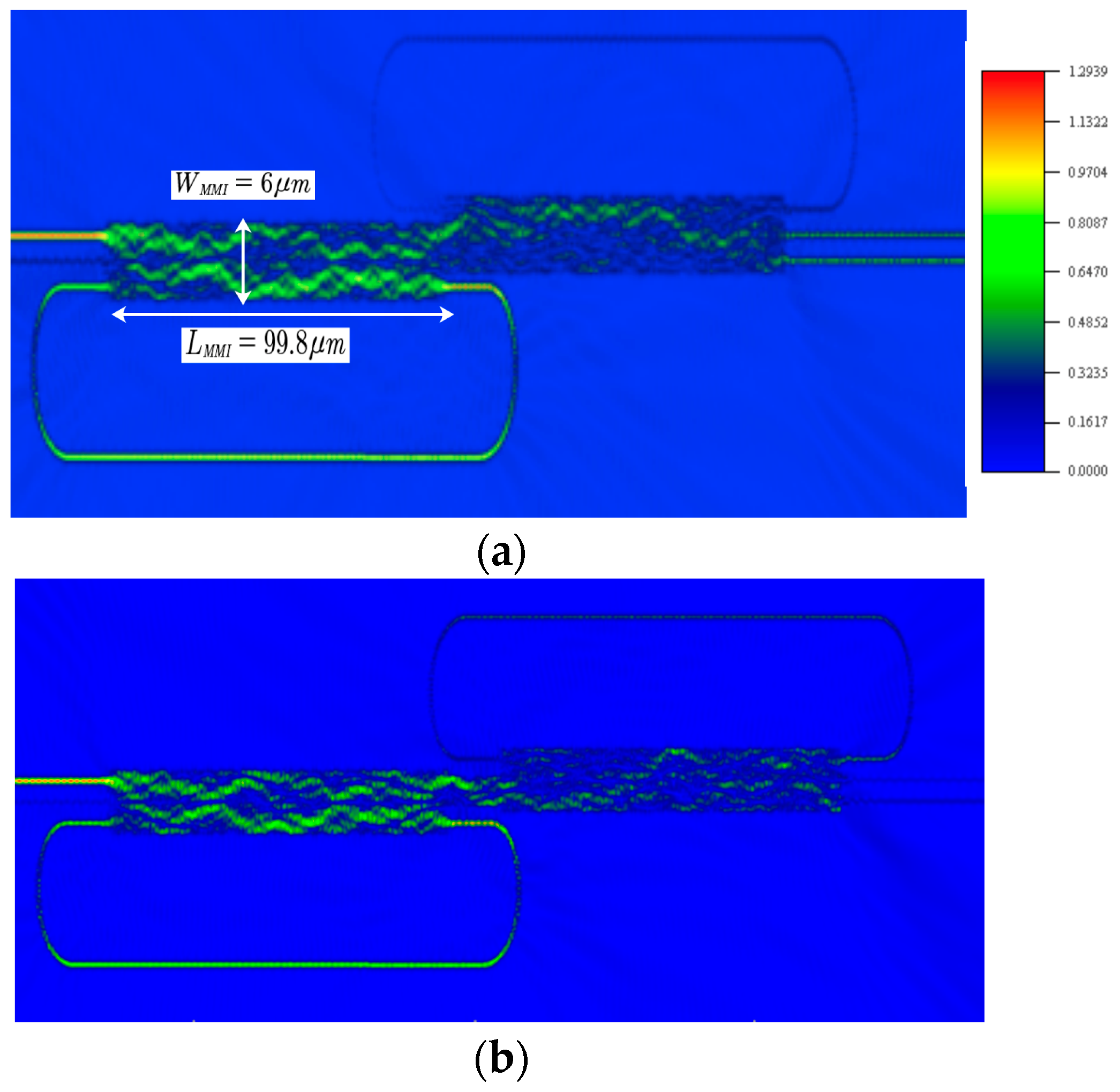
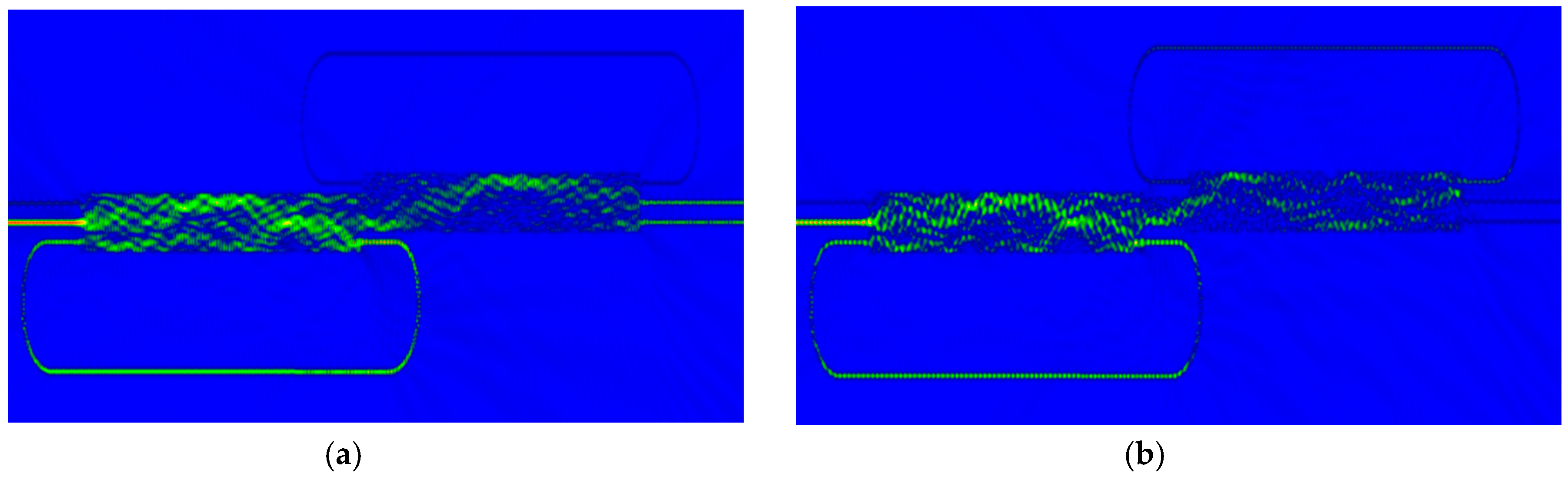
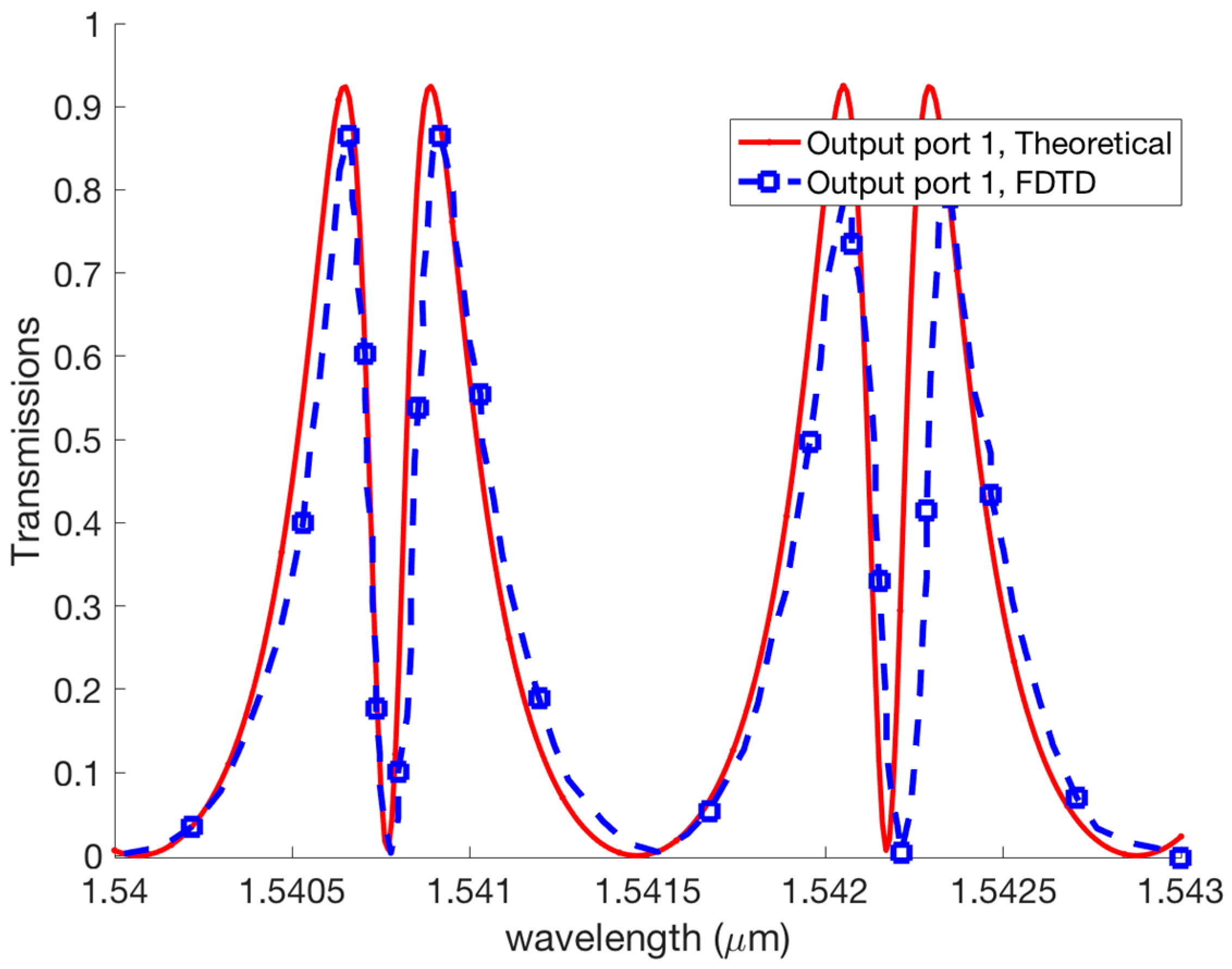
3. Coupled Fano Resonances and Generation of the EIT Effect
4. Conclusions
Funding
Conflicts of Interest
References
- Zhou, X.; Zhang, L.; Pang, W.; Zhang, H.; Yang, Q.; Zhang, D. Phase characteristics of an electromagnetically induced transparency analogue in coupled resonant systems. New J. Phys. 2013, 15, 103033. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Lvovsky, A.I.; Sanders, B.C.; Tittel, W. Optical quantum memory. Nat. Photonics 2009, 3, 706–714. [Google Scholar] [CrossRef]
- Harris, S.E. Lasers without inversion: Interference of lifetime-broadened resonances. Phys. Rev. Lett. 1989, 62, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Chin, S.; Thévenaz, L. Tunable photonic delay lines in optical fibers. Laser Photonics Rev. 2012, 6, 724–738. [Google Scholar] [CrossRef]
- Tanji-Suzuki, H.; Chen, W.; Landig, R.; Simon, J.; Vuletić, V. Vacuum-induced transparency. Science 2011, 361. [Google Scholar] [CrossRef]
- Tassin, P.; Zhang, L.; Zhao, R.; Jain, A.; Koschny, T.; Soukoulis, C.M. Electromagnetically induced transparency and absorption in metamaterials: The radiating two-oscillator model and its experimental confirmation. Phys. Rev. Lett. 2012, 109, 187401. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Liu, Y.; Yu, L.; Yu, Z.; Chen, L.; Li, R.; Ma, R.; Liu, C.; Zhang, J.; Ye, H. Plasmonic metamaterial for electromagnetically induced transparency analogue and ultra-high figure of merit sensor. Sci. Rep. 2017, 7, 45210. [Google Scholar] [CrossRef] [PubMed]
- Totsuka, K.; Kobayashi, N.; Tomita, M. Slow light in coupled-resonator-induced transparency. Phys. Rev. Lett. 2007, 98, 213904. [Google Scholar] [CrossRef] [PubMed]
- Chremmos, I.; Schwelb, O. Photonic Microresonator Research and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Xu, Q.; Sandhu, S.; Povinelli, M.L.; Shakya, J.; Fan, S.; Lipson, M. Experimental realization of an on-chip all-optical analogue to electromagnetically induced transparency. Phys. Rev. Lett. 2006, 96, 123901. [Google Scholar] [CrossRef] [PubMed]
- Garrido Alzar, C.L.; Martinez, M.A.G.; Nussenzveig, P. Classical analog of electromagnetically induced transparency. Am. J. Phys. 2002, 70, 37–41. [Google Scholar] [CrossRef]
- Liu, N.; Langguth, L.; Weiss, T.; Kästel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Weis, P.; Garcia-Pomar, J.L.; Beigang, R.; Rahm, M. Hybridization induced transparency in composites of metamaterials and atomic media. Opt. Express 2011, 19, 23573–23580. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.D.; Chang, H.; Fuller, K.A.; Rosenberger, A.T.; Boyd, R.W. Coupled-resonator-induced transparency. Phys. Rev. A 2004, 69, 063804. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Chen, W.; Nori, F.; Yang, L. What is and what is not electromagnetically induced transparency in whispering-gallery microcavities. Nat. Commun. 2014, 5, 5082. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Song, X.; Duan, G.; Wang, L.; Yu, L. Multiple fano resonances control in mim side-coupled cavities systems. IEEE Photonics J. 2015, 7, 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Zhang, Y.; Yu, L. Independently formed multiple fano resonances for ultra-high sensitivity plasmonic nanosensor. Plasmonics 2018, 13, 107–113. [Google Scholar] [CrossRef]
- Li, J.; Qu, Y.; Wu, Y. Add-drop double bus microresonator array local oscillators for sharp multiple fano resonance engineering. J. Appl. Phys. 2018, 123, 104305. [Google Scholar] [CrossRef]
- Dong, C.-H.; Zou, C.-L.; Xiao, Y.-F.; Cui, J.-M.; Han, Z.-F.; Guo, G.-C. Modified transmission spectrum induced by two-mode interference in a single silica microsphere. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 215401. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Chern, R.-L.; Lin, H.-Y. Multiple fano resonances in metallic arrays of asymmetric dual stripes. Appl. Opt. 2010, 49, 2819–2826. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Ding, P.; Wang, J.; Fan, C.; Liang, E. Double fano-type resonances in heptamer-hole array transmission spectra with high refractive index sensing. J. Mod. Opt. 2015, 62, 1241–1247. [Google Scholar] [CrossRef]
- Liu, H.; Leong Eunice Sok, P.; Wang, Z.; Si, G.; Zheng, L.; Liu, Y.J.; Soci, C. Multiple and multipolar fano resonances in plasmonic nanoring pentamers. Adv. Opt. Mater. 2013, 1, 978–983. [Google Scholar] [CrossRef]
- Liang, W.; Yang, L.; Poon, J.K.; Huang, Y.; Vahala, K.J.; Yariv, A. Transmission characteristics of a fabry-perot etalon-microtoroid resonator coupled system. Opt. Lett. 2006, 31, 510–512. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-C.; Li, B.-B.; Xiao, Y.-F. Electromagnetically induced transparency in optical microcavities. Nanophotonics 2017, 6, 789–811. [Google Scholar] [CrossRef]
- Le, T.T.; Cahill, L.W.; Elton, D. The design of 2 × 2 SOI MMI couplers with arbitrary power coupling ratios. Electron. Lett. 2009, 45, 1118–1119. [Google Scholar] [CrossRef]
- Soldano, L.B.; Pennings, E.C.M. Optical multi-mode interference devices based on self-imaging: Principles and applications. IEEE J. Lightwave Tech. 1995, 13, 615–627. [Google Scholar] [CrossRef]
- Le, T.-T.; Cahill, L. Generation of two fano resonances using 4 × 4 multimode interference structures on silicon waveguides. Opt. Commun. 2013, 301, 100–105. [Google Scholar] [CrossRef]
- Le, T.-T. Fano resonance based on 3 × 3 multimode interference structures for fast and slow light applications. Int. J. Microwave Opt. Technol. 2017, 13, 406–412. [Google Scholar]
- Le, D.-T.; Le, T.-T. Fano resonance and EIT-like effect based on 4 × 4 multimode interference structures. Int. J. Appl. Eng. Res. 2017, 12, 3784–3788. [Google Scholar]
- Huang, W.P.; Xu, C.L.; Lui, W.; Yokoyama, K. The perfectly matched layer (PML) boundary condition for the beam propagation method. IEEE Photonics Technol. Lett. 1996, 8, 649–651. [Google Scholar] [CrossRef]
- Fan, S. Sharp asymmetric line shapes in side-coupled waveguide-cavity systems. Appl. Phys. Lett. 2002, 80, 908–910. [Google Scholar] [CrossRef]
- Le, D.-T.; Le, T.-T. Coupled resonator induced transparency (CRIT) based on interference effect in 4 × 4 MMI coupler. Int. J. Comput. Syst. 2017, 4, 95–98. [Google Scholar]
- Hon, K.Y.; Poon, A. Silica polygonal micropillar resonators: Fano line shapes tuning by using a mach-zehnder interferometer. In Proceedings of the Lasers and Applications in Science and Engineering, San Jose, CA, USA, 23 February 2006. [Google Scholar]
- Chen, Z.-Q.; Qi, J.-W.; Jing, C.; Li, Y.-D. Fano resonance based on multimode interference in symmetric plasmonic structures and its applications in plasmonic nanosensors. Chin. Phys. Lett. 2013, 30, 057301. [Google Scholar] [CrossRef]
- Zhang, B.-H.; Wang, L.-L.; Li, H.-J.; Zhai, X.; Xia, S.-X. Two kinds of double fano resonances induced by an asymmetric MIM waveguide structure. J. Opt. 2016, 18, 065001. [Google Scholar] [CrossRef]
- Le, D.-T.; Do, T.-D.; Nguyen, V.-K.; Nguyen, A.-T.; Le, T.-T. Sharp asymmetric resonance based on 4 × 4 multimode interference coupler. Int. J. Appl. Eng. Res. 2017, 12, 2239–2242. [Google Scholar]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569–572. [Google Scholar] [CrossRef]
- Le, T.-T.; Cahill, L. Microresonators based on 3 × 3 restricted interference MMI couplers on an soi platform. In Proceedings of the Annual Meeting Conference (LEOS 2009), Belek-Antalya, Turkey, 4–8 October 2009. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Bogaerts, W.; Heyn, P.D.; Vaerenbergh, T.V. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Le, T.-T. The design of optical signal transforms based on planar waveguides on a silicon on insulator platform. Int. J. Eng. Technol. 2010, 2, 245–251. [Google Scholar]
- Xia, F.; Sekaric, L.; Vlasov, Y.A. Mode conversion losses in silicon-on-insulator photonic wire based racetrack resonators. Opt. Express 2006, 14, 3872–3886. [Google Scholar] [CrossRef] [PubMed]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Le, T.-T. Highly sensitive sensor based on 4 × 4 multimode interference coupler with microring resonators. J. Opt. Adv. Mater. 2018, 5, 264–270. [Google Scholar]
- Le, D.-T.; Nguyen, M.-C.; Le, T.-T. Fast and slow light enhancement using cascaded microring resonators with the sagnac reflector. Optik Int. J. Light Elect. Opt. 2017, 131, 292–301. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-T. Electromagnetically Induced Transparency (EIT) Like Transmission Based on 3 × 3 Cascaded Multimode Interference Resonators. Micromachines 2018, 9, 417. https://doi.org/10.3390/mi9080417
Le T-T. Electromagnetically Induced Transparency (EIT) Like Transmission Based on 3 × 3 Cascaded Multimode Interference Resonators. Micromachines. 2018; 9(8):417. https://doi.org/10.3390/mi9080417
Chicago/Turabian StyleLe, Trung-Thanh. 2018. "Electromagnetically Induced Transparency (EIT) Like Transmission Based on 3 × 3 Cascaded Multimode Interference Resonators" Micromachines 9, no. 8: 417. https://doi.org/10.3390/mi9080417
APA StyleLe, T.-T. (2018). Electromagnetically Induced Transparency (EIT) Like Transmission Based on 3 × 3 Cascaded Multimode Interference Resonators. Micromachines, 9(8), 417. https://doi.org/10.3390/mi9080417



