1. Introduction
Microrobot actuation studies have focused on electromagnetic methodologies associated with different control approaches. Their locomotion techniques have a crucial role for some major areas such as invasive diagnostics and targeted drug and living cell delivery. Due to the non-linear nature of the magnetic field, the precise localization of microrobots in the in-vitro/vivo application is becoming a challenging field for researchers [
1]. Promising solutions can be developed by implementing not only material-based solutions, but also a combination of sensors and control models. Miniaturization strategies of existing robotic technologies and biomimetic approaches make effort towards moving microrobots in a predefined trajectory in different media [
2,
3]. For example, a levitated microrobot in liquid media cannot move parallel to the surface during horizontal movements due to their hydrodynamic structures. We named this problem the “head-tilting” reaction. Previous studies were applied to various levitation techniques for the stabilization and control of the horizontal movements of microrobots [
2,
3,
4,
5]. Based on these studies, active levitation techniques that use an electromagnet give better results compared to passive levitation techniques that use permanent magnets. However, an application of active levitation requires expensive and complex feedback mechanisms, and has a higher energy consumption rate. Passive levitation is generally more favorable, since it is more compact, consumes less energy, and can be applied at room temperature [
6,
7,
8]. Furthermore, it is observed that open loop control methods yield good results when applied to passively levitated microrobots. It is possible to obtain satisfactory results in microrobot studies by using various control methods such as single degree-of-freedom models [
9,
10]. With these methods, even with simple control strategies, good results can be observed. Moreover, there exist previous studies in which passive levitation was applied to living cells and water bubbles to levitate them to a target position [
11,
12,
13]. In another study, Perline and his team applied open-loop controllers to colonies of diamagnetically levitated microrobots [
8]. It can be seen that high-accuracy motion control is crucial for many applications, such as tissue engineering, cell manipulation, drug delivery, microassembly, and protein-crystal handling [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27].
When working with micro-scale robots, the fluidic environment shows laminar flow characteristics; therefore, the Reynolds Number of the flow cannot be neglected. Nelson and his team investigated the effects of drag force during electromagnetic levitation [
28]. However, they could not get adequate results in the control of the robot due to lack of modelling of environmental effects. Similarly, Sitti and his team had difficulties controlling microrobots due to lack of theoretical calculation of net force [
29]. Assumptions made about the drag force hindered their accuracy of motion. Khamesee and his team obtained similar results, even though they added drag force into their control model [
5]. Arai and his team applied high-frequency ultrasound vibrations on the surface upon which the microrobot moves and consequently achieved better results [
30]. However, the drag force on the microrobot still exists and their motion control strategy does not answer it. Feng Lin and his team manufactured a microrobot using pyrolytic graphite and a diamagnetic material and levitated it using an electromagnet with four poles [
31]. However, their motion range was limited to 1 mm, and no accuracy of motion was studied. Also, since the study does not contain any mathematical model of the motion characteristics, the deviation of experimental results from the theoretical calculations cannot be seen.
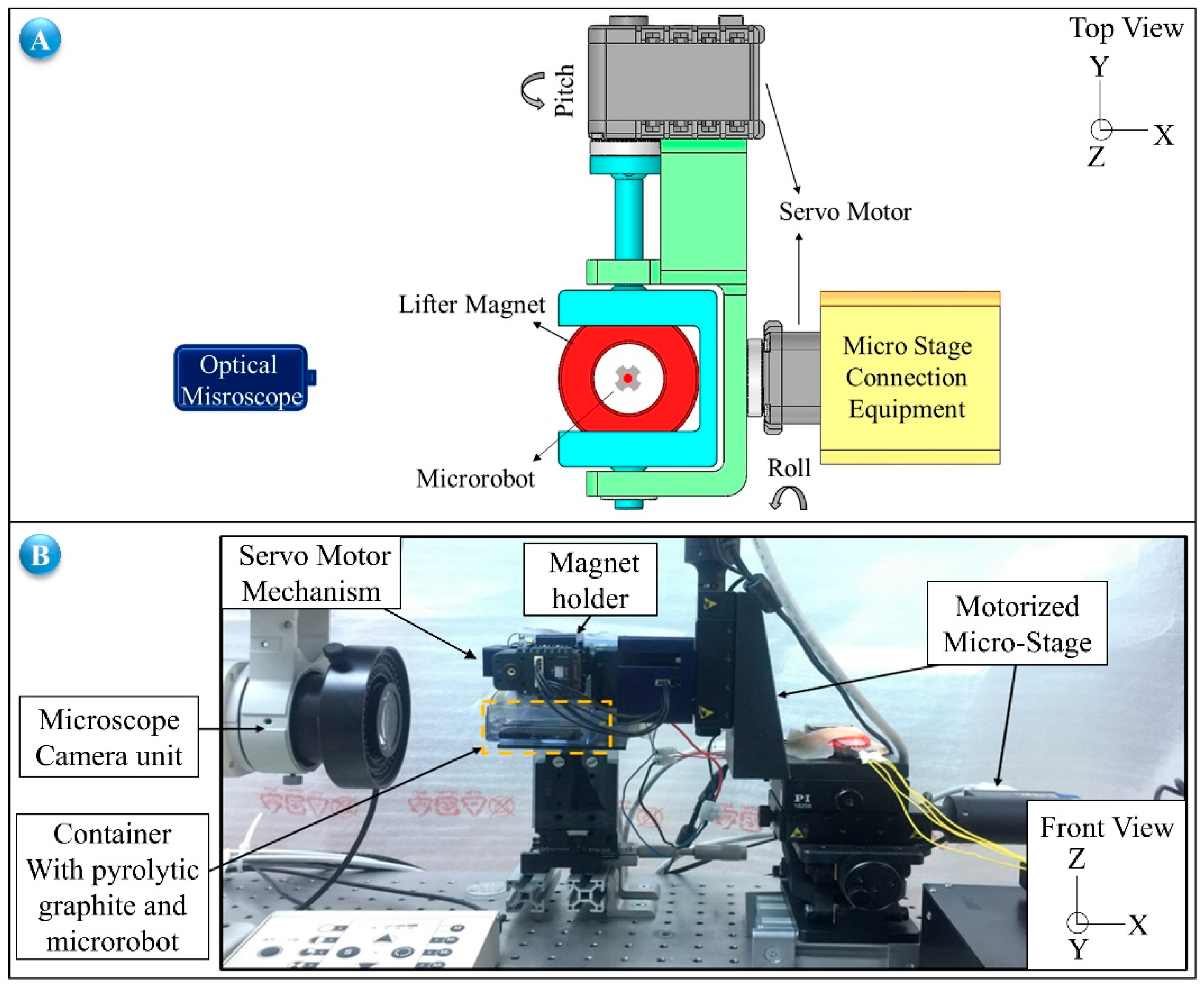
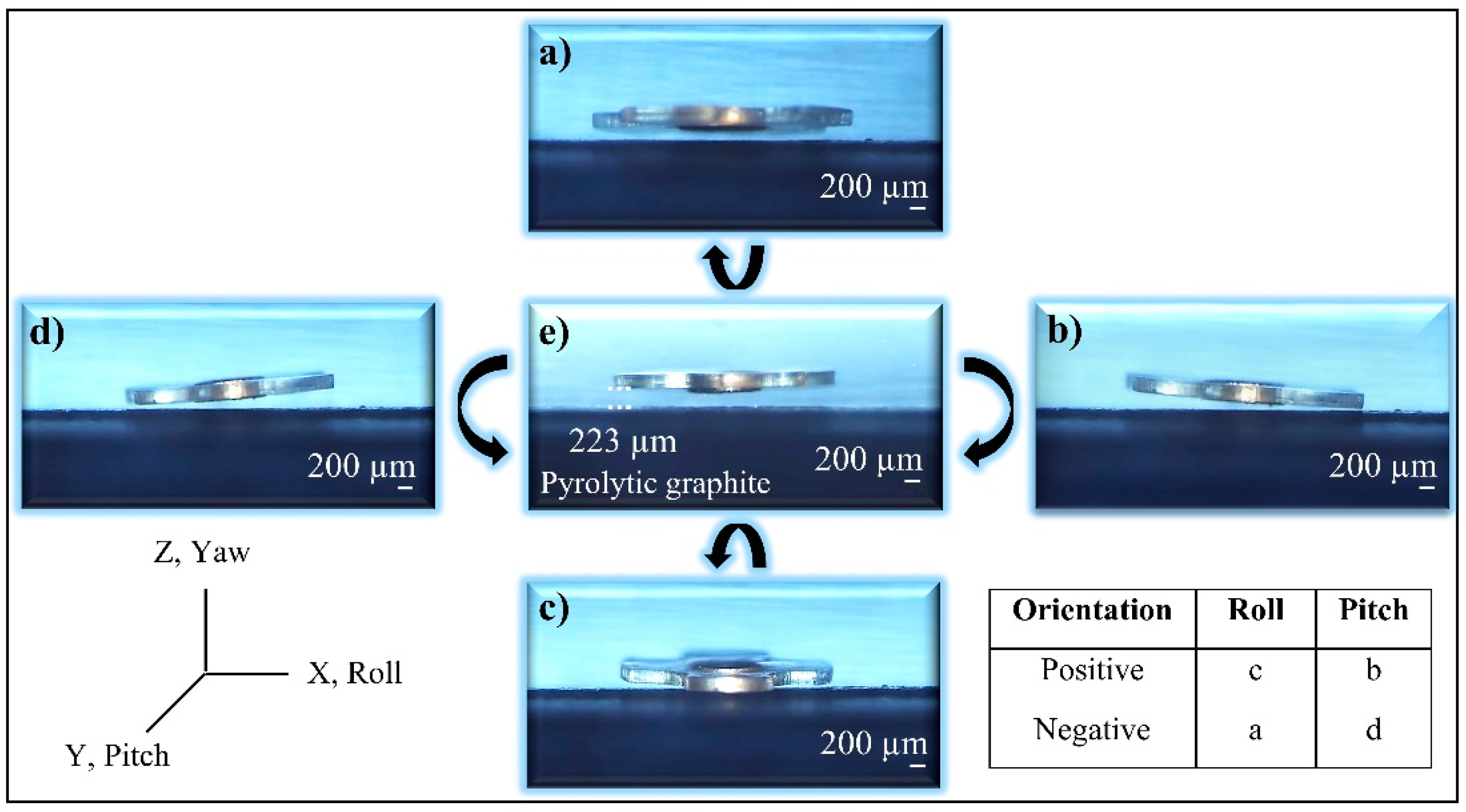
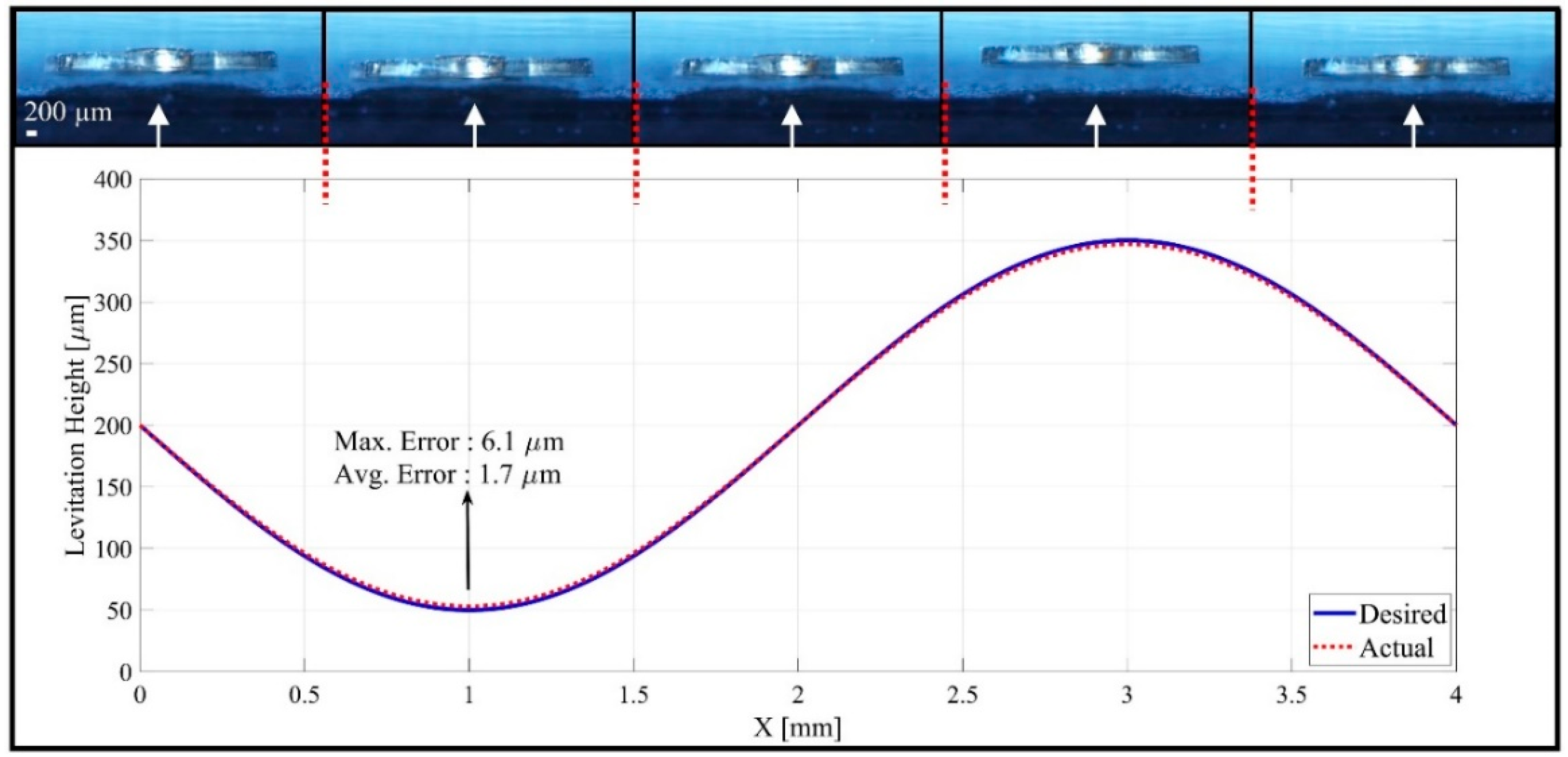
In our study, we control the lateral motions of an untethered microrobot via passive diamagnetic levitation in a fluidic environment. A disc-shaped magnet (N48 grade neodymium) with ø1 mm and 200 µm thickness, called the “carrier-magnet”, is used at the center of a microrobot and it is also placed above on a pyrolytic graphite surface in a liquid medium. A ring-shape magnet (N48 grade neodymium) with dimension of ø40 mm × ø20 mm × 8 mm, called the “lifter-magnet”, is attached on a micro-stage and aligned with the microrobot in order to provide stable magnetic levitation. This setup, compared to others, is more compact and requires less energy to operate than actively controlled magnetic levitation systems. While the microrobot motion trajectory is on the horizontal axis, it cannot accelerate parallel to the pyrolytic graphite surface. The head-tilting reaction starts and develops depending on the horizontal speed of the microrobot and increases exponentially in time. Furthermore, the drag force also increases exponentially as a function of microrobot’s speed, and it cannot be omitted. Therefore, before determining control parameters, the speed, mechanical delay between permanent magnets, and orientation of carrier-magnet were modelled in COMSOL® (version 5.3, COMSOL Inc., Stockholm, Sweden). Afterwards, control strategies were applied to minimize the drag force’s effect to realize stable locomotion characteristics even at a much higher speed (>5 mm/s). Experimental results show that the microrobot may successfully have followed a sinusoidal trajectory of 150 µm amplitude and 4 mm period with an average error of 1.73 µm.
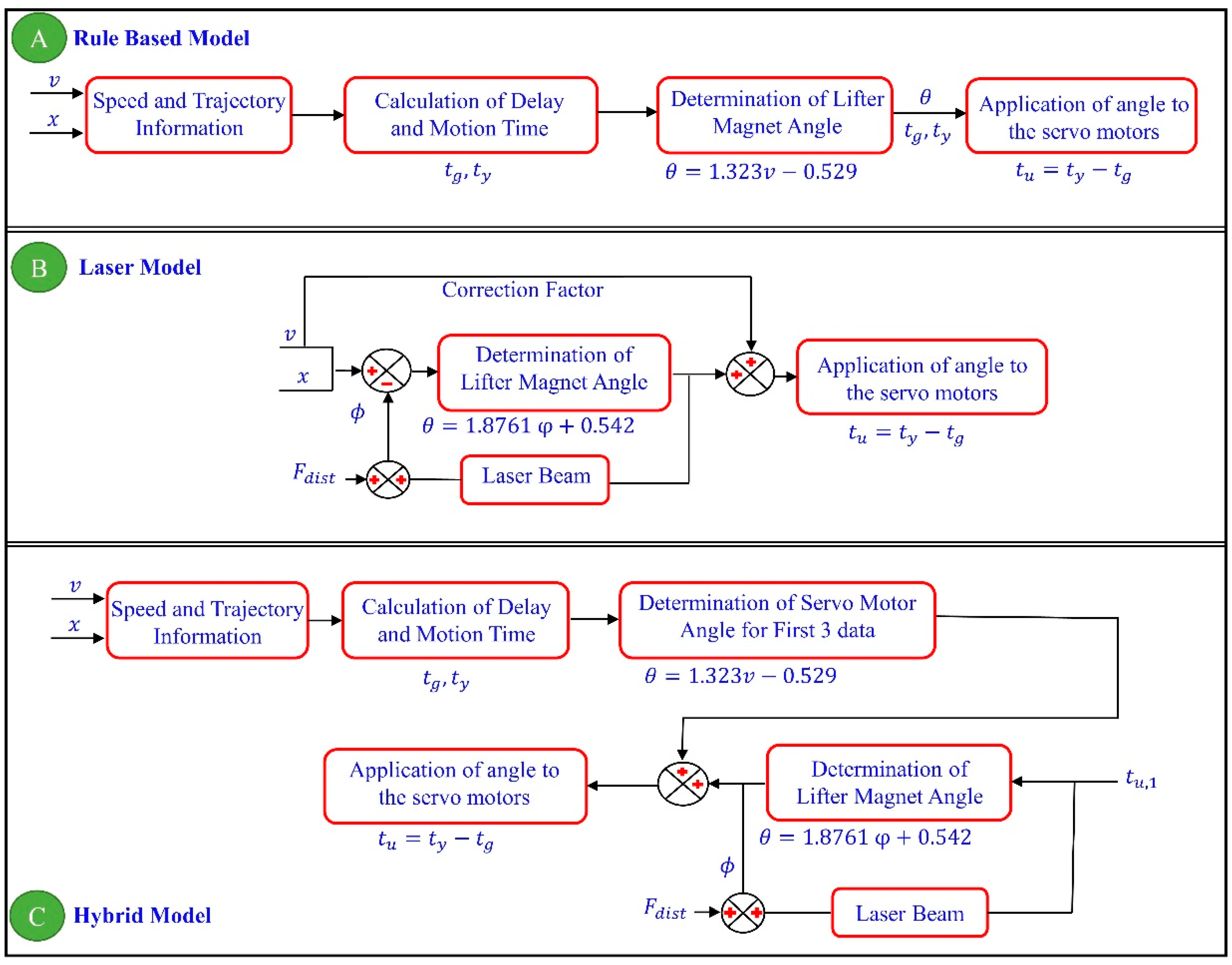
Our contribution to this study is to design 3 control models that take hydrodynamic effects exerted on the microrobot into account. Also, for the first time, the problem of head-tilting reaction is investigated and solutions are presented based on these three control models, which are the rule-based model, the laser model, and the hybrid model. The main purpose of the developed control techniques is the minimization of the drag force’s effect on the microrobot, which moves inside a fluidic environment in an untethered manner. Thus, they can be utilized in any application that requires complex trajectories tracking and precise transportation of micro and nano structures. The rule-based model uses a constant angle, which is calculated via projected duration of motion and motion speed, as input parameters. For the laser model, the control input frequency changes between 15 (66.7 ms) Hz and 58 (17.2 ms) Hz. On the other hand, the hybrid model takes advantage of those two previous strategies and combines them into a single model. In the experimental results section, the reliability of these three models is verified, and the results are presented. All control techniques are compared to the uncontrolled head-tilting reaction.
2. Mathematical Model
In this section, we explain the mathematical model that can be used for calculating the minimum and maximum levitation heights of the microrobot, the microrobot’s speed-phase difference of the stage, and its head-tilting angle equations. In our experiments, we observed that the horizontal motion of the microrobot causes a head-tilting reaction; consequently, it is unable to move parallel to the surface. Two main reasons were concluded for this situation. These reasons are the “phase difference” between the center of the microrobot and the center of the carrier-magnet, and the drag force that acts on the robot due to its hydrodynamic structure. The phase difference occurs because of the fact that the acceleration of microrobot is lower than the carrier-magnet. This difference in acceleration is caused by the air resistance acting only on the lifter-magnet, which is connected to the micro-stages during its movement. While the resistance of air is negligible, the drag force acting on the microrobot in the fluid cannot be omitted. For this reason, while the lifter-magnet follows a step function like a motion profile with sharp edges, and the microrobot has a parabolic motion profile with smoother edges [
32].
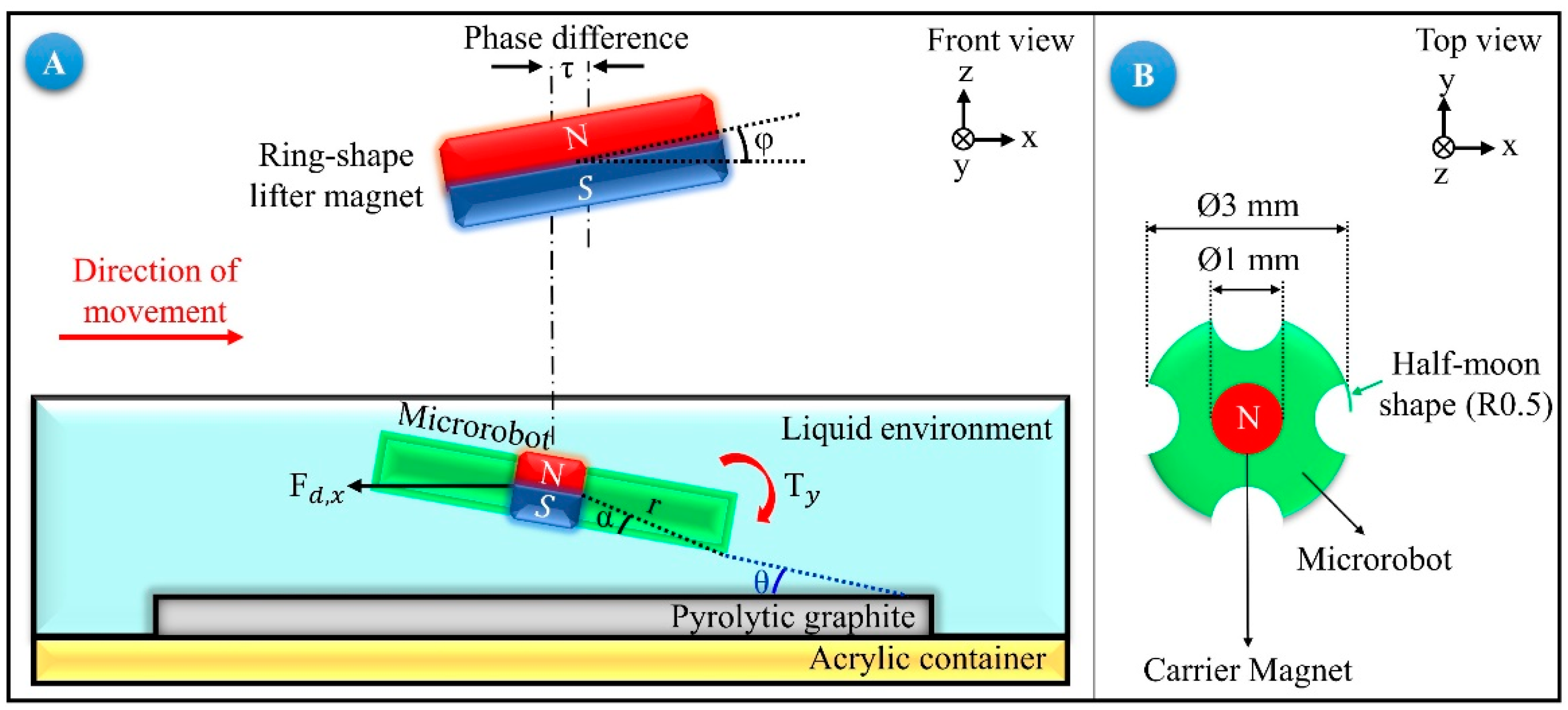
Figure 1 shows the schematic diagram of the head-tilting reaction and phase difference for the microrobot moving in the
x axis. In this figure, a pyrolytic graphite is placed on the surface of an acrylic container. The microrobot is located above the pyrolytic graphite in liquid media. For our model and further experiments, the liquid media is chosen as de-ionized (DI) water. Since the pyrolytic graphite is a diamagnetic material with a magnetic permeability of
, it encloses the microrobot within the boundaries of magnetic field lines of the lifter-magnet. Because of this, we can achieve more stable levitation characteristics inside the liquid [
32,
33].
During this movement, an undesired torque in the y axis is exerted on the microrobot, which causes it to tilt in the direction of motion. Also, a phase difference, τ, is observed, which is caused by the aforementioned reasons. The lifter-magnet’s position is controlled in three-axes using microcarrier stages, and its orientation is controlled in two axes by using two servo motors. The orientation angle of the lifter-magnet in the direction of motion is expressed by . The microrobot radius is shown by r, the angle between the corner point and the center by α, the angle between the corner point and the pyrolytic graphite by θ, and the drag force acting on the movement in the axis direction by .
As shown in
Figure 1, the microrobot moving in the x direction is not parallel to the surface during its motion due to the undesired torque
acting on it. For a microrobot, for which the moment of inertia is taken as
(μg mm
2), a relation between the angular acceleration and undesired torque can be determined [
32,
33,
34]. Accordingly, Equation (1) will be used to calculate the angle value at which the lifter-magnet should be held in order to avoid the generation of undesired torque values (
Figure 2).
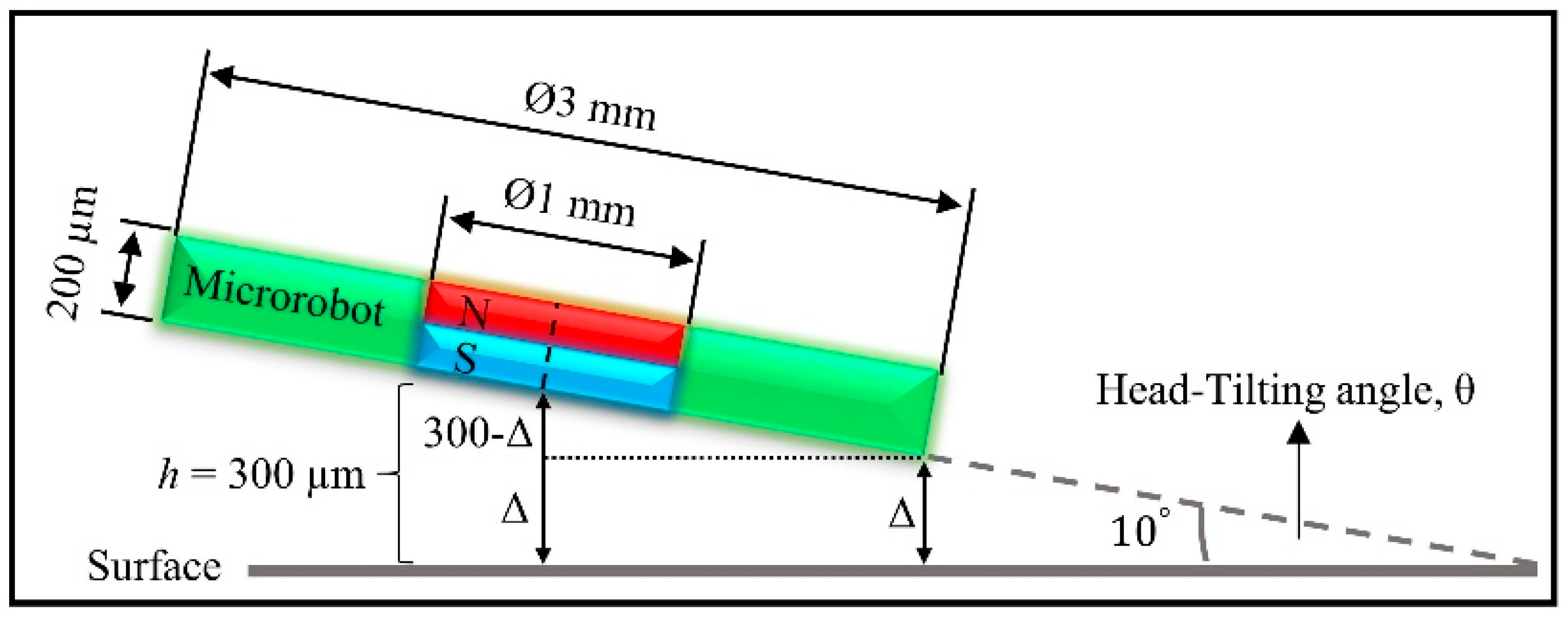
The head-tilting angle,
θ, increases with the speed of motion, and this has some implications for robot levitation. Increasing head-tilting angles can cause the microrobot to hit the surface during its motion. In
Figure 3, the head-tilting amount, Δ, can be calculated for a robot with
α = 3.814°,
θ = 10°,
and
r = 1503.33
Δ = 39.528 μm is obtained for
, which is the instantaneous levitation height. According to this calculation, if the angle of diversion of the microrobot is 10°, and if the levitation height is lower than 260 μm, it is determined that the robot is likely to be hit the surface. If the instantaneous levitation height is lower than the required tolerance between the microrobot and the surface, the robot may hit the surface. For this reason, the working boundaries of the microrobot should firstly be determined. To find these boundaries, a free-body diagram needs to be generated, and each force acting on the robot needs to be calculated.
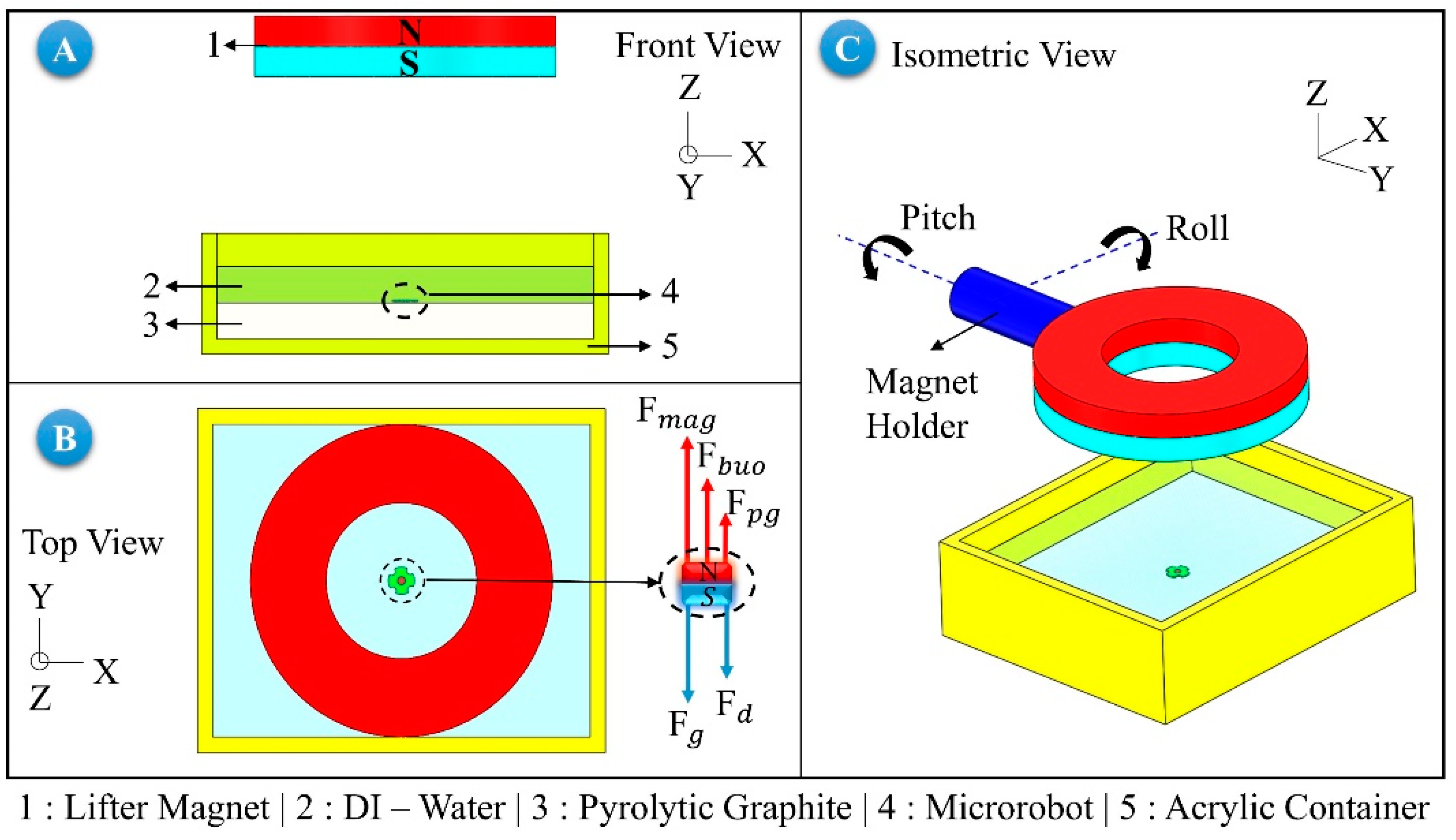
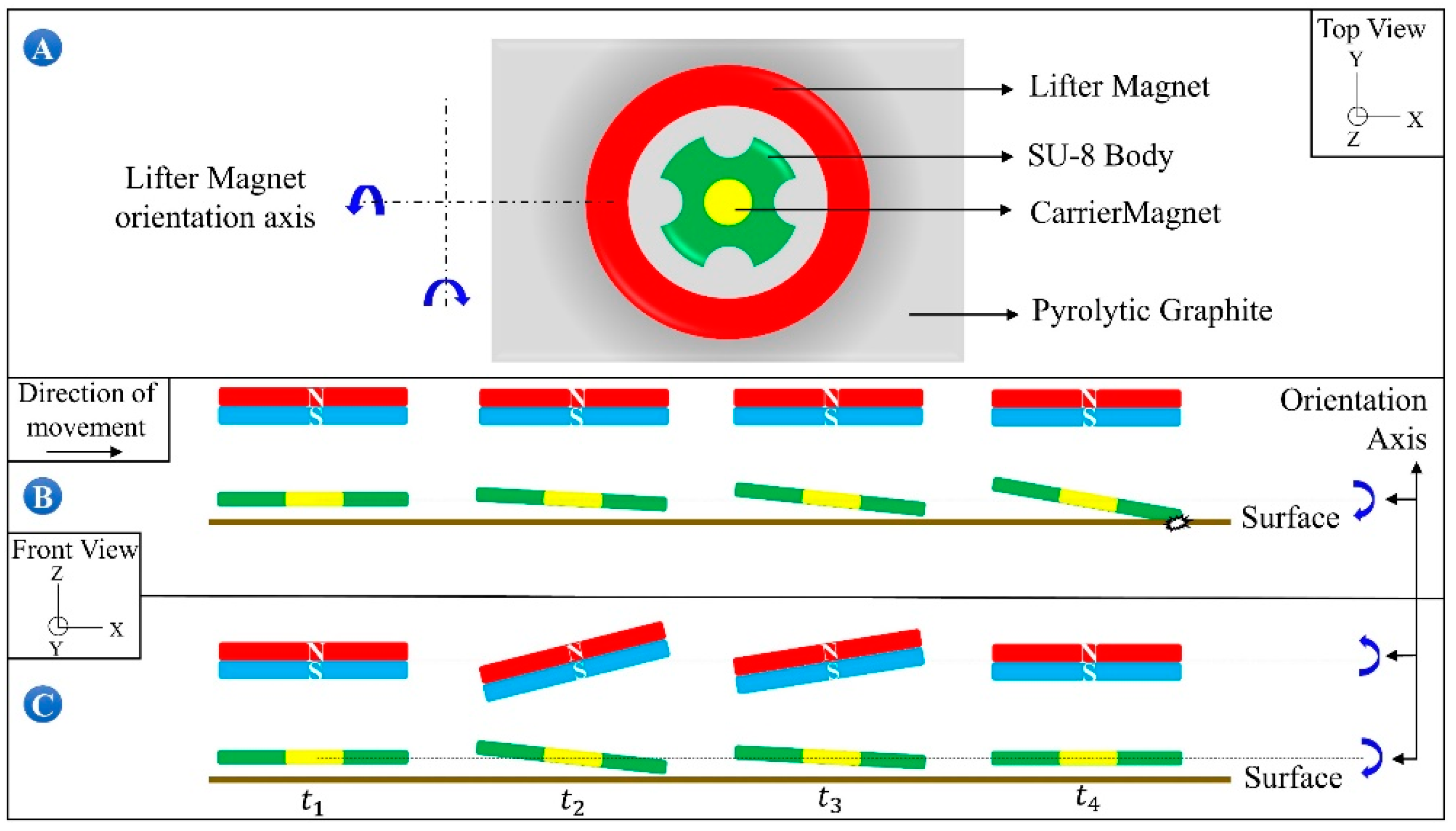
Figure 4A shows the front view of the levitation system. The top view of the system and the forces acting on the robot are shown at
Figure 4B, and the isometric view of the lifter-magnet and the test setup is shown in
Figure 4C. In
Figure 4B, the magnetic force of the lifter-magnet acting on the microrobot is illustrated as
; the buoyant force due to liquid media as
; the diamagnetic force induced by the pyrolytic graphite, which is located on the surface of the acrylic container (shown in
Figure 1A and
Figure 4A), as
; the gravitational force as
and the drag force as
.
The acceleration-dependent mathematical model is expressed in Equations (3)–(5), in which the robot mass is
mr [
32,
33,
34]. The forces exerted on the microrobot are shown in
Figure 4B. For a robot with a mass of 2.92 μg, robot acceleration can be determined for known values of lifting force (12.788 μN), speed-dependent friction force [
33], and gravitational force (28.741 μN). The relationship between phase difference and the microrobot acceleration has been investigated in a different study [
32].
Using a mathematical model with 3 degrees of freedom, which takes into account gravity, lift, friction, and magnetic and diamagnetic forces, it is calculated that the net magnetic force should be 16.74 μN in order to levitate the microrobot [
32,
33,
34]. Applying these forces on the microrobot causes it to levitate in the fluidic environment. It is necessary to calculate the robot and lifter-magnet accelerations so that the approximate values for phase difference can be found during the lateral motion of the robot. The aim of the experiments was to control microrobot motion in high accuracy so that it could complete a predetermined trajectory in a repeatable manner at desired speed. Also, how fast this task can be accomplished is another important criteria. Since the lifter-magnet speed profile is determined (step function), the value of the acceleration can also be found. However, the acceleration of the microrobot depends on the speed of the lifter-magnet. For example, although the lifter-magnet completes a trajectory of 5 mm in 1 s with a speed of 5 mm/s, it takes time for the microrobot to reach a speed of 5 mm/s due to existence of the drag force. It has been shown that the value of
is 0.125 μN for 5 mm/s speed [
33]. For a microrobot with a constant mass, it has been stated that the speed profile, and thus the acceleration, may be of parabolic increasing-decreasing characteristic against the variable drag force [
32]. The value of the microrobot acceleration can be determined according to Equation (6).
For the microrobot whose acceleration is determined, instantaneous speed values can be found by assuming that it has an acceleration characteristic. Using microrobot speed rating,
, Equation (7) can be used to calculate the time required to reach a speed of 5 mm/s.
The drag force, which is equal to about 1/134 of the net magnetic force [
35], causes the microrobot to have a delay of 103.1 ms in total, because the starting values are 7.46 ms and 5 mm/s. As a result, according to the speed value, it is expected that the robot will move with
τ = 515.5 μm. In addition, a linear expression can be obtained from previous works done with the phase difference, and approximate phase difference expression can be related to the speed by Equation (8) [
32,
33].
3. Simulation Studies
In the mathematical model section, it was shown that the robot head can hit the surface if the levitation height is not sufficient, and the definitions for head-tilting and phase difference were stated. Also, a method for determining acceleration of microrobot in order to find the phase difference was given. In this section, the simulation studies are presented, which were conducted in order to develop a method for improving the head-tilting action that acts during the lateral movements of the microrobot. Using the simulation results, we also obtained the following microrobot control parameters via orientation equations, the operation limits, and the expression for surface impact condition. In addition to them, a first-order linear equation for the phase difference is calculated. The aim is to perform the robot motion parallel to the surface as shown in
Figure 4C. In the analyses made on the COMSOL
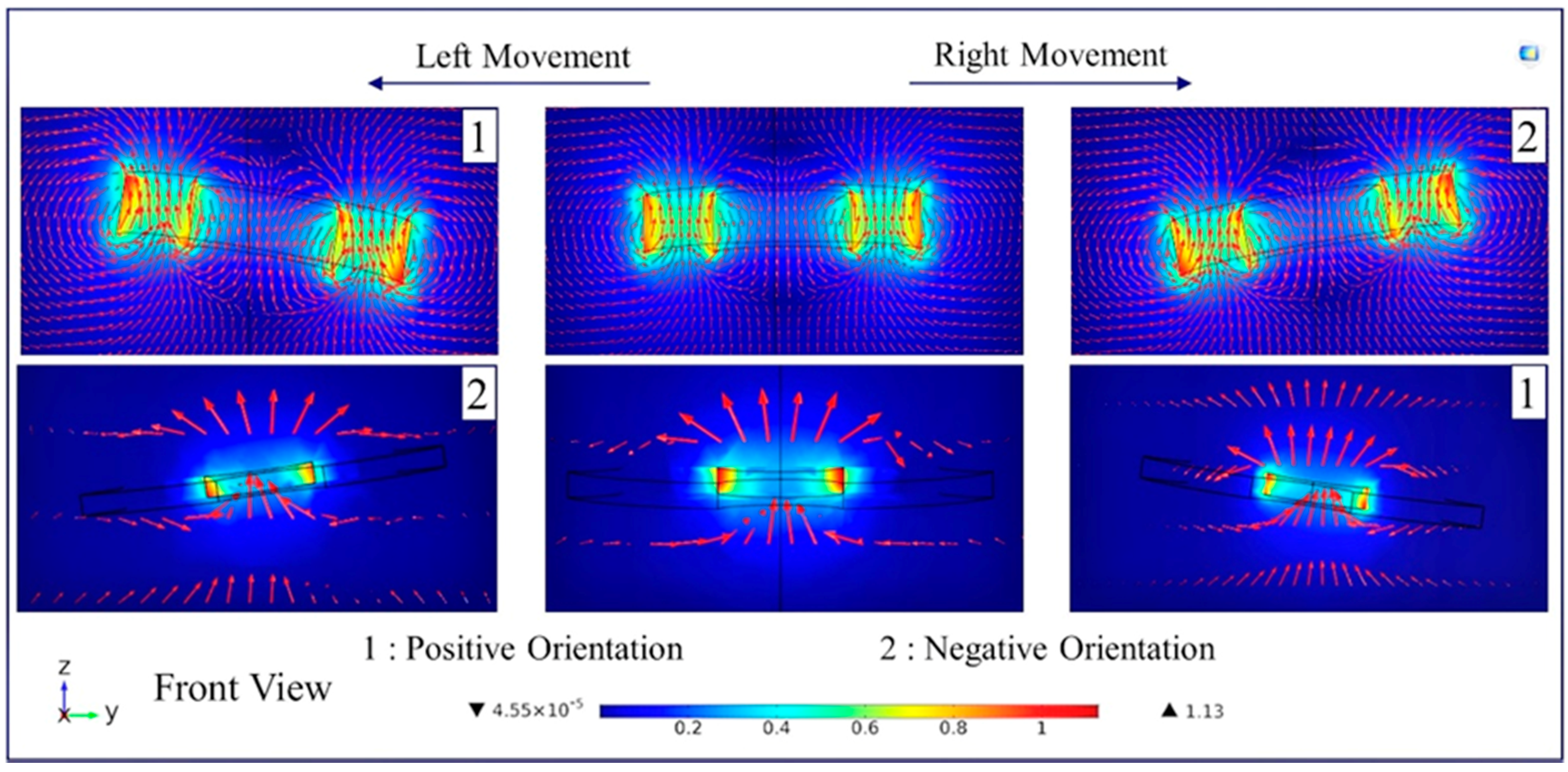
® AC/DC module, the orientation that must be applied on the lifter-magnet should firstly be determined. In
Figure 5, the magnetic field force lines that pass through the lifter-magnet and microrobot surface are shown when they are parallel to the surface. It has been determined that the field lines on the robot with levitation on the
z axis are perpendicular to the robot. A parametric analysis on the tilting angle of the microrobot is performed in order to determine the direction of the force applied during right and left movements. As a result of the analysis, it was found that the robot and the lifter-magnet must have opposite orientations. In this case, the active force lines on the robot were observed to remain perpendicular to its surface.
Microrobots have a small characteristic length
L and a small characteristic velocity
; this leads to a small Reynolds (
Re) number (Equation (9)) and Stokes flow (Equation (10)) [
35].
At low
Re, the Navier-Stokes Equation becomes time-independent [
36],
in which
is the velocity vector field and
is the hydrodynamic pressure scalar field. A low
Re number can be due to a slower motion, a small working environment, or high viscosity [
37]. Navier can be omitted, since
[
38] and inertial terms of fluid become negligible, while viscous force and surface tension are more dominant at the small length scale. In the studies with a low
Re regime, it can be seen that size effects can be neglected, and locomotion of a microrobot can be achieved by vibrating it. Depending on the vibration frequency, the
value is changed, and motion under low
Re can be obtained [
35,
36,
37,
38]. In our work, velocity of the microrobot determines the flow characteristic, since DI water remains stationary in the container. Thus, the motion characteristics of the microrobot in a low
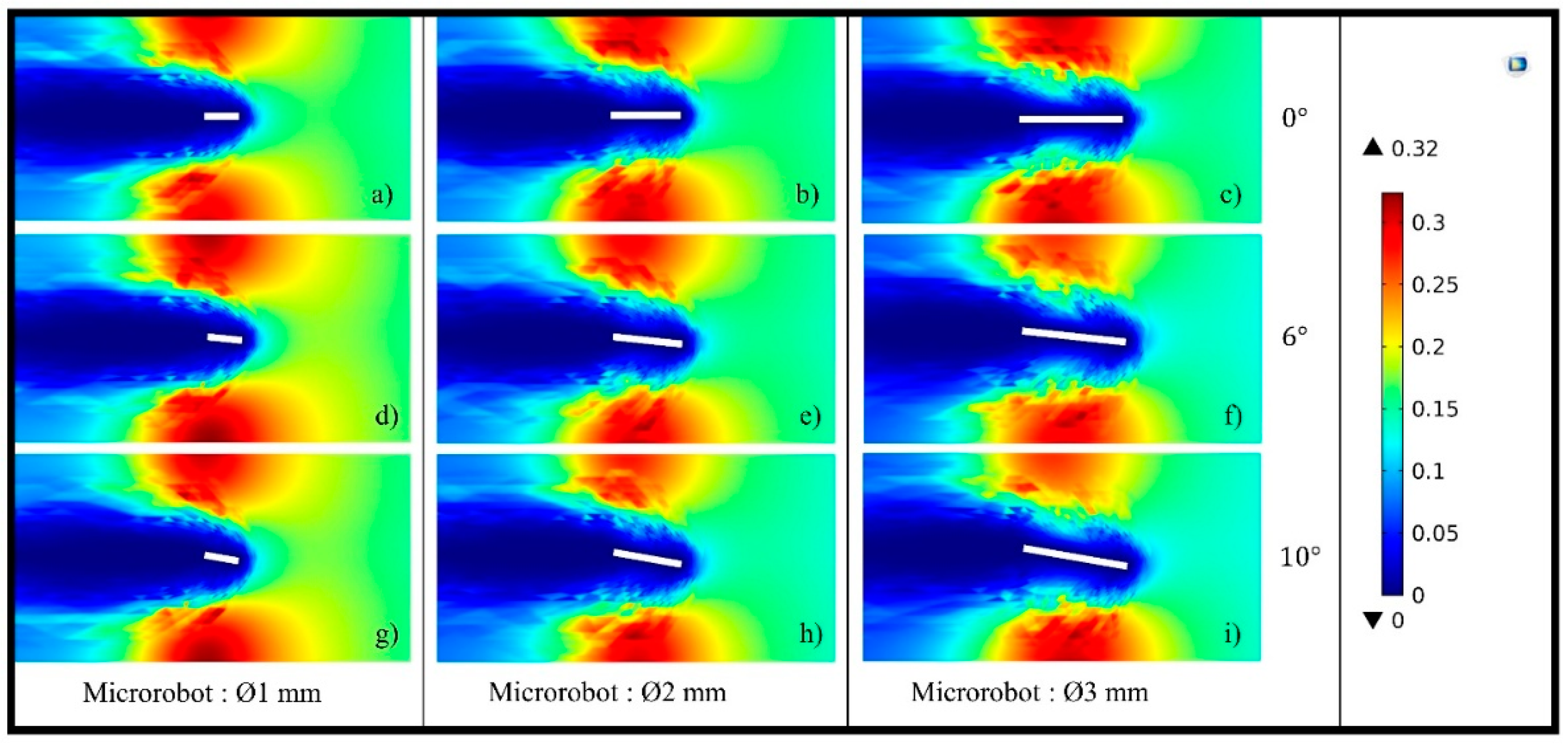
Re flow regime is investigated depending on its scale and with a head-tilting angle, which varies between 0–10° (
Figure 6). Creeping Flow Physics in COMSOL
® is used for three different sizes of microrobot (1 mm, 2 mm, and 3 mm). In this case, when the experimental conditions are kept constant, the change in the Reynolds number is dependent on the speed of the robot, not its size and head-tilting angle. In addition, for microrobots of different sizes with the same flow characteristics, the drag force does not change in the movements parallel to the surface [
32,
33,
34]. However, for microrobots that are working in the same experimental conditions, have the same speed, same head-tilting angle and different sizes, the drag force will change proportionally with the cross-sectional area. From Equation (1), the torque value that should be applied to the microrobot can also be calculated.
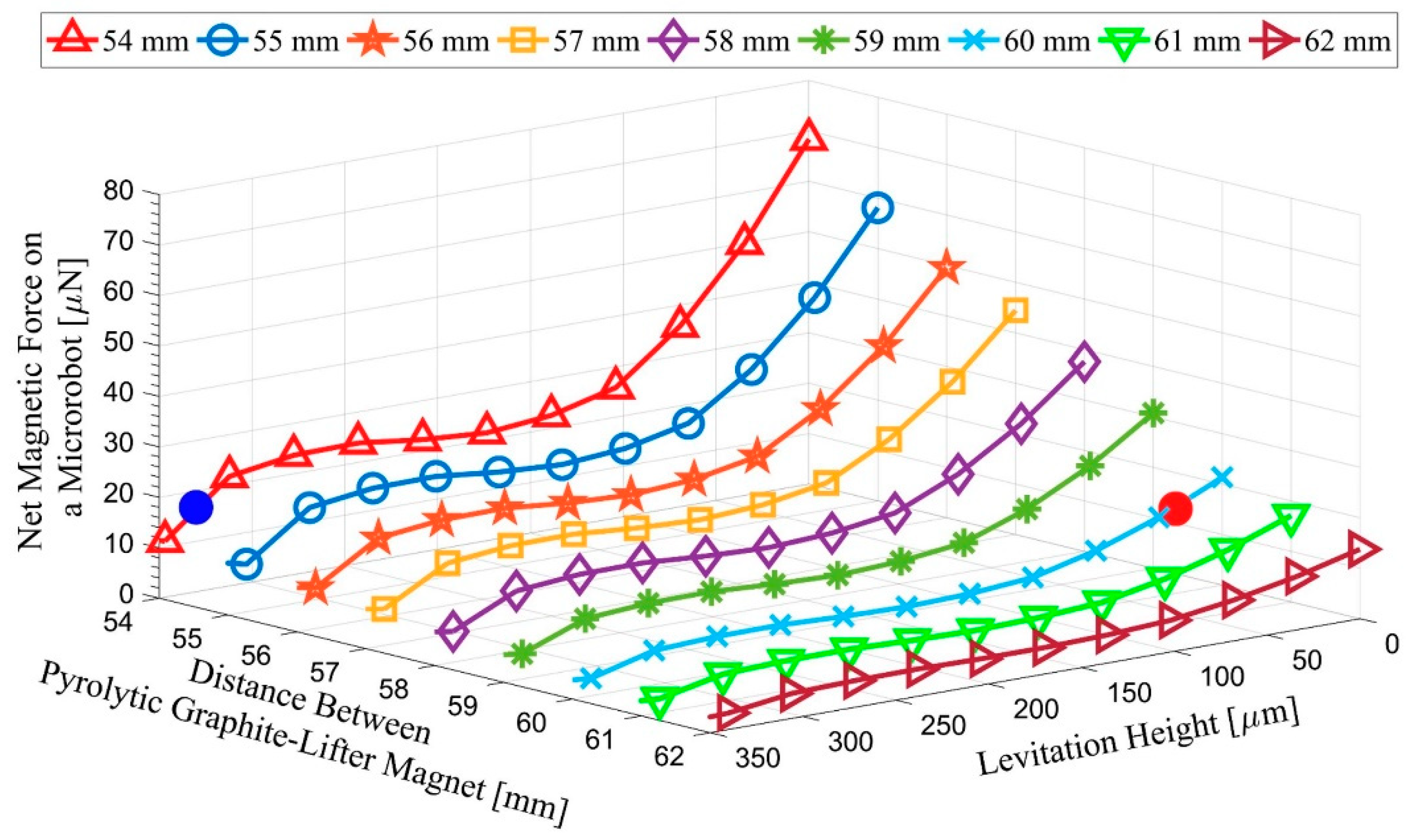
Once the lifter-magnet orientation is found, it is also very important to determine the operation limits of the microrobot. As indicated in the mathematical model section, the robot has a risk of surface collision, depending on its levitation height and speed. There is a risk of the microrobot surfacing in an uncontrolled manner due to close proximity to the lifter-magnet. These situations can be addressed by setting a lower and an upper limit to the levitation height. Here,
Figure 7 represents a graph for the net force exerted on the microrobot against microrobot lifter-magnet distance at different levitation heights. According to the net magnetic force value of 16.74 μN [
32,
33,
34], the microrobot was observed to be at the maximum levitation height of 329.1 μm when the lifter-magnet was at a distance of 54 mm (marked with a blue dot) from the pyrolytic graphite. On the other hand, the microrobot was at the minimum 31.0 μm levitation height when the lifter-magnet was located at 60 mm height (marked with a red dot). Since the magnetic force exhibits an exponential characteristic, the linear region of 100–300 μm was chosen as the operation limits. In particular, this region is affected less by the nonlinear magnitudes for experimental speed ranges.
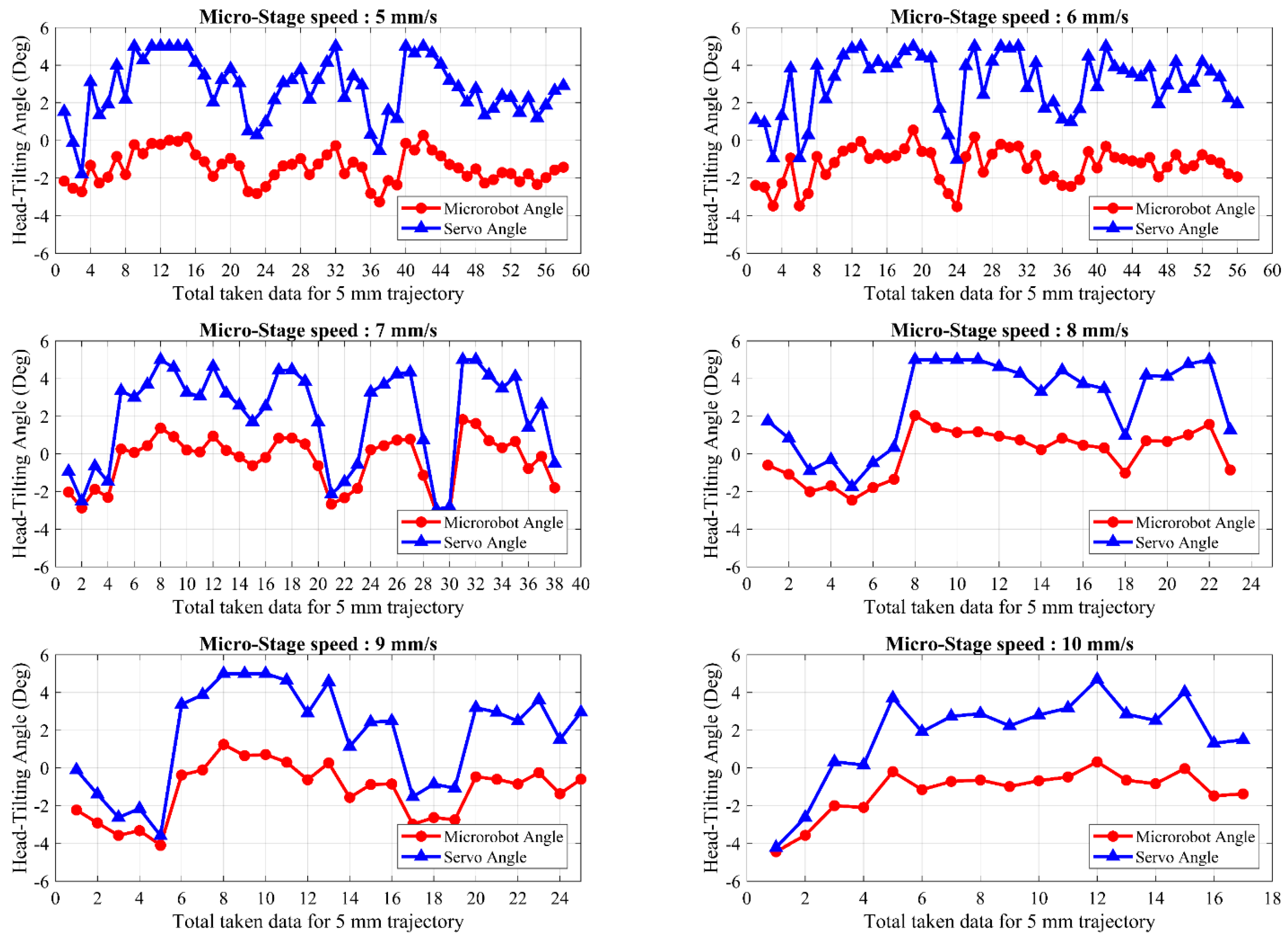
Following the determination of operation limits, the head-tilting reaction after certain time intervals is examined, and results are presented. By the time the microrobot reaches a desired speed with a certain delay parameter due to a lower acceleration, the tilting angle is also found to be dependent on this parameter.
Figure 8A shows the top view of the system and the orientation of the lifter-magnet.
Figure 8B shows a depiction of the microrobot that is starting to move by tilting its head gradually in the x direction at
t1 until it reaches the desired speed at
t4. At
t4, the microrobot is depicted as hitting the surface due to its higher speed. Moreover, the simulation data presented in
Figure 8C shows that the lifter-magnet is given an opposite orientation relative to microrobot. It is observed that the head-tilting angle of the microrobot is reduced starting from time
t2. At time
t4, instantaneous speeds are equal and the motion characteristic is depicted as being parallel to the surface.
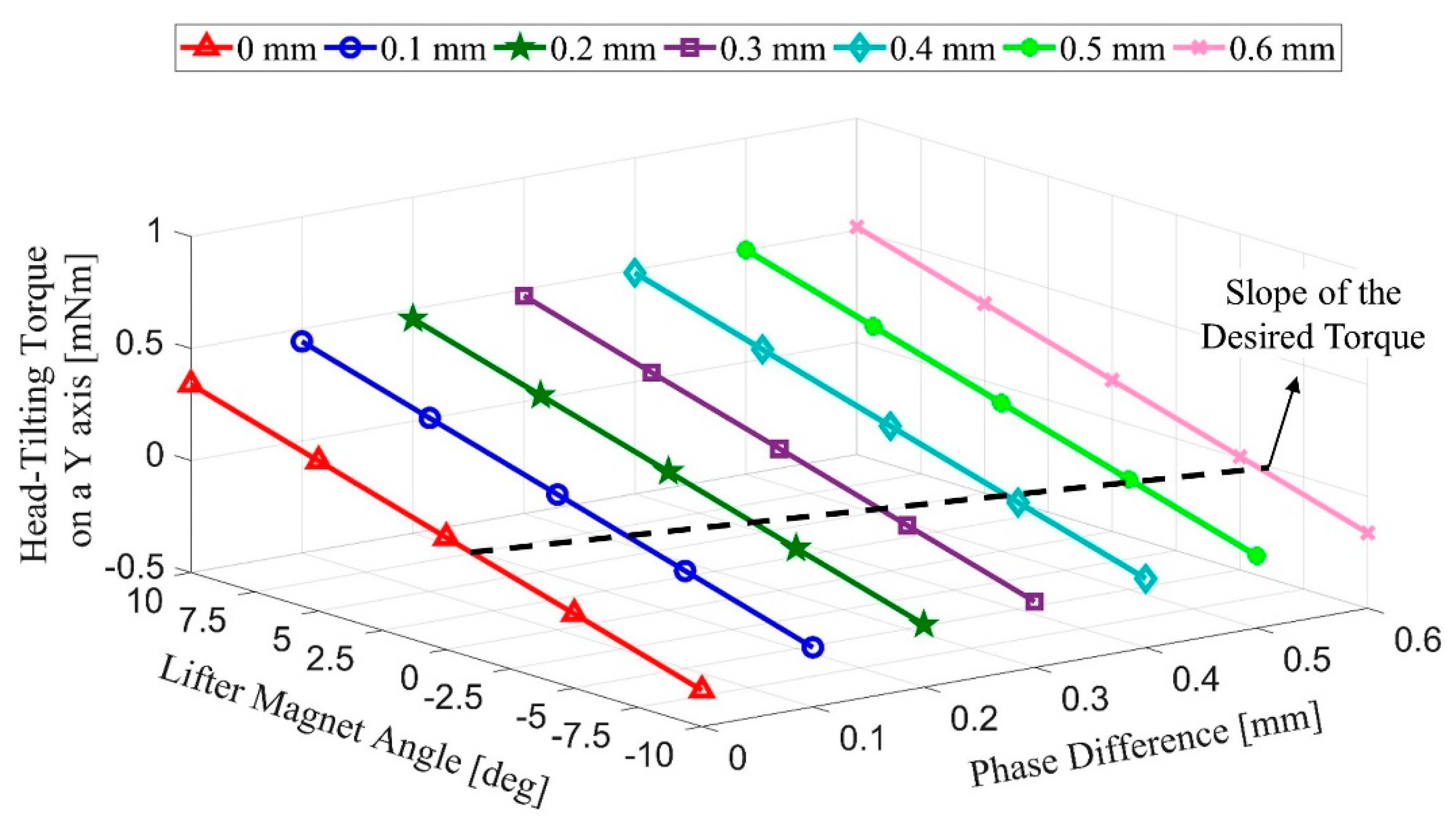
For all cases mentioned in the mathematical model section, finite element method (FEM) studies were conducted, and their results are given in this section. After the determination of these results, we need to derive the equations necessary for rule-based model design. To this end, various tilting angle values of microrobot were studied in COMSOL
® by parametric analysis. Different phase difference values are presented relative to the
x-axis with the upper legend in
Figure 8, while different angles of microrobot are given on the
y-axis. On the
z-axis, undesired torque values for different phase differences and carrier-magnet angles are shown. In this graph, a black dashed line is used to show the values where the torque equals zero. This line shows the angle that must be applied to the lifter-magnet in order to overcome the undesired torque.
Equations (11) and (12) are derived using the dashed line shown in
Figure 8. These equations are related to the speed of the micro-stage and its tilting angle to be applied to the rule-based model and the laser model, respectively.
As a result of using these equations with a certain time delay depending on the speed, the head-tilting angle can be improved, as presented with the results in experimental study section.
5. Conclusions and Discussion
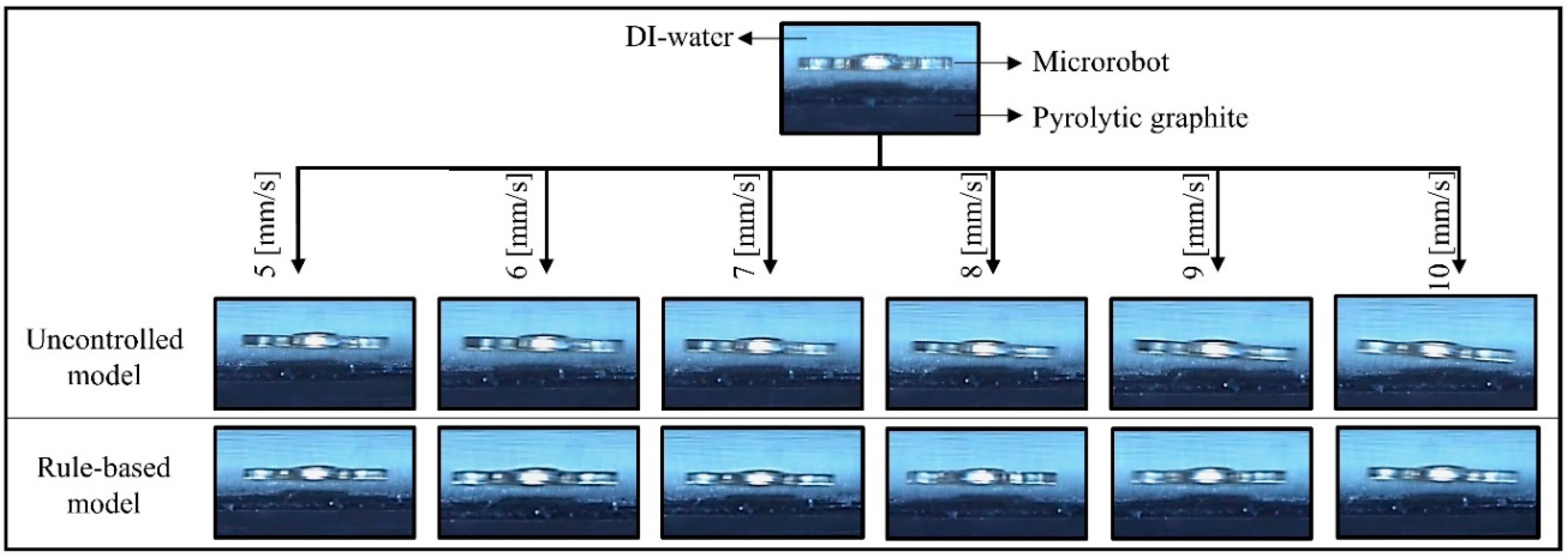
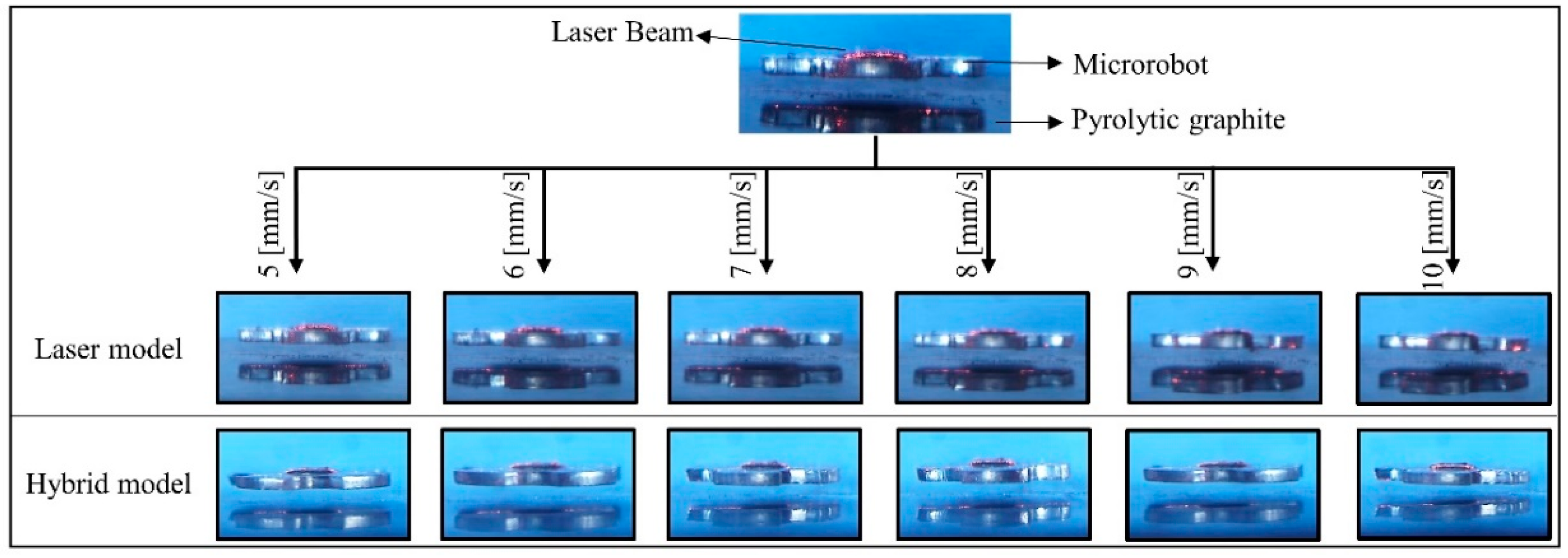
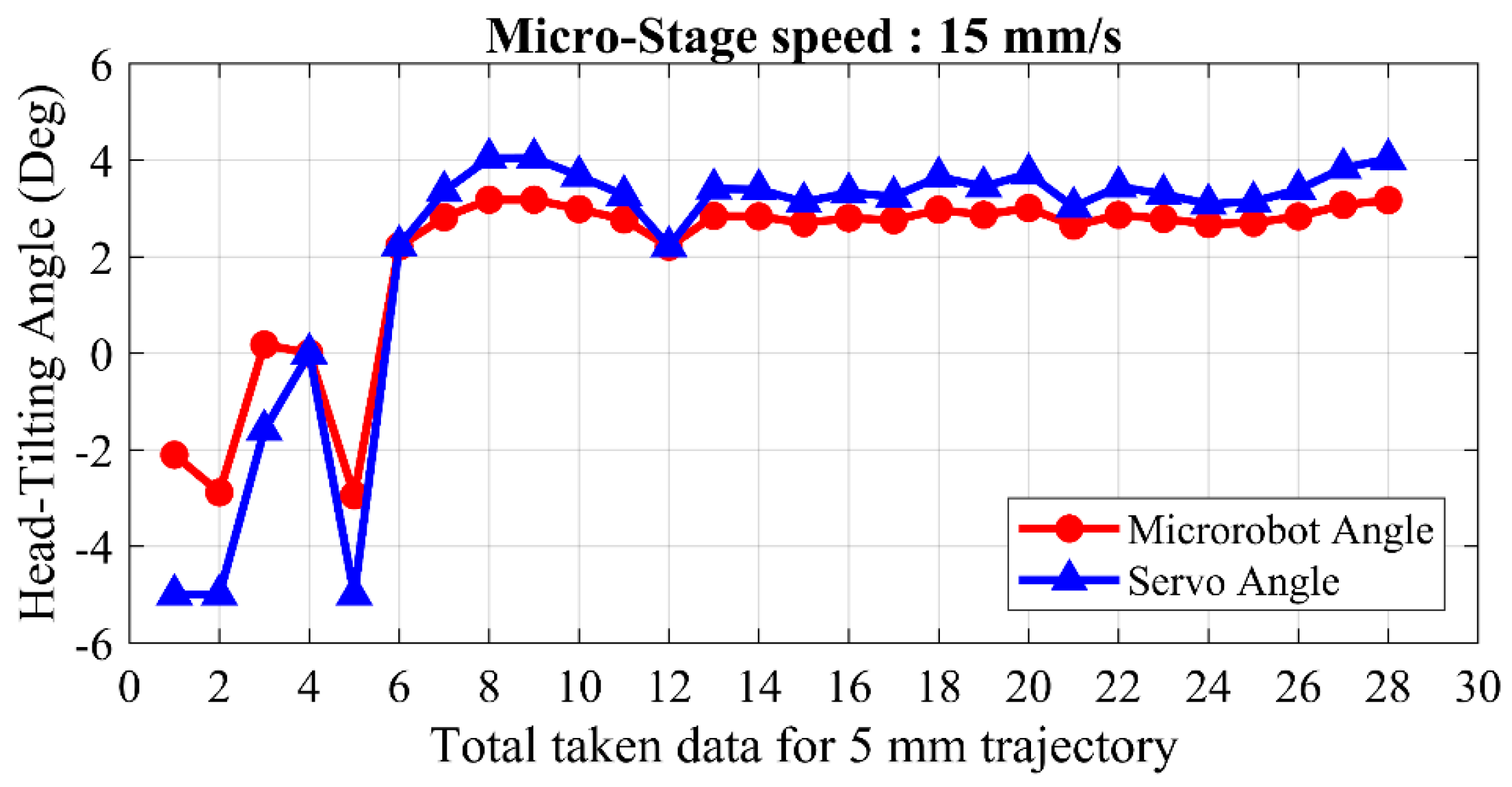
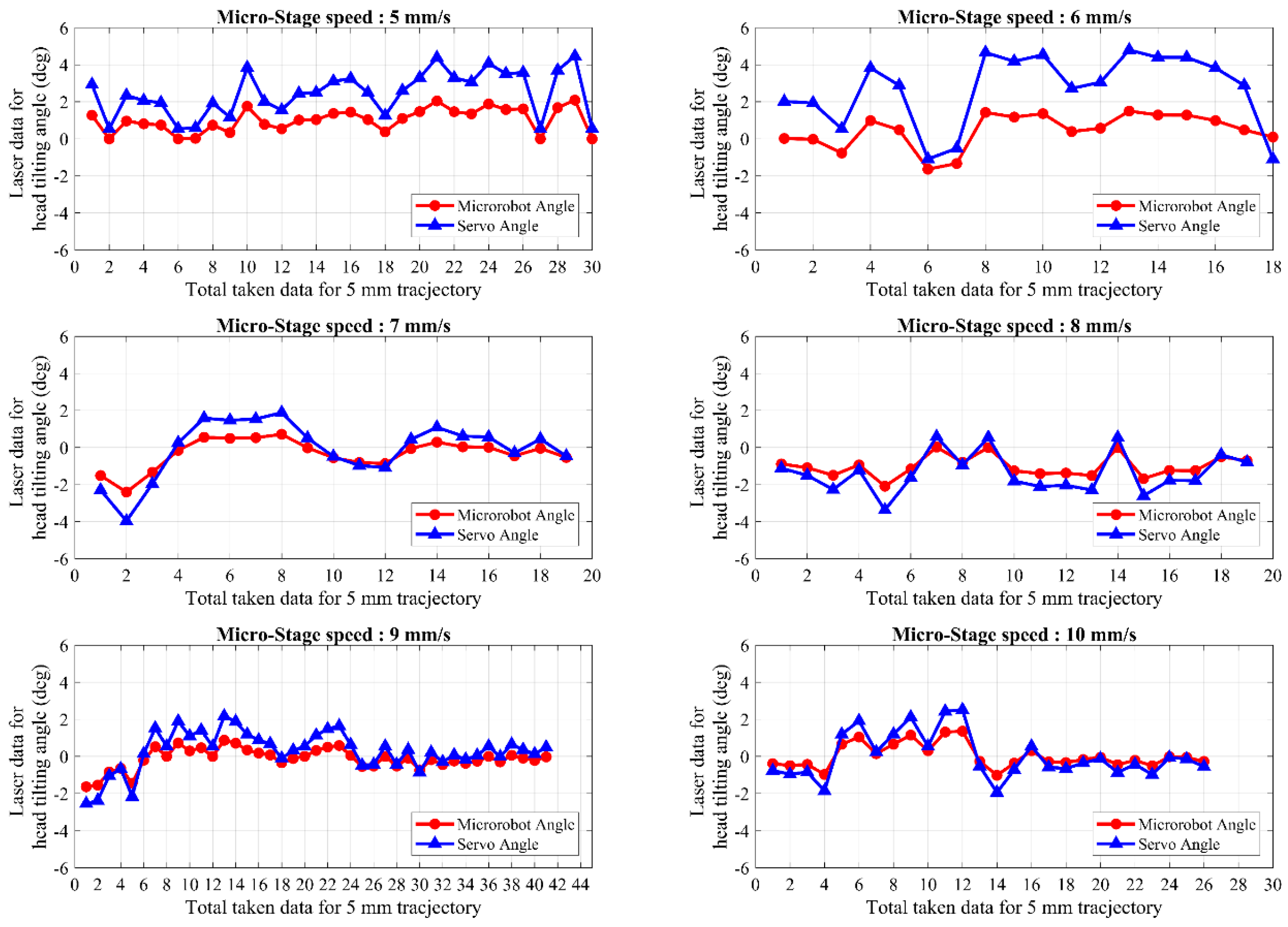
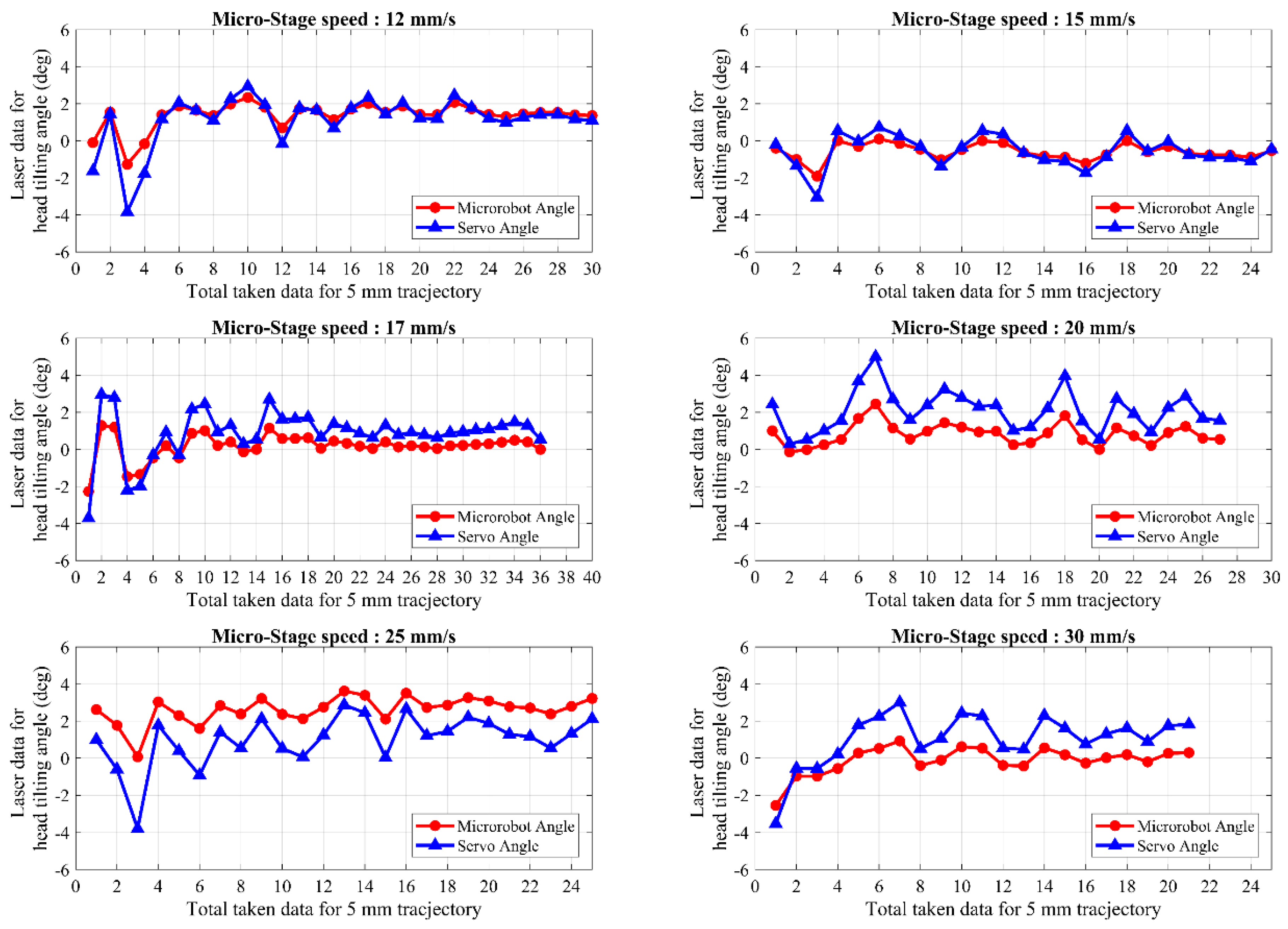
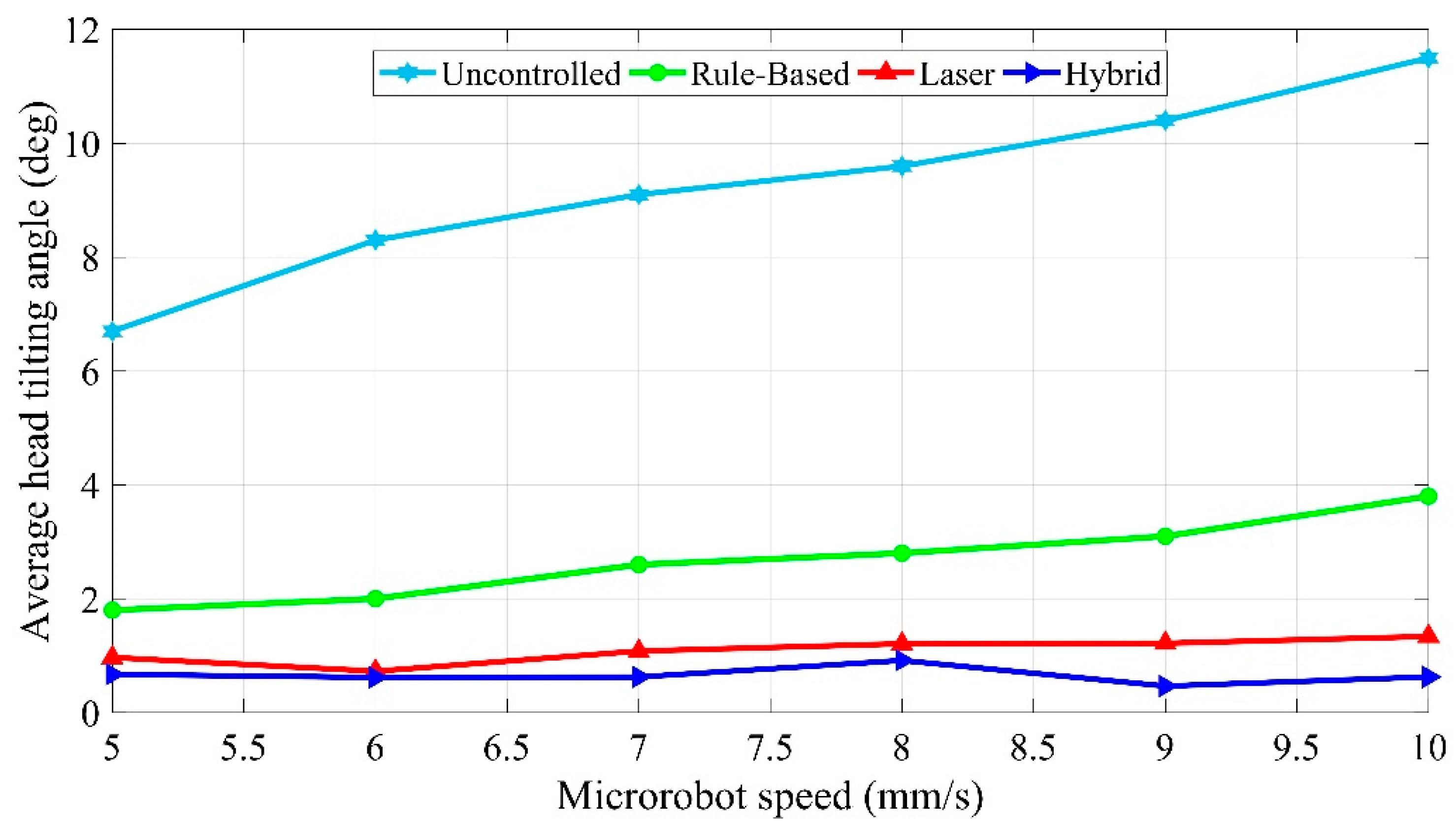
The microrobot was intended to track a 5 mm linear trajectory at 200 μm levitation height to compare the controller performances of different models. All conducted experiments were repeated at different speeds for each control model separately, while the trajectories and levitation heights remain constant. Firstly, the microrobot movement was performed at a speed range of 5–10 mm/s in the uncontrolled model. We found that the head-tilting angle increases with respect to speed of the microrobot. At higher speeds, the robot is likely to hit the surface of the pyrolytic graphite. In experiments with the uncontrolled model, the reason for the head-tilting reaction in the z-axis is the drag force generated by the DI-water medium. Thus, to reduce the head-tilting angle, we developed a rule-based controller model. However, during the experimental test, it was observed that steady-state error cannot be eliminated with this model, whereas transient response can be improved. Since the rule-based model is an open-loop controller and non-linearities in the system are not taken into account for simplicity, the obtained results were unsatisfactory. Moreover, when the microrobot moves faster than 10 mm/s, the steady-state error is more likely to increase, and as a result, the microrobot head hits the surface. In the laser model, although steady state error is less than the steady-state error of the rule-based model, due to hardware limitation of sensing speed, this technique is not reliable enough for a closed-loop controller. This model can be used to control the microrobot up to speeds of 15 mm/s in stable conditions. Thus, it is not suitable for applications in which higher speeds are required. Therefore, the rule-based control system and laser calibration were merged to create a hybrid control model, resulting in a more stable control at high speeds of up to 30 mm/s. It was verified that the microrobot with the hybrid model enabled one to achieve more precise localization over a number of test results. Furthermore, in the hybrid model, the aggressiveness and the transient system response can be tuned via the rule-based model. This ensures a speed-independent, stable, closed-loop control structure and low steady-state error.
In this study, we developed various control algorithms based on discussed three models for the stabilization of the lateral motion of microrobots. There exists no prior study for the solution to this problem. By taking into consideration the complex motion tasks of microrobots in 3D space, a sinusoidal trajectory with 150 µm amplitude and 4 mm length is also tested, with an average error rate of 1.73 µm. The fact that this motion did not take place at a constant levitation height and that the microrobot has a wide range of levitation height shows the high performance of the microrobot design and orientation control. In the mathematical model section, starting from a free body diagram with head-tilting angle, the relation between the head-tilting angle and levitation height and phase difference equation depending on the micro-stage speed were derived. Thus, the mechanical delays in the controller were calculated based on the differences in the accelerations of the lifter-magnet and the microrobot. According to the calculated delay, the time required for the lifter-magnet to be held at the target orientation was determined, which in turn allowed the control of the lateral motion of the microrobot. By conducting parametric FEM analyses in COMSOL®, the equations that depend on micro-stage speed and microrobot head-tilting angle were determined for open-loop and closed-loop controllers. The head-tilting reaction, which can be determined using the first-order equations of angle-correction, generated undesired torque on the microrobot. It brought out, as a result, average 9.3° head-tilting angle in the case of uncontrolled model. On the other hand, by using control strategies, we achieved following results:
2.7° head-tilting angle for the Rule-based Model
1.1° head-tilting angle for the Laser Model,
0.7° head-tilting angle for the Hybrid Model
Moreover, the hybrid model was also experimented with at a speed of 30 mm/s and received an average angle error of 1°. This result proved that the microrobot can be used in cases in which a high speed and a complex and long trajectory are necessary. Furthermore, since the microrobot is capable of 5 axes orientation, its head position can also be utilized in various object manipulation tasks.
As a result, through the developed control models, a solution methodology for the head-tilting problem was developed and implemented for different tasks that require high-speed and low positioning error rates. The presented control models are particularly important for the purposes of cell and particle manipulation applications. In future studies, we will focus on developing fully autonomous control techniques.