Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit
Abstract
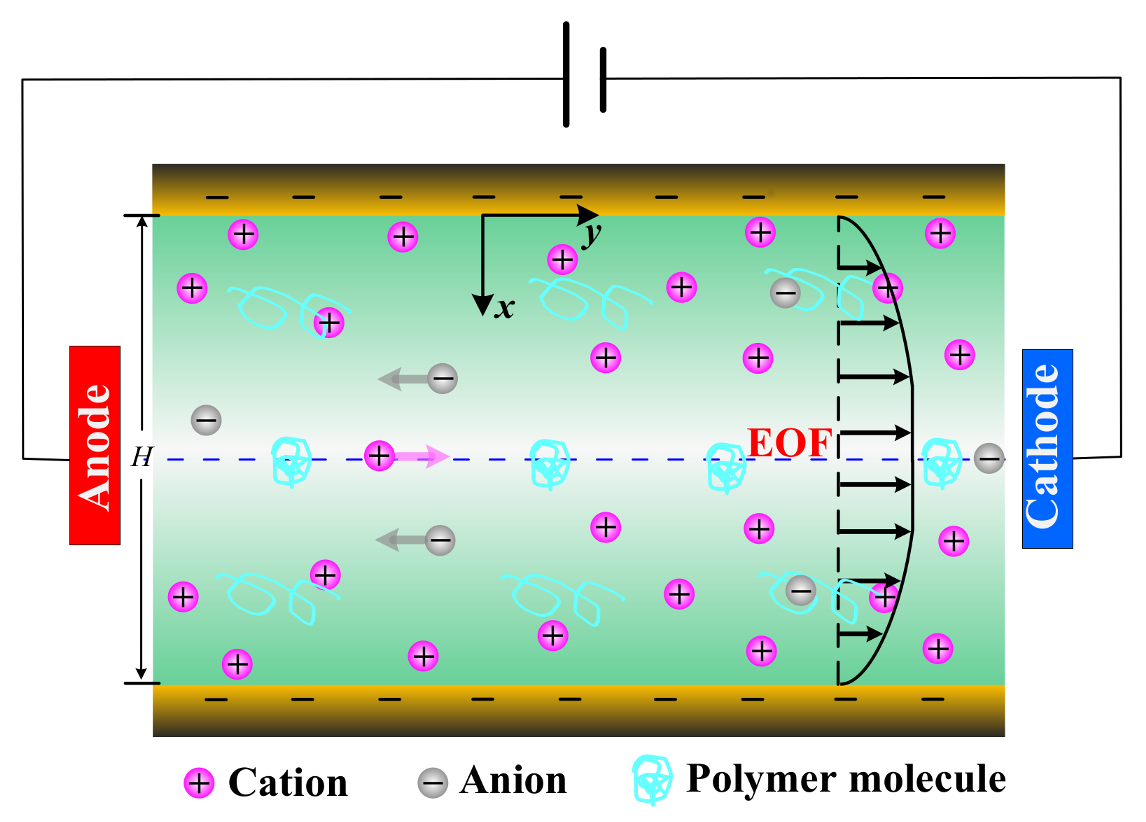
1. Introduction
2. Mathematical Model
3. Numerical Method and Validation
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vogel, R.; Anderson, W.; Eldridge, J.; Glossop, B.; Willmott, G. A Variable Pressure Method for Characterizing Nanoparticle Surface Charge Using Pore Sensors. Anal. Chem. 2012, 84, 3125–3131. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.L.; Daiguji, H. Manipulation of Protein Translocation through Nanopores by Flow Field Control and Application to Nanopore Sensors. Anal. Chem. 2016, 88, 9251–9258. [Google Scholar] [CrossRef] [PubMed]
- Mei, L.; Chou, T.H.; Cheng, Y.S.; Huang, M.J.; Yeh, L.H.; Qian, S. Electrophoresis of pH-regulated Nanoparticles: Impact of the Stern Layer. Phys. Chem. Chem. Phys. 2016, 18, 9927–9934. [Google Scholar] [CrossRef] [PubMed]
- Karnik, R.; Fan, R.; Yue, M.; Li, D.; Yang, P.; Majumdar, A. Electrostatic Control of Ions and Molecules in Nanofluidic Transistors. Nano Lett. 2005, 5, 943–948. [Google Scholar] [CrossRef] [PubMed]
- Siria, A.; Poncharal, P.; Biance, A.L.; Fulcrand, R.; Blase, X.; Purcell, S.T.; Bocquet, L. Giant Osmotic Energy Conversion Measured in a Single Transmembrane Boron Nitride Nanotube. Nature 2013, 494, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Garcia, A.L.; Lopez, G.P.; Petsev, D.N. Electrokinetic Transport and Separations in Fluidic Nanochannels. Electrophoresis 2007, 28, 595–610. [Google Scholar] [CrossRef] [PubMed]
- Sparreboom, W.; van den Berg, A.; Eijkel, J.C.T. Principles and Applications of Nanofluidic Transport. Nat. Nanotechnol. 2009, 4, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Green, N.G.; Ramos, A.; Morgan, H. Ac Electrokinetics: A Survey of Sub-micrometre Particle Dynamics. J. Phys. D Appl. Phys. 2000, 33, 632–641. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Advances in Electrokinetics and Their Applications in Micro/Nano Fluidics. Microfluid. Nanofluid. 2012, 13, 179–203. [Google Scholar] [CrossRef]
- Mei, L.; Yeh, L.H.; Qian, S. Buffer Anions Can Enormously Enhance the Electrokinetic Energy Conversion in Nanofluidics with Highly Overlapped Double Layers. Nano Energy 2017, 32, 374–381. [Google Scholar] [CrossRef]
- Reuss, F.F. Charge-induced Flow. Proc. Imp. Soc. Nat. Mosc. 1809, 3, 327–344. [Google Scholar]
- Tang, Z.; Hong, S.; Djukic, D.; Modi, V.; West, A.C.; Yardley, J.; Osgood, R.M. Electrokinetic Flow Control for Composition Modulation in a Microchannel. J. Micromech. Microeng. 2002, 12, 870–877. [Google Scholar] [CrossRef]
- Haywood, D.G.; Harms, Z.D.; Jacobson, S.C. Electroosmotic Flow in Nanofluidic Channels. Anal. Chem. 2014, 86, 11174–11180. [Google Scholar] [CrossRef] [PubMed]
- Prabhakaran, R.A.; Zhou, Y.; Zhao, C.; Hu, G.; Song, Y.; Wang, J.; Yang, C.; Xuan, X. Induced Charge Effects on Electrokinetic Entry Flow. Phys. Fluids 2017, 29, 062001. [Google Scholar] [CrossRef]
- Burgreen, D.; Nakache, F.R. Electrokinetic Flow in Ultrafine Capillary Slits. J. Phys. Chem. 1964, 68, 1084–1091. [Google Scholar] [CrossRef]
- Petsev, D.N.; Lopez, G.P. Electrostatic Potential and Electroosmotic Flow in a Cylindrical Capillary Filled with Symmetric Electrolyte: Analytic Solutions in Thin Double Layer Approximation. J. Colloid Interface Sci. 2006, 294, 492–498. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wong, T.N.; Yang, C.; Ooi, K.T. Characterization of Electroosmotic Flow in Rectangular Microchannels. Int. J. Heat Mass Transf. 2007, 50, 3115–3121. [Google Scholar] [CrossRef]
- Yossifon, G.; Mushenheim, P.; Chang, Y.C.; Chang, H.C. Nonlinear Current-Voltage Characteristics of Nanochannels. Phys. Rev. E 2009, 79, 046305. [Google Scholar] [CrossRef] [PubMed]
- Atalay, S. Role of Surface Chemistry in Nanoscale Electrokinetic Transport. Ph.D. Thesis, Old Dominion University, Norfolk, VA, USA, 2014. [Google Scholar]
- Huang, M.J.; Mei, L.; Yeh, L.H.; Qian, S. ph-Regulated Nanopore Conductance with Overlapped Electric Double Layers. Electrochem. Commun. 2015, 55, 60–63. [Google Scholar] [CrossRef]
- Baldessari, F. Electrokinetics in Nanochannels: Part I. Electric Double Layer Overlap and Channel-to-Well Equilibrium. J. Colloid Interface Sci. 2008, 325, 526–538. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chakraborty, S. Implications of Interactions between Steric Effects and Electrical Double Layer Overlapping Phenomena on Electro-Chemical Transport in Narrow Fluidic Confinements. arXiv, 2010; arXiv:1010.5731. [Google Scholar]
- Choi, W.; Joo, S.W.; Lim, G. Electroosmotic Flows of Viscoelastic Fluids with Asymmetric Electrochemical Boundary Conditions. J. Non-Newton. Fluid Mech. 2012, 187, 1–7. [Google Scholar] [CrossRef]
- Zhao, C.L.; Yang, C. Electro-osmotic Mobility of Non-Newtonian Fluids. Biomicrofluidics 2011, 5, 014110. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chakraborty, S. Analytical Solutions for Velocity, Temperature and Concentration Distribution in Electroosmotic Microchannel Flows of a Non-Newtonian Bio-Fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Zimmerman, W.B.; Rees, J.M.; Craven, T.J. Rheometry of Non-Newtonian Electrokinetic Flow in a Microchannel T-Junction. Microfluid. Nanofluid. 2006, 2, 481–492. [Google Scholar] [CrossRef]
- Olivares, M.L.; Vera-Candioti, L.; Berli, C.L.A. The EOF of Polymer Solutions. Electrophoresis 2009, 30, 921–929. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of Electroosmotic Flow of Power-Law Fluids in a Slit Microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Park, H.M.; Lee, W.M. Helmholtz–Smoluchowski Velocity for Viscoelastic Electroosmotic Flows. J. Colloid Interface Sci. 2008, 317, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Park, H.M.; Lee, W.M. Effect of Viscoelasticity on the Flow Pattern and the Volumetric Flow Rate in Electroosmotic Flows through a Microchannel. Lab Chip 2008, 8, 1163–1170. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.M.; Alves, M.A.; Pinho, F.T. Analytical Solution of Mixed Electro-osmotic/Pressure Driven Flows of Viscoelastic Fluids in Microchannels. J. Non-Newton. Fluid Mech. 2009, 159, 50–63. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Afonso, A.M.; Alves, M.A.; Nóbrega, J.M.; Pinho, F.T. Analytical and Numerical Study of the Electro-osmotic Annular Flow of Viscoelastic Fluids. J. Colloid Interface Sci. 2014, 420, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.M.; Alves, M.A.; Pinho, F.T. Electro-osmotic Flow of Viscoelastic Fluids in Microchannels under Asymmetric Zeta Potentials. J. Eng. Math. 2011, 71, 15–30. [Google Scholar] [CrossRef]
- Sousa, J.J.; Afonso, A.M.; Pinho, F.T.; Alves, M.A. Effect of the Skimming Layer on Electro-osmotic-Poiseuille Flows of Viscoelastic Fluids. Microfluid. Nanofluid. 2011, 10, 107–122. [Google Scholar] [CrossRef]
- Dhinakaran, S.; Afonso, A.M.; Alves, M.A.; Pinho, F.T. Steady Viscoelastic Fluid Flow between Parallel Plates under Electro-osmotic Forces: Phan-Thien-Tanner Model. J. Colloid Interface Sci. 2010, 344, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Yeh, L.H.; Lin, C.Y.; Mei, L.; Qian, S. ph-Regulated Ionic Conductance in a Nanochannel with Overlapped Electric Double Layers. Anal. Chem. 2015, 87, 4508–4514. [Google Scholar] [CrossRef] [PubMed]
- Mei, L.; Yeh, L.H.; Qian, S. Gate Modulation of Proton Transport in a Nanopore. Phys. Chem. Chem. Phys. 2016, 18, 7449–7458. [Google Scholar] [CrossRef] [PubMed]
- Keunings, R. On the High Weissenberg Number Problem. J. Non-Newton. Fluid Mech. 1986, 20, 209–226. [Google Scholar] [CrossRef]
- El-Kareh, A.W.; Leal, L.G. Existence of Solutions for All Deborah Numbers for a Non-Newtonian Model Modified to Include Diffusion. J. Non-Newton. Fluid Mech. 1989, 33, 257–287. [Google Scholar] [CrossRef]
- Min, T.; Yoo, J.Y.; Choi, H. Effect of Spatial Discretization Schemes on Numerical Solutions of Viscoelastic Fluid Flows. J. Non-Newton. Fluid Mech. 2001, 100, 27–47. [Google Scholar] [CrossRef]
- Vaithianathan, T.; Collins, L.R. Numerical Approach to Simulating Turbulent Flow of a Viscoelastic Polymer Solution. J. Comput. Phys. 2003, 187, 1–21. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Constitutive Laws for the Matrix-Logarithm of the Conformation Tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Zhang, H.N.; Li, D.Y.; Li, X.B.; Cai, W.H.; Li, F.C. Numerical Simulation of Heat Transfer Process of Viscoelastic Fluid Flow at High Weissenberg Number by Log-Conformation Reformulation. J. Fluids Eng. Trans. ASME 2017, 139, 091402. [Google Scholar] [CrossRef]
- Leonard, B.P. A Stable and Accurate Convective Modelling Procedure Based on Quadratic Upstream Interpolation. Comput. Meth. Appl. Mech. Eng. 1979, 19, 59–98. [Google Scholar] [CrossRef]
- Harten, A. High Resolution Schemes for Hyperbolic Conservation Laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Issa, R.I.; Gosman, A.D.; Watkins, A.P. The Computation of Compressible and Incompressible Recirculating Flow by a Non-Iterative Implicit Scheme. J. Comput. Phys. 1986, 62, 66–82. [Google Scholar] [CrossRef]








| Variable | |||
|---|---|---|---|
| Maximum velocity | 0.15 | 0.34 | 0.22 |
| Enhancement of the maximum velocity | 2.50 | 2.05 | 1.75 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, L.; Zhang, H.; Meng, H.; Qian, S. Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit. Micromachines 2018, 9, 155. https://doi.org/10.3390/mi9040155
Mei L, Zhang H, Meng H, Qian S. Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit. Micromachines. 2018; 9(4):155. https://doi.org/10.3390/mi9040155
Chicago/Turabian StyleMei, Lanju, Hongna Zhang, Hongxia Meng, and Shizhi Qian. 2018. "Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit" Micromachines 9, no. 4: 155. https://doi.org/10.3390/mi9040155
APA StyleMei, L., Zhang, H., Meng, H., & Qian, S. (2018). Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit. Micromachines, 9(4), 155. https://doi.org/10.3390/mi9040155




