Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique
Abstract
:1. Introduction
2. Mathematical Models
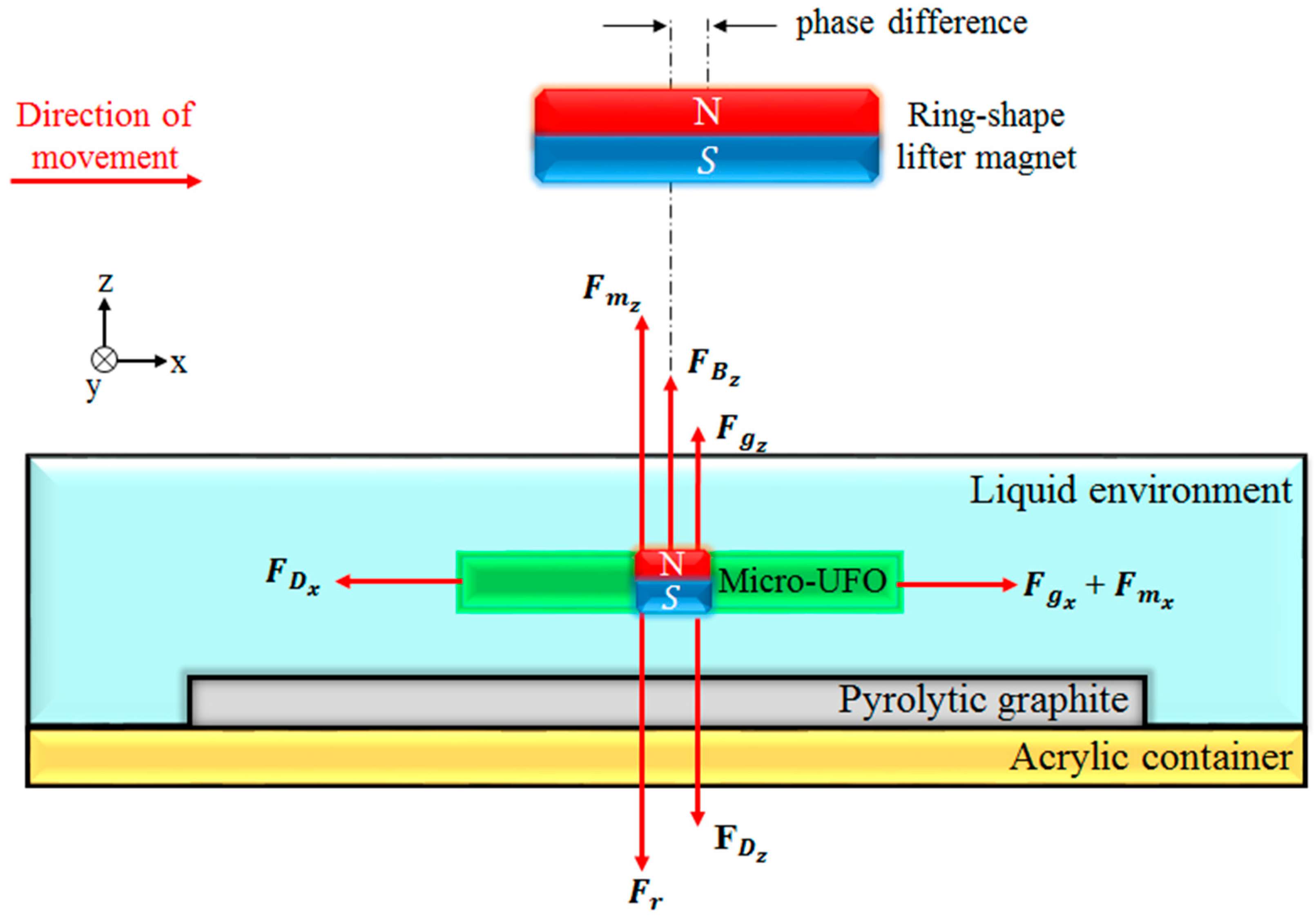
2.1. Schematic of Micro-UFO
2.2. Theoretical Background
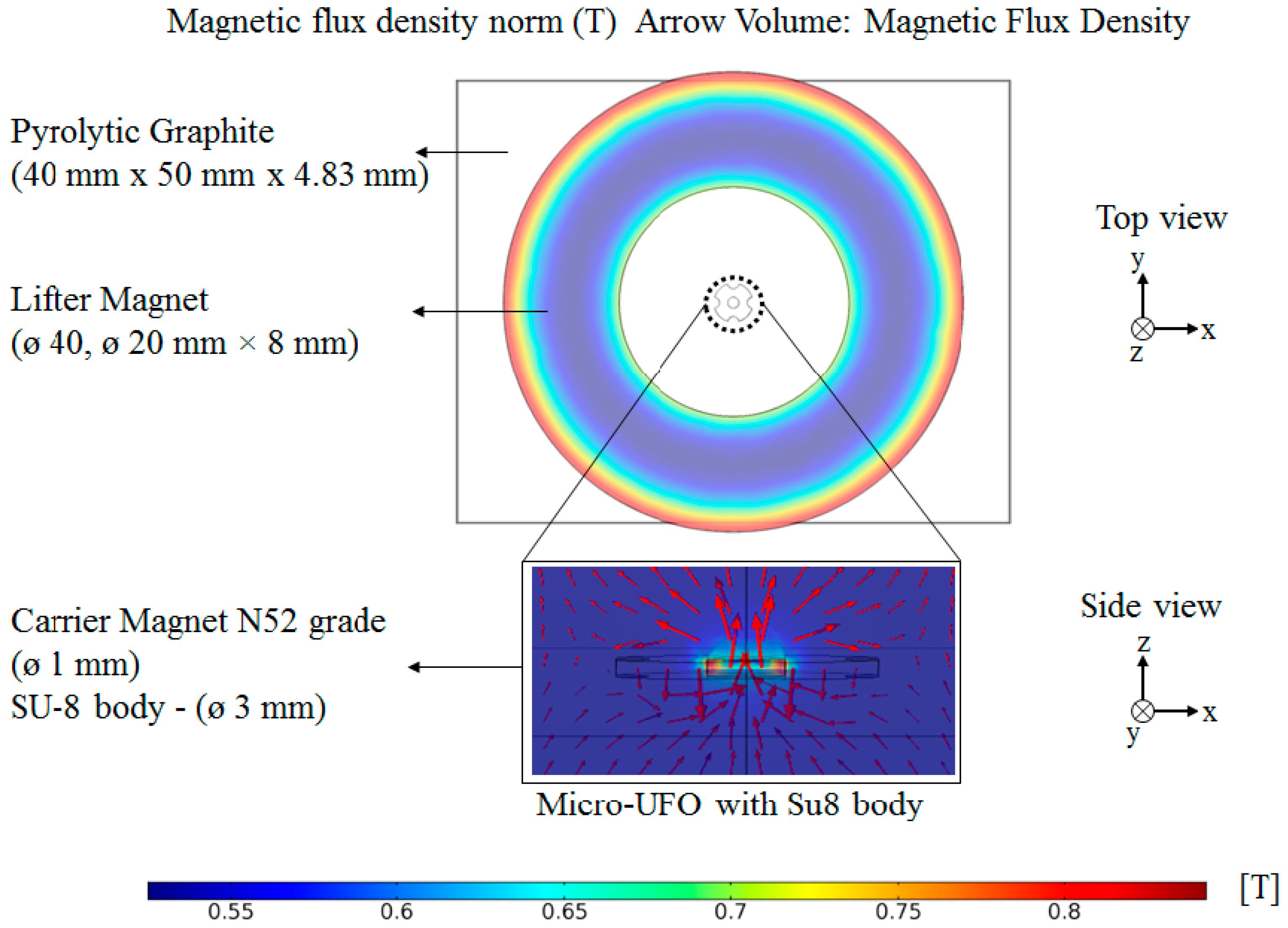
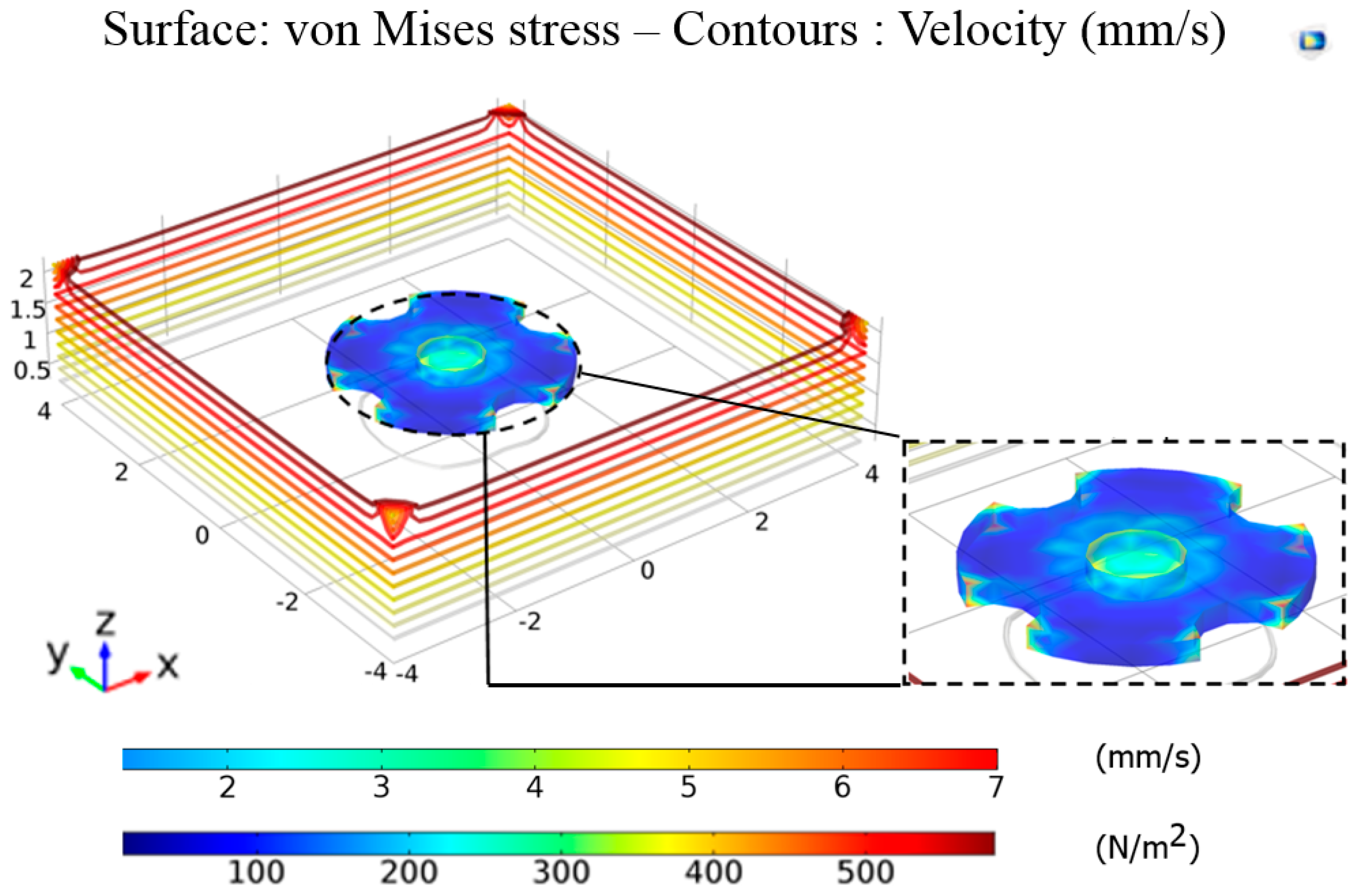
2.3. FEM Analysis
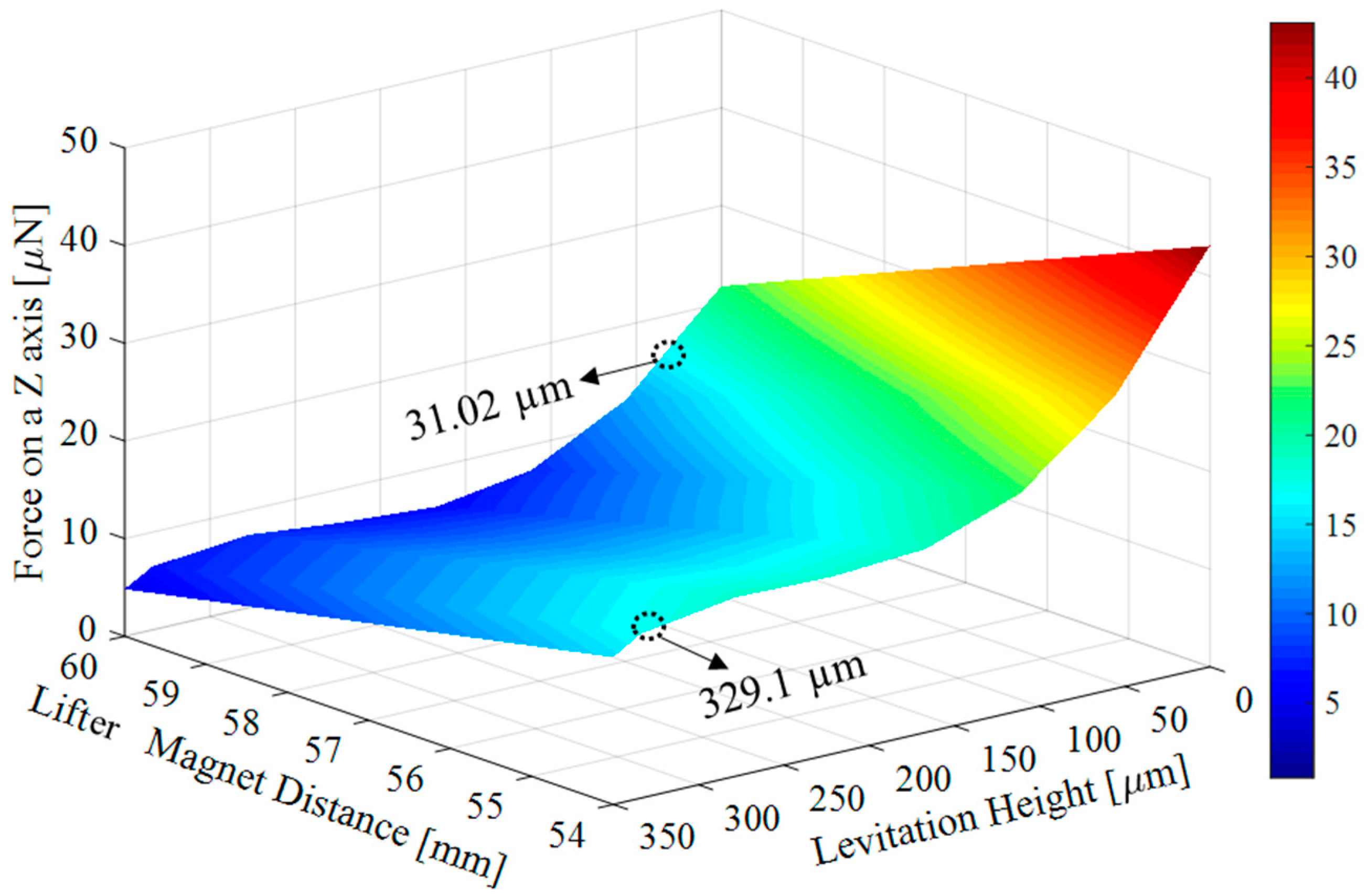
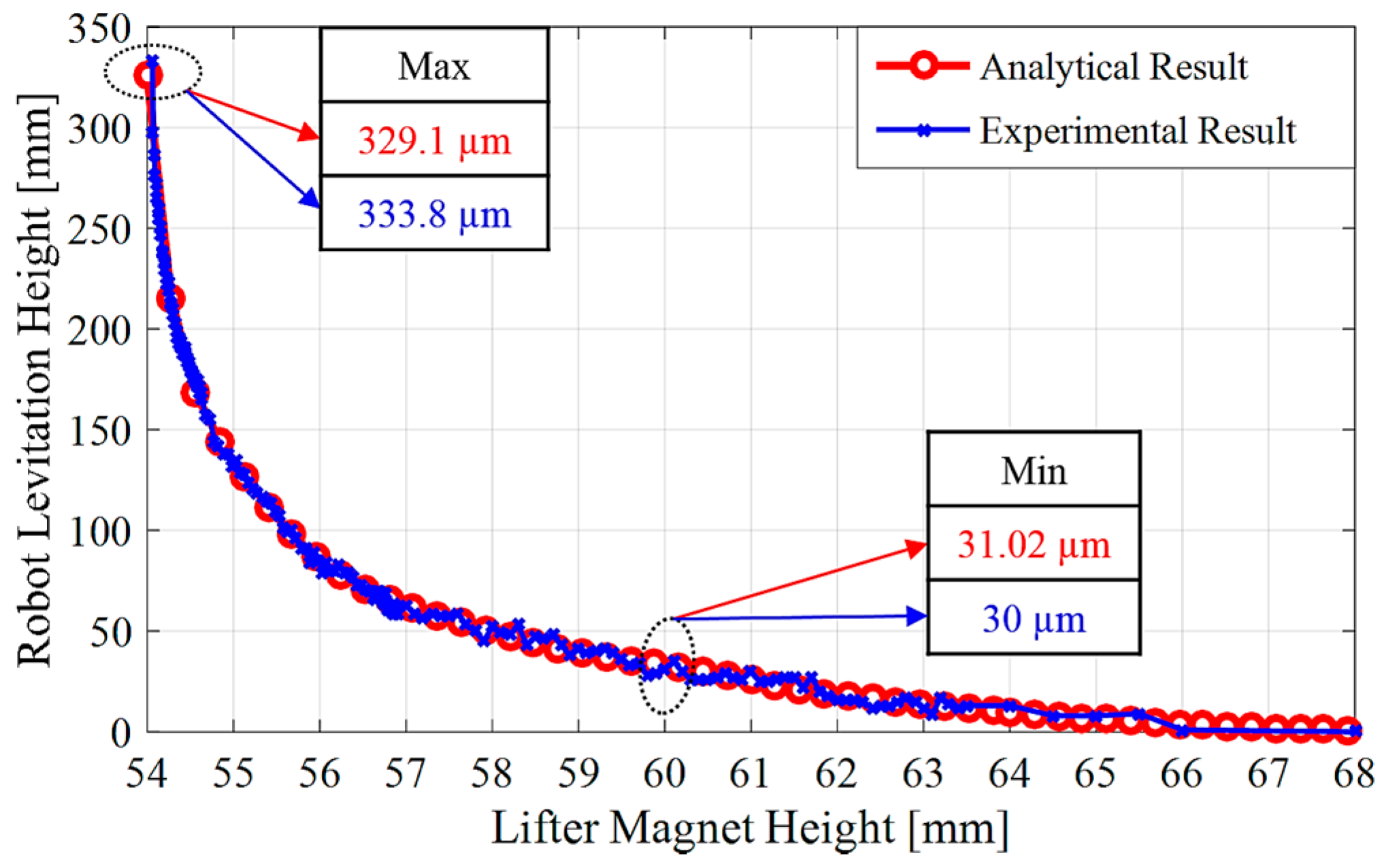
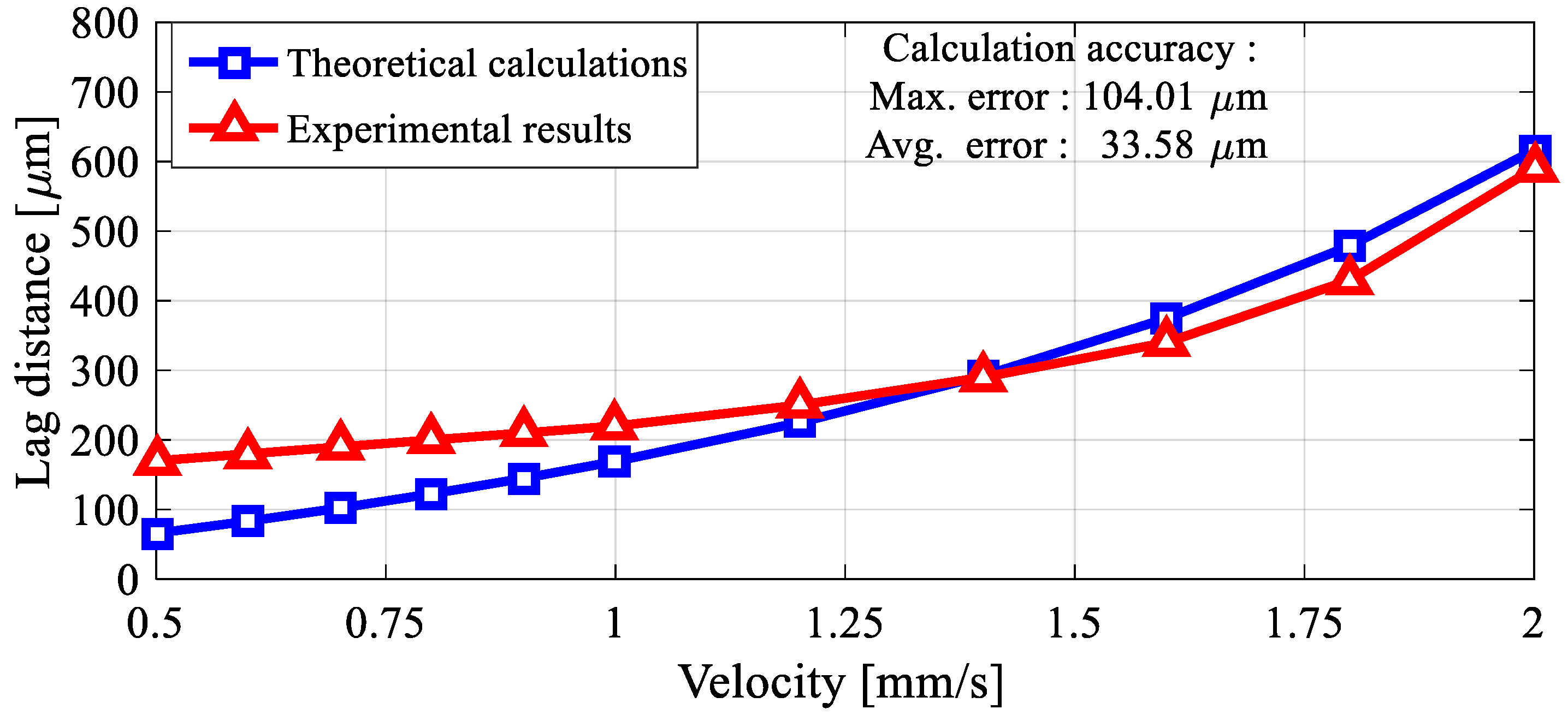
2.4. FEM Analysis of Levitation Characteristic’s Result
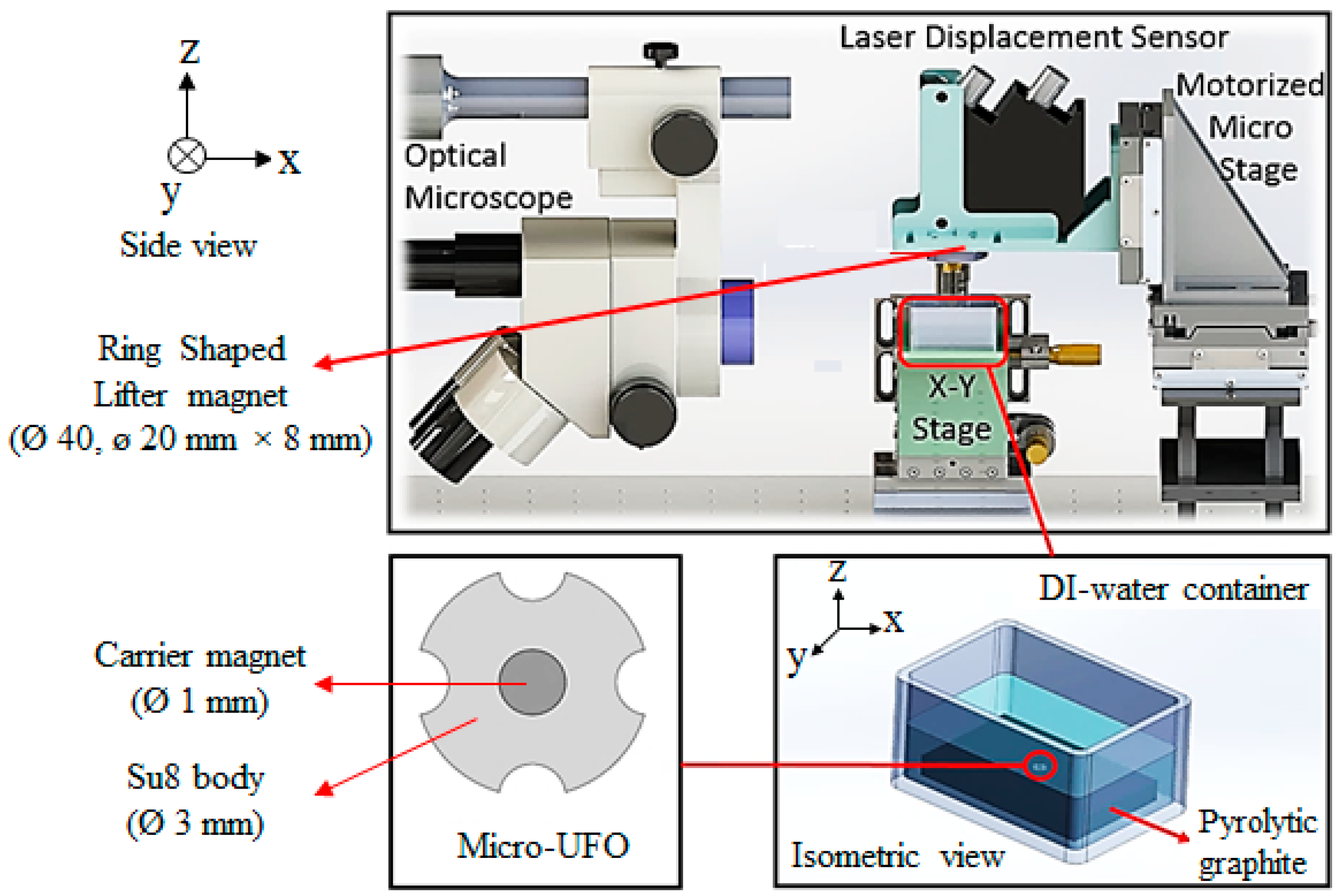
3. Materials and Methods
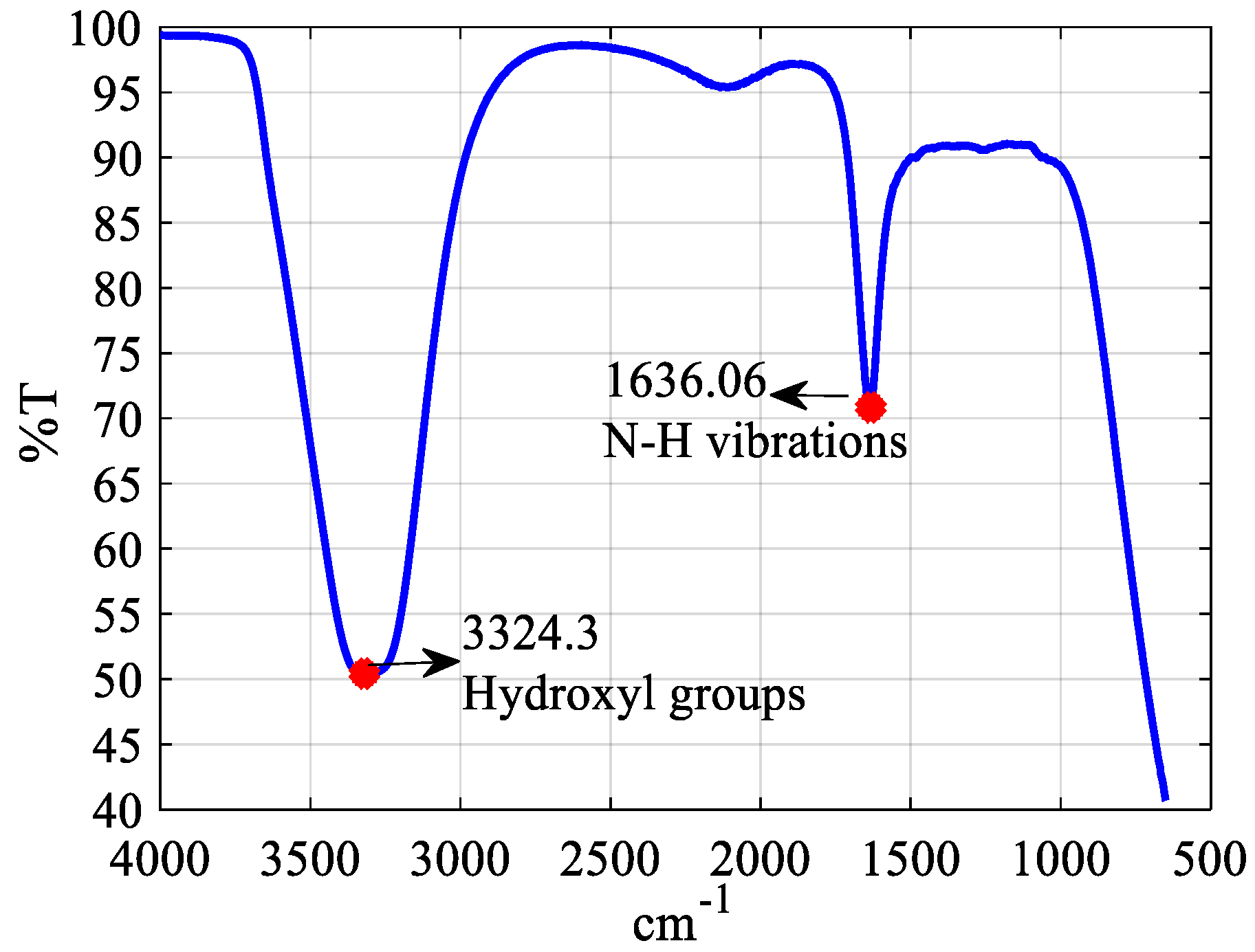
3.1. Permanent Magnet Surface Coating
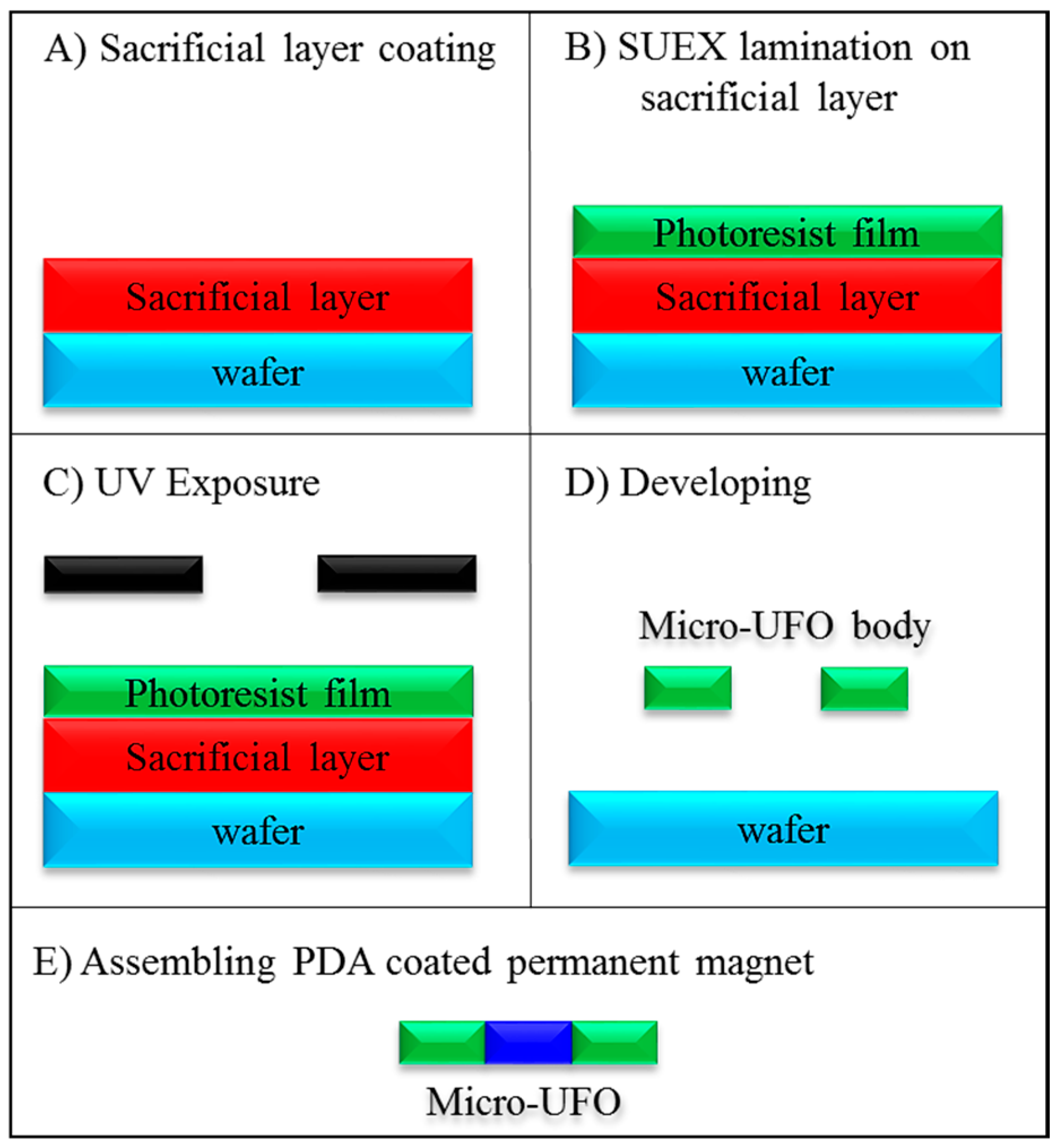
3.2. Micro-UFO Fabrication
4. Experimental Setup and Test Results
4.1. Experimental Setup
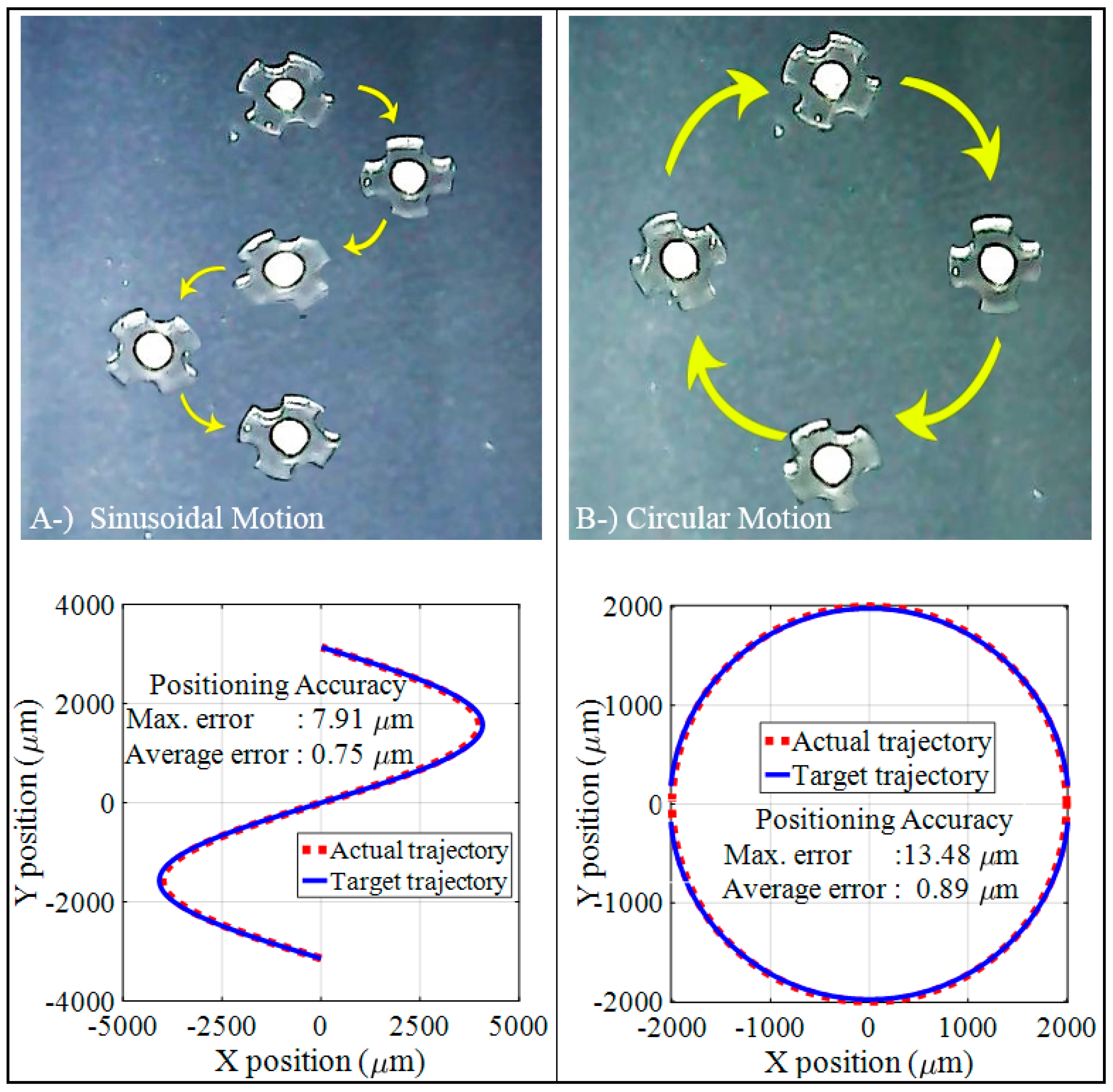
4.2. Accurate Positioning and Phase Difference Characterization
4.3. Head Bending Reaction
5. Discussion and Conclusions
5.1. General
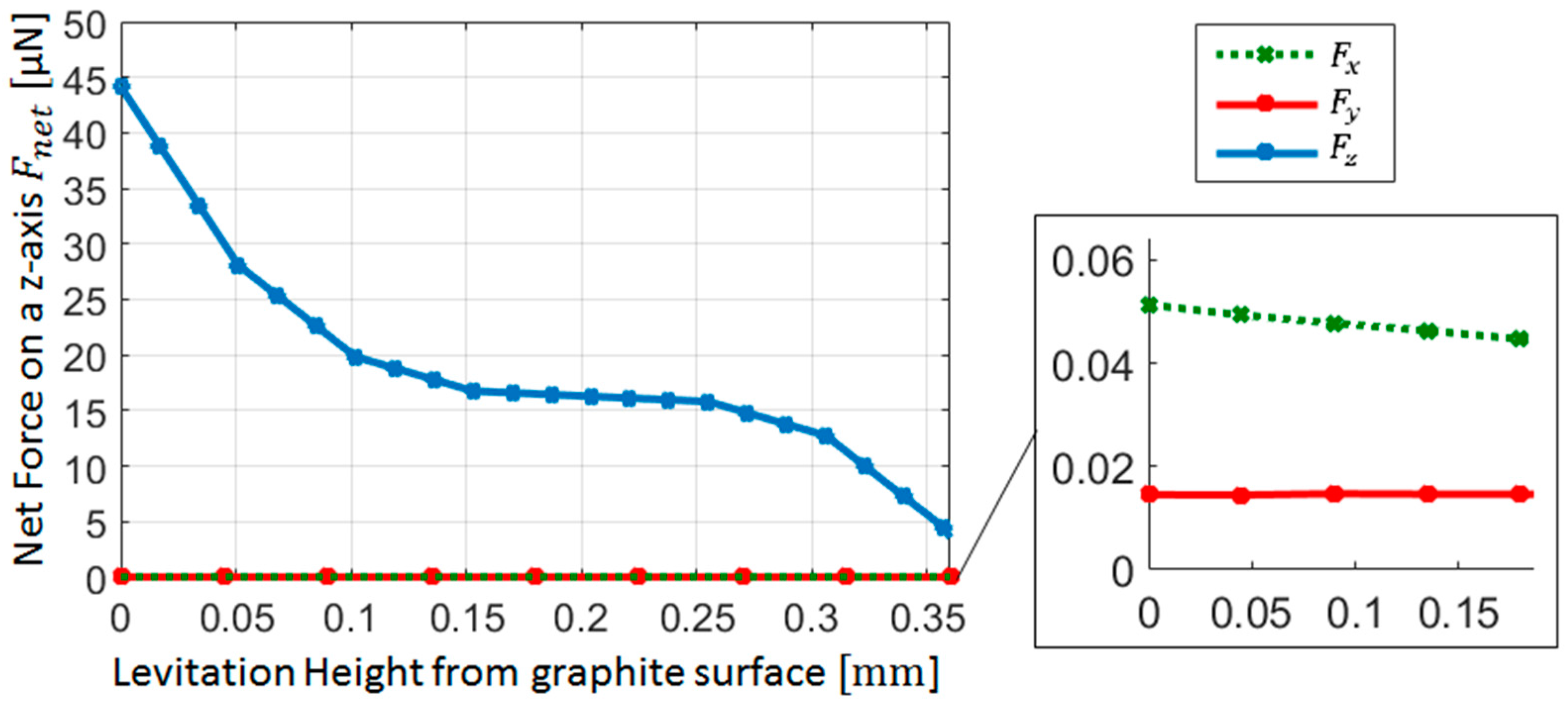
5.2. Levitation on z-Axis
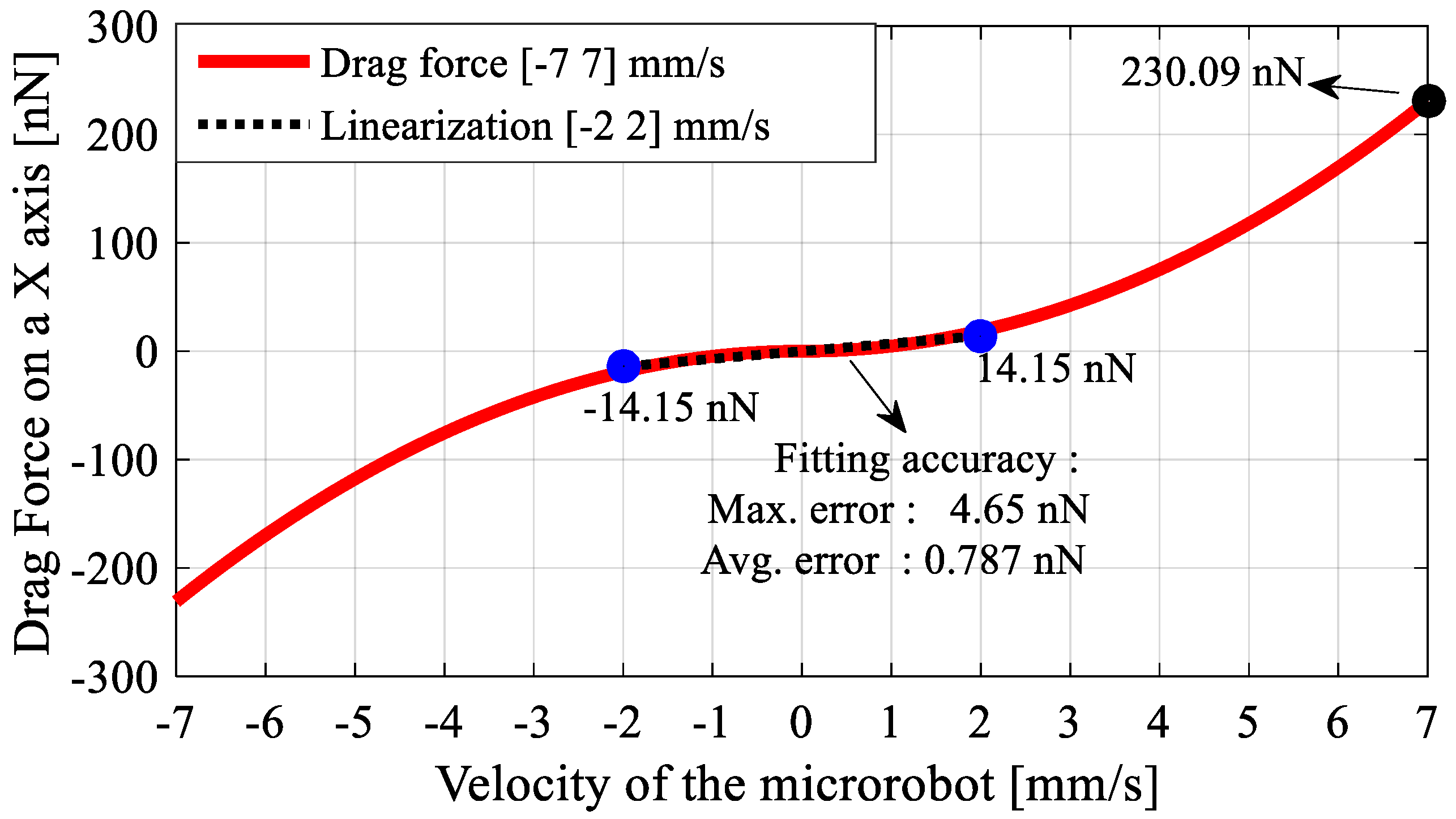
5.3. Drag Force—Lifter Magnet Effects
5.4. Center Alignment
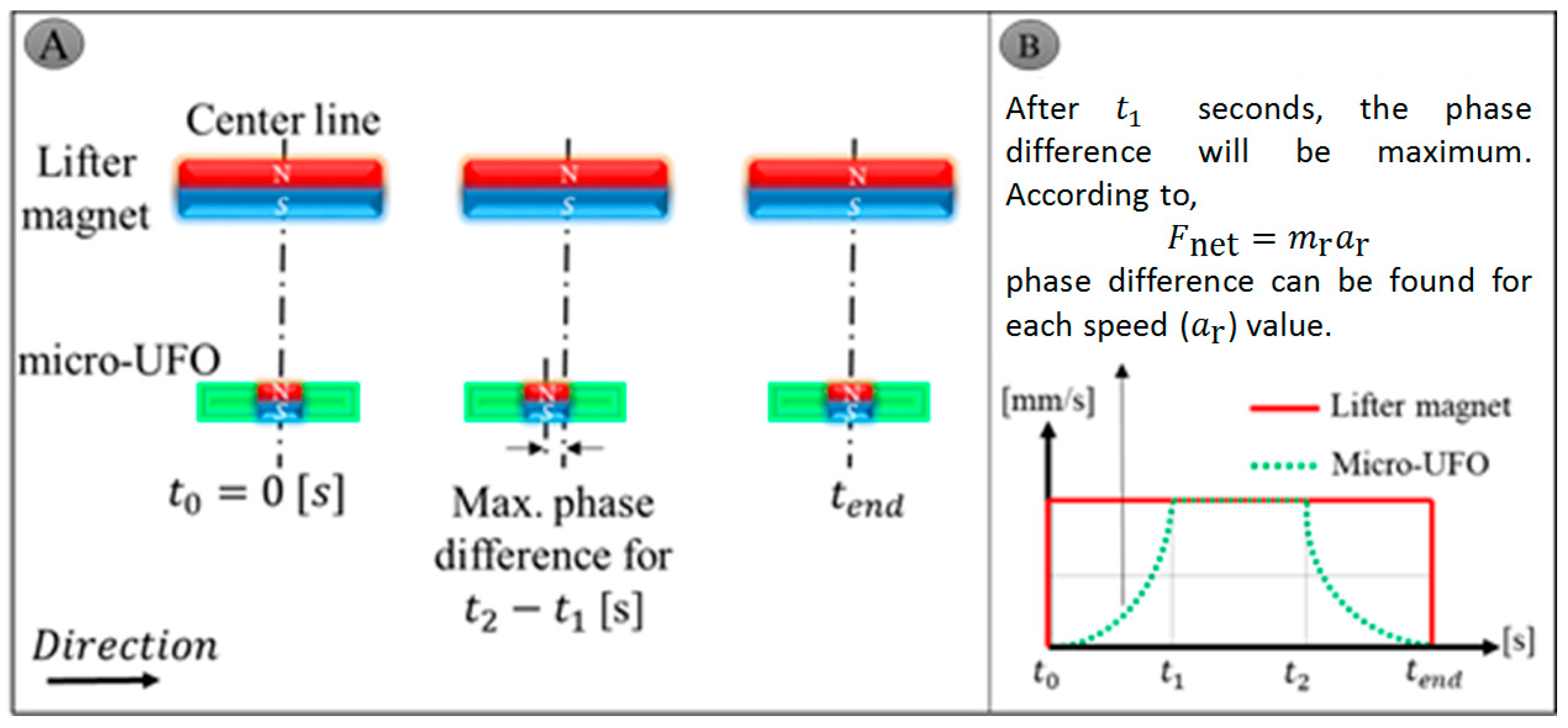
5.5. Phase Difference
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fusco, S.; Sakar, M.S.; Kennedy, S.; Peters, C.; Bottani, R.; Starsich, F.; Mooney, D. An integrated icrorobotic platform for on-demand, targeted therapeutic interventions. Adv. Mater. 2014, 26, 952–957. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Ichikawa, A.; Arai, F.; Hagiwara, M. Continuous enucleation of bovine oocyte by microrobot with local flow distribution control. In Proceedings of the 2012 International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Xi’an, China, 29 August–1 September 2012; pp. 59–64. [Google Scholar]
- Hagiwara, M.; Kawahara, T.; Yamanishi, Y.; Arai, F. Driving method of microtool by horizontally arranged permanent magnets for single cell manipulation. Appl. Phys. Lett. 2010, 97, 013701. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, M.; Cui, T. Microfluidic valves based on TiO2 coating with tunable surface wettability between super hydrophilic and super hydrophobic. In Proceedings of the 2011 16th Internationa Solid-State Sensors, Actuators and Microsystems Conference (TRANSDUCERS), Beijing, China, 5–9 June 2011; pp. 306–309. [Google Scholar]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [PubMed]
- Lucarini, G.; Iacovacci, V.; Gouveia, P.J.; Ricotti, L.; Menciassi, A. Design of a novel magnetic platform for cell manipulation. J. Micromech. Microeng. 2018, 28, 025009. [Google Scholar] [CrossRef]
- Ceylan, H.; Giltinan, J.; Kozielski, K.; Sitti, M. Mobile microrobots for bioengineering applications. Lab Chip 2017, 17, 1705–1724. [Google Scholar] [CrossRef] [PubMed]
- Peyer, K.E.; Zhang, L.; Nelson, B.J. Bio-inspired magnetic swimming microrobots for biomedical applications. Nanoscale 2013, 5, 1259–1272. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Ishii, K.S.; Fan, Q.; Ohta, A.T. Hydrogel microrobots actuated by optically generated vapour bubbles. Lab Chip 2012, 12, 3821–3826. [Google Scholar] [CrossRef] [PubMed]
- Fusco, S.; Huang, H.W.; Peyer, K.E.; Peters, C.; Häberli, M.; Ulbers, A.; Nelson, B.J. Shape-switching microrobots for medical applications: The influence of shape in drug delivery and locomotion. ACS Appl. Mater. Interfaces 2015, 7, 6803–6811. [Google Scholar] [CrossRef] [PubMed]
- Tung, H.W.; Sargent, D.F.; Nelson, B.J. Protein crystal harvesting using the RodBot: A wireless mobile microrobot. J. Appl. Crystallogr. 2014, 47, 692–700. [Google Scholar] [CrossRef]
- Hagiwara, M.; Kawahara, T.; Feng, L.; Yamanishi, Y.; Arai, F. High performance magnetically driven microtools with ultrasonic vibration for biomedical innovations. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3453–3454. [Google Scholar]
- Zhang, L.; Abbott, J.J.; Dong, L.; Kratochvil, B.E.; Bell, D.; Nelson, B.J. Artificial bacterial flagella: Fabrication and magnetic control. Appl. Phys. Lett. 2009, 94, 064107. [Google Scholar] [CrossRef]
- Hagiwara, M.; Kawahara, T.; Yamanishi, Y.; Masuda, T.; Feng, L.; Arai, F. On-chip magnetically actuated robot with ultrasonic vibration for single cell manipulations. Lab Chip 2011, 11, 2049–2054. [Google Scholar] [CrossRef] [PubMed]
- Chung, S.E.; Dong, X.; Sitti, M. Three-dimensional heterogeneous assembly of coded microgels using an untethered mobile microgripper. Lab Chip 2015, 15, 1667–1676. [Google Scholar] [CrossRef] [PubMed]
- Erin, O.; Giltinan, J.; Tsai, L.; Sitti, M. Design and actuation of a magnetic millirobot under a constant unidirectional magnetic field. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3404–3410. [Google Scholar]
- Feng, L.; Di, P.; Arai, F. High-precision motion of magnetic microrobot with ultrasonic levitation for 3-D rotation of single oocyte. Int. J. Robot. Res. 2016, 35, 1445–1458. [Google Scholar] [CrossRef]
- Lucarini, G.; Palagi, S.; Levi, A.; Mazzolai, B.; Dario, P.; Menciassi, A.; Beccai, L. Navigation of magnetic microrobots with different user interaction levels. IEEE Trans. Autom. Sci. Eng. 2014, 11, 818–827. [Google Scholar] [CrossRef]
- Profijt, H.B.; Pigot, C.; Reyne, G.; Grechishkin, R.M.; Cugat, O. Stable diamagnetic self-levitation of a micro-magnet by improvement of its magnetic gradients. J. Magn. Magn. Mater. 2009, 321, 259–262. [Google Scholar] [CrossRef]
- Pigot, C.; Chetouani, H.; Poulin, G.; Reyne, G. Diamagnetic levitation of solids at microscale. IEEE Trans. Magn. 2008, 44, 4521–4524. [Google Scholar] [CrossRef]
- Pelrine, R.; Wong-Foy, A.; McCoy, B.; Holeman, D.; Mahoney, R.; Myers, G.; Low, T. Diamagnetically levitated robots: An approach to massively parallel robotic systems with unusual motion properties. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), St. Paul, MN, USA, 14–18 May 2012; pp. 739–744. [Google Scholar]
- Pelrine, R.; Hsu, A.; Wong-Foy, A.; McCoy, B.; Cowan, C. Optimal control of diamagnetically levitated milli robots using automated search patterns. In Proceedings of the 2016 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Paris, France, 18–22 July 2016; pp. 1–6. [Google Scholar]
- Feng, L.; Zhang, S.; Jiang, Y.; Zhang, D.; Arai, F. Microrobot with passive diamagnetic levitation for microparticle manipulations. J. Appl. Phys. 2017, 122, 243901. [Google Scholar] [CrossRef]
- Demircali, A.; Uvet, H.; Kahraman, Y.; Kose, T.; Sisu, S.; Erkan, K. Precise Positioning of Diamagnetically Levitated Microrobot. In Proceedings of the CBU International Conference Proceedings, Prague, Czech Republic, 22–24 March 2017; Volume 5, pp. 1071–1077. [Google Scholar]
- Demircali, A.; Erkan, K.; Uvet, H. A study on finding optimum parameters of a diamagnetically driven untethered microrobot. J. Magn. 2017, 22, 539–549. [Google Scholar] [CrossRef]
- Ye, Z.; Duan, Z.; Su, Y. Theoretic and numerical analysis of diamagnetic levitation and its experimental verification. In Proceedings of the International Conference on Photonics and Optical Engineering and the Annual West China Photonics Conference (icPOE 2014), Xi’an, China, 13–15 October 2014; p. 944907. [Google Scholar]
- Chen, J.Y.; Zhou, J.B.; Meng, G. Diamagnetic bearings for MEMS: Performance and stability analysis. Mech. Res. Commun. 2008, 35, 546–552. [Google Scholar] [CrossRef]
- Küstler, G. Diamagnetic levitation-historical milestones. Electrotech. Energ. 2007, 52, 265–282. [Google Scholar]
- Boukallel, M.; Piat, E.; Abadie, J. Passive diamagnetic levitation: Theoretical foundations and application to the design of a micro-nano force sensor. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; pp. 1062–1067. [Google Scholar]
- Katz, V.J. The history of Stokes’ theorem. Math. Mag. 1979, 52, 146–156. [Google Scholar] [CrossRef]
- Liao, N.; Wu, M.; Pan, F.; Lin, J.; Li, Z.; Zhang, D.; Liu, J. Poly (dopamine) coated superparamagnetic iron oxide nanocluster for noninvasive labeling, tracking, and targeted delivery of adipose tissue-derived stem cells. Sci. Rep. 2016, 6, 18746. [Google Scholar] [CrossRef] [PubMed]



| Symbol | Quantity | Units |
|---|---|---|
| Buoyant force | N | |
| Diamagnetic force | N | |
| Drag force | N | |
| Magnetic force | N | |
| Gravitational force | N | |
| Unwanted torque | Nm | |
| Magnetic flux density | T | |
| Magnetic field strength | A/m | |
| Magnetization vector | A/m | |
| Magnetic insulation coefficient | - | |
| Relative permeability | - | |
| Volume of a particle | ||
| Robot mass | kg | |
| Gravitational acceleration | ||
| Robot volume | ||
| Fluid density | ||
| Robot density | ||
| Robot acceleration |
| Symbol | Quantity | Units |
|---|---|---|
| 2.929751 × | kg | |
| 9.81 | m/ | |
| 1798.374 | kg/ | |
| 998.2071 | kg/ | |
| 1.229066 × | ||
| 1.229066 × | ||
| 8.15402 × | ||
| 1.61911 × | ||
| I | 23.62 × | kg· |
| 12.788 | μN | |
| 28.741 | μN |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uvet, H.; Demircali, A.A.; Kahraman, Y.; Varol, R.; Kose, T.; Erkan, K. Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique. Micromachines 2018, 9, 126. https://doi.org/10.3390/mi9030126
Uvet H, Demircali AA, Kahraman Y, Varol R, Kose T, Erkan K. Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique. Micromachines. 2018; 9(3):126. https://doi.org/10.3390/mi9030126
Chicago/Turabian StyleUvet, Hüseyin, Ali Anil Demircali, Yusuf Kahraman, Rahmetullah Varol, Tunc Kose, and Kadir Erkan. 2018. "Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique" Micromachines 9, no. 3: 126. https://doi.org/10.3390/mi9030126
APA StyleUvet, H., Demircali, A. A., Kahraman, Y., Varol, R., Kose, T., & Erkan, K. (2018). Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique. Micromachines, 9(3), 126. https://doi.org/10.3390/mi9030126





