Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section
Abstract
1. Introduction
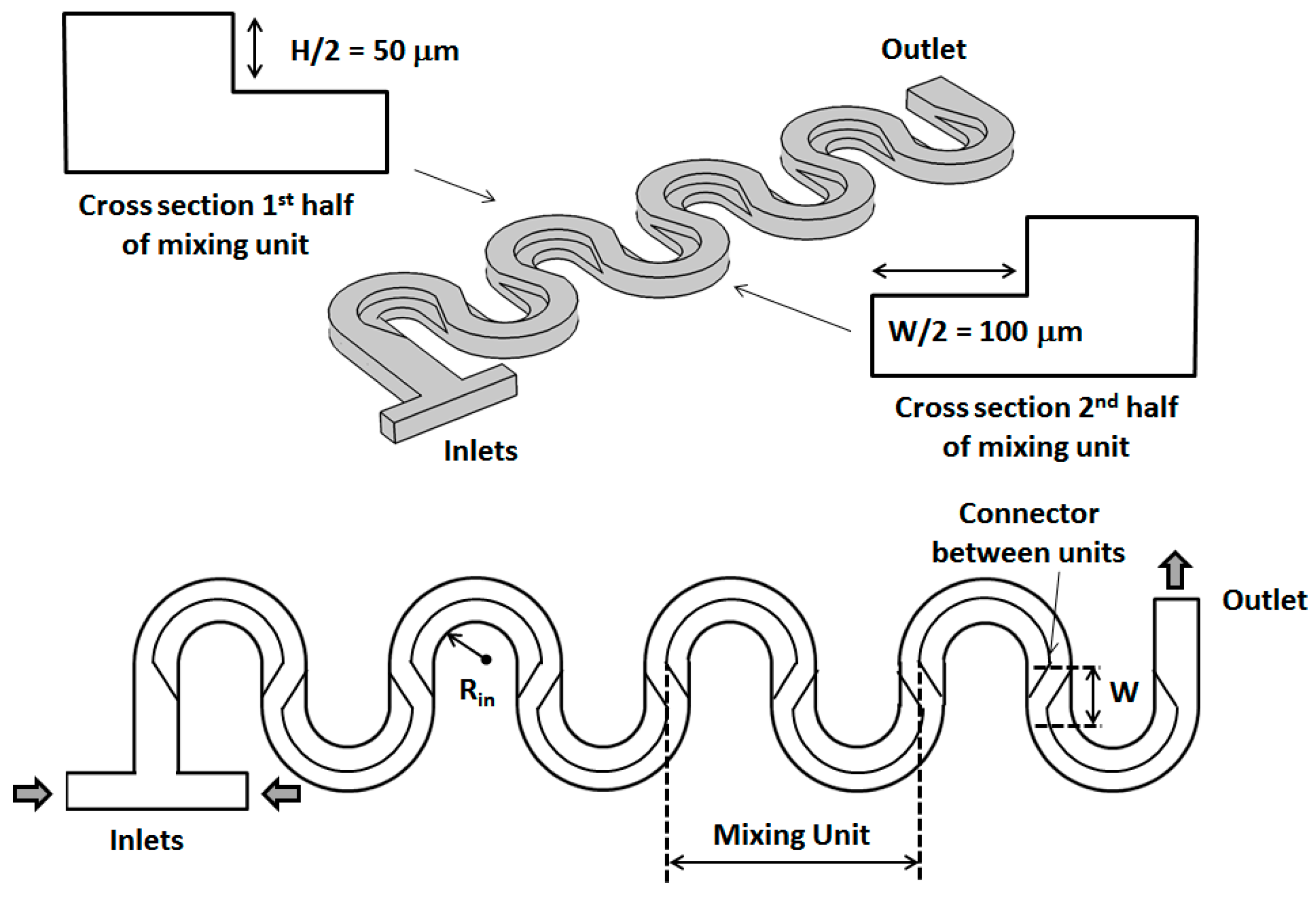
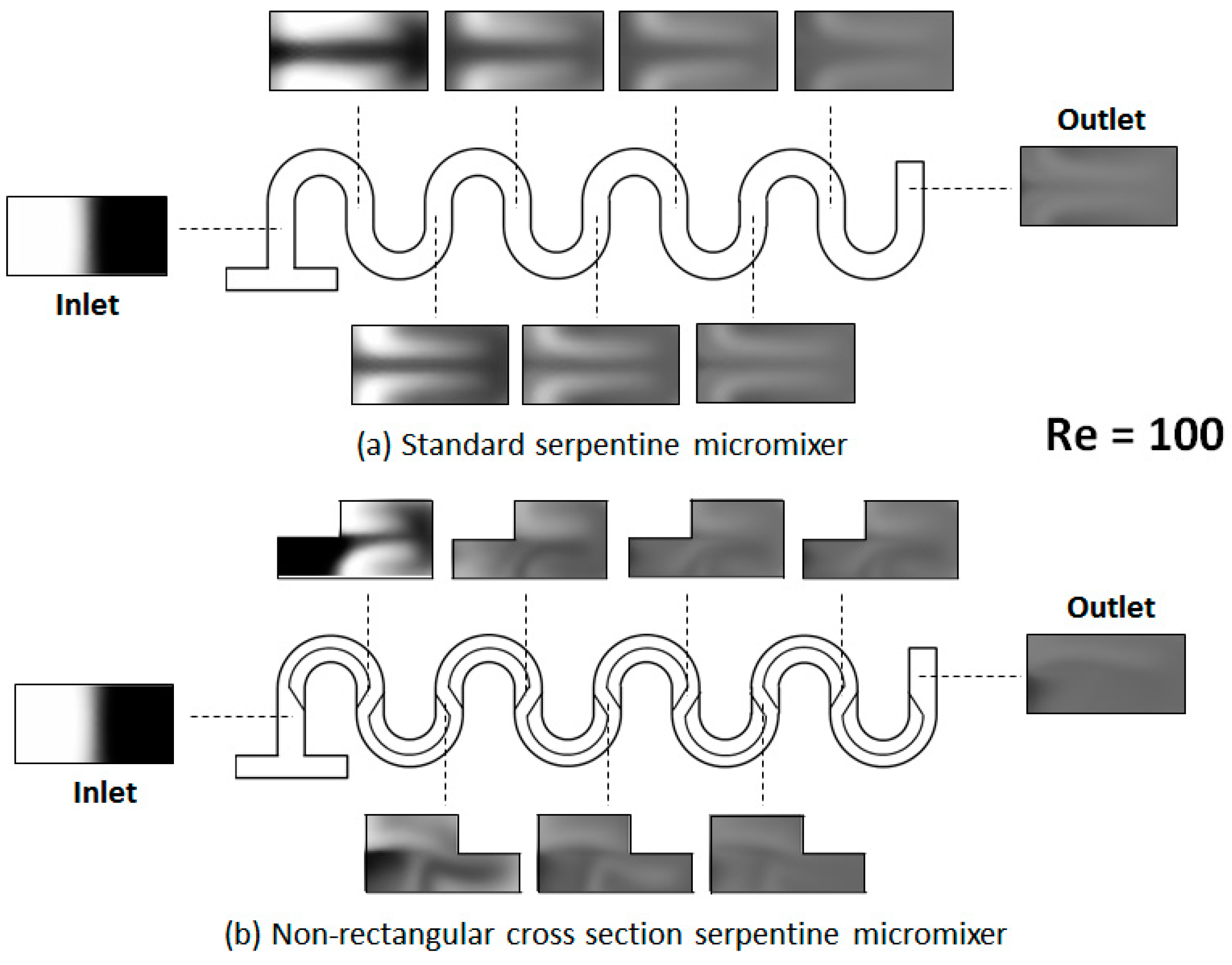
2. Geometrical Design of the Micromixer
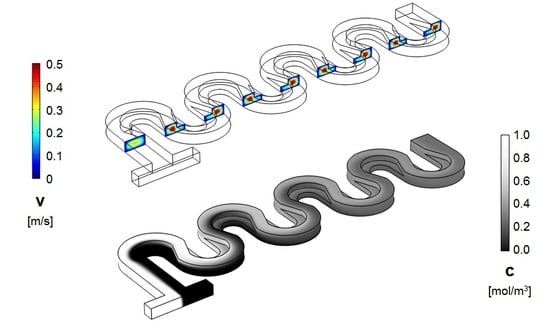
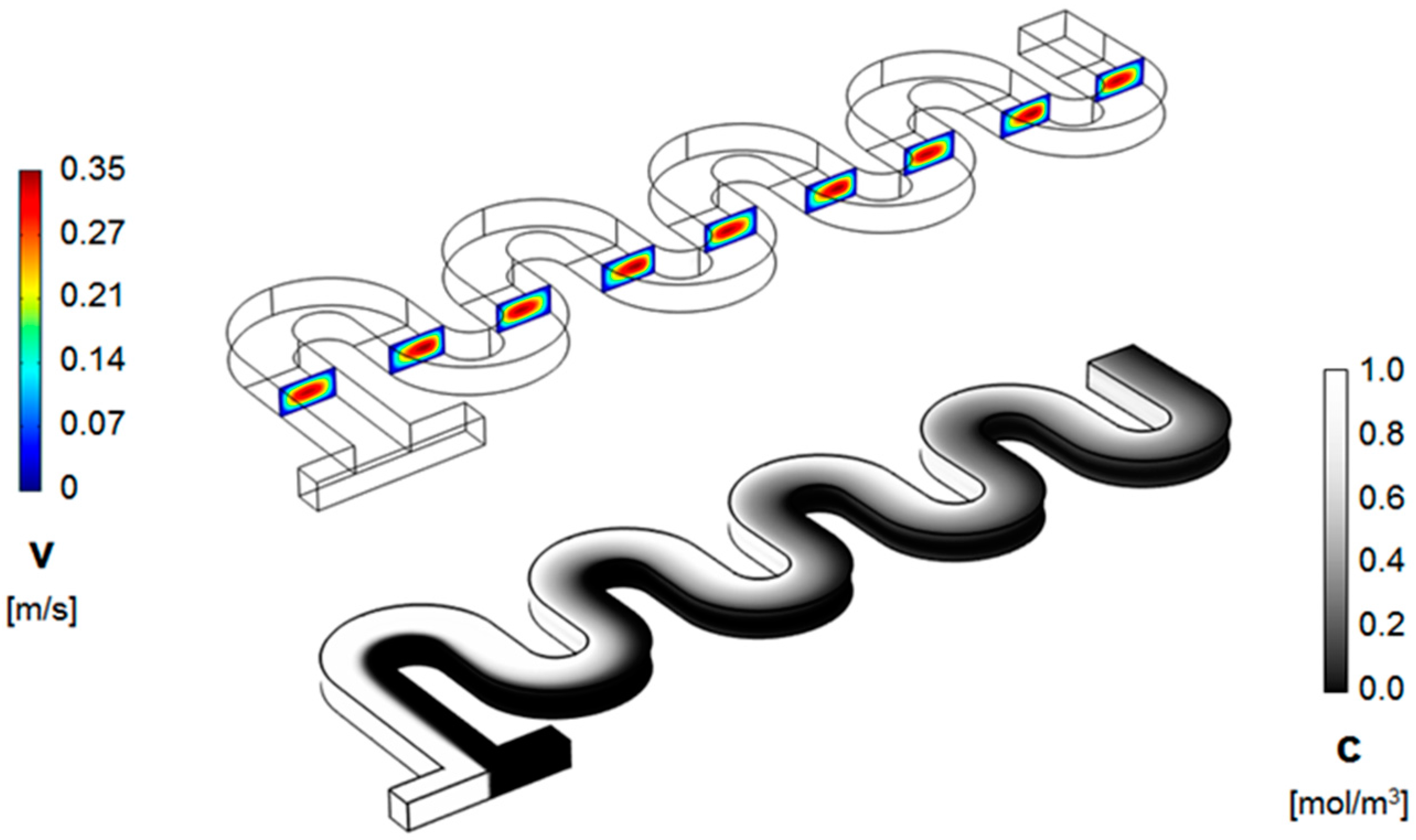
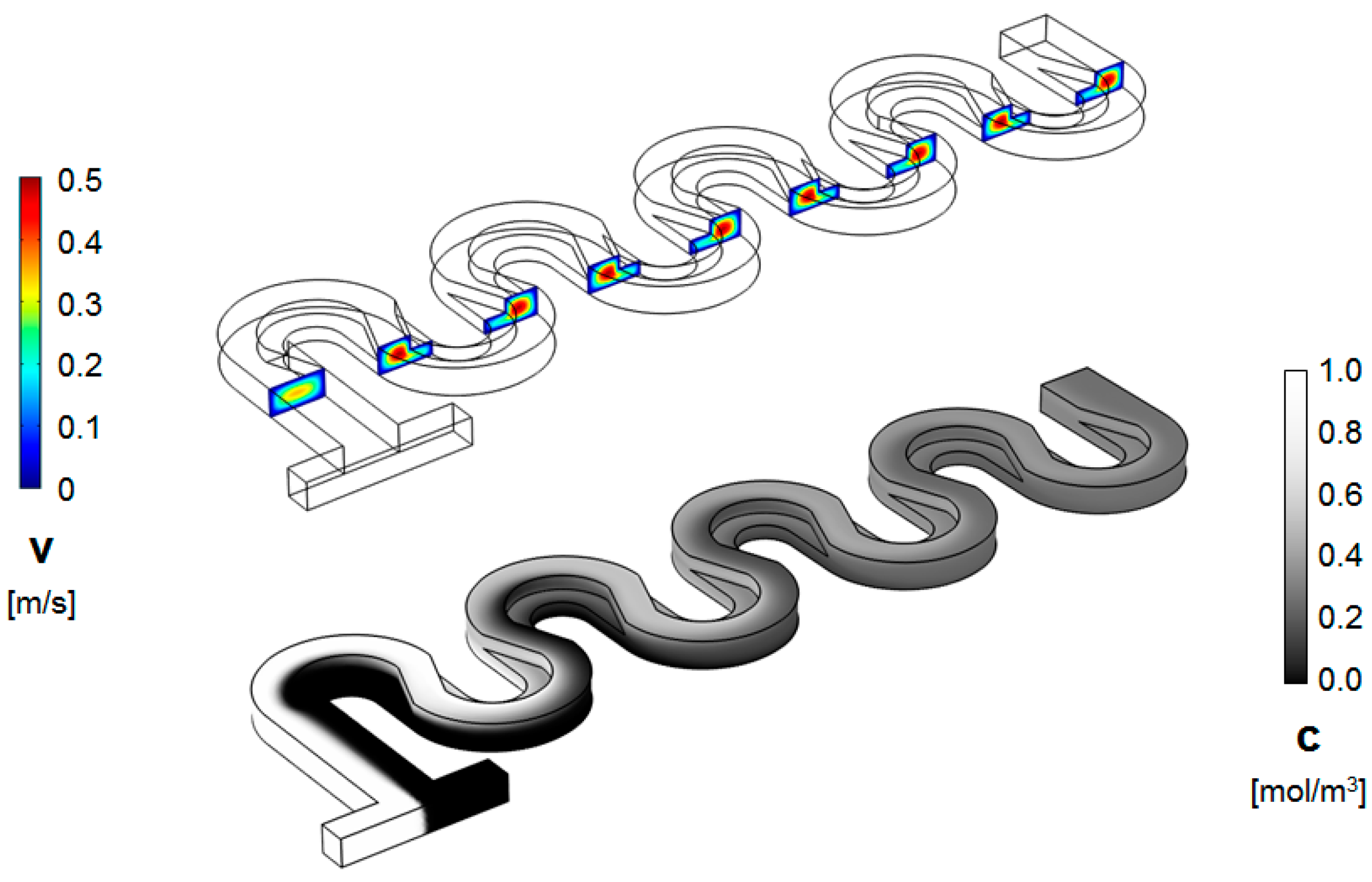
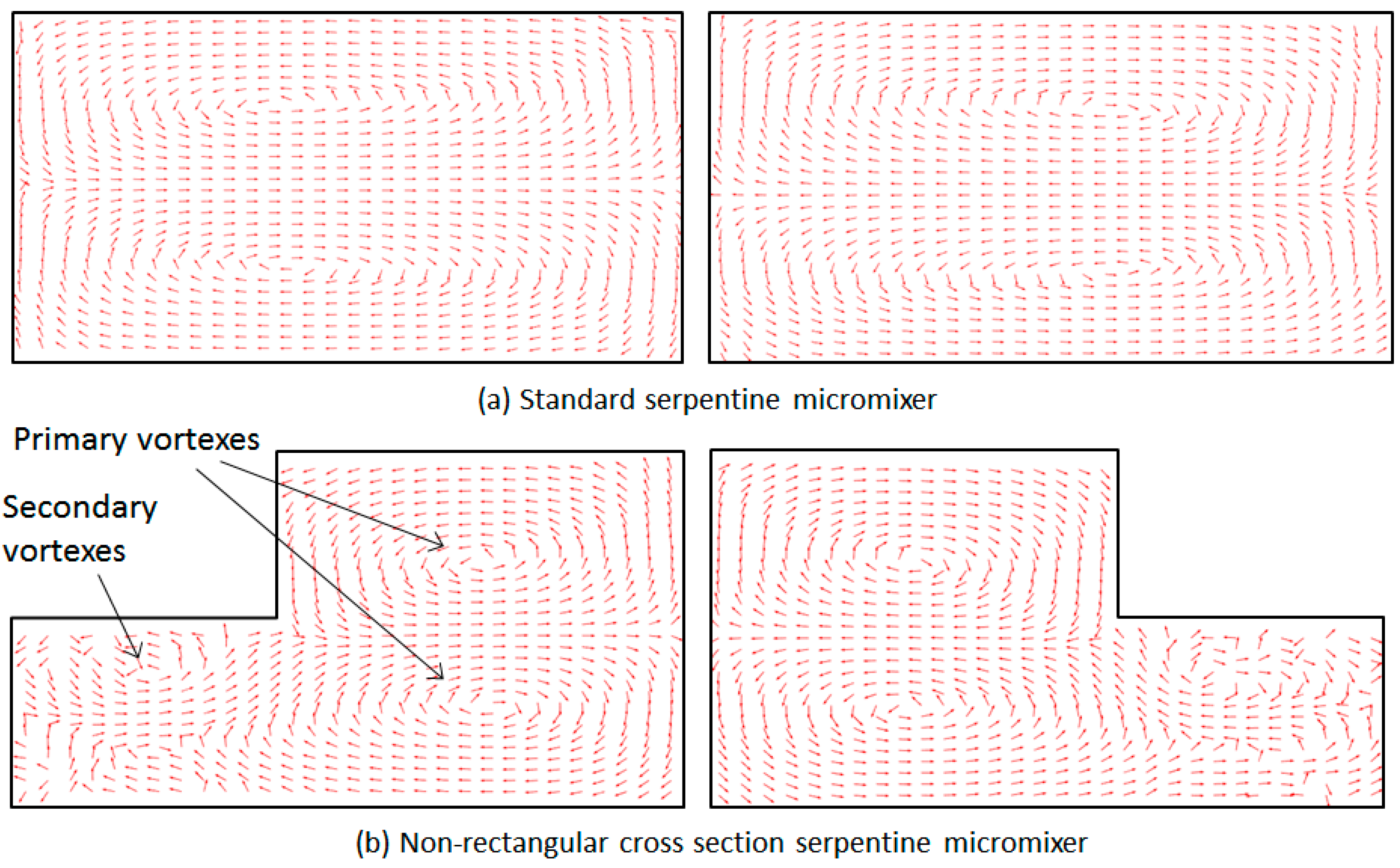
3. Numerical Model and Mixing Assessment
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Capretto, L.; Carugo, D.; Mazzitelli, S.; Nastruzzi, C.; Xunli, Z. Microfluidic and lab-on-a-chip preparation routes for organic nanoparticles and vesicular systems for nanomedicine applications. Adv. Drug Deliv. Rev. 2013, 65, 1496–1543. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.D.; Linder, V.; Sia, S.K. Lab-on-a-chip devices for global health: Past studies and future opportunities. Lab Chip 2007, 7, 41–57. [Google Scholar] [CrossRef] [PubMed]
- Fair, R.B. Digital microfluidics: Is a true lab-on-a-chip possible? Microfluid. Nanofluid. 2007, 3, 245–281. [Google Scholar] [CrossRef]
- Geong, G.S.; Chung, S.; Kim, C.B. Applications of micromixing technology. Analyst 2010, 135, 460–473. [Google Scholar] [CrossRef]
- Chiu, D.T.; deMello, A.J.; Di Carlo, D.; Doyle, P.S.; Hansen, C.; Maceiczyk, R.M.; Wootton, R.C.R. Small but perfectly formed? Successes, challenges, and opportunities for microfluidics in the chemical and biological sciences. Chem 2017, 2, 201–223. [Google Scholar] [CrossRef]
- Jayamohan, H.; Sant, H.J.; Gale, B.K. Applications of microfluidics for molecular diagnostics. Methods Mol. Biol. 2013, 949, 305–334. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Li, L.; Nichols, K.P.; Ismagilov, R.F. SlipChip. Lab Chip 2009, 9, 2286–2292. [Google Scholar] [CrossRef] [PubMed]
- Bamford, R.A.; Smith, A.; Metz, J.; Glover, G.; Titball, R.W.; Pagliara, S. Investigating the physiology of viable but non-culturable bacteria by microfluidics and time-lapse microscopy. BMC Biol. 2017, 15, 121. [Google Scholar] [CrossRef] [PubMed]
- Zilionis, R.; Nainys, J.; Veres, A.; Savova, V.; Zemmour, D.; Klein, A.M.; Mazutis, L. Single-cell barcoding and sequencing using droplet microfluidics. Nat. Protoc. 2017, 12, 44–73. [Google Scholar] [CrossRef] [PubMed]
- Junkin, M.; Tay, S. Microfluidic single-cell analysis for systems immunology. Lab Chip 2014, 14, 1246–1260. [Google Scholar] [CrossRef] [PubMed]
- Pagliara, S.; Franze, K.; McClain, C.R.; Wylde, G.W.; Fisher, C.L.; Franklin, R.J.M.; Kabla, A.J.; Keyser, U.F.; Chalut, K.J. Auxetic nuclei in embryonic stem cells exiting pluripotency. Nat. Mater. 2014, 13, 638–644. [Google Scholar] [CrossRef] [PubMed]
- Tsao, C.-W. Polymer microfluidics: Simple, low-cost fabrication process bridging academic lab research to commercialized production. Micromachines 2016, 7, 225. [Google Scholar] [CrossRef]
- Waheed, S.; Cabot, J.M.; Macdonald, N.P.; Lewis, T.; Guijt, R.M.; Paullab, B.; Breadmore, M.C. 3D printed microfluidic devices: Enablers and barriers. Lab Chip 2016, 11, 1993–2013. [Google Scholar] [CrossRef] [PubMed]
- Shan, C.; Chen, F.; Yang, Q.; Jiang, Z.; Hou, X. 3D multi-microchannel helical mixer fabricated by femtosecond laser inside fused silica. Micromachines 2018, 9, 29. [Google Scholar] [CrossRef]
- Sun, G.; Panpan, W.; Shenguang, G.; Lei, G.; Jinghua, Y.; Mei, Y. Photoelectrochemical sensor for pentachlorophenol on microfluidic paper-based analytical devicebased on the molecular imprinting technique. Biosens. Bioelectron. 2014, 56, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic mixing: A review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T. Micromixers: Fundamentals, Design and Fabrication, 2nd ed.; Elsevier: Oxford, UK, 2012; ISBN 978-1-43-773520-8. [Google Scholar]
- Nguyen, N.-T.; Wu, Z. Mixers—A review. J. Micromech. Microeng. 2005, 15, R1–R16. [Google Scholar] [CrossRef]
- Cai, G.; Xue, L.; Zhang, H.; Lin, J. A review of micromixers. Micromachines 2018, 8, 274. [Google Scholar] [CrossRef]
- Brandhoff, L.; Zirath, H.; Salas, M.; Haller, A.; Peham, J.; Wiesinger-Mayr, H.; Spittler, A.; Schnetz, G.; Lang, W.; Vellekoop, M.J. A multi-purpose ultrasonic streaming mixer for integrated magnetic bead ELISAs. J. Micromech. Microeng. 2015, 25, 104001. [Google Scholar] [CrossRef]
- Phan, H.V.; Coskun, M.B.; Sesen, M.; Pandraud, G.; Neild, A.; Alan, T. Vibrating membrane with discontinuities for rapid and efficient microfluidic mixing. Lab Chip 2015, 15, 4206–4216. [Google Scholar] [CrossRef] [PubMed]
- Nama, N.; Huang, P.-H.; Huang, T.J.; Constanzo, F. Investigation of micromixing by acoustically oscillated sharp-edges. Biomicrofluidics 2016, 10, 024124. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.V.; Tovar, A.R.; Lee, A.P. Lateral cavity acoustic transducer as an on-chip cell/particle microfluidic switch. Lab Chip 2012, 12, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.-H.; Ren, L.; Nama, N.; Li, S.; Li, P.; Yao, X.; Cuento, R.A.; Wei, C.-H.; Chen, Y.; Xie, Y.; et al. An acoustofluidic sputum liquefier. Lab Chip 2015, 15, 3125–3131. [Google Scholar] [CrossRef] [PubMed]
- Destgeer, G.; Im, S.; Ha, B.H.; Jung, J.H.; Ansari, M.A.; Sung, H.J. Adjustable, rapidly switching microfluidic gradient generation using focused travelling surface acoustic wave. Appl. Phys. Lett. 2014, 104, 023506. [Google Scholar] [CrossRef]
- Krishnaveni, T.; Renganathan, T.; Picardo, J.R.; Pushpavanam, S. Numerical study of enhanced mixing in pressure-driven flows in microchannels using a spatially periodic electric field. Phys. Rev. E 2017, 96, 033117. [Google Scholar] [CrossRef] [PubMed]
- Ryu, K.S.; Shaikh, K.; Goluch, E.; Fana, Z.; Liu, C. Micro magnetic stir-bar mixer integrated with parylene microfluidic channels. Lab Chip 2004, 6, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Abbas, Y.; Miwa, J.; Zengerle, R.; von Stetten, F. Active continuous-flow micromixer using an external braille pin actuator array. Micromachines 2013, 4, 80–89. [Google Scholar] [CrossRef]
- Tofteberg, T.; Skolimowski, M.; Andreassen, E.; Geschke, O. A novel passive micromixer: Lamination in a planar channel system. Microfluid. Nanofluid. 2010, 8, 209–215. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Kee, S.P.; Gavriilidis, A. Design and characterization of the staggered herringbone mixer. Chem. Eng. J. 2008, 142, 109–121. [Google Scholar] [CrossRef]
- Fodor, P.S.; Kaufman, M. The evolution of mixing in the staggered herring bone micromixer. Mod. Phys. Lett. B 2011, 25, 1111–1125. [Google Scholar] [CrossRef]
- Alam, A.; Afzal, A.; Kim, K.-Y. Mixing performance of a planar micromixer with circular obstructions in a curved microchannel. Chem. Eng. Res. Des. 2014, 92, 423–434. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, S.W.; Kwon, T.H.; Lee, S.S. A barrier embedded chaotic micromixer. J. Micromech. Microeng. 2004, 15, 798–805. [Google Scholar] [CrossRef]
- Scherr, T.; Quitadamo, C.; Tesvich, P.; Park, D.S.; Tiersch, T.; Hayes, D.; Choi, J.W.; Nandakumar, K.; Monroe, W.T. A planar microfluidic mixer based on logarithmic spirals. J. Micromech. Microeng. 2012, 22, 055019. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, T. A novel design for passive misscromixers based on topology optimization method. Biomed. Microdevices 2016, 18, 57. [Google Scholar] [CrossRef] [PubMed]
- Shamloo, A.; Madadelahi, M.; Akbari, A. Numerical simulation of centrifugal serpentine micromixers and analyzing mixing quality parameters. Chem. Eng. Process. Process Intensif. 2016, 104, 243–252. [Google Scholar] [CrossRef]
- Dean, W.R. Note on the motion of a fluid in a curved pipe. Philos. Mag. 1927, 4, 208–223. [Google Scholar] [CrossRef]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beebe, D.J. Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Araci, I.E.; Robles, M.; Quake, S.R. A reusable microfluidic device provides continuous measurement capability and improves the detection limit of digital biology. Lab Chip 2016, 16, 1573–1578. [Google Scholar] [CrossRef] [PubMed]
- Mengeaud, V.; Josserand, J.; Girasult, H.H. Mixing processes in a zigzag microchannel: Finite element simulation and optical study. Anal. Chem. 2002, 74, 4279–4286. [Google Scholar] [CrossRef] [PubMed]
- Alam, A.; Kim, K.Y. Analysis of mixing in a curved microchannel with rectangular grooves. Chem. Eng. J. 2012, 181–182, 708–716. [Google Scholar] [CrossRef]
- Cook, K.J.; Fan, Y.; Hassan, I. Mixing evaluation of a passive scaled-up serpentine micromixer with slanted grooves. J. Fluids Eng. 2013, 135, 081102. [Google Scholar] [CrossRef]
- Javaid, M.U.; Cheema, T.A.; Park, C.W. Analysis of passive mixing in a serpentine microchannel with sinusoidal side walls. Micromachines 2018, 9, 8. [Google Scholar] [CrossRef]
- Hossain, S.; Kim, K.-Y. Mixing performance of a serpentine micromixer with non-aligned inputs. Micromachines 2015, 6, 842–854. [Google Scholar] [CrossRef]
- Sayah, A.; Gijs, M.A.M. Understanding the mixing process in 3D microfluidic nozzle/diffuser systems: Simulations and experiments. J. Micromech. Microeng. 2016, 26, 115017. [Google Scholar] [CrossRef]
- Fodor, P.S.; Itomlenskis, M.; Kaufman, M. Assessment of mixing in passive microchannels with fractal surface patterning. Eur. Phys. J. Appl. Phys. 2009, 47, 31301. [Google Scholar] [CrossRef]
- D’Alessandro, J.; Fodor, P.S. Use of grooved microchannels to improve the performance of membrane-less fuel cells. Fuel Cells 2014, 14, 818–826. [Google Scholar] [CrossRef]
- Jiang, F.; Drese, K.S.; Hardt, S.; Küpper, M.; Schönfeld, F. Helical flows and chaotic mixing in curved micro channels. AIChE J. 2004, 50, 2297–2305. [Google Scholar] [CrossRef]
- Camesasca, M.; Kaufman, M.; Manas-Zloczower, I. Quantifying fluid mixing with the Shannon entropy. Macromol. Theory Simul. 2006, 15, 595–607. [Google Scholar] [CrossRef]
- Fodor, P.S.; Vyhnalek, B.; Kaufman, M. Entropic Evaluation of Dean Flow Micromixers. In Proceedings of the 2013 COMSOL Conference, Boston, MA, USA, 9–11 October 2013; Available online: https://www.comsol.com/paper/entropic-evaluation-of-dean-flow-micromixers-15053 (accessed on 21 January 2018).
- Alemaskin, K.; Manas-Zloczover, I.; Kaufman, M. Entropic analysis of color homogeneity. Polym. Eng. Sci. 2005, 45, 1031–1038. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. Soft lithography. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clark, J.; Kaufman, M.; Fodor, P.S. Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section. Micromachines 2018, 9, 107. https://doi.org/10.3390/mi9030107
Clark J, Kaufman M, Fodor PS. Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section. Micromachines. 2018; 9(3):107. https://doi.org/10.3390/mi9030107
Chicago/Turabian StyleClark, Joshua, Miron Kaufman, and Petru S. Fodor. 2018. "Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section" Micromachines 9, no. 3: 107. https://doi.org/10.3390/mi9030107
APA StyleClark, J., Kaufman, M., & Fodor, P. S. (2018). Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section. Micromachines, 9(3), 107. https://doi.org/10.3390/mi9030107