Research and Development of a 3D Jet Printer for High-Viscosity Molten Liquids
Abstract
:1. Introduction
2. Principle of the 3D Jet Printer
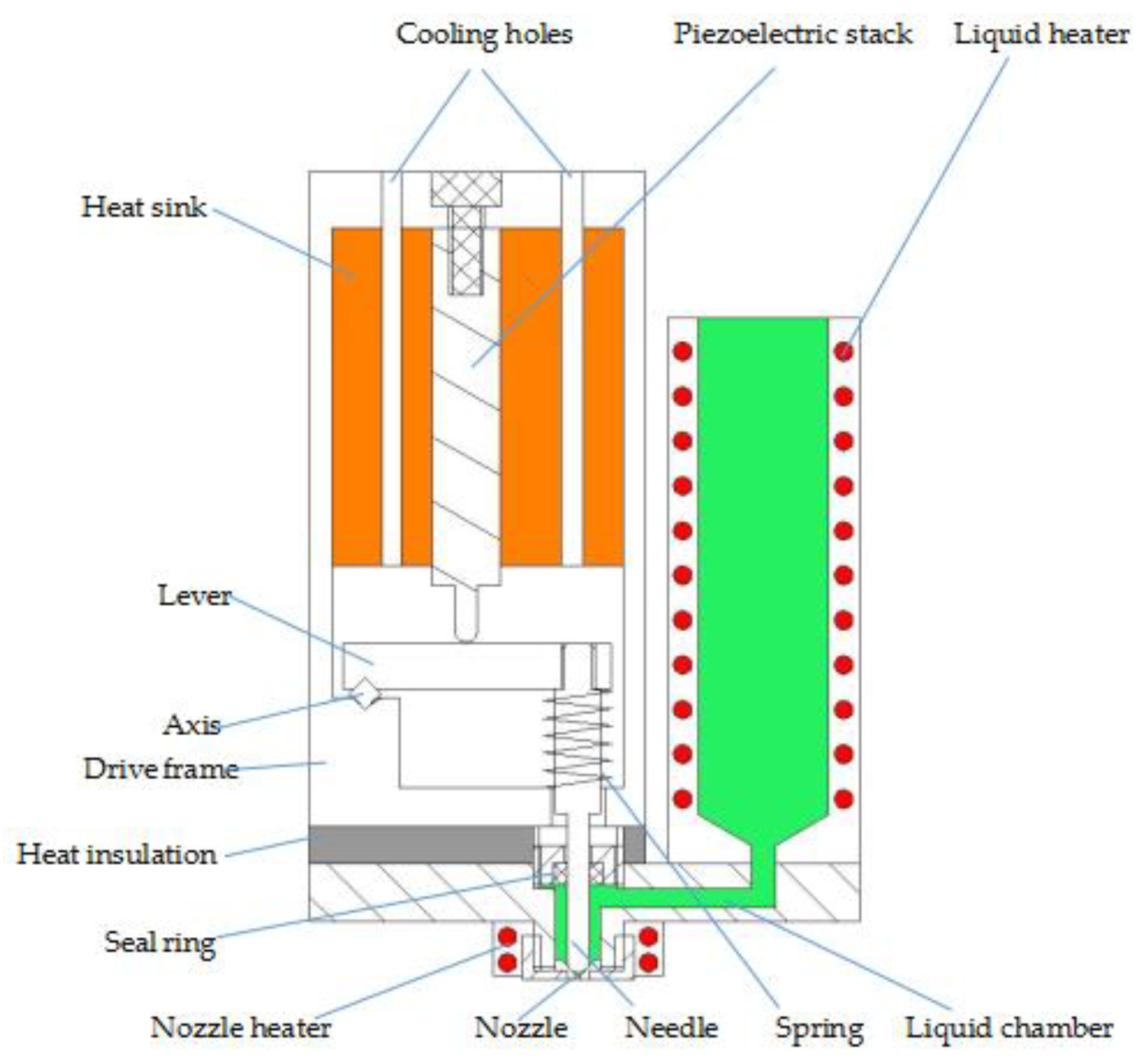
2.1. Structure of the Device
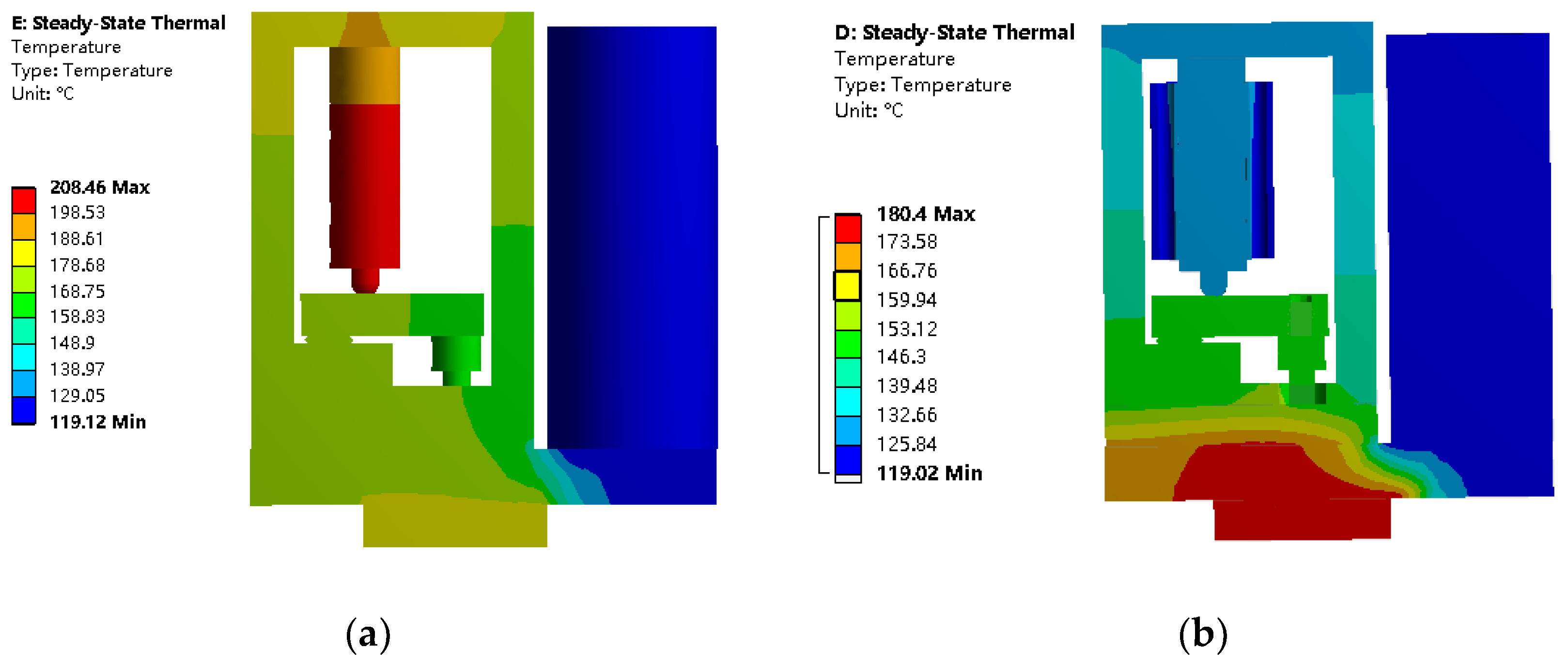
2.2. Thermodynamic Analysis
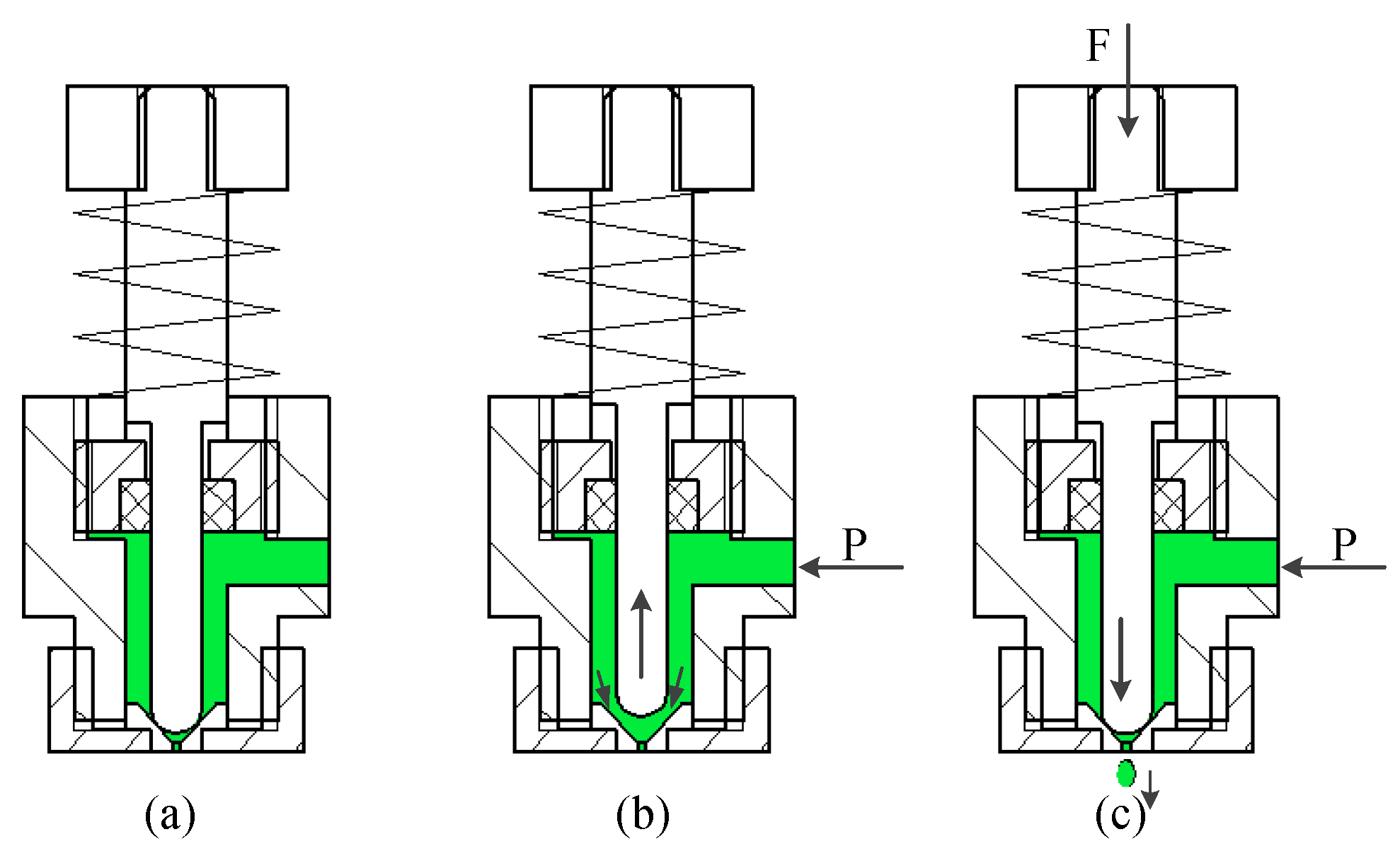
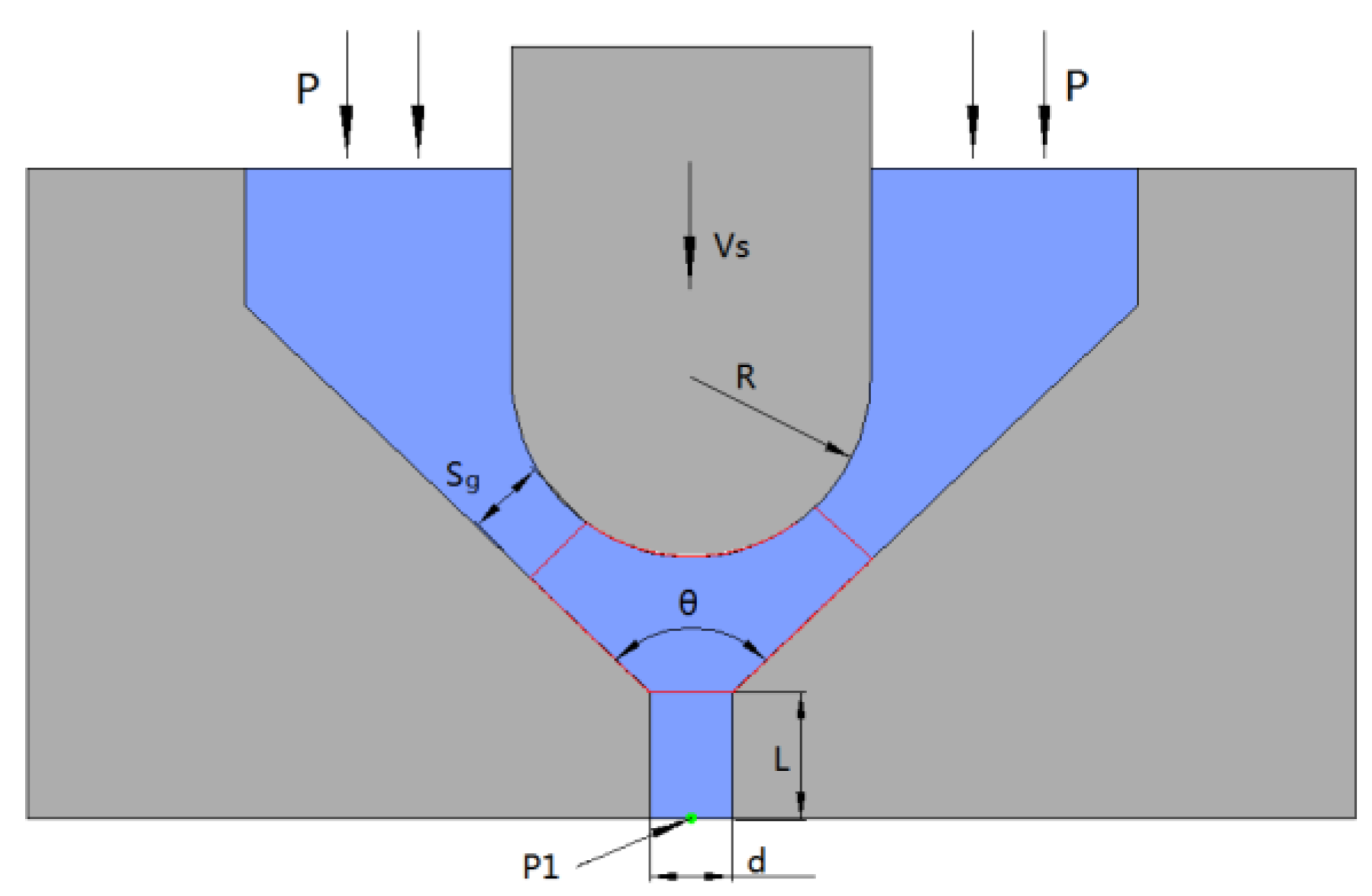
2.3. Theoretical Analysis of Jetting
2.4. Analysis of Jetting
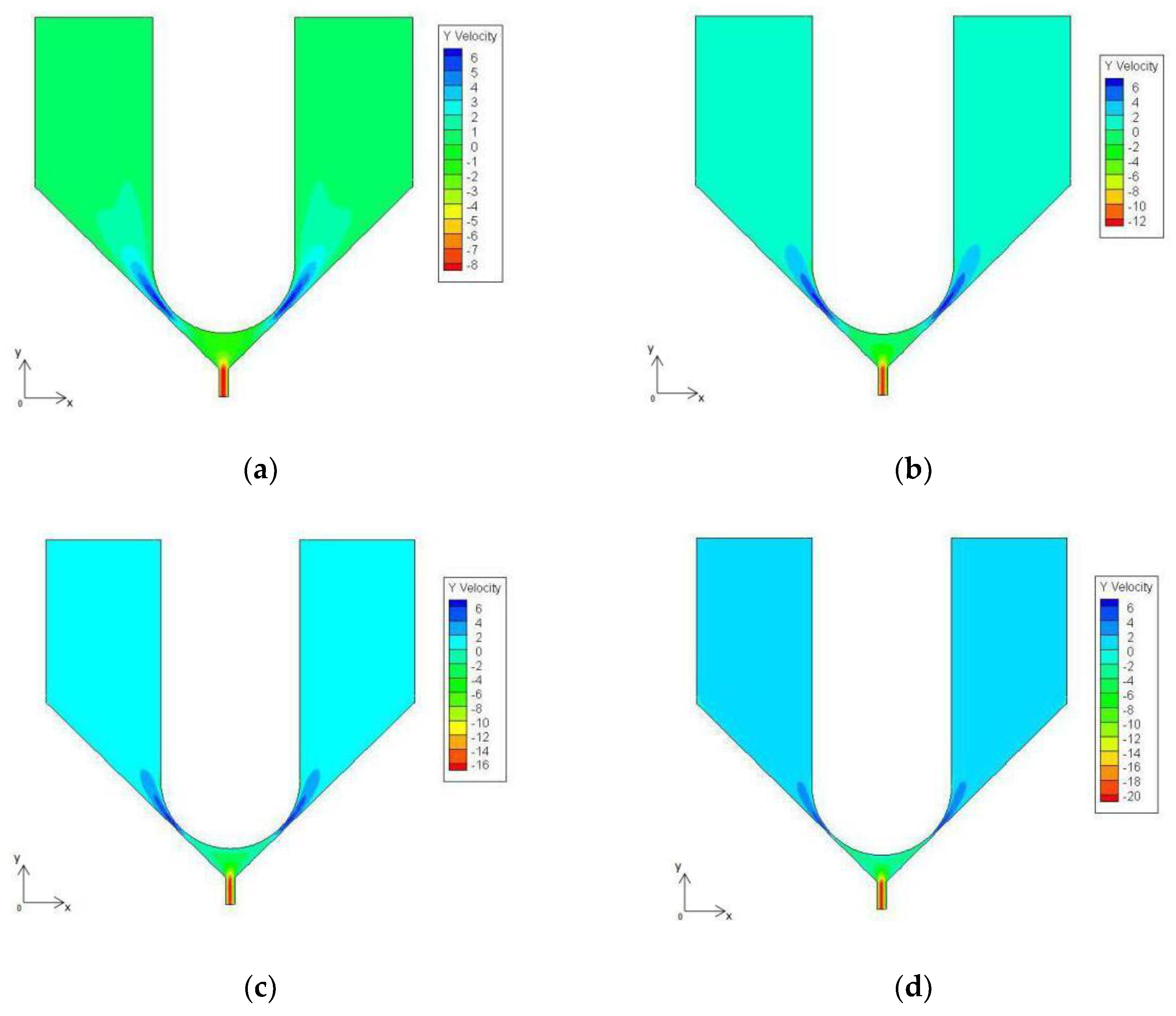
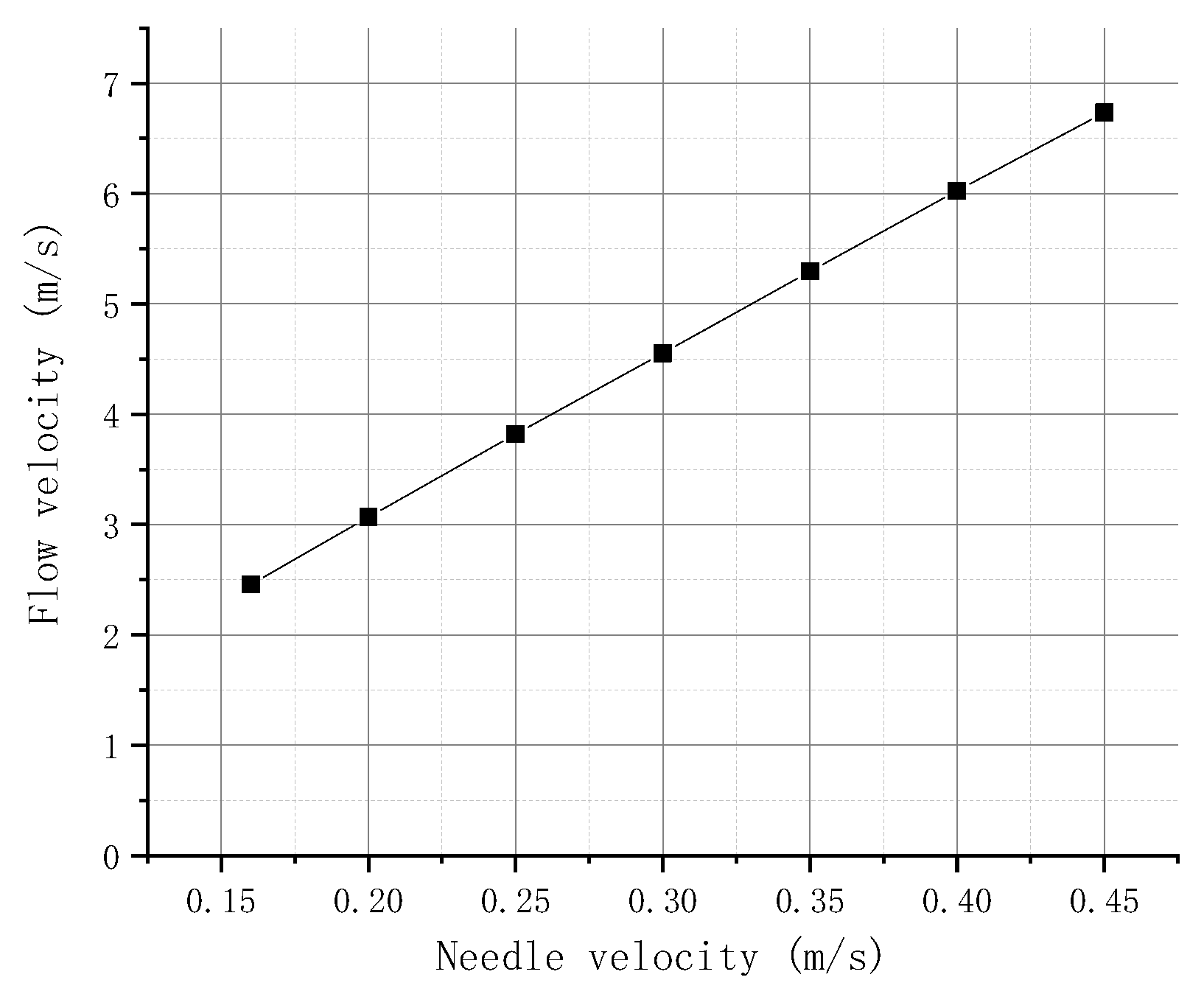
2.4.1. Simulation of the Needle Velocity
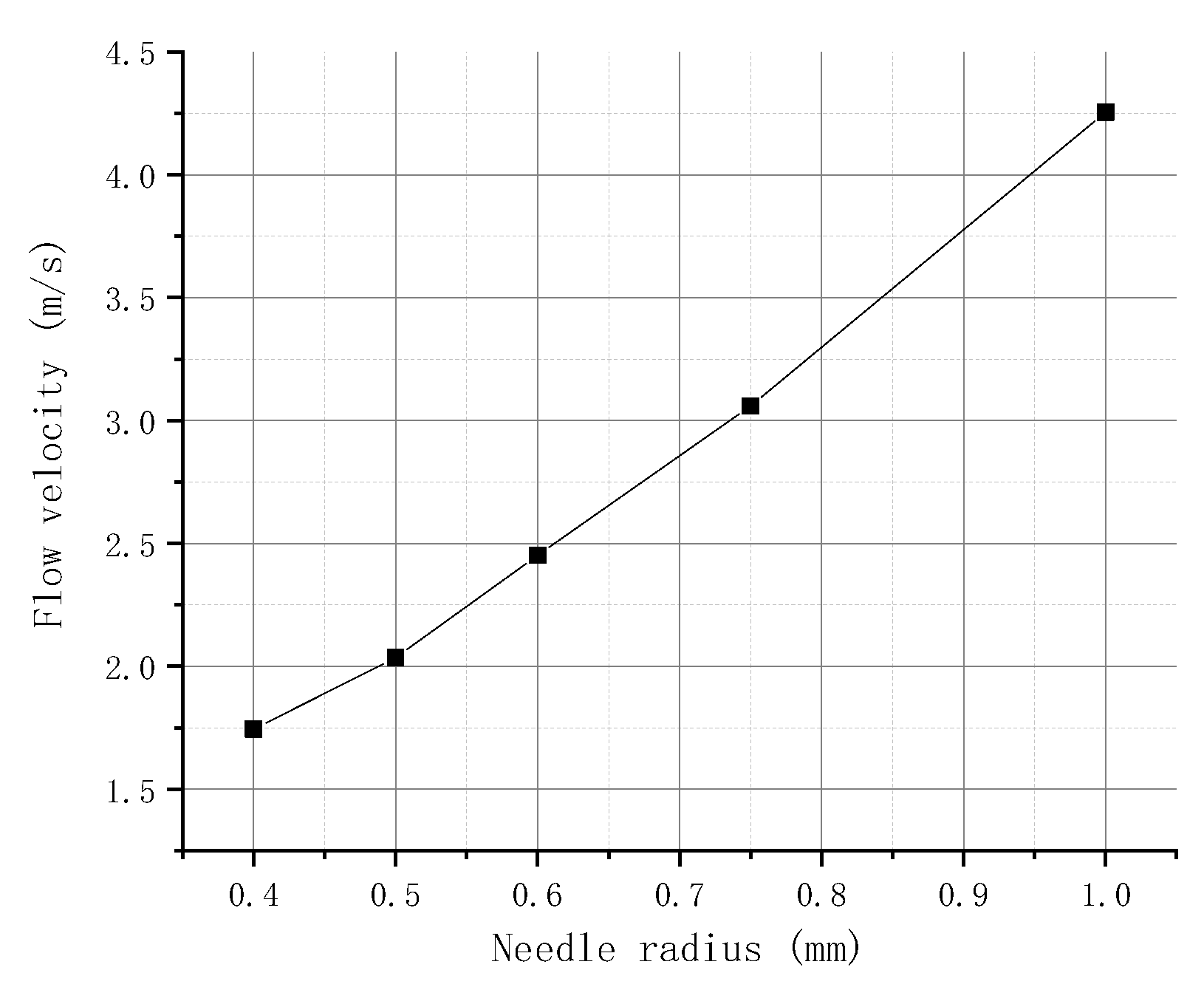
2.4.2. Simulation of the Needle Radius
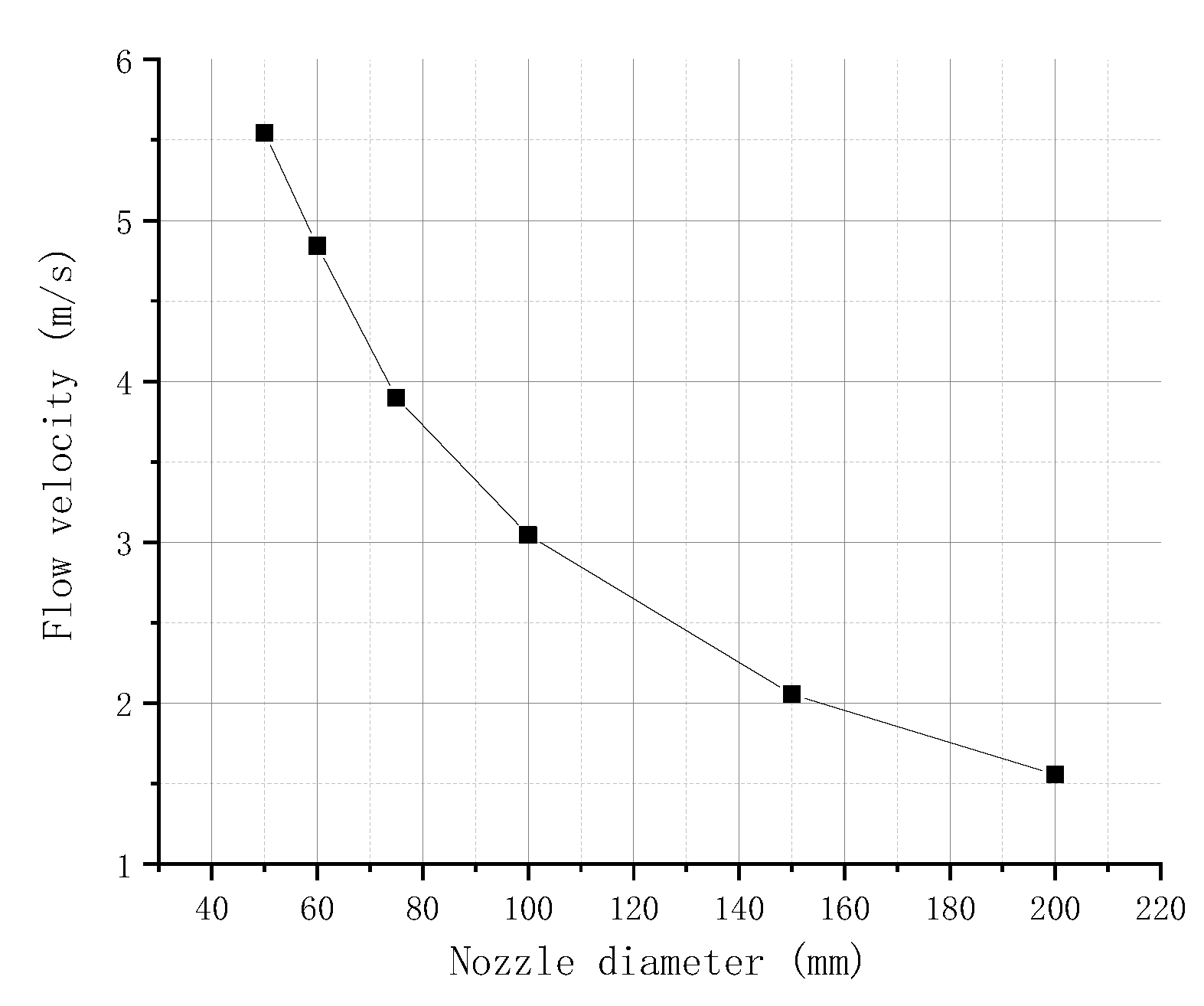
2.4.3. Simulation of the Nozzle Diameter
2.4.4. Simulation of the Nozzle Taper Angle
3. Experiment and Discussion
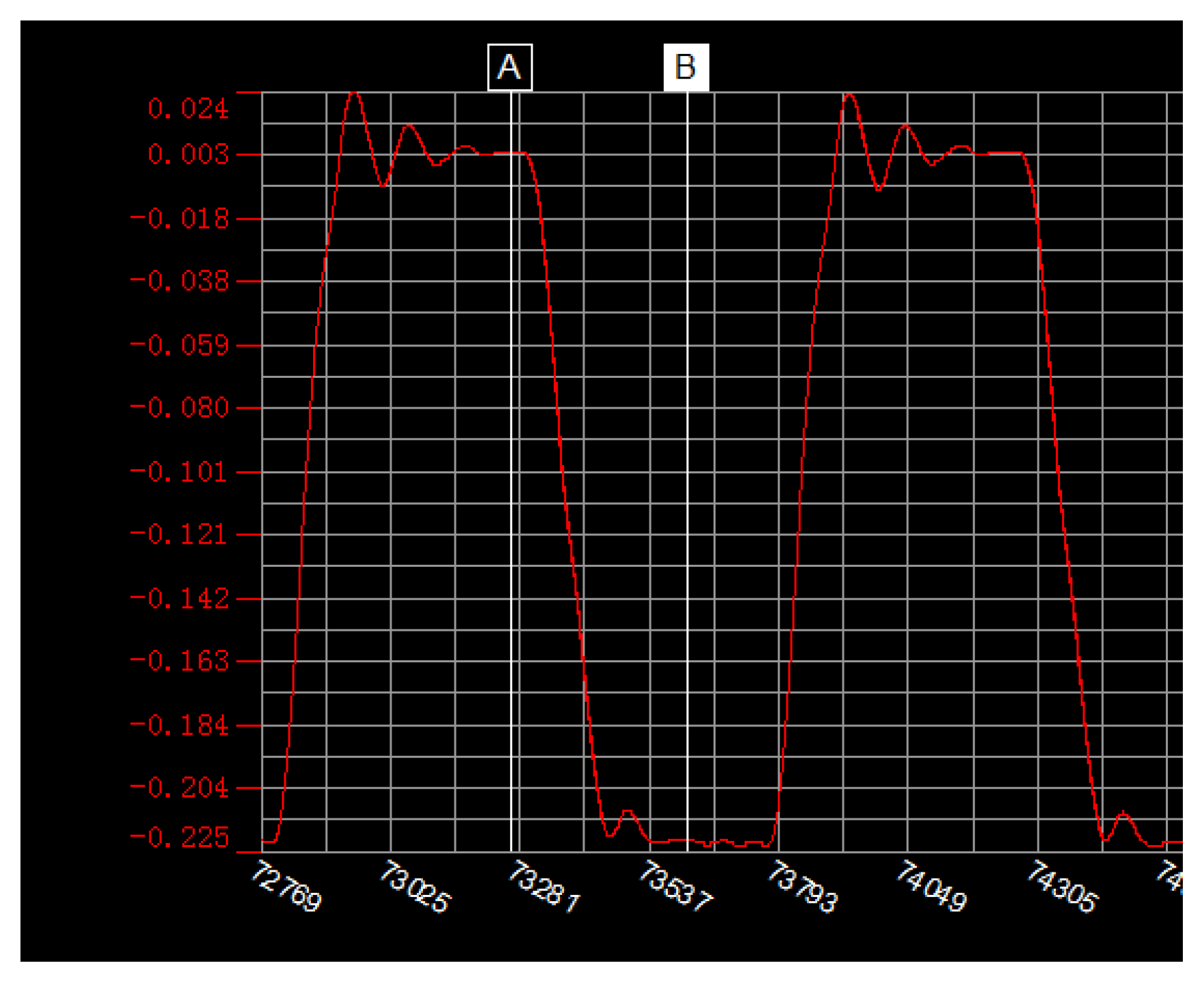
3.1. Experiment on the Needle Velocity
3.2. Experiment on Influencing Factors of Injection
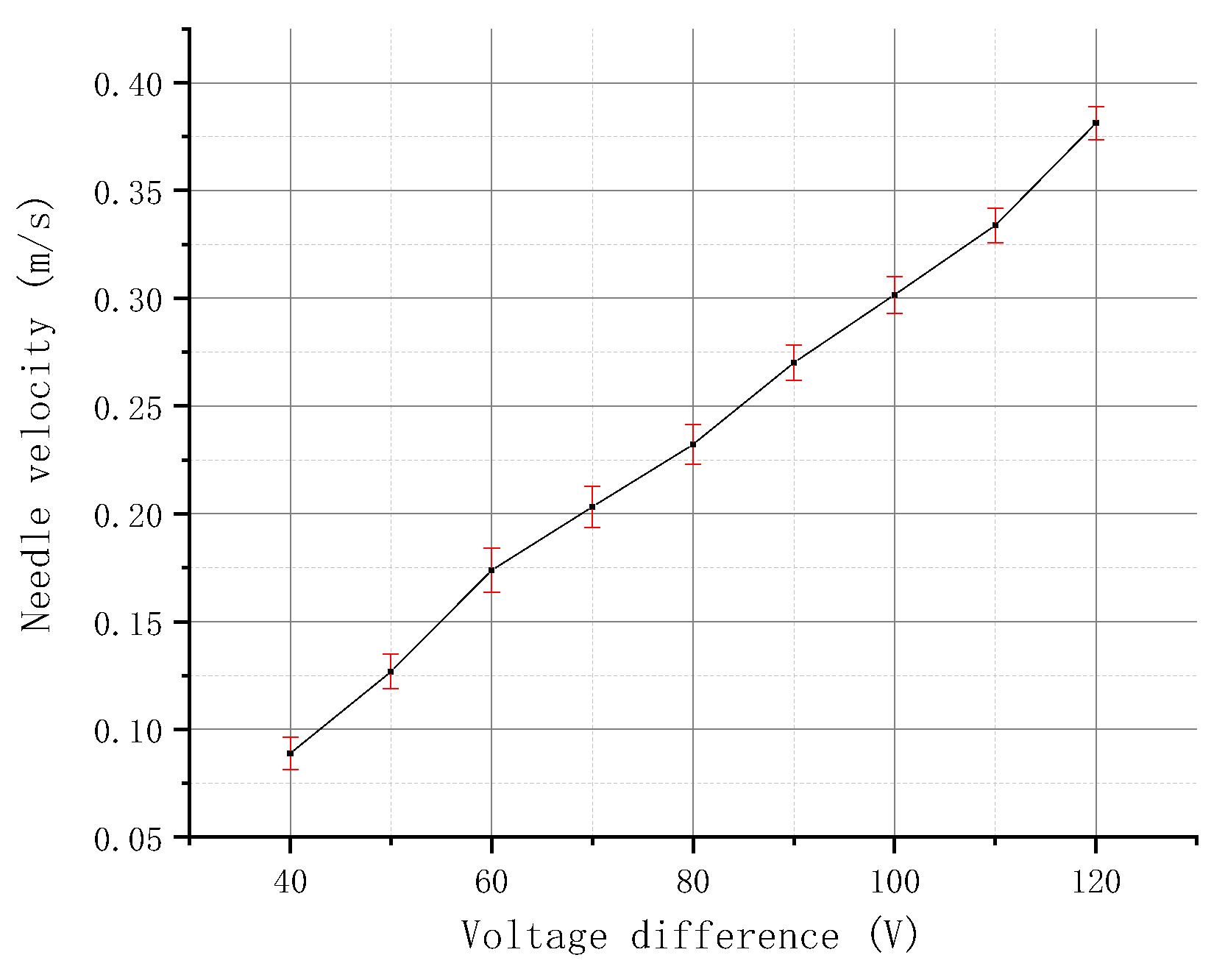
3.2.1. Experiment on the Voltage Difference
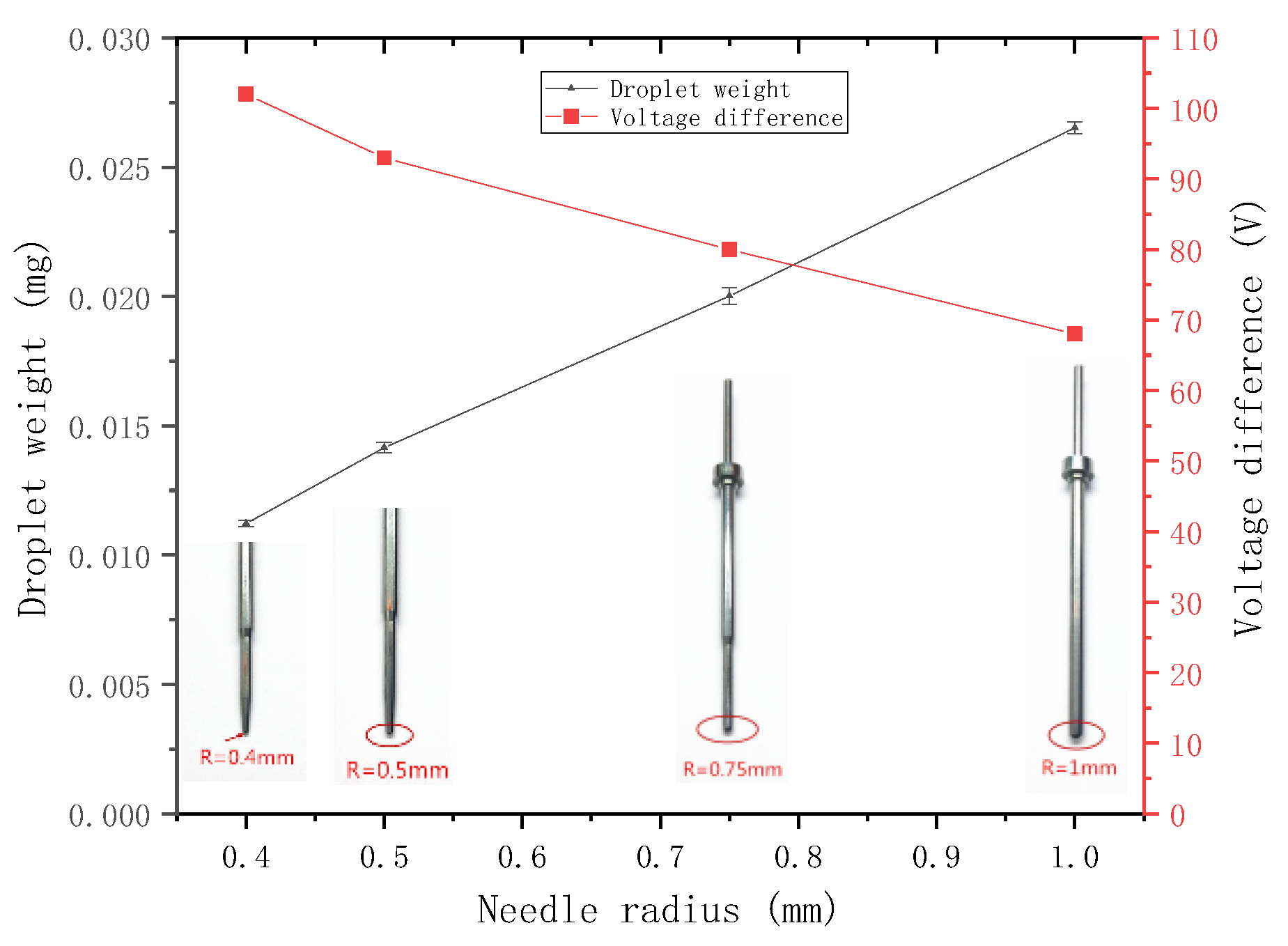
3.2.2. Experiment on the Needle Radius
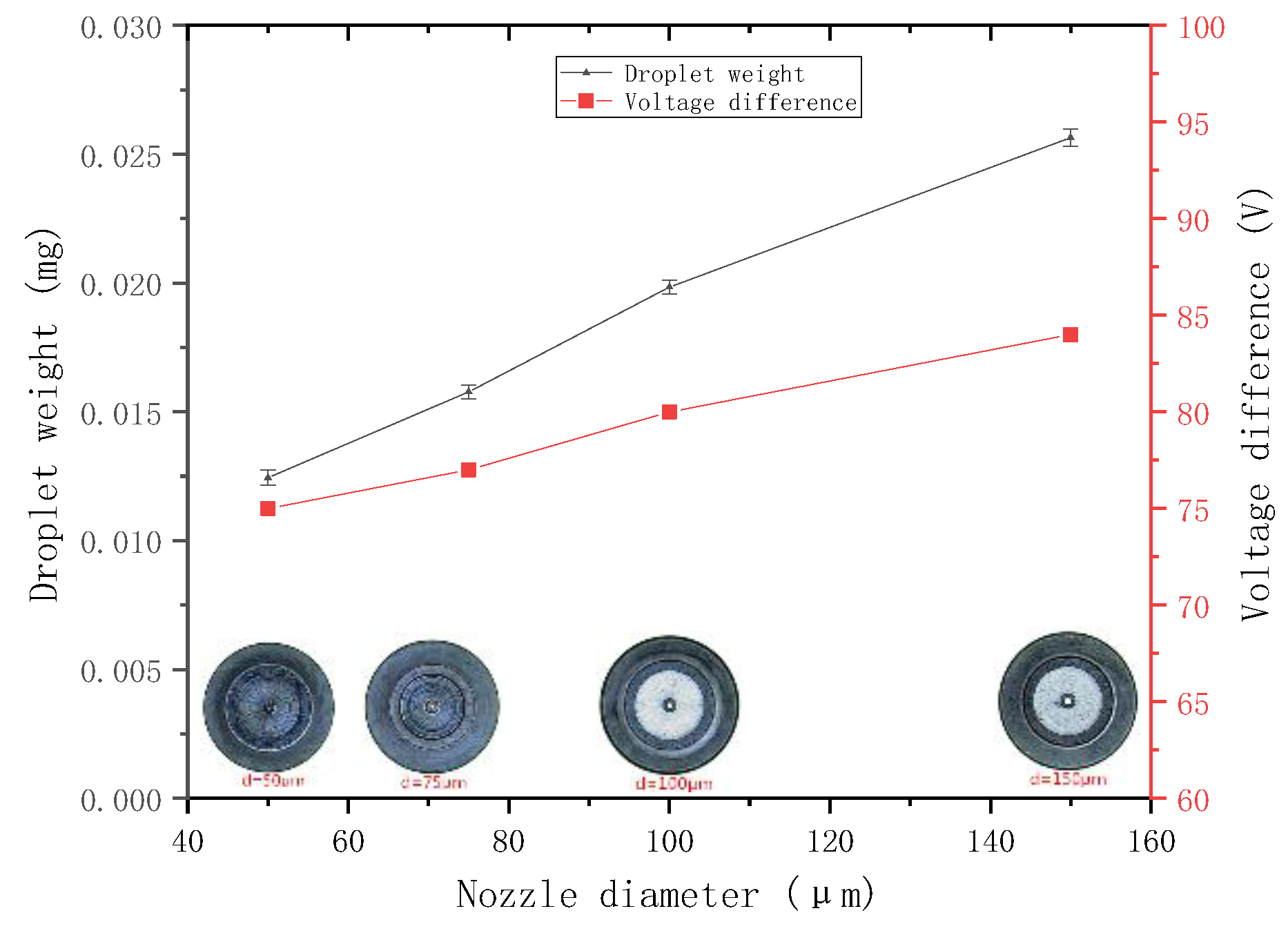
3.2.3. Experiment on the Nozzle Diameter
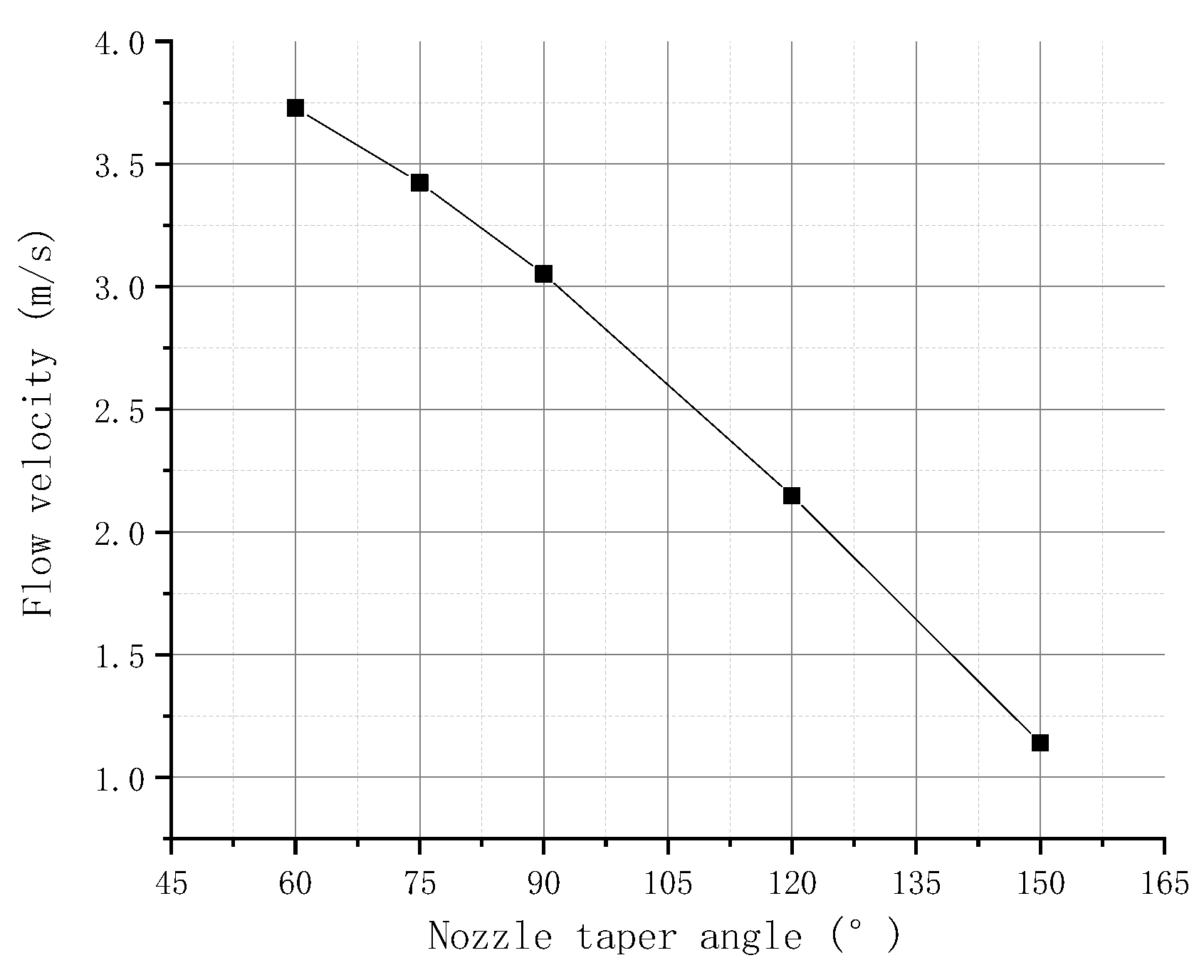
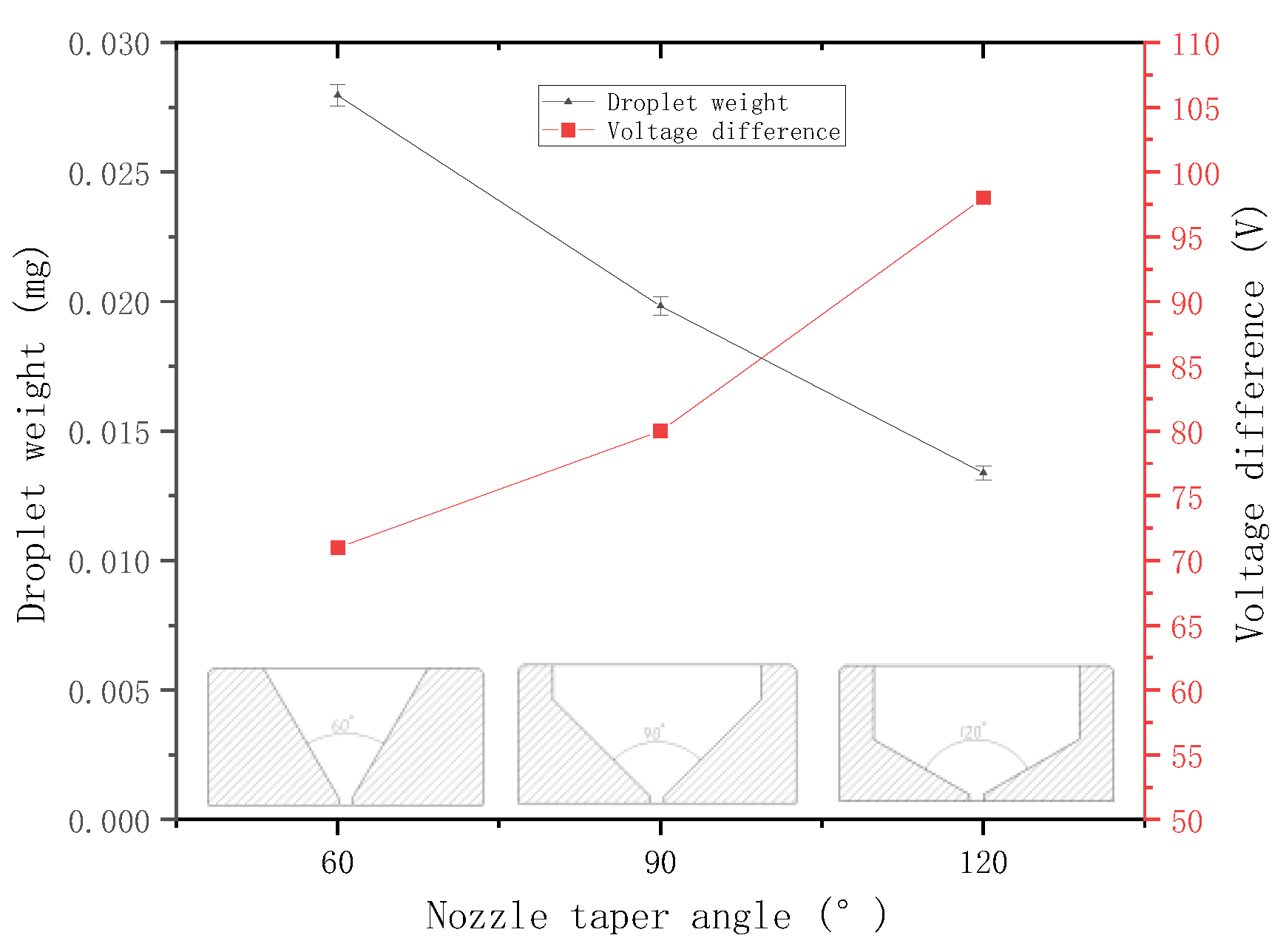
3.2.4. Experiment on the Nozzle Taper Angle
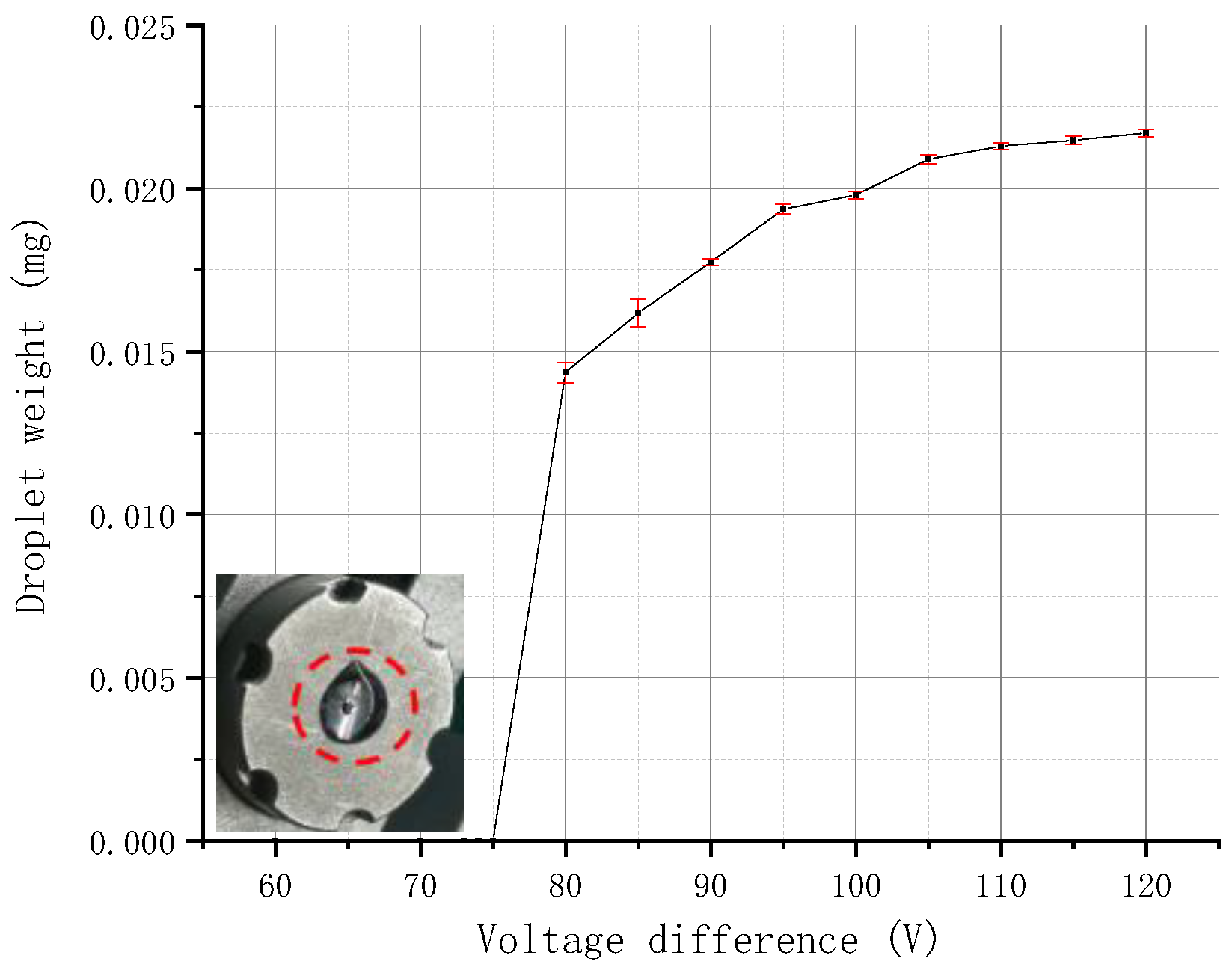
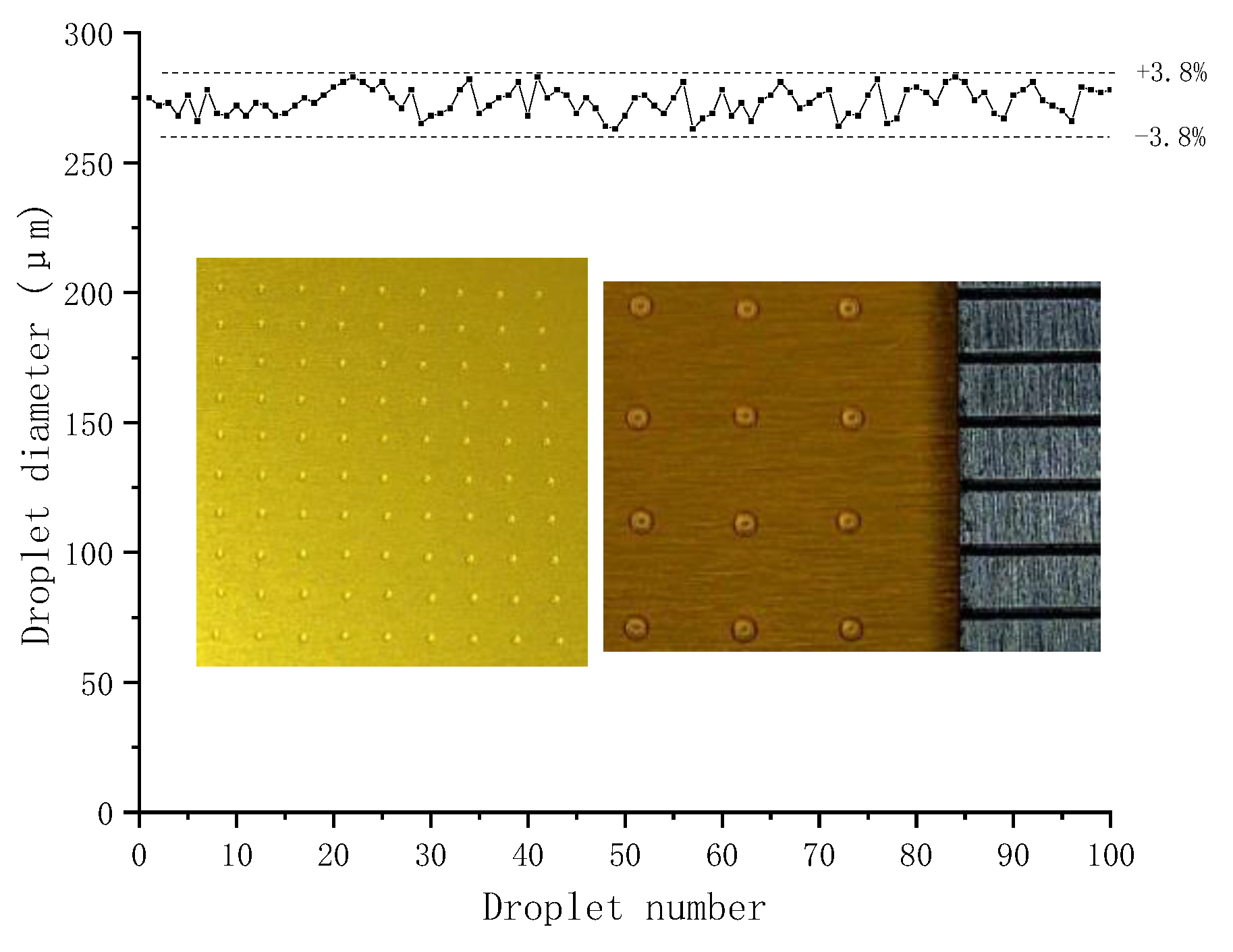
3.3. Minimum Droplet and Consistency Analysis
4. Conclusions
- The defect that the piezoelectric stacks cannot operate in high-temperature conditions can be solved by the cooling mechanism designed in this paper.
- The experiments verified that the velocity of the needle is positively correlated with the voltage difference of the piezoelectric stacks.
- Through simulation analysis and experimental research, the ejection capacity of the jet printer is positively correlated with the velocity and the radius of the needle and negatively correlated with the diameter and taper angle of the nozzle.
- Through experimental comparison, by using a needle with a radius of 0.4 mm, a nozzle with a diameter of 50 μm, a taper angle of 90°, a supply pressure of 0.05 Mpa, and a voltage difference of 98 V, a molten liquid with a viscosity of 8000 cps can be sprayed with the minimum average droplet diameter of 275 μm, and the variation of the droplet diameter was within ±3.8%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muth, J.T.; Vogt, D.M.; Truby, R.L.; Mengüç, Y.; Kolesky, D.B.; Wood, R.J.; Lewis, J.A. 3D printing: Embedded 3D printing of strain sensors within highly stretchable elastomers. Adv. Mater. 2014, 26, 6307–6312. [Google Scholar] [CrossRef] [PubMed]
- Shangguan, H.; Kang, J.; Yi, J.; Zhang, X.; Wang, X.; Wang, H.; Huang, T. The design of 3D-printed lattice-reinforced thickness-varying shell molds for castings. Materials 2018, 11, 535. [Google Scholar] [CrossRef] [PubMed]
- Comina, G.; Suska, A.; Filippini, D. 3D printed unibody lab-on-a-chip: Features survey and check-valves integration. Micromachines 2015, 6, 437–451. [Google Scholar] [CrossRef]
- Park, S.; Kwon, J.; Lim, J.; Shin, W.; Lee, Y.; Lee, H.; Kim, H.J.; Han, S.; Yeo, J.; Ko, S.H. Micropatterning of metal nanoparticle ink by laser-induced thermocapillary flow. Nanomaterials 2018, 8, 645. [Google Scholar] [CrossRef] [PubMed]
- Nazarov, A.; Skornyakov, I.; Shishkovsky, I. The setup design for selective laser sintering of high-temperature polymer materials with the alignment control system of layer deposition. Machines 2018, 6, 11. [Google Scholar] [CrossRef]
- Thrimurthulu, K.; Pandey, P.M.; Reddy, N.V. Optimum part deposition orientation in fused deposition modeling. Int. J. Mach. Tools Manuf. 2004, 44, 585–594. [Google Scholar] [CrossRef]
- Singamneni, S.; Smith, D.; Leguen, M.J.; Truong, D. Extrusion 3D printing of polybutyrate-adipate-terephthalate-polymer composites in the pellet form. Polymers 2018, 10, 922. [Google Scholar] [CrossRef]
- Tao, Y.; Malshe, A.P.; Brown, W.D. Selective bonding and encapsulation for wafer-level vacuum packaging of mems and related micro systems. Microelectron. Reliab. 2004, 44, 251–258. [Google Scholar] [CrossRef]
- Cima, M.; Sachs, E.; Fan, T.; Bredt, J.F.; Michaels, S.P.; Khanuja, S.; Lauder, A.; Lee, S.J.J.; Brancazio, D.; Curodeau, A. Three-Dimensional Printing Techniques. U.S. Patent 5,204,055, 20 April 1993. [Google Scholar]
- Shu, X.Y.; Zhang, H.H.; Liu, H.Y.; Dan, X.; Xiao, J.F. Experimental study on high viscosity fluid micro-droplet jetting system. Sci. China Technol. Sci. 2010, 53, 182–187. [Google Scholar] [CrossRef]
- Hayes, D.J.; Cox, W.R. Micro-jet printing of polymers for electronics manufacturing. In Proceedings of the International Conference on Adhesive Joining and Coating Technology in Electronics Manufacturing, Binghamton, NY, USA, 28–30 September 1998; pp. 168–173. [Google Scholar]
- Orme, M.; Liu, Q.; Smith, R. Molten aluminum micro-droplet formation and deposition for advanced manufacturing applications. Alum. Trans. 2000, 3, 95–103. [Google Scholar]
- Usuda, H. Droplet Jetting Apparatus, Method of Operating Droplet Jetting Apparatus, and Device Manufacturing Method. U.S. Patent 7,255,420, 14 August 2007. [Google Scholar]
- Lu, D.; Dong, W.; Fu, Y.; Li, Y.; Zhao, L.; Xu, F.; Tan, Y. Preparation technology of micron-sized sphere sn-pb particles by pulsed orifice ejection method. Weld. Join. 2013, 11, 010. [Google Scholar]
- Yao, Y.; Gao, S.; Cui, C. Rapid prototyping based on uniform droplet spraying. J. Mater. Process. Tech. 2004, 146, 389–395. [Google Scholar]
- Lee, T.M.; Kang, T.G.; Yang, J.S.; Jo, J.; Kim, K.Y.; Choi, B.O.; Kim, D.S. Drop-on-demand solder droplet jetting system for fabricating microstructure. IEEE Trans. Electron. Packag. Manuf. 2008, 31, 202–210. [Google Scholar]
- Lee, T.M.; Kang, T.G.; Yang, J.S.; Jo, J.D.; Kim, K.Y.; Choi, B.O.; Kim, D.S. 3D metal microstructure fabrication using a molten metal DoD inkjet system. In Proceedings of the Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1637–1640. [Google Scholar]
- Partovi, F.Y. An analytic model to quantify strategic service vision. Int. J. Serv. Ind. Manag. 2001, 12, 476–499. [Google Scholar] [CrossRef]
- Hongwei, Z. Basic Theory and Experimental Research of Ruler-Type Piezoelectric Actuator; Jilin University: Changchun, China, 2006. [Google Scholar]
- Wehl, W.; Wild, J.; Lemmermeyer, B. A Drop-on-demand metal jet printer for wafer bumping. In Proceedings of the 14th European Microelectronics and Packaging Conference & Exhibition, Friedrichshafen, Germany, 23–25 June 2003; pp. 1–6. [Google Scholar]



| Influencing Factor | Droplet Weight | Injection Capacity |
|---|---|---|
| voltage difference | ↑ | ↑ |
| Needle radius | ↑ | ↑ |
| Nozzle diameter | ↑ | ↓ |
| Nozzle taper angle | ↓ | ↓ |
| Serial Number | Needle Radius (mm) | Taper Angle (°) | Nozzle Diameter (μm) | Minimum Voltage Difference (V) | Supply Pressure (MPa) | Droplet Diameter (μm) |
|---|---|---|---|---|---|---|
| 1 | 0.4 | 60 | 50 | 90 | 0.05 | 295 |
| 2 | 0.4 | 90 | 50 | 98 | 0.05 | 275 |
| 3 | 0.4 | 120 | 50 | 120 | 0.05 | - |
| 4 | 0.5 | 120 | 50 | 112 | 0.05 | 305 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Gu, S.; Liu, J.; Tian, H.; Lv, Q. Research and Development of a 3D Jet Printer for High-Viscosity Molten Liquids. Micromachines 2018, 9, 554. https://doi.org/10.3390/mi9110554
Yang Y, Gu S, Liu J, Tian H, Lv Q. Research and Development of a 3D Jet Printer for High-Viscosity Molten Liquids. Micromachines. 2018; 9(11):554. https://doi.org/10.3390/mi9110554
Chicago/Turabian StyleYang, Yang, Shoudong Gu, Jianfang Liu, Hongyu Tian, and Qingqing Lv. 2018. "Research and Development of a 3D Jet Printer for High-Viscosity Molten Liquids" Micromachines 9, no. 11: 554. https://doi.org/10.3390/mi9110554
APA StyleYang, Y., Gu, S., Liu, J., Tian, H., & Lv, Q. (2018). Research and Development of a 3D Jet Printer for High-Viscosity Molten Liquids. Micromachines, 9(11), 554. https://doi.org/10.3390/mi9110554




