Numerical Demonstration of In-Tube Liquid-Column Migration Driven by Photoisomerization
Abstract
1. Introduction
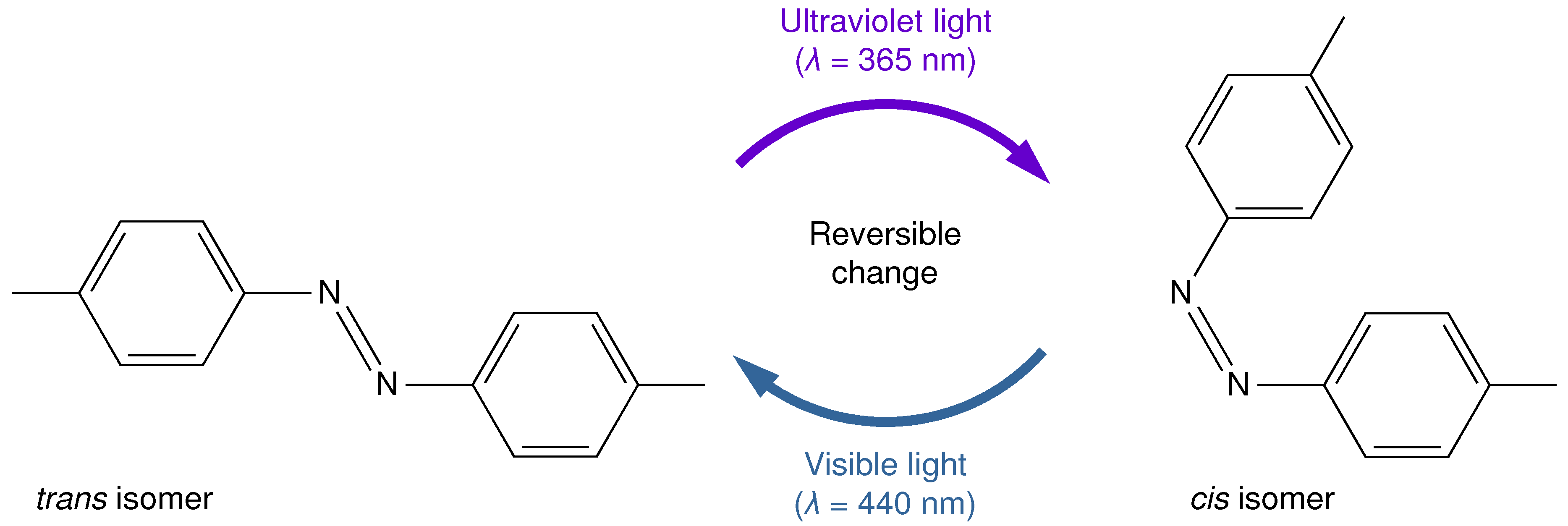
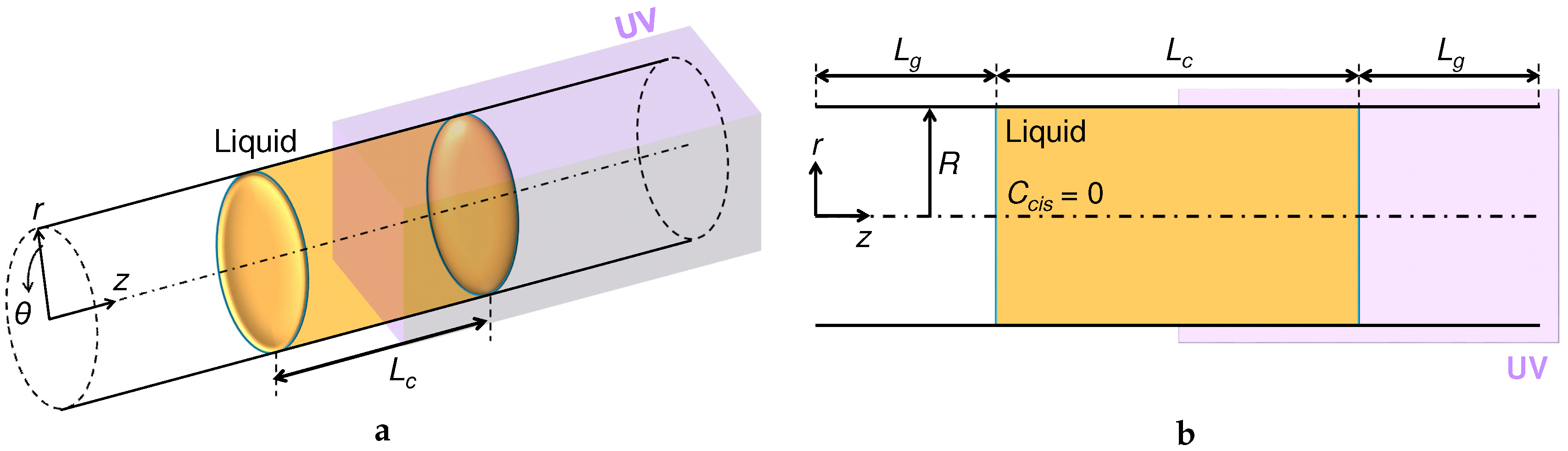
2. Problem Setting: A Photoisomerizable Liquid Column in a Tube
3. Numerical Procedure
3.1. Governing Equations for Fluid Motions
3.2. Representation of Cis-/Trans-Isomer Liquid
3.3. Transport of the Cis/Trans Isomer with the CST Method
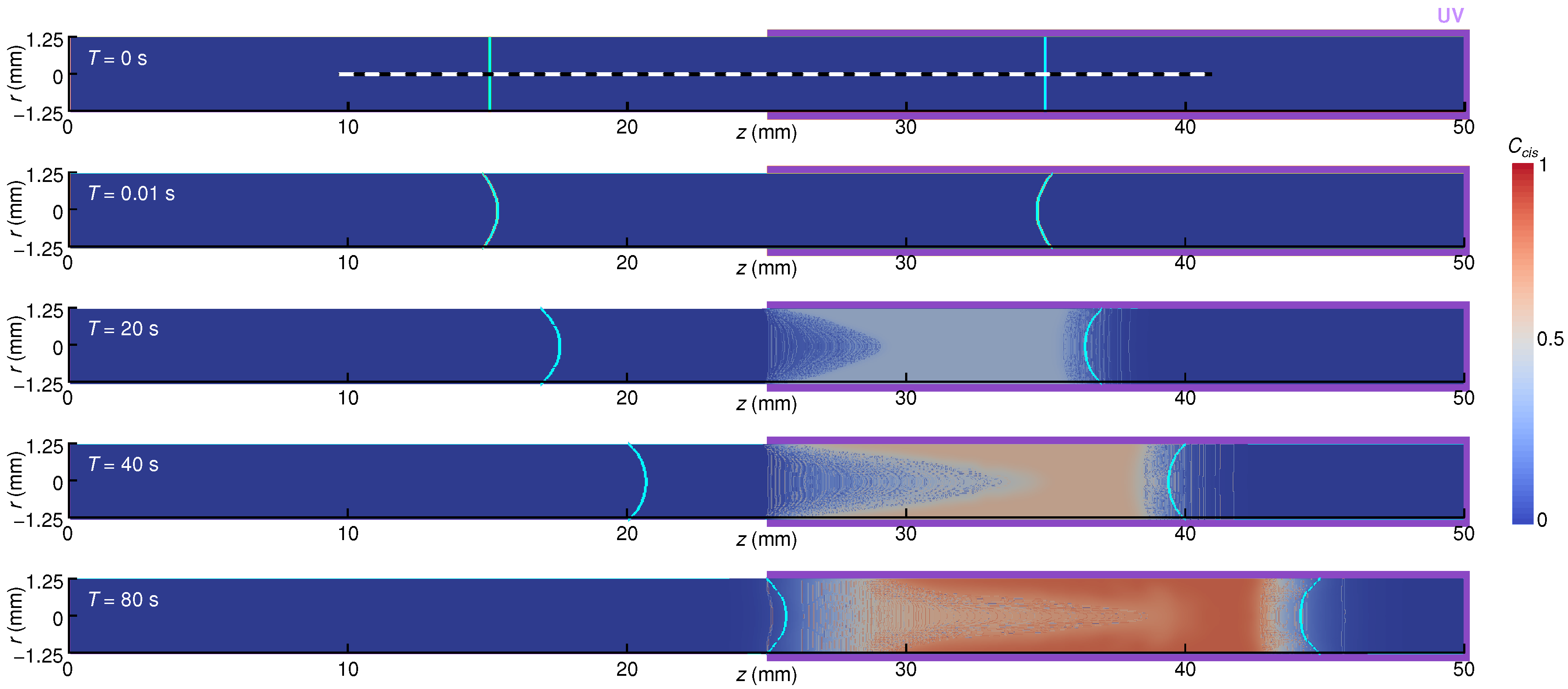
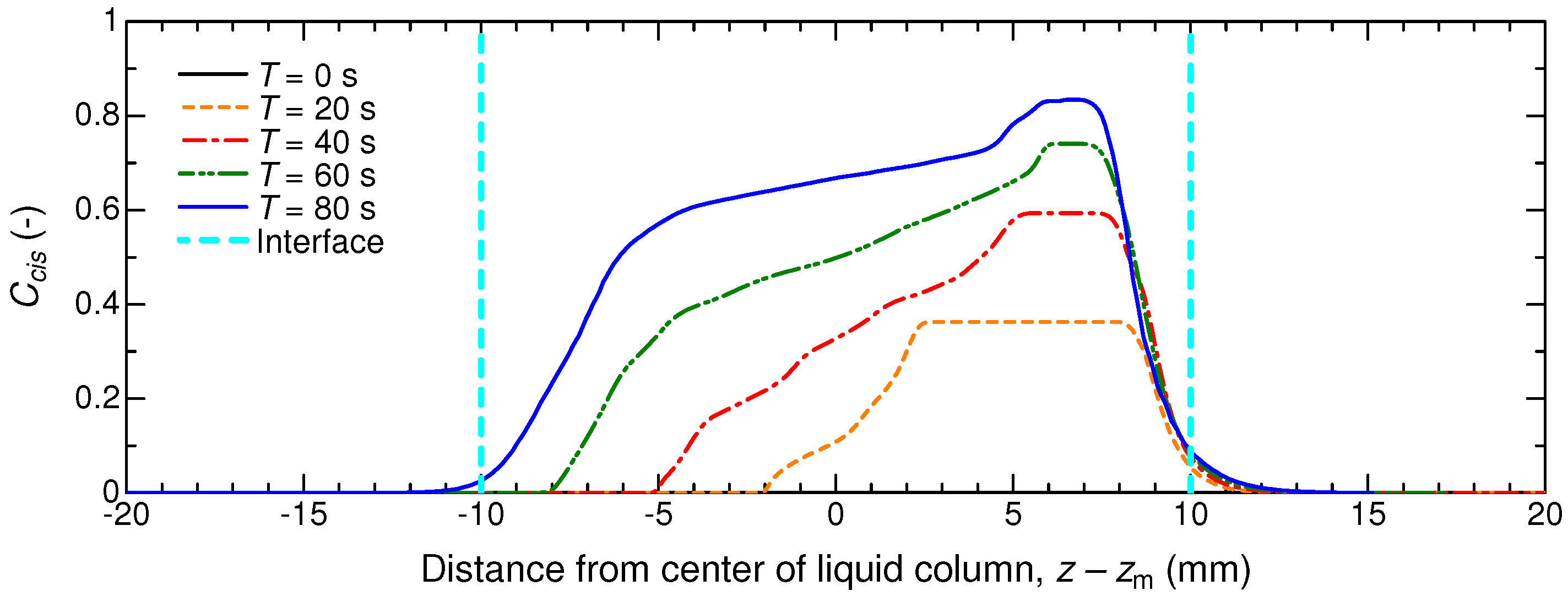
4. Results
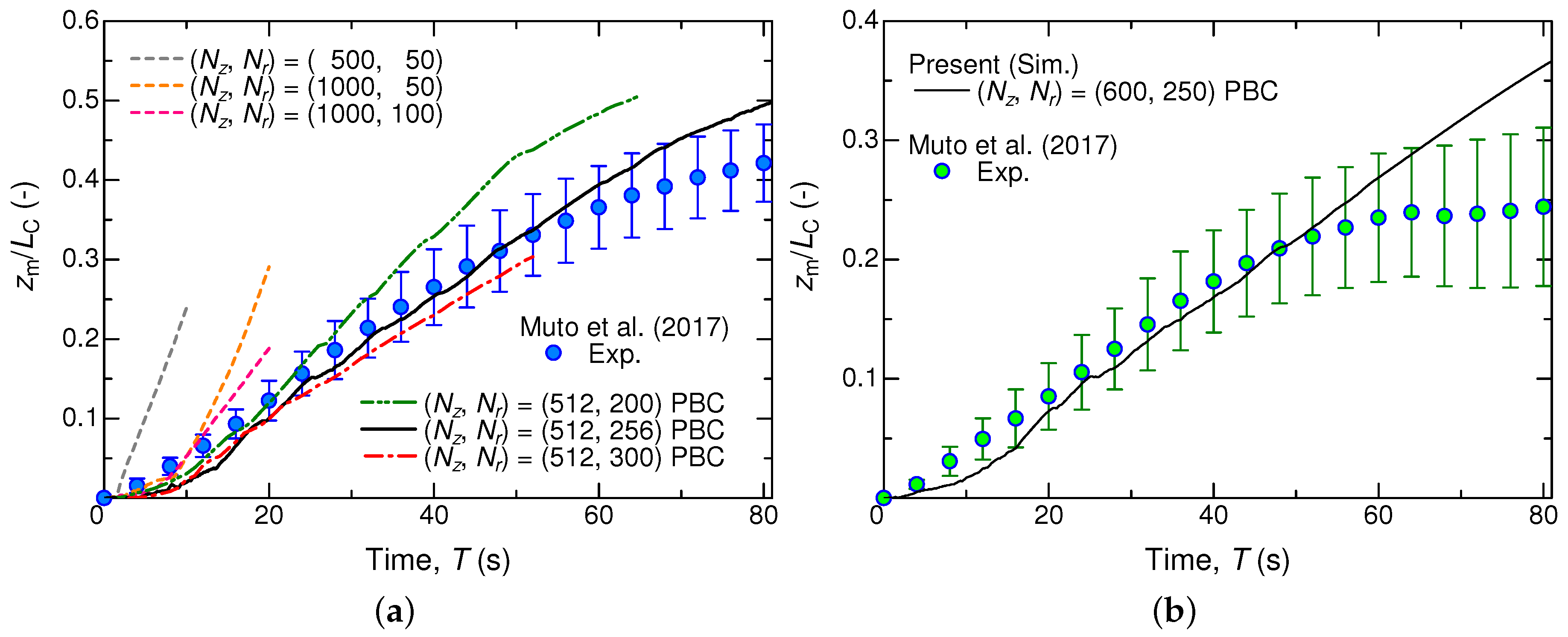
4.1. Grid Resolution: Comparative Validation with Experimental Results
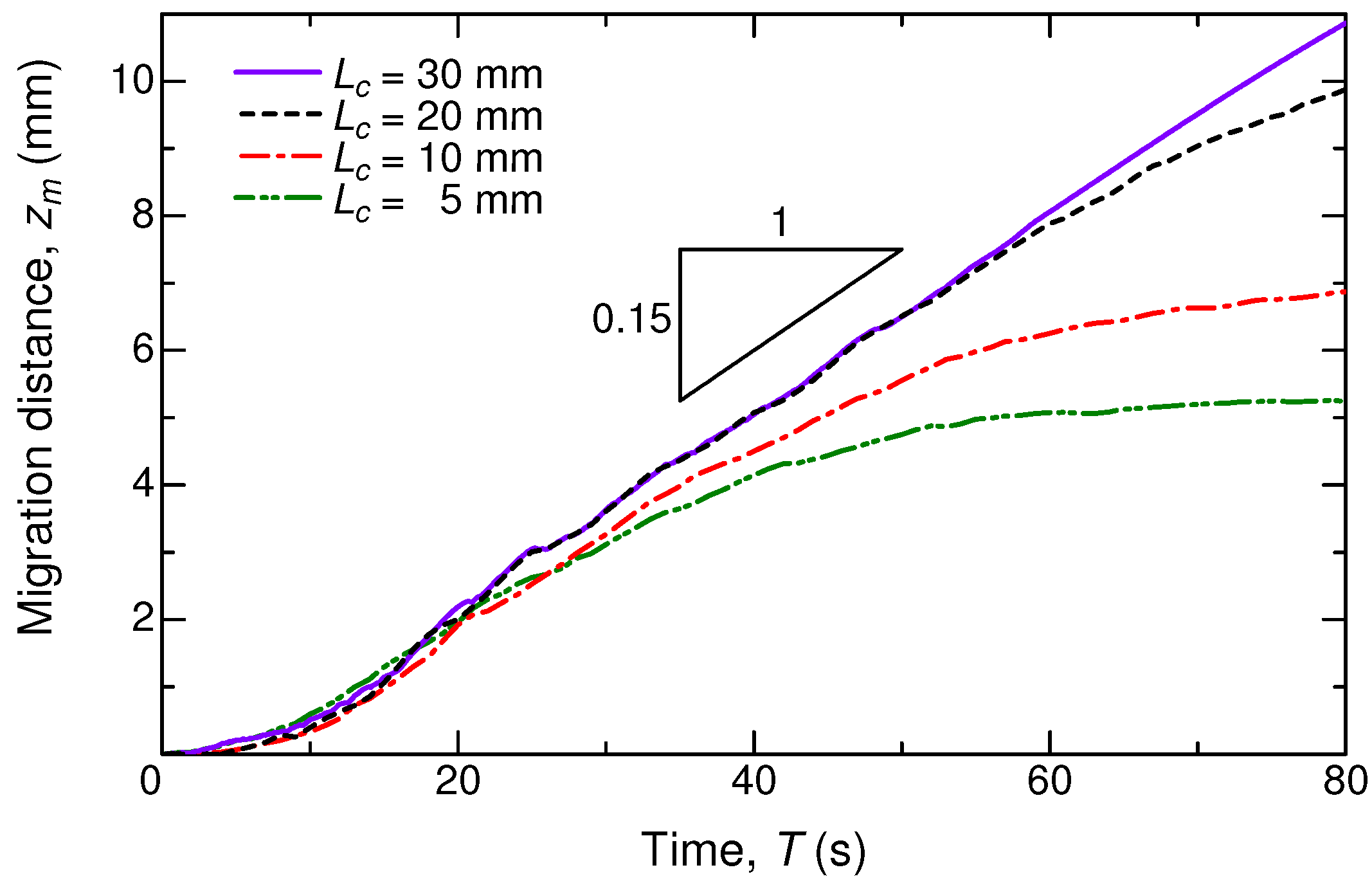
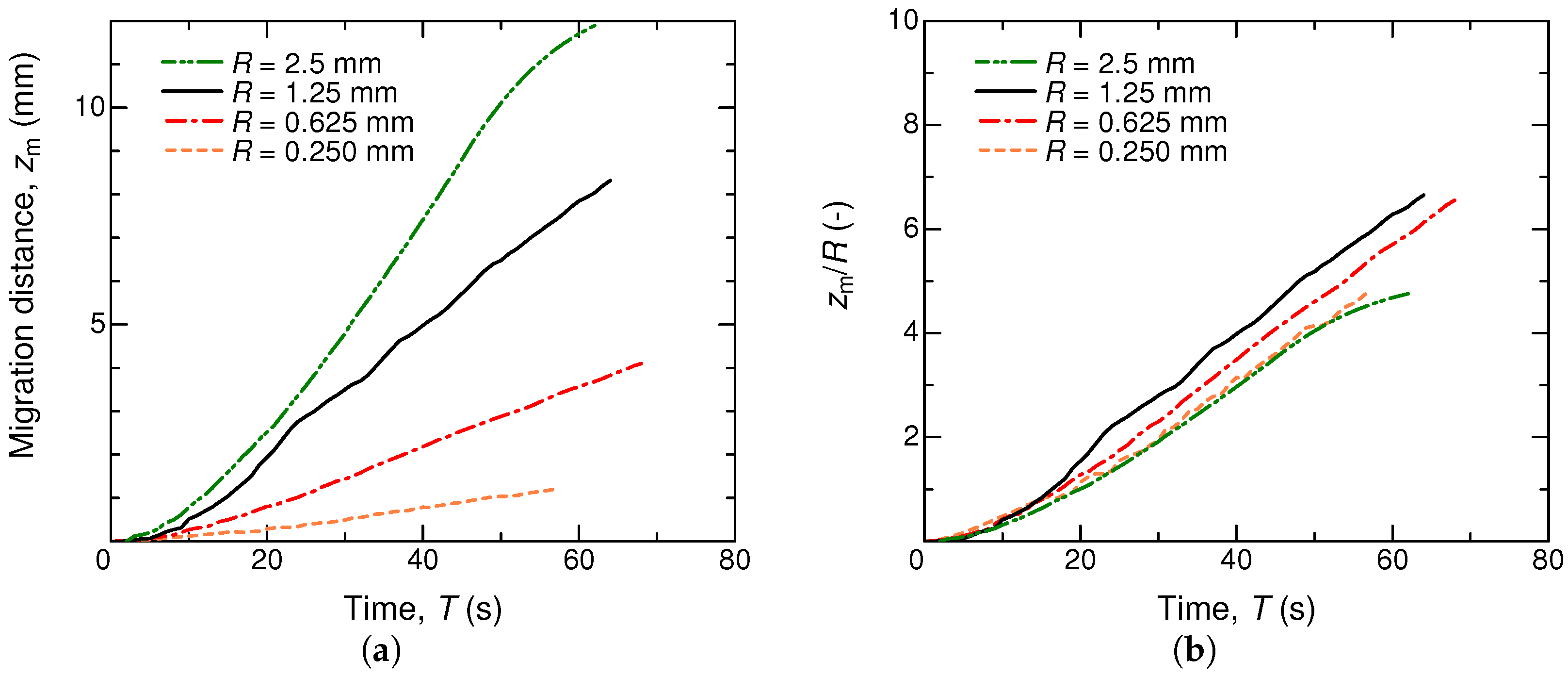
4.2. Influence of the Liquid Column Length and Tube Radius
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
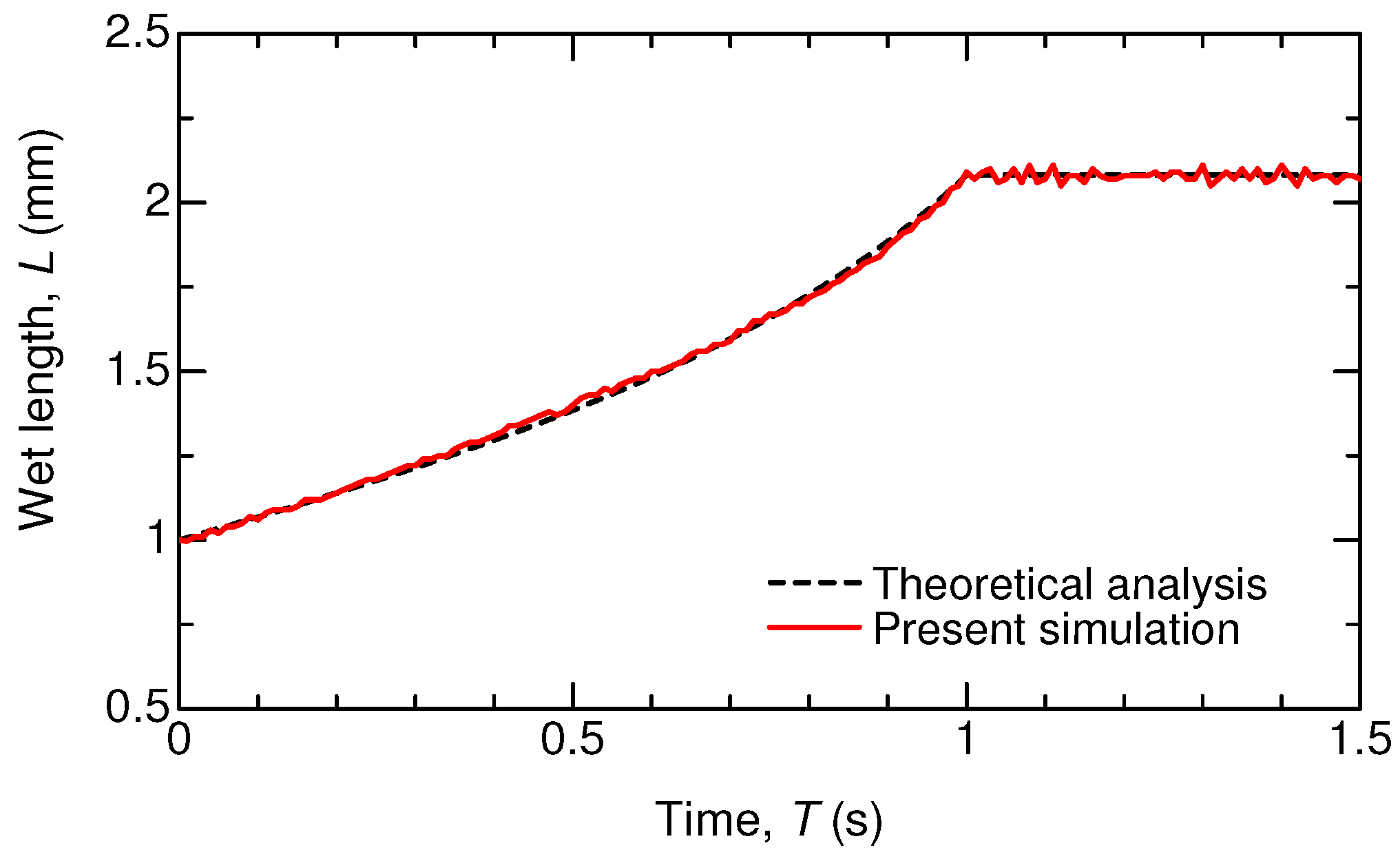
Appendix A. Preliminary Tests
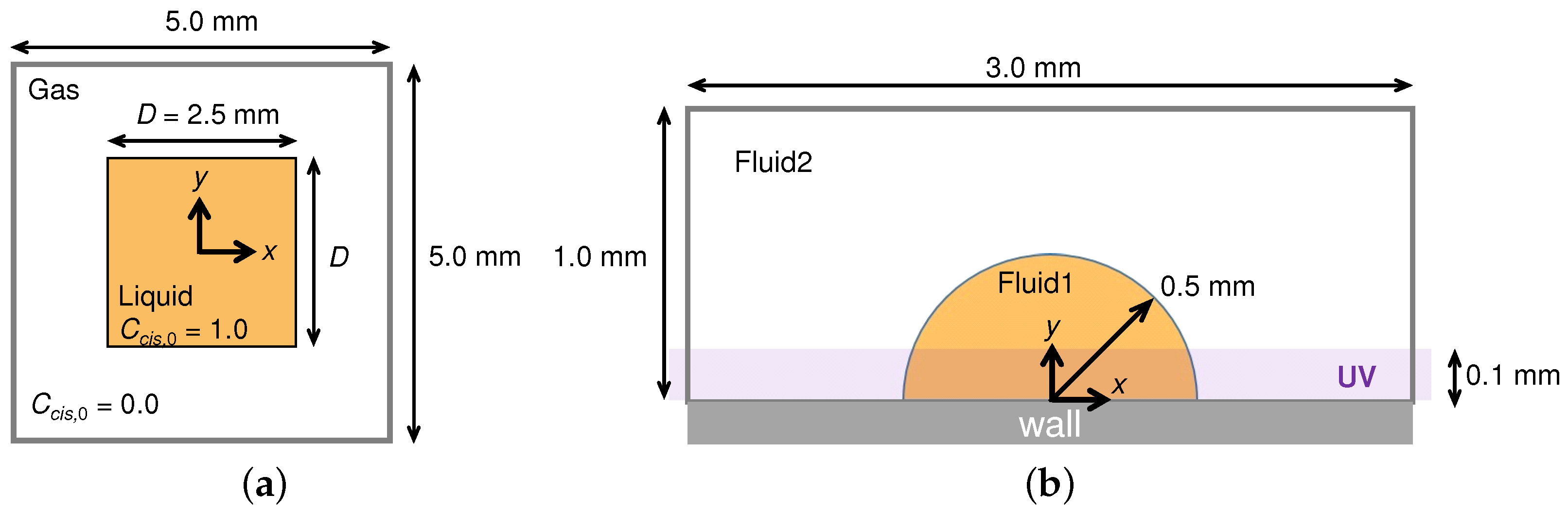
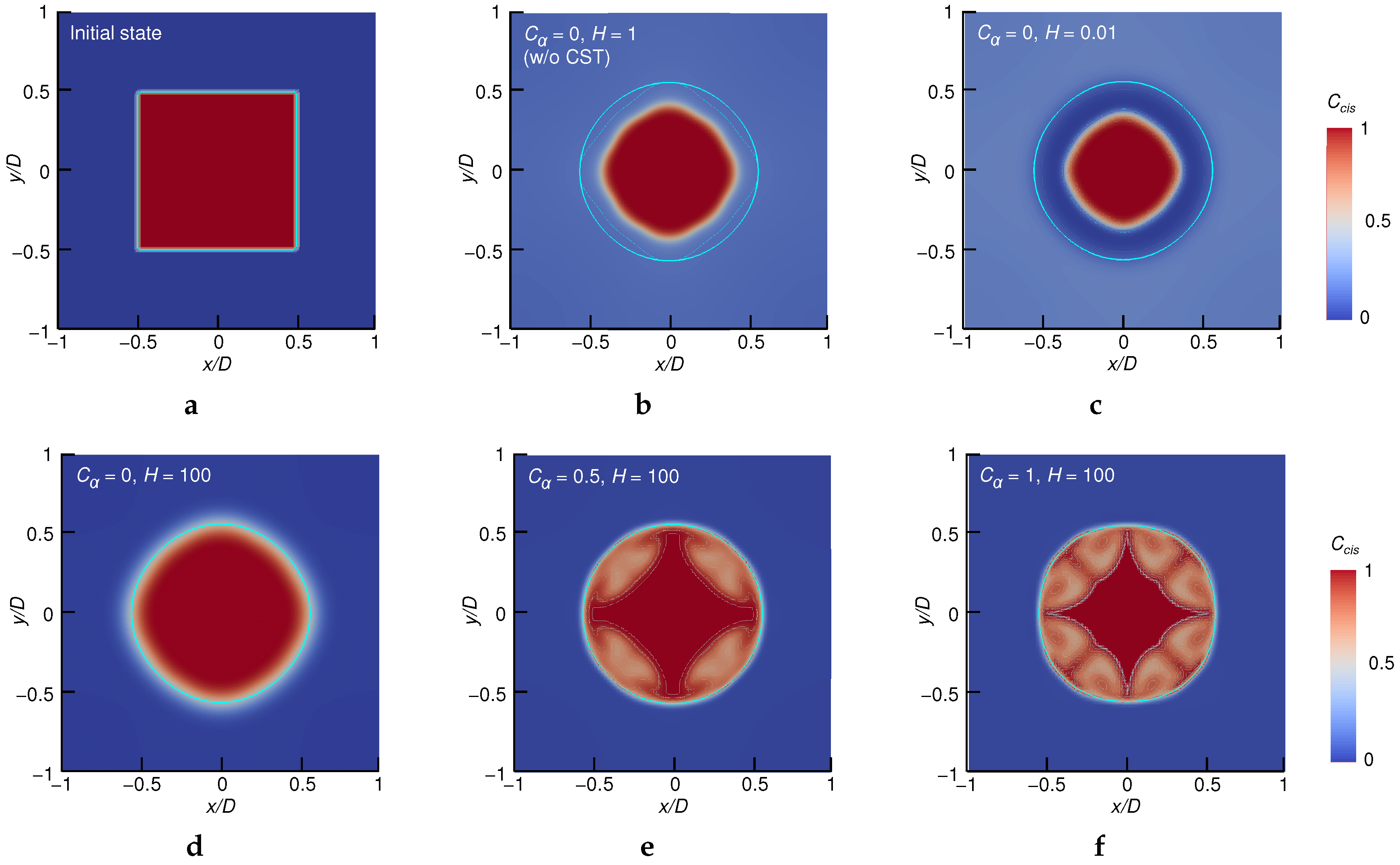
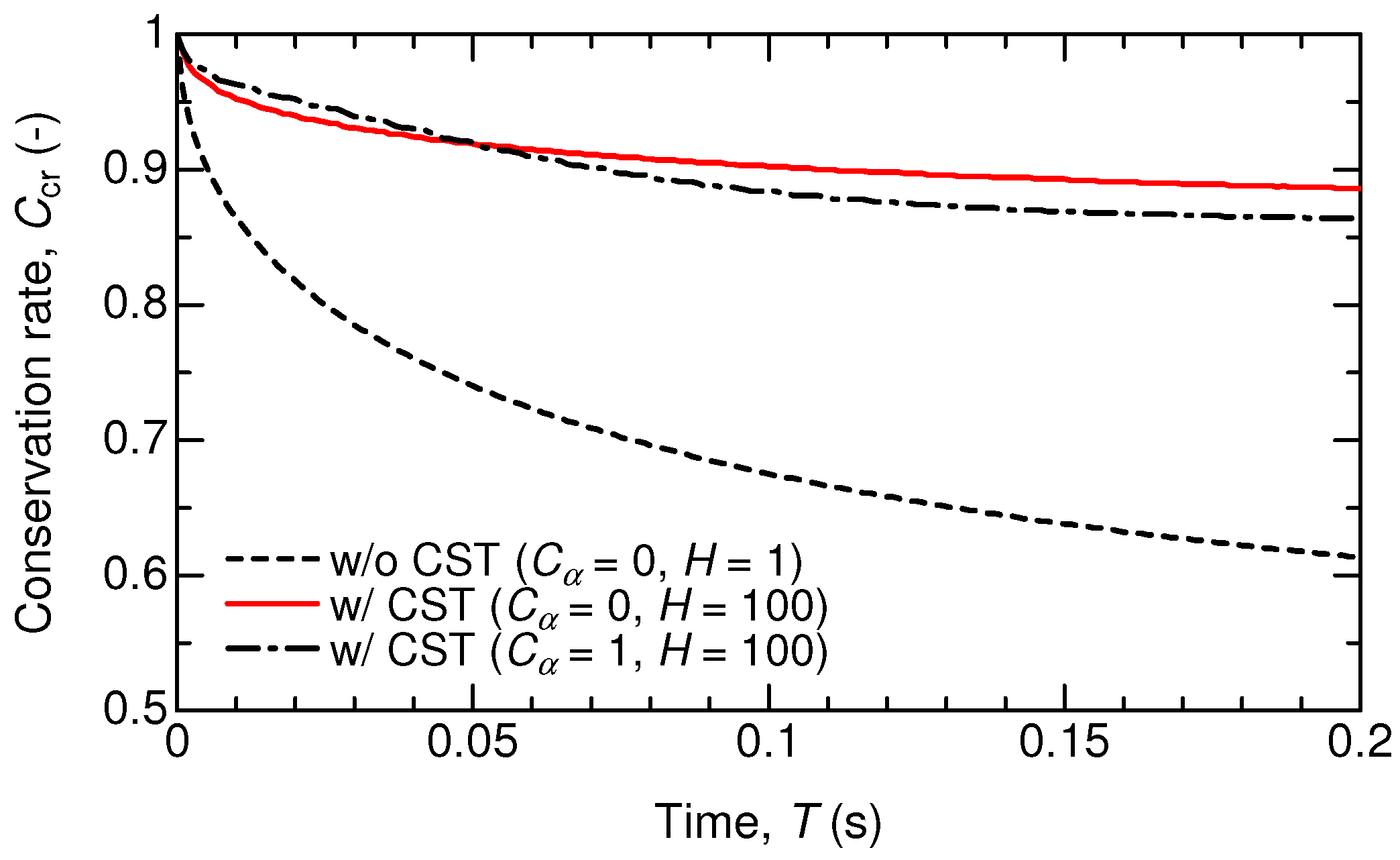
Appendix A.1. Scalar Transport Near the Interface
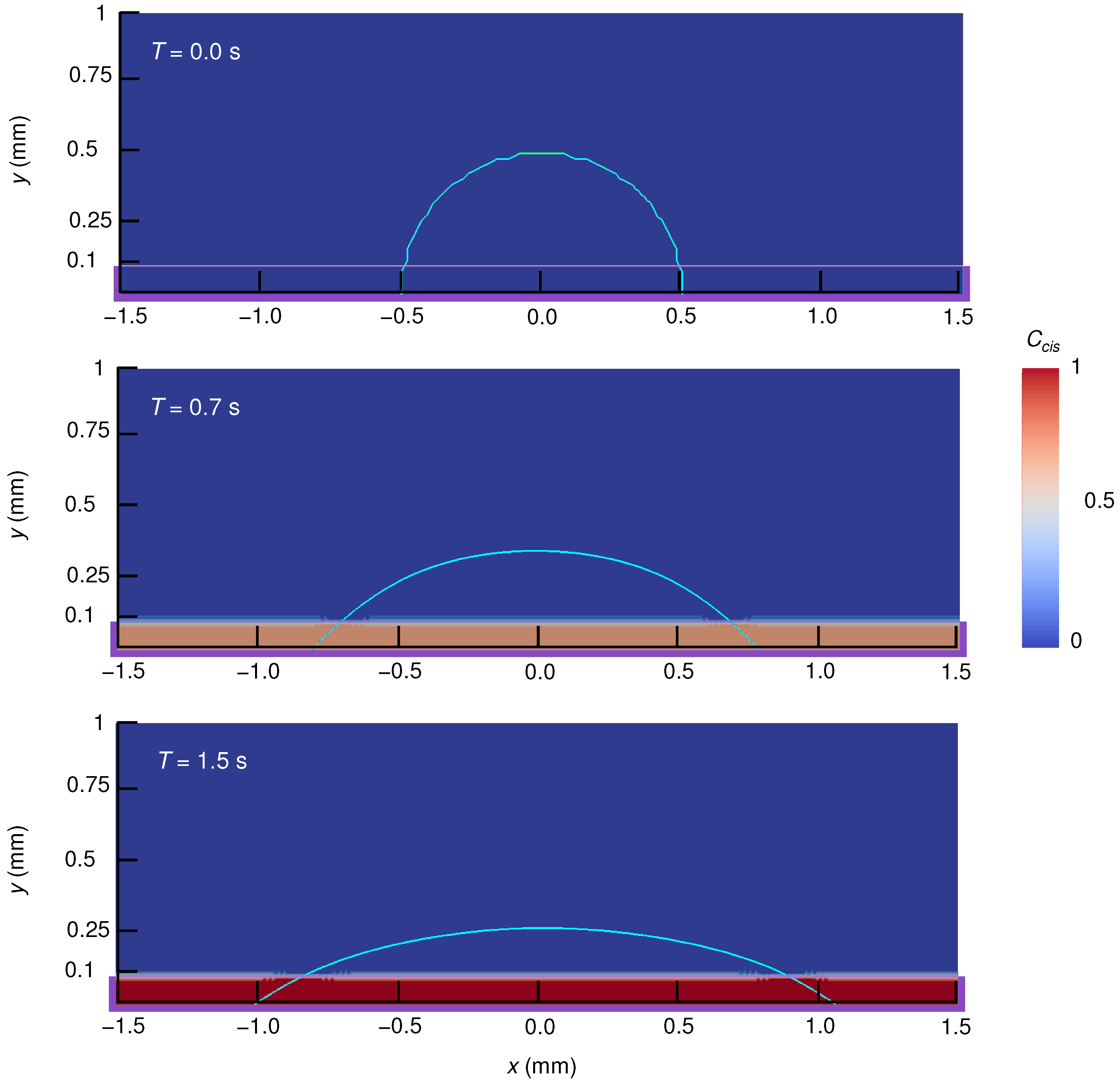
Appendix A.2. Changed Static Contact Angle by Photoisomerization
References
- Mark, D.; Haeberle, S.; Roth, G.; Stetten, F.; Zengerle, R. Microfluidic lab-on-a-chip platforms: Requirements, characteristics and applications. Chem. Soc. Rev. 2010, 39, 1153–1182. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhe, J. Recent advances in particle and droplet manipulation for lab-on-a-chip devices based on surface acoustic waves. Lab Chip 2011, 11, 1280–1285. [Google Scholar] [CrossRef] [PubMed]
- Elvira, K.S.; Solvas, X.C.I.; Wootten, R.R.; de Mello, A.J. The past, present and potential for microfluidic reactor technology in chemical synthesis. Nat. Chem. 2013, 5, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical reserch. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Pit, A.M.; Duits, M.H.; Mugele, F. Droplet manipulations in two phase flow microfluidics. Micromachines 2015, 6, 1768–1793. [Google Scholar] [CrossRef]
- Du, K.; Jiang, Y.; Liu, Y.; Wathuthanthri, I.; Choi, C.H. Manipulation of the superhydrophobicity of plasma-etched polymer nanostructures. Micromachines 2018, 9, 304. [Google Scholar] [CrossRef]
- Wu, T.; Suzuki, Y.; Kasagi, N. Low-voltage droplet manipulation using liquid dielectrophoresis on electret. J. Micromech. Microeng. 2010, 20, 085043. [Google Scholar] [CrossRef]
- Lee, J.; Moon, H.; Fowler, J.; Schoellhammer, T.; Kim, C.-J. Electrowetting and electrowetting-on-dielectric for microscale liquid handling. Sens. Actuators A Phys. 2002, 95, 259–268. [Google Scholar] [CrossRef]
- Baigl, D. Photo-actuation of liquids for light-driven microfluidics: State of the art and perspective. Lab Chip 2012, 12, 3637–3653. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M. Radiation pressure on a free liquid surface. Phys. Rev. Lett. 1973, 30, 139–142. [Google Scholar] [CrossRef]
- Kuo, S.C.; Sheetz, M.P. Force of single kinesin molecules measured with optical tweezers. Science 1993, 260, 232–234. [Google Scholar] [CrossRef] [PubMed]
- Baroud, C.N.; Delville, J.P.; Gallaire, F.; Wunenburger, R. Thermocapillary valve for droplet production and sorting. Phys. Rev. E 2007, 75, 046302. [Google Scholar] [CrossRef] [PubMed]
- Namura, K.; Nakajima, K.; Kimura, K.; Suzuki, M. Photothermally controlled Marangoni flow around a micro bubble. Appl. Phys. Lett. 2015, 106, 043101. [Google Scholar] [CrossRef]
- Muto, M.; Yamamoto, M.; Motosuke, M. A noncontact picolitor droplet handling by photothermal control of interfacial flow. Anal. Sci. 2016, 32, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Kazuno, N.; Tsukahara, T.; Motosuke, M. Laplace pressure versus Marangoni convection in photothermal manipulation of micro droplet. Eur. Phys. J.-Spec. Top. 2017, 226, 1337–1348. [Google Scholar] [CrossRef]
- Ichimura, K.I.; Oh, S.-K.; Nakagawa, M. Light-driven motion of liquids on a photoresponsive surface. Science 2000, 288, 1624–1626. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.-K.; Nakagawa, M.; Ichimura, K. Photocontrol of liquid motion on an azobenzene monolayer. J. Mater. Chem. 2002, 12, 2262–2269. [Google Scholar] [CrossRef]
- Berna, J.; Leigh, D.A.; Lubomska, M.; Mendoza, S.M.; Perez, E.M.; Rudolf, P.; Teobaldi, G.; Zerbetto, F. Macroscopic transport by synthetic molecular machines. Nat. Mater. 2005, 4, 704–710. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Piech, M.; Bell, N.S.; Gust, D.; Vail, S.; Garcia, A.A.; Schneider, J.; Park, C.-D.; Hayes, M.A.; Picraux, S.T. Photon control of liquid motion on reversibly photoresponsive surfaces. Langmuir 2007, 23, 10864–10872. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Liu, Y.; Wei, J.; Chen, E.; Qin, L.; Yu, Y. Photocontrol of fluid slugs in liquid crystal polymer microactuators. Nature 2016, 537, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Diguet, A.; Guillermic, R.-M.; Magome, N.; Saint-Jalmes, A.; Chen, Y.; Yoshikawa, K.; Baigl, D. Photomanipulation of a droplet by the chromocapillary effect. Angew. Chem. Int. Ed. 2009, 48, 9281–9284. [Google Scholar] [CrossRef] [PubMed]
- Diguet, A.; Li, H.; Queyriaux, N.; Chen, Y.; Baigl, D. Photoreversible fragmentation of a liquid interface for micro-droplet generation by light actuation. Lab Chip 2011, 11, 2666–2669. [Google Scholar] [CrossRef] [PubMed]
- Muto, M.; Ayako, Y.; Yamamoto, K.; Yamamoto, M.; Kondo, Y.; Motosuke, M. Photochemical migration of liquid column in a glass tube. Eur. Phys. J.-Spec. Top. 2017, 226, 1199–1205. [Google Scholar] [CrossRef]
- Orihara, Y.; Matsumura, A.; Saito, Y.; Ogawa, N.; Saji, T.; Yamaguchi, A.; Sakai, H.; Abe, M. Reversible release control of an oily substance using photoresponsive micelles. Langmuir 2001, 17, 6072–6076. [Google Scholar] [CrossRef]
- Shin, J.Y.; Abbott, N.L. Using light to control dynamics surface tensions of aqueous solutions of water soluble surfactants. Langmuir 1999, 15, 4404–4410. [Google Scholar] [CrossRef]
- Eastoe, J.; Dominguez, M.S.; Wyatt, P. Properties of a stilbene-containing gemini photosurfactant: Light-triggered changes in surface tension and aggregation. Langmuir 2002, 18, 7837–7844. [Google Scholar] [CrossRef]
- Shang, T.; Smith, K.A.; Hatton, T.A. Photoresponsive surfactants exhibiting unusually large, reversible surface tension changes under varying illumination conditions. Langmuir 2003, 19, 10764–10773. [Google Scholar] [CrossRef]
- Chevallier, E.; Mamane, A.; Srone, H.A.; Tribet, C.; Lequeux, F.; Monteux, C. Pumping-out photo-surfactants from an air-water interface using light. Soft Matter 2011, 7, 7866–7874. [Google Scholar] [CrossRef]
- OpenFAOM. Available online: https://www.openfoam.org/ (accessed on 30 September 2018).
- Deshpande, S.S.; Anumolu, L.; Trujillo, M.F. Evaluating the performance of the two-phase flow solver interFoam. Comput. Sci. Discov. 2012, 5, 014016. [Google Scholar] [CrossRef]
- Hoang, D.A.; Steijn, V.; Portela, L.M.; Kreutzer, M.T.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Klostermann, J.; Schaake, K.; Schwarze, R. Numerical simulation of a single rising bubble by VOF with surface compression. Int. J. Numer. Mech. Fluids 2013, 71, 960–982. [Google Scholar] [CrossRef]
- Nieves-Remacha, M.J.; Yang, L.; Jensen, K.F. OpenFOAM computational fluid dynamic simulations of two-phase flow and mass transfer in an advanced-flow reactor. Ind. Eng. Chem. Res. 2015, 54, 6649–6659. [Google Scholar] [CrossRef]
- Yang, L.; Nieves-Remacha, M.J.; Jensen, K.F. Simulations and analysis of multiphase transport and reaction in segmented flow microreactors. Chem. Eng. Sci. 2017, 169, 106–116. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Deising, D.; Marschall, H.; Bothe, D. A unified single-field model framework for Volume-Of-Fluid simulations of interfacial species transfer applied to bubble flows. Chem. Eng. Sci. 2016, 139, 173–195. [Google Scholar] [CrossRef]
- Quickenden, T.I.; Irvin, J.A. The ultraviolet absorption spectrum of liquid water. J. Chem. Phys. 1980, 72, 4416. [Google Scholar] [CrossRef]
- Motosuke, M.; Muto, M. (Tokyo University of Science, Tokyo, Japan). Personal communication, 2018.
| (kg/m) | (mPa·s) | D (m/s) | () | (mN/m) | k (s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Liquid | Air | Liquid | Air | Liquid | Air | Cis | Trans | Cis | Trans | ||||||
| 992.3 | 1.247 | 0.890 | 0.018 | 31.4 | 36.6 | 41.0 | 40.0 | ||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nitta, K.; Tsukahara, T. Numerical Demonstration of In-Tube Liquid-Column Migration Driven by Photoisomerization. Micromachines 2018, 9, 533. https://doi.org/10.3390/mi9100533
Nitta K, Tsukahara T. Numerical Demonstration of In-Tube Liquid-Column Migration Driven by Photoisomerization. Micromachines. 2018; 9(10):533. https://doi.org/10.3390/mi9100533
Chicago/Turabian StyleNitta, Kei, and Takahiro Tsukahara. 2018. "Numerical Demonstration of In-Tube Liquid-Column Migration Driven by Photoisomerization" Micromachines 9, no. 10: 533. https://doi.org/10.3390/mi9100533
APA StyleNitta, K., & Tsukahara, T. (2018). Numerical Demonstration of In-Tube Liquid-Column Migration Driven by Photoisomerization. Micromachines, 9(10), 533. https://doi.org/10.3390/mi9100533






