A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges
Abstract
:1. Introduction
2. Materials and Methods
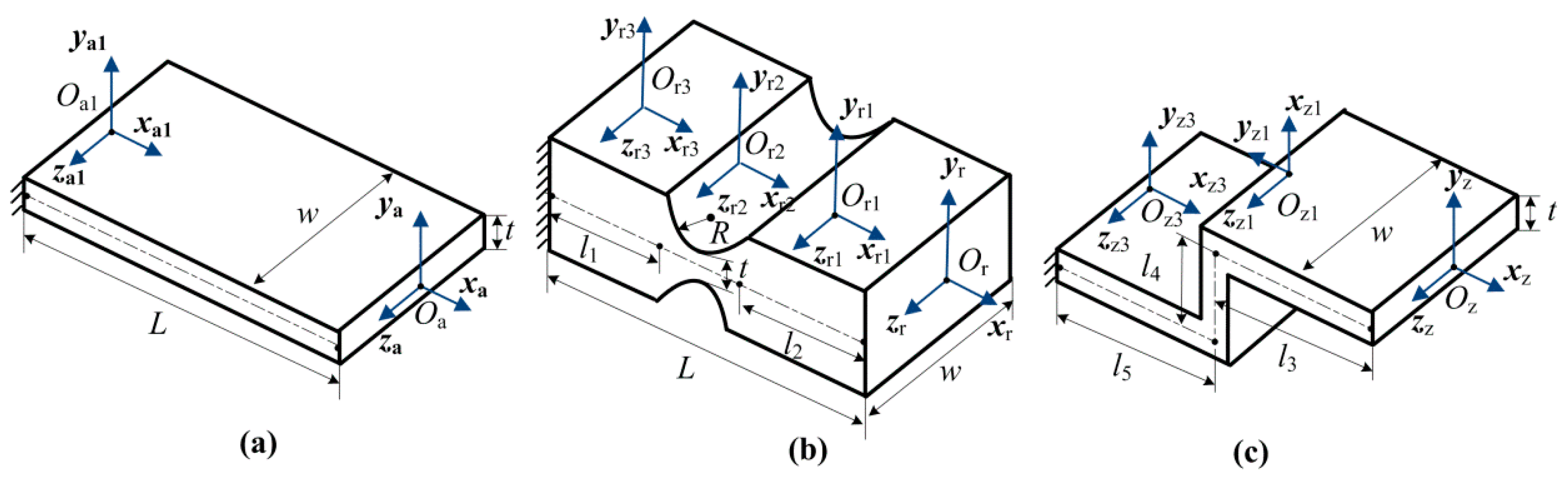
2.1. Calculation of the “Z-shaped” Flexure Hinge
2.2. Platform Design
2.3. Dynamic Calculation
3. Results and Discussion
3.1. Experimental System
3.2. Output Performance
3.3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, D.H.; Lee, M.G.; Kim, B.; Sun, Y. A superelastic alloy microgripper with embedded electromagnetic actuators and piezoelectric force sensors: A numerical and experimental study. Smart Mater. Struct. 2005, 14, 1265. [Google Scholar] [CrossRef]
- Tanikawa, T.; Arai, T. Development of a micro-manipulation system having a two-fingered micro-hand. IEEE Trans. Robot. Autom. 2012, 15, 152–162. [Google Scholar] [CrossRef]
- Xu, Q. Robust impedance control of a compliant microgripper for high-speed position/force regulation. IEEE Trans. Ind. Electron. 2015, 62, 1201–1209. [Google Scholar] [CrossRef]
- Hao, G.; Kong, X. A novel large-range XY compliant parallel manipulator with enhanced out-of-plane stiffness. J. Mech. Des. 2012, 134, 061009. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Constraint-based design of parallel kinematic XY flexure mechanisms. J. Mech. Des. 2007, 129, 816–830. [Google Scholar] [CrossRef]
- Hao, G.; Li, H. Conceptual designs of multi-degree of freedom compliant parallel manipulators composed of wire-beam based compliant mechanisms. Proc. Inst. Mech. Eng. Part C 2015, 229, 538–555. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. Design and Analysis of a New High Precision Decoupled XY Compact Parallel Micromanipulator. Micromachines 2017, 8, 82. [Google Scholar] [CrossRef]
- PI Company. Available online: http://www.pi-usa.us/piezo_motion_tutorial/ (accessed on 29 July 2017).
- Attocube Company. Available online: http://www.attocube.com/attomotion/ (accessed on 29 July 2017).
- SmarACT Company. Available online: http://www.smaract.com/products/ (accessed on 29 July 2017).
- Zhou, M.; Fan, Z.; Ma, Z.; Zhao, H.; Guo, Y.; Hong, K.; Wu, D. Design and Experimental Research of a Novel Stick-Slip Type Piezoelectric Actuator. Micromachine 2017, 8, 150. [Google Scholar] [CrossRef]
- Nomura, Y.; Aoyama, H. Development of inertia driven microrobot with nano tilting stage for SEM operation. Microsyst. Technol. 2007, 13, 1347–1352. [Google Scholar] [CrossRef]
- Li, J.; Zhou, X.; Zhao, H.; Shao, M.; Hou, P.; Xu, X. Design and experimental performances of a piezoelectric linear actuator by means of lateral motion. Smart Mater. Struct. 2015, 24, 065007. [Google Scholar] [CrossRef]
- Shimizu, Y.; Peng, Y.; Kaneko, J.; Azuma, T.; Ito, S.; Gao, W.; Lu, T.F. Design and construction of the motion mechanism of an XY micro-stage for precision positioning. Sens. Actuat. A 2013, 201, 395–406. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H.; Qu, H.; Cui, T.; Fu, L.; Huang, H.; Ren, L.; Fan, Z. A piezoelectric-driven rotary actuator by means of inchworm motion. Sens. Actuat. A 2013, 194, 269–276. [Google Scholar] [CrossRef]
- Kim, S.C.; Soo, H.K. Precise rotary motor by inchworm motion using dual wrap belts. Rev. Sci. Instrum. 1999, 70, 2546–2550. [Google Scholar] [CrossRef]
- Heijer, M.; Fokkema, V.; Saedi, A.; Schakel, P.; Rost, M.J. Improving the accuracy of walking piezo motors. Rev. Sci. Instrum. 2014, 85, 055007. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhao, C. A new standing-wave-type linear ultrasonic motor based on in-plane modes. Ultrasonics 2011, 51, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Morita, T.; Kurosawa, M.K.; Higuchi, T. A cylindrical micro ultrasonic motor using PZT thin film deposited by single process hydrothermal method (/spl phi/2.4 mm, L = 10 mm stator transducer). IEEE Trans. Ultrason. Ferr. 2002, 45, 1178–1187. [Google Scholar] [CrossRef] [PubMed]
- Uchino, K. Piezoelectric ultrasonic motors: Overview. Smart Mater. Struct. 1998, 7, 273. [Google Scholar] [CrossRef]
- Rong, W.; Zhang, S.; Yu, M.; Sun, L. A 3D stick-slip nanopositioner for nanomanipulation. In Proceedings of the 2011 International Conference on Mechatronics and Automation (ICMA), Beijing, China, 7–10 August 2011; pp. 195–199. [Google Scholar]
- Matsunami, G.; Kawamata, A.; Hosaka, H.; Morita, T. Multilayered LiNbO 3 actuator for XY-stage using a shear piezoelectric effect. Sens. Actuat. A 2008, 144, 337–340. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H.; Qu, X.; Qu, H.; Zhou, X.; Fan, Z.; Fu, H. Development of a compact 2-DOF precision piezoelectric positioning platform based on inchworm principle. Sens. Actuat. A 2015, 222, 87–95. [Google Scholar] [CrossRef]
- Kim, H.; Gweon, D.G. Development of a compact and long range XYθz nano-positioning stage. Rev. Sci. Instrum. 2012, 83, 085102. [Google Scholar] [CrossRef] [PubMed]
- Min, K.S.; Choi, W.C.; Song, S.H.; Hwang, E.J. Static and dynamic analysis of a nanopositioning flexure-hinge stage with a flexible lever mechanism. Proc. Inst. Mech. Eng. Part B 2005, 219, 447–454. [Google Scholar] [CrossRef]
- Gao, P.; Swei, S.M.; Yuan, Z. A new piezodriven precision micropositioning stage utilizing flexure hinges. Nanotechnology 1999, 10, 394. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, D.; Shirinzadeh, B. Dynamic modelling of a flexure-based mechanism for ultra-precision grinding operation. Precis. Eng. 2011, 35, 554–565. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.N. Design of Circular Cross-Section Corner-Filleted Flexure Hinges for Three-Dimensional Compliant Mechanisms. Mech. Des. 2002, 124, 479. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Z. Design calculations for flexure hinges. Rev. Sci. Instrum. 2002, 73, 3101. [Google Scholar] [CrossRef]











| Method | Right-Angle | Right-Circular | Z-Shaped |
|---|---|---|---|
| MCM (Matrix-based compliance modeling) | 265.8 μm | 28.0 μm | 323.5 μm |
| FEM (Fine element method) | 261.4 μm | 27.4 μm | 340.1 μm |
| Error | 1.7% | 2.2% | 4.9% |
| Modal Number | Frequency (Hz) | Resonance Direction |
|---|---|---|
| First | 678 | y |
| Second | 965 | z |
| Third | 1297 | θx |
| Fourth | 1553 | x |
| Fifth | 1832 | θz |
| Sixth | 2002 | θy |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, H.; Zhao, H. A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges. Micromachines 2017, 8, 245. https://doi.org/10.3390/mi8080245
Li J, Liu H, Zhao H. A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges. Micromachines. 2017; 8(8):245. https://doi.org/10.3390/mi8080245
Chicago/Turabian StyleLi, Jianping, Hui Liu, and Hongwei Zhao. 2017. "A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges" Micromachines 8, no. 8: 245. https://doi.org/10.3390/mi8080245
APA StyleLi, J., Liu, H., & Zhao, H. (2017). A Compact 2-DOF Piezoelectric-Driven Platform Based on “Z-Shaped” Flexure Hinges. Micromachines, 8(8), 245. https://doi.org/10.3390/mi8080245




