Development of Novel Platform to Predict the Mechanical Damage of a Miniature Mobile Haptic Actuator
Abstract
:1. Introduction
2. Drop Tester
2.1. Drop Tester Configuration
2.2. Drop Tester Verification
3. Finite Element Analysis of Impact Behavior of the LRA
3.1. Determination of Damping Ratio for the Spring
3.2. Micro-Tensile Test for Spring
3.3. Experimental Verification of Analytical Model
3.4. FE Simulation
4. Conclusions
- (1)
- For the analysis, a series of preparations were carried out. First, the drop tester was newly-developed for experimental verification of the FE model. Its experimental verification satisfied the free fall conditions while assisting the drop with a test apparatus. Second, a micro-tensile test was performed to obtain the material properties considering the size effect of the thin LRA springs. Third, structural damping was modeled by measuring the vibration displacement of a spring with the excitation signal.
- (2)
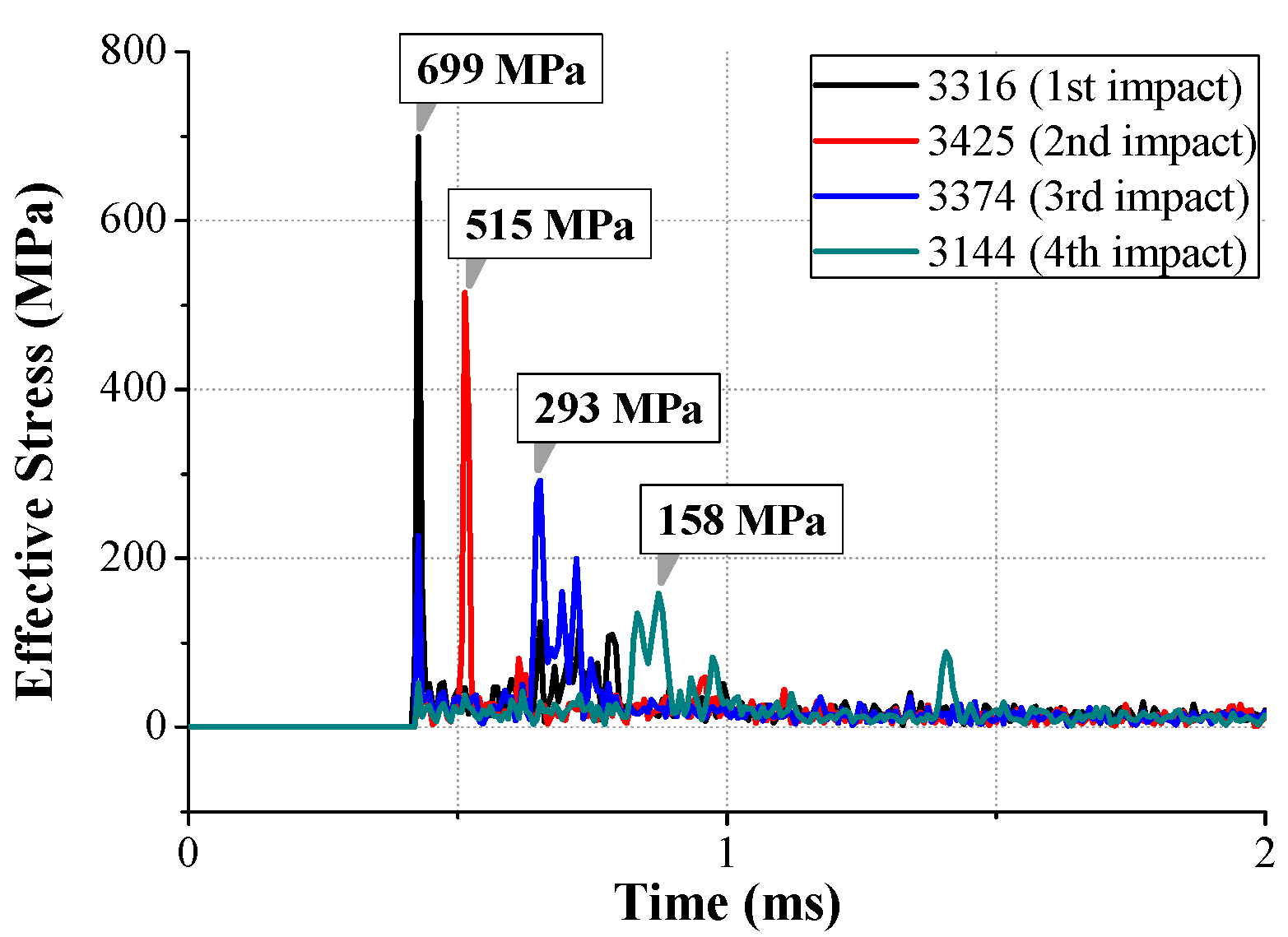
- Based on the previous study, the impact FE modeling of a dummy phone including an LRA was performed, and its experimental verification was carried out by comparison of the impact deformation and force during the impact behavior. Despite the error in the impact force (7.5%) and pulse width (33%), the analytical model and experimental model were well correlated. Additionally, the impact rebound displacement is well matched.
- (3)
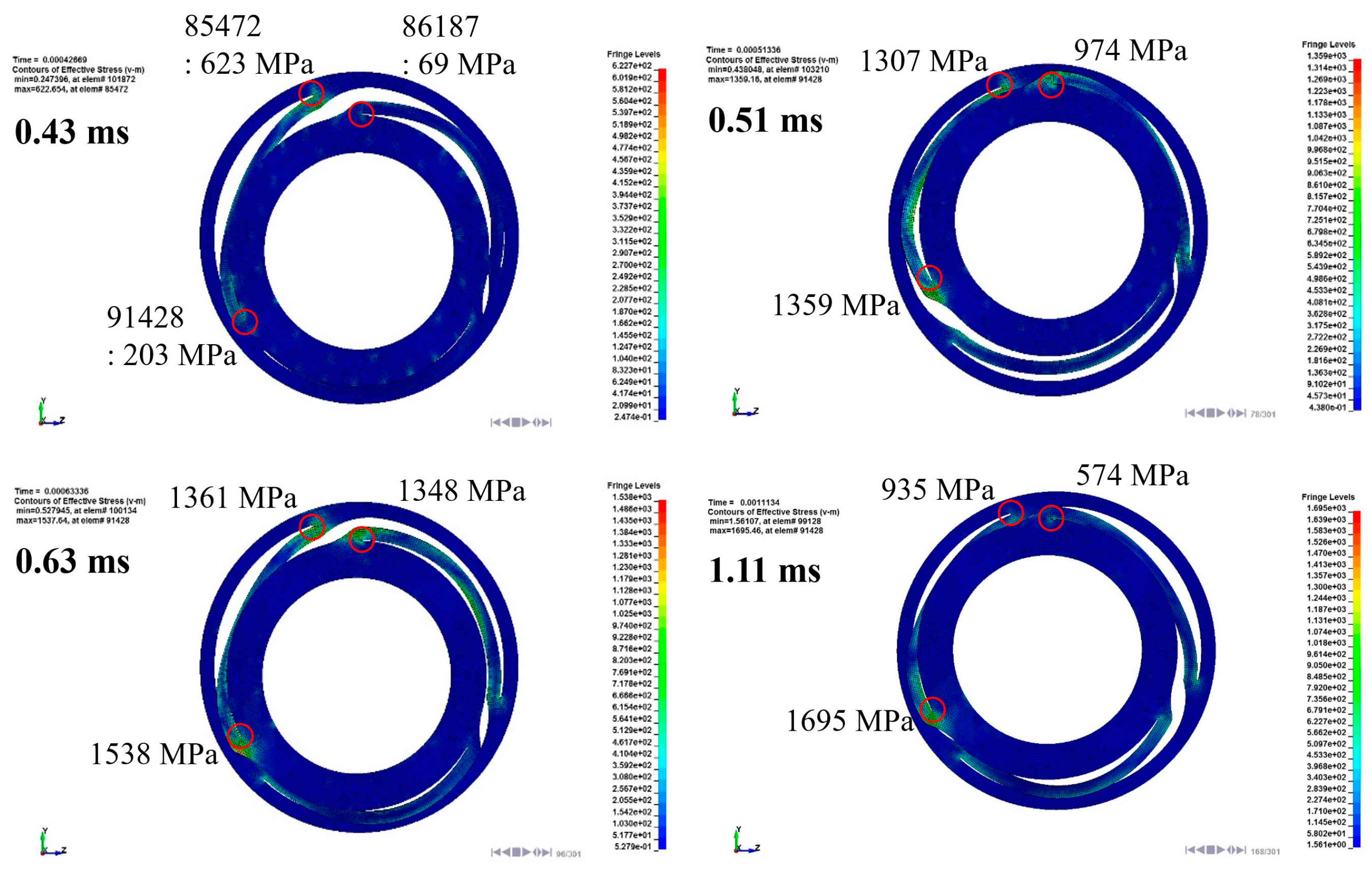
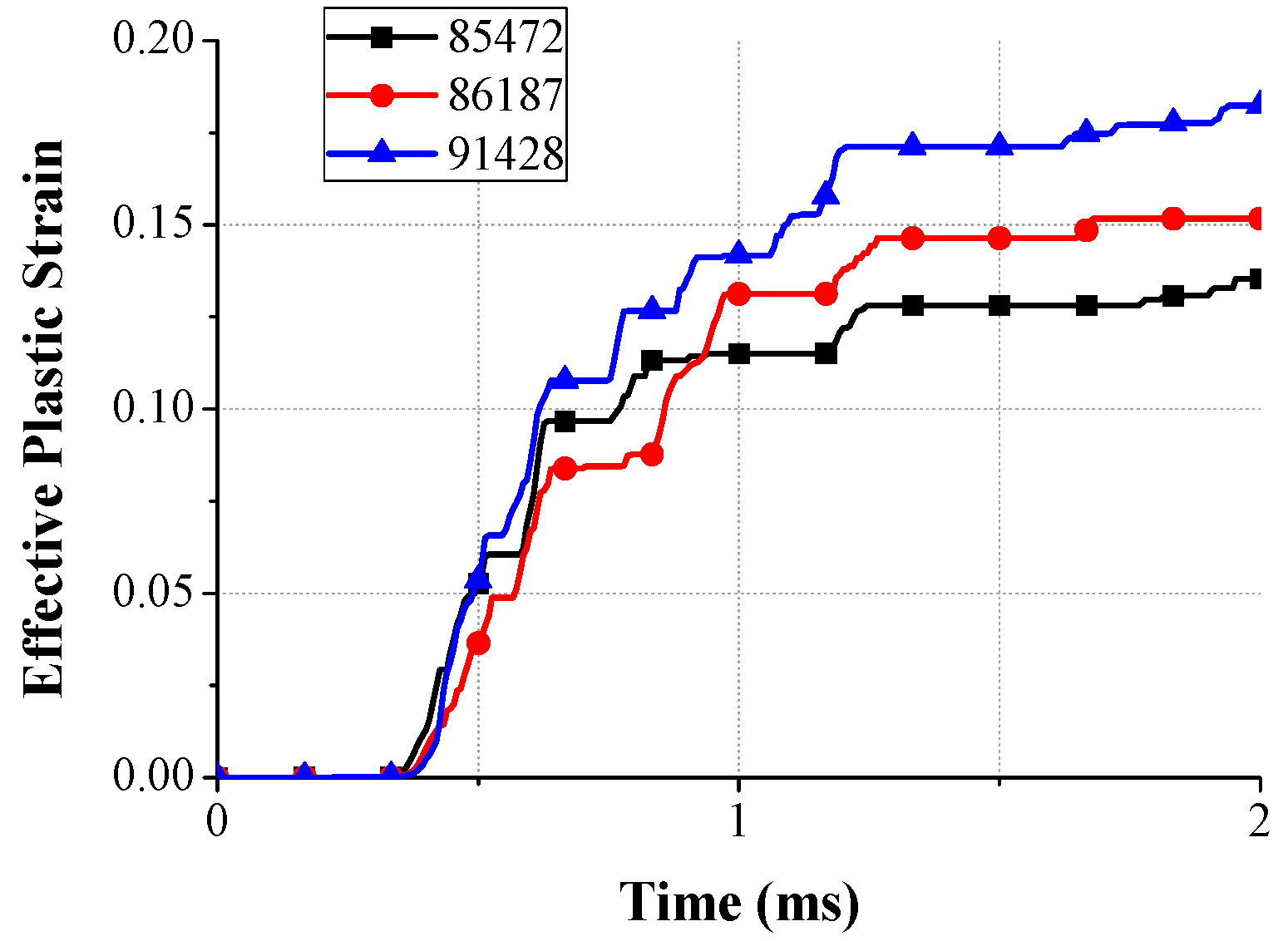
- Consequently, the damage of the FE model was analyzed. The external impact and secondary internal impact of the LRA moving mass were concentrated on the LRA spring. Primary and secondary impact generated a maximum impact stress of 1695 MPa. Further, effective strain at the same position was evaluated as 0.182. The damaged shape of the spring was confirmed and a vibration characteristic change was expected.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kern, T.A. Engineering Haptic Devices; Springer Heidelberg: Berlin, Germany, 2009. [Google Scholar]
- Cho, Y.J.; Yang, T.H.; Kwon, D.S. A new miniature smart actuator based on piezoelectric material and solenoid for mobile devices. In Proceedings of the 5th International Conference on the Advanced Mechatronics (ICAM), Osaka, Japan, 4–6 October 2010; pp. 615–620. [Google Scholar]
- Yang, T.H.; Pyo, D.B.; Kim, S.Y.; Cho, Y.J.; Bae, Y.D. A New Subminiature Impact Actuator for Mobile Devices. In Proceedings of the IEEE World Haptics Conference, New York, NY, USA, 21–24 June 2011; pp. 95–100. [Google Scholar]
- Pyo, D.B. A Novel Impact-Resonant Actuator for Mobile Devices. Master’s Thesis, Korea Advanced Institute of Science and Technology (KAIST), DaeJeon, Korea, 2012. [Google Scholar]
- Kim, K.H.; Choi, Y.M.; Gweon, D.G.; Lee, M.G. A novel laser micro/nano-machining system for FPD process. J. Mater. Process. Technol. 2008, 201, 497–501. [Google Scholar] [CrossRef]
- Goyal, S.; Buratynski, E. Methods for Realistic Drop-Testing. Int. Microelectron. Packag. Soc. 2000, 23, 45–52. [Google Scholar]
- Kim, J.G.; Lee, J.Y.; Lee, S.Y. Drop/Impact Simulation and Experimental Verification of Mobile Phone. Trans. Korean Soc. Mech. Eng. 2001, 25, 695–702. [Google Scholar]
- Kim, J.G.; Park, Y.K. Experimental Verification of Drop/Impact Simulation for a Cellular Phone. Exp. Mech. 2004, 44, 375–380. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Yu, T.X.; Lee, S.W. Drop/impact tests and analysis of typical portable electronics devices. Int. J. Mech. Sci. 2008, 50, 905–917. [Google Scholar] [CrossRef]
- Karppine, J.; Li, J.; Pakarinen, J.; Mattila, T.T.; Paulasto-Krockel, M. Shock impact reliablity characterization of a handheld product in accelerated tests and use environment. Microelectron. Reliab. 2012, 52, 190–198. [Google Scholar] [CrossRef]
- Mattila, T.T.; Vajavaara, L.; Hokka, J.; Hussa, E.; Makela, M.; Halkola, V. Evaluation of the drop response of handheld electronic products. Microelectron. Reliab. 2014, 54, 601–609. [Google Scholar] [CrossRef]
- Choi, B.J.; Yeom, H.H.; Jeon, Y.H.; Lee, M.G. Experimental verification of drop impact test and analysis for mobile electronics. In Proceedings of the 11th International Conference on Multi-Material Micro Manufacture (4M) and the 10th International Workshop on Microfactories (IWMF), Kongens Lyngby, Denmark, 13–15 September 2016; pp. 125–128. [Google Scholar]
- Metz, R. Impact and Drop Testing with ICP Force Sensors. Sound Vib. 2007, 11, 18–20. [Google Scholar]
- Inman, D.J. Engineering Vibration; Pearson Education: London, UK, 2008. [Google Scholar]
- Bazant, Z.P. Size effect on structural strength: A review. Arch. Appl. Mech. 1999, 69, 703–725. [Google Scholar]
- Gupta, R.K.; Mathew, C.; Ramkumar, P. Strain Hardening in Aerospace Alloys. Front. Aerosp. Eng. 2015, 4, 1–13. [Google Scholar] [CrossRef]
- Magd, E.E. Mechanical properties at high strain rates. J. Phys. IV Colloq. 1994, 4, 149–170. [Google Scholar]


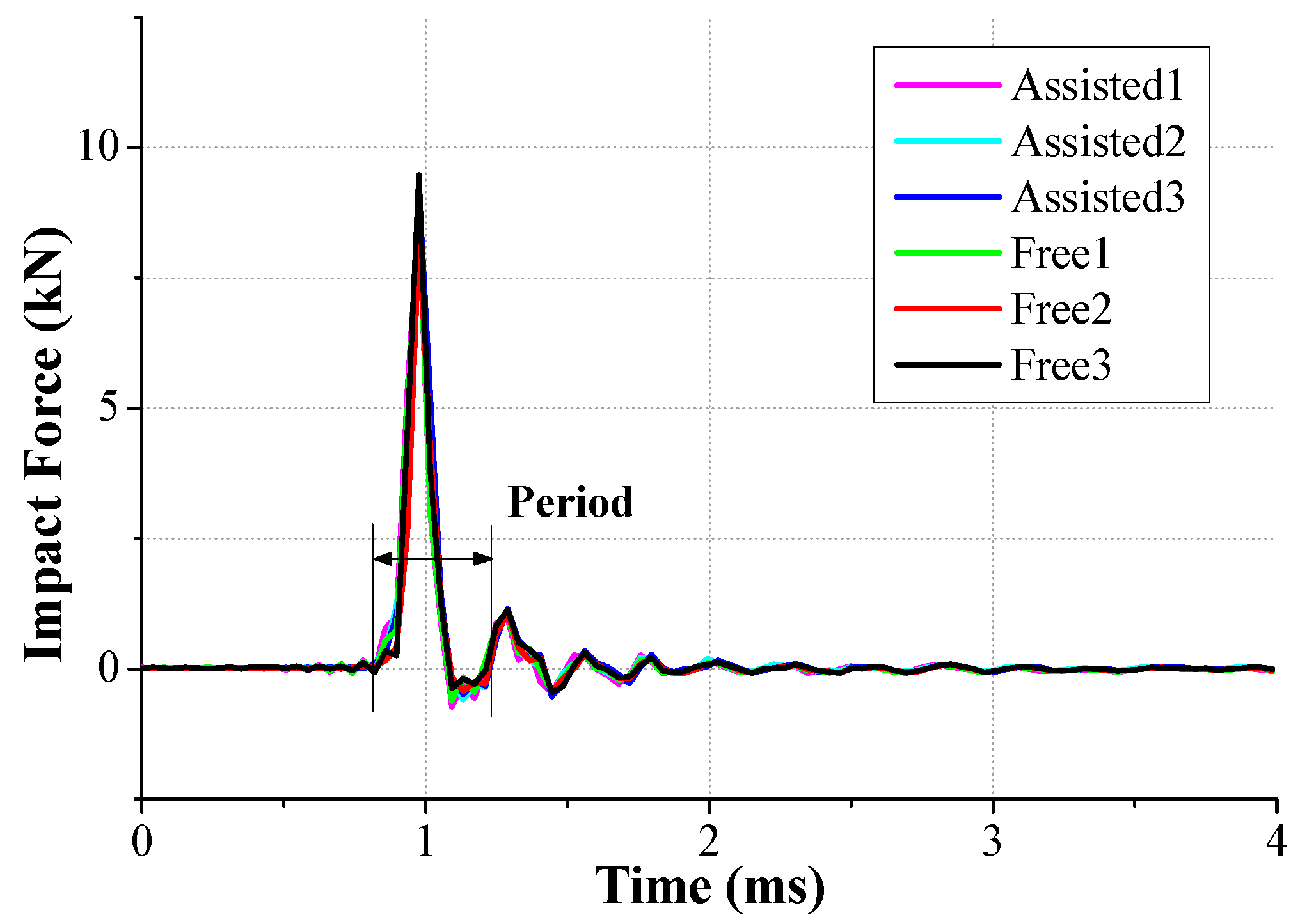


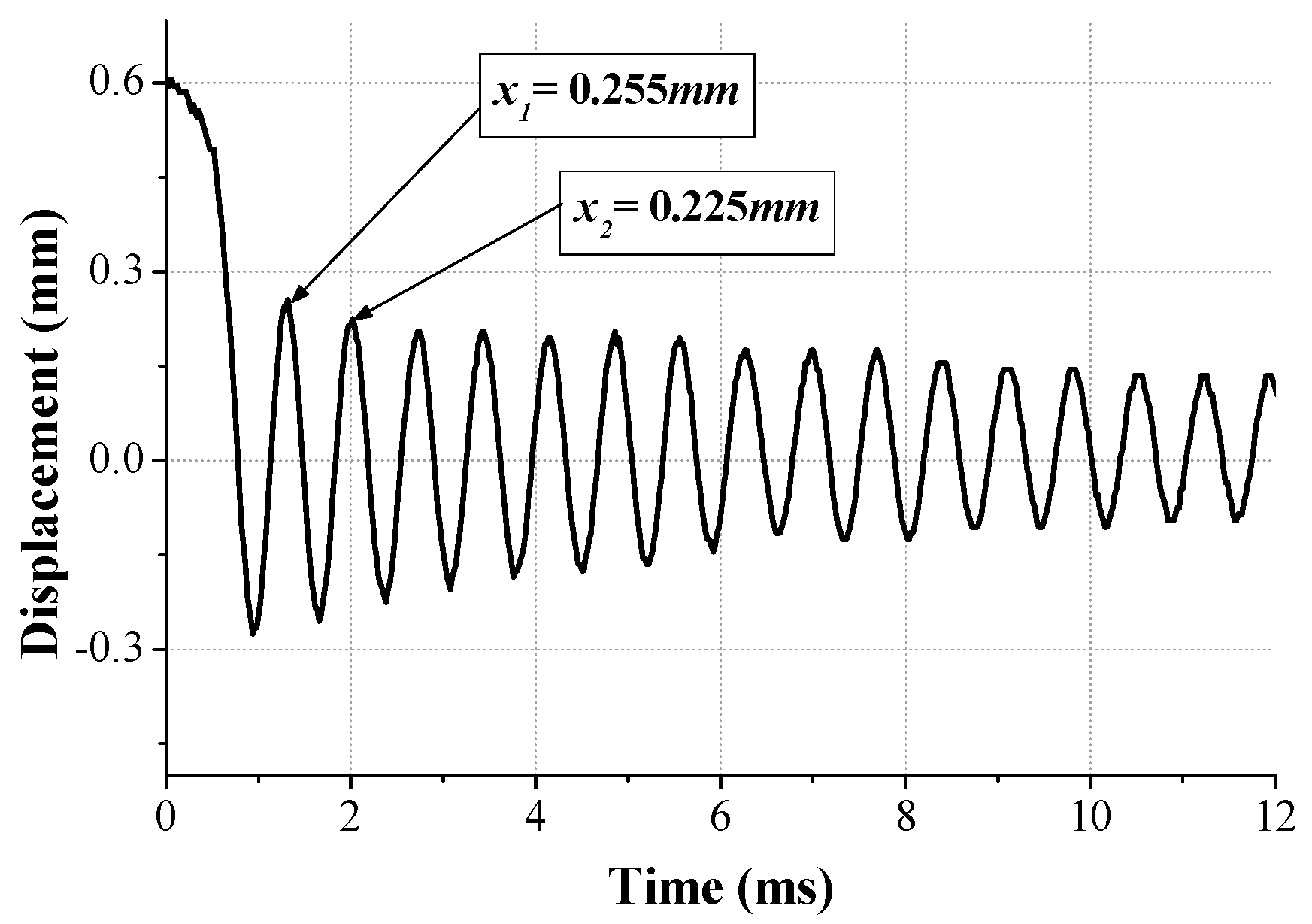

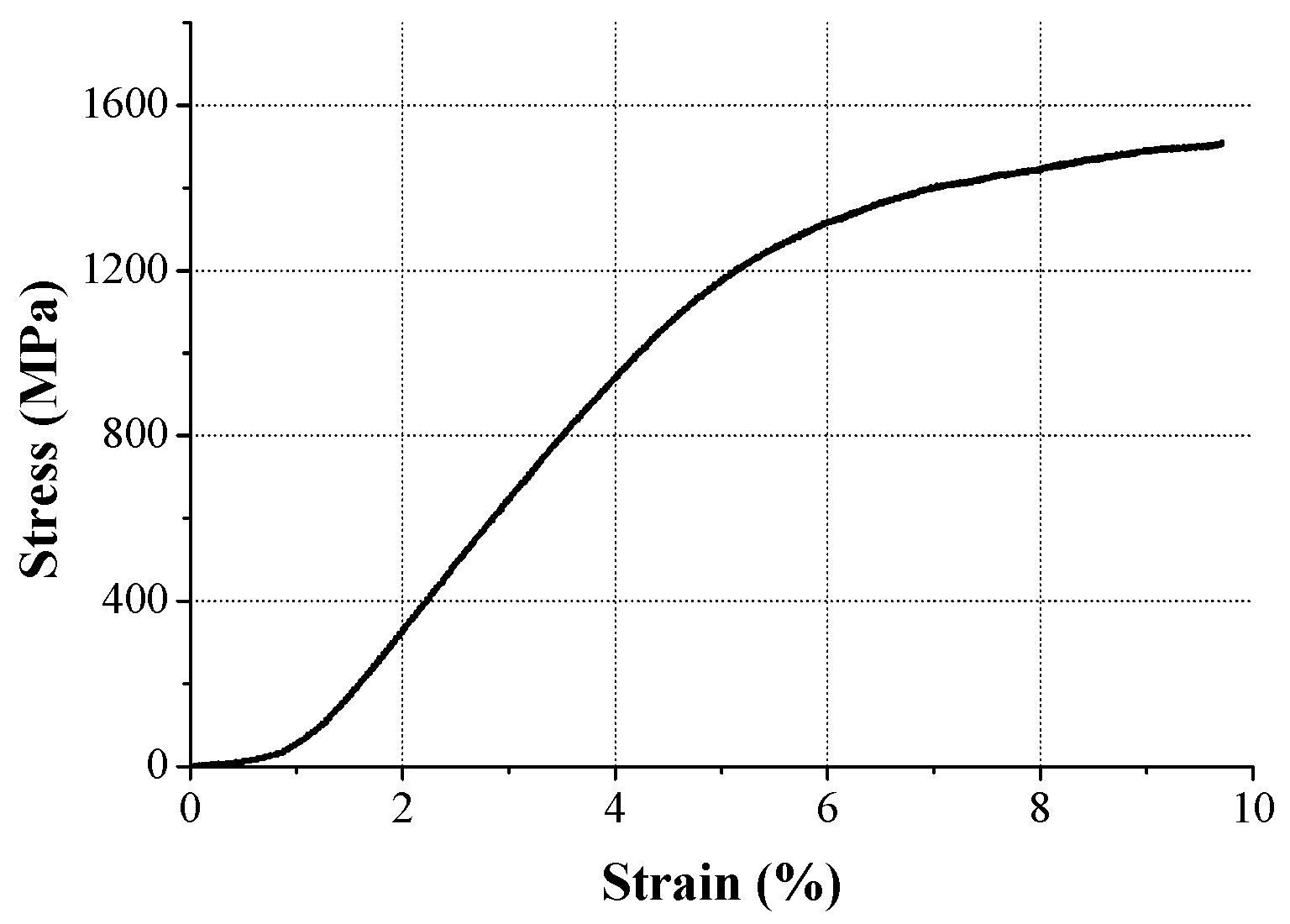
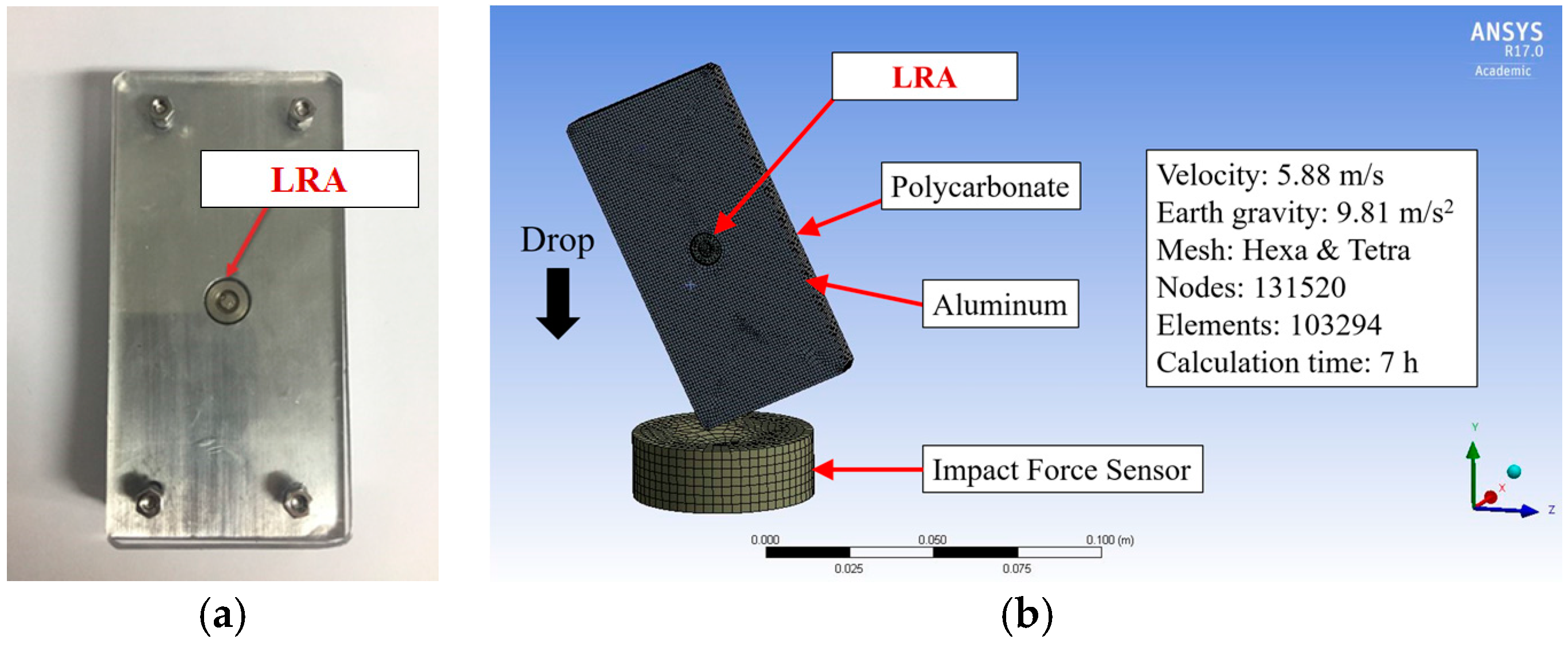

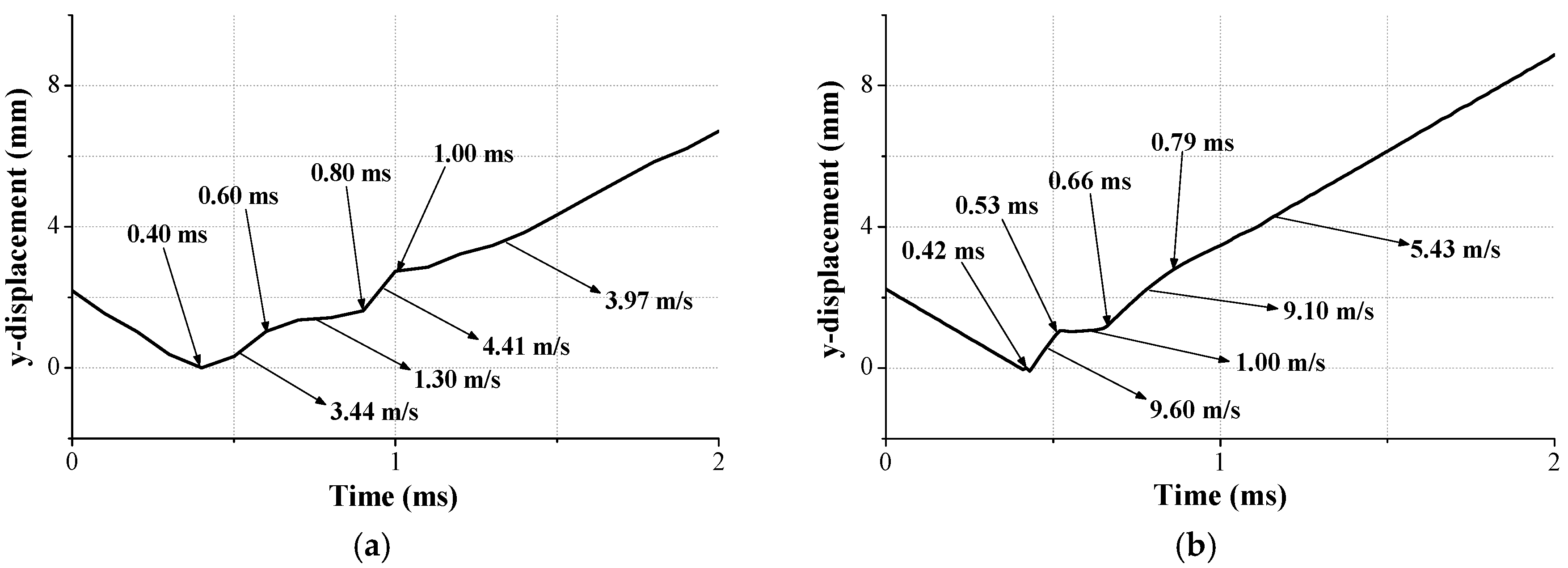
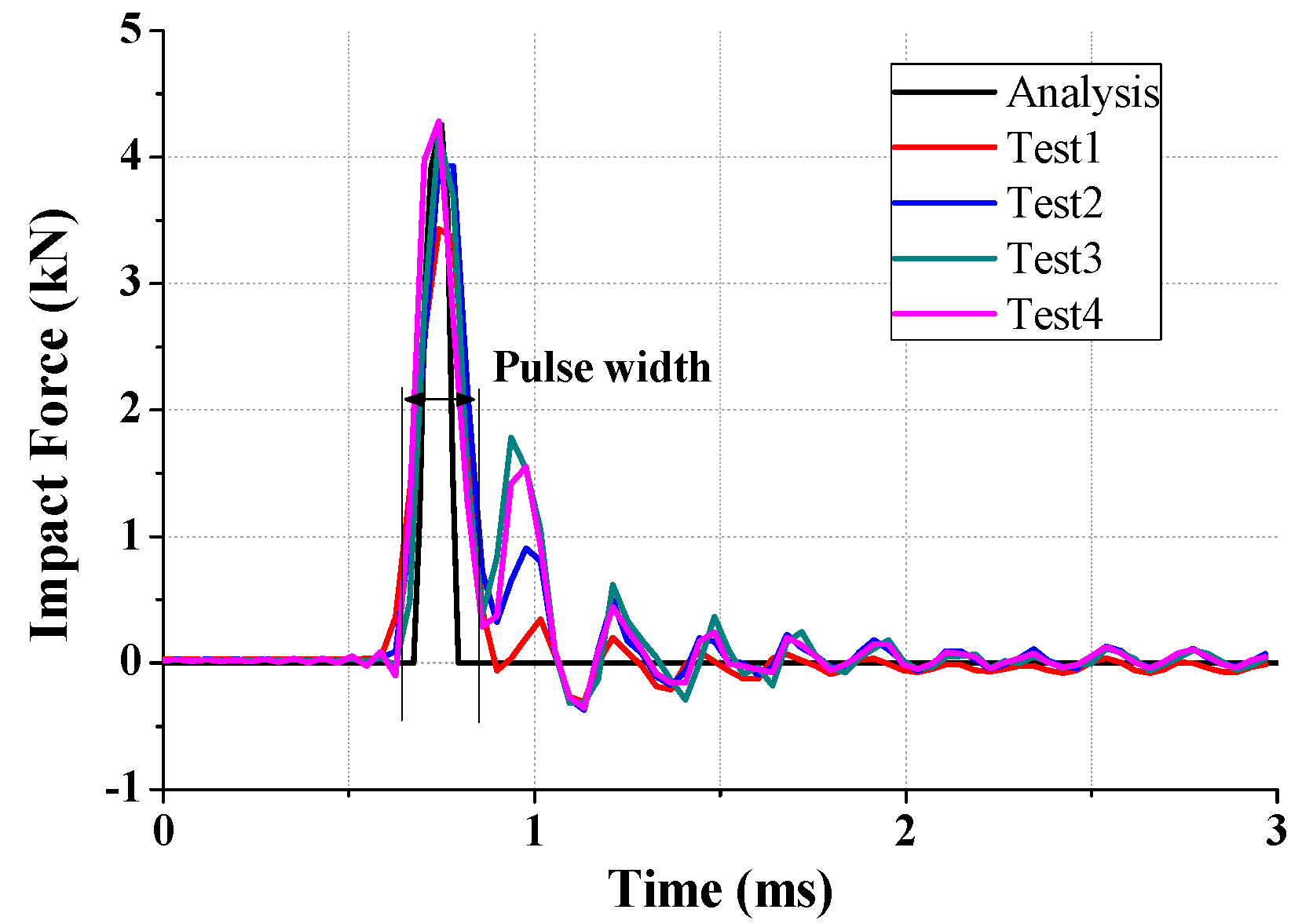
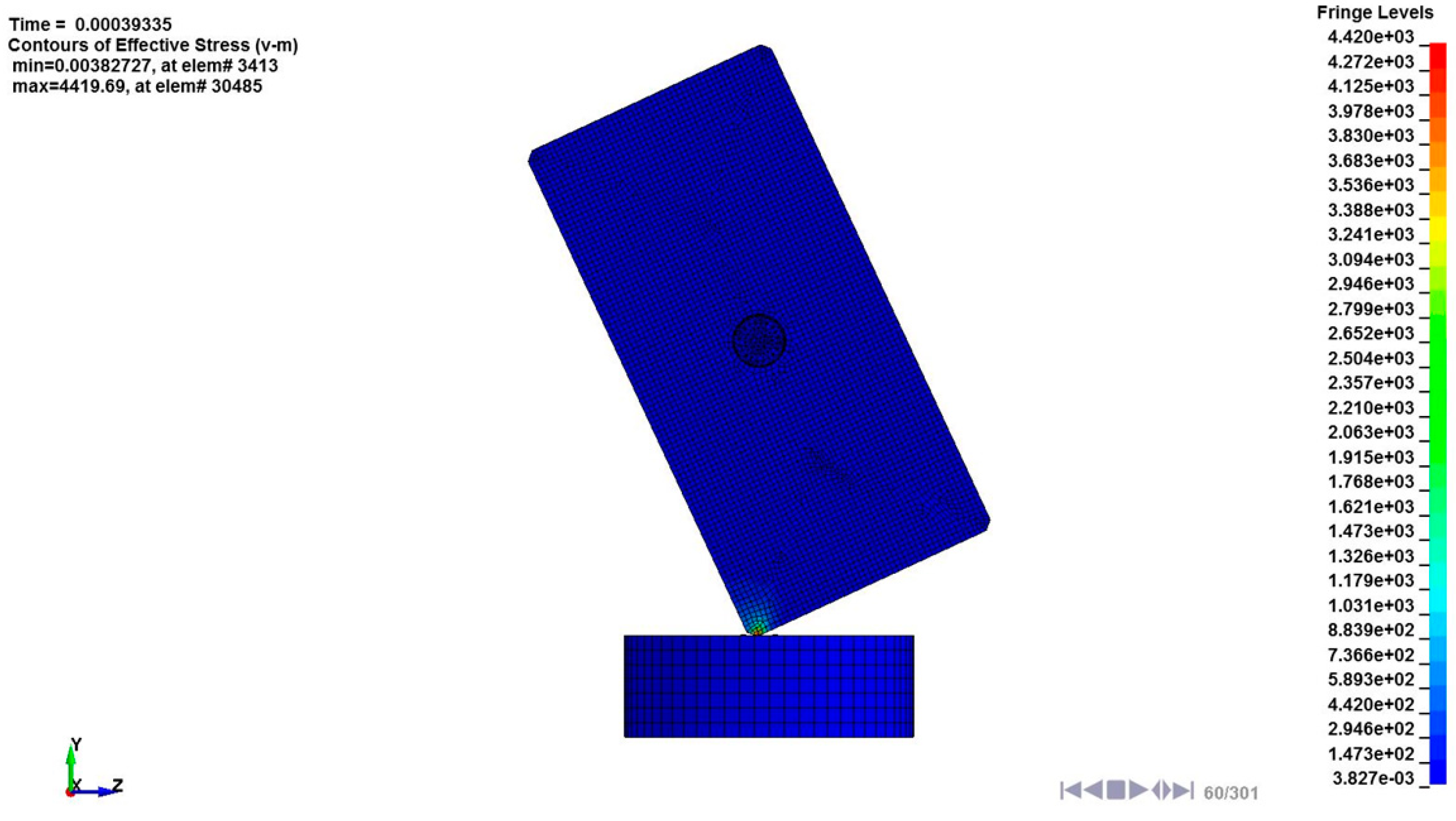
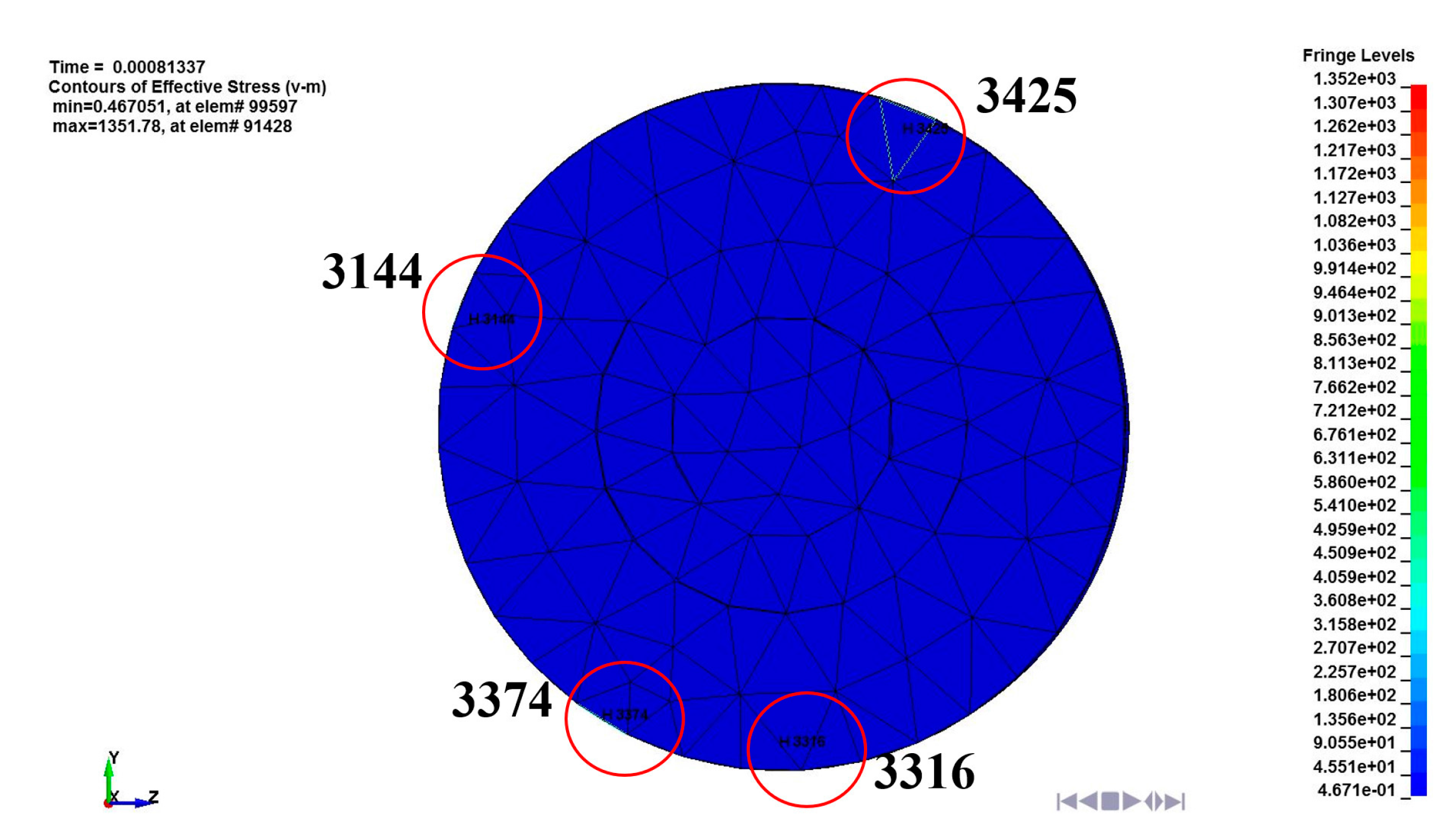

| No. | Peak Impact Force (kN) | Period (ms) | Force Error (%) |
|---|---|---|---|
| Assisted1 | 8.68 | 0.39 | 2.36 |
| Assisted2 | 8.84 | 0.47 | 0.56 |
| Assisted3 | 9.23 | 0.47 | 3.82 |
| Free1 | 8.78 | 0.39 | 1.24 |
| Free2 | 8.31 | 0.43 | 6.52 |
| Free3 | 9.48 | 0.43 | 6.64 |
| No. | Peak Force (N) | Pulse Width (ms) |
|---|---|---|
| Analysis | 4255.94 | 0.083 |
| Test1 | 3433.23 | 0.128 |
| Test2 | 3934.92 | 0.126 |
| Test3 | 4186.65 | 0.118 |
| Test4 | 4284.30 | 0.121 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, B.; Kwon, J.; Jeon, Y.; Lee, M.G. Development of Novel Platform to Predict the Mechanical Damage of a Miniature Mobile Haptic Actuator. Micromachines 2017, 8, 156. https://doi.org/10.3390/mi8050156
Choi B, Kwon J, Jeon Y, Lee MG. Development of Novel Platform to Predict the Mechanical Damage of a Miniature Mobile Haptic Actuator. Micromachines. 2017; 8(5):156. https://doi.org/10.3390/mi8050156
Chicago/Turabian StyleChoi, Byungjoo, Jiwoon Kwon, Yongho Jeon, and Moon Gu Lee. 2017. "Development of Novel Platform to Predict the Mechanical Damage of a Miniature Mobile Haptic Actuator" Micromachines 8, no. 5: 156. https://doi.org/10.3390/mi8050156
APA StyleChoi, B., Kwon, J., Jeon, Y., & Lee, M. G. (2017). Development of Novel Platform to Predict the Mechanical Damage of a Miniature Mobile Haptic Actuator. Micromachines, 8(5), 156. https://doi.org/10.3390/mi8050156






