Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters
Abstract
:1. Introduction
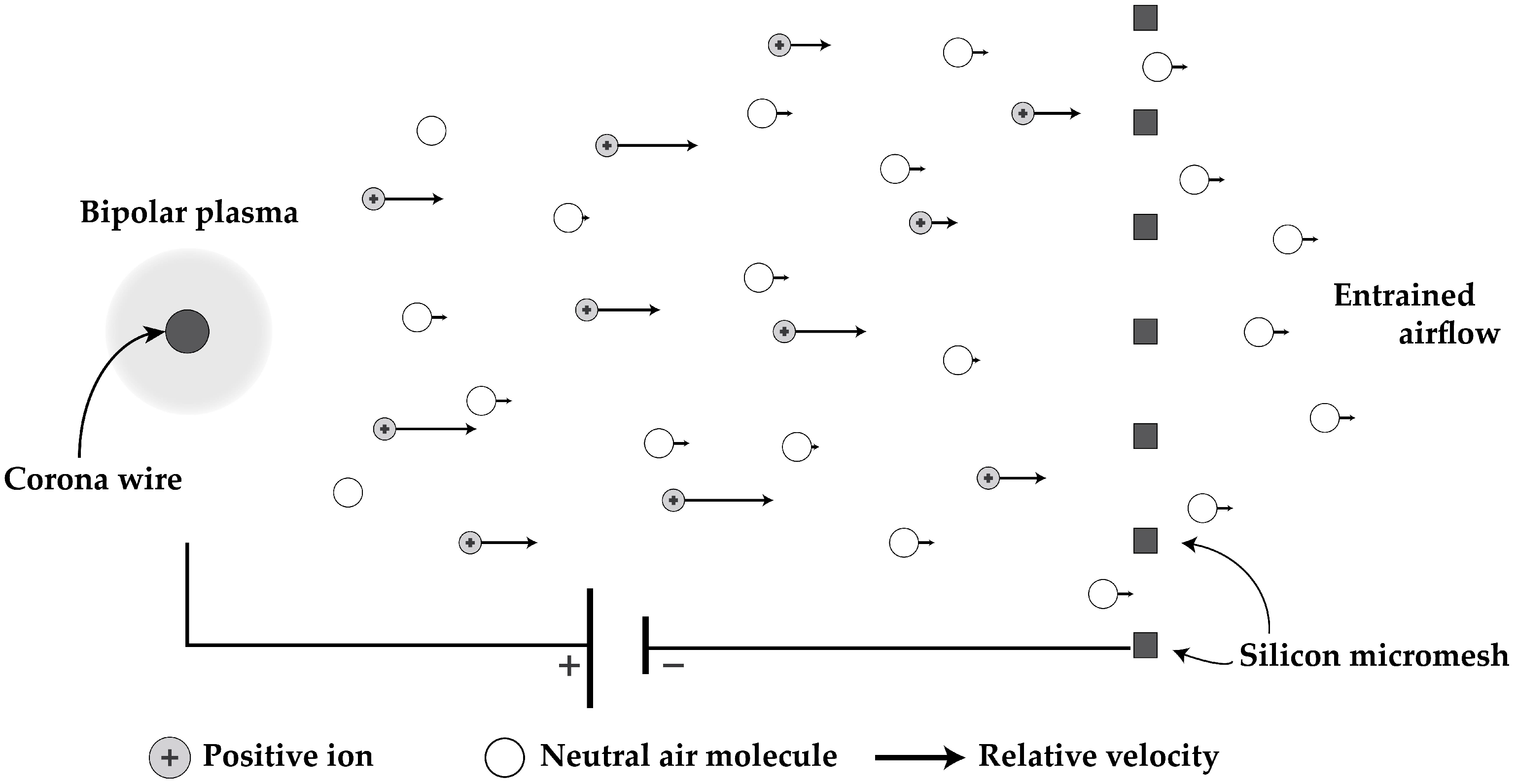
1.1. Electrohydrodynamic Force Scaling
1.2. Corona Discharge Scaling
1.3. Collector Electrode Effects
2. Materials and Methods
2.1. Electrode Design and Fabrication
2.2. Characterization Setup
3. Results
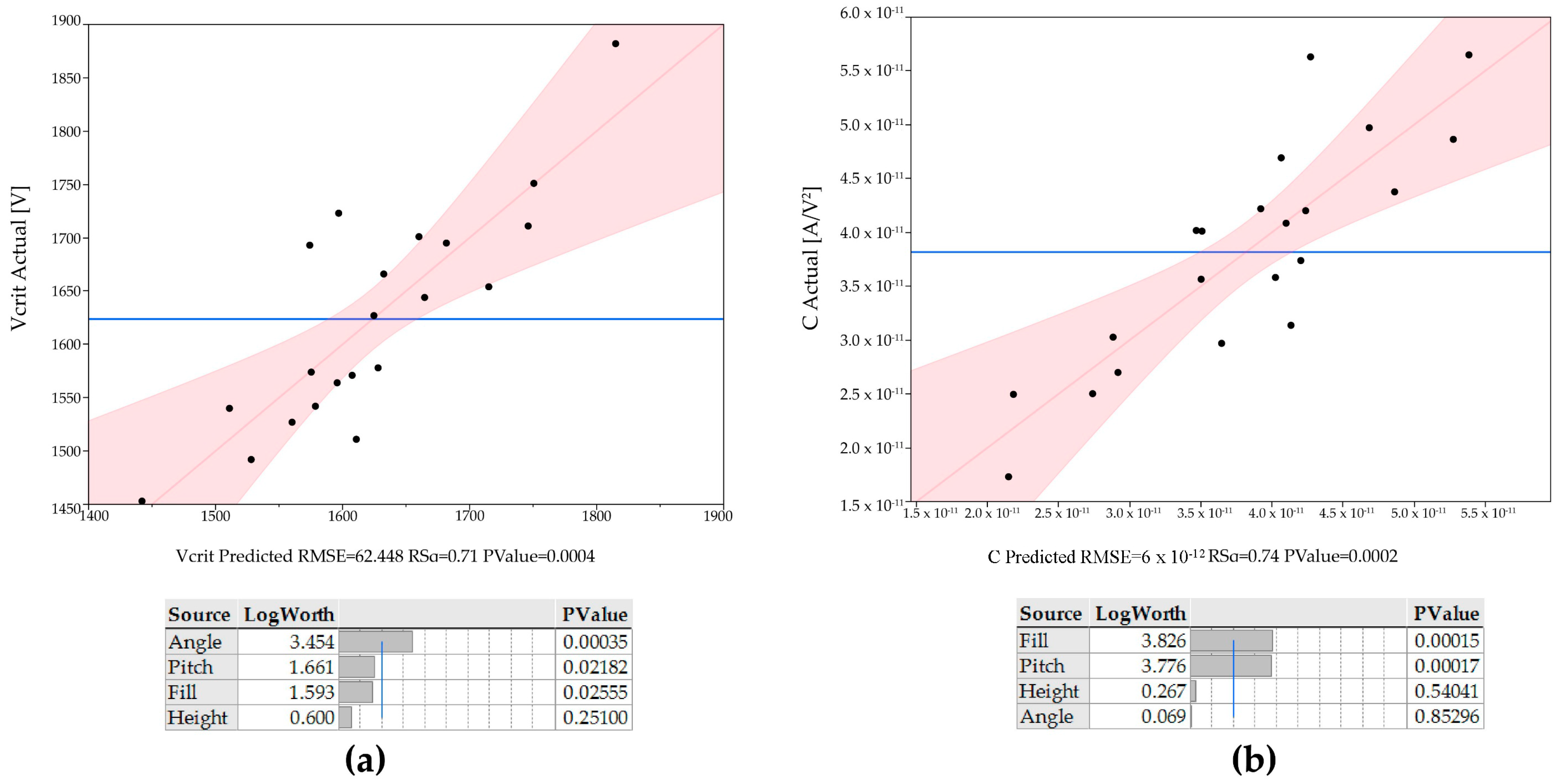
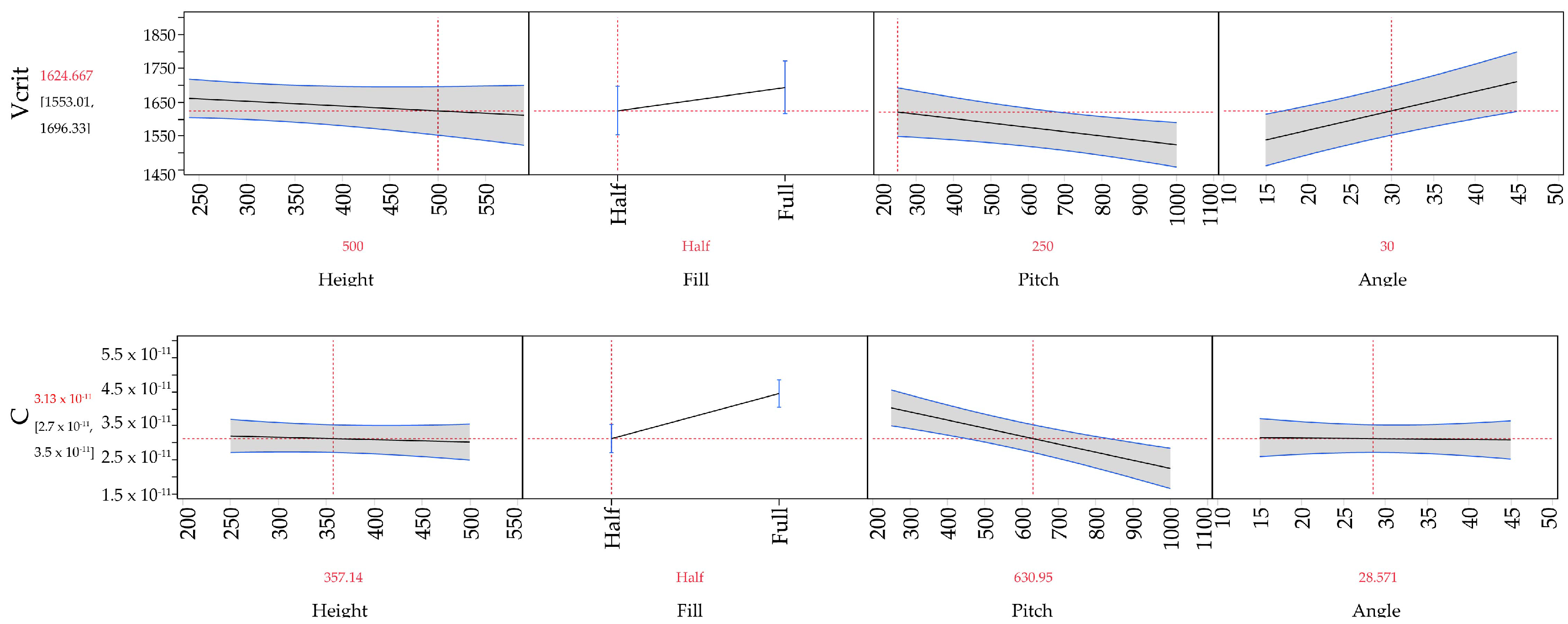
3.1. Corona Inception Voltage and Current
3.2. Loss Factor
3.3. Failure Modes
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| EHD | Electrohydrodynamic |
| MEMS | Micro electromechnical systems |
| DRIE | Deep reactive ion etch |
| IC | Integrated circuit |
References
- Flynn, A.M. Gnat Robots (and How They Will Change Robotics); Working Papers 295; MIT Artificial Intelligence Laboratory: Cambridge, MA, USA, 1987. [Google Scholar]
- Wood, R.J.; Finio, B.; Karpelson, M.; Ma, K.; Pérez-Arancibia, N.O.; Sreetharan, P.S.; Tanaka, H.; Whitney, J.P. Progress on ‘pico’air vehicles. Int. J. Robot. Res. 2012, 31, 1292–1302. [Google Scholar] [CrossRef]
- Wood, R.J. The first takeoff of a biologically inspired at-scale robotic insect. IEEE Trans. Robot. 2008, 24, 341–347. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, W.; Zhang, Z. Liftoff of an Electromagnetically Driven Insect-Inspired Flapping-Wing Robot. IEEE Trans. Robot. 2016, 32, 1285–1289. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, X.; Qi, M.; Lin, L. Electrostatic flapping wings with pivot-spar brackets for high lift force. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016; pp. 1133–1136. [Google Scholar]
- Robinson, M. A history of the electric wind. Am. J. Phys. 1962, 30, 366–372. [Google Scholar] [CrossRef]
- Fylladitakis, E.D.; Theodoridis, M.P.; Moronis, A.X. Review on the history, research, and applications of electrohydrodynamics. IEEE Trans. Plasma Sci. 2014, 42, 358–375. [Google Scholar] [CrossRef]
- Tabrizchi, M.; Khayamian, T.; Taj, N. Design and optimization of a corona discharge ionization source for ion mobility spectrometry. Rev. Sci. Instrum. 2000, 71, 2321–2328. [Google Scholar] [CrossRef]
- Robinson, M. Movement of air in the electric wind of the corona discharge. Trans. Ame. Inst. Electr. Eng. Part I Commun. Electron. 1961, 80, 143–150. [Google Scholar] [CrossRef]
- Christenson, E.A.; Moller, P.S. Ion-neutral propulsion in atmospheric media. AIAA J. 1967, 5, 1768–1773. [Google Scholar] [CrossRef]
- Pekker, L.; Young, M. Model of ideal electrohydrodynamic thruster. J. Propuls. Power 2011, 27, 786–792. [Google Scholar] [CrossRef]
- Drew, D.; Contreras, D.S.; Pister, K.S. First thrust from a microfabricated atmospheric ion engine. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 346–349. [Google Scholar]
- Drew, D.S.; Pister, K.S. First takeoff of a flying microrobot with no moving parts. In Proceedings of the International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Paris, France, 18–22 July 2016; pp. 1–6. [Google Scholar]
- Karpelson, M.; Wei, G.Y.; Wood, R.J. Driving high voltage piezoelectric actuators in microrobotic applications. Sens. Actuators A Phys. 2012, 176, 78–89. [Google Scholar] [CrossRef]
- Wang, H.C.; Jewell-Larsen, N.E.; Mamishev, A.V. Thermal management of microelectronics with electrostatic fluid accelerators. Appl. Ther. Eng. 2013, 51, 190–211. [Google Scholar] [CrossRef]
- Ong, A.O.; Abramson, A.R.; Tien, N.C. Electrohydrodynamic microfabricated ionic wind pumps for thermal management applications. J. Heat Transf. 2014, 136, 061703. [Google Scholar]
- Moreau, E.; Benard, N.; Lan-Sun-Luk, J.D.; Chabriat, J.P. Electrohydrodynamic force produced by a wire-to-cylinder dc corona discharge in air at atmospheric pressure. J. Phys. D Appl. Phys. 2013, 46, 475204. [Google Scholar] [CrossRef]
- Chang, J.S.; Lawless, P.A.; Yamamoto, T. Corona discharge processes. IEEE Trans. Plasma Sci. 1991, 19, 1152–1166. [Google Scholar] [CrossRef]
- Peek, F.W. Dielectric Phenomena in High Voltage Engineering; McGraw-Hill Book Company, Incorporated: New York, NY, USA, 1920. [Google Scholar]
- Tirumala, R.; Li, Y.; Pohlman, D.; Go, D. Corona discharges in sub-millimeter electrode gaps. J. Electrost. 2011, 69, 36–42. [Google Scholar] [CrossRef]
- Vuhuu, Q.; Comsa, R. Influence of gap length on wire-plane corona. IEEE Trans. Power Appar. Syst. 1969. [Google Scholar] [CrossRef]
- Moreau, E.; Touchard, G. Enhancing the mechanical efficiency of electric wind in corona discharges. J. Electrost. 2008, 66, 39–44. [Google Scholar] [CrossRef]
- O’Hern, T.; Torczynski, J. Reynolds number dependence of the drag coefficient for laminar flow through fine-scale photoetched screens. Exp. Fluids 1993, 15, 75–81. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Wotton-under-Edge, UK, 1881; Volume 1. [Google Scholar]
- Eifert, A.; Baier, T.; Hardt, S. Small onset voltages in negative corona discharges using the edges of gold and aluminum foils as nano-structured electrodes. Appl. Phys. Lett. 2013, 103, 023114. [Google Scholar] [CrossRef]

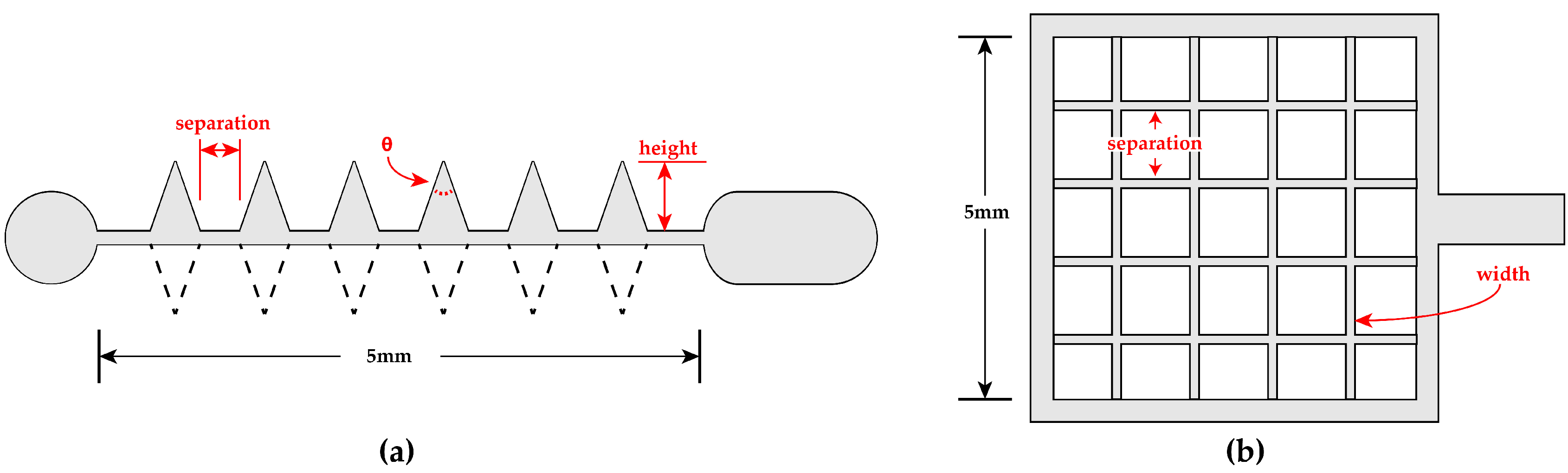

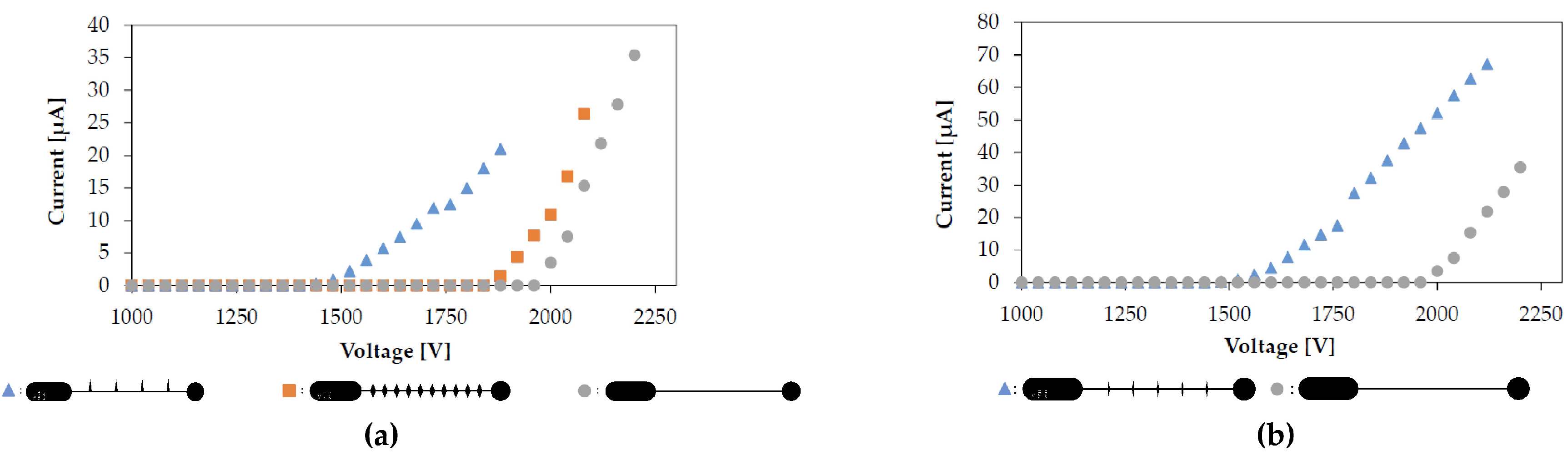
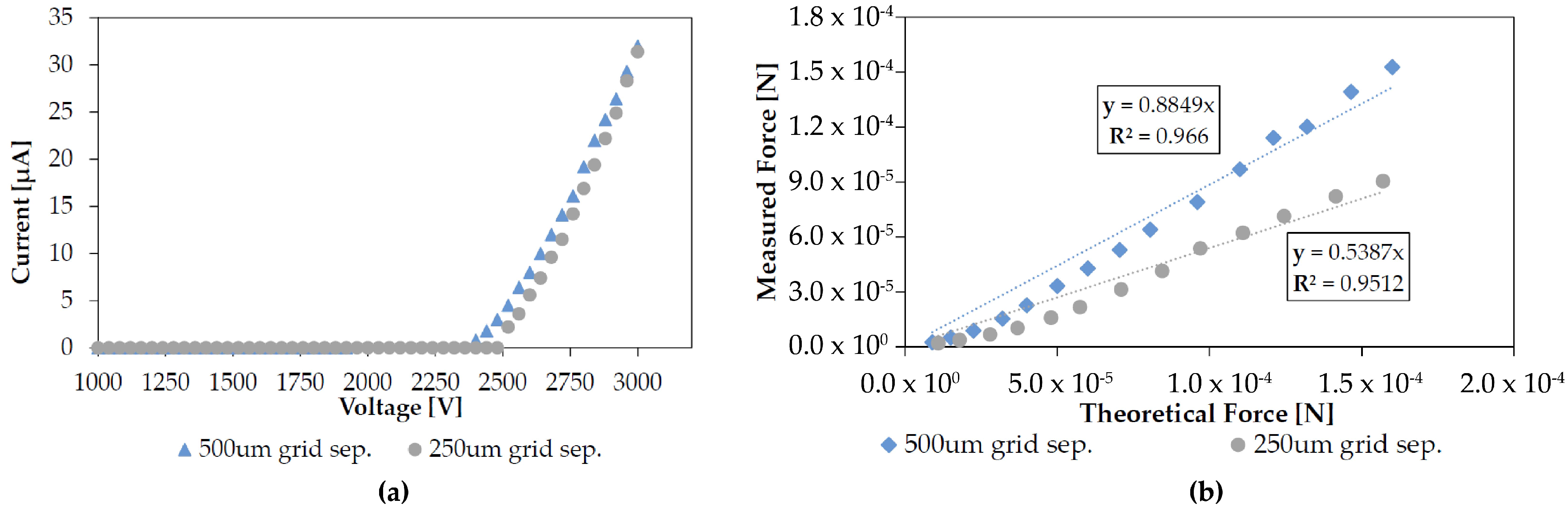
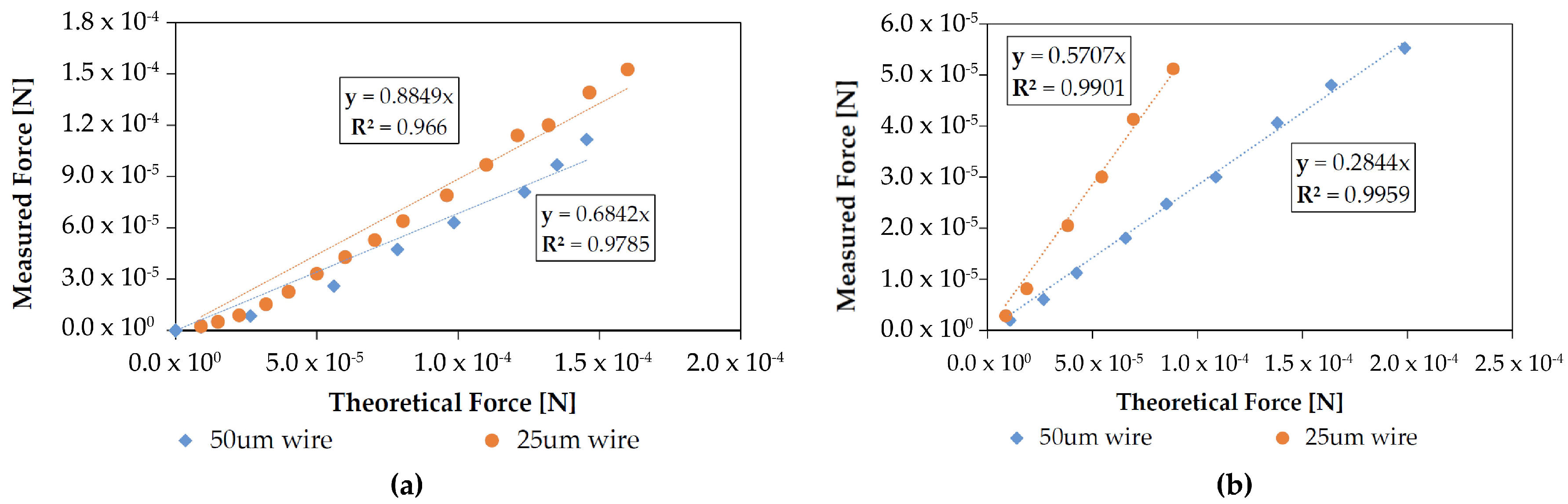
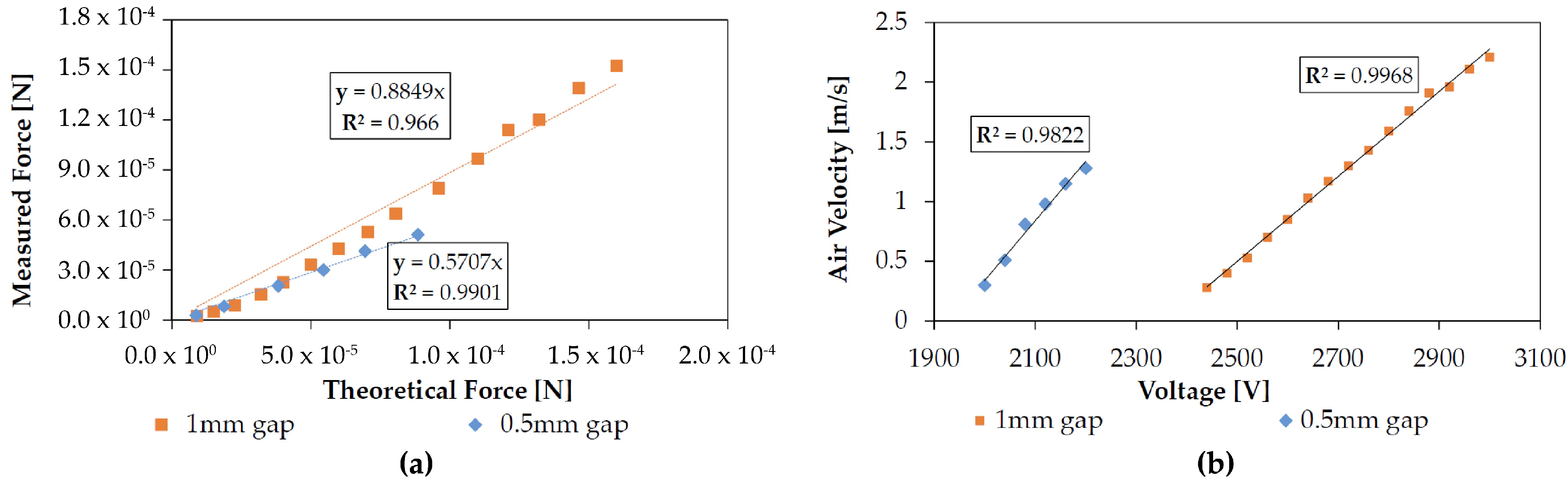


| Emitter Wires | Collector Grids | ||||
|---|---|---|---|---|---|
| Separation | Height | Angle | Fill | Separation | Width |
| 250 | 250 | 15 | Half | 250 | 10 |
| 500 | 500 | 30 | Full | 500 | 25 |
| 750 | - | 45 | - | 750 | 50 |
| 1000 | - | - | - | 1000 | - |
| - | - | - | - | 1250 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drew, D.S.; Pister, K.S.J. Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters. Micromachines 2017, 8, 141. https://doi.org/10.3390/mi8050141
Drew DS, Pister KSJ. Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters. Micromachines. 2017; 8(5):141. https://doi.org/10.3390/mi8050141
Chicago/Turabian StyleDrew, Daniel S., and Kristofer S. J. Pister. 2017. "Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters" Micromachines 8, no. 5: 141. https://doi.org/10.3390/mi8050141
APA StyleDrew, D. S., & Pister, K. S. J. (2017). Geometric Optimization of Microfabricated Silicon Electrodes for Corona Discharge-Based Electrohydrodynamic Thrusters. Micromachines, 8(5), 141. https://doi.org/10.3390/mi8050141






