Modeling of MEMS Mirrors Actuated by Phase-Change Mechanism
Abstract
:1. Introduction
2. Experimental Procedures
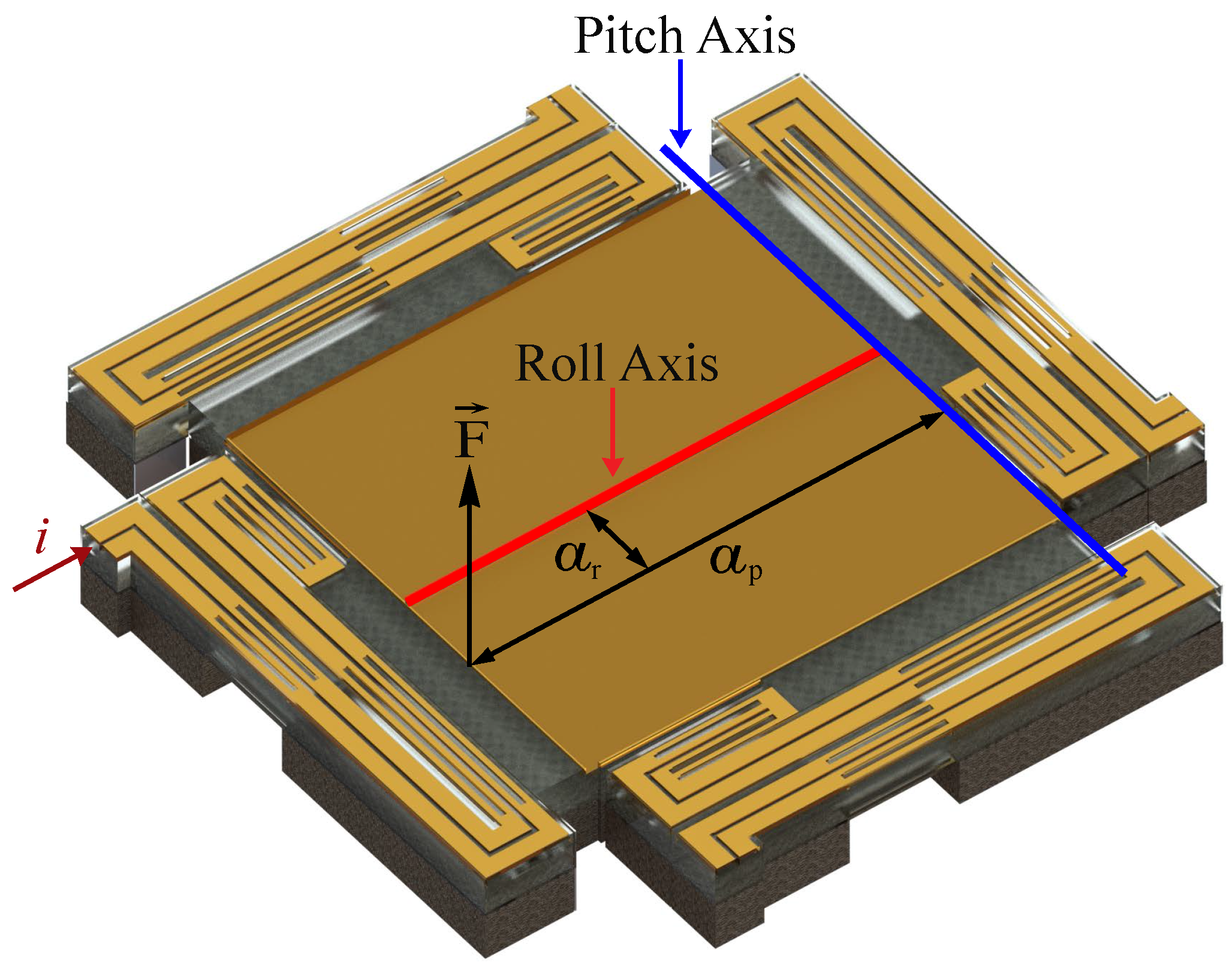
2.1. Design and Fabrication of VO2-Based MEMS Mirrors
2.2. Increasing Yield by Reducing Intrinsic Stress
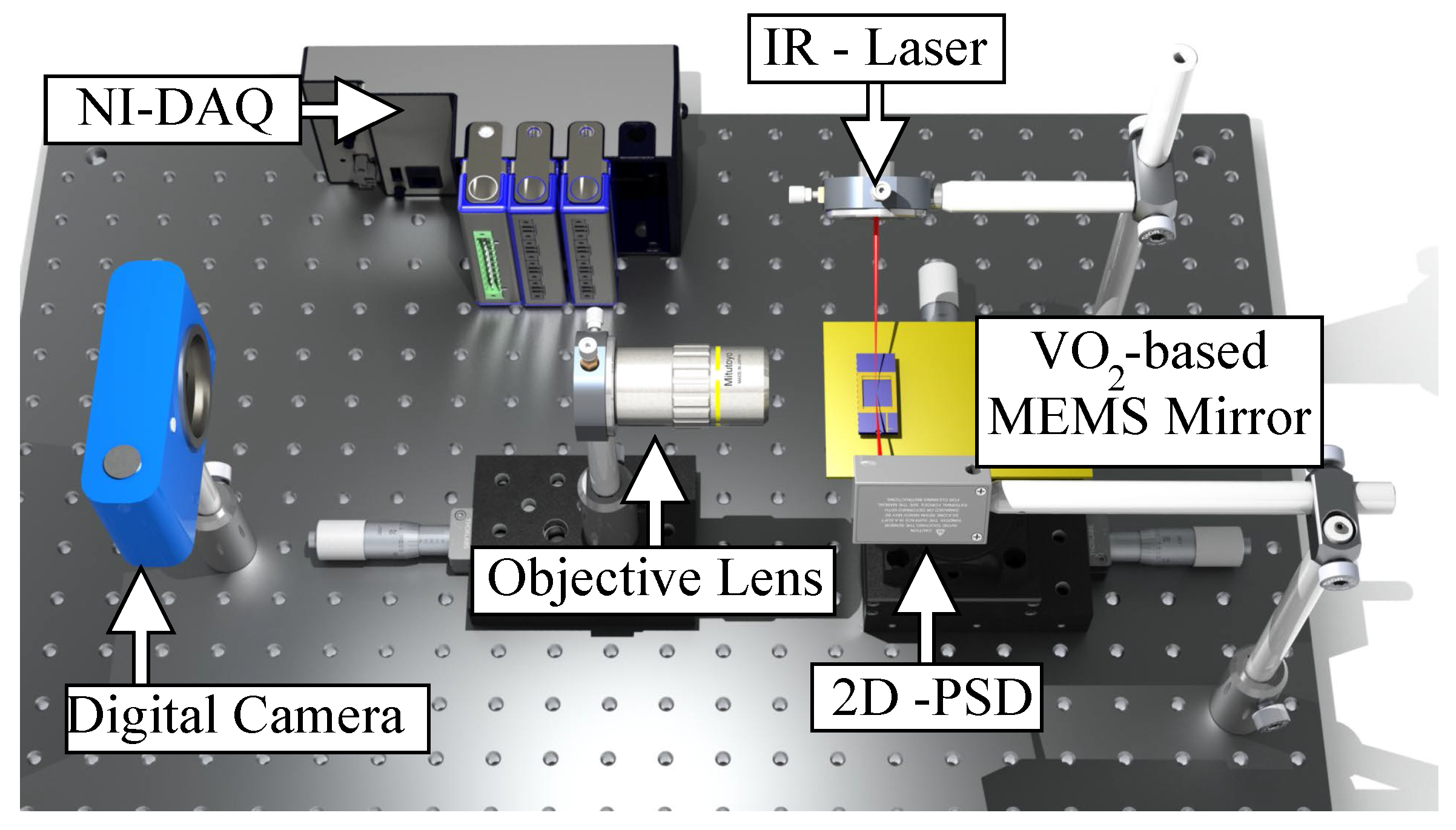
2.3. Experimental Setup
3. Modeling
3.1. Linear Model
3.2. Nonlinear Model
3.2.1. Phase Transition-Induced Force
3.2.2. Differential Thermal Expansion-Induced Force
4. Results and Discussion
4.1. Simulation Results
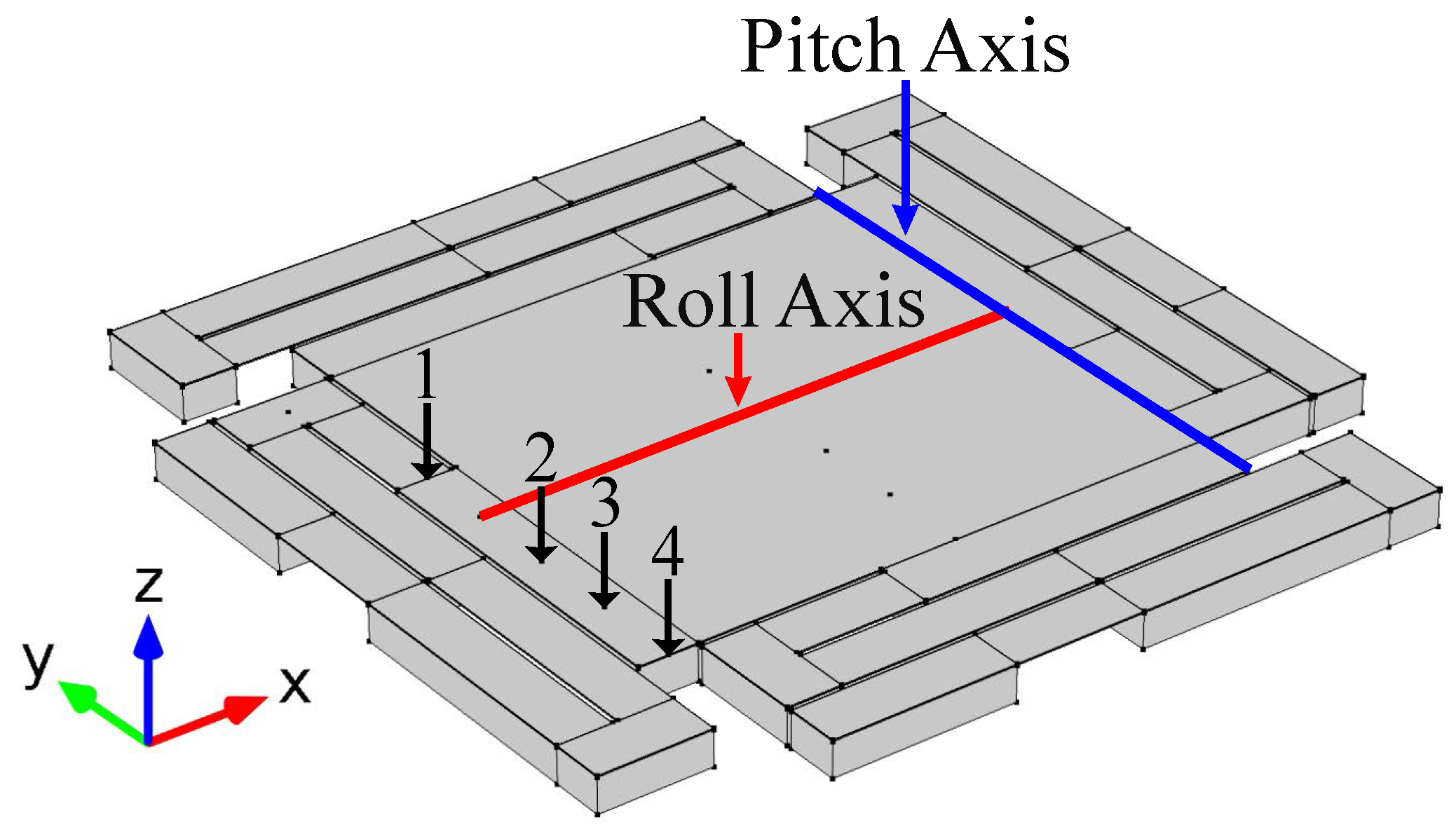
4.2. MEMS Mirror Mechanical Model
4.3. Identification and Verification
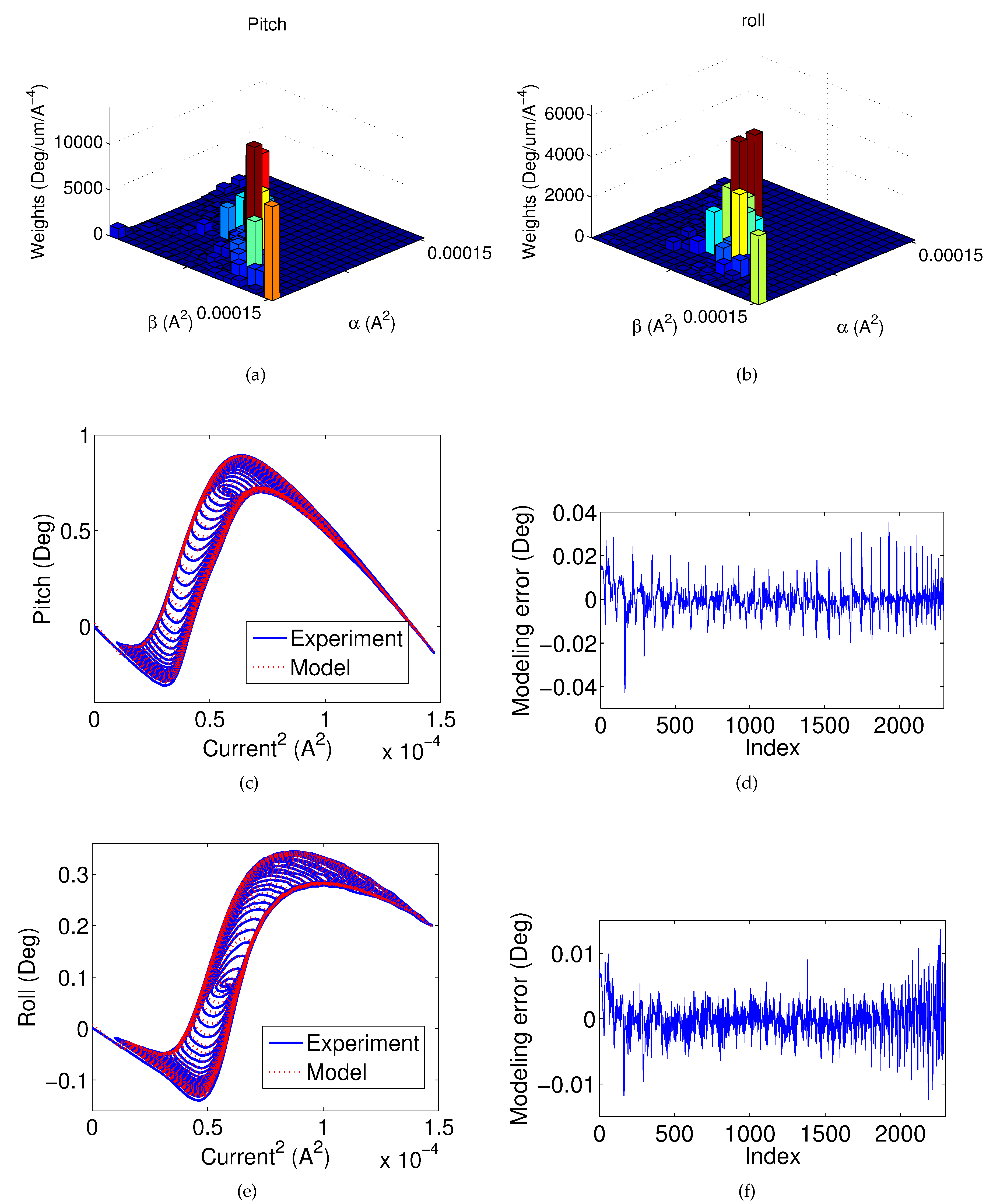
4.3.1. Identification
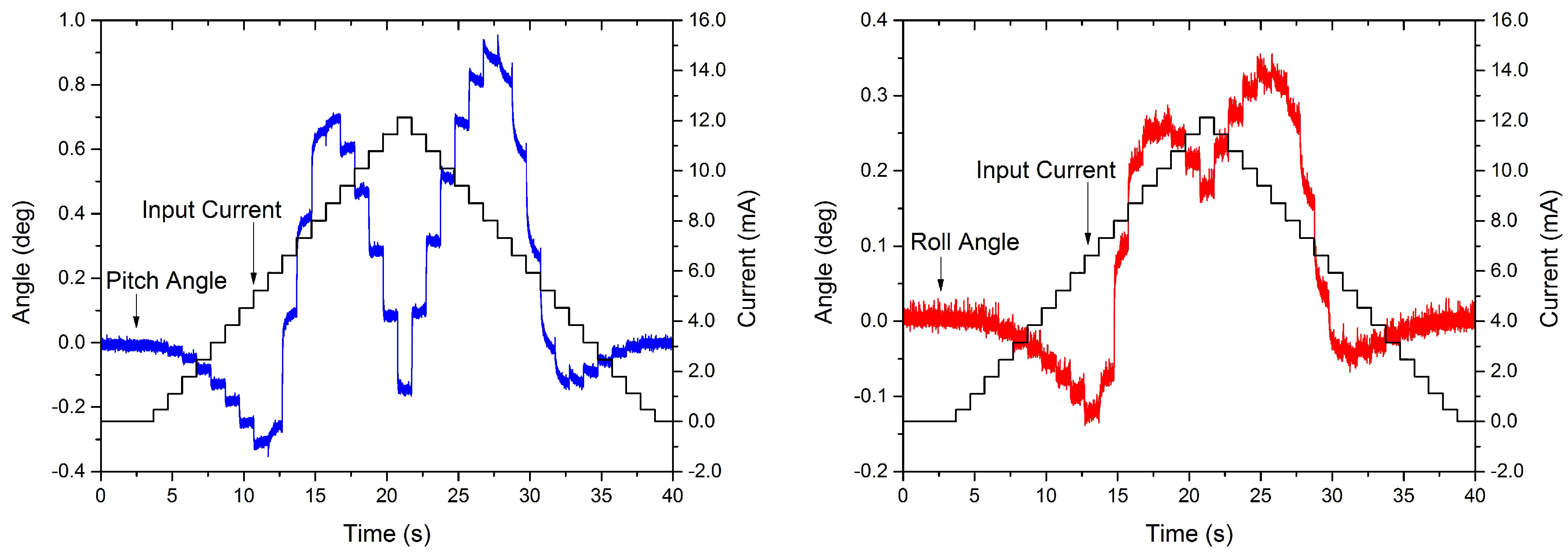
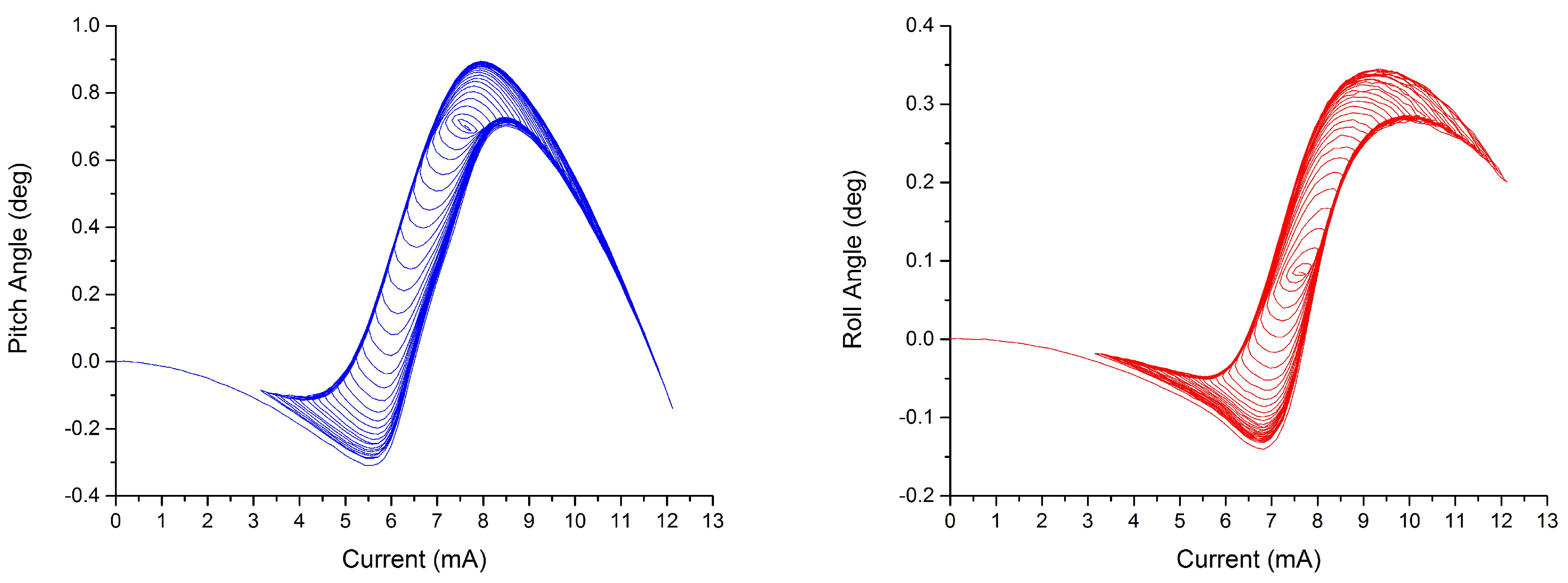
4.3.2. Quasi-Static Verification
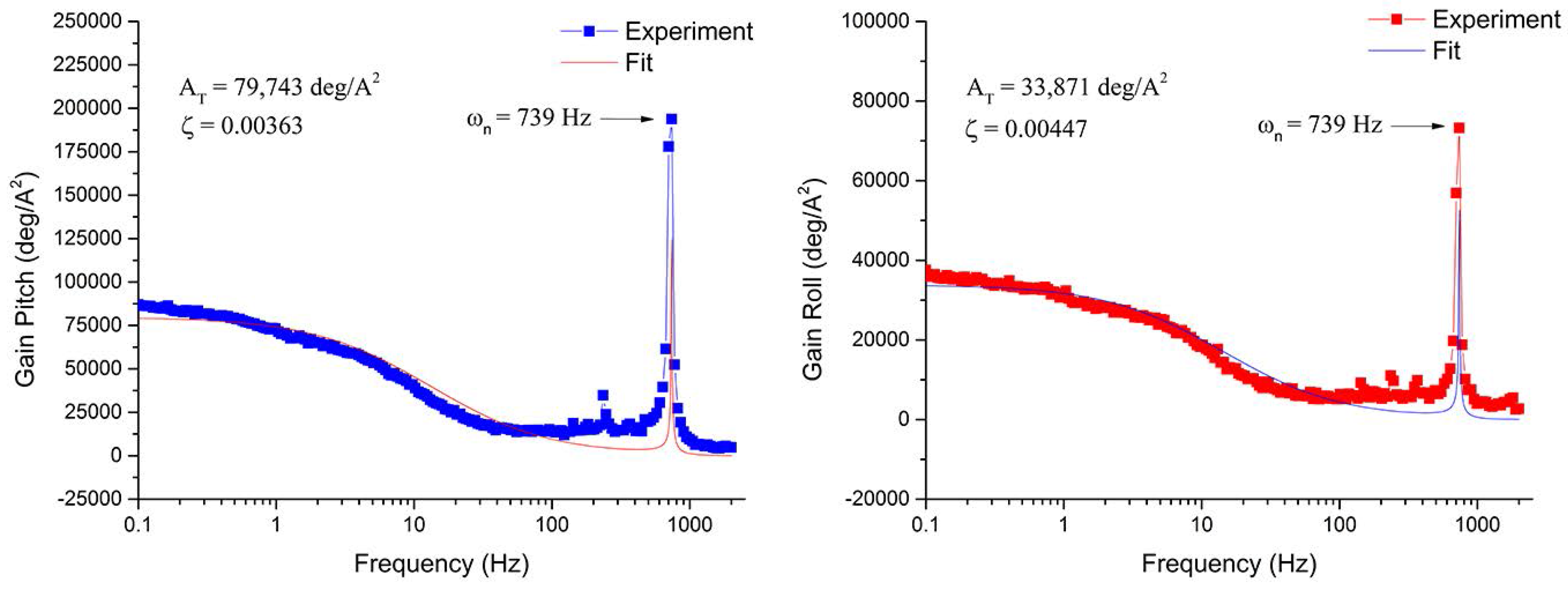
4.3.3. Frequency Verification
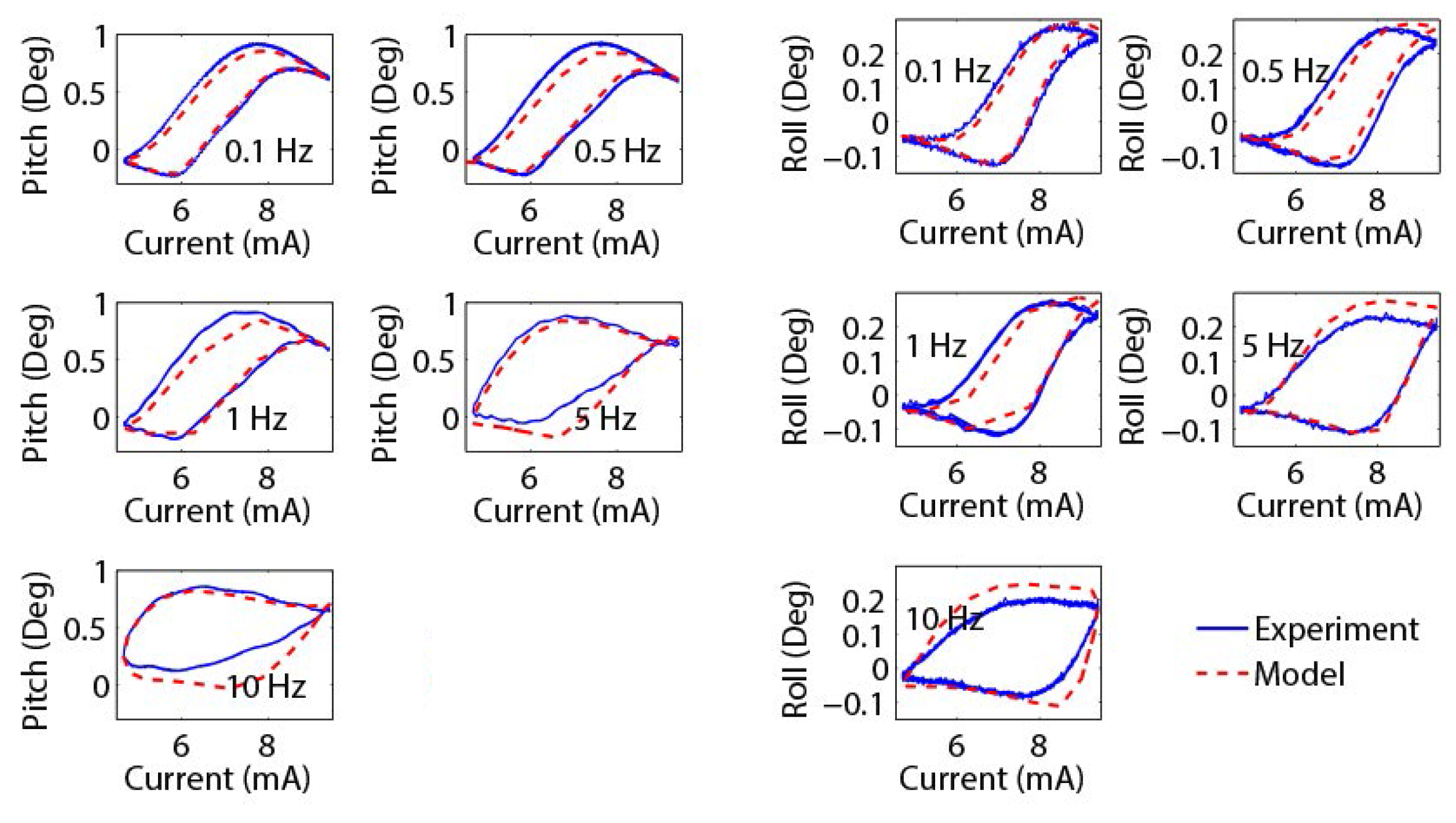
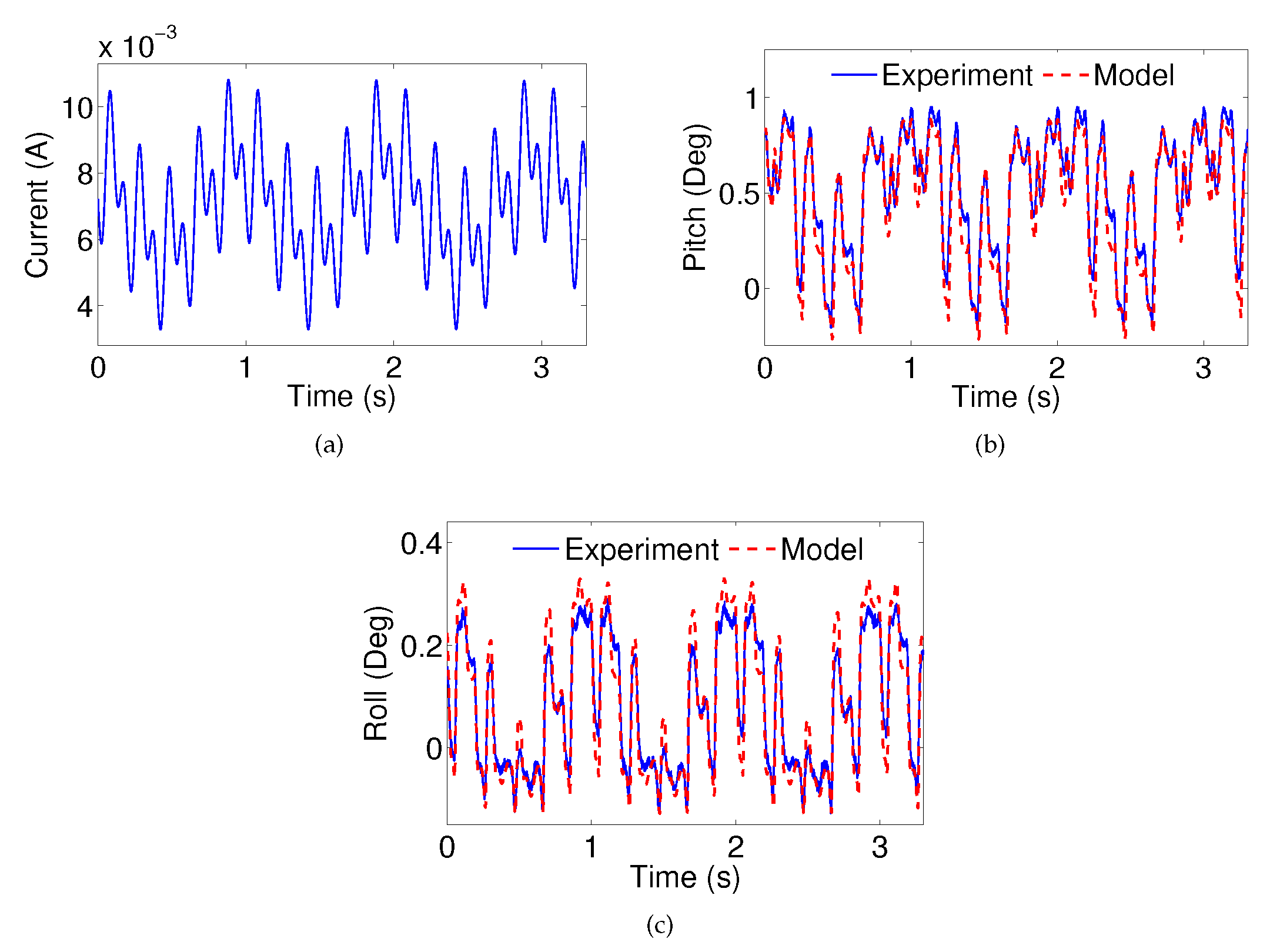
4.3.4. Multi-Frequency Verification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xie, H.; Pan, Y.; Fedder, G.K. A CMOS-MEMS mirror with curled-hinge comb drives. J. Microelectromech. Syst. 2003, 12, 450–457. [Google Scholar]
- Koh, K.H.; Kobayashi, T.; Lee, C. A 2-D MEMS scanning mirror based on dynamic mixed mode excitation of a piezoelectric PZT thin film S-shaped actuator. Opt. Express 2011, 19, 13812–13824. [Google Scholar] [CrossRef] [PubMed]
- Hung, A.C.L.; Lai, H.Y.H.; Lin, T.W.; Fu, S.G.; Lu, M.S.C. An electrostatically driven 2D micro-scanning mirror with capacitive sensing for projection display. Sens. Actuators A Phys. 2015, 222, 122–129. [Google Scholar] [CrossRef]
- Naono, T.; Fujii, T.; Esashi, M.; Tanaka, S. Non-resonant 2-D piezoelectric MEMS optical scanner actuated by Nb doped PZT thin film. Sens. Actuators A Phys. 2015, 233, 147–157. [Google Scholar] [CrossRef]
- Yalcinkaya, A.; Urey, H.; Brown, D.; Montague, T.; Sprague, R. Two-axis electromagnetic microscanner for high resolution displays. J. Microelectromech. Syst. 2006, 15, 786–794. [Google Scholar] [CrossRef]
- Cho, A.R.; Han, A.; Ju, S.; Jeong, H.; Park, J.H.; Kim, I.; Bu, J.U.; Ji, C.H. Electromagnetic biaxial microscanner with mechanical amplification at resonance. Opt. Express 2015, 23, 16792–16802. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Dooley, S.; Watson, E.; McManamon, P.F.; Xie, H. A Tip-Tilt-Piston Micromirror Array for Optical Phased Array Applications. J. Microelectromech. Syst. 2010, 19, 1450–1461. [Google Scholar] [CrossRef]
- Jain, A.; Qu, H.; Todd, S.; Xie, H. A thermal bimorph micromirror with large bi-directional and vertical actuation. Sens. Actuators A Phys. 2005, 122, 9–15. [Google Scholar] [CrossRef]
- Samuelson, S.R.; Xie, H. A Large Piston Displacement MEMS Mirror With Electrothermal Ladder Actuator Arrays for Ultra-Low Tilt Applications. J. Microelectromech. Syst. 2014, 23, 39–49. [Google Scholar] [CrossRef]
- Torres, D.; Wang, T.; Zhang, J.; Zhang, X.; Dooley, S.; Tan, X.; Xie, H.; Sepúlveda, N. VO2-Based MEMS Mirrors. J. Microelectromech. Syst. 2016, 25, 780–787. [Google Scholar] [CrossRef]
- Sepulveda, N.; Rua, A.; Cabrera, R.; Fernández, F. Young’s modulus of VO2 thin films as a function of temperature including insulator-to-metal transition regime. Appl. Phys. Lett. 2008, 92, 1913. [Google Scholar] [CrossRef]
- Zylbersztejn, A.; Mott, N. Metal-insulator transition in vanadium dioxide. Phys. Rev. B 1975, 11, 4383. [Google Scholar] [CrossRef]
- Barker, A., Jr.; Verleur, H.; Guggenheim, H. Infrared optical properties of vanadium dioxide above and below the transition temperature. Phys. Rev. Lett. 1966, 17, 1286. [Google Scholar] [CrossRef]
- Mlyuka, N.R.; Niklasson, G.A.; Granqvist, C.G. Mg doping of thermochromic VO2 films enhances the optical transmittance and decreases the metal-insulator transition temperature. Appl. Phys. Lett. 2009, 95, 171909. [Google Scholar] [CrossRef]
- Cao, J.; Gu, Y.; Fan, W.; Chen, L.; Ogletree, D.; Chen, K.; Tamura, N.; Kunz, M.; Barrett, C.; Seidel, J.; et al. Extended mapping and exploration of the vanadium dioxide stress-temperature phase diagram. Nano Lett. 2010, 10, 2667–2673. [Google Scholar] [CrossRef] [PubMed]
- Breckenfeld, E.; Kim, H.; Burgess, K.; Charipar, N.; Cheng, S.F.; Stroud, R.; Piqué, A. Strain Effects in Epitaxial VO2 Thin Films on Columnar Buffer-Layer TiO2/Al2O3 Virtual Substrates. ACS Appl. Mater. Interfaces 2017, 9, 1577–1584. [Google Scholar] [CrossRef] [PubMed]
- Merced, E.; Tan, X.; Sepúlveda, N. Strain energy density of VO2-based microactuators. Sens. Actuators A Phys. 2013, 196, 30–37. [Google Scholar] [CrossRef]
- Rúa, A.; Fernández, F.l.E.; Sepúlveda, N. Bending in VO2-coated microcantilevers suitable for thermally activated actuators. J. Appl. Phys. 2010, 107, 074506. [Google Scholar] [CrossRef]
- Cabrera, R.; Merced, E.; Sepúlveda, N. Performance of Electro-Thermally Driven VO2-Based MEMS Actuators. J. Microelectromech. Syst. 2014, 23, 243–251. [Google Scholar] [CrossRef]
- Cabrera, R.; Merced, E.; Sepúlveda, N. A micro-electro-mechanical memory based on the structural phase transition of VO2. Phys. Status Solidi 2013, 210, 1704–1711. [Google Scholar] [CrossRef]
- Merced, E.; Cabrera, R.; Dávila, N.; Fernández, F.E.; Sepúlveda, N. A micro-mechanical resonator with programmable frequency capability. Smart Mater. Struct. 2012, 21, 035007. [Google Scholar] [CrossRef]
- Bai, Y.; Yeow, J.T.W.; Wilson, B.C. A Characteristic Study of Micromirror with Sidewall Electrodes. Int. J. Optomech. 2007, 1, 231–258. [Google Scholar] [CrossRef]
- Isikman, S.O.; Urey, H. Dynamic Modeling of Soft Magnetic Film Actuated Scanners. IEEE Trans. Magn. 2009, 45, 2912–2919. [Google Scholar] [CrossRef]
- Han, F.; Wang, W.; Zhang, X.; Xie, H. Modeling and Control of a Large-Stroke Electrothermal MEMS Mirror for Fourier Transform Microspectrometers. J. Microelectromech. Syst. 2016, 25, 750–760. [Google Scholar] [CrossRef]
- Zhang, J.; Merced, E.; Sepúlveda, N.; Tan, X. Optimal compression of generalized Prandtl–Ishlinskii hysteresis models. Automatica 2015, 57, 170–179. [Google Scholar] [CrossRef]
- Zhang, J.; Merced, E.; Sepúlveda, N.; Tan, X. Modeling and Inverse Compensation of Nonmonotonic Hysteresis in VO2-Coated Microactuators. IEEE/ASME Trans. Mech. 2014, 19, 579–588. [Google Scholar] [CrossRef]
- Zhang, J.; Torres, D.; Ebel, J.L.; Sepúlveda, N.; Tan, X. A Composite Hysteresis Model in Self-Sensing Feedback Control of Fully Integrated VO2 Microactuators. IEEE/ASME Trans. Mech. 2016, 21, 2405–2417. [Google Scholar] [CrossRef]
- Merced, E.; Torres, D.; Tan, X.; Sepúlveda, N. An Electrothermally Actuated VO2-Based MEMS Using Self-Sensing Feedback Control. J. Microelectromech. Syst. 2015, 24, 100–107. [Google Scholar] [CrossRef]
- Xie, H. Vertical Displacement Device. US Patent 6,940,630, 6 September 2005. [Google Scholar]
- Wu, L.; Xie, H. A large vertical displacement electrothermal bimorph microactuator with very small lateral shift. Sens. Actuators A Phys. 2008, 145, 371–379. [Google Scholar] [CrossRef]
- Zhang, L.; Tsaur, J.; Maeda, R. Residual Stress Study of SiO2/Pt/Pb(Zr,Ti)O3/Pt Multilayer Structure for Micro Electro Mechanical System Applications. Jpn. J. Appl. Phys. 2003, 42, 1386. [Google Scholar] [CrossRef]
- Matsui, Y.; Hiratani, M.; Kumagai, Y.; Miura, H.; Fujisaki, Y. Thermal Stability of Pt Bottom Electrodes for Ferroelectric Capacitors. Jpn. J. Appl. Phys. 1998, 37, L465. [Google Scholar] [CrossRef]
- Kinbara, A.; Haraki, H. Internal Stress of Evaporated Thin Gold Films. Jpn. J. Appl. Phys. 1965, 4, 243. [Google Scholar] [CrossRef]
- Kebabi, B.; Malek, C.; Ladan, F. Stress and microstructure relationships in gold thin films. Vacuum 1990, 41, 1353–1355. [Google Scholar] [CrossRef]
- Leo, D.J. Engineering Analysis of Smart Material Systems; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mayergoyz, I. Mathematical Models of Hysteresis and Their Applications; Springer: New York, NY, USA, 1991. [Google Scholar]
- Tan, X.; Baras, J. Modeling and control of hysteresis in magnetostrictive actuators. Automatica 2004, 40, 1469–1480. [Google Scholar] [CrossRef]
- Nye, J. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Wortman, J.J.; Evans, R.A. Young’s Modulus, Shear Modulus, and Poisson’s Ratio in Silicon and Germanium. J. Appl. Phys. 1965, 36, 153–156. [Google Scholar] [CrossRef]
- Gall, K.; Dunn, M.L.; Zhang, Y.; Corff, B.A. Thermal cycling response of layered gold/polysilicon MEMS structures. Mech. Mater. 2004, 36, 45–55. [Google Scholar] [CrossRef]
- Gall, K.; West, N.; Spark, K.; Dunn, M.L.; Finch, D.S. Creep of thin film Au on bimaterial Au/Si microcantilevers. Acta Mater. 2004, 52, 2133–2146. [Google Scholar] [CrossRef]
- Tsai, K.Y.; Chin, T.S.; Shieh, H.P.D.; Ma, C.H. Effect of as-deposited residual stress on transition temperatures of VO2 thin films. J. Mater. Res. 2004, 19, 2306–2314. [Google Scholar] [CrossRef]
- Case, F.C. Modifications in the phase transition properties of predeposited VO2 films. J. Vac. Sci. Technol. A Vac. Surf. Films 1984, 2, 1509–1512. [Google Scholar] [CrossRef]


| Properties | Materials | |||
|---|---|---|---|---|
| Si | SiO2 | Au | VO2 | |
| Density [Kg/m] | 2320 | 2200 | 19300 | 4670 |
| Young’s Modulus [GPa] | 187 [38,39] | 70 | 70 | 140 |
| Poisson Ratio | 0.22 | 0.17 | 0.44 | 0.33 |
| Point Load Location | Rotational Spring Constant | |
|---|---|---|
| Pitch () | Roll () | |
| 1 | 2.29 | 1.219 |
| 2 | 2.29 | 1.217 |
| 3 | 2.29 | 1.217 |
| 4 | 2.29 | 1.217 |
| Constant | Name and Units | Pitch () | Roll () |
|---|---|---|---|
| Gain [deg/A] | 79,743 | 33,871 | |
| Time response [s] | 0.0014 | 0.001479 | |
| Resonant Frequency [rad/s] | 4643 | 4643 | |
| Damping ratio | 0.00363 | 0.00447 | |
| J | Moment of Inertia [Kgm] | ||
| G | Rotational Damping coefficient [Nms/rad] | ||
| k | Rotational Spring coefficient [Nm/rad] | ||
| a | Position of the force with respect to the axis [ ] | 600 | 115 |
| Constant bias of Preisach model [ ] | 0.99 | 0.38 | |
| Thermal expansion-induced force term [N/°C] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, D.; Zhang, J.; Dooley, S.; Tan, X.; Sepúlveda, N. Modeling of MEMS Mirrors Actuated by Phase-Change Mechanism. Micromachines 2017, 8, 138. https://doi.org/10.3390/mi8050138
Torres D, Zhang J, Dooley S, Tan X, Sepúlveda N. Modeling of MEMS Mirrors Actuated by Phase-Change Mechanism. Micromachines. 2017; 8(5):138. https://doi.org/10.3390/mi8050138
Chicago/Turabian StyleTorres, David, Jun Zhang, Sarah Dooley, Xiaobo Tan, and Nelson Sepúlveda. 2017. "Modeling of MEMS Mirrors Actuated by Phase-Change Mechanism" Micromachines 8, no. 5: 138. https://doi.org/10.3390/mi8050138
APA StyleTorres, D., Zhang, J., Dooley, S., Tan, X., & Sepúlveda, N. (2017). Modeling of MEMS Mirrors Actuated by Phase-Change Mechanism. Micromachines, 8(5), 138. https://doi.org/10.3390/mi8050138





