Integrated Optofluidic Chip for Low-Volume Fluid Viscosity Measurement
Abstract
:1. Introduction
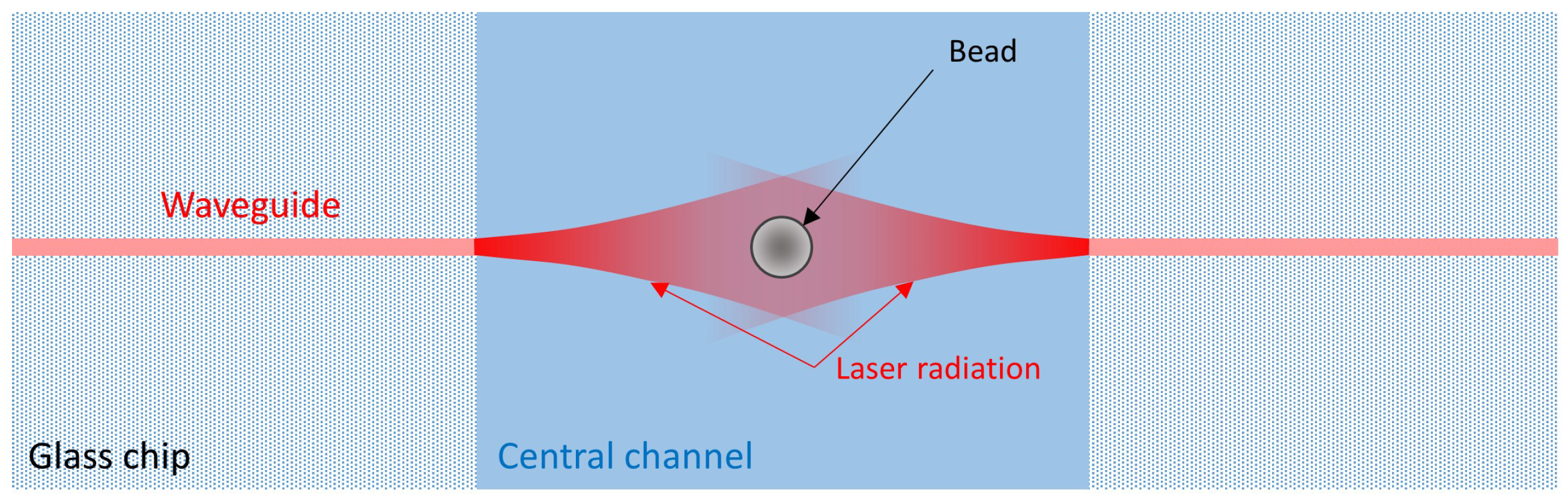
2. Device Structure and Working Principle
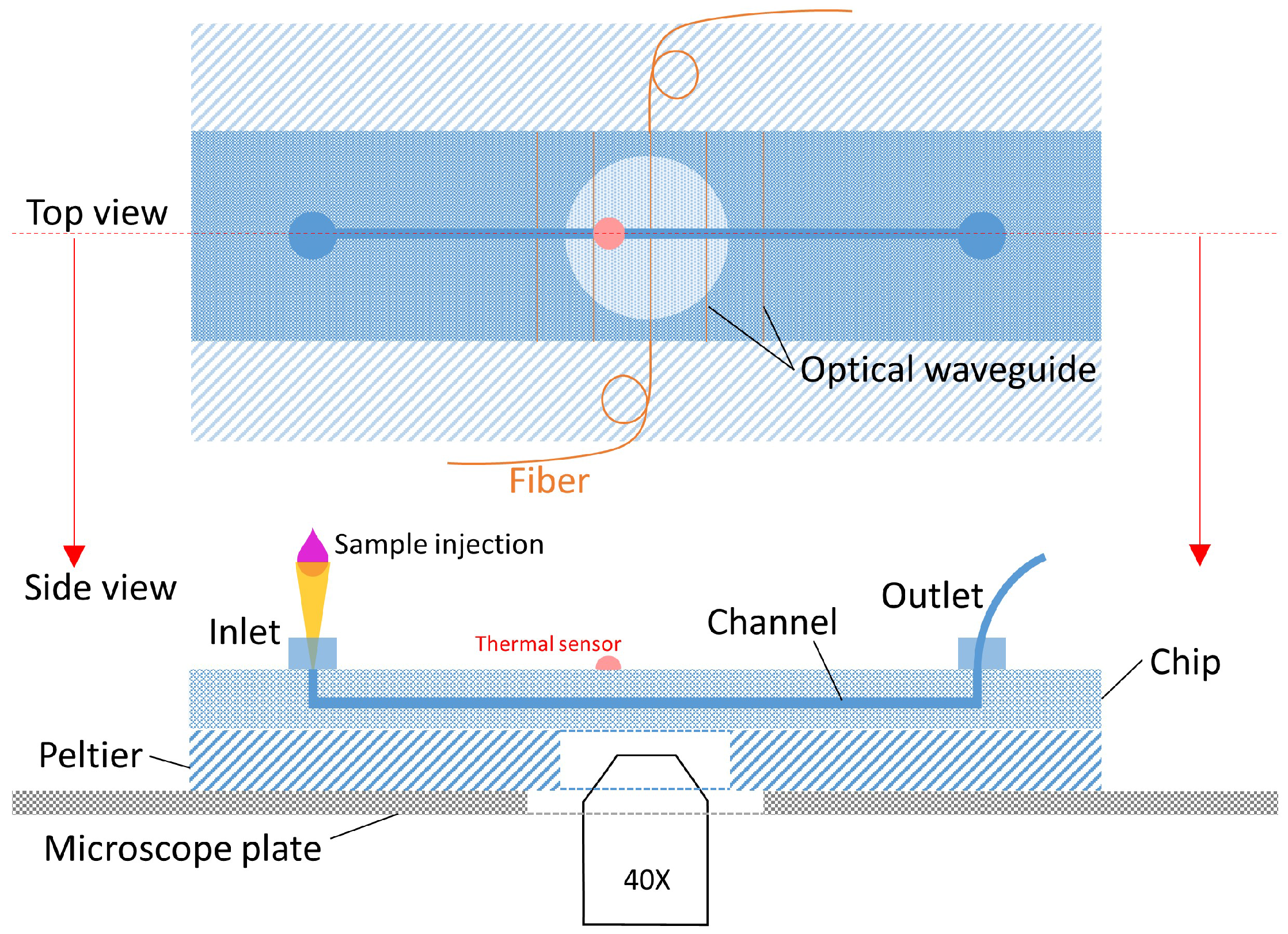
2.1. Chip Design and Fabrication
2.2. Fluid Viscosity Derivation
3. Experiment and Methods
3.1. Experimental Setup
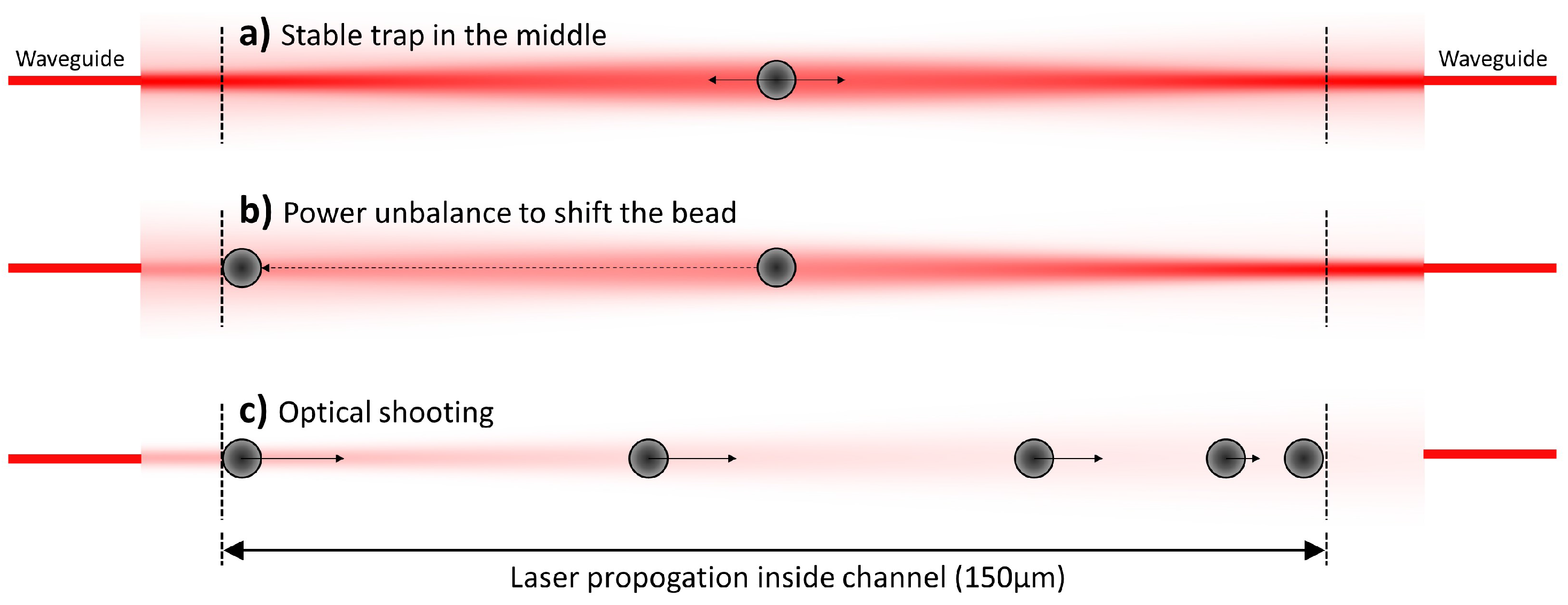
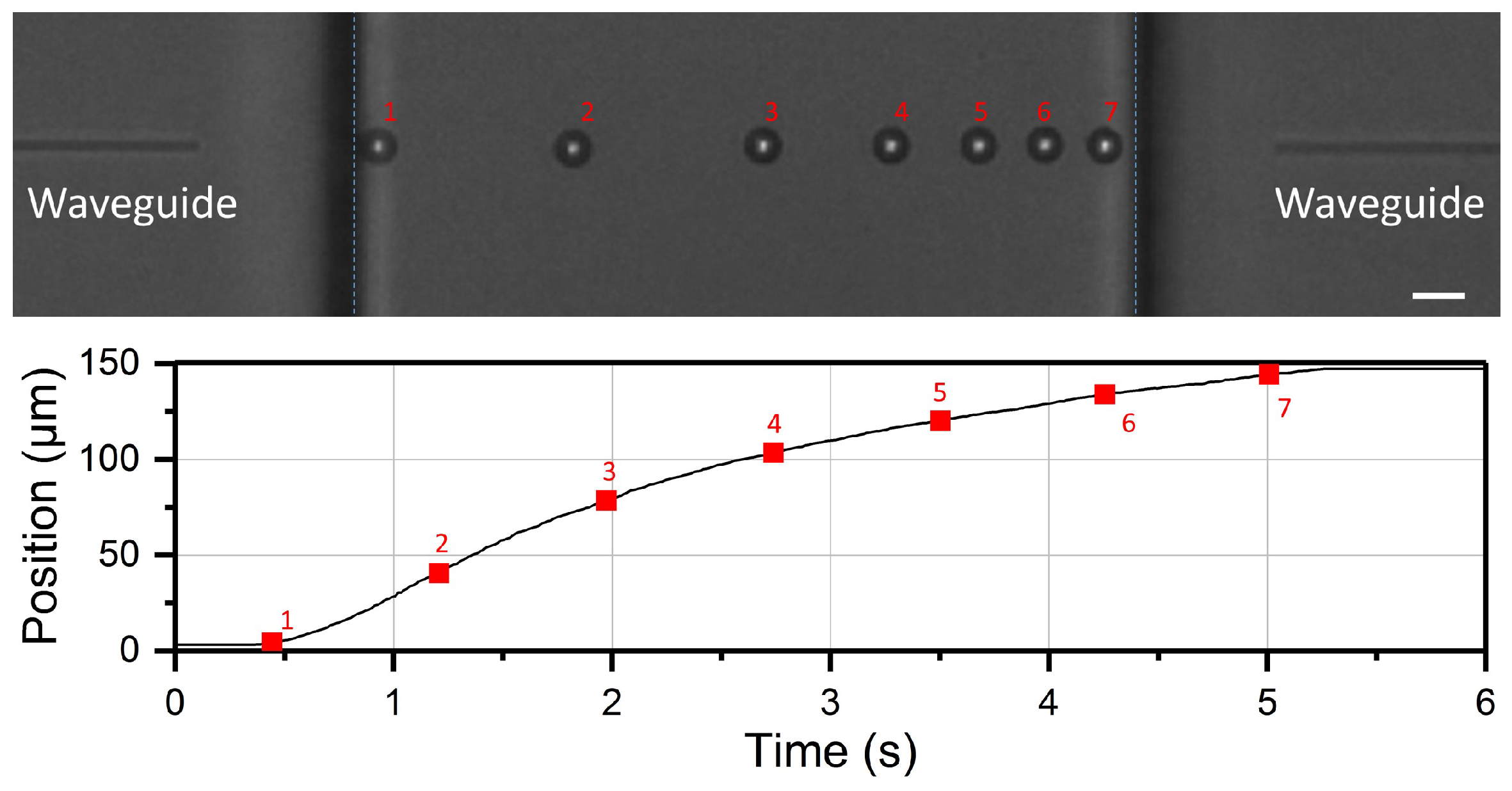
3.2. Optical Shooting Protocol and Data Acquisition
4. Results and Discussion
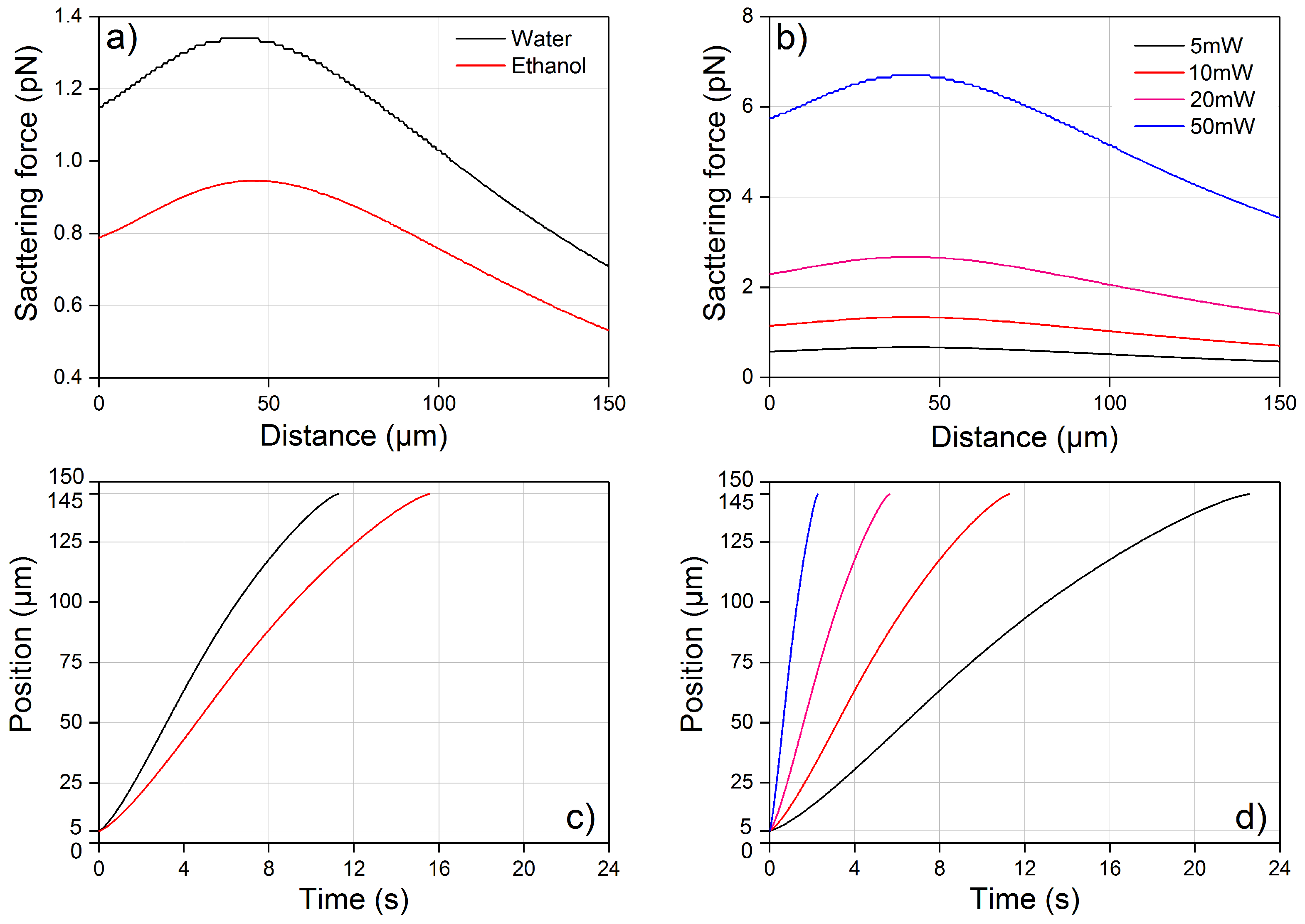
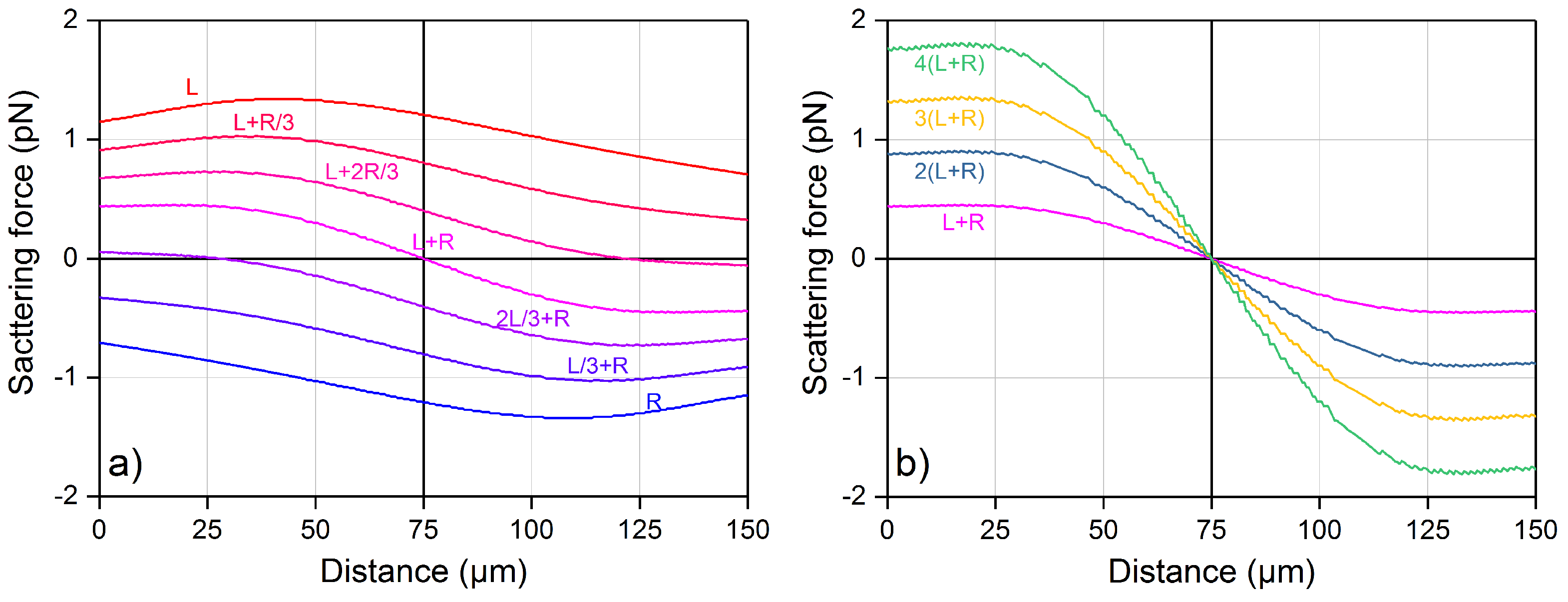
4.1. Optical Force Profile and Theoretical Trajectory
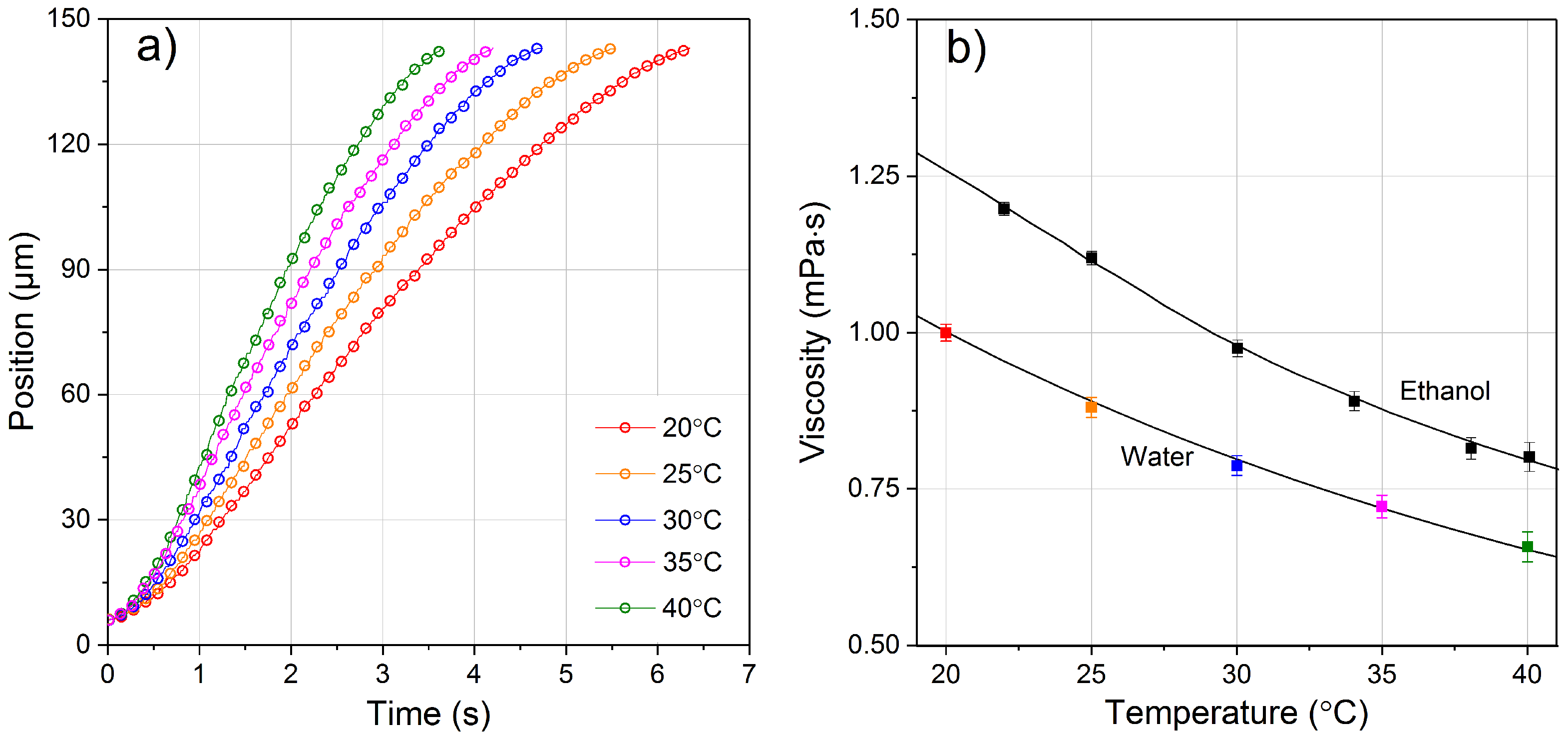
4.2. Viscosity of Water and Ethanol as a Function of Temperature
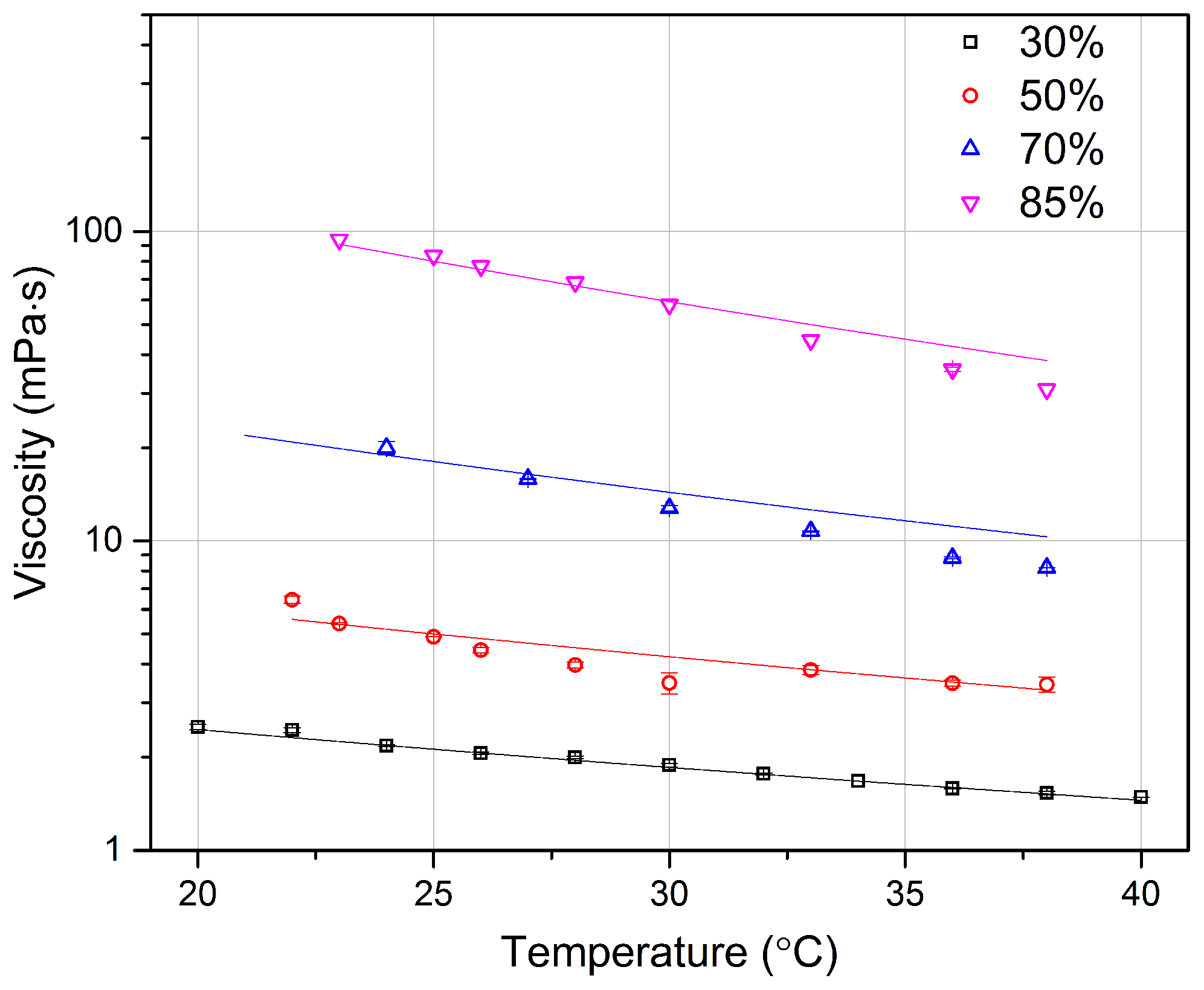
4.3. Glycerol Viscosity Measurement
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Chapman, C.D.; Robertson-Anderson, R.M. Nonlinear microrheology reveals entanglement-driven molecular-level viscoelasticity of concentrated DNA. Phys. Rev. Lett. 2014, 113, 098303. [Google Scholar] [CrossRef] [PubMed]
- Gardel, M.L.; Valentine, M.T.; Crocker, J.C.; Bausch, A.R.; Weitz, D.A. Microrheology of entangled F-actin solutions. Phys. Rev. Lett. 2003, 91, 158302. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M.; Mason, T.G. Fluid mechanics of microrheology. Ann. Rev. Fluid Mech. 2010, 42, 413–438. [Google Scholar] [CrossRef]
- Mason, T.G.; Weitz, D.A. Linear viscoelasticity of colloidal hard sphere suspensions near the glass transition. Phys. Rev. Lett. 1995, 75, 2770–2773. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M. Active microrheology in the continuum limit: Can the macrorheology be recovered? Differences 2005, 91125, 4. [Google Scholar]
- Tassieri, M.; Gibson, G.M.; Evans, R.M.L.; Yao, A.M.; Warren, R.; Padgett, M.J.; Cooper, J.M. Measuring storage and loss moduli using optical tweezers: Broadband microrheology. Phys. Rev. E 2010, 81, 026308. [Google Scholar] [CrossRef] [PubMed]
- Atakhorrami, M.; Sulkowska, J.I.; Addas, K.M.; Koenderink, G.H.; Tang, J.X.; Levine, A.J.; MacKintosh, F.C.; Schmidt, C.F. Correlated fluctuations of microparticles in viscoelastic solutions: Quantitative measurement of material properties by microrheology in the presence of optical traps. Phys. Rev. E 2006, 73, 061501. [Google Scholar] [CrossRef] [PubMed]
- Tassieri, M.; Giudice, F.D.; Robertson, E.J.; Jain, N.; Fries, B.; Wilson, R.; Glidle, A.; Greco, F.; Netti, P.A.; Maffettone, P.L.; Bicanic, T.; Cooper, J.M. Microrheology with optical tweezers: Measuring the relative viscosity of solutions ‘at a glance’. Sci. Rep. 2015, 5, 8831. [Google Scholar] [CrossRef] [PubMed]
- Keen, S.; Yao, A.; Leach, J.; Di Leonardo, R.; Saunter, C.; Love, G.; Cooper, J.; Padgett, M. Multipoint viscosity measurements in microfluidic channels using optical tweezers. Lab Chip 2009, 9, 2059. [Google Scholar] [CrossRef] [PubMed]
- Bellini, N.; Vishnubhatla, K.C.; Bragheri, F.; Ferrara, L.; Minzioni, P.; Ramponi, R.; Cristiani, I.; Osellame, R. Femtosecond laser fabricated monolithic chip for optical trapping and stretching of single cells. Opt. Express 2010, 18, 4679–4688. [Google Scholar] [CrossRef] [PubMed]
- Bragheri, F.; Minzioni, P.; Martinez Vazquez, R.; Bellini, N.; Paie, P.; Mondello, C.; Ramponi, R.; Cristiani, I.; Osellame, R. Optofluidic integrated cell sorter fabricated by femtosecond lasers. Lab Chip 2012, 12, 3779–3784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Watts, B.; Guo, T.; Zhang, Z.; Xu, C.; Fang, Q. Optofluidic device based microflow cytometers for particle/cell detection: A review. Micromachines 2016, 7, 70. [Google Scholar] [CrossRef]
- Yang, T.; Bragheri, F.; Minzioni, P. A comprehensive review of optical stretcher for cell mechanical characterization at single-cell level. Micromachines 2016, 7, 90. [Google Scholar] [CrossRef]
- Matteucci, M.; Triches, M.; Nava, G.; Kristensen, A.; Pollard, M.; Berg-Sørensen, K.; Taboryski, R. Fiber-based, injection-molded optofluidic systems: Improvements in assembly and applications. Micromachines 2015, 6, 1971–1983. [Google Scholar] [CrossRef]
- Yang, T.; Paiè, P.; Nava, G.; Bragheri, F.; Vazquez, R.M.; Minzioni, P.; Veglione, M.; Di Tano, M.; Mondello, C.; Osellame, R.; et al. An integrated optofluidic device for single-cell sorting driven by mechanical properties. Lab Chip 2015, 15, 1262–1266. [Google Scholar] [CrossRef] [PubMed]
- Nava, G.; Bragheri, F.; Yang, T.; Minzioni, P.; Osellame, R.; Cristiani, I.; Berg-Sørensen, K. All-silica microfluidic optical stretcher with acoustophoretic prefocusing. Microfluid. Nanofluid. 2015, 19, 837–844. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A. Trapping of atoms by resonance radiation pressure. Phys. Rev. Lett. 1978, 40, 729–732. [Google Scholar] [CrossRef]
- Ferrara, L.; Baldini, E.; Minzioni, P.; Bragheri, F.; Liberale, C.; Fabrizio, E.D.; Cristiani, I. Experimental study of the optical forces exerted by a Gaussian beam within the Rayleigh range. J. Opt. 2011, 13, 075712. [Google Scholar] [CrossRef]
- Bragheri, F.; Ferrara, L.; Bellini, N.; Vishnubhatla, K.C.; Minzioni, P.; Ramponi, R.; Osellame, R.; Cristiani, I. Optofluidic chip for single cell trapping and stretching fabricated by a femtosecond laser. J. Biophotonics 2010, 3, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef]
- Minzioni, P.; Bragheri, F.; Liberale, C.; Di Fabrizio, E.; Cristiani, I. A novel approach to fiber-optic tweezers: Numerical analysis of the trapping efficiency. IEEE J. Select. Top. Quantum Electron. 2008, 14, 151. [Google Scholar] [CrossRef]
- Svoboda, K.; Block, S.M. Biological applications of optical forces. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 247–285. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Li, R. Optical force exerted on a Rayleigh particle by a vector arbitrary-order Bessel beam. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 234–243. [Google Scholar] [CrossRef]
- Ebert, S.; Travis, K.; Lincoln, B.; Guck, J. Fluorescence ratio thermometry in a microfluidic dual-beam laser trap. Opt. Express 2007, 15, 15493. [Google Scholar] [CrossRef] [PubMed]
- Thermophysical Properties of Water and Steam. International Association for the Properties of Water and Steam. Available online: http://www.viscopedia.com/viscosity-tables/substances/water/ (accessed on 25 November 2015).
- Tables of Physical and Chemical Constants. Kaye and Laby Online. Available online: http://www.viscopedia.com/viscosity-tables/substances/ethanol/ (accessed on 22 November 2016).
- Cheng, N.S. Formula for the viscosity of a glycerol–water mixture. Ind. Eng. Chem. Res. 2008, 9, 3285–3288. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Nava, G.; Vitali, V.; Bragheri, F.; Osellame, R.; Bellini, T.; Cristiani, I.; Minzioni, P. Integrated Optofluidic Chip for Low-Volume Fluid Viscosity Measurement. Micromachines 2017, 8, 65. https://doi.org/10.3390/mi8030065
Yang T, Nava G, Vitali V, Bragheri F, Osellame R, Bellini T, Cristiani I, Minzioni P. Integrated Optofluidic Chip for Low-Volume Fluid Viscosity Measurement. Micromachines. 2017; 8(3):65. https://doi.org/10.3390/mi8030065
Chicago/Turabian StyleYang, Tie, Giovanni Nava, Valerio Vitali, Francesca Bragheri, Roberto Osellame, Tommaso Bellini, Ilaria Cristiani, and Paolo Minzioni. 2017. "Integrated Optofluidic Chip for Low-Volume Fluid Viscosity Measurement" Micromachines 8, no. 3: 65. https://doi.org/10.3390/mi8030065
APA StyleYang, T., Nava, G., Vitali, V., Bragheri, F., Osellame, R., Bellini, T., Cristiani, I., & Minzioni, P. (2017). Integrated Optofluidic Chip for Low-Volume Fluid Viscosity Measurement. Micromachines, 8(3), 65. https://doi.org/10.3390/mi8030065








