Faraday Waves-Based Integrated Ultrasonic Micro-Droplet Generator and Applications
Abstract
:1. Introduction
2. Silicon-Based MHz Multiple Fourier Horn Ultrasonic Nozzles
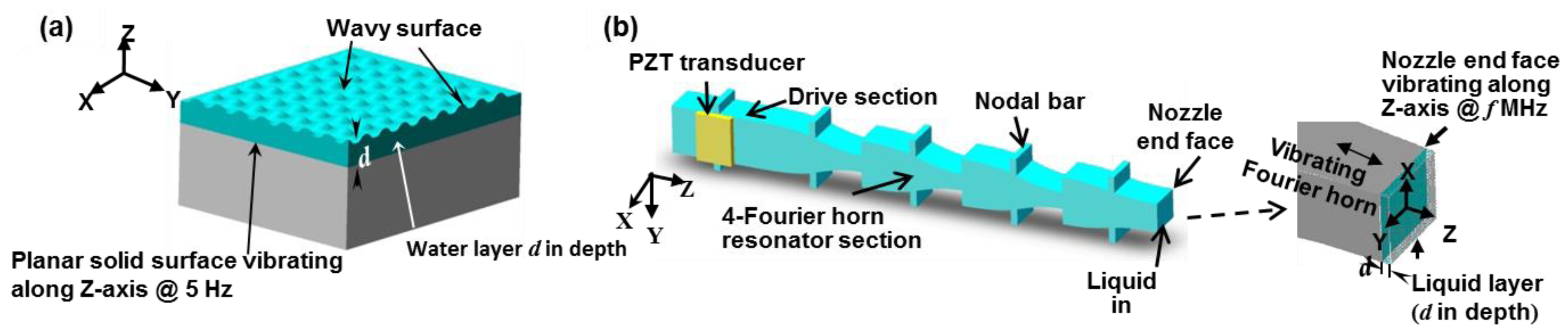
2.1. Multiple Fourier Horn Nozzle Architecture and Working Principle
2.2. Simulation and Design
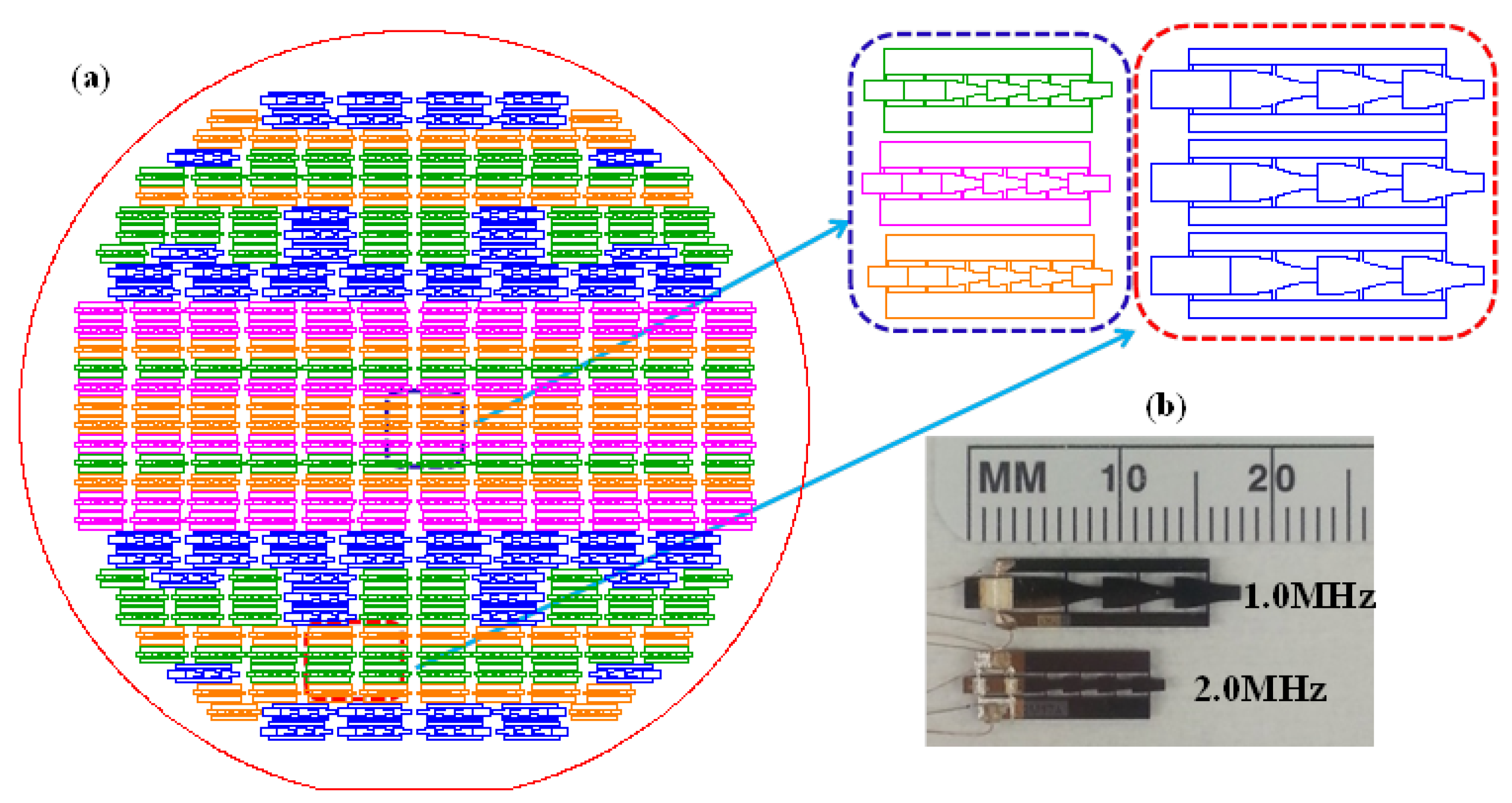
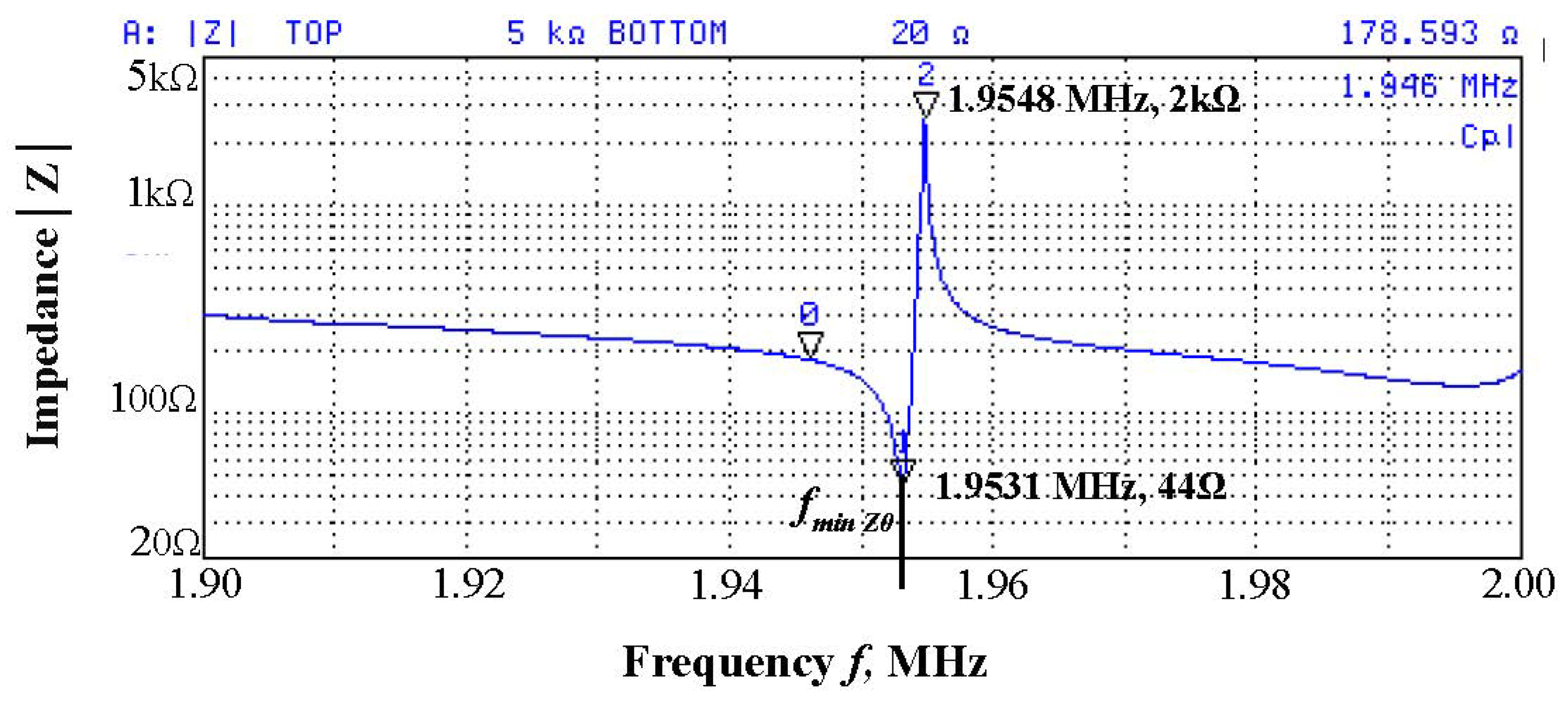
2.3. Fabrication and Characterization
3. Temporal Instability of MHz Faraday Waves for Micro Droplet Ejection
3.1. Linear Theory
3.2. Dynamics of Droplet Ejection and Droplet Diameter
4. Droplet Ejection Experiments and Verifications
4.1. Critical Vibration Amplitude (hcr) for Droplet Ejection
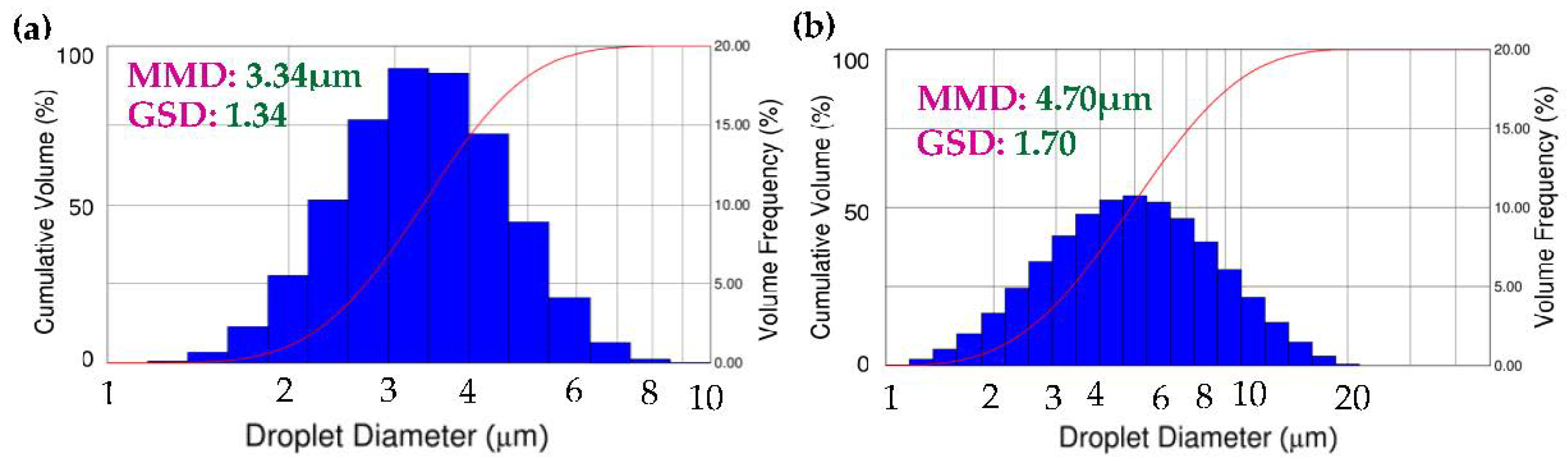
4.2. Droplet Diameter/Size Distribution and Electrical Drive Power
5. Battery-Run Pocket-Size Clogging-Free Integrated Ultrasonic Micro Droplet Generator
6. Applications
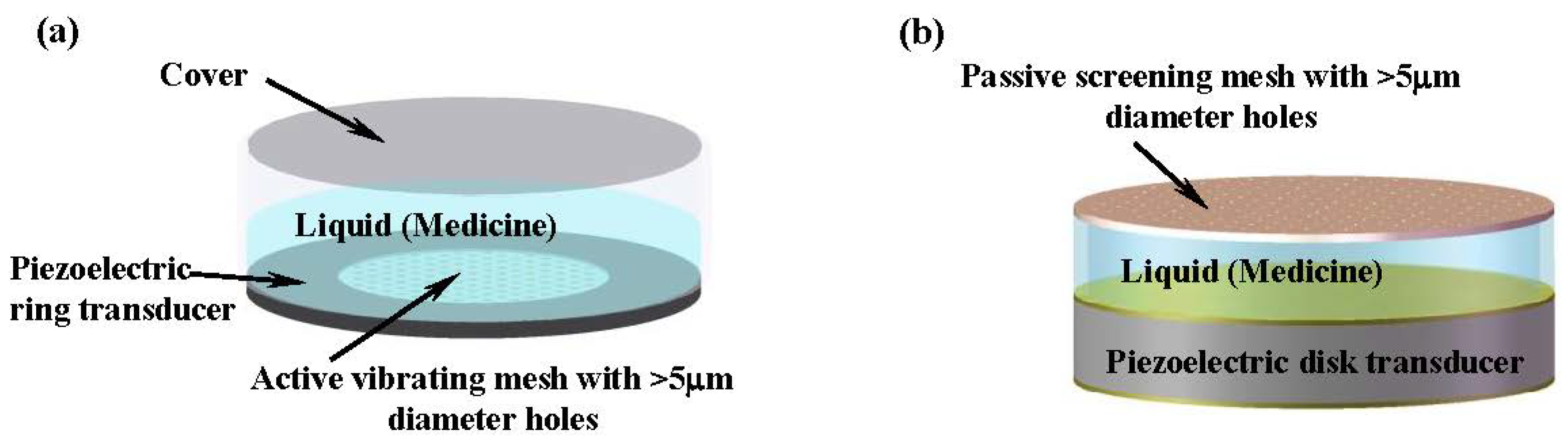
6.1. Imminent Application to Inhalation Drug Delivery
6.2. Other Potential Applications
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghazanfari, T.; Elhissi, A.M.A.; Ding, Z.; Taylor, K.M.G. The influence of fluid physicochemical properties on vibrating-mesh nebulization. Int. J. Pharm. 2007, 339, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Rottier, B.L.; van Erp, C.J.P.; Sluter, T.S.; Heijerman, H.G.M.; Frijlink, H.W.; de Boer, A.H. Changes in performance of the Pari eFlow Rapid and Pari LC Plus during 6 months use by CF patients. J. Aerosol Med. Pulm. Drug Deliv. 2009, 22, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Elrod, S.A.; Hadimioglu, B.; Khuri-Yakub, B.T.; Rawson, E.G.; Richley, E.; Quate, C.F. Nozzless droplet formation with focused acoustic beams. J. Appl. Phys. 1989, 65, 3441–3447. [Google Scholar] [CrossRef]
- Meacham, J.M.; Ejimofor, C.; Kumar, S.; Degertekin, A.G.; Fedorov, F.L. Micromachined ultrasonic droplet generator based on a liquid horn structure. Rev. Sci. Instrum. 2004, 75, 1347–1352. [Google Scholar] [CrossRef]
- Lee, C.H.; Lal, A. Single microdroplet ejection using an ultrasonic longitudinal mode with a PZT/Tapered glass capillary. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 1514–1522. [Google Scholar] [PubMed]
- Perçin, G.; Khuri-Yakub, B.T. Piezoelectrically actuated flextensional micromachined ultrasound transducers. I: Theory. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 573–584. [Google Scholar] [CrossRef] [PubMed]
- Perçin, G.; Khuri-Yakub, B.T. Piezoelectrically actuated flextensional micromachined ultrasound transducers. II: Fabrication and experiments. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 585–595. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.W.; Yu, H.; Zou, Q.; Kim, E.S. Directional droplet ejection by nozzleless acoustic ejectors built on ZnO and PZT. J. Micromech. Microeng. 2006, 16, 2697–2704. [Google Scholar] [CrossRef]
- Ai, Y.; Marrone, B.L. Droplet translocation by focused acoustic waves. Microfluid. Nanofluid. 2012, 13, 715–722. [Google Scholar] [CrossRef]
- Qi, A.; Friend, J.M.; Yeo, L.Y.; Morton, A.V.; McIntosh, M.P.; Spiccin, L. Miniature inhalation therapy using surface acoustic wave microfluidic atomization. Lab Chip 2009, 9, 2184–2193. [Google Scholar] [CrossRef] [PubMed]
- Faraday, M. On a peculiar class of acoustical figures and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 1831, 121, 299–340. [Google Scholar] [CrossRef]
- Rayleigh, B. On the crispation of fluid resting upon a vibrating support. Philos. Mag. 1883, 16, 50–58. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ursell, F. The Stability of the Plane Free Surface of a Liquid in Vertical Periodic Motion. Proc. R. Soc. Lond. A 1954, 225, 505–515. [Google Scholar] [CrossRef]
- Cerda, E.A.; Tirapegui, E.L. Faraday’s instability for viscous liquids. Phys. Rev. Lett. 1997, 78, 859–862. [Google Scholar] [CrossRef]
- Yule, A.J.; Al-Suleimani, Y. On droplet formation from capillary waves on a vibrating surface. Proc. R. Soc. Lond. A 2000, 456, 1069–1085. [Google Scholar] [CrossRef]
- Tsai, S.C.; Tsai, C.S. Linear theory of temporal instability of megahertz Faraday waves for monodisperse microdroplet ejection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1746–1754. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.S.; Mao, R.W.; Lin, S.K.; Zhu, Y.; Tsai, S.C. Faraday instability-based micro droplet ejection for inhalation drug delivery. Technology 2014, 2, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.C.; Song, Y.L.; Tseng, T.K.; Chou, Y.F.; Chen, W.J.; Tsai, C.S. High-frequency silicon-based ultrasonic nozzles using multiple Fourier horns. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 277–285. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.C.; Cheng, C.H.; Wang, N.; Song, Y.L.; Lee, C.T.; Tsai, C.S. Silicon-based Megahertz ultrasonic nozzles for production of monodisperse micrometer-sized droplets. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1968–1979. [Google Scholar] [CrossRef] [PubMed]
- McAuley, S.A.; Ashraf, H.; Atabo, L.; Chambers, A.; Hall, S.; Hopkins, J.; Nicholls, G. Silicon micromachining using a high-density plasma source. J. Phys. D 2001, 34, 2769–2774. [Google Scholar] [CrossRef]
- Tsai, S.C.; Song, Y.L.; Tsai, C.S.; Chou, Y.F.; Cheng, C.H. Ultrasonic atomization using MHz silicon-based multiple-Fourier horn nozzles. Appl. Phys. Lett. 2006, 88, 014102. [Google Scholar] [CrossRef]
- Tsai, S.C.; Lin, S.K.; Mao, R.W.; Tsai, C.S. Ejection of uniform micrometer-sized droplets from Faraday waves on a millimeter-sized water drop. Phys. Rev. Lett. 2012, 108, 154501. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.S.; Mao, R.W.; Lin, S.K.; Wang, N.; Tsai, S.C. Miniaturized multiple Fourier-horn ultrasonic droplet generators for biomedical applications. Lab Chip 2010, 10, 2733–2740. [Google Scholar] [CrossRef] [PubMed]
- Langer, R. Perspectives: Drug delivery—Drugs on target. Science 2001, 293, 58–59. [Google Scholar] [CrossRef] [PubMed]
- Patton, J.S.; Byron, P.R. Inhaling medicines: Delivering drugs to the body through the lungs. Nat. Rev. Drug Discov. 2007, 6, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Sangwan, S.; Condos, R.; Smaldone, G.C. Lung deposition and respirable mass during wet nebulization. J. Aerosol Med. 2003, 16, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Sagalla, R.B.; Smaldone, G.C. Capturing the efficiency of vibrating mesh nebulizers: Minimizing upper airway deposition. J. Aerosol Med. Pulm. Drug Deliv. 2014, 27, 341–348. [Google Scholar] [CrossRef] [PubMed]
- Diaz, K.T.; Skaria, S.; Harris, S.K.; Solomita, M.; Lau, S.; Bauer, K.; Smaldone, G.C.; Condos, R. Delivery and safety of inhaled interferon-γ in idiopathic pulmonary fibrosis. J. Aerosol Med. Pulm. Drug Deliv. 2012, 25, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.C.; Mao, R.W.; Zhu, Y.; Chien, E.; Maduzia, J.; Tsai, C.S.; Brenner, M.; Mahon, S.; Mukai, D.; Boss, G.; et al. Hand-Held High-Throughput Ultrasonic Monodisperse Aerosol Inhalers for Detoxification of Massive Cyanide Poisoning. In Proceedings of the 2012 IEEE International Ultrasonics Symposium (IUS-2012), Dresden, Germany, 7–10 October 2012; pp. 1632–1634.
- Tsai, C.S.; Lin, S.K.; Mao, R.W.; Tsai, S.C.; Brenner, M.; Mahon, S.; Mukai, D.; Boss, G. Pocket-Sized Ultrasonic Nebulizer for Inhalation Drug Delivery. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS-2013), Prague, Czech Republic, 21–25 July 2013; pp. 1190–1192.
- Mao, R.W.; Lin, S.K.; Tsai, S.C.; Brenner, M.; Mahon, S.; Boss, G.; Smaldone, G.C.; Tsai, C.S. MEMS-Based Silicon Ultrasonic Twin-Nozzle Nebulizer for Inhalation Drug Delivery. In Proceedings of the 2014 IEEE International Ultrasonics Symposium (IUS-2014), Chicago, IL, USA, 3–6 September 2014; pp. 742–744.
- Tsai, C.S.; Mao, R.W.; Lin, S.K.; Tsai, S.C.; Boss, G.; Brenner, M.; Smaldone, G.C.; Mahon, S.; Shahverdi, K.; Zhu, Y. Ultrasound-driven megahertz Faraday waves for generation of monodisperse micro droplets and applications. In Proceedings of the 2015 International Congress on Ultrasonics, Metz, France, 10–14 May 2015.
- Aerni, H.R.; Cornett, D.S.; Caprioli, R.M. Automated acoustic matrix deposition for MALDI sample preparation. Anal. Chem. 2006, 78, 827–834. [Google Scholar] [CrossRef] [PubMed]
- Lal, A.; White, R.M. Micromachined silicon ultrasonic atomizer. In Proceedings of the IEEE International Ultrasonics Symposium, San Antonio, TX, USA, 3–6 November 1996; Volume 1, pp. 339–342.
- Dang, J.M.; Leong, K.W. Natural polymers for gene delivery and tissue engineering. Adv. Drug Deliv. Rev. 2006, 58, 487–499. [Google Scholar] [CrossRef] [PubMed]
- Zarnitsyn, V.G.; Meacham, J.M.; Varady, M.J.; Hao, C.H.; Degertekin, F.L.; Fedorov, A.G. Electrosonic ejector microarray for drug and gene delivery. Biomed. Microdevices 2008, 10, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Garstecki, P.M.; Fuerstman, J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.-C.; Hettiarachchi, K.; Siu, M.; Pan, Y.-R.; Lee, A.P. Controlled Microfluidic Encapsulation of Cells, Proteins, and Microbeads in Lipid Vesicles. J. Am. Chem. Soc. 2006, 128, 5656–5658. [Google Scholar] [CrossRef] [PubMed]





| Medicine | Medicine Concentration | Nebulizer Unit | Droplet MMD (µm) | Output Rate (µL/min) | Disease |
|---|---|---|---|---|---|
| Albuterol * | 25 mg/mL | Bench-scale | 4.5 | 150 | Asthma |
| Humulin, U100 * | 100 units/mL | Bench-scale | 4.5 | 100 | Diabetes |
| Cobinamide | 100 mM | Pocket-size | 3.7 | 150 | Cyanide poisoning |
| Magnesium thiosulfate | 1.0 M | Pocket-size | 3.8 | 150 | Sulfide poisoning |
| Interferon-γ | 100 µg/0.5 mL | Pocket-size | 2.9 | 100 | Pulmonary fibrosis |
| Budesonide suspension | 0.5 mg/2.0 mL | Pocket-size | 3.1 | 350 | Asthma |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.S.; Mao, R.W.; Tsai, S.C.; Shahverdi, K.; Zhu, Y.; Lin, S.K.; Hsu, Y.-H.; Boss, G.; Brenner, M.; Mahon, S.; et al. Faraday Waves-Based Integrated Ultrasonic Micro-Droplet Generator and Applications. Micromachines 2017, 8, 56. https://doi.org/10.3390/mi8020056
Tsai CS, Mao RW, Tsai SC, Shahverdi K, Zhu Y, Lin SK, Hsu Y-H, Boss G, Brenner M, Mahon S, et al. Faraday Waves-Based Integrated Ultrasonic Micro-Droplet Generator and Applications. Micromachines. 2017; 8(2):56. https://doi.org/10.3390/mi8020056
Chicago/Turabian StyleTsai, Chen S., Rong W. Mao, Shirley C. Tsai, Kaveh Shahverdi, Yun Zhu, Shih K. Lin, Yu-Hsiang Hsu, Gerry Boss, Matt Brenner, Sari Mahon, and et al. 2017. "Faraday Waves-Based Integrated Ultrasonic Micro-Droplet Generator and Applications" Micromachines 8, no. 2: 56. https://doi.org/10.3390/mi8020056
APA StyleTsai, C. S., Mao, R. W., Tsai, S. C., Shahverdi, K., Zhu, Y., Lin, S. K., Hsu, Y.-H., Boss, G., Brenner, M., Mahon, S., & Smaldone, G. C. (2017). Faraday Waves-Based Integrated Ultrasonic Micro-Droplet Generator and Applications. Micromachines, 8(2), 56. https://doi.org/10.3390/mi8020056





