The Optimal Locomotion of a Self-Propelled Worm Actuated by Two Square Waves
Abstract
:1. Introduction
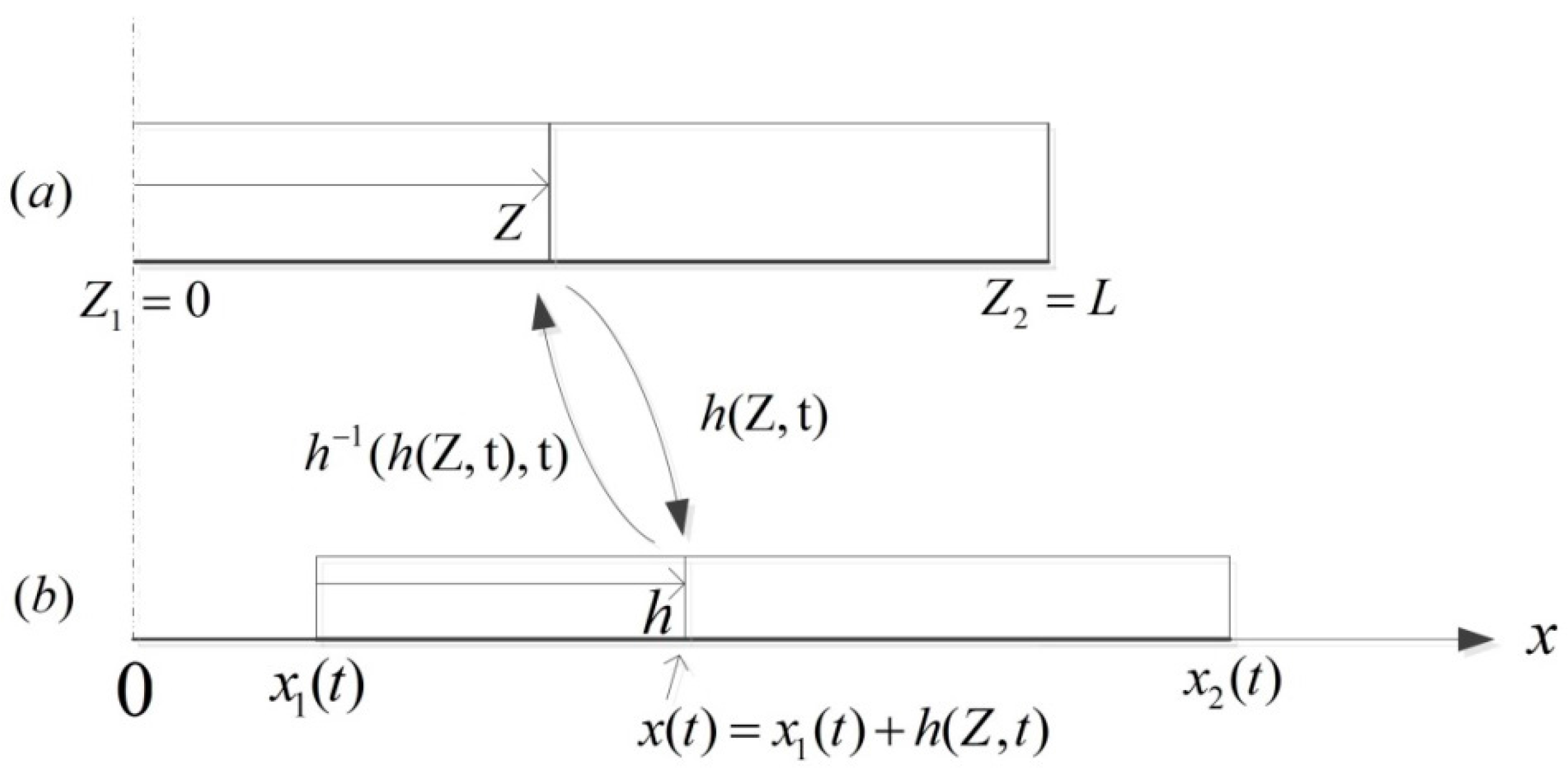
2. The Mathematical Description of Worm-Like Locomotion
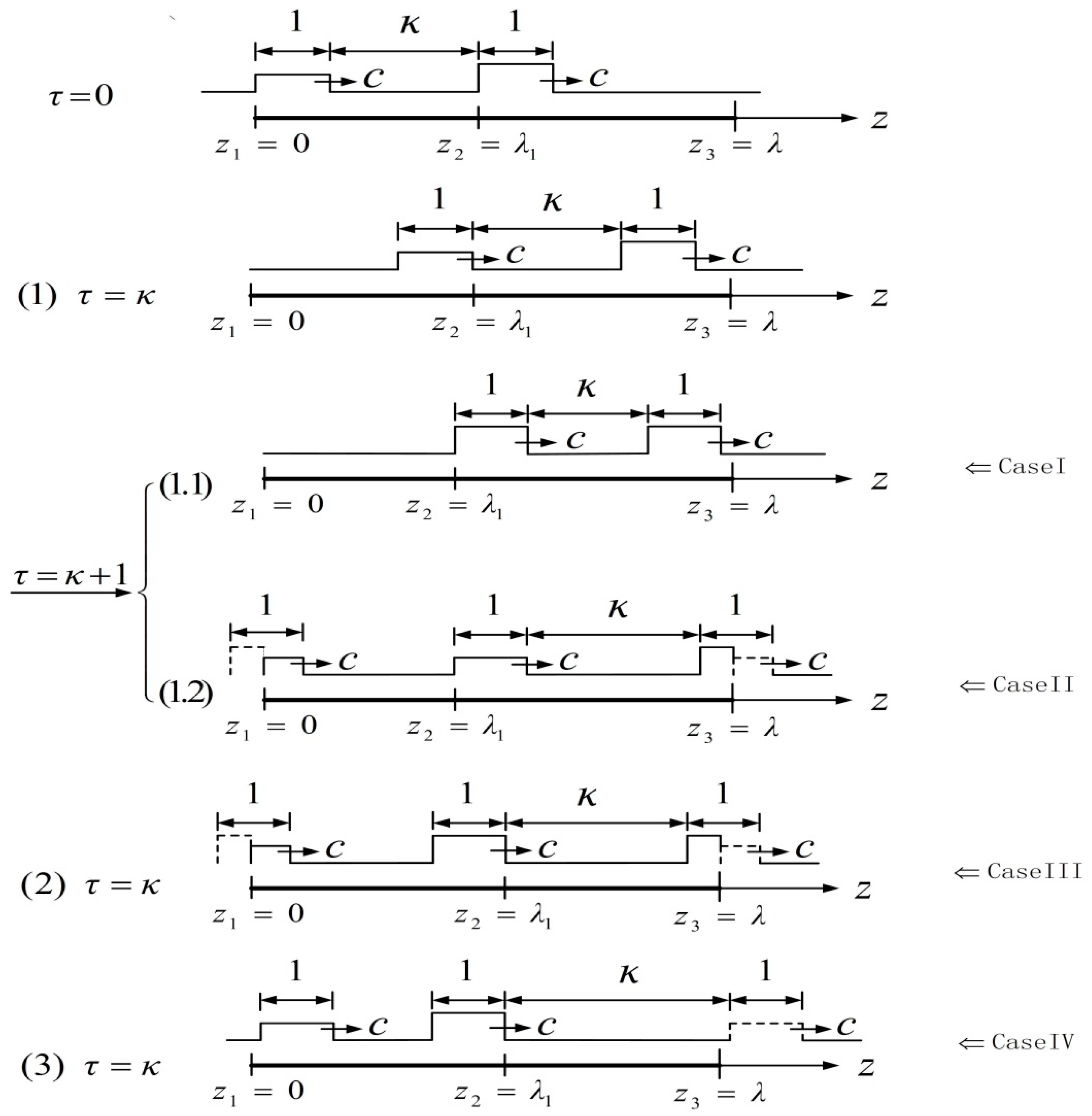
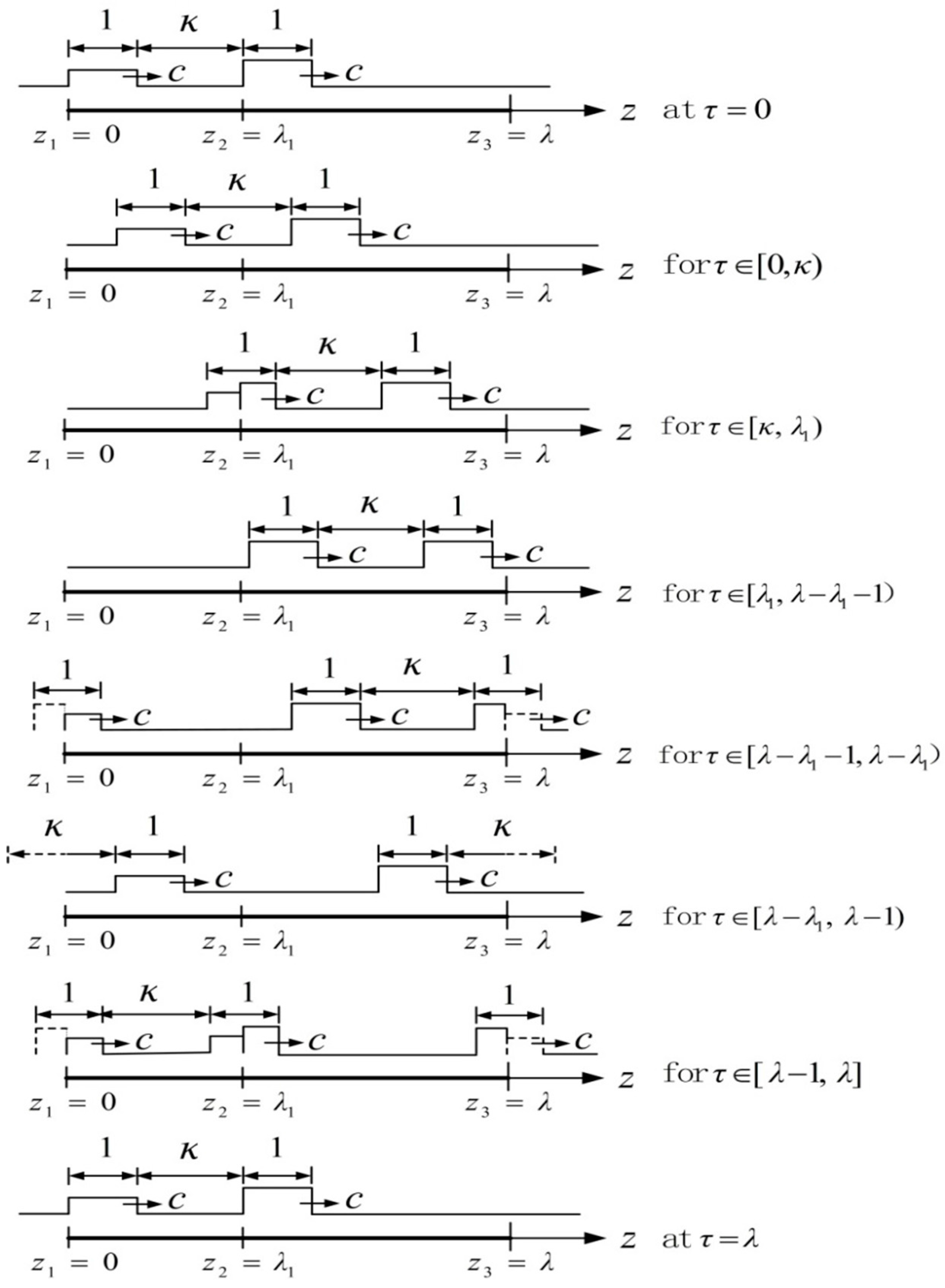
3. Square Strain Waves (SSW)
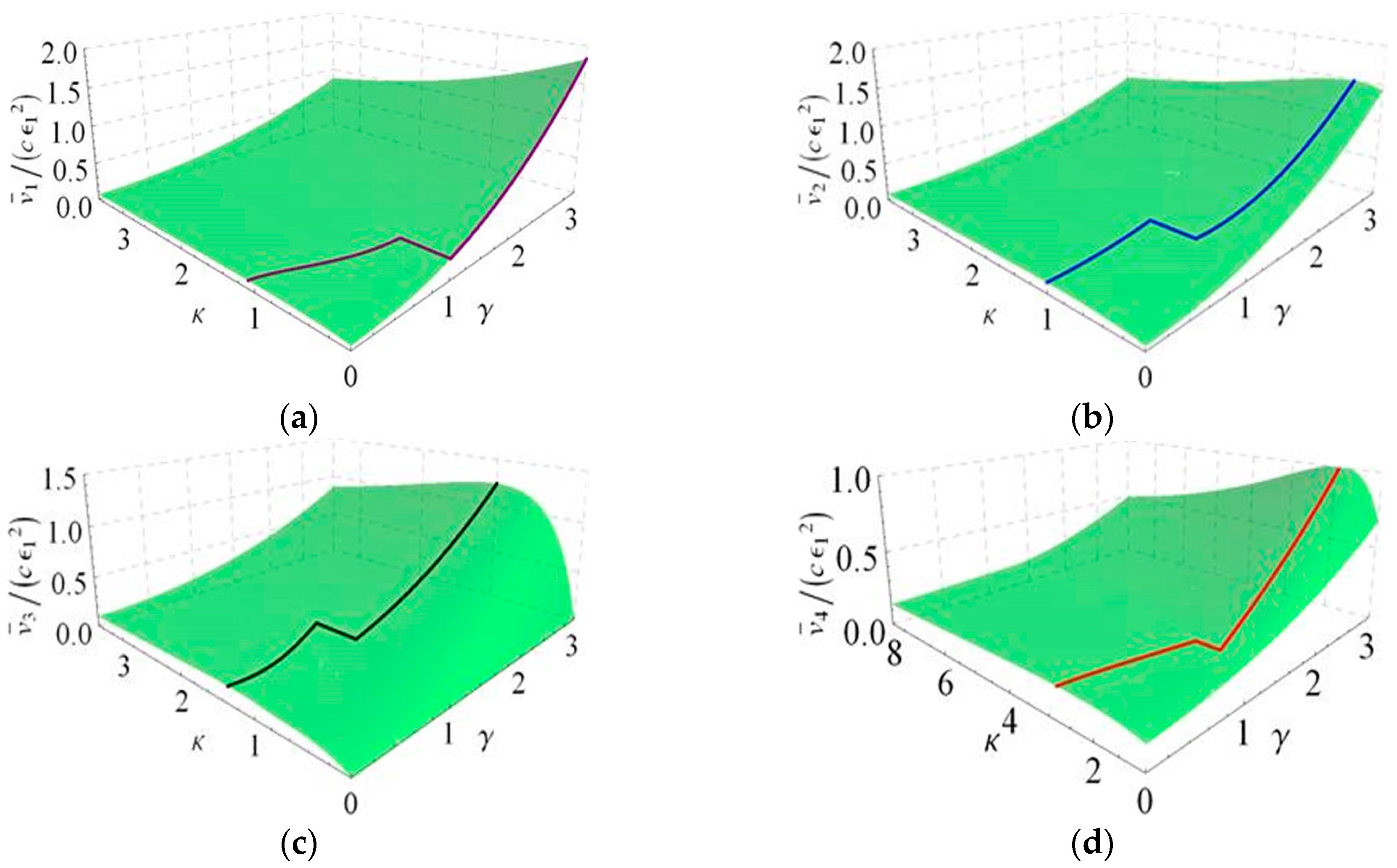
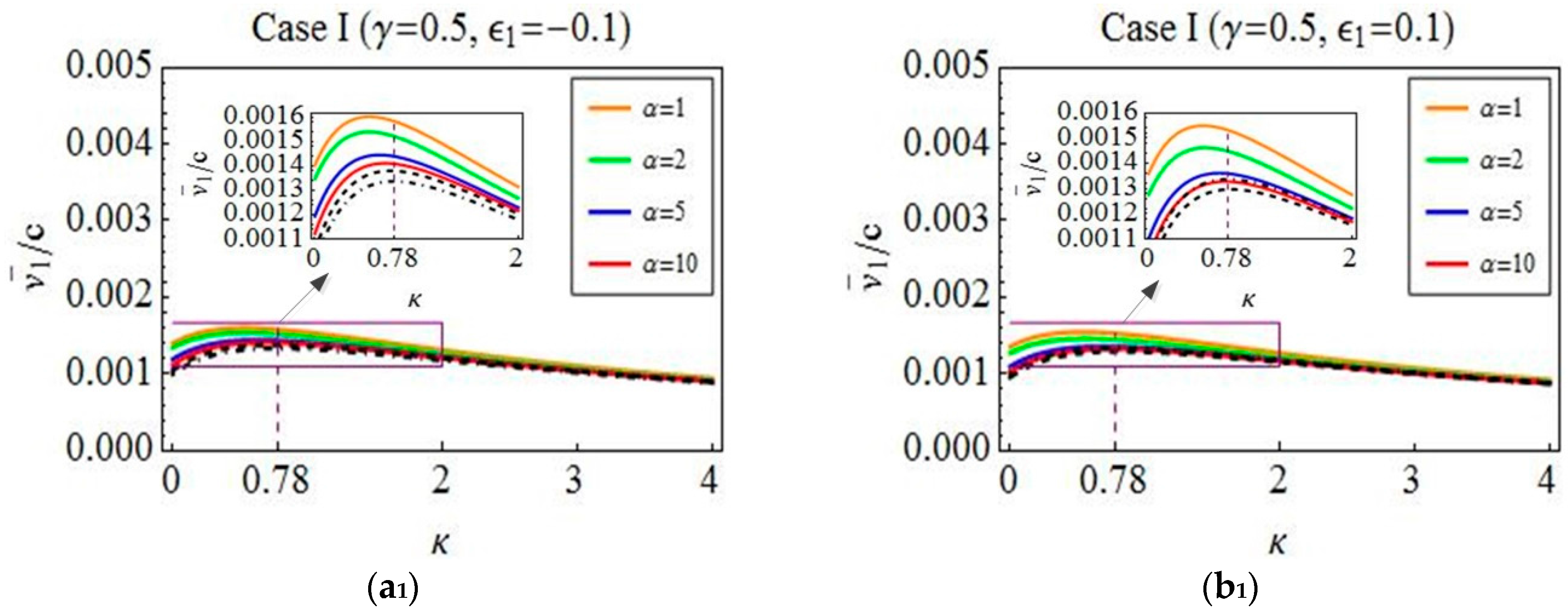
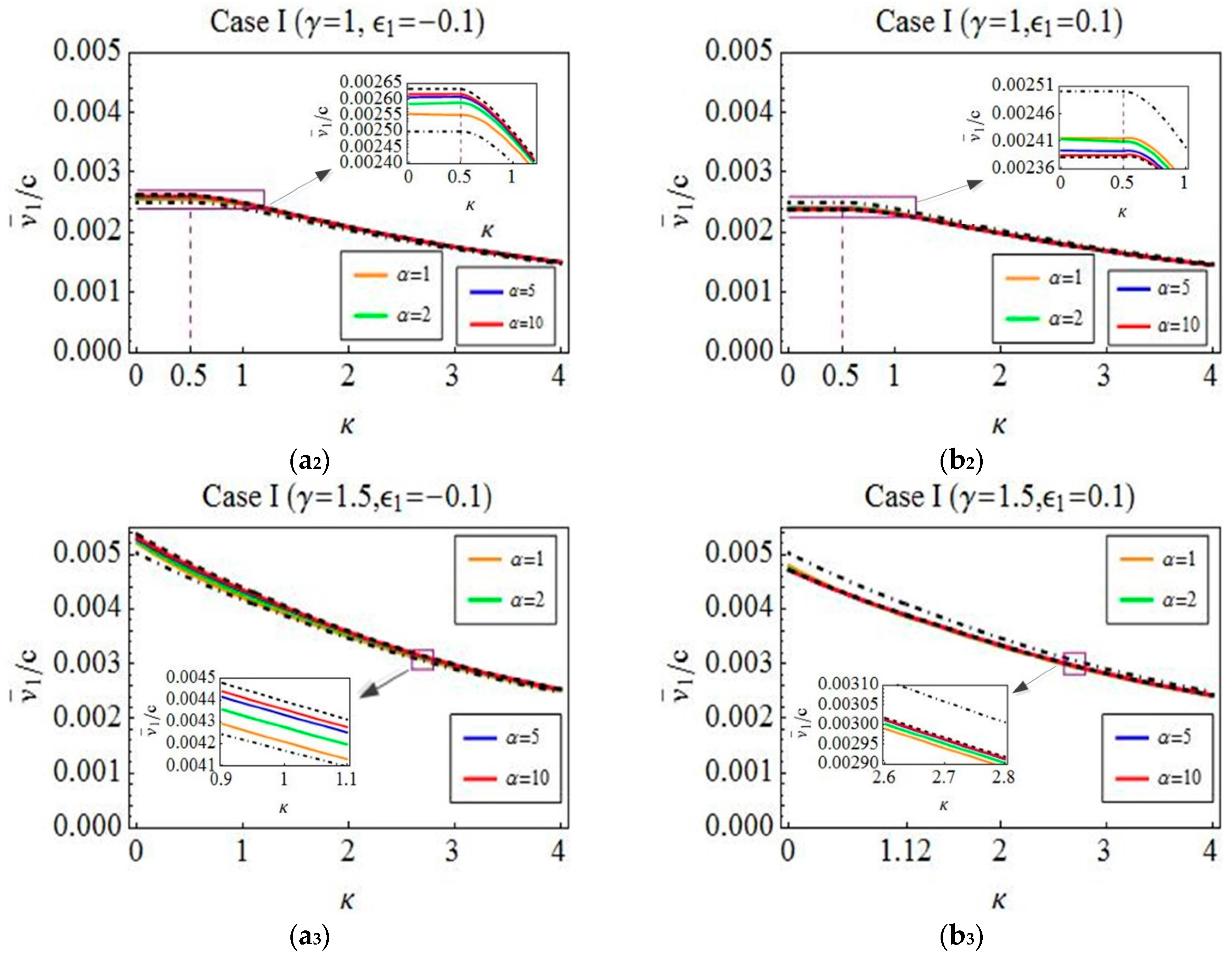
4. Optimization
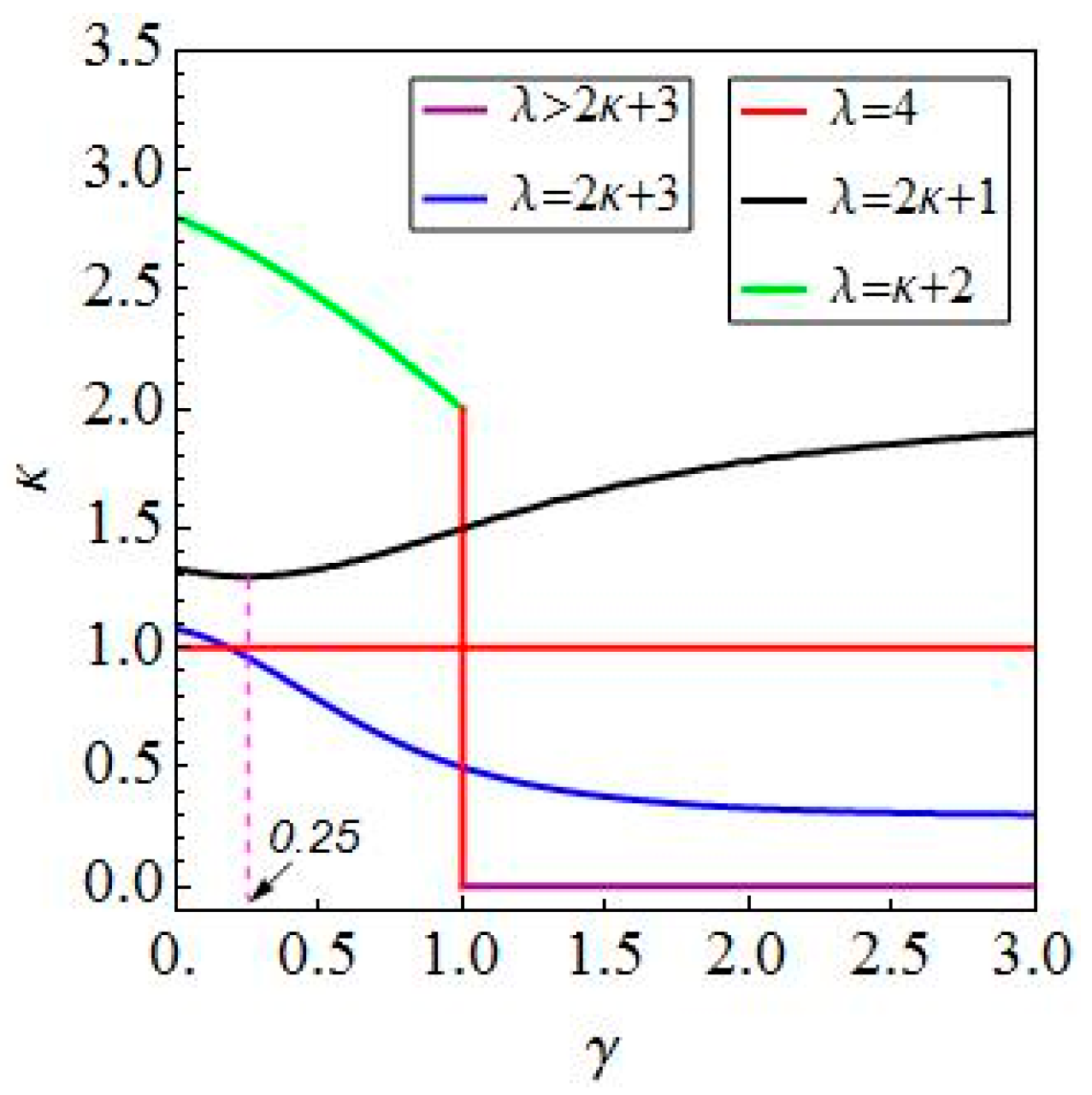
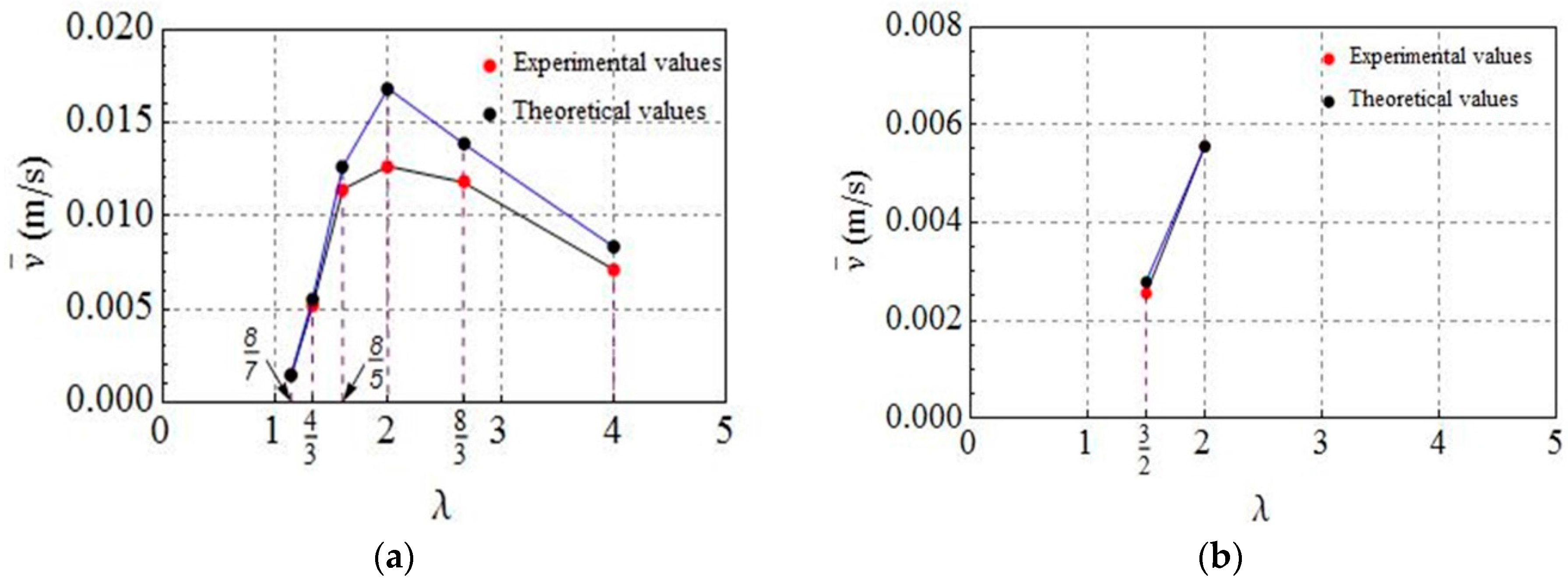
5. Verification and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Expression of and
Appendix B. Expression of for
- (1)
- WhenWhen
- (2)
- When
- (3)
- When
- (4)
- When
- (5)
- When
References
- Boxerbaum, A.; Chiel, H.J.; Quinn, R.D. Softworm: A soft, biologically inspired worm-like robot. Neurosc. Abstr. 2009, 315, 44106. [Google Scholar]
- Tyrakowski, T.; Kaczorowski, P.; Pawłowicz, W.; Ziółkowski, M.; Smuszkiewicz, P.; Trojanowska, I.; Marszaek, A.; Żebrowska, M.; Lutowska, M.; Kopczyńska, E.; et al. Discrete movements of foot epithelium during adhesive locomotion of a land snail. Folia Biol. 2012, 60, 99–106. [Google Scholar] [CrossRef]
- Gray, J.; Lissmann, H. Studies In Animal Locomotion. J. Exp. Biol. 1938, 15, 506–517. [Google Scholar]
- Chapman, G. The hydrostatic skeleton in the invertebrates. Biol. Rev. 1958, 33, 338–371. [Google Scholar] [CrossRef]
- Boxerbaum, A.S.; Shaw, K.M.; Chiel, H.J.; Quinn, R.D. Continuous wave peristaltic motion in a robot. Int. J. Robot. Res. 2012, 31, 302–318. [Google Scholar] [CrossRef]
- Agersborg, H.K. Notes on the locomotion of the nudibranchiate mollusk Dendronotus giganteus O’Donoghue. Biol. Bull. 1922, 42, 257–266. [Google Scholar] [CrossRef]
- Jones, H. Observations on the locomotion of two British terrestrial planarians (Platyhelminthes, Tricladida). J. Zool. 1978, 186, 407–416. [Google Scholar] [CrossRef]
- Yanagida, T.; Adachi, K.; Yokojima, M.; Na kamura, T. Development of a peristaltic crawling robot attached to a large intestine endoscope using bellows-type artificial rubber muscles. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Omori, H.; Murakami, T.; Nagai, H.; Nakamura, T.; Kubota, T. Planetary subsurface explorer robot with propulsion units for peristaltic crawling. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Tanaka, Y.; Ito, K.; Nakagaki, T.; Kobayashi, R. Mechanics of peristaltic locomotion and role of anchoring. J. R. Soc. Interface 2012, 9, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Dobrolyubov, A.I. The Mechanism of Locomotion of Some Terrestrial Animals by Trveling Waves of Deformation. J. Theor. Biol. 1986, 119, 457–466. [Google Scholar] [CrossRef]
- DeSimone, A.; Guarnieri, F.; Noselli, G.; Tatone, A. Crawlers in viscous environments: Linear vs non-linear rheology. Int. J. Non-Linear Mech. 2013, 56, 142–147. [Google Scholar] [CrossRef]
- Noselli, G.; Tatone, A.; DeSimone, A. Discrete one-dimensional crawlers on viscous substrates: Achievable net displacements and their energy cost. Mech. Res. Commun. 2014, 58, 73–81. [Google Scholar] [CrossRef]
- Gidoni, P.; Noselli, G.; DeSimone, A. Crawling on directional surfaces. Int. J. Non-Linear Mech. 2014, 61, 65–73. [Google Scholar] [CrossRef]
- Fang, H.; Wang, C.; Li, C.; Wang, K.W.; Xu, J. A comprehensive study on the locomotion characteristics of a metameric earthworm-like robot: A. Modeling and gait generation. Multibody Syst. Dyn. 2015, 34, 391–413. [Google Scholar] [CrossRef]
- Jung, K.; Koo, J.C.; Lee, Y.K.; Choi, H.R. Artificial annelid robot driven by soft actuators. Bioinspir. Biomim. 2007, 2, S42–S49. [Google Scholar] [CrossRef] [PubMed]
- Boxerbaum, A.S.; Chiel, H.J.; Quinn, R.D. A New Theory and Methods for Creating Peristaltic Motion in a Robotic Platform. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (Icra), Anchorage, AK, USA, 3–7 May 2010; pp. 1221–1227. [Google Scholar]
- Onal, C.D.; Wood, R.J.; Rus, D. Towards printable robotics: Origami-inspired planar fabrication of three-dimensional mechanisms. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Quinn, R.D.; Boxerbaum, A.; Palmer, L.; Chiel, H.; Diller, E.; Hunt, A.; Bachmann, R. Novel Locomotion via Biological Inspiration. In Proceedings of the Unmanned Systems Technology Xiii, Orlando, FL, USA, 27–29 April 2011; p. 8045. [Google Scholar]
- Fang, H.; Li, S.; Wang, K.W.; Xu, J. Phase coordination and phase–velocity relationship in metameric robot locomotion. Bioinspir. Biomim. 2015, 10, 066006. [Google Scholar] [CrossRef] [PubMed]
- Keller, J.B.; Falkovitz, M.S. Crawling of Worms. J. Theor. Biol. 1983, 104, 417–442. [Google Scholar] [CrossRef]
- Gidoni, P.; DeSimone, A. Stasis domains and slip surfaces in the locomotion of a bio-inspired two-segment crawler. Meccanica 2017, 52, 587–601. [Google Scholar] [CrossRef]
- DeSimone, A.; Tatone, A. Crawling motility through the analysis of model locomotors: Two case studies. Eur. Phys. J. E 2012, 35, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Xu, J. Analysis of worm-like locomotion driven by the sine-squared strain wave in a linear viscous medium. Mech. Res. Commun. 2017, 85, 33–44. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear Programming; Athena scientific Belmont: Belmont, MA, USA, 1999. [Google Scholar]
- Fang, H.; Wang, C.; Li, S.; Wang, K.W.; Xu, J. A comprehensive study on the locomotion characteristics of a metameric earthworm-like robot: B. Gait analysis and experiments. Multibody Syst. Dyn. 2015, 35, 153–177. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Xu, J. The Optimal Locomotion of a Self-Propelled Worm Actuated by Two Square Waves. Micromachines 2017, 8, 364. https://doi.org/10.3390/mi8120364
Jiang Z, Xu J. The Optimal Locomotion of a Self-Propelled Worm Actuated by Two Square Waves. Micromachines. 2017; 8(12):364. https://doi.org/10.3390/mi8120364
Chicago/Turabian StyleJiang, Ziwang, and Jian Xu. 2017. "The Optimal Locomotion of a Self-Propelled Worm Actuated by Two Square Waves" Micromachines 8, no. 12: 364. https://doi.org/10.3390/mi8120364
APA StyleJiang, Z., & Xu, J. (2017). The Optimal Locomotion of a Self-Propelled Worm Actuated by Two Square Waves. Micromachines, 8(12), 364. https://doi.org/10.3390/mi8120364




