The Multitasking System of Swarm Robot based on Null-Space-Behavioral Control Combined with Fuzzy Logic
Abstract
:1. Introduction
2. Building the Function of the Suction/Thrust Ford Based on Fuzzy Logic
- First step
- ➢
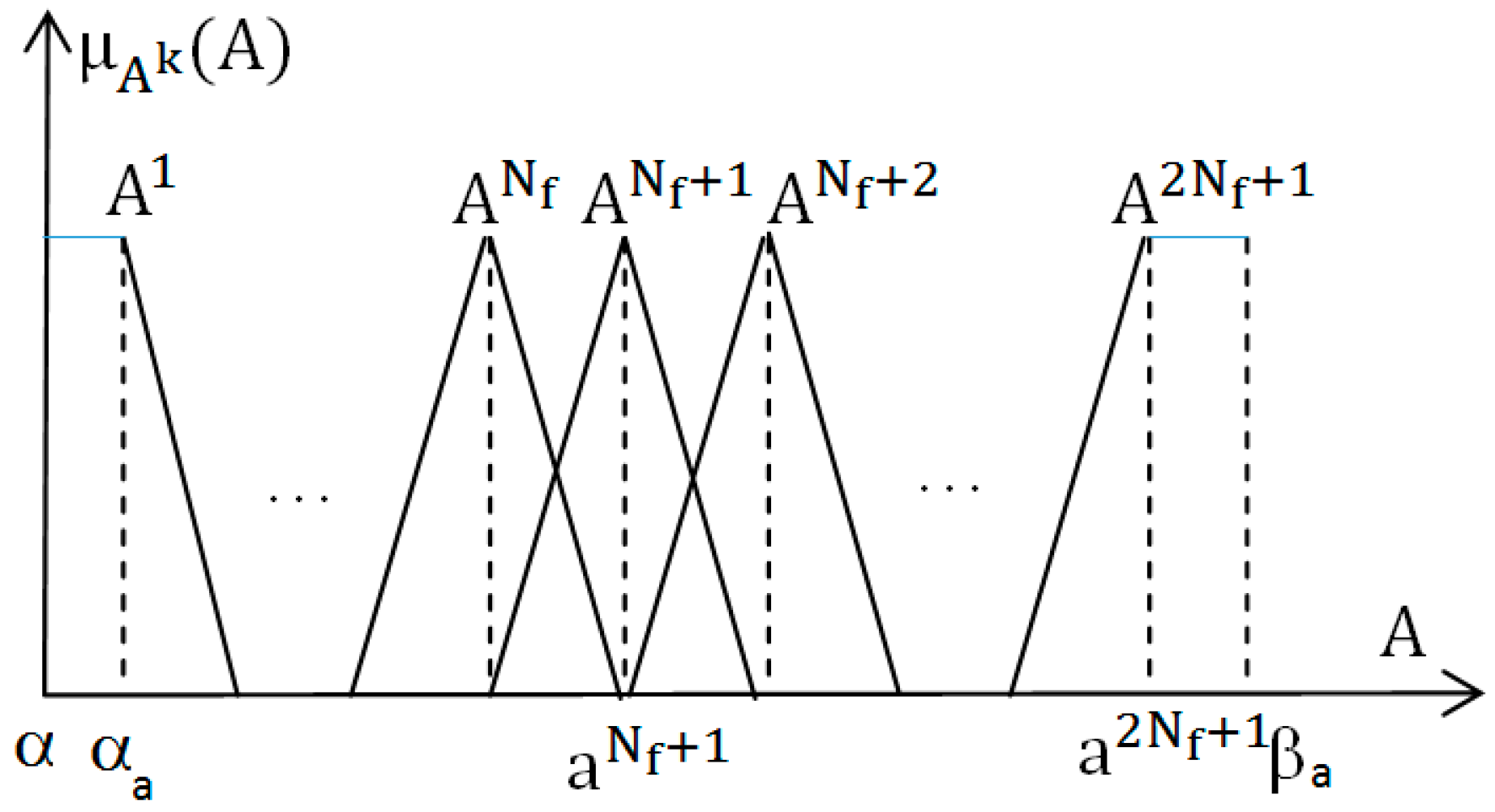
- The input signal is , assume that the value domain of u is [αb, βb] ∈ R, divide this domain into 2Nf + 1 in the range Bk as shown in Figure 1.
- ➢
- The output signal is A with the value domain [αa, βa], divide this value domain into 2Nf + 1 in the range Ak as shown in Figure 2 (k = 1, 2, …, 2Nf + 1). is the focus of the fuzzy range Ak:
- The second step: establishing 2Nf + 1 rule IF-THEN with the form: IF: , THEN:
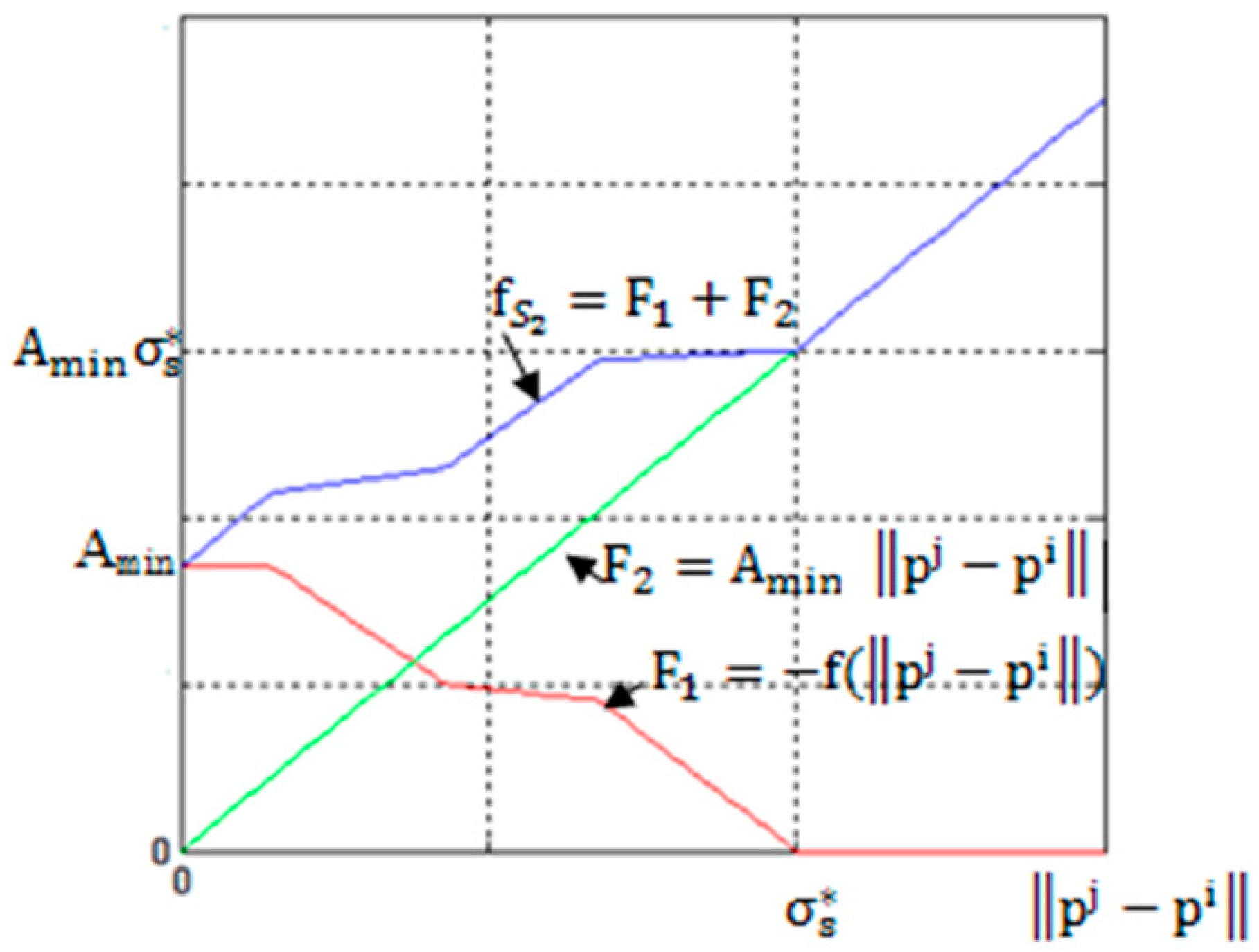
- The third step: defuzzifier using the central area method, we have control laws as follows [36]:
- Upper and lower limits:where:
- The equation of a part linearization:where: ,
3. The Stability of the System
- If increases, the thrust increases, the restricted area of the swarm robot increases.
- If increases, the restricted area of the swarm robot decreases.
- If the size of the swarm (N) is bigger, the restricted area is lower.
4. Multitasking-Control System of Swarm Robot
- The first task is avoiding obstacles
- The second task is moving to the destination.
- The third task is maintaining the swarm: Avoiding collisions among individuals in the swarm, but not splitting the group.
4.1. Determining the Speed Component Avoiding Obstacles
4.2. Determining the Speed Component Moving to the Target
4.3. Determining the Maintained-Swarm Speed Component
4.4. The Algorithm of Swarm Robot Control for Performing Multiple-Task
- The first step
- ➢
- Enter the number (N) of robots in the swarm.
- ➢
- Enter the number (M) of obstacles in the moving space.
- ➢
- Initially the position of individual robots in n-dimensional space:
- ➢
- Placement of M obstacles and the destination (g) in n-dimensional space:
- ➢
- Enter the safe distance between the individual robot and obstacle , the safe distance among robot individuals
- ➢
- Enter the coefficients and
- ➢
- Enter the number of steps to calculate (K).
- The second step
- ➢
- Calculating the distance between each robot (i) and each obstacle , the distance between each robot and target, the distance between robot (i) and robot (j).
- ➢
- Calculating the suction/thrust force according to Equation (3), satisfying Condition (4).
- The third step
- ➢
- Comparing the actual distance and safe distance from the robot (i) to the obstacle (m):
- ▪
- If , the robot (i) does not need to avoid the obstacle (o), it means .
- ▪
- If , the robot (i) needs to avoid the obstacle (o), calculating by Formula (26). Calculating , , .
- ➢
- Comparing the actual distance and the desired distance from the robot (i) to the target:
- ▪
- If , the robot (i) reached the target g, .
- ▪
- If , the robot (i) has not reached the target, calculating by the Formula (24).
- ▪
- Calculating ,,, calculating: , , .
- ➢
- Comparing the actual distance and the desired distance from the robot (i) to the robot (j):
- ▪
- If , the robot (i) and the robot (j) move towards each other by the suction force .
- ▪
- If , the robot (i) and the robot (j) move away from each other by the thrust force .
- ▪
- If , the robot (i) and the robot (j) keep their route because of .
- ▪
- Calculating , , .
- The fourth step
- ➢
- The speed of the individual (i) at the step k (k = 0 ÷ K − 1) is determined by the formula:
- ➢
- The distance moved of the robot (i) in a step time():
- ➢
- The new position of the robot (i) after k + 1 steps:
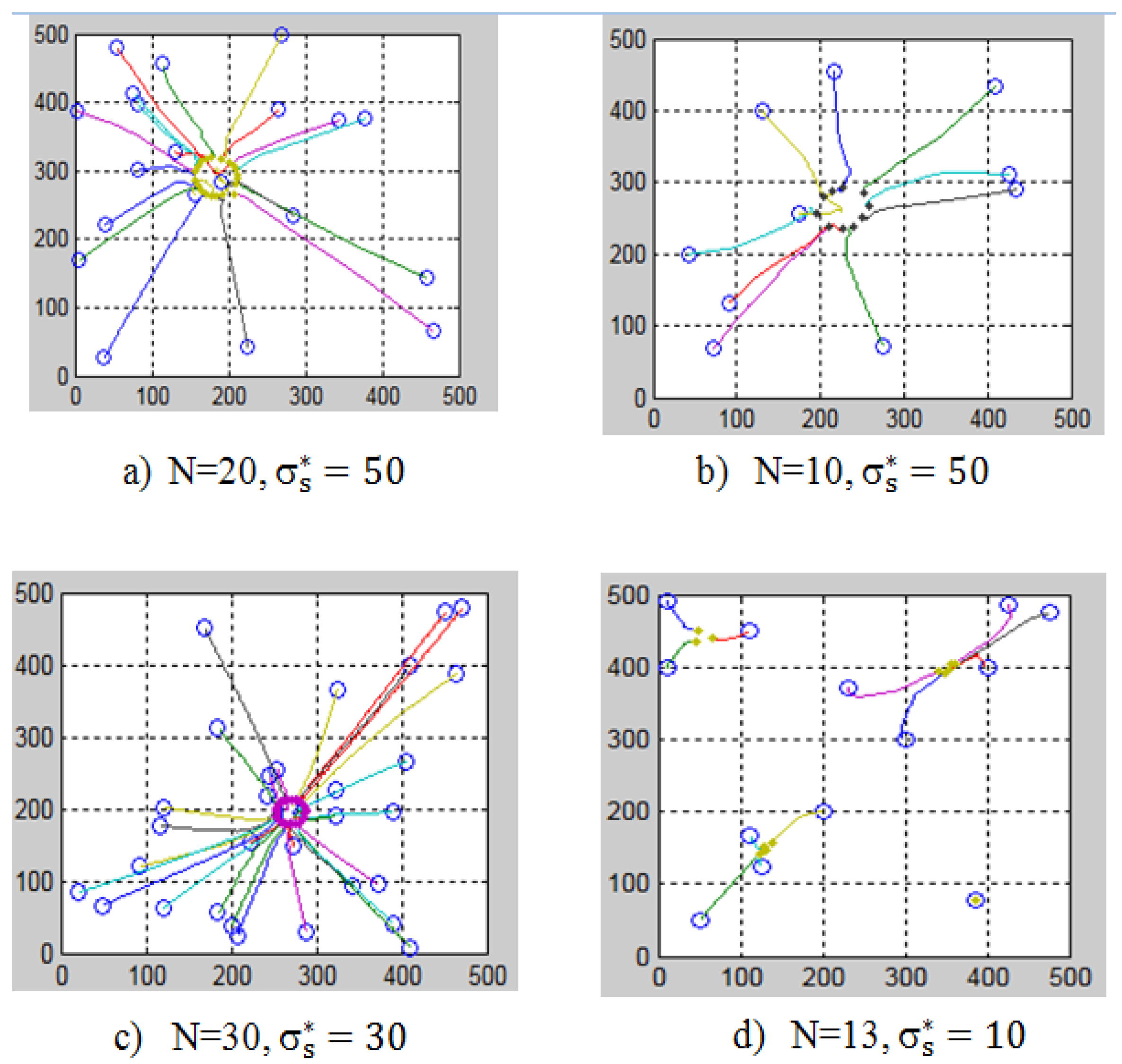
5. Simulation Results and Analysis
- If the size of the swarm (N) increases, the convergence radius decreases;
- If the safe distance increases, the convergence radius increases;
- The actual convergent radius (R) is always smaller than the calculated value (σ).
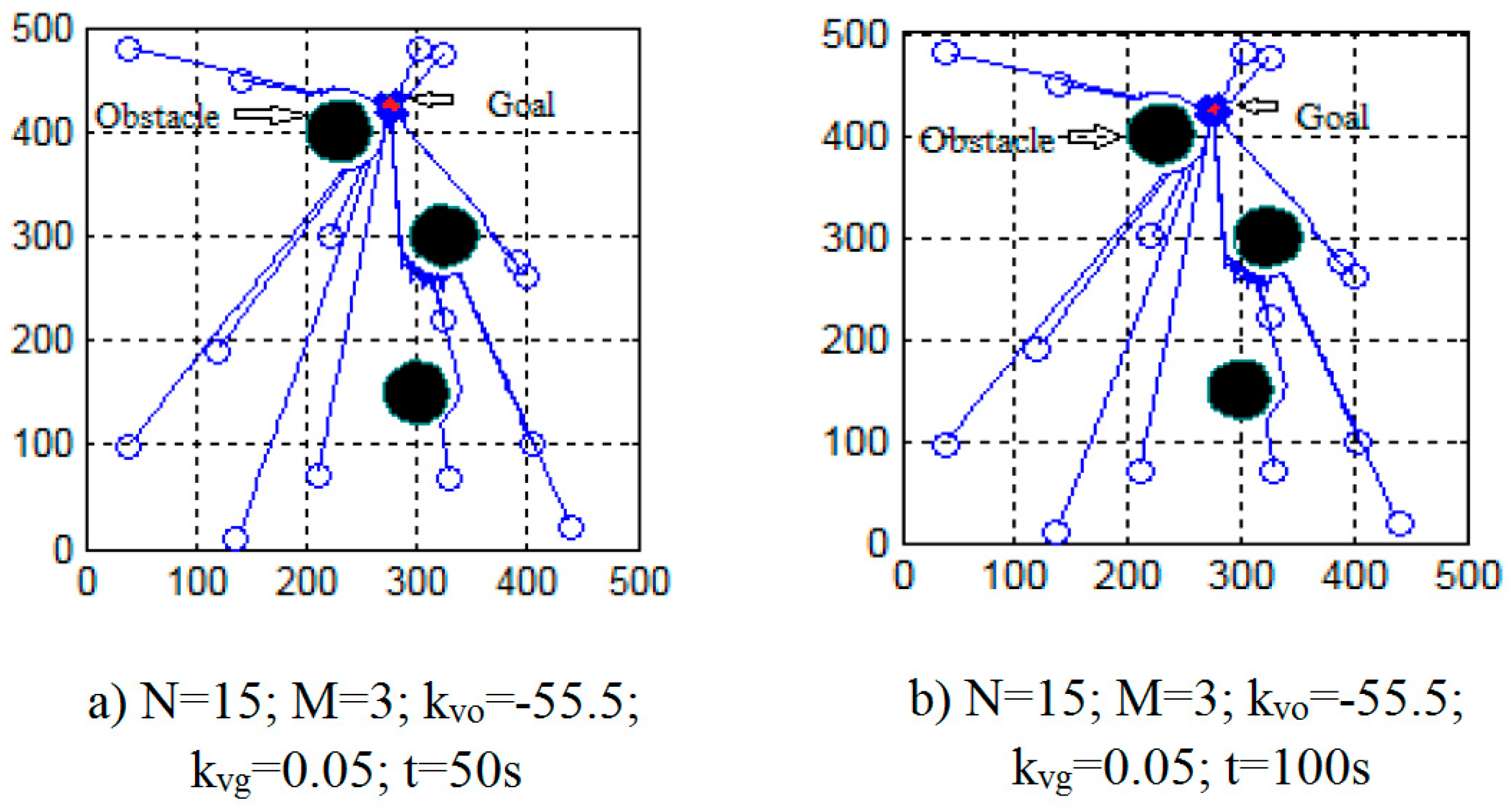
- If the coefficient is larger, the individual movement to the target is faster.
- If we want to increase the coefficient but not let the robot collide with obstacles, we must reduce the coefficient . This means, if is more positive, must be more negative.
- If the number of obstacles (M) is bigger, the avoid-obstacle-coefficient ( must be more negative. If the coefficient is more negative, the ability of the robots to avoid obstacles is better, but the moving time to the destination will be longer.
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Darmanin, R.N.; Bugeja, M.K. A review on multi-robot systems categorised by application domain. In Proceedings of the 2017 25th Mediterranean Conference on Control and Automation (MED), Valletta, Malta, 3–6 July 2017; pp. 701–706. [Google Scholar]
- Li, D.; Fan, Q.; Dai, X. Research status of multi-robot systems task allocation and uncertainty treatment. J. Phys. Conf. Ser. 2017, 887, 012081. [Google Scholar] [CrossRef]
- Gautam, A.; Mohan, S. A review of research in multi-robot systems. In Proceedings of the 2012 7th IEEE International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012; pp. 1–5. [Google Scholar]
- Bruemmer, D.J.; Dudenhoeffer, D.D.; McKay, M.D.; Anderson, M.O. A Robotic Swarm for Spill Finding and Perimeter Formation. 2002. Available online: https://pdfs.semanticscholar.org/baa7/5fc5db081a730a01ecfccb42167c62d39c58.pdf (access on 9 December 2017).
- Mataric, M.J. Behaviour-based control: Examples from navigation, learning, and group behaviour. J. Exp. Theor. Artif. Intell. 1997, 9, 323–336. [Google Scholar] [CrossRef]
- Correll, N.; Martinoli, A. Multirobot inspection of industrial machinery. IEEE Robot. Autom. Mag. 2009, 16, 103–112. [Google Scholar] [CrossRef]
- Kube, C.R.; Bonabeau, E. Cooperative transport by ants and robots. Robot. Auton. Syst. 2000, 30, 85–101. [Google Scholar] [CrossRef]
- Miyata, N.; Ota, J.; Arai, T.; Asama, H. Cooperative transport by multiple mobile robots in unknown static environments associated with real-time task assignment. IEEE Trans. Robot. Autom. 2002, 18, 769–780. [Google Scholar] [CrossRef]
- Farinelli, A.; Iocchi, L.; Nardi, D. Multirobot systems: A classification focused on coordination. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2004, 34, 2015–2028. [Google Scholar] [CrossRef]
- Parker, L.E. Multiple mobile robot systems. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 921–941. [Google Scholar]
- Cai, Y.; Yang, S.X. A survey on multi-robot systems. In Proceedings of the World Automation Congress (WAC), Puerto Vallarta, Mexico, 24–28 June 2012; pp. 1–6. [Google Scholar]
- Yan, Z.; Jouandeau, N.; Cherif, A.A. A survey and analysis of multi-robot coordination. Int. J. Adv. Robot. Syst. 2013, 10, 399. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Inf. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. Coop. Robot. Sens. Netw. 2015, 604, 31–51. [Google Scholar]
- Dias, M.B.; Zlot, R.; Kalra, N.; Stentz, A. Market-based multirobot coordination: A survey and analysis. Proc. IEEE 2006, 94, 1257–1270. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Dorigo, M.; Floreano, D.; Gambardella, L.M.; Mondada, F.; Nolfi, S.; Baaboura, T.; Burnier, D. Swarmanoid: a novel concept for the study of heterogeneous robotic swarms. IEEE Robot. Autom. Mag. 2013, 20, 60–71. [Google Scholar] [CrossRef]
- Champion, B.T.; Joordens, M.A. Underwater swarm robotics review. In Proceedings of the 2015 10th System of Systems Engineering Conference (SoSE), San Antonio, Texas, USA, 17–20 May 2015; pp. 111–116. [Google Scholar]
- Son, J.H.; Ahn, H.S. Cooperative reinforcement learning: brief survey and application to bio-insect and artificial robot interaction. In Proceedings of the IEEE/ASME International Conference on Mechtronic and Embedded Systems and Applications, 2008 (MESA 2008), Beijing, China, 12–15 October 2008; pp. 71–76. [Google Scholar]
- Goodrich, M.A.; Schultz, A.C. Human-robot interaction: A survey. Found. Trends Hum.-Comput. Interact. 2007, 1, 203–275. [Google Scholar] [CrossRef]
- Chen, J.Y.; Barnes, M.J. Human-agent teaming for multirobot control: A review of human factors issues. IEEE Trans. Hum.-Mach. Syst. 2014, 44, 13–29. [Google Scholar] [CrossRef]
- Guanghua, W.; Deyi, L.; Wenyan, G.; Peng, J. Study on formation control of multi-robot systems. In Proceedings of the 2013 Third International Conference on Intelligent System Design and Engineering Applications (ISDEA), Hong Kong, China, 16–18 January 2013; pp. 1335–1339. [Google Scholar]
- Yang, M.; Yan, G.G.; Tian, Y.T. A review of studies in flocking for multi-robot system. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering (CMCE), Changchun, China, 24–26 August 2010; pp. 28–31. [Google Scholar]
- Portugal, D.; Rocha, R. A Survey on Multi-Robot Patrolling Algorithms. 2011. Available online: http://ap.isr.uc.pt/archive/dportugalPR11_Doceis2011.pdf (access on 9 December 2017).
- Liu, Y.; Nejat, G. Robotic urban search and rescue: A survey from the control perspective. J. Intell. Robot. Syst. 2013, 72, 147. [Google Scholar] [CrossRef]
- Cook, D.; Vardy, A.; Lewis, R. A survey of AUV and robot simulators for multi-vehicle operations. In Proceedings of the 2014 IEEE/OES Autonomous Underwater Vehicles (AUV), Oxford, MS, USA, 6–9 October 2014; pp. 1–8. [Google Scholar]
- Xiong, N.; He, J.; Yang, Y.; He, Y.; Kim, T.H.; Lin, C. A survey on decentralized flocking schemes for a set of autonomous mobile robots. JCM 2010, 5, 31–38. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Contr. 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Gazi, V.; Passino, K.M. Stability analysis of swarms. IEEE Trans. Autom. Contr. 2003, 48, 692–697. [Google Scholar] [CrossRef]
- Wang, L.; Fang, H. Stability analysis of practical anisotropie swarms. In Proceedings of the 2010 11th International Conference on Control Automation Robotics & Vision (ICARCV), Singapore, 7–10 December 2010; pp. 768–772. [Google Scholar]
- Chen, X.B.; Pan, F.; Li, L.; Fang, H. Practical stability analysis for swarm systems. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 3904–3909. [Google Scholar]
- Xue, Z.; Zeng, J.; Feng, C.; Liu, Z. Swarm target tracking collective behavior control with formation coverage search agents & globally asymptotically stable analysis of stochastic swarm. JCP 2011, 6, 1772–1780. [Google Scholar]
- Brooks, R. A robust layered control system for a mobile robot. IEEE J. Robot. Autom. 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Marino, A.; Parker, L.E.; Antonelli, G.; Caccavale, F. A decentralized architecture for multi-robot systems based on the null-space-behavioral control with application to multi-robot border patrolling. J. Intell. Robot. Syst. 2013, 71, 423–444. [Google Scholar] [CrossRef]
- Wolkenhauer, O. A course in fuzzy systems and control. Int. J. Electr. Eng. Educ. 1997, 34, 282. [Google Scholar] [CrossRef]



| N | α | β | σ | R | |
|---|---|---|---|---|---|
| 10 | 10 | 0.02 | 9.74 | 15.61 | 6.18 |
| 10 | 30 | 0.02 | 25.37 | 43.62 | 17.06 |
| 20 | 10 | 0.02 | 8.40 | 10.25 | 4.10 |
| 20 | 30 | 0.02 | 25.33 | 30.82 | 15.18 |
| 30 | 10 | 0.02 | 8.23 | 8.77 | 3.91 |
| 30 | 30 | 0.02 | 25.25 | 25.23 | 15.04 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Thi Thuy, N.; Nguyen Trong, T. The Multitasking System of Swarm Robot based on Null-Space-Behavioral Control Combined with Fuzzy Logic. Micromachines 2017, 8, 357. https://doi.org/10.3390/mi8120357
Le Thi Thuy N, Nguyen Trong T. The Multitasking System of Swarm Robot based on Null-Space-Behavioral Control Combined with Fuzzy Logic. Micromachines. 2017; 8(12):357. https://doi.org/10.3390/mi8120357
Chicago/Turabian StyleLe Thi Thuy, Nga, and Thang Nguyen Trong. 2017. "The Multitasking System of Swarm Robot based on Null-Space-Behavioral Control Combined with Fuzzy Logic" Micromachines 8, no. 12: 357. https://doi.org/10.3390/mi8120357
APA StyleLe Thi Thuy, N., & Nguyen Trong, T. (2017). The Multitasking System of Swarm Robot based on Null-Space-Behavioral Control Combined with Fuzzy Logic. Micromachines, 8(12), 357. https://doi.org/10.3390/mi8120357





