Low-Cost High-Speed In-Plane Stroboscopic Micro-Motion Analyzer
Abstract
:1. Introduction
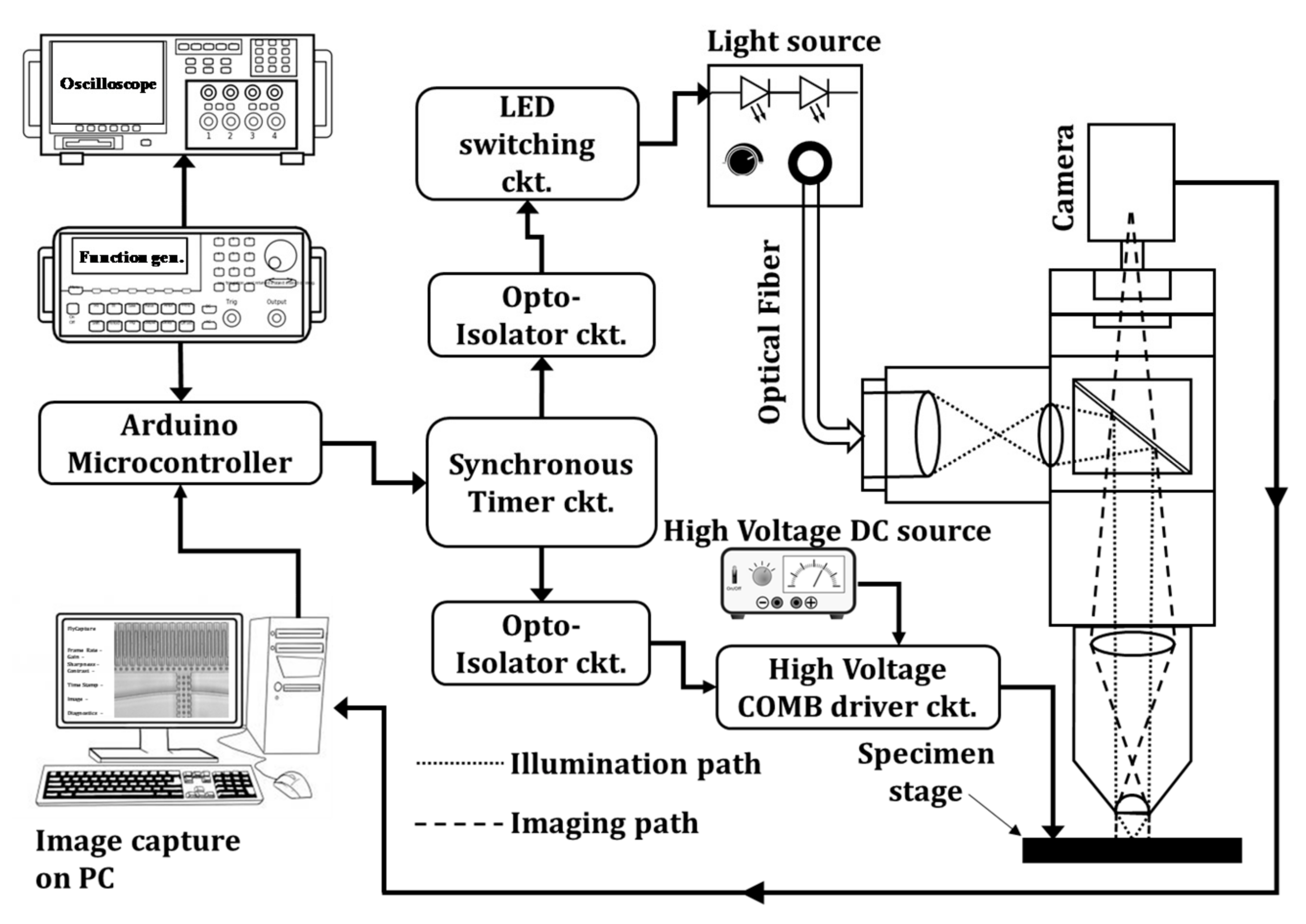
2. Low-Cost Stroboscopy Imaging System
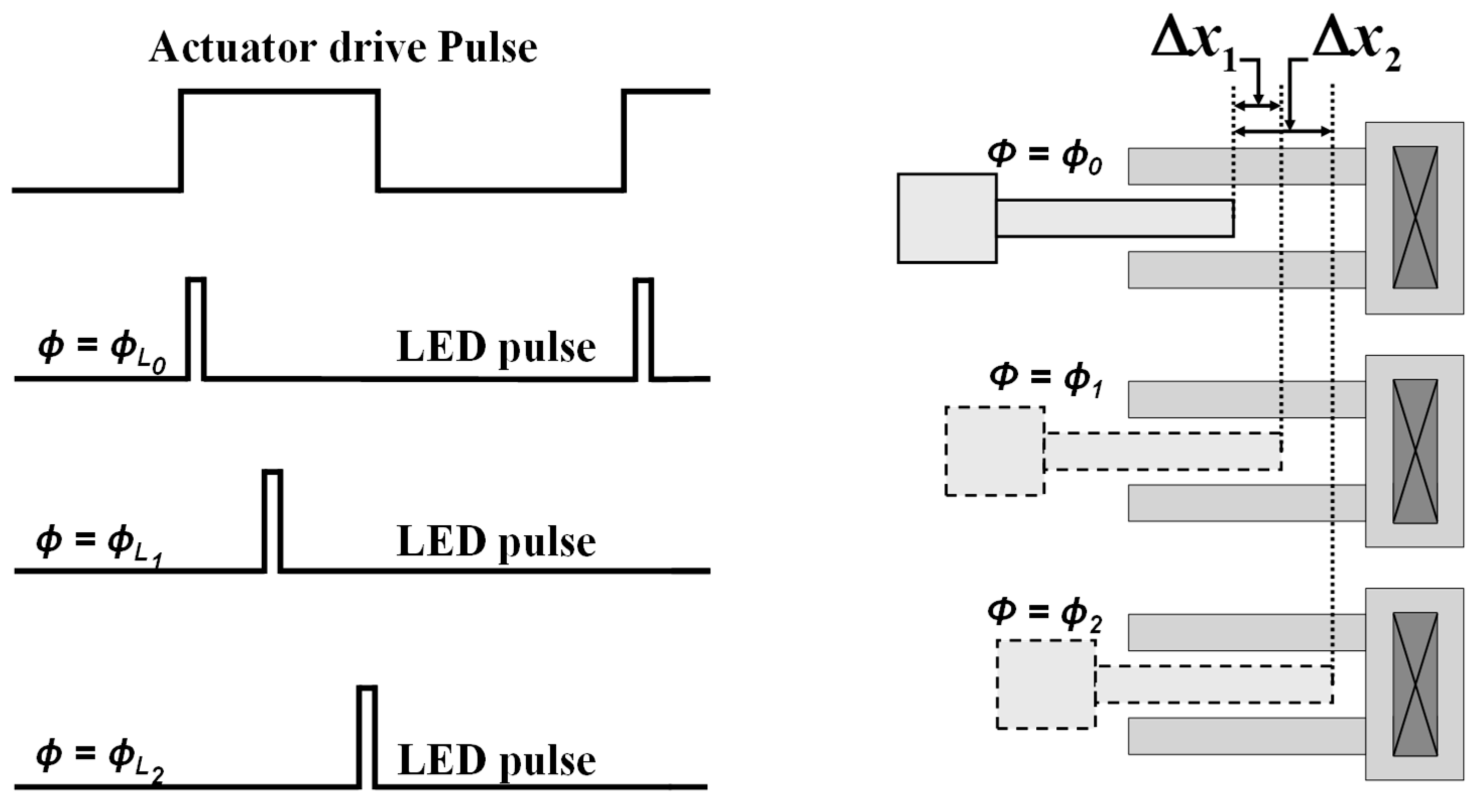
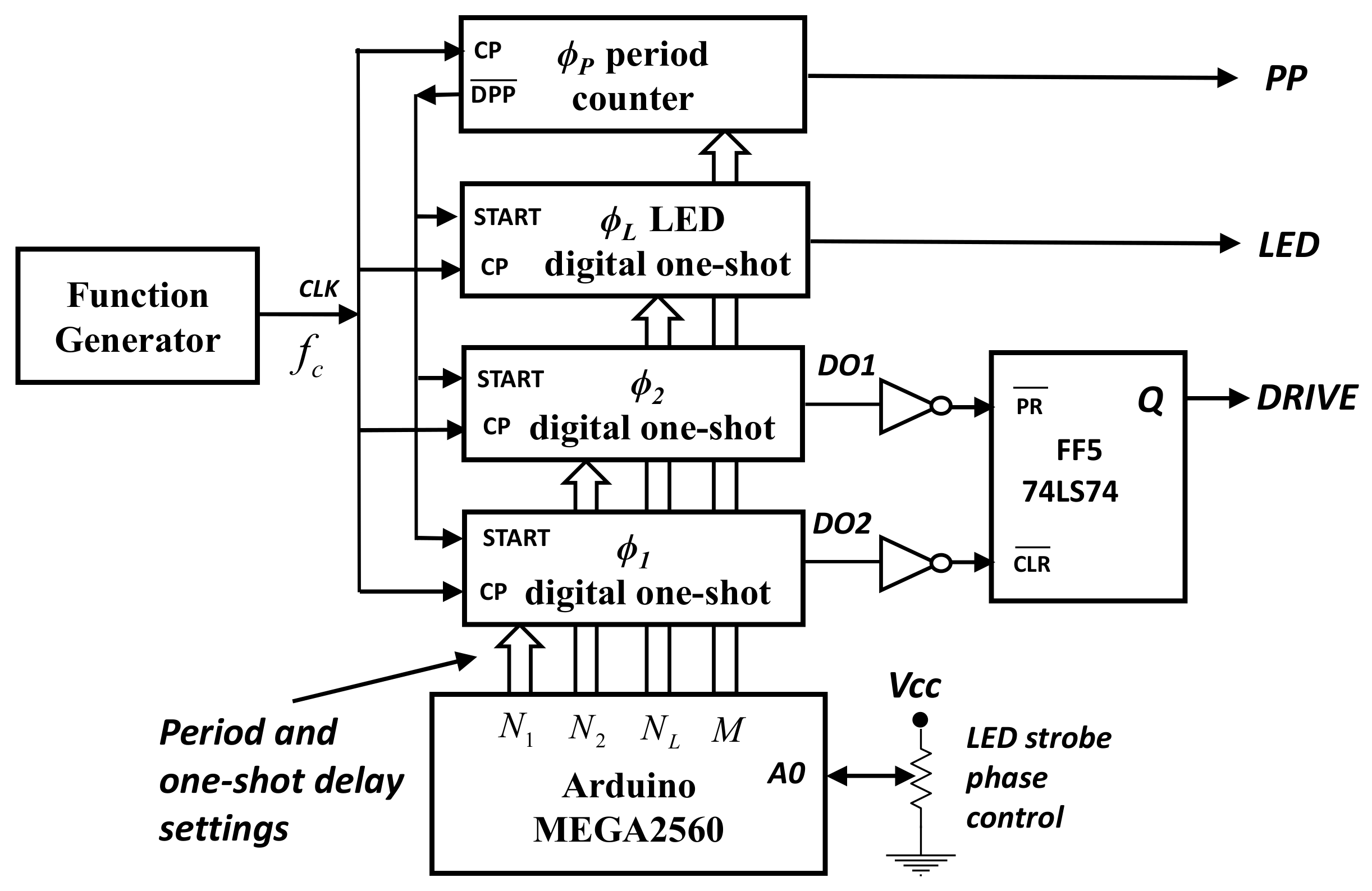
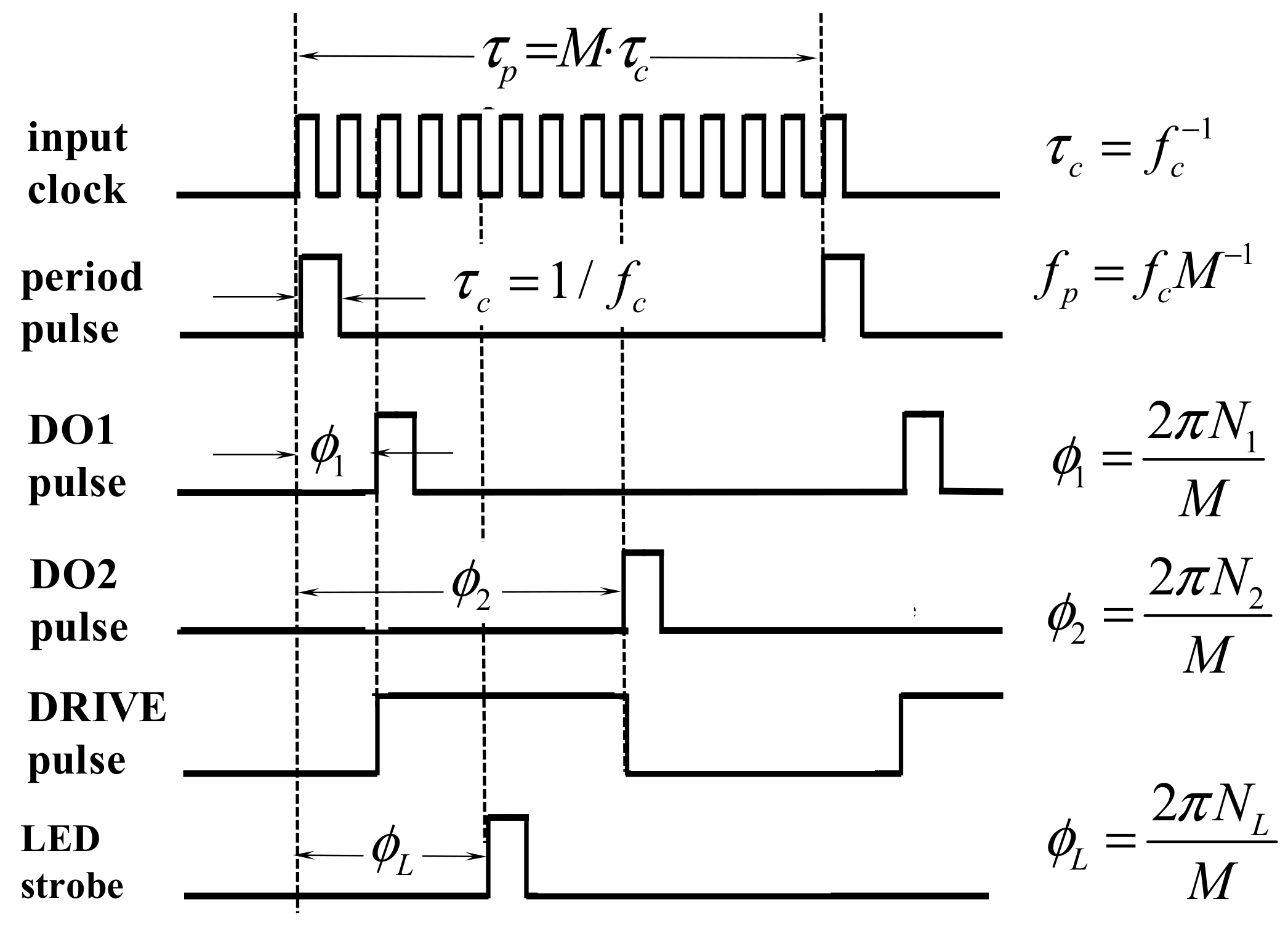
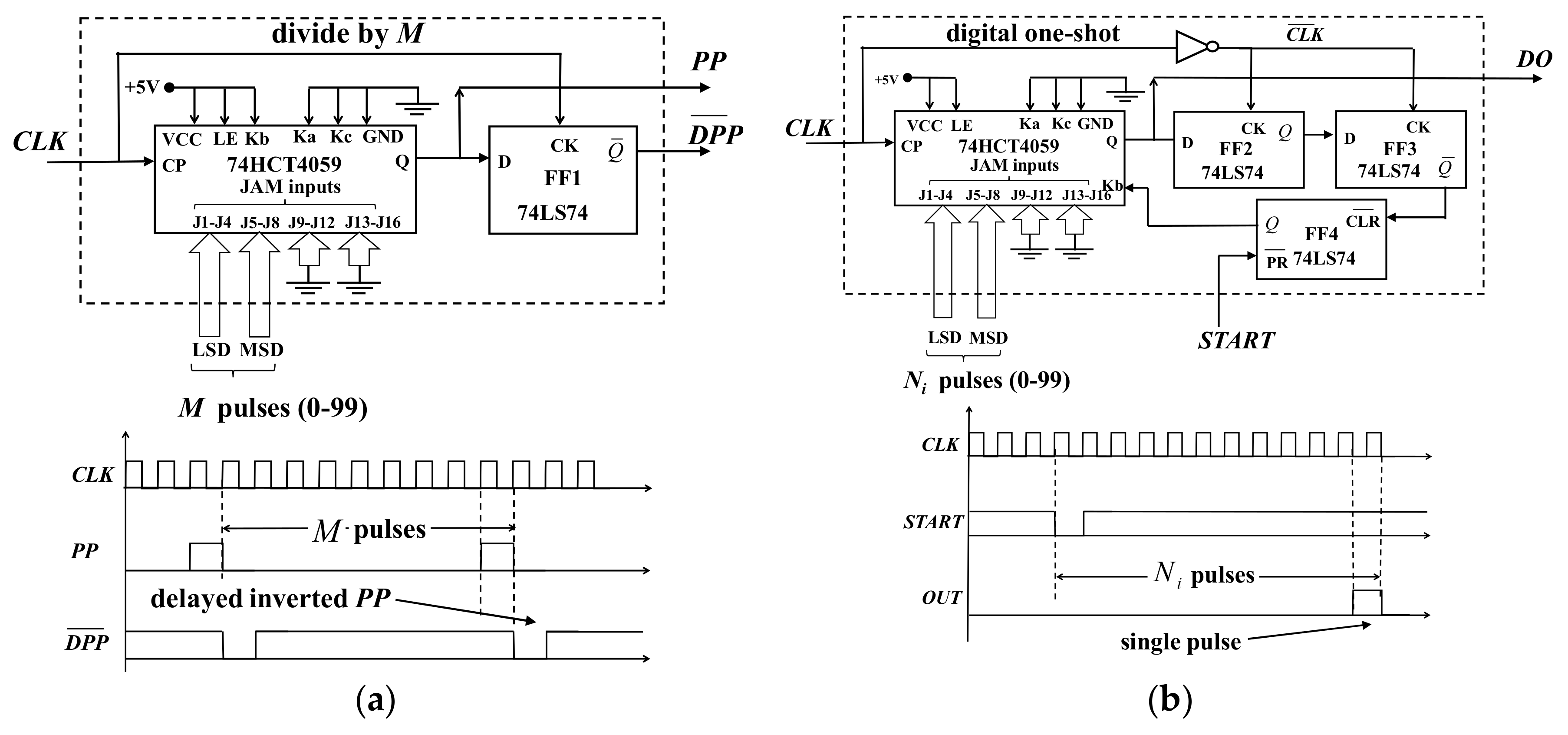
2.1. Timer Generator Circuit
2.2. High Voltage MEMS and LED Driver Circuits
2.3. Imaging Optics
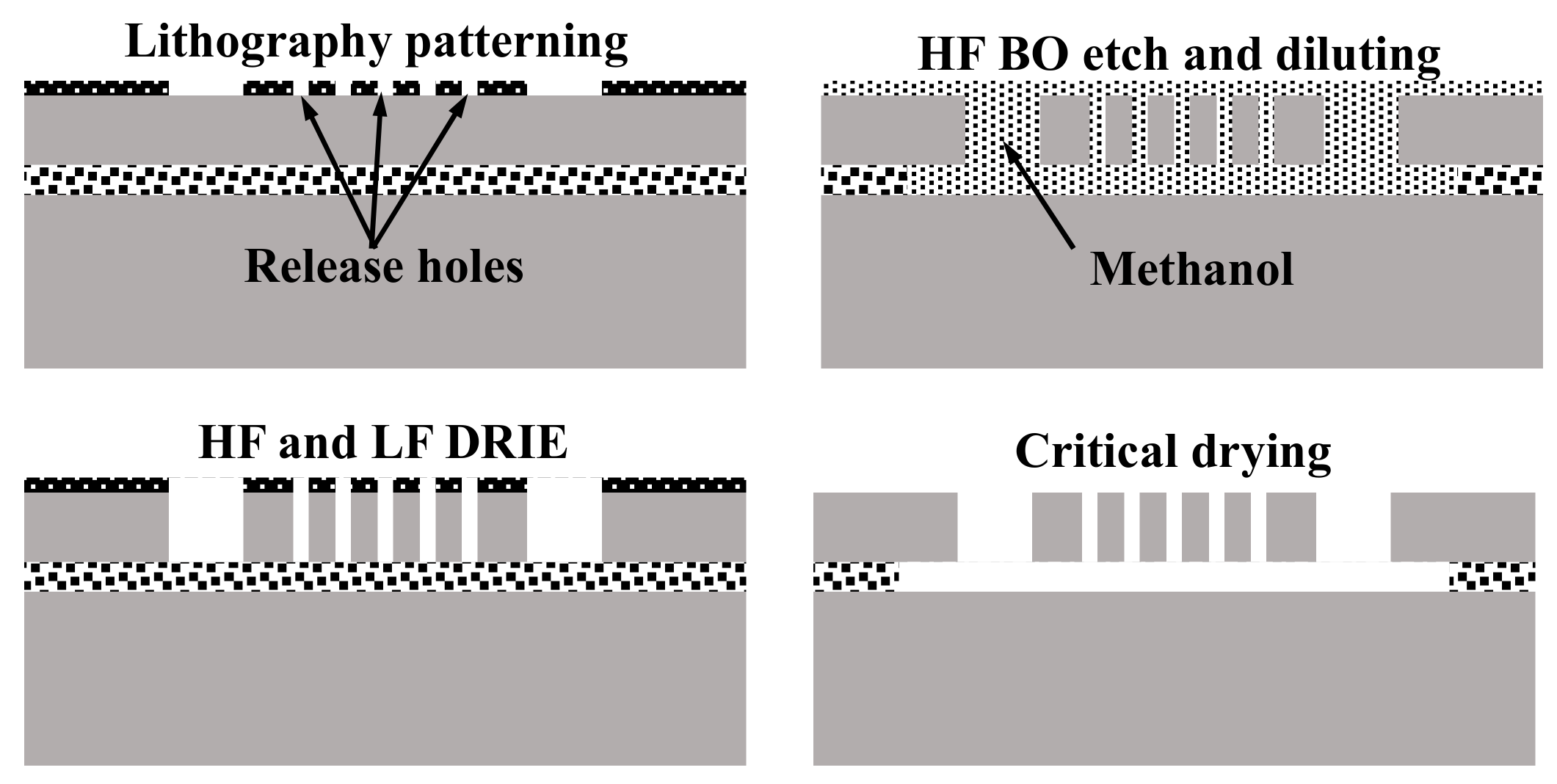
3. Test Device Fabrication
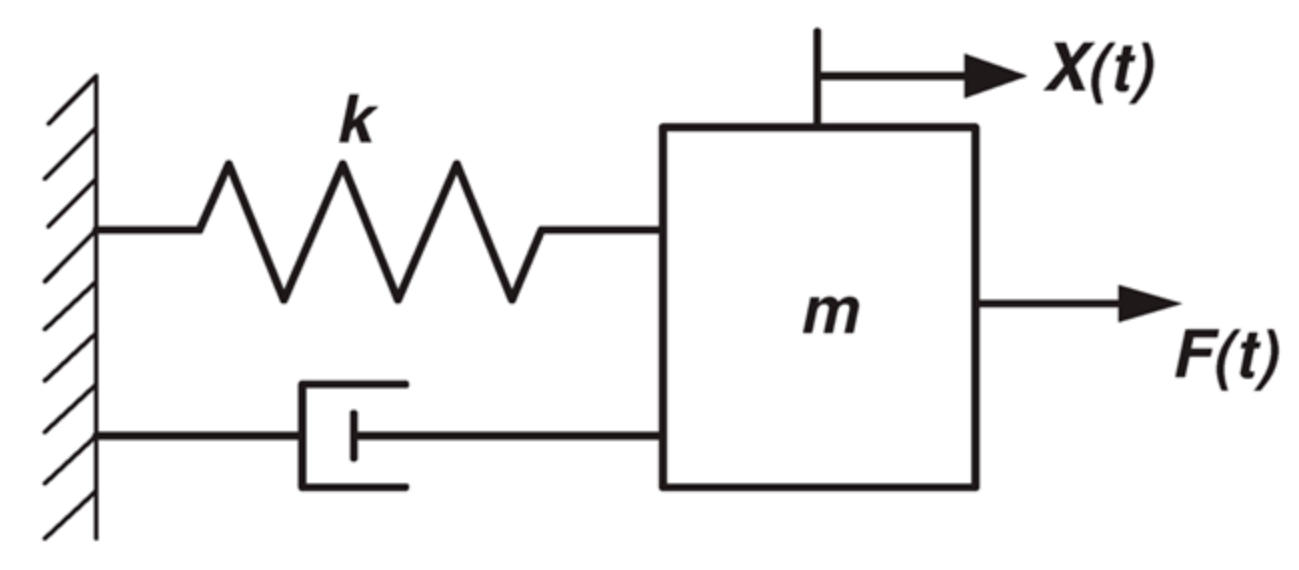
4. Comb Drive Motion
5. Experimental Imaging Results
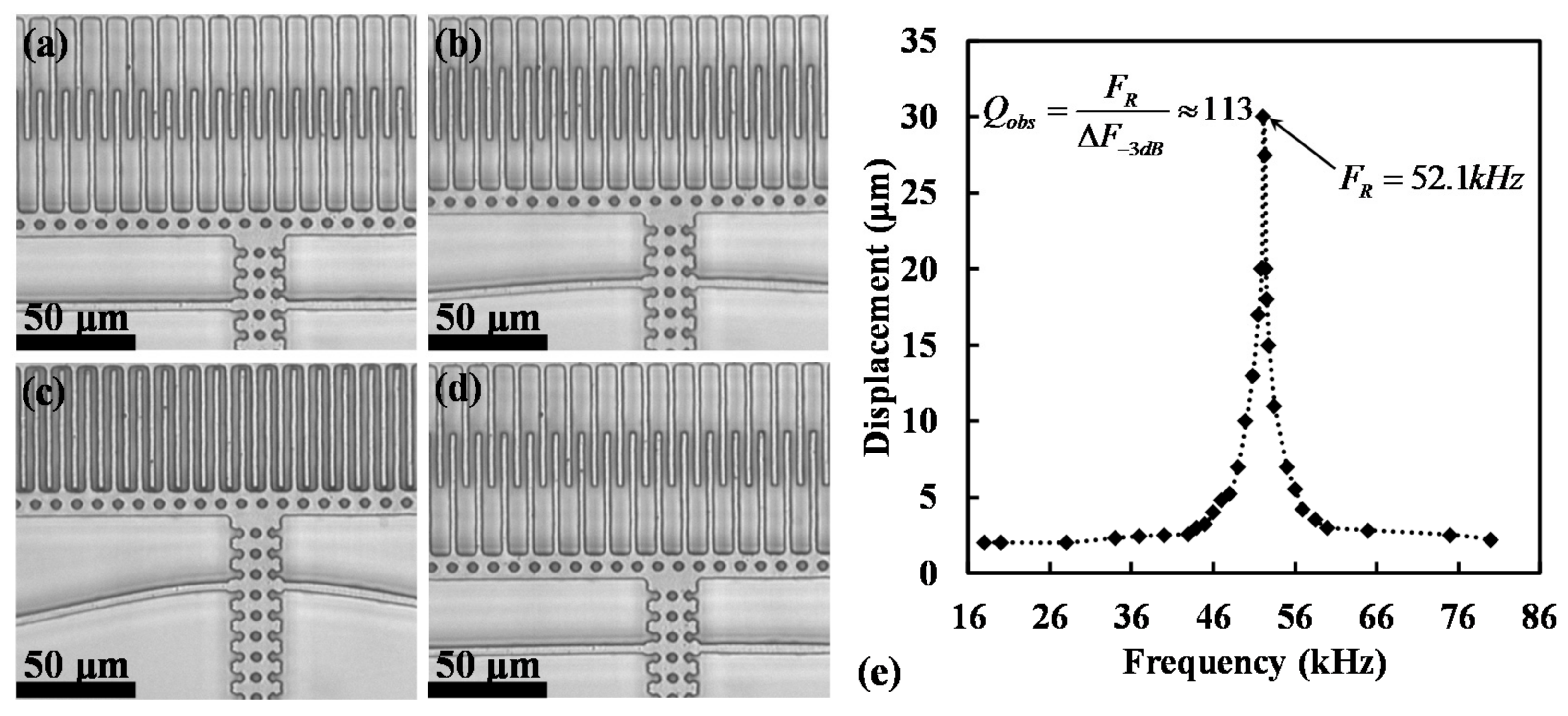
5.1. Frequency Analysis
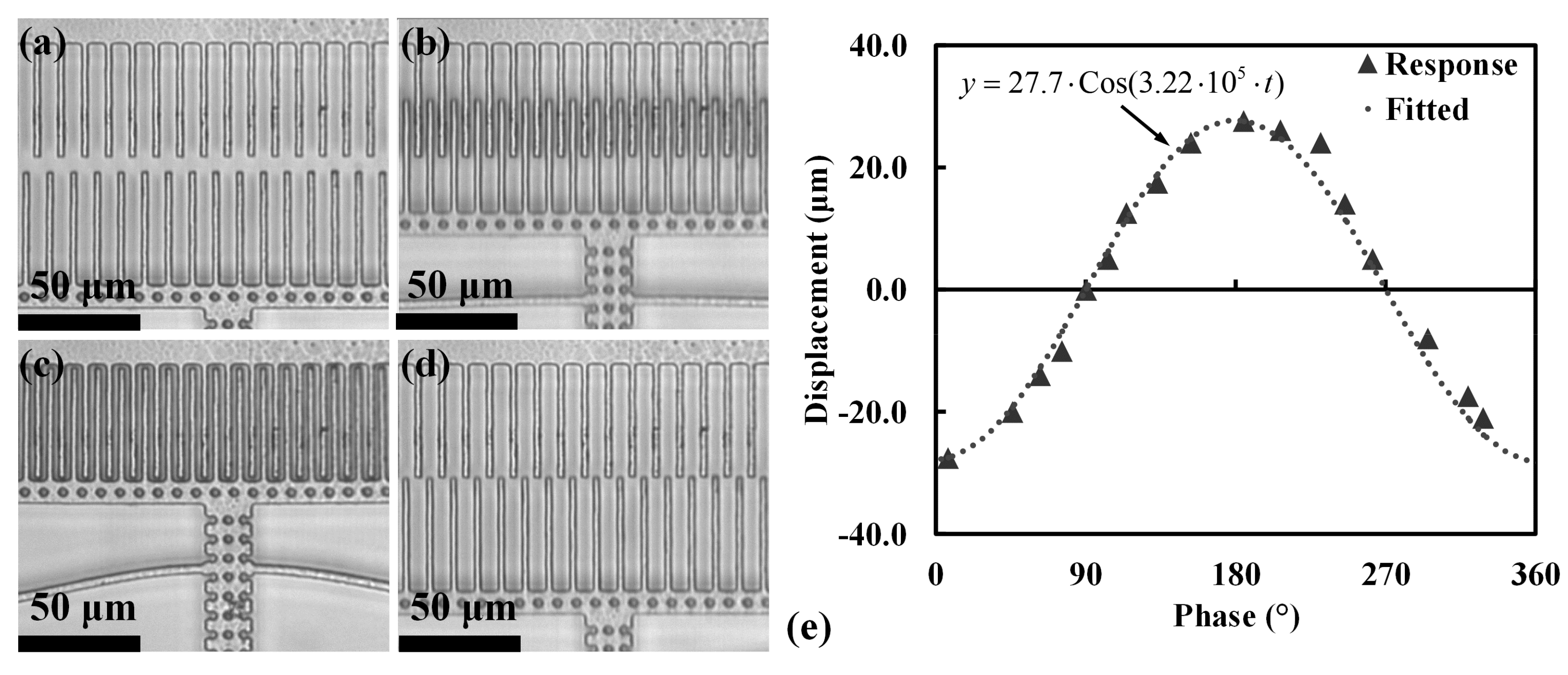
5.2. Phase Analysis
5.3. Stroke vs. Applied Voltage
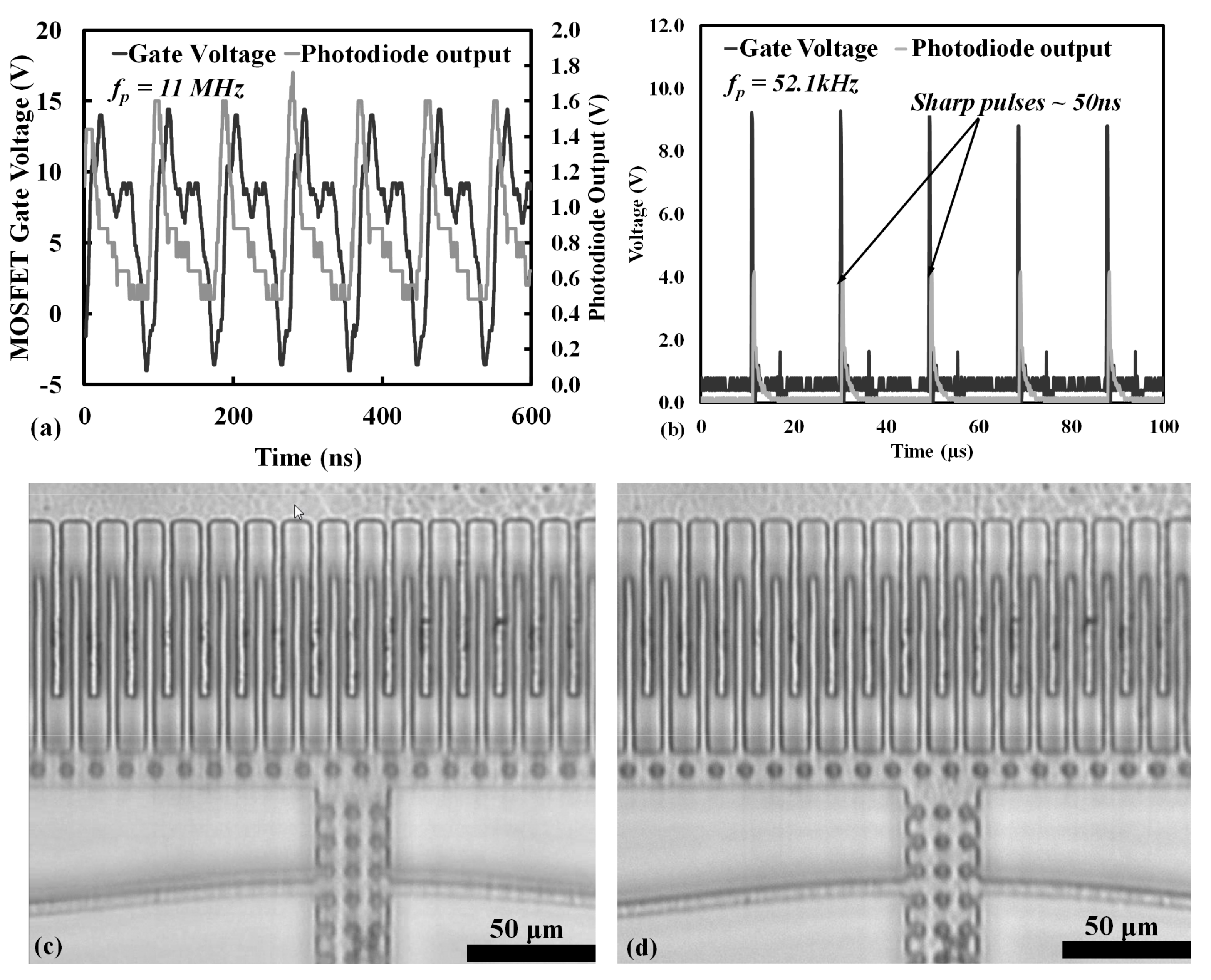
5.4. Stroboscopic System Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Lawrence, E. Optical Measurement Techniques for Dynamic Characterization of MEMS Devices. Available online: http://www.polytec.com/fileadmin/user_uploads/Applications/Micro_Nano_Technology/Documents/OM_TP_MEMS_Whitepaper_2012_07_E.pdf (accessed on 6 September 2017).
- Lawrence, E.M.; Speller, K.E.; Yu, D. MEMS characterization using laser doppler vibrometry. Proc. SPIE 2003, 4980, 51–62. [Google Scholar]
- Davis, C.; Freeman, D.M. Statistics of subpixel registration algorithms based on spatiotemporal gradients or block matching. Opt. Eng. 1997, 37, 1290–1298. [Google Scholar] [CrossRef]
- Davis, C.; Freeman, D.M. Using a light microscope to measure motions with nanometer accuracy. Opt. Eng. 1997, 37, 1299–1304. [Google Scholar] [CrossRef]
- Smith, N.F.; Tanner, D.M.; Swanson, S.E.; Miller, S.L. Non-destructive resonant frequency measurement on MEMS actuators. In Proceedings of the 39th Annual IEEE International Reliability Physics Symposium, Orlando, FL, USA, 30 April–3 May 2001; pp. 99–105. [Google Scholar]
- Rembe, C.; Muller, L.; Muller, R.S.; Howe, R.T. Full three-dimensional motion characterization of a gimballed electrostatic microactuator. In Proceedings of the 39th Annual IEEE International Reliability Physics Symposium, Orlando, FL, USA, 30 April–3 May 2001; pp. 91–98. [Google Scholar]
- Hart, M.; Conant, R.A.; Lau, K.Y.; Muller, R.S. Time-resolved measurement of optical MEMS using stroboscopic interferometry. Proc. Transducers 1999, 99, 470–473. [Google Scholar]
- Rembe, C.; Muller, R.S. Measurement system for full three-dimensional motion characterization of MEMS. J. Microelectromech. Syst. 2002, 11, 479–488. [Google Scholar] [CrossRef]
- Hart, M.R.; Conant, R.A.; Lau, K.Y.; Muller, R.S. Stroboscopic interferometer system for dynamic MEMS characterization. J. Microelectromech. Syst. 2000, 9, 409–418. [Google Scholar] [CrossRef]
- Rembe, C.; Tibken, B.; Hofer, E.P. Analysis of the dynamics in microactuators using high-speed cine photomicrography. J. Microelectromech. Syst. 2001, 10, 137–145. [Google Scholar] [CrossRef]
- Guo, T.; Chang, H.; Chen, J.; Fu, X.; Hu, X. Micro-motion analyzer used for dynamic MEMS characterization. Opt. Lasers Eng. 2009, 47, 512–517. [Google Scholar] [CrossRef]
- Petitgrand, S.; Bosseboeuf, A. Simultaneous mapping of out-of-plane and in-plane vibrations of MEMS with (sub) nanometer resolution. J. Micromech. Microeng. 2004, 14, S97. [Google Scholar] [CrossRef]
- LM_BR_MSA-400.pdf. Available online: http://www.ects.pl/files/uploader/Producenci/Polytec/Wibrometry_do_pomiarow_mikrostruktur/MSA-500/LM_BR_MSA-400.pdf (accessed on 6 September 2017).
- Lyncée Tec. Reflection Configured Digital Holographic Microscope (DHM®), a Non-Scanning and Non-Contact Method for Static and Dynamic 3D Topography as Well as Vibration Characterization. Available online: https://www.lynceetec.com/wp-content/uploads/2014/02/LynceeTec_DHM_Rseries_Datasheet_2014.pdf (accessed on 6 September 2017).
- 74HCT4059 Datasheet (PDF)—NXP Semiconductors. Available online: http://www.alldatasheet.com/datasheet-pdf/pdf/15613/PHILIPS/74HCT4059.html (accessed on 6 September 2017).
- Tang, W.C.K. Electrostatic Comb Drive for Resonant Sensor and Actuator Applications. Ph.D. Thesis, University of California, Berkeley, CA, USA, 21 November 1990. [Google Scholar]
- Zhou, G.; Dowd, P. Tilted folded-beam suspension for extending the stable travel range of comb-drive actuators. J. Micromech. Microeng. 2002, 13, 178. [Google Scholar] [CrossRef]
- Dennis, J.O.; Ahmed, A.Y.; Khir, M.H.M.; Rabih, A.A.S. Modelling and simulation of the effect of air damping on the frequency and quality factor of a CMOS-MEMS resonator. Appl. Math. Inf. Sci. 2015, 9, 729–737. [Google Scholar]
- Eltagoury, Y.M.; Soliman, M.; Sabry, Y.M.; Alotaibi, M.J.; Khalil, D. Electrostatic comb-drive actuator with high in-plane translational velocity. Micromachines 2016, 7, 188. [Google Scholar] [CrossRef]

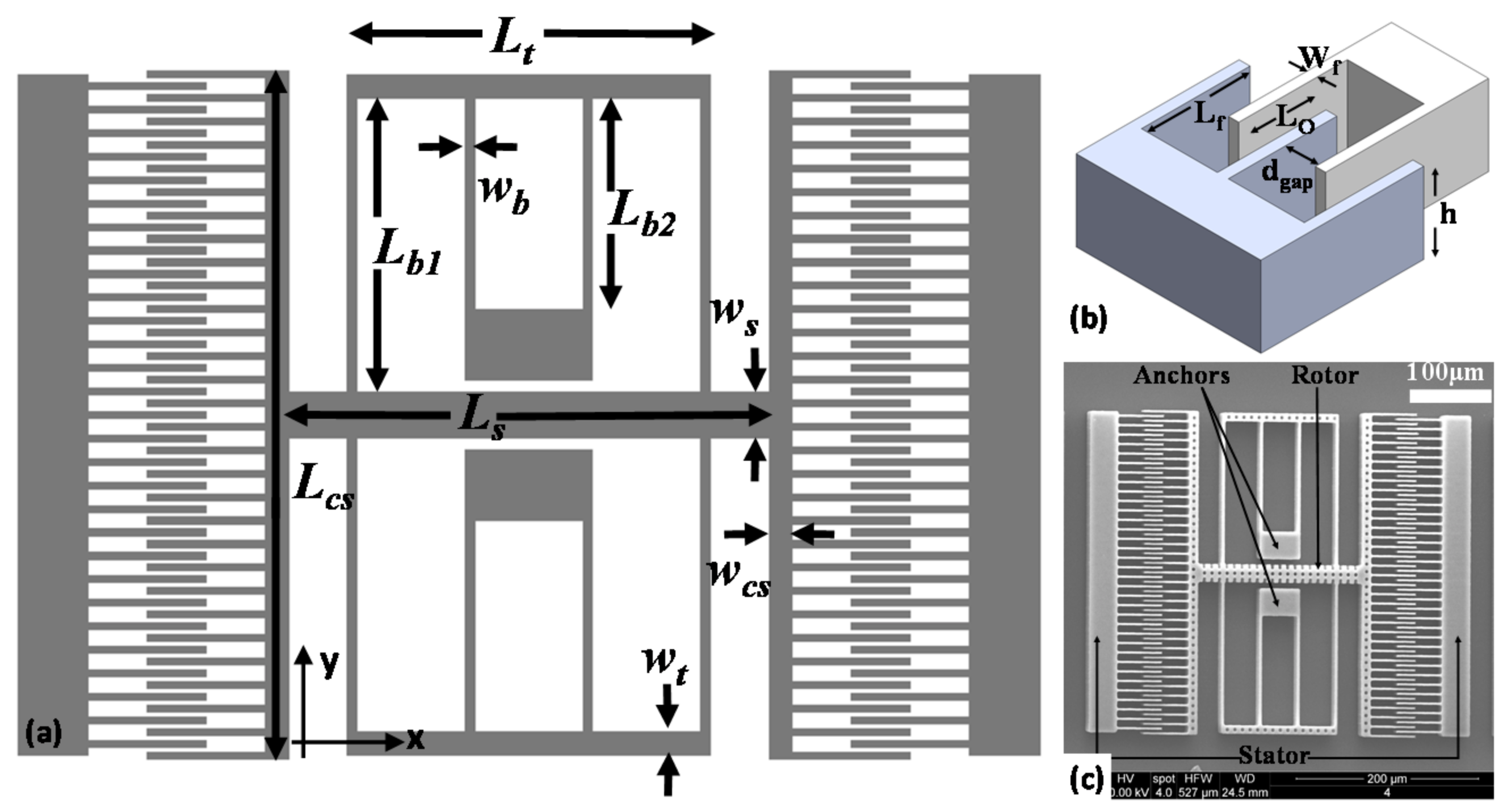

| Name | Parameter | Value | Unit |
|---|---|---|---|
| Shuttle length | Ls | 294 | µm |
| Truss length | Lt | 153 | µm |
| Width shuttle | ws | 20 | µm |
| Width truss | wt | 10 | µm |
| 1st beam length | Lb1 | 125 | µm |
| 2nd beam length | Lb2 | 90 | µm |
| Beam width | wb | 2.5 | µm |
| Support length | Lcs | 293 | µm |
| Support width | wcs | 10 | µm |
| Finger length | Lf | 50 | µm |
| Finger width | wf | 3 | µm |
| Finger gap | dgap | 2 | µm |
| Finger overlap length | Lo | 22 | µm |
| Number of rotor fingers | Nfr | 60 | - |
| Number of stator fingers | Nfs | 58 | - |
| Finger height | h | 30 | µm |
| Young’s modulus for silicon | ESi | 150 | GPa |
| Density of silicon | ρSi | 2330 | Kg · m−3 |
| Buffer oxide thickness | dSiO2 | 1 | µm |
| Kinematic viscosity of air | νair | 1.57 × 10−5 | m2/s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, S.S.; Banerjee, A.; Karkhanis, M.U.; Mastrangelo, C.H. Low-Cost High-Speed In-Plane Stroboscopic Micro-Motion Analyzer. Micromachines 2017, 8, 351. https://doi.org/10.3390/mi8120351
Pandey SS, Banerjee A, Karkhanis MU, Mastrangelo CH. Low-Cost High-Speed In-Plane Stroboscopic Micro-Motion Analyzer. Micromachines. 2017; 8(12):351. https://doi.org/10.3390/mi8120351
Chicago/Turabian StylePandey, Shashank S., Aishwaryadev Banerjee, Mohit U. Karkhanis, and Carlos H. Mastrangelo. 2017. "Low-Cost High-Speed In-Plane Stroboscopic Micro-Motion Analyzer" Micromachines 8, no. 12: 351. https://doi.org/10.3390/mi8120351
APA StylePandey, S. S., Banerjee, A., Karkhanis, M. U., & Mastrangelo, C. H. (2017). Low-Cost High-Speed In-Plane Stroboscopic Micro-Motion Analyzer. Micromachines, 8(12), 351. https://doi.org/10.3390/mi8120351




