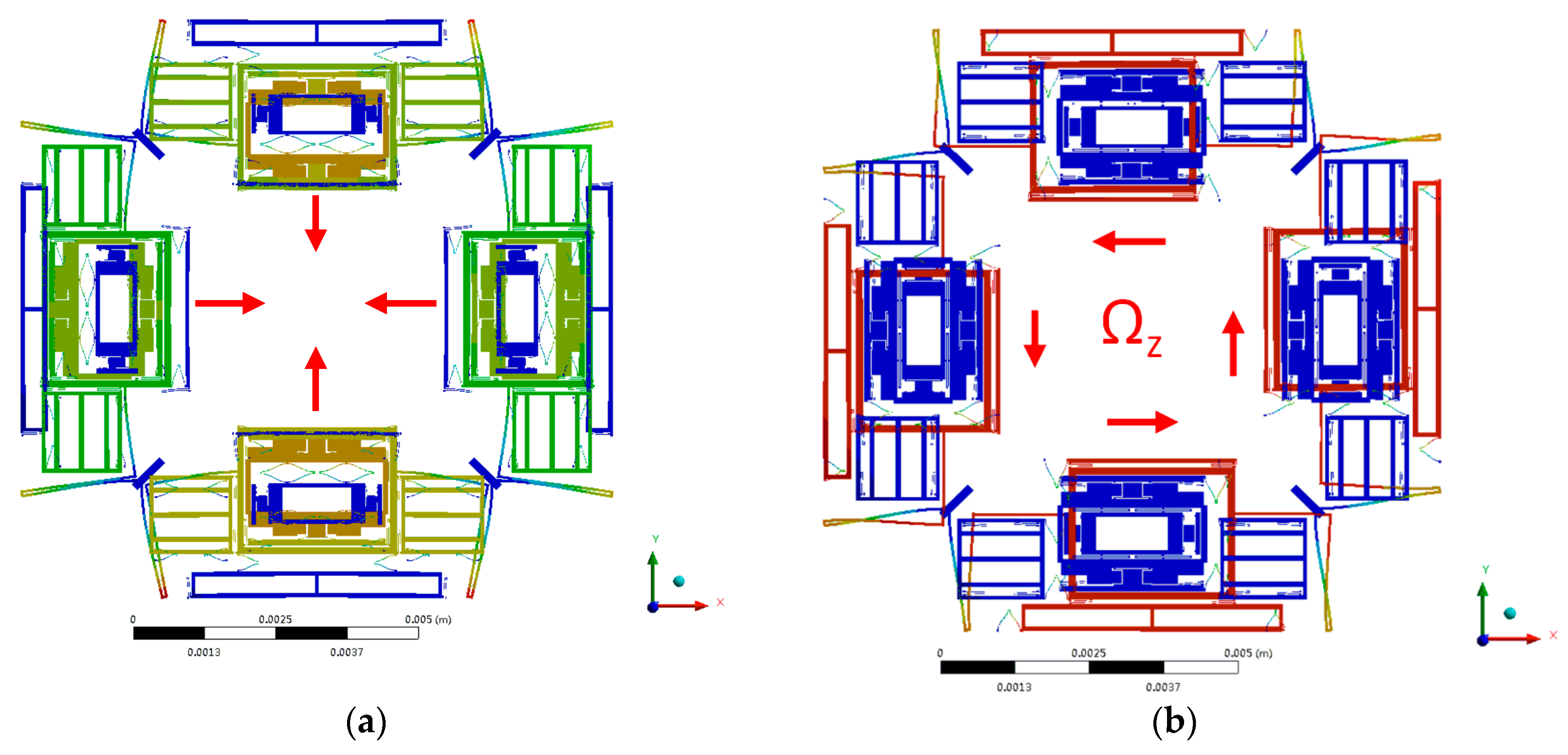
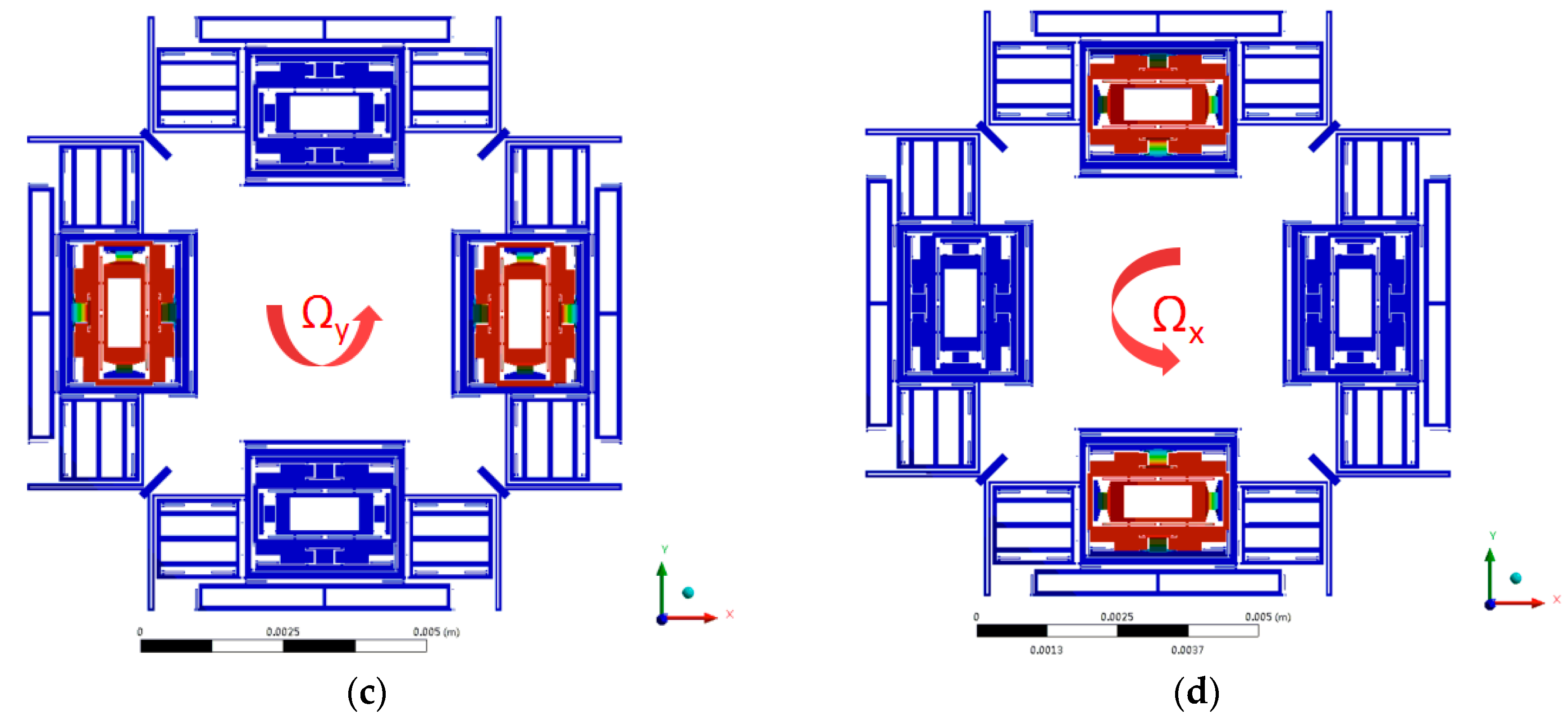
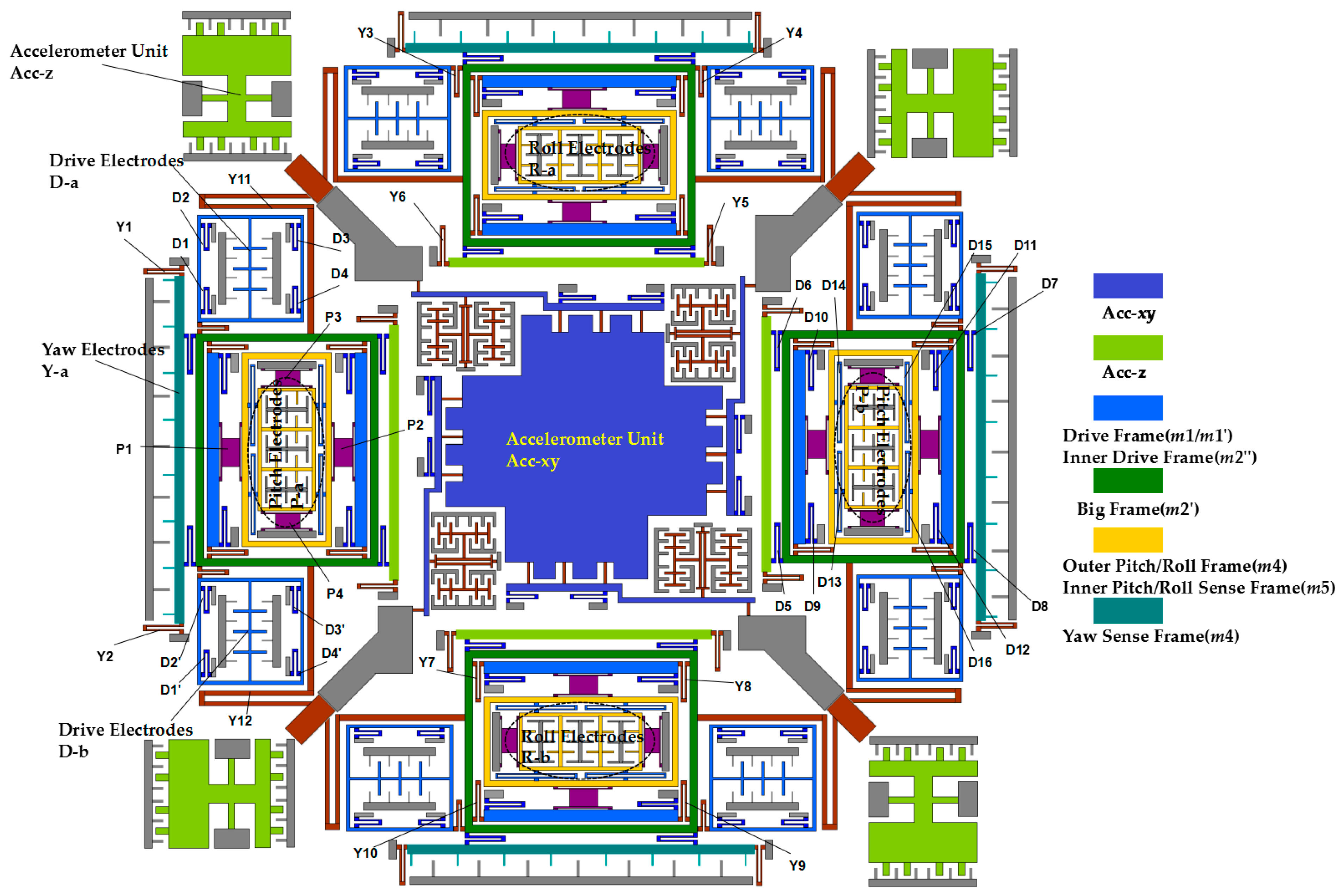
The Drive Frame is driven to move in the drive direction with the driving beams (D1, D2, D3, D4, D1’, D2’, D3’, D4’), when a driving voltage is applied on the drive electrodes. Under the participation of yaw coupling beams (Y3, Y4, Y5, Y6, Y11, Y12), the Big Frame will move together with the Drive Frames. The driving beams (D5, D6, D7, D8) will bring the yaw sense electrodes to move together with the Big Frame. Yaw sensing beams (Y1, Y2) will limit the yaw sense electrodes to have 2-DOF in-plane movement, when an angular rate in z-direction is applied on the gyroscope.
The isolation mass for Pitch/Roll Modes and the Outer Frame in Pitch/Roll Modes will be driven to move together with the driving beams (D
9, D
10, D
11, D
12, D
13, D
14, D
15, D
16). When an angular rate in
x/
y-direction is applied on the gyroscope, under the participation of pitch/roll sensing beams (P
1, P
2, P
3, P
4), the Outer Frame in Pitch/Roll Modes has 2-DOF in the in-plane drive direction and out-of-plane sensing direction. The schematic diagrams for the gyroscope and various beams are shown in
Figure 3 and a summary of all the driving and sensing beams and frames mentioned above is shown in
Table 1.
Since all the drive and sense movements are transferred by various kinds of beams, it is necessary to establish the stiffness matrix for different beams of the gyroscope unit, and analyze the relationship between stiffness coupling coefficients and the structural parameters of the gyroscope unit.
3.1. Mechanical Error Analysis
Once the Drive Mode is stably driven, a quasi-stable vibration will exist in the Sense Mode even without angular rate input, due to the coupling stiffness in structure. The response of the beam force introduced by the coupling stiffness, widely known as quadrature error, is always orthogonal to the Coriolis response. This is one of the main sources of zero-rate output (ZRO) of the micro-gyroscope [
25]. The quadrature error, as well as cross-axis error introduced by fabrication process are greatly in connection with the ZRO, and ultimately influence the output of the MIMU.
Processing techniques such as the lithography process, silicon etching, bonding process etc. may introduce fabrication imperfection. Characterizing the non-idealities inherent in micro-gyroscope and accelerometers, including cross-axis sensitivity, offset bias and non-linearity, is quite necessary for industrial viability. The beams of the structure are relatively symmetrical in design, and the elastic system axes coincides to the proof mass axes in design, which makes the gyroscope unit structure fully decoupled. The in-plane and out-of-plane rotation of the elastic system axes introduced from fabrication has the maximum effect on mode decoupling.
Since all the beam geometries are identical, and the layout is totally symmetrical, the system stiffness matrix is diagonal because the off-diagonal can be cancelled out. Due to fabrication imperfection, the beams are not perfectly matched leading to a non-diagonal stiffness matrix (Equation (1)). The simplified elements of these off-diagonal terms can be expressed by the diagonal terms with some parameters, usually equivalent rotation [
26].
where
ksystem is the stiffness matrix of an ideal beam;
ksystem’ is the stiffness matrix of beam with fabrication imperfection, which can be approximately expressed by diagonal terms.
In fabrication processing, especially in dry etching with SF
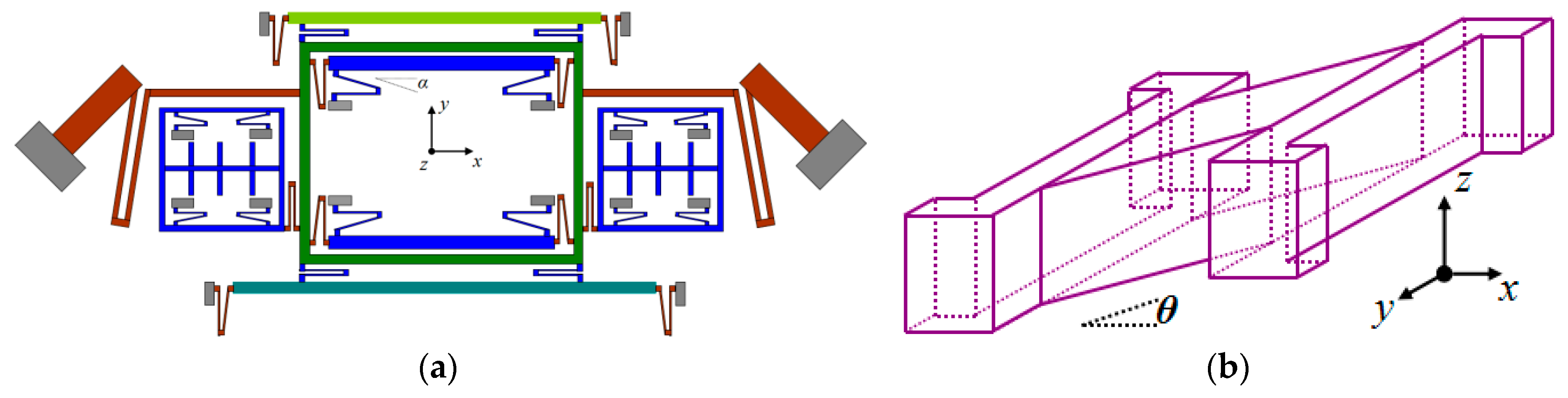
6, the gas pressure difference between two U-shaped coupling beam arms can have the different etching rates. For specific performance, one of the two arms that are close to the anchor will be etched slower than that of the other arm as shown in
Figure 4a, which is equivalent to having an additional angle α on the whole U-shaped beam and greatly affects the terms of the coupling stiffness (
kxy/kyx). Due to the terms of the coupling stiffness introduced by fabrication imperfection, the whole gyroscope unit will have an undesired in-plane movement when the Drive Frames are steadily driven without angular velocity (Ω
z) input, which will mostly affect the quadrature error for Drive Mode to Yaw Mode.
Analysis of fabrication imperfection for Trampoline decoupling beams can introduce an additional angle
θ (
Figure 4b) and lead to an out-of-plane movement in Pitch/Roll mode, when the Drive Frames are steadily driven without angular velocity (Ω
y/Ω
x) input.
Assuming the rotation angle is
α and taking into consideration from the perspective of system stiffness, the transfer matrix can be expressed as:
Substituting the ideal system stiffness matrix into Equation (2), the current equation can be calculated as:
where
KRtot’ is the current system stiffness matrix with rotation movement,
TR is the transfer matrix and
Ktot is the ideal system stiffness matrix.
Actually, the contribution to quadrature error for Drive Mode to Yaw Mode is the summation of all the decoupling beams associated with the above two modes. Therefore, the equivalent matrix consists of driving beams in Drive Frame (D
1, D
2, D
3, D
4, D
1’, D
2’, D
3’, D
4’), yaw coupling beams with Big Frame (D
5, D
6, D
7, D
8, Y
3, Y
4, Y
5, Y
6, Y
11, Y
12) and yaw sensing beams in Yaw Frame (Y
1, Y
2). Take all the beams above into consideration, the equivalent matrix
k is obviously the summation of each matrix for the coupling beams, the equation is shown below:
where the
kxx and
kyy are the diagonal coefficients, while
kxy and
kyx are the off-diagonal coefficients in Equation (4).
Similarly, the equivalent matrix for Drive Mode to Pitch/Roll Mode consists of Pitch/Roll drive beams with Inner Drive Frame (D
9, D
10, D
11, D
12), Pitch/Roll coupling beams in Outer Pitch/Roll Frame (P
1, P
2) and pitch/roll sensing beams in Inner Pitch/Roll Frame (D
13, D
14, D
15, D
16, P
3, P
4).
Table 2 shows the part of the structural dimensions with fabrication error, for example 0.1°.
To ensure the requirement of smooth vibration and acquire the needed working mode, the MIMU is completely symmetrical and center-symmetrically distributed in design, including the proof mass and coupling beams. As mentioned in the previous Section, due to the existence of fabrication error introduced by lithography process, silicon etching, bonding process etc., anisoelasticity of decoupling beams will be generated and affect the output of the MIMU.
Considering the dynamics equations of the MIMU under the existence of anisoelasticity of decoupling beams, two types of dynamic models can be confirmed: Drive Mode to Yaw Mode, Drive Mode to Pitch/Roll Mode.
Table 3 shows the weight different frames in a quarter of the structure.
3.1.1. Dynamics Analysis for Drive Mode to Yaw Mode
As is mentioned about the working principle of the MIMU in
Section 2, different frames can be classified according to the degrees of freedom and establish the simplified dynamic models for analyzing the motion of the gyroscope in the drive direction.
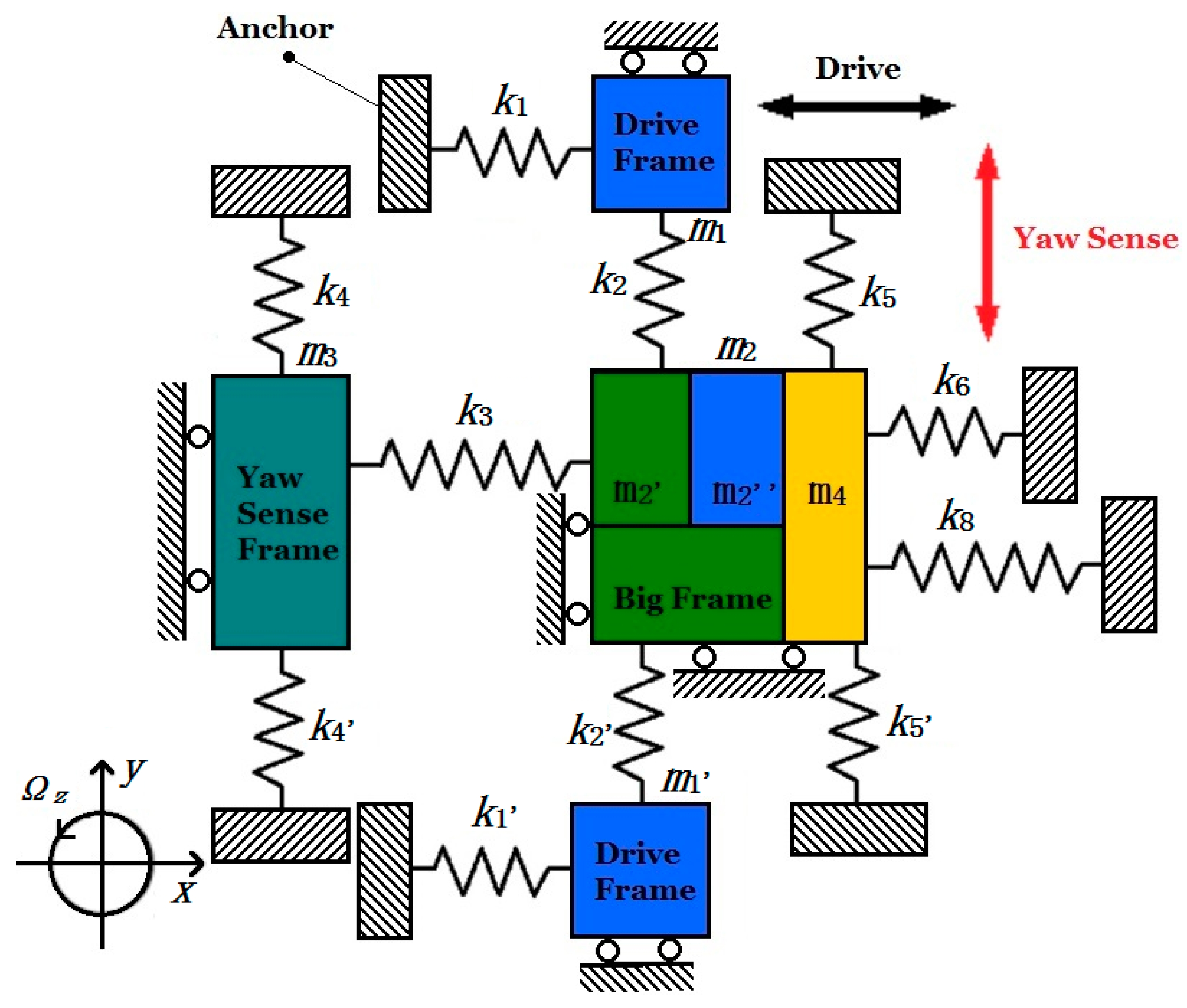
In
Figure 5,
k1 and
k1’ are the summation of stiffnesses of U-shaped coupling beams D
1, D
2, D
3, D
4 and D
1’, D
2’, D
3’, D
4’;
k2 and
k2’ are the stiffness of decoupling beams Y
3 and Y
4;
k4 and
k4’ are the stiffness of coupling beams Y
1, Y
2, Y
5 and Y
6;
k3 is summation of the stiffness of coupling beams D
7 and D
8 between Yaw Sense Frame and Big Frame;
k5 and
k5’ are the stiffness of crab-leg beams Y
11 and Y
12;
k6 is the summation of the stiffness of coupling beams D
9, D
10, D
11, D
12;
k8 is the summation of the stiffness of decoupling beams P
1 and P
2. All the labels of decoupling beams are shown in
Figure 3.
Moreover, m1 and m1’ represent the masses of Drive Frame, m3 represents the Yaw Sense Frame; m2’ and m2” represent the Big Frame and Inner Drive Frame respectively and m4 is the Outer Plane Frame (Pitch/Roll Mode). To simplify the dynamic model and equations, the related masses are classified in degrees of freedom: Drive Frames (m1 and m1’) and Inner Drive Frame (m2”) have one degree of freedom in direction x; Yaw Sense Frame (m3) has one degree of freedom in direction y. In particular, Big Frame (m2′) has two degrees of freedom in direction x and y, while Outer Plane Frame (m2”) has two degrees of freedom in direction x and z. Since m2’, m2” and m4 are driven together in direction x, when driving force is applied on the MIMU, so the three masses can be treated as a whole mass.
One significant point of the MIMU is that both Yaw Mode and Pitch/Roll Mode share the same driving equation, since Big Frame (
m2’), Inner Drive Frame (
m2”) and Outer Pitch/Roll Frame (
m4) move together by the driving force. The simplified dynamic equation in driving direction is shown below:
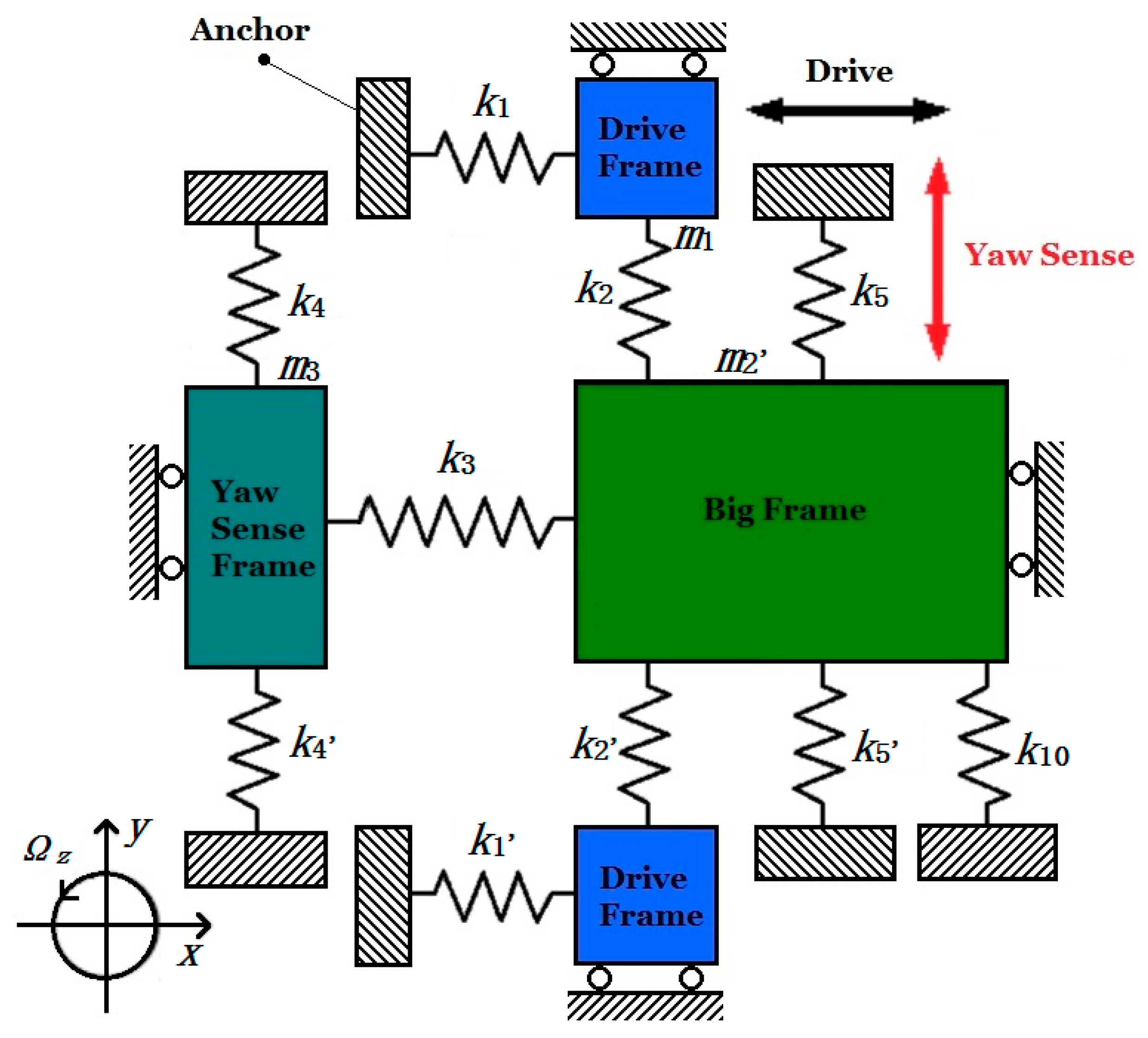
In Yaw Mode, the Coriolis mass is the Big Frame (
m2’) only with two degrees of freedom in direction
x and
y. So insulating the inner masses of the Big Frame, including the Inner Drive Frame (
m2”) and Pitch/Roll Frames, the simplified dynamic model for Yaw Mode is shown in
Figure 6.
In
Figure 6,
k10 represents the summation of U-shaped decoupling beams Y
7, Y
8, Y
9 and Y
10 (
Figure 3). The other springs are the same in
Figure 5. So the simplified dynamic equation in Yaw Sense direction is shown below:
According to Equations (6) and (7), when the angular input Ωz = 0, owning to the existence of coupling stiffness kyx, coupling force kyxx generated by driving force in direction x will attach to the MIMU in direction y, and make the Big frame vibrate in the sense direction.
Since the sensing displacement is far less than driving displacement, the coupling term (2
k5xy + k6xy + k8xy)
y can be neglected, and the dynamic equations of the gyroscope in drive direction x and sense direction y can be rewritten as follow:
Assuming the electrostatic force
Fd =
Fe sin
ωdt, the equation of driving displacement can be expressed below:
where
Fe is the amplitude of the electrostatic force, the
kxx is the summation of 2
k1xx,
k3xx, 2
k5xx,
k6xx,
k8xx.
ωd is the frequency of driving voltage and
ωx is the natural resonant frequency of Drive Mode,
Qdrive is the quality factor of the Drive Mode.
Ax,drive below is the amplitude of driving displacement when
ωd ≈
ωx.
In Equation (8), upon being steadily driven, even if there is no angular velocity input (Ω
z = 0), the yaw sensing electrodes will be driven in direction y under the coupling term (
k5yxα + k10yxα)x, and quadrature error
yQerror,yaw between Drive Mode to Yaw Mode can be expressed below:
where
ωy is the natural resonant frequency of Yaw Mode.
Qyaw is the quality factor of the Yaw Mode.
k5yxα and
k10yxα are the coupling stiffness terms of decoupling beams Y
11, Y
12 and Y
7, Y
8, Y
9, Y
10 correspondingly. From the equation above, by eliminating the coupling stiffness terms 2
k5yxα + k10yxα, the quadrature error
yQerror,yaw can simultaneously be reduced.
As mentioned in Equation (4), the terms of the coupling stiffness kxyα(kyxα) introduced by fabrication imperfection can be expressed as (kxx − kyy)α. By reducing the equivalent angle of etching error α or conducting pre-compensation in the structural design on the key decoupling beams (Y7, Y8, Y9, Y10 and Y11, Y12), the quadrature error between Drive Mode to Yaw Mode can be reduced effectively.
Since the mechanical sensitivity of the Yaw Mode is linked with the input angular velocity Ω
z, to simplify calculation, the coupling term (2
k5yx + k10yx)x which leads to the quadrature error of Yaw Mode can be neglected in Equation (8). When the Drive Mode is in resonant state (
ωx ≈
ωd), and the mechanical sensitivity
Syaw of Drive Mode to Yaw Mode can be easily calculated and expressed below:
3.1.2. Dynamics Analysis for Drive Mode to Pitch/Roll Mode
The Pitch Sense Frame and Roll Sense Frame are symmetrically distributed in four directions of the MIMU. Since the whole structure of the MIMU is totally symmetrical (
Figure 1 and
Figure 3), the analyzing process for Pitch Mode is the same as Roll Mode. Take the Pitch Sense Frame into consideration, upon being driven steadily by the Drive Frame, the pitch sensing electrodes have an out-of-plane movement in direction z when input angular velocity Ω
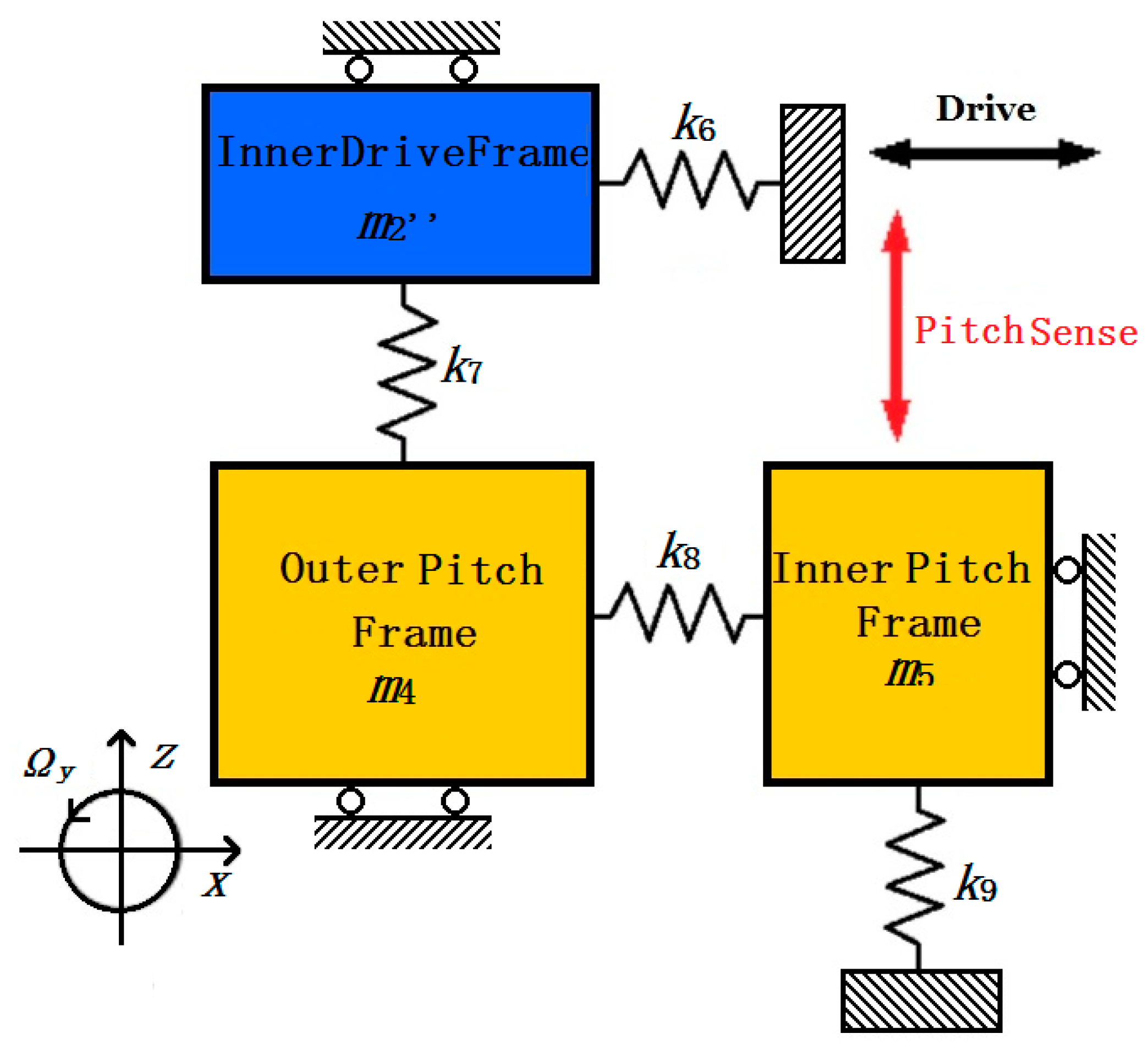
y applied on the MIMU. The simplified dynamic model of Pitch Mode is shown in
Figure 7.
In
Figure 7, the Inner Drive Frame (
m2”) is driven together with the Big Frame (
m2’) via decoupling beams Y
7, Y
8, Y
9 and Y
10 in
Figure 3, so Pitch mode shares the same driving equation (Equation (6)) with the other sense mode as that in Yaw Mode.
k6 represents the summation of U-shaped driving beams D
9, D
10, D
11, D
12. Besides,
k7 is the summation of Trampoline beams P
1 and P
2, and
k9 is the summation of Trampoline beams P
3 and P
4.
k8 represents the summation of four double U-shaped beams D
13, D
14, D
15 and D
16. The Outer Pitch Frame (
m4) has two degrees of freedom and takes the Inner Pitch Frame (
m5) move in direction
z via double U-shaped beams (D
13, D
14, D
15, D
16). The dynamic equation of Pitch Mode in drive direction
x and sense direction z can be written below:
From analysis about the working principle in
Section 2, the driving force in Drive Frame is the same as that in Inner Drive Frame, in other words, the Yaw Frame and Pitch/Roll Frame (Outer Pitch/Roll Frame and Inner Pitch/Roll Frame) are driven by the same driving force. Therefore, to simplify the calculation of mechanical sensitivity in Pitch/Roll Mode, the equation of driving movement in direction
x (Equation (9)) can be reused.
The solving process of Pitch Mode is similar to that of Yaw Mode above, the mechanical sensitivity
Spitch of Pitch Mode can be expressed below:
where
ωz is the natural resonant frequency of Pitch/Roll Mode,
Qpitch is the quality factor of the Pitch Mode. When the frequency of driving force
ωd is equal to the natural resonant frequency of Drive Mode
ωd, the mechanical sensitivity of Pitch/Roll Mode can be expressed in Equation (14).
The source of the quadrature error
zQerror,pitch of Drive Mode to Pitch/Roll Mode is led by the coupling term
kzxθ = (
k7zx + k9zx)
θ, where
θ is the equivalent offset angle by etching error of decoupling beams P
1, P
2, P
3 and P
4 in
Figure 4. The calculation process is the same as that in Equation (11) and expressed below.
By reducing the equivalent offset angle θ or making pre-compensation in the structural design on the key decoupling beams (P1, P2, P3 and P4), the quadrature error from Drive Mode to Pitch/Roll Mode can be reduced effectively.
3.2. Cross-Axis Error Analysis between Sense Modes
The sources of the total sense mode output can be divided into three parts: Coriolis effect output, quadrature error, and cross-axis error between sense modes [
27,
28]. However, the whole MIMU is totally symmetric in structure, whereas in separate structural part, since the decoupling beams are not symmetrically distributed and the existence of fabrication imperfection, there also exists a coupling effect between two different sense modes.
To calculate the cross-axis error between two different sense modes, one Sensing frame can be applied an assumed displacement, and by analyzing the coupling paths composed of various decoupling beams, the output of the other Sense Frame can be expressed. Since the Pitch Sense Frame and Roll Sense Frame are totally symmetric, the most significant cross-axis errors are those from Yaw Mode to Pitch/Roll Mode, and from Pitch/Roll Mode to Yaw Mode.
3.2.1. Cross-Axis Error from Yaw Mode to Pitch Mode
As is shown in
Figure 3, if the Yaw Frame is driven in y axis by Coriolis force under the angular velocity input Ω
z, the Inner Pitch Frame (
m5) will be motionless in theory. Due to the existence of fabrication imperfection of the coupling beams (D
7, D
8, Y
7, Y
8, Y
9, Y
10, Y
11, Y
12), however, the Big Frame (
m2’) together with the Inner Drive Frame (
m2”) will be driven in turn by Yaw Frame, and further leads to the movement of Pitch Frame (
m4 and
m5), which will have an extra output signal called cross-axis error [
23]. To analyze the cross-axis error, the dynamic model is established in
Figure 8.
All the tabs of coupling beams correspond with those in the above figures. Assuming the “drive part” of the model is the yaw electrodes and angular input is Ωz only, and Yaw Sense Frame (m3) and Big Frame (m2’) move together in direction y, the displacement can be expressed by Equation (12) with mechanical sensitivity Syaw. Due to the existence of coupling terms k5xyα, Big Frame (m2’) as well as two Drive Frame (m1/m1’) have an extra displacement in direction x. By the transmission of decoupling beams Y11, Y12 and Y7, Y8, Y9, Y10 (k5/k5’ and k10), the extra displacement will be delivered to Inner Drive Frame (m2”), and further leads to the movement of Outer Pitch Frame (m4) and Inner Pitch Frame (m5).
The dynamic equation is similar to Equation (11). To express the driving displacement for Inner Drive Frame (
m2”). The dynamic equations are written below:
where
ωx is the equivalent resonant frequency for Inner Drive Mode.
Qdrive is the equivalent natural quality factors for Inner Drive Mode.
Asx is the amplitude of the drive displacement for Inner Drive Frame (
m2”). Actually, Inner Drive Mode shares the same resonant frequency and quality factor with Drive Mode. If Yaw Mode works in driving frequency
ωd, Equation (16) can be simplified as above.
The calculation process for the output of the Pitch Mode is similar to that in
Section 3.1.2, and the dynamic model is the same as
Figure 7. Since the only input angular velocity is Ω
z, the output of Pitch Mode is only from fabrication error of Pitch Mode, more specifically, from the terms of the coupling stiffness
k7zxθ + k9zxθ, and Equation (14) can be taken for referenced. So the cross-axis error from Yaw Mode to Pitch Mode can be expressed below:
As is known, the smaller the cross-axis errors between two different sense modes, the better [
29,
30]. Since the main source of the cross-axis error from Yaw Mode to Pitch Mode is the coupling stiffness terms 2
k5xyα + k9zxα and
k7zxθ + k9zxθ, more specifically, the coupling stiffness terms of crab-leg beams Y
11, Y
12, U-shaped beams Y
7, Y
8, Y
9, Y
10, trampoline beams P
1, P
2, P
3 and P
4, that the equivalent fabrication angle
α and
θ matters most (
Figure 4), should be decreased as much as possible to reduce the value of cross-axis error
Syaw2pitch.
3.2.2. Cross-Axis Error from Pitch Mode to Yaw Mode
The mechanism of cross-axis error from Pitch Mode to Yaw Mode is similar with that from Yaw Mode to Pitch Mode. If the Inner Pitch Frame (m5) is driven in direction z by Coriolis force under the angular velocity input Ωy, the Yaw Sense Frame (m3) will be motionless in theory. Fabrication imperfection of the coupling beams (D9, D10, D11, D12, P1, P2) will lead to the movement of Outer Pitch Frame (m4) in direction z, together with the Inner Drive Frame (m2”) and Big Frame (m2’) in direction x, and further lead to the movement of Yaw Sense Frame (m3). The extra output signal of Yaw Frame is the cross-axis error from Pitch Mode to Yaw Mode.
Assuming the “drive part” of the model is the pitch electrodes. Due to the existence of
k7zxθ + k9zxθ, Inner Drive Frame (
m2”) will have an extra movement, and further leads to the movement of Big Frame (
m2’), under the decoupling beams Y
7, Y
8, Y
9, Y
10 (
k10). Then, Yaw Sense Frame (
m3) will further be driven by Y
11, Y
12 (
k5yxα/k5yxα’). Dynamic model in
Figure 5 can be taken for reference and the dynamic equations are written below, from which the equivalent drive displacement for Inner Drive frame together with the Big Frame can be calculated.
where
ωx,
Qsx,
Asx and
ωd are the same parameters as those in Equation (16). Therefore, Equation (18) can be simplified as above.
The calculation process for the output of the Yaw Mode is similar to that in
Section 3.1.1, and the dynamic model is the same as
Figure 6. Since the only input angular is Ω
y, the output of Yaw Mode is only from fabrication error of decoupling beams Y
11, Y
12 and Y
7, Y
8, Y
9, Y
10, more specifically, from the terms of the coupling stiffness 2
k5yxα + k10yxα, and Equation (11) can be taken for reference. So the cross-axis error from Pitch Mode to Yaw Mode can be expressed below:
The main source of the cross-axis error from Pitch Mode to Yaw Mode is the coupling stiffness terms 2
k5yxα + k10yxα and
k7zxθ + k9zxθ, more specifically, the coupling stiffness terms of the crab-leg beams Y
11/Y
12 and Y
7, Y
8, Y
9, Y
10, linked with the Big Frame (
m2’), and trampoline beams P
1, P
2, P
3 and P
4. The equivalent fabrication angle
α, and
θ (
Figure 4), should be decreased as much as possible to reduce the value of cross-axis error
Spitch2yaw. Equation (20) shows the mechanical output of three sense modes, when the Drive Mode is in resonant state and been make mode-matching with sense modes for high sensitivity.
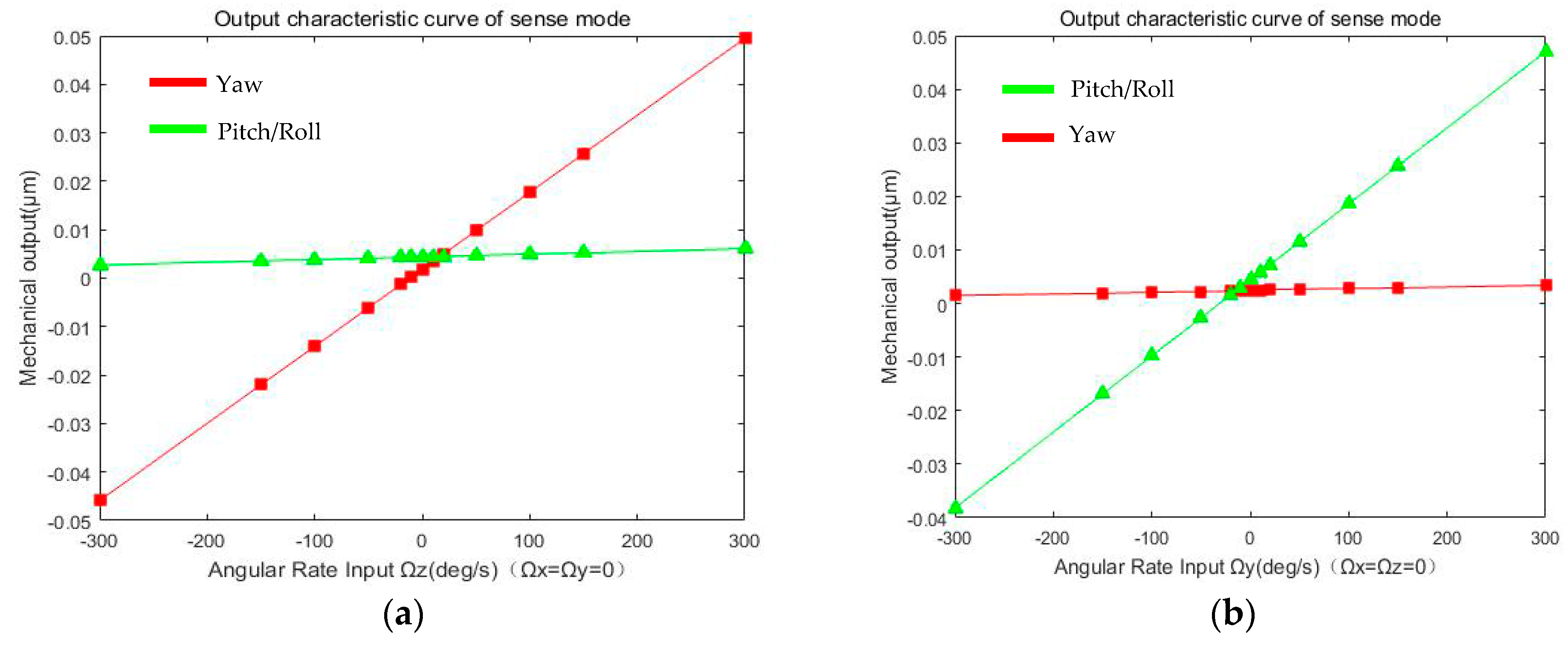
Figure 9 shows the simulation of the mechanical output for sense modes.
The Syaw, Spitch, Sroll represent the mechanical sensitivity of three sense modes; The Syaw2pitch (Syaw2roll), Spitch2yaw (Sroll2yaw), Sroll2pitch (Spitch2roll) represent the cross-axis error from one sense mode to the other mode, respectively. In addition, the yQerror,yaw, zQerror,pitch, zQerror,roll are the quadrature error corresponding to the sense modes.
Cross-axis error from Pitch/Roll Mode to Yaw mode is about 5.6 × 10
−6 μm/°/s, and the mechanical sensitivity of Yaw Mode is about 1.59 × 10
−4 μm/°/s, with quality factor (
Qyaw) of in-plane movement in vacuum about 300. Quadrature error of Yaw Mode is 1.849 × 10
−3 μm with fabrication error
α = 0.1° of decoupling beams
k5/
k5’ (Y
11/Y
12) and
k10 (Y
7, Y
8, Y
9, Y
10). Likewise, cross-axis error from Yaw Mode to Pitch/Roll Mode is about 2.4 × 10
−6 μm/°/s, and the mechanical sensitivity of Pitch/Roll Mode is about 1.42 × 10
−4 μm/°/s, with quality factor (
Qpitch/Qroll) of out-of-plane movement in vacuum about 1000. Quadrature error of Pitch/Roll Mode is 4.397 × 10
−3 μm with fabrication error
θ = 0.1° of decoupling beams
k7 (P
1/P
2) and
k9 (P
3/P
4). Summary of all the parameters above is shown in
Table 4.