Nonlinear Dynamic Behavior of a Bi-Axial Torsional MEMS Mirror with Sidewall Electrodes
Abstract
:1. Introduction
2. Static Simulation
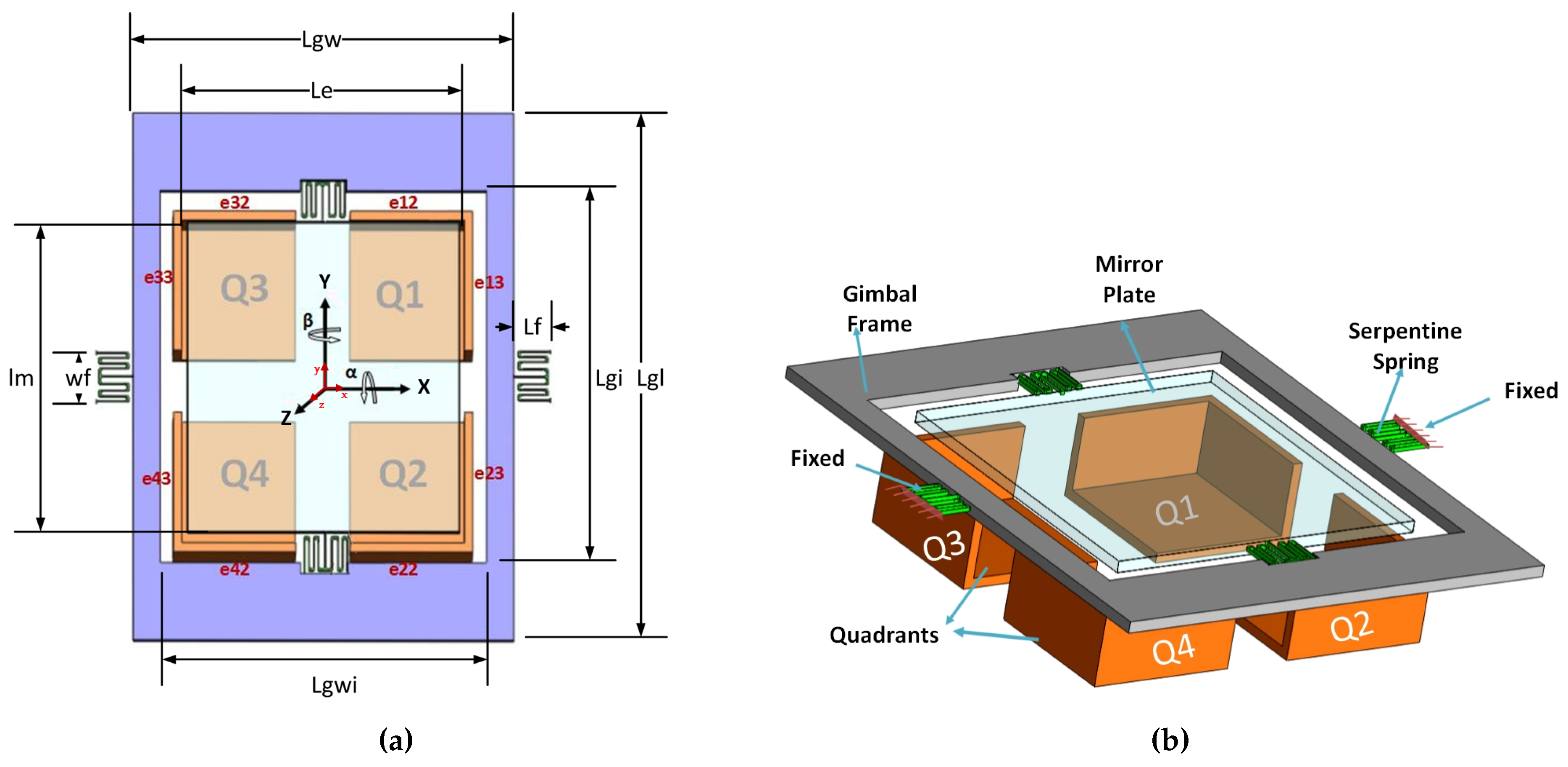
2.1. Operation Principles
2.2. System Model
2.2.1. Electrostatic Forces and Torques
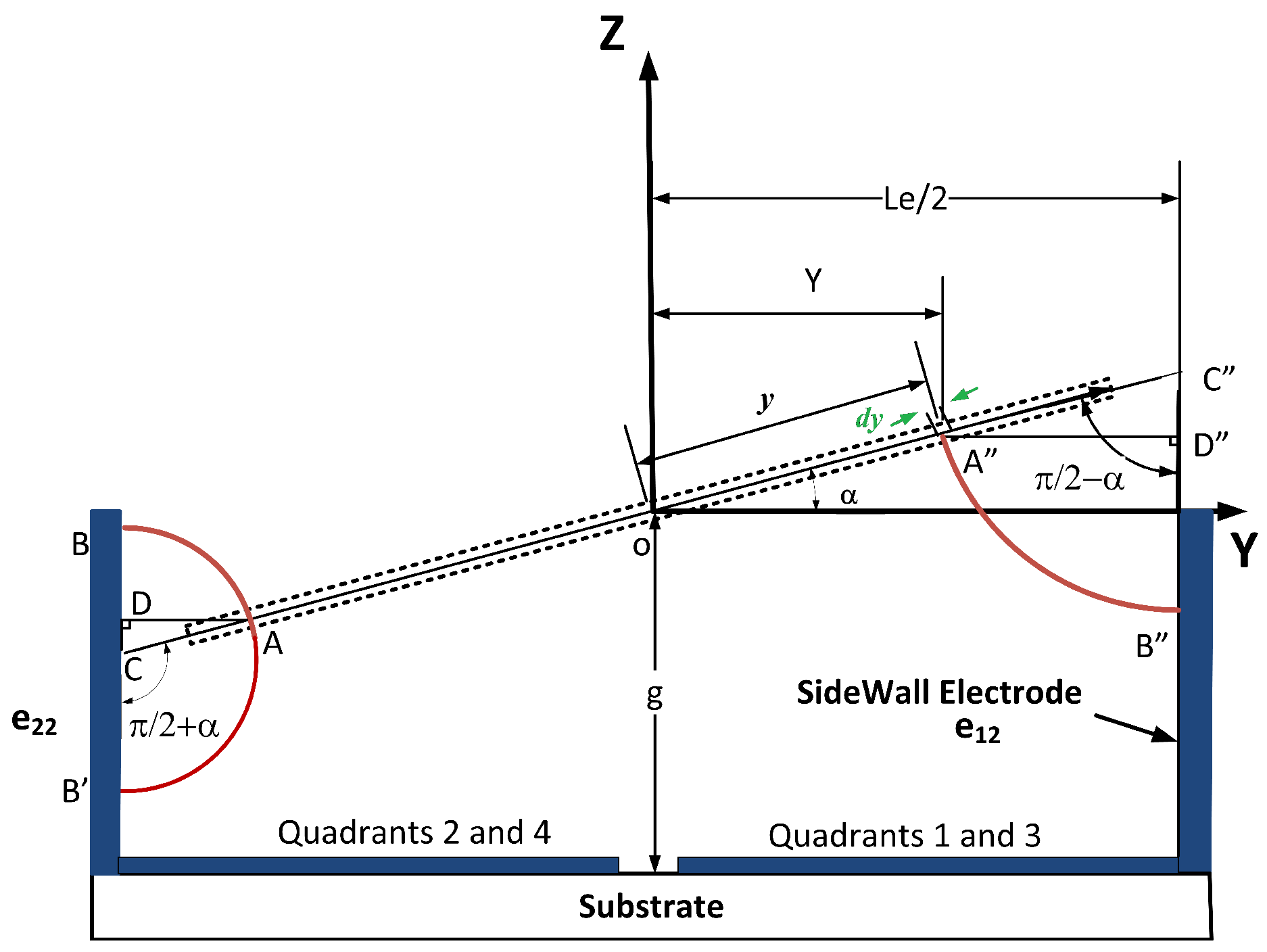
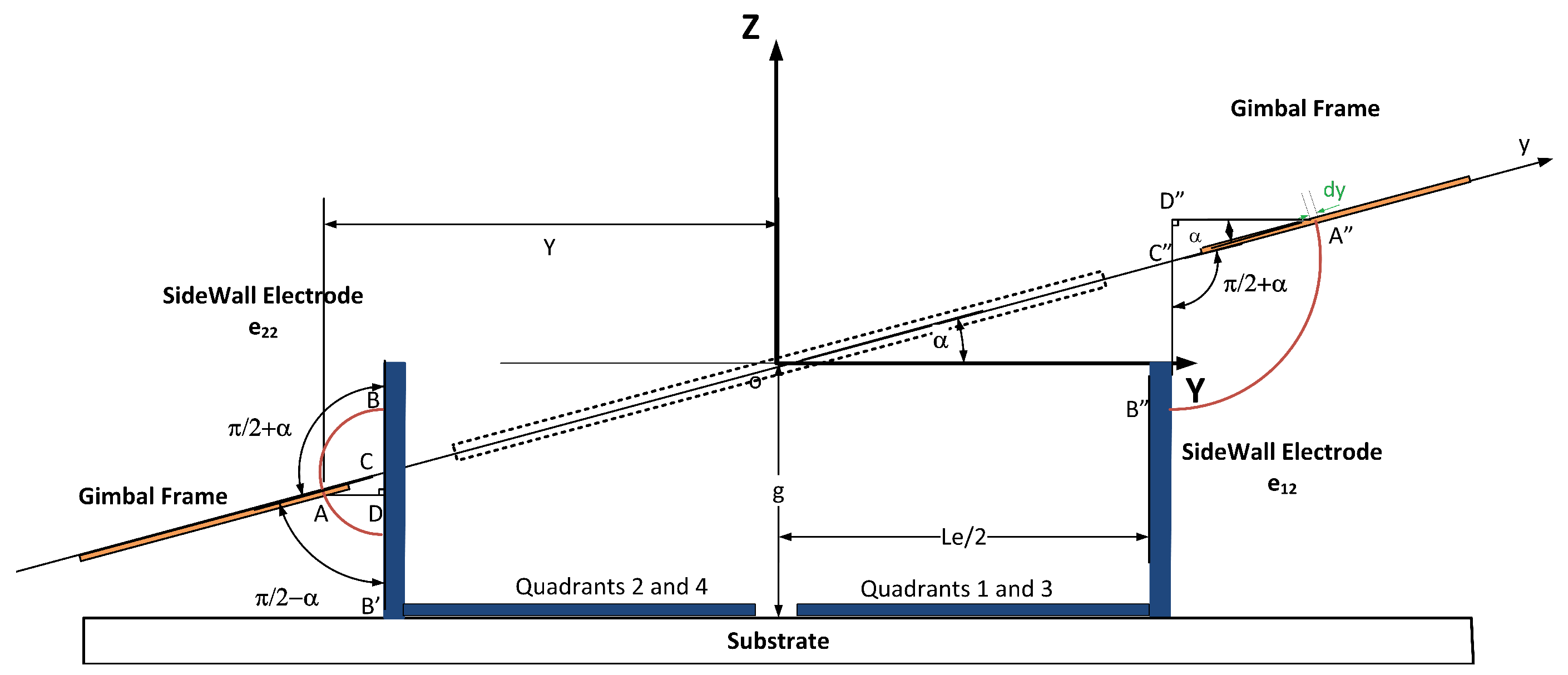
Sidewall Electrodes
Mechanical Spring Force
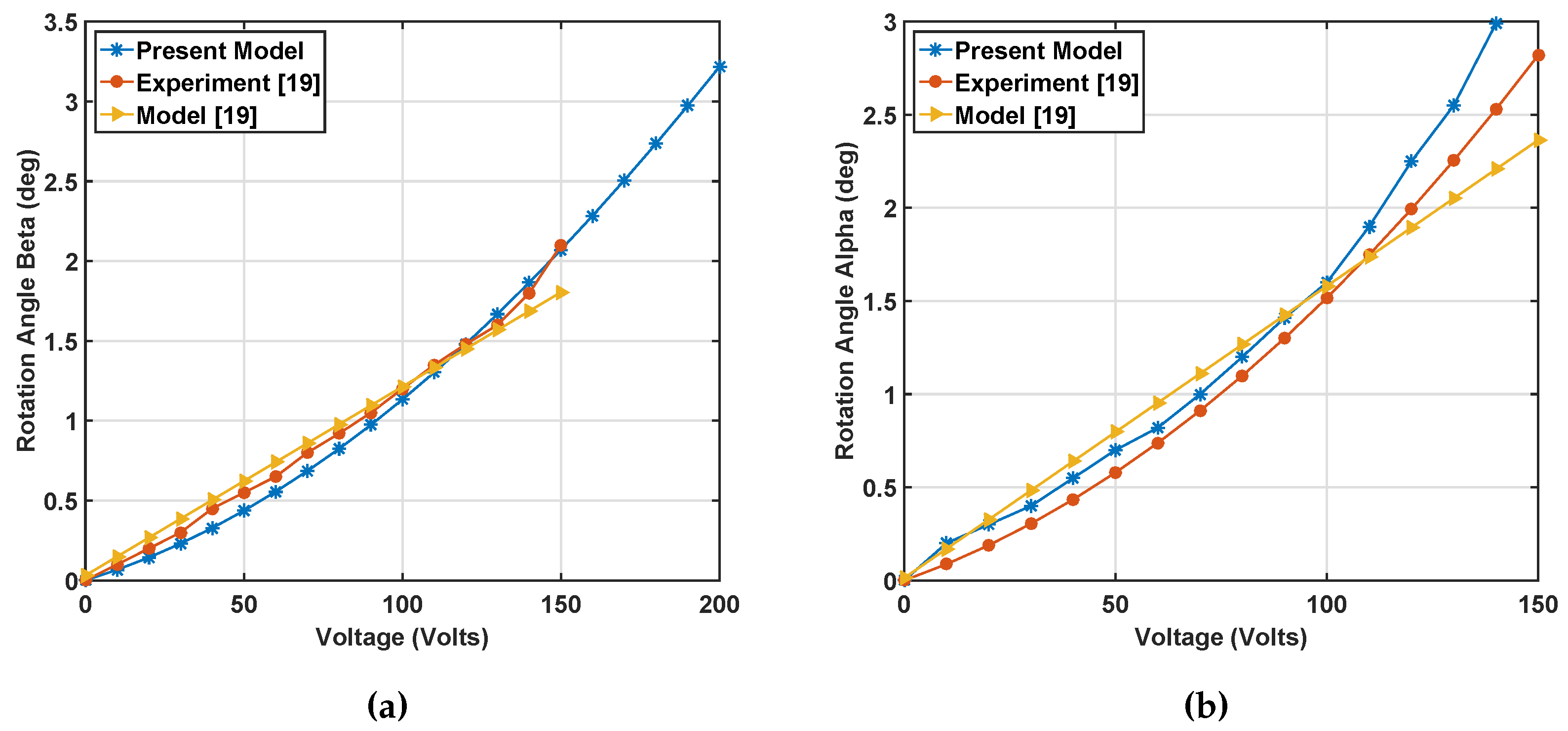
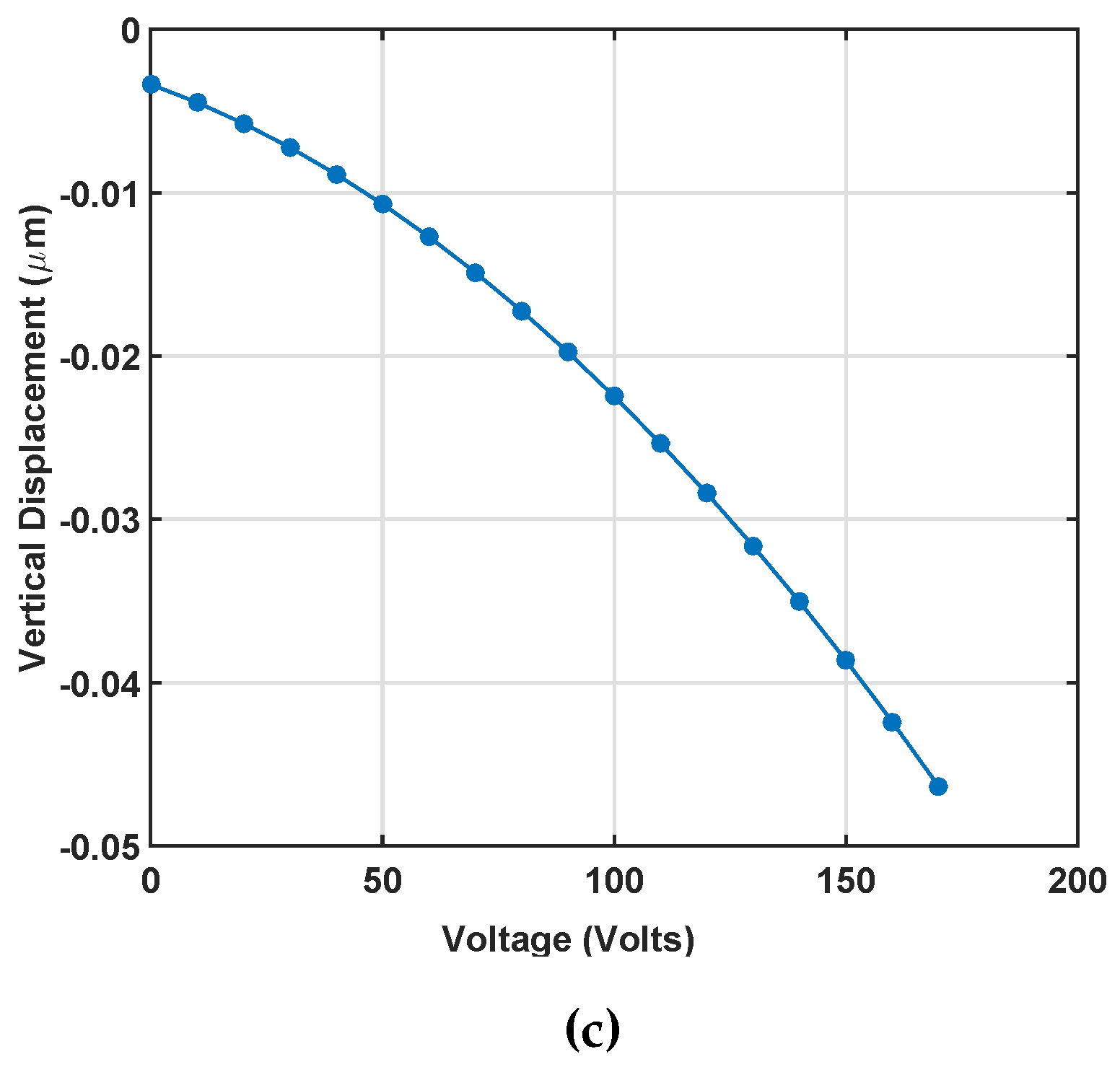
2.3. Static Simulation Results
3. Dynamic Simulation
3.1. Equations of Motion
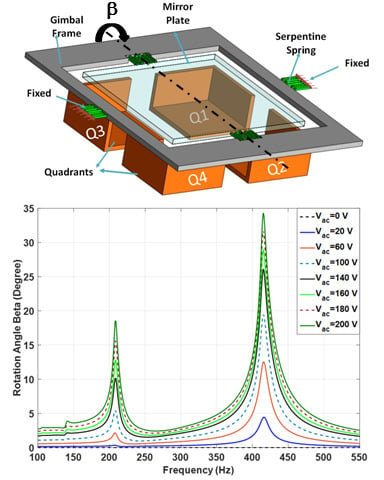
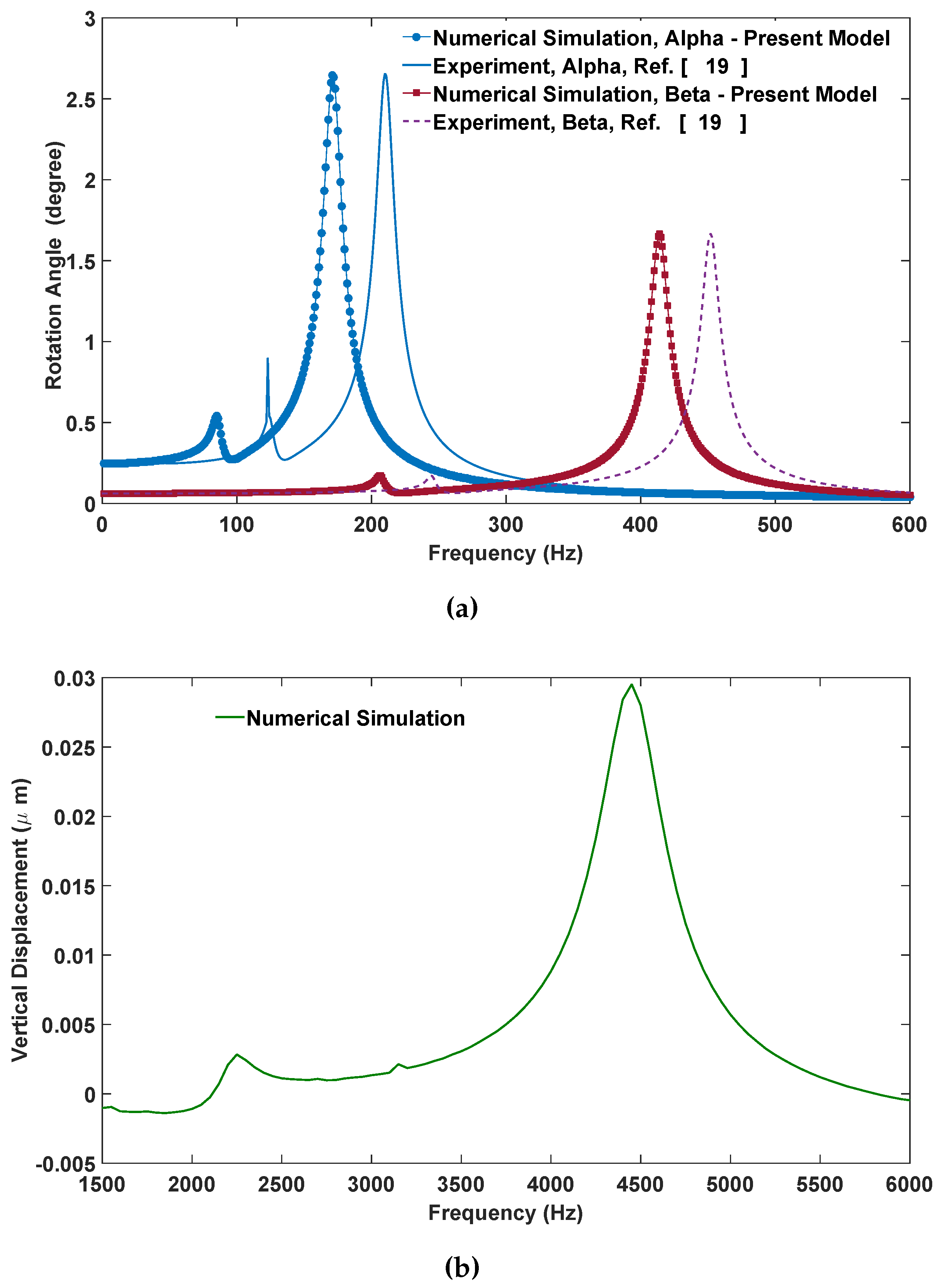
3.2. Dynamic Simulation Results
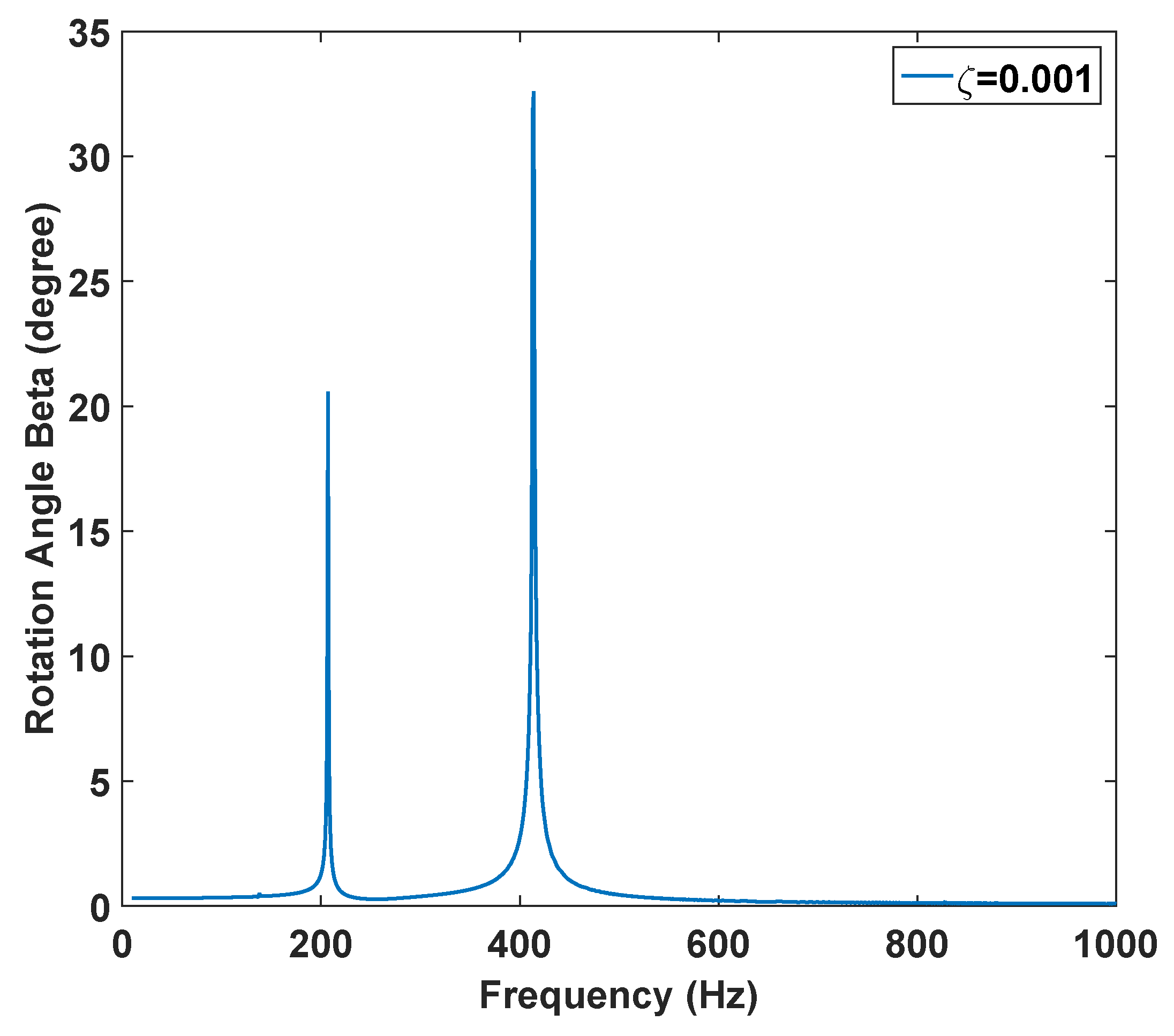
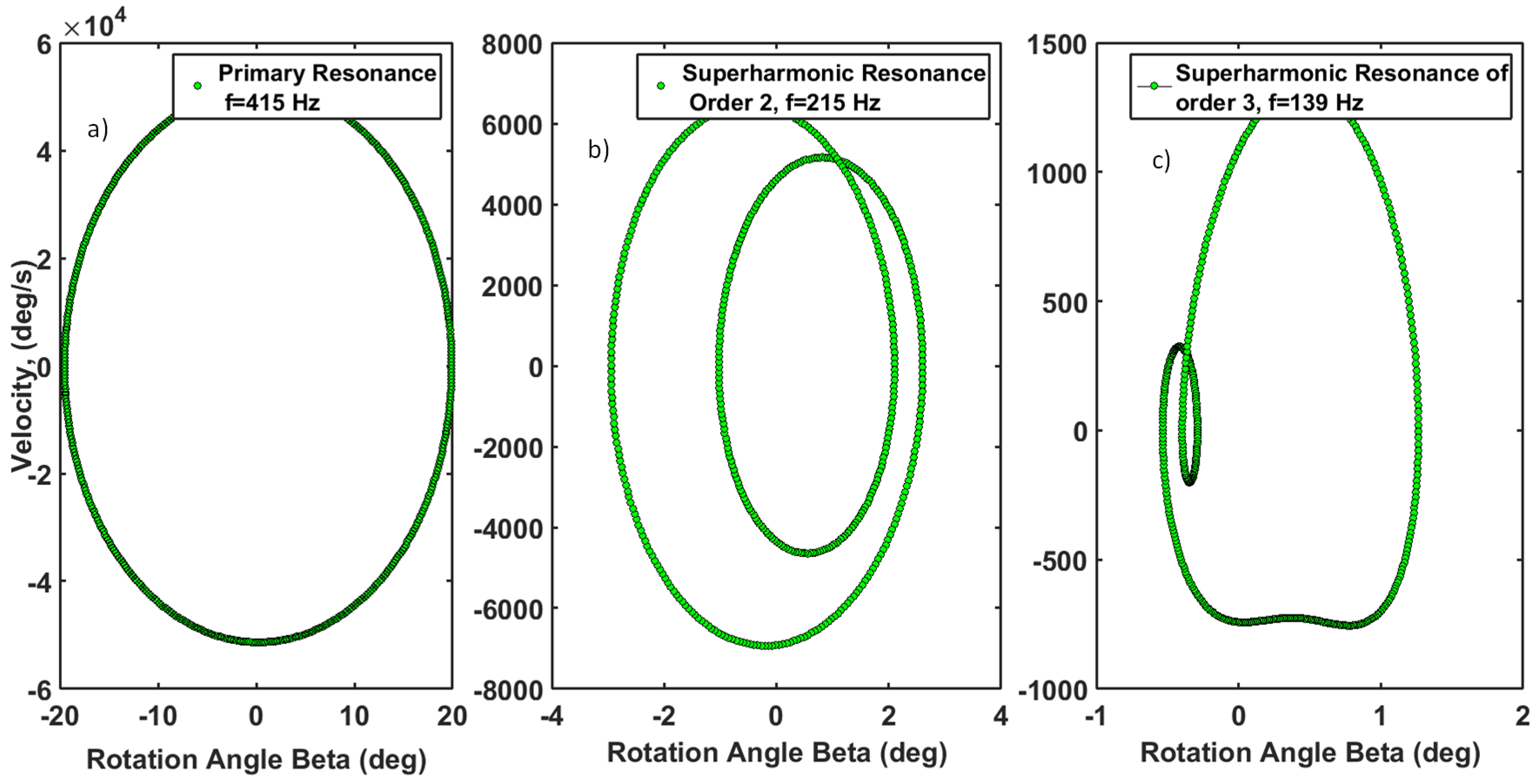
3.3. Analytical Explanation of Secondary Resonances
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix: Integral Boundaries
References
- Rodgers, M.; Sniegowski, J. Designing microelectromechanical systems-on-a chip in a 5 level surface technology. In Proceedings of the 2nd International Conference on Engineering Design and Automation, Maui, HI, USA, 9–12 August 1998.
- Hofmann, U.; Janes, J.; Quenzer, H.J. High-Q MEMS resonators for laser beam scanning displays. Micromachines 2012, 3, 509–528. [Google Scholar] [CrossRef]
- Pengwang, E.; Rabenorosoa, K.; Rakotondrabe, M.; Andreff, N. Scanning micromirror platform based on MEMS technology for medical application. Micromachines 2016, 7, 24. [Google Scholar] [CrossRef]
- Toshiyoshi, H.; Piyawattanametha, W.; Wu, M. Linearization of electrostatically actuated surface micromachined 2-D optical scanner. J. Microelectromech. Syst. 2001, 10, 205–214. [Google Scholar] [CrossRef]
- Moeenfard, H.; Ahmadian, M.T. Analytical modeling of bending effect on the torsional response of electrostatically actuated micromirrors. Opt. Int. J. Light Electron Opt. 2013, 124, 1278–1286. [Google Scholar] [CrossRef]
- Hu, F.; Tang, Y.; Qian, Y. Design of a MEMS micromirror actuated by electrostatic repulsive force. Opt. Int. J. Light Electron Opt. 2012, 123, 387–390. [Google Scholar] [CrossRef]
- Janes, J.; Quenzer, J.; Hofmann, U.; Kaden, D.; Wagne, B. Design, fabrication and characterization of low voltage piezoelectric two axis gimballess microscanners. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 2489–2492.
- Liao, W.; Liu, W.; Rogers, J.E.; Tang, Y.; Wang, B.P.; Xie, H. A Tip-tilt-piston piezoelectric scanning micromirror with folded PZT unimorph actuators. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 526–529.
- Ogando, K.; la Forgia, N.; Zárate, J.; Pastoriza, H. Design and characterization of a fully compliant out-of-plane thermal actuator. Sens. Actuators A Phys. 2012, 183, 95–100. [Google Scholar] [CrossRef]
- Gokdel, Y.D.; Sarioglu, B.; Mutlu, S.; Yalcinkaya, A.D. Design and fabrication of two-axis micromachined steel scanners. J. Micromech. Microeng. 2009, 19, 075001. [Google Scholar] [CrossRef]
- Yalcinkaya, A.; Urey, H.; Brown, D.; Montague, T.; Sprague, R. Two-axis wlectromagnetic microscanner for high resolution displays. J. Micromech. Microeng. 2006, 15, 786–794. [Google Scholar] [CrossRef]
- Jung, W.; McCormick, D.T.; Zhang, J.; Wang, L.; Tien, N.C.; Chen, Z. Three-dimensional endoscopic optical coherence tomography by sse of a two-axis Microelectromechanical scanning mirror. Appl. Phys. Lett. 2006, 88, 163901. [Google Scholar] [CrossRef]
- Zhang, W.M.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic pull-in instability in MEMS/NEMS: A review. Sens. Actuators A Phys. 2014, 214, 187–218. [Google Scholar] [CrossRef]
- Singh, J.; Teo, J.H.S.; Xu, Y.; Premachandran, C.S.; Chen, N.; Kotlanka, R.; Olivo, M.; Sheppard, C.J.R. A Two axes scanning SOI MEMS micromirror for endoscopic bioimaging. J. Micromech. Microeng. 2008, 18, 025001. [Google Scholar]
- Vyasarayani, C.; Abdel-Rahman, E.M.; McPhee, J. Modeling of contact and stiction in electrostatic microcantilever actuators. J. Nanotechnol. Eng. Med. 2012, 3, 011003. [Google Scholar] [CrossRef]
- Zega, V.; Nitzan, S.; Li, M.; Ahn, C.H.; Ng, E.; Hong, V.; Yang, Y.; Kenny, T.; Corigliano, A.; Horsley, D.A. Predicting the closed-loop stability and oscillation amplitude of nonlinear parametrically amplified oscillators. Appl. Phys. Lett. 2015, 106, 233111. [Google Scholar] [CrossRef]
- Caspani, A.; Comi, C.; Corigliano, A.; Langfelder, G.; Zega, V.; Zerbini, S. Dynamic nonlinear behavior of torsional resonators in MEMS. J. Micromech. Microeng. 2014, 24, 095025. [Google Scholar] [CrossRef]
- Ramini, A.; Bellaredj, M.L.F.; Hafiz, M.A.A.; Younis, M.I. Experimental investigation of snap-through motion of in-plane MEMS shallow arches under electrostatic excitation. J. Micromech. Microeng. 2016, 26, 015012. [Google Scholar] [CrossRef]
- Bai, Y. Design, Fabrication, and Characterization of a 2-D SOI MEMS Micromirror with Sidewall Electrodes for Confocal MACROscope Imaging. Ph.D. Thesis, University Of Waterloo, Waterloo, ON, Canada, August 2010. [Google Scholar]
- Towfighian, S.; Ozdogan, M. Static modeling of a Bi-axial micro-mirror with sidewall electrodes. ASME Int. Mech. Eng. Congress Expo. 2014, 10, IMECE2014-38834. [Google Scholar]
- Griffiths, D.J.; College, R. Introduction to Electrodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1999; Volume 3. [Google Scholar]
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 20. [Google Scholar]
- Nayfeh, A.H.; Pai, P.F. Linear and Nonlinear Structural Mechanics; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Alsaleem, F.M.; Younis, M.I.; Ouakad, H.M. On the nonlinear resonances and dynamic pull-in of electrostatically actuated resonators. J. Micromech. Microeng. 2009, 19, 045013. [Google Scholar] [CrossRef]


© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozdogan, M.; Towfighian, S. Nonlinear Dynamic Behavior of a Bi-Axial Torsional MEMS Mirror with Sidewall Electrodes. Micromachines 2016, 7, 42. https://doi.org/10.3390/mi7030042
Ozdogan M, Towfighian S. Nonlinear Dynamic Behavior of a Bi-Axial Torsional MEMS Mirror with Sidewall Electrodes. Micromachines. 2016; 7(3):42. https://doi.org/10.3390/mi7030042
Chicago/Turabian StyleOzdogan, Mehmet, and Shahrzad Towfighian. 2016. "Nonlinear Dynamic Behavior of a Bi-Axial Torsional MEMS Mirror with Sidewall Electrodes" Micromachines 7, no. 3: 42. https://doi.org/10.3390/mi7030042
APA StyleOzdogan, M., & Towfighian, S. (2016). Nonlinear Dynamic Behavior of a Bi-Axial Torsional MEMS Mirror with Sidewall Electrodes. Micromachines, 7(3), 42. https://doi.org/10.3390/mi7030042