Design of a Weighted-Rotor Energy Harvester Based on Dynamic Analysis and Optimization of Circular Halbach Array Magnetic Disk
Abstract
:1. Introduction
2. Overall Design of the WREH
2.1. Weighted Rotor for Energy Harvester
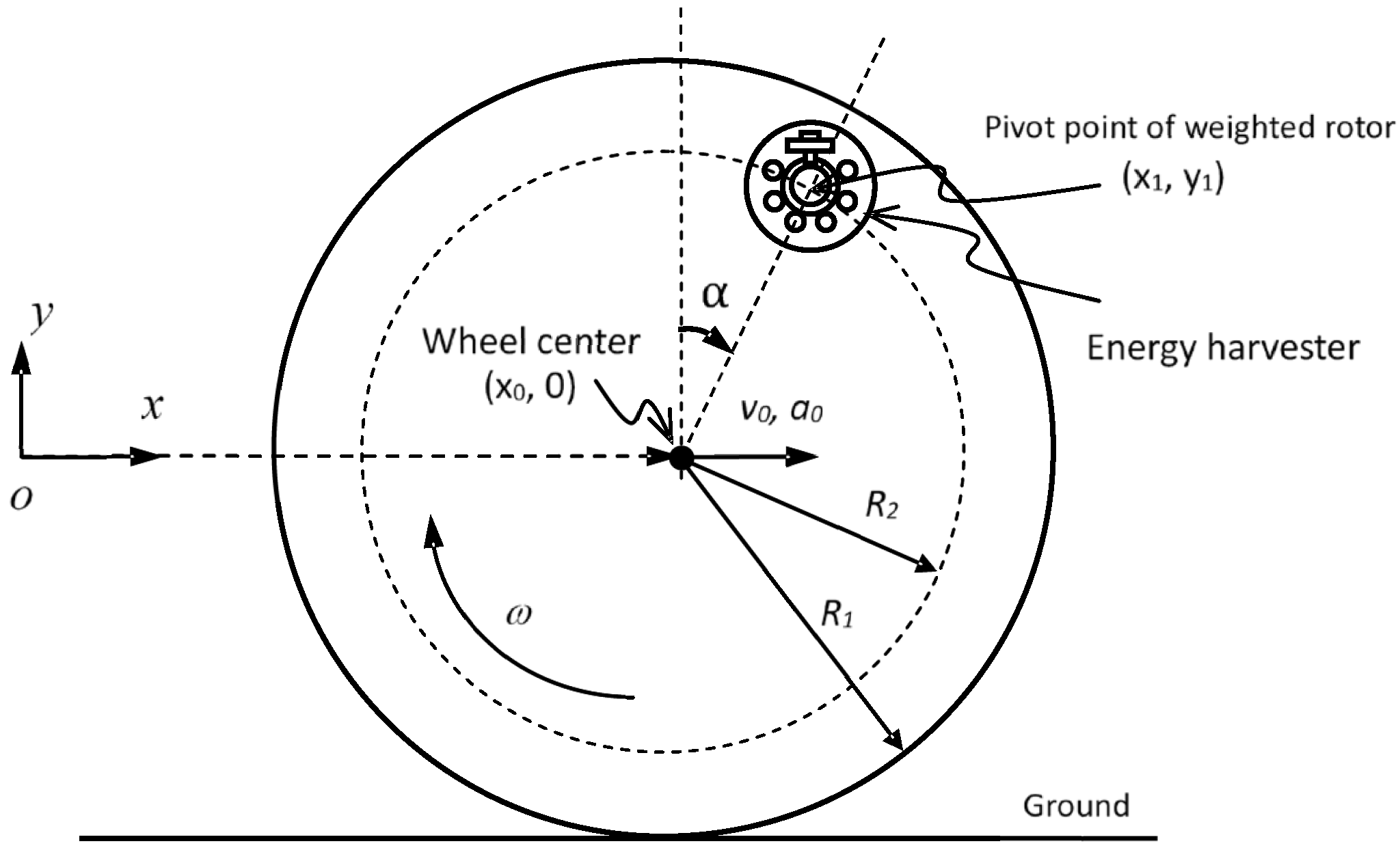
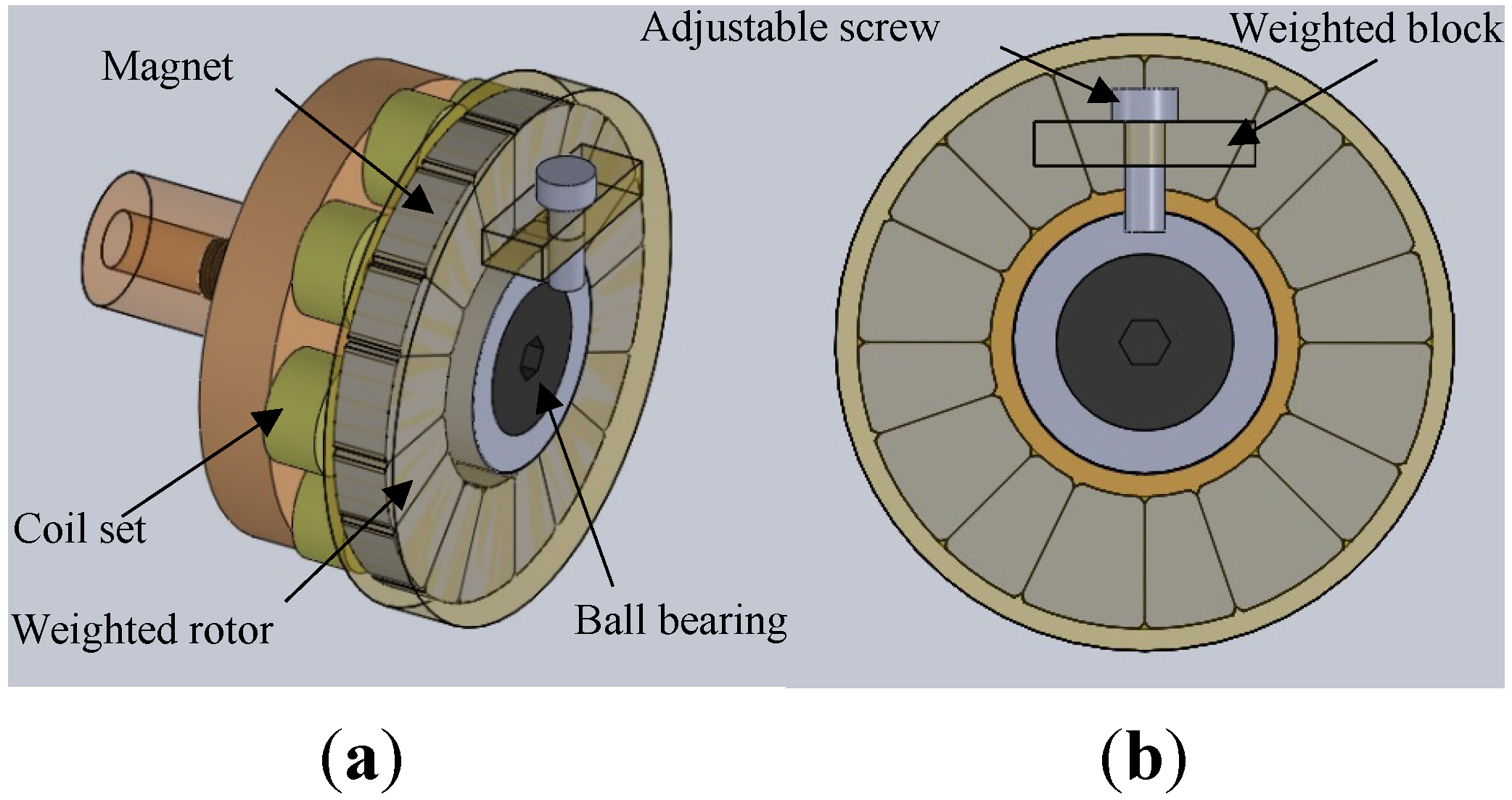

2.2. Output Voltage and Electromagnetic Damping
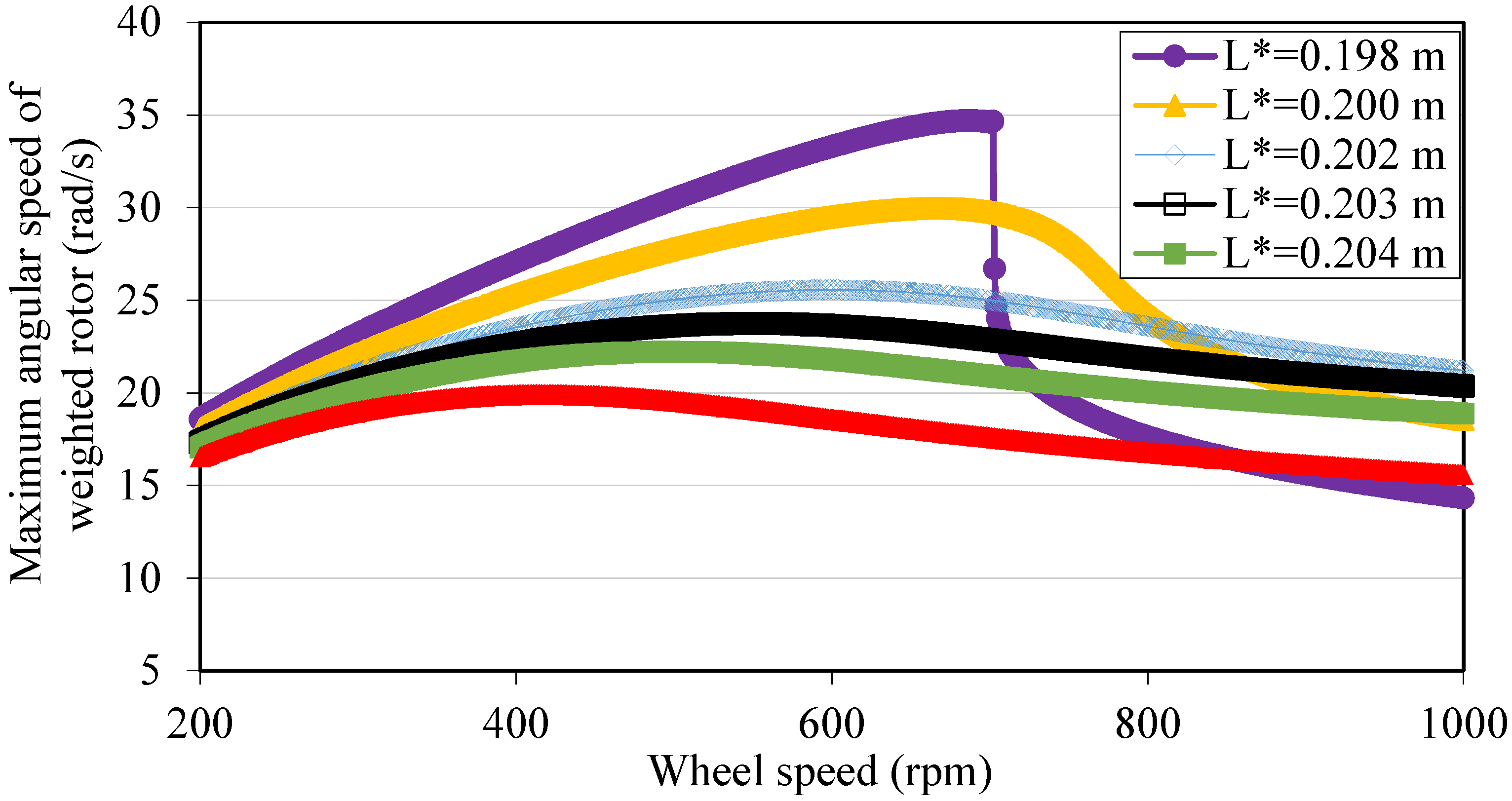
2.3. Optimization of Halbach Array Magnetic Circuit
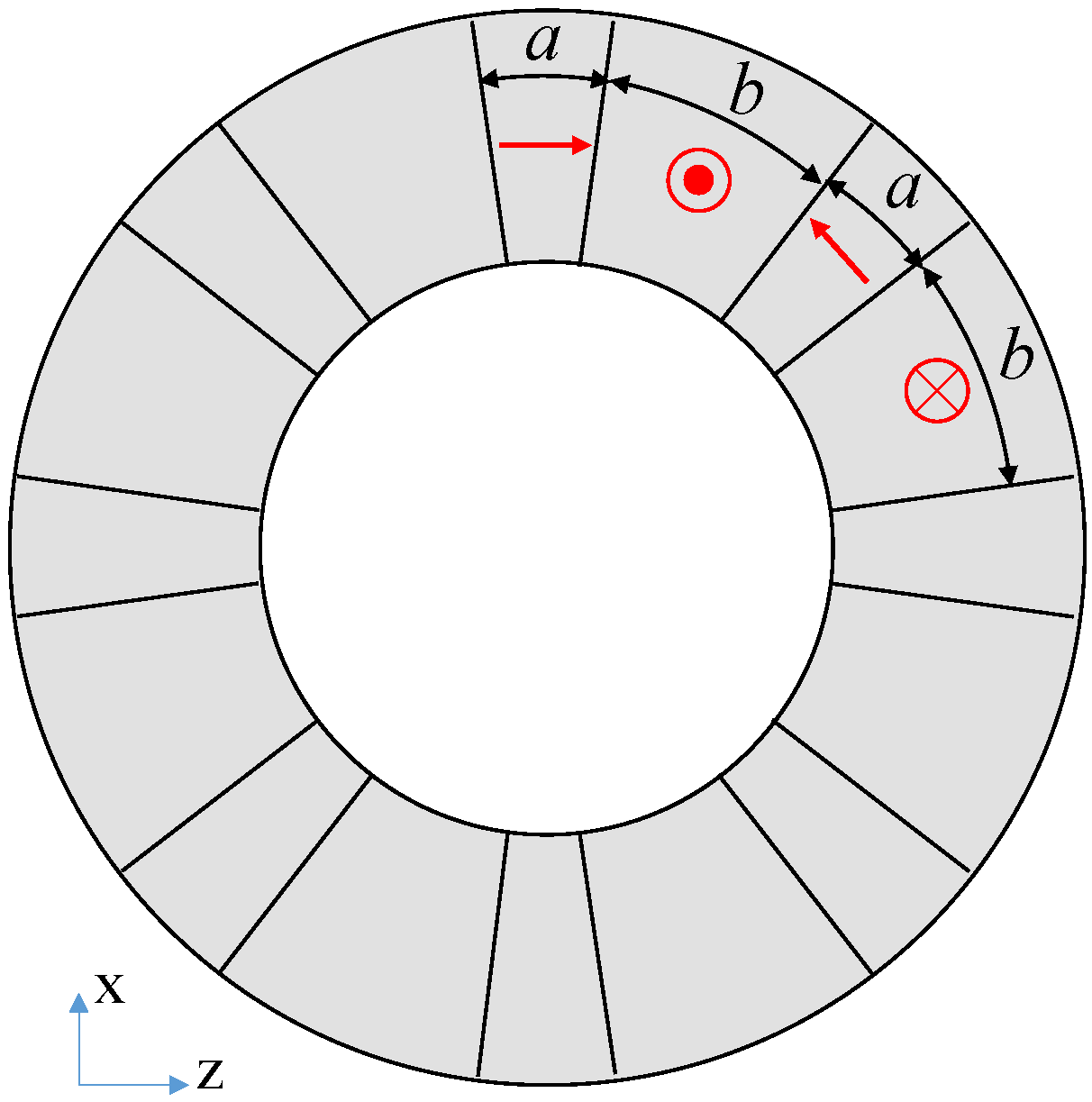
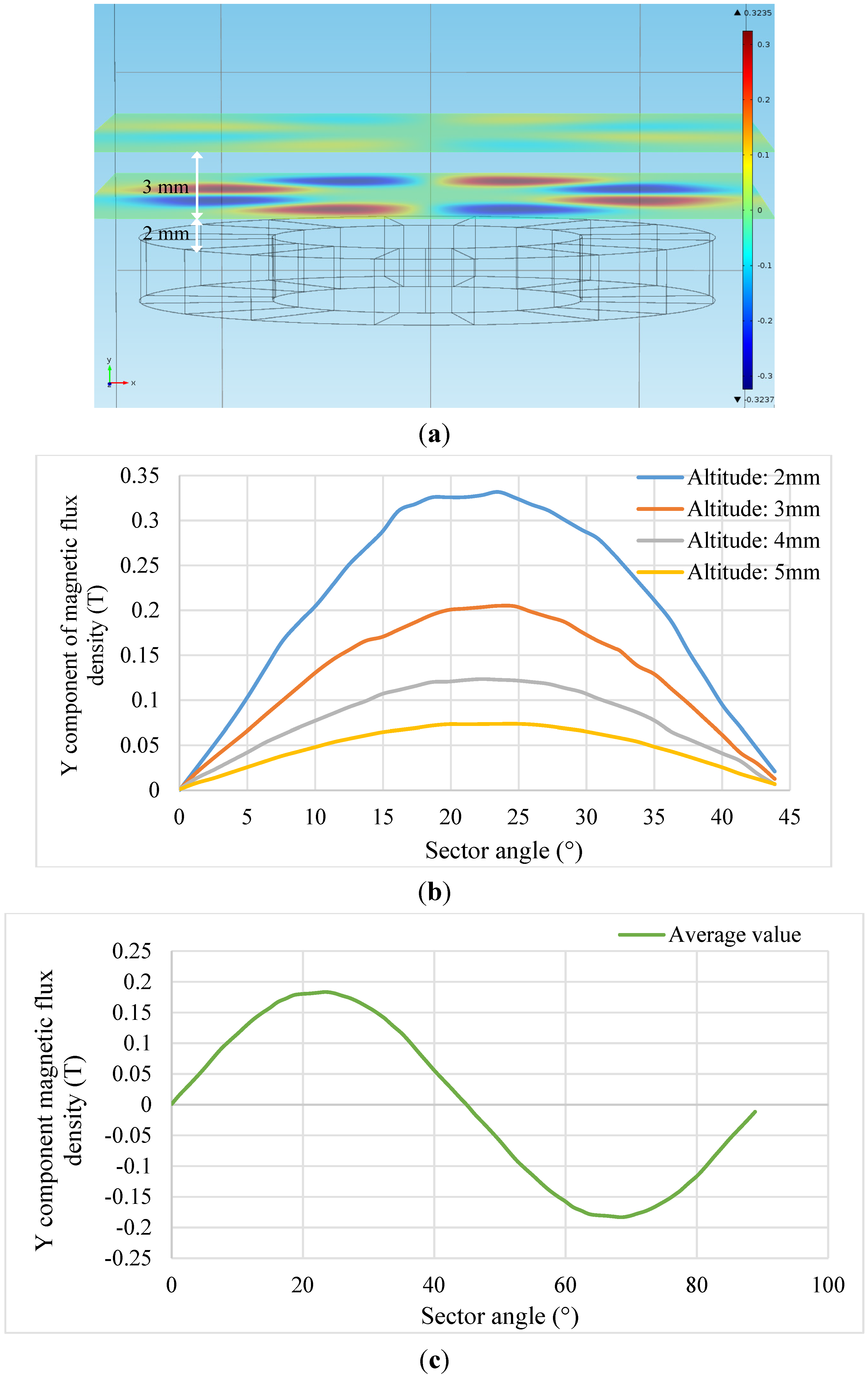
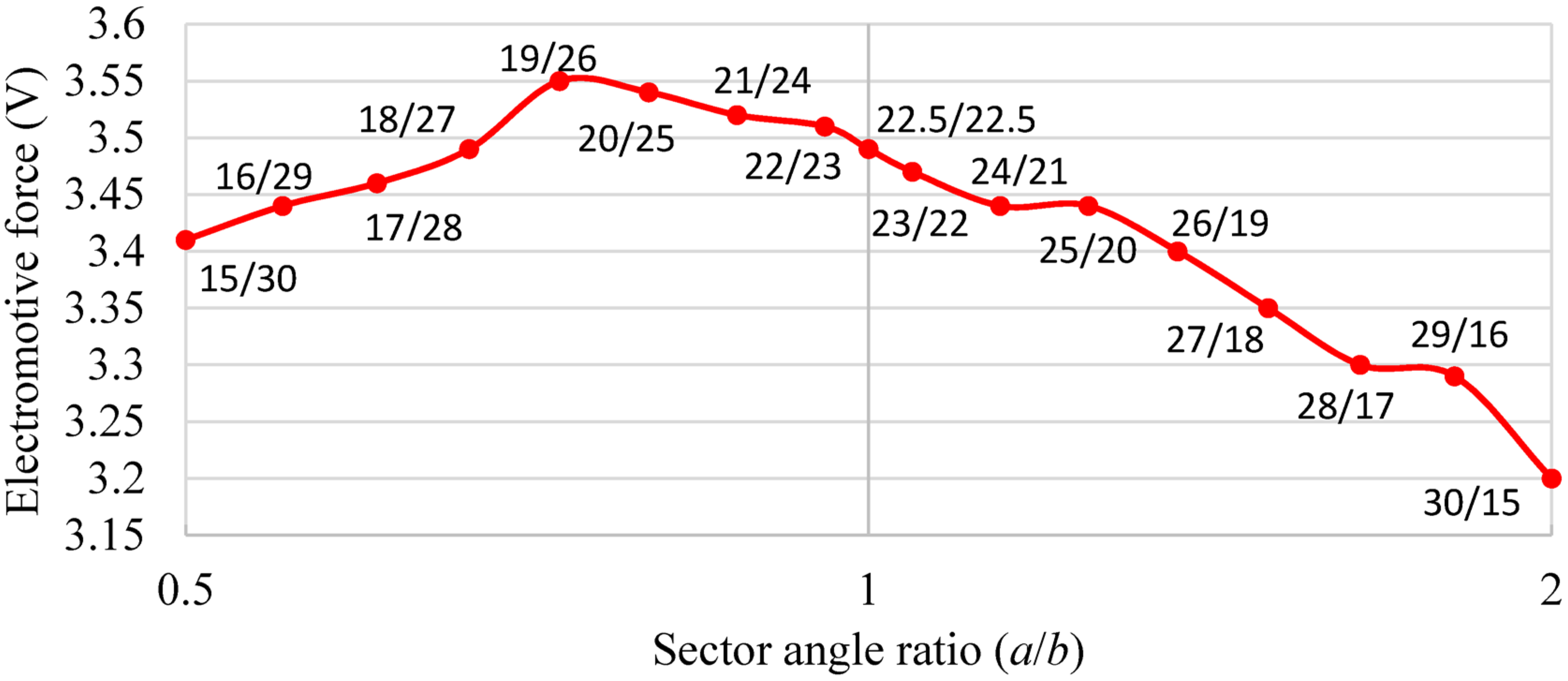
| Parameter | Circular Halbach Array Disk |
|---|---|
| Dimensions of individual magnet | rout = 13.0 mm |
| rin = 7.0 mm | |
| tm = 3.0 mm | |
| Residual magnetism of magnet by axial magnetization | Br = 1.4 T |
| Coil wire diameter | d = 0.1 mm |
| Coil turns in a layer | Nr = 20 |
| Coil layers in a set | Nt = 30 |
| Thickness of coil set | tc = 3.0 mm |
| Inside diameter of the coil set | Din = 2.0 mm |
| Outside diameter of the coil set | Dout = 6.0 mm |
| Air gap between magnetic disk and coil sets | tp = 1.0 mm |
| Number of coil turn | 600 |
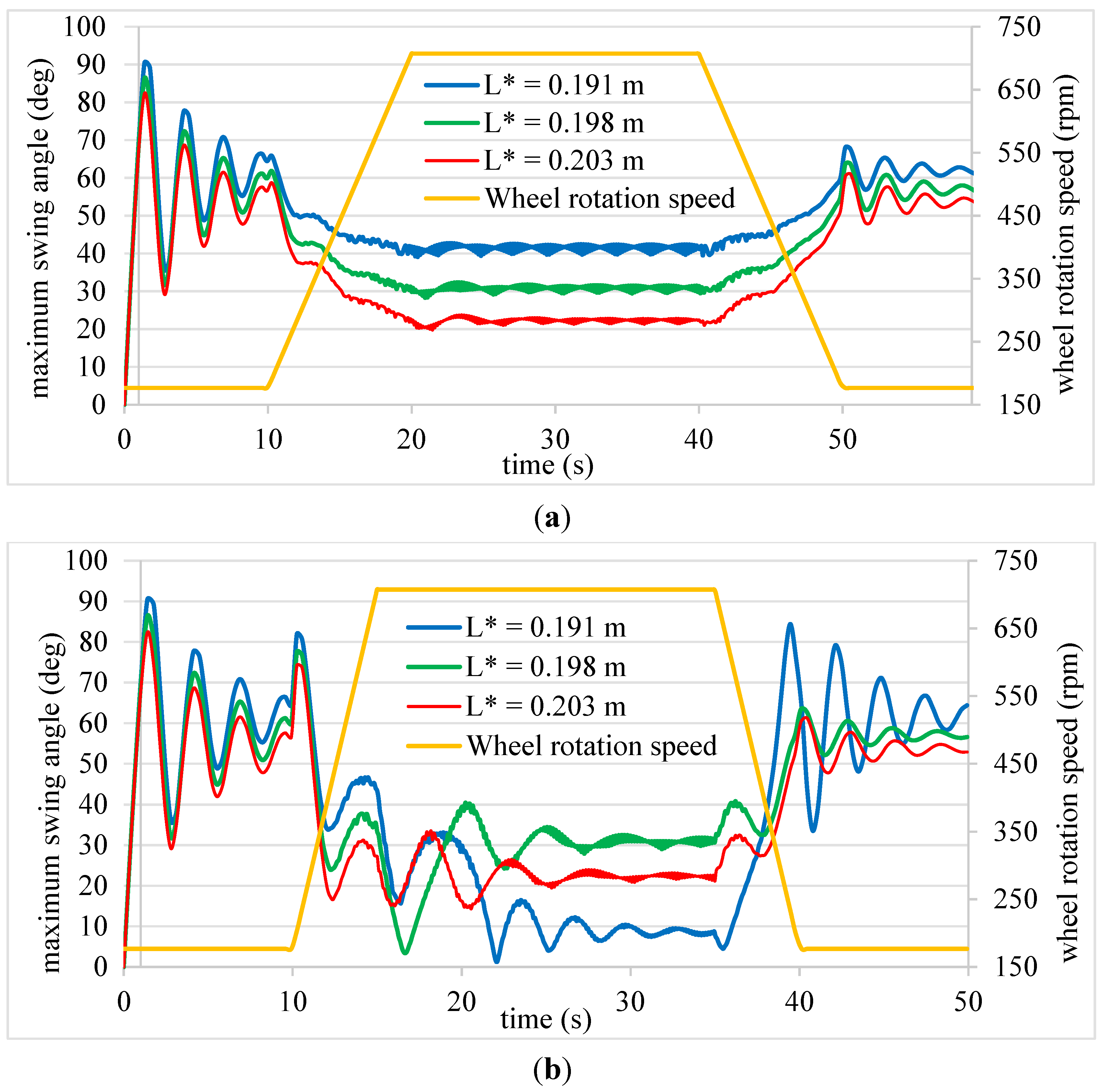
3. Experiments and Results


| Plate rotation speed (rpm) | Average power generation simulation (μw) | Average voltage simulation (V) | Average power generation experiment (μw) | Average voltage experiment (V) |
|---|---|---|---|---|
| 300 | 404 | 0.471 | 399 | 0.468 |
| 350 | 454 | 0.499 | 445 | 0.494 |
| 400 | 507 | 0.528 | 491 | 0.520 |
| 450 | 555 | 0.552 | 526 | 0.538 |
| 500 | 585 | 0.567 | 535 | 0.541 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Wright, P.K.; Sundararajan, V. Improving power output for vibration-based energy scavengers. IEEE Pervas. Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Arnold, D.P. Review of microscale magnetic power generation. IEEE Trans. Magn. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Todoroki, A. Wireless monitoring of automobile tires for intelligent tires. Sensors 2008, 8, 8123–8138. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Lin, C.C.; Yu, J.H. A nonlinear suspended energy harvester for a tire pressure monitoring system. Micromachines 2015, 6, 312–327. [Google Scholar] [CrossRef]
- Schaijk, R.V.; Elfrink, R.; Oudenhoven, J.; Pop, V.; Wang, Z.; Renaud, M. A MEMS vibration energy harvester for automotive applications. Prco. SPIE 2013, 8763, 876305. [Google Scholar]
- Leland, E.S.; Wright, P.K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload. Smart Mater. Struct. 2006, 15, 1413–20. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Reversible hysteresis for broadband magnetopiezoelastic energy havesting. Appl. Phys. Lett. 2009, 95, 174103. [Google Scholar] [CrossRef]
- Sari, I.; Balkan, T.; Kulah, H. An electromagnetic micro power generator for wideband environmental vibrations. Sens. Actuators A 2008, 145–146, 405–413. [Google Scholar] [CrossRef]
- Lee, D.G.; Carman, G.P.; Murphy, D.; Schulenburg, C. Novel micro vibration energy harvesting device using frequency up conversion. In Proceeding of Sensors Solid-State Actuators and Microsystems Conference Transducers, Lyon, French, 10–14 June 2007.
- Daminakis, M.; Goethals, J.; Kowtke, J. Enhancing power harvesting using a tuned auxiliary structure. J. Intell. Mater. Syst. Struct. 2005, 16, 825–834. [Google Scholar] [CrossRef]
- Spreemann, D.; Manoli, Y.; Folkmer, B.; Mintenbeck, D. Non-resonant vibration conversion. J. Micromech. Microeng. 2006, 16, 169–173. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K. Design of a frequency-adjusting device for harvesting energy from a rotating wheel. Sens. Actuators A 2010, 159, 196–203. [Google Scholar] [CrossRef]
- Guizzi, G.L.; Mannon, M.; Manzi, G.; Salvatori, M. Preliminary study on a kinetic energy recovery system for sailing yachts. Renew. Energy 2014, 62, 216–225. [Google Scholar] [CrossRef]
- Lu, C.H.; Wang, Y.J.; Sung, C.K.; Chao, P.C.P. A hula-hoop energy-harvesting system. IEEE Trans. Magn. 2011, 47, 2395–2398. [Google Scholar] [CrossRef]
- Barton, D.A.W.; Burrow, S.G.; Clare, L.R. Energy harvesting from vibrations with a nonlinear oscillator. J. Vib. Acoustics 2010, 132, 021009. [Google Scholar] [CrossRef]
- Singh, K.B.; Bedekar, V.; Taheri, S.; Priya, S. Piezoelectric vibration energy harvesting system with an adaptive frequency tuning mechanism for intelligent tires. Mechatronics 2012, 22, 970–988. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K. System design of a weighted-rotor type electromagnetic generator for harvesting energy from a rotating wheel. IEEE/ASME Trans. Mechatron. 2013, 18, 754–763. [Google Scholar] [CrossRef]
- Wu, X.; Parmar, M.; Lee, D.W. A seesaw-structured energy harvester with super wide bandwidth for TPMS application. IEEE/ASME Trans. Mechatron. 2013, 19, 1514–1522. [Google Scholar]
- Manla, G.; White, N.M.; Tudor, M.J. Numerical model of a non-contact piezoelectric energy harvester for rotating objects. IEEE Sens. J. 2011, 12, 1785–1793. [Google Scholar] [CrossRef]
- Lee, J.; Choi, B. Development of a piezoelectric energy harvesting system for implementing wireless sensors on the tires. Energy Convers. Manag. 2014, 78, 32–38. [Google Scholar] [CrossRef]
- Introduction of TPMS. Orange Electronic. Available online: http://www.orange-electronic.com (accessed on 19 March 2015).
- Wang, Y.J.; Chen, C.D. Design and jump phenomenon analysis of an eccentric ring energy harvester. Smart Mater. Struct. 2013, 22, 105019. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K.; Li, C. Natural frequency self-tuning energy harvester using a circular Halbach array magnetic disk. J. Intell. Mater. Syst. Struct. 2012, 23, 933–943. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-J.; Hao, Y.-T.; Lin, H.-Y. Design of a Weighted-Rotor Energy Harvester Based on Dynamic Analysis and Optimization of Circular Halbach Array Magnetic Disk. Micromachines 2015, 6, 375-389. https://doi.org/10.3390/mi6030375
Wang Y-J, Hao Y-T, Lin H-Y. Design of a Weighted-Rotor Energy Harvester Based on Dynamic Analysis and Optimization of Circular Halbach Array Magnetic Disk. Micromachines. 2015; 6(3):375-389. https://doi.org/10.3390/mi6030375
Chicago/Turabian StyleWang, Yu-Jen, Yu-Ti Hao, and Hao-Yu Lin. 2015. "Design of a Weighted-Rotor Energy Harvester Based on Dynamic Analysis and Optimization of Circular Halbach Array Magnetic Disk" Micromachines 6, no. 3: 375-389. https://doi.org/10.3390/mi6030375
APA StyleWang, Y.-J., Hao, Y.-T., & Lin, H.-Y. (2015). Design of a Weighted-Rotor Energy Harvester Based on Dynamic Analysis and Optimization of Circular Halbach Array Magnetic Disk. Micromachines, 6(3), 375-389. https://doi.org/10.3390/mi6030375





