Noise Reduction of MEMS Gyroscope Based on Direct Modeling for an Angular Rate Signal
Abstract
:1. Introduction
2. Modeling of Stochastic Error for MEMS Gyroscope
| Noise Terms | Allan Variance | Slope | Coefficient | Unit |
|---|---|---|---|---|
| ARW | N2/τ | −1/2 | N = σ(1) | °/h0.5 |
| Bias instability | (0.6643B)2 | 0 | B = σ(f0)/0.6643 | °/h |
| RRW | K2τ/3 | +1/2 | K = σ(3) | °/h1.5 |
3. Optimal KF Algorithm for Gyroscope Noise Reduction
3.1. KF State and Measurement Equation
3.2. Analysis of KF Observability
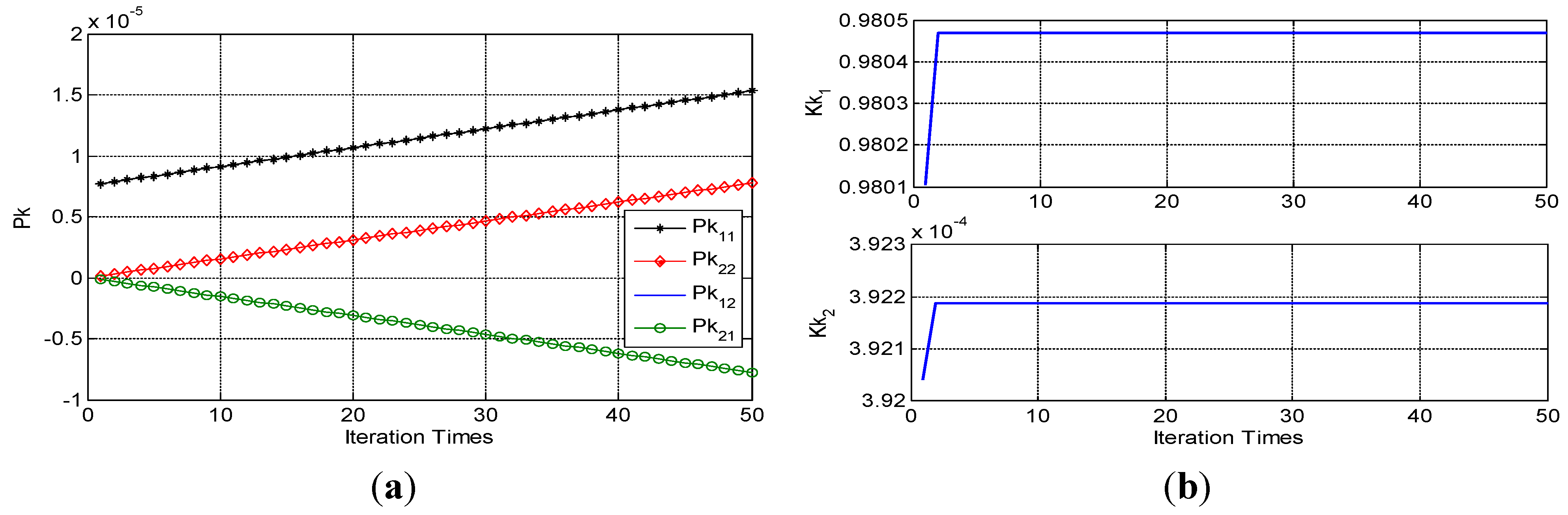
3.3. Discrete-Time KF for True Rate Signal Estimate
- Step 1: Form the covariance matrices Q and R by the ARW and RRW noise variance and variance qω;
- Step 2: Analyze the steady-state filtering gain Ks off-line by using of Equations (9)–(11), ;
- Step 3: Perform the eigenvalue decomposition of matrix m, ;
- Step 4: Extract the eigenvectors matrix S and eigenvalues λ1 and λ2;
- Step 5: Calculate the matrices A and B,
- Step 6: Perform the discrete-time KF equation,
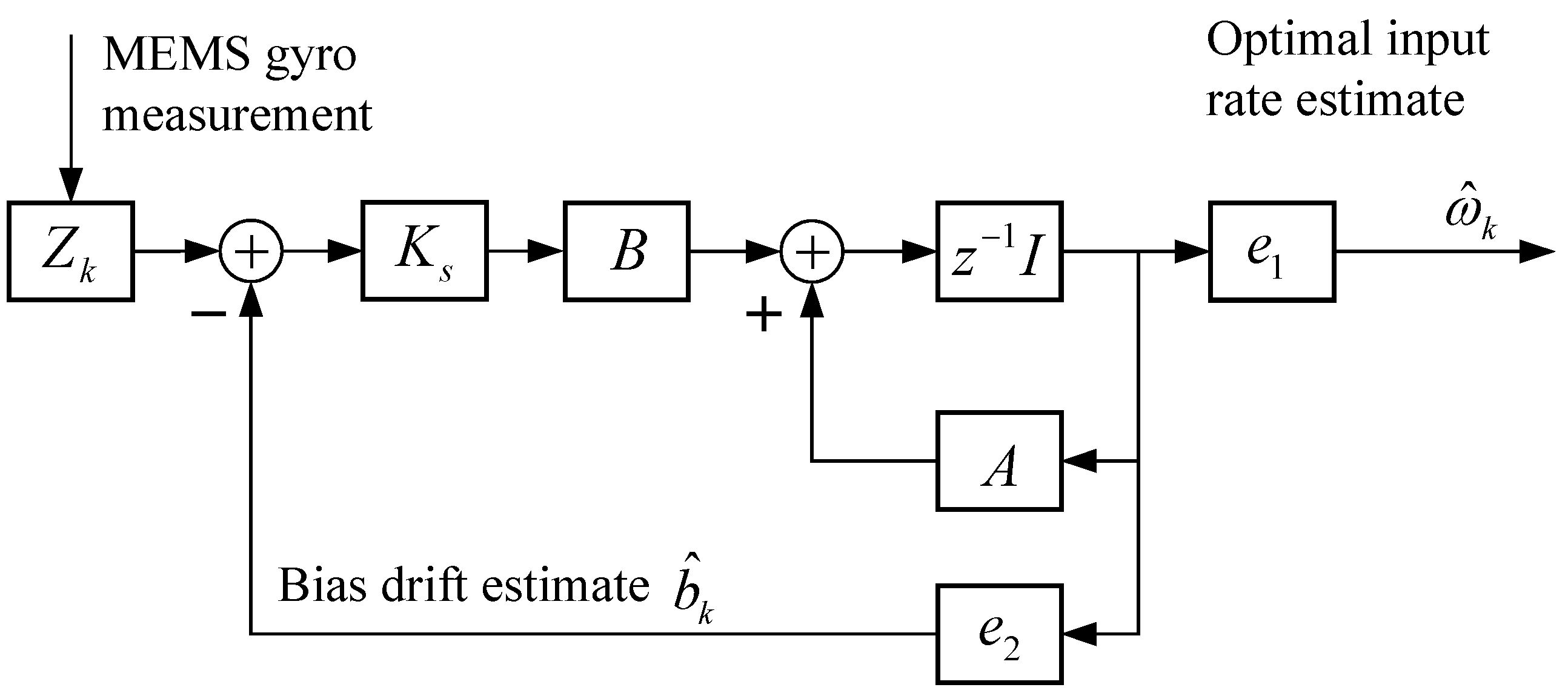
3.4. Analysis of KF Bandwidth

4. Experiment and Discussion
4.1. Static Drift Test Result
| Terms | Noise (°/s/Hz0.5) | ARW (°/h0.5) | Bias drift (°/h) |
|---|---|---|---|
| Original gyro | 0.150 | 4.8668 | 44.4129 |
| BW = 10 Hz | 0.013 | 0.4006 | 4.1344 |
| BW = 20 Hz | 0.040 | 1.2037 | 12.1383 |
| BW = 30 Hz | 0.061 | 1.8879 | 19.7388 |
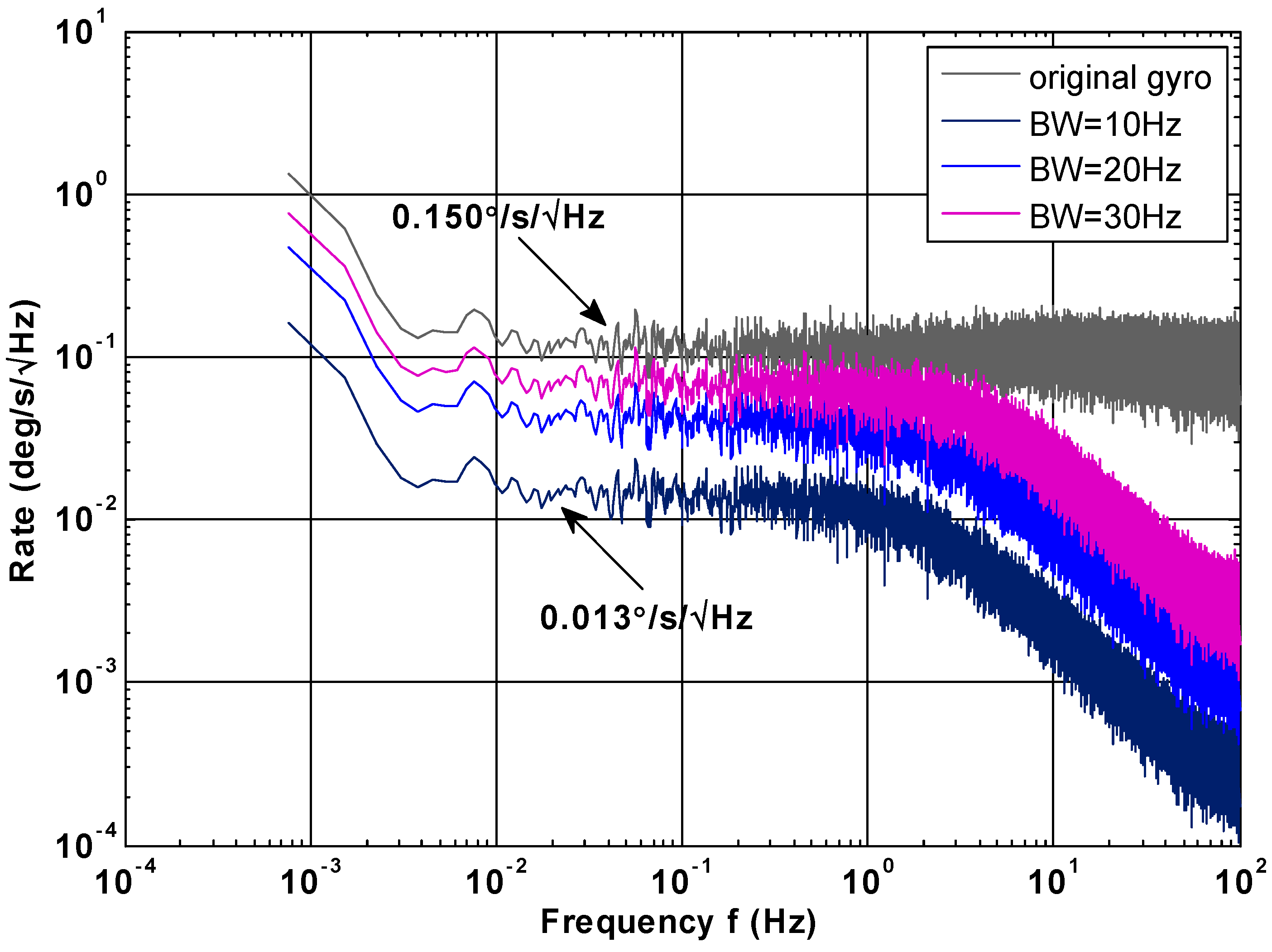
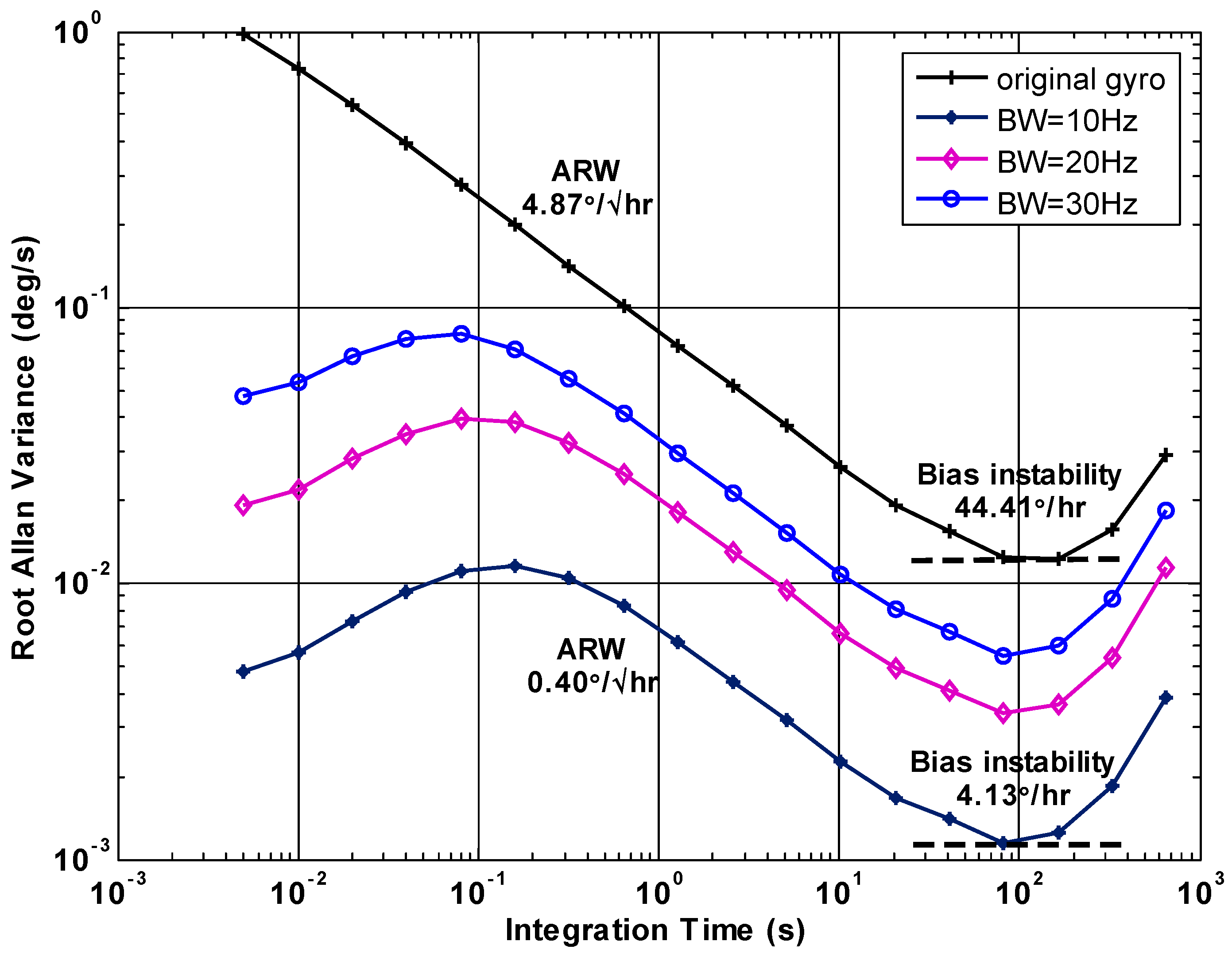

4.2. Constant Rate Test Result
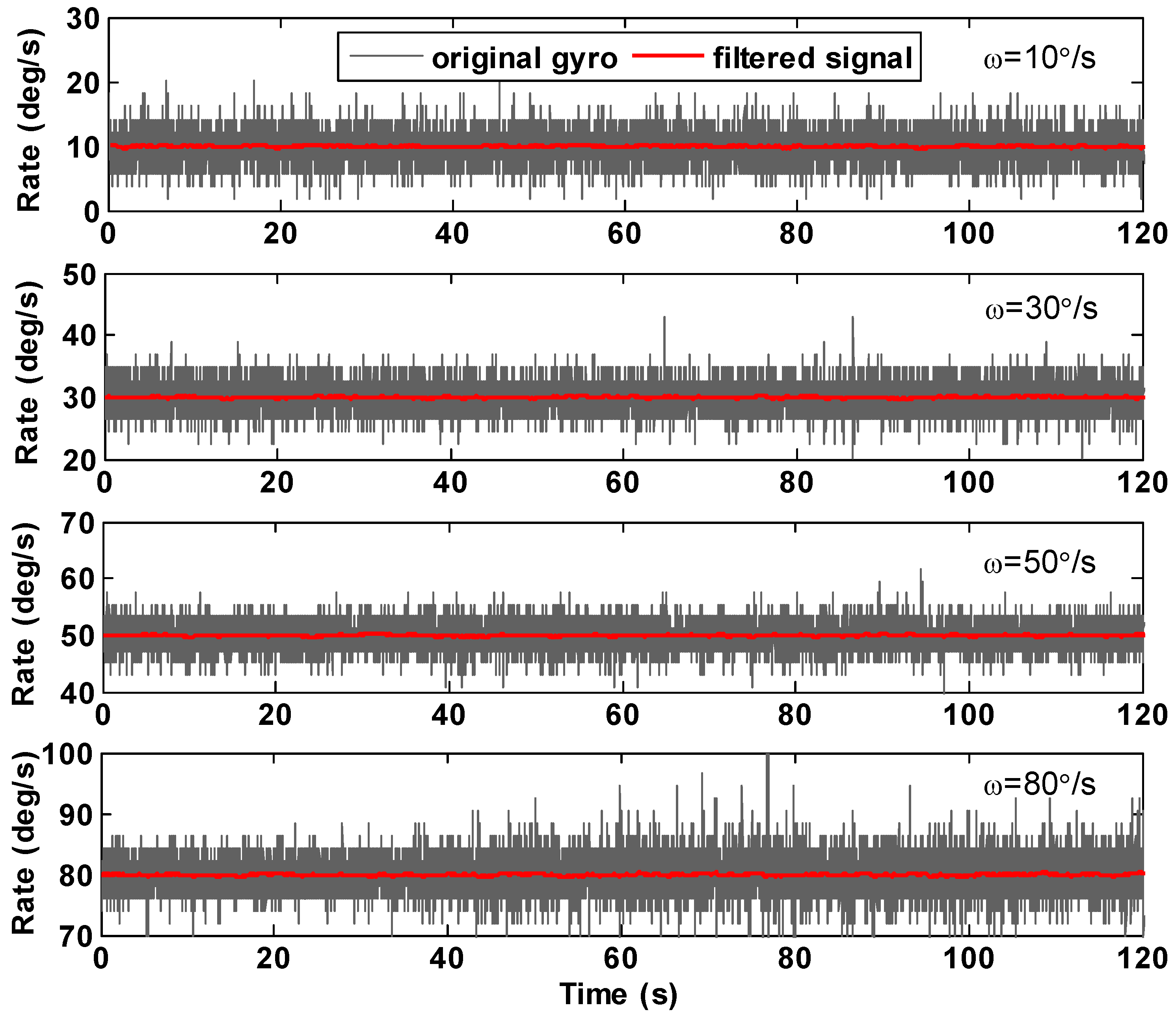
| Rate (°/s) | Mean of Estimated Error (°/s) | STD of Estimated Error (°/s) | ||
|---|---|---|---|---|
| Original Gyro | After Filtering | Original Gyro | After Filtering | |
| 10 | 0.0413 | −0.0421 | 1.9378 | 0.1120 |
| 30 | 0.0197 | −0.0209 | 2.0195 | 0.1075 |
| 50 | 0.0582 | −0.0607 | 1.9751 | 0.1069 |
| 80 | 0.0776 | −0.0812 | 2.6189 | 0.1407 |
4.3. Swing Rate Test Result
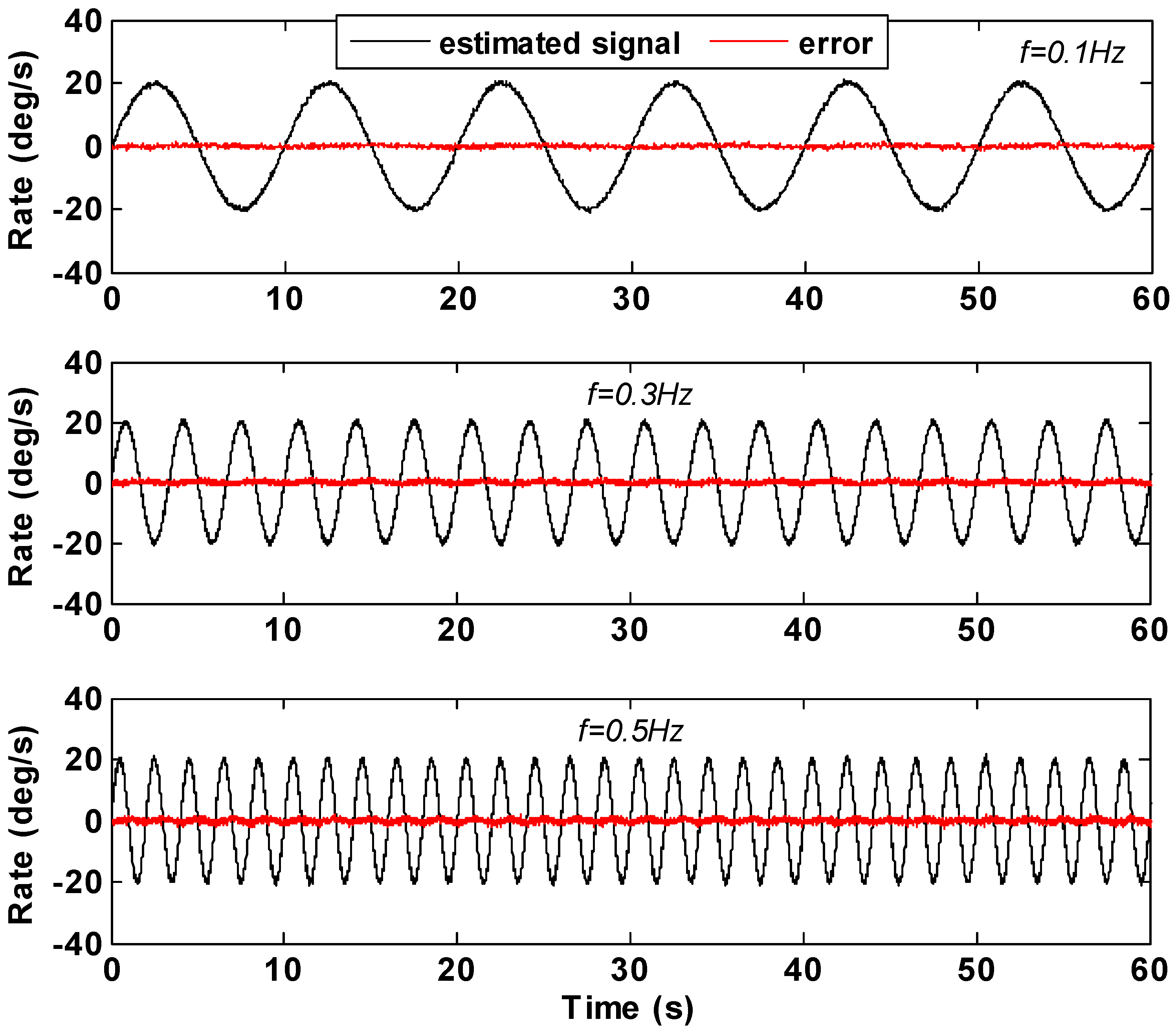
| Frequency f (Hz) | Amplitude (°/s) | STD Error (°/s) | ||
|---|---|---|---|---|
| Original Gyro | After Filtering | Original Gyro | After Filtering | |
| 0.1 | 22.4481 | 20.0973 | 1.6749 | 0.3836 |
| 0.3 | 22.6760 | 20.1926 | 1.6242 | 0.5510 |
| 0.5 | 23.1104 | 20.7806 | 1.7234 | 0.6866 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Acar, C.; Shkel, A.M. Nonresonant micromachined gyroscopes with structural mode-decoupling. IEEE Sens. J. 2003, 3, 497–506. [Google Scholar] [CrossRef]
- Al-Majed, M.I.; Alsuwaidan, B.N. A new testing platform for attitude determination and control subsystems: Design and applications. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 1318–1323.
- Liu, K.; Zhang, W.P.; Chen, W.Y.; Li, K.; Dai, F.Y.; Cui, F.; Wu, X.S.; Ma, G.Y.; Xiao, Q.J. The development of micro-gyroscope technology. J. Micromech. Microeng. 2009, 19, 157–185. [Google Scholar]
- Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. North-finding with 0.004 radian precision using a silicon MEMS quadruple mass gyroscope with Q-factor of 1 million. In Proceedings of the IEEE 25th International Conference on Micro Electro Mechanical Systems, Paris, France, 29 January–2 February 2012; pp. 164–167.
- Nitzan, S.; Ahn, C.H.; Su, T.-H.; Li, M.; Ng, E.J.; Wang, S.; Yang, Z.M.; O’Brien, G.; Boser, B.E.; Kenny, T.W.; et al. Epitaxially-encapsulated polysilicon disk resonator gyroscope. In Proceedings of the IEEE 26th International Conference on Micro Electro Mechanical Systems, Taipei, Taiwan, 20–24 January 2013; pp. 625–628.
- Sahin, E.; Alper, S.E.; Akin, T. Experimental evaluation of alternative drive-mode control electronics developed for high-performance MEMS gyroscopes. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 2817–2820.
- Ezekwe, C.D.; Boser, B.E. A mode-matching ΔΣ closed-loop vibratory gyroscope readout interface with a 0.004°/s/Hz noise floor over a 50 Hz band. IEEE J. Solid-State Circuits 2008, 43, 3039–3048. [Google Scholar] [CrossRef]
- Chen, X.Y. Modeling random gyro drift by time series neural networks and by traditional method. In Proceedings of the IEEE conference on Neural Networks and Signal Processing, Nanjing, China, 14–17 December 2003; pp. 810–813.
- Zhang, Y.S.; Wang, Y.Y.; Yang, T.; Yin, R.; Fang, J.C. Dynamic angular velocity modeling and error compensation of one-fiber fiber optic gyroscope (OFFOG) in the whole temperature range. Meas. Sci. Technol. 2012, 23, 1–6. [Google Scholar]
- Sharaf, R.; Noureldin, A.; Osman, A.; El-Sheimy, N. Online INS/GPS integration with a radial basis function neural network. IEEE Aerosp. Electron. Syst. Mag. 2004, 20, 8–14. [Google Scholar] [CrossRef]
- Mao, B.; Wu, J.W.; Wu, J.T.; Zhou, X.M. MEMS gyro denoising based on second generation wavelet transform. In Proceedings of the First International Conference on Pervasive Computing Signal Processing and Applications (PCSPA), Harbin, China, 17–19 September 2010; pp. 255–258.
- Bekkeng, J.K. Calibration of a novel MEMS inertial reference unit. IEEE Trans. Instrum. Meas. 2009, 58, 1967–1974. [Google Scholar] [CrossRef]
- Jamshaid, A.; Muhammad, U. A consistent and robust Kalman filter design for in-motion alignment of inertial navigation system. Measurement 2009, 42, 577–582. [Google Scholar] [CrossRef]
- Bayard, D.S.; Ploen, S.R. High Accuracy Inertial Sensors from Inexpensive Components. U.S. Patent US20030187623A1, 2 October 2003. [Google Scholar]
- Chang, H.L.; Xue, L.; Jiang, C.Y.; Kraft, M.; Yuan, W.Z. Combining numerous uncorrelated MEMS gyroscopes for accuracy improvement based on an optimal Kalman filter. IEEE Trans. Instrum. Meas. 2012, 61, 3084–3093. [Google Scholar] [CrossRef]
- Xue, L.; Jiang, C.Y.; Chang, H.L.; Yang, Y.; Qin, W.; Yuan, W.Z. A novel Kalman filter for combining outputs of MEMS gyroscope array. Measurement 2012, 45, 745–754. [Google Scholar] [CrossRef]
- Lam, Q.M.; Crassidis, J.L. Precision attitude determination using a multiple model adaptive estimation scheme. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–20.
- Stearns, H.; Tomizuka, M. Multiple model adaptive estimation of satellite attitude using MEMS gyros. In Proceedings of the American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3490–3495.
- Guerrier, S.; Skaloud, J.; Stebler, Y.; Victoria-Feser, M.-P. Wavelet variance based estimation for composite stochastic processes. J. Am. Stat. Assoc. 2013, 108, 1021–1030. [Google Scholar] [CrossRef] [PubMed]
- Vaccaro, R.J.; Zaki, A.S. Statistical modeling of rate gyros. IEEE Trans. Instrum. Meas. 2012, 61, 673–684. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Hou, H.; Niu, X. Analysis and modeling of inertial sensors using Allan variance. IEEE Trans. Instrum. Meas. 2008, 57, 140–149. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering Theory and Practice Using Matlab, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001; pp. 119–121. [Google Scholar]
- Analog Devices, ADXRS300. Available online: http://www.analog.com/static/imported-files/data_sheets/ADXRS300.pdf (accessed on 4 November 2014).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, L.; Jiang, C.; Wang, L.; Liu, J.; Yuan, W. Noise Reduction of MEMS Gyroscope Based on Direct Modeling for an Angular Rate Signal. Micromachines 2015, 6, 266-280. https://doi.org/10.3390/mi6020266
Xue L, Jiang C, Wang L, Liu J, Yuan W. Noise Reduction of MEMS Gyroscope Based on Direct Modeling for an Angular Rate Signal. Micromachines. 2015; 6(2):266-280. https://doi.org/10.3390/mi6020266
Chicago/Turabian StyleXue, Liang, Chengyu Jiang, Lixin Wang, Jieyu Liu, and Weizheng Yuan. 2015. "Noise Reduction of MEMS Gyroscope Based on Direct Modeling for an Angular Rate Signal" Micromachines 6, no. 2: 266-280. https://doi.org/10.3390/mi6020266
APA StyleXue, L., Jiang, C., Wang, L., Liu, J., & Yuan, W. (2015). Noise Reduction of MEMS Gyroscope Based on Direct Modeling for an Angular Rate Signal. Micromachines, 6(2), 266-280. https://doi.org/10.3390/mi6020266






