1. Introduction
Tunable microlenses are widely used in microfluidic or lab-on-chip systems [
1] due to their fine tuning of the light. A tunable microlens adaptively reshapes the input light including adjusting its focal position, intensity, beam profile, and even propagation direction [
2]. They can also be used for ordinary coupling, collimating and focusing, and in wide range of lab-on-a-chip applications such as flow cytometry [
3,
4,
5], on-chip optical tweezers and single molecule detection [
6,
7].
Several kinds of tunable microlenses are developed for providing adaptive focusing with adjustable curved refractive surfaces [
2], such as a micromeniscus surface actuated by electro-wetting [
8], liquid microlenses based on the dielectrophoretic effect [
9,
10,
11], microlenses based on the thermal effect [
12], or hydraulically actuated polydimethylsiloxane (PDMS) membranes [
13,
14]. Among them, electro-wetting and dielectrophoresis lenses are electrically driven, while other microlenses whose focal lengths are variable are either based on pressure-induced systems using an elastic membrane, or on thermal effect. A mechanical lens whose focal length is controlled by pumping liquid in and out of the lens chamber caused great interest. The operation mechanism of this lens is simple because it only requires a fluid pumping system. There are two working mechanisms which are often used to implement these tunable liquid microlenses. One is to achieve the refraction of light at curved, optically smooth, liquid-liquid interfaces between two flowing fluids by controlling laminar flows. Recently, the Whitesides group has developed a dynamically reconfigurable liquid-liquid lens [
15] with the convex shape of liquid-liquid interfaces in a microfluidic expansion chamber. The curvatures in the liquid-liquid interfaces were controlled by adjusting hydrodynamic flow conditions, and then adjustable focal length was produced. However, in the liquid-liquid lens, a higher speed of the laminar flows is necessary, which means large amounts of fluid have to be supplied discontinuously for keeping the microlens working. Utilization of so-called liquid gradient refractive index (L-GRIN) microlenses [
16] is the other approach and also the preferable way to achieve a tunable microlens. Similarly, with the traditional solid self-focusing lens, the refractive index of the L-GRIN microlens increases continuously from the cladding region to the core optical axis. However, a gradient refractive index of the L-GRIN microlens is achieved by dynamically adjusting hydrodynamic flow conditions rather than by changing the geometrical structure of the lens for the traditional one. In contrast to the liquid-liquid interface-based microlens, the L-GRIN lens operates through the diffusion in multiple flows rather than by relying on a clearly defined, curved liquid-liquid interface. Therefore, the flow consumption rate is much lower in the L-GRIN lens [
17]. These lenses focus a light beam through a liquid medium with a two-dimensional (2D) refractive index gradient. The two-dimensional (2D) refractive index profile and, subsequently, the focal length of the L-GRIN lens can be tuned by changing the ratio of the flow rates of the two inlets [
17]. However, most L-GRIN microlenses are only capable of out-of-plane focusing. In-plane-focusing tunable microlens are, however, proven to be preferable in integrative devices, which can be fabricated and seamlessly integrated with other on-chip fluidic and optical components such as a lab-on-a-chip lasers [
18] and optical waveguides [
19]. In particular, it has inspired the creation of a variety of innovative devices controlled by flow rates and liquid compositions, and variable light focusing was measured and shown, but the quantitative relation between liquid parameters and focal length has not been demonstrated clearly. It will lead to the unpredictability of the focusing effect in the device.
In this paper, an in-plane tunable L-GRIN microlens was designed for dynamically adjusting the beam focusing, which can be more readily integrated for lab-on-a-chip applications. The convection-diffusion process of liquids in the microfluidic chamber is firstly simulated with the finite element method (FEM) when a high-refractive-index solution is injected side-by-side into a low-refractive-index solution. During the convection and diffusing process, the diffusion profile of the liquids, and hence the refractive index profile within the L-GRIN microlens, varies with the hydrodynamic flow conditions. Thus, the refractive index profile of the L-GRIN microlens is calculated and discussed numerically under different flow conditions, and the beam transmission and focusing process in the L-GRIN microlens is simulated using the ray tracing method. The effects of the diffusion coefficient, mass fraction and flow rate of liquids on the input beam focusing effect, including the focal length and the size of the focal spot, were demonstrated. Therefore, an in-plane tunable beam focusing is achieved using a simple planar microfluidic structure; in addition, with the simulation of the convection and diffusing process, the ray tracing method gives us approaches to predict the focusing effect of an L-GRIN microlens.
2. Structure and Principle of L-GRIN Micrlens
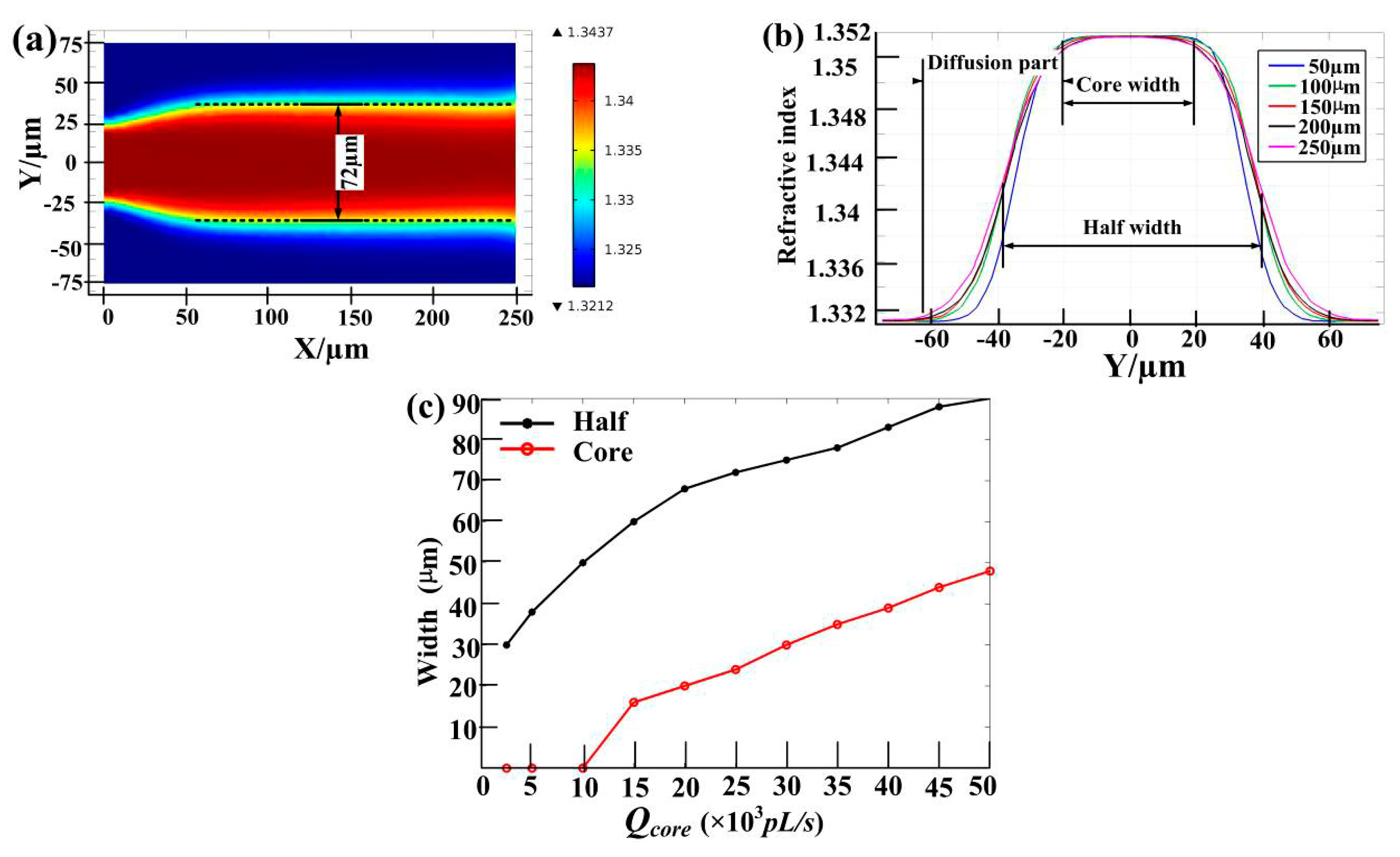
The schematic of the L-GRIN microlens designed is shown in
Figure 1. The structure of the microlens as shown in
Figure 1a consists of the microfluid chamber, core inlet, cladding inlet and outlet. The core liquid and the cladding liquid are injected through the core inlet and cladding inlet, respectively, which flow out through the outlet.
Hin_core,
Win_core, Hin_clad,
Win_clad, Hout,
Wout represent the height and width of the core inlet, cladding inlet and outlet, respectively. The main part of the L-GRIN microlens is a micro-cylindrical chamber, where the diffusion and convection process of liquids occurs and the gradient refractive index profile appears. The
xoy cross-sectional view of the L-GRIN microlens together with the substrate is also illustrated in
Figure 1a, where
dcore which is designed to be 50 μm stands for the diameter of the core inlet. Similarly,
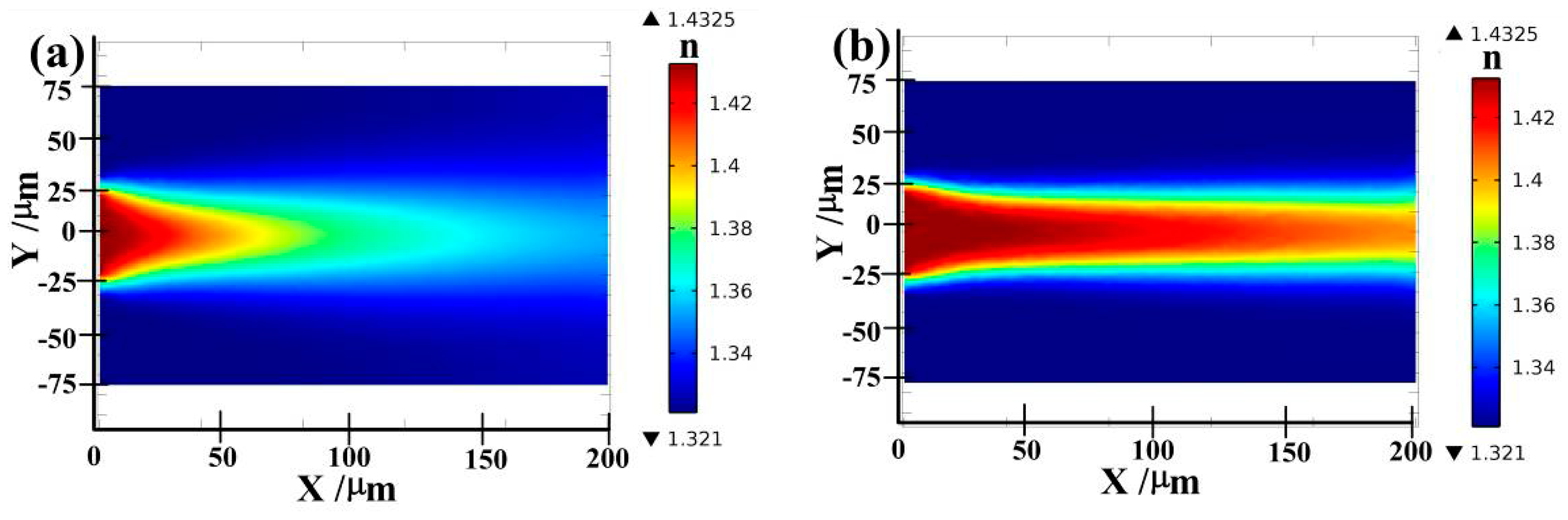
dclad is the diameter of the cladding inlet and is designed to be 150 μm. In the chamber, ethylene glycolsolution (core liquid) is injected side-by-side into de-ionized (DI) water (cladding liquid) from the same direction as shown in
Figure 1b. On account of the well-known manner in which the refractive index of liquids varies with the wavelength of incident light, in our simulation, the wavelength of incident light is set to be 500nm without considering the dispersion of light. The diffusion and convection process between ethylene glycol solution and DI water results in a 2D refractive index profile in the lens chamber, as shown in the left graph of
Figure 1c.An axis-symmetric refractive index gradient is accordingly achieved in the
xoy plane and the simulation result is given in the right graph of
Figure 1c, which shows that the refractive index of the L-GRIN microlens increases continuously from the cladding region to the core optical axis. The maximum refractive index comes near the inlet, and under the influence of diffusion, the refractive index decreases along the flowing direction of the liquids.
Figure 1.
(a) Structure diagram of the tunable L-GRIN microlens (left graph), in which Hin_core = 50 μm, Win_core = 30 μm, Hin_clad = 150 μm, Win_clad = 50 μm, Hout = 150 μm, Wout = 50 μm. The xoy cross-sectional view of the L-GRIN microlens together with the substrate (right graph), in which dcore = 50 μm, dclad = 150 μm; (b)The simplified model of the microfluidic chamber; (c) Simulated refractive index profile in the microfluidic chamber (left graph) and the refractive index profile in the xoy plane (right graph).
Figure 1.
(a) Structure diagram of the tunable L-GRIN microlens (left graph), in which Hin_core = 50 μm, Win_core = 30 μm, Hin_clad = 150 μm, Win_clad = 50 μm, Hout = 150 μm, Wout = 50 μm. The xoy cross-sectional view of the L-GRIN microlens together with the substrate (right graph), in which dcore = 50 μm, dclad = 150 μm; (b)The simplified model of the microfluidic chamber; (c) Simulated refractive index profile in the microfluidic chamber (left graph) and the refractive index profile in the xoy plane (right graph).
To simulate and optimize the refractive index profile and light propagation in the L-GRIN microlens under different conditions, the FEM and optical ray tracing method are adopted. The refractive index profile can be calculated by simulating the diffusion and convection process of liquids in the microfluidic chamber. When the refractive index of liquids is mainly affected by diffusion, the process can be described by Fick’s second law:
In which
C is the solution concentration and
t is the diffusion time.
D represents the diffusion coefficient that may determine the diffusion speed between the core liquid and the cladding liquid. As shown in Equation (1), the solution concentration changes with time and space. However, in the microfluidic chamber, the diffusion and the convection have a combined effect on the refractive index profile of the L-GRIN microlens. The convective-diffusive process in the chamber is therefore rewritten as [
20]:
where
U is defined to be the average flow velocity in the chamber. For a steady state flow, the distribution of concentration in the device does not vary with time, which means that
. Considering the symmetry of the lens structure, the convective-diffusive process can be simplified as:
The concentration distribution for the full, developed, steady-state flow can be expressed as Equation (4) [
21].
In the normalized coordinate system, , , where R is the radius of the microfluidic chamber. Then c′ = c/C0 is the normalized concentration, and C0 stands for the initial concentration. Pe is called the Peclet number, which is a dimensionless number and represents the relative proportion of convection to diffusion. Pe is proportional to the laminar velocity across the transversal section of the microfluidic chamber and the length of the microfluidic chamber, and Pe is also inversely proportional to the diffusion coefficient. Pe is usually used to describe the coefficient involved in the convection and diffusion process for a common analysis. However, the effect caused by convection and diffusion is analyzed separately in the present paper in order to dynamically reshape the light beam of the L-GRIN microlens.
For the structure we designed,
is defined as the average velocity, where
Qcore is the flow rate of the core liquid and
Qcore is the flow rate of the cladding liquid;
r is the normalized initial boundary ratio between the core and cladding liquids and is expressed as [
22]:
where
,
, and μ
core is the liquid viscosity of the core liquid and μ
clad is the liquid viscosity of the cladding liquid. The initial parameters are set as
,
and
, in which
stands for the full mixing state at the outlet and
represents the full mixing state at the chamber walls.
Once the liquids for the core and the cladding liquids are determined, the liquid viscosity and diffusion coefficient are considered to be constant. The position of the focal point can be tuned along the
x-direction by changing the refractive index profile, which can be achieved by adjusting the flow rate of the core or cladding liquid. According to Equation (2), if the average velocity
U is large, the diffusion in the
xoy plane can be neglected and only the refractive index profile in the
yoz plane needs to be calculated, where the plane is perpendicular to the liquid flow direction. On the contrary, when the average velocity
U is small, the diffusion in both
and
directions has to be discussed. The refractive index profile can be obtained according to the concentration profile [
23].
where
n(x’, y’) is the refractive index profile of the L-GRIN microlens in the
x’oy’ plane, and
and
are the normalized concentration profile of the core and cladding liquids in the
x’oy’ plane, respectively. The focusing of the input light beam through the microlens is determined by the refractive index profile.
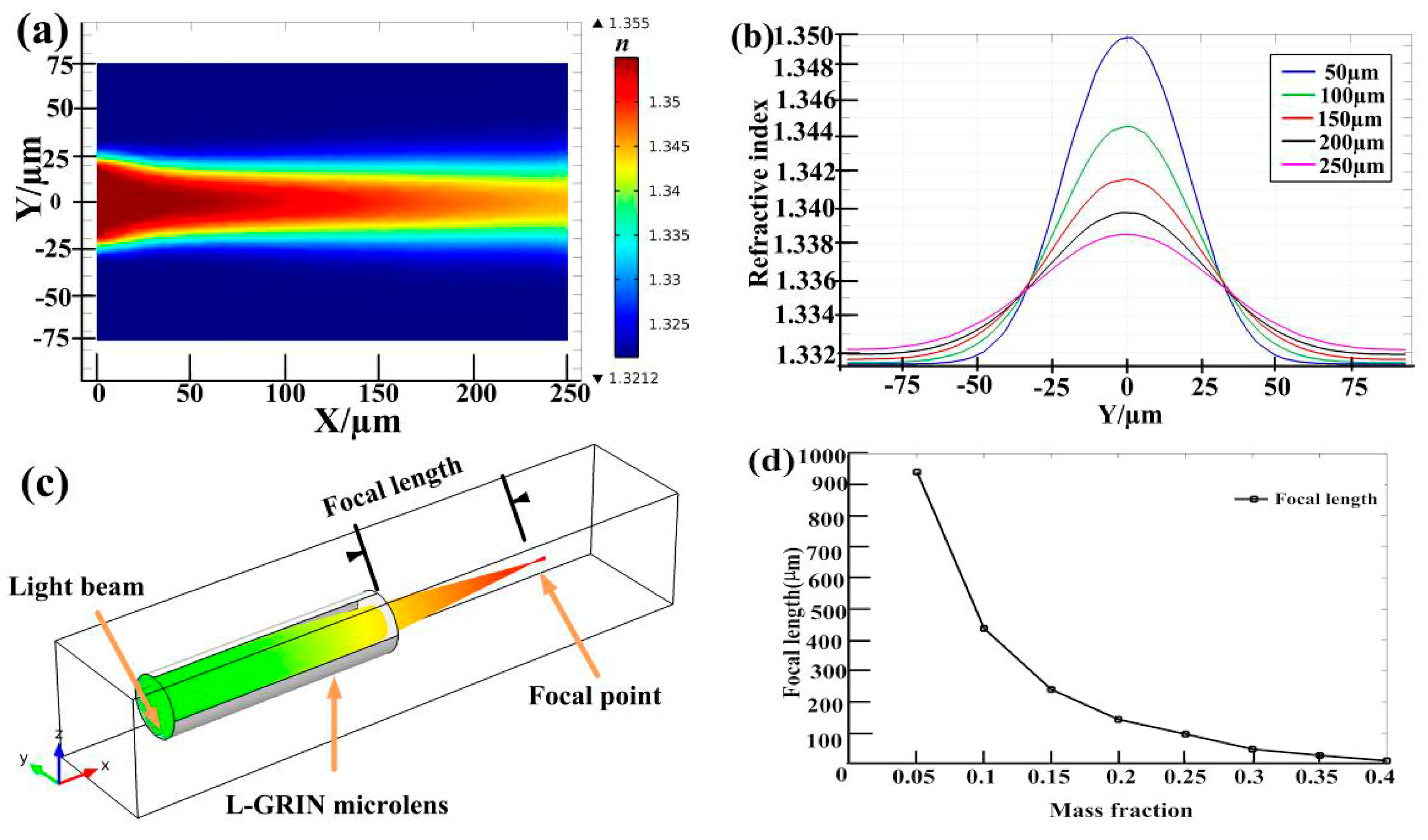
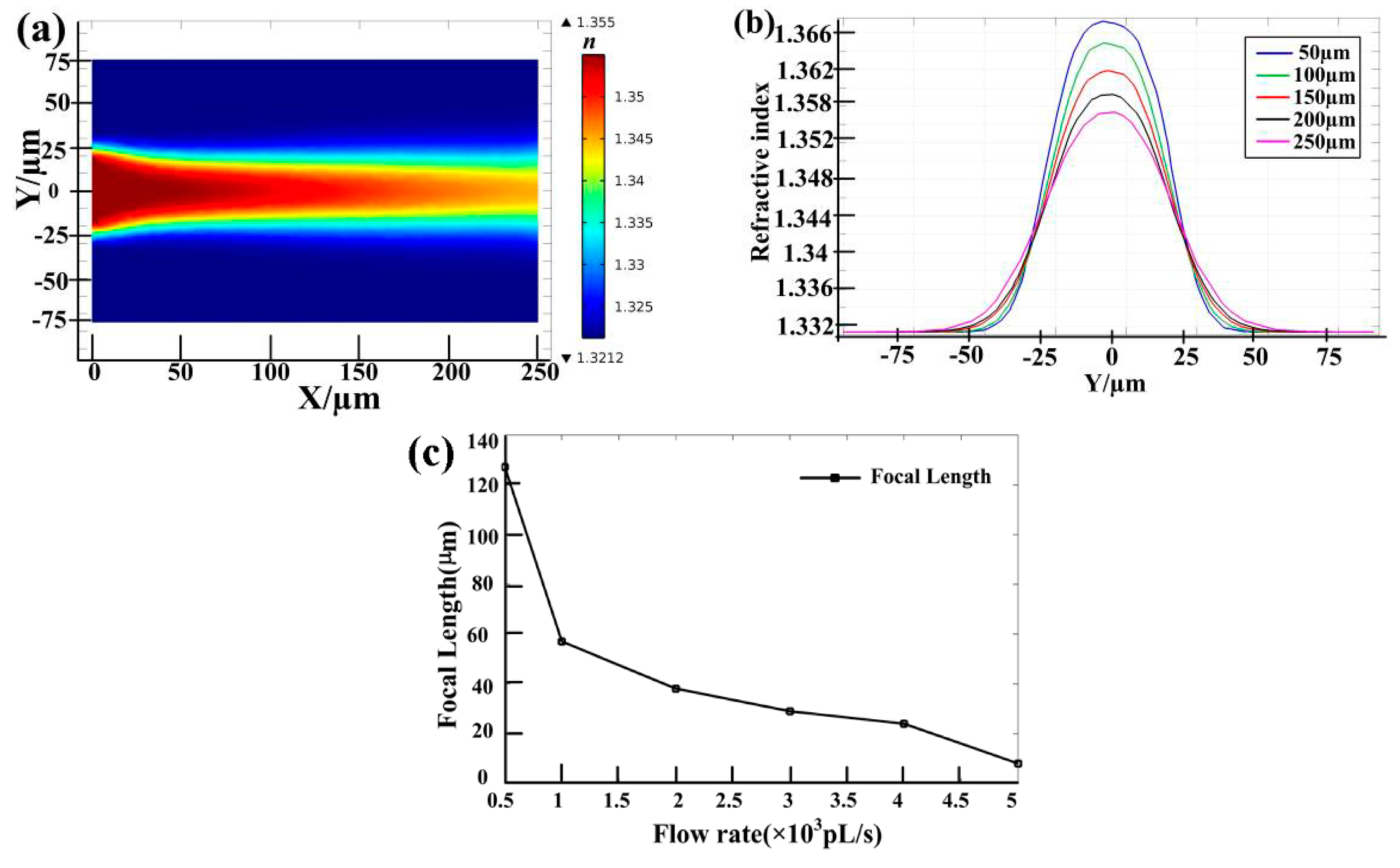
Because of the decisive effect of the convection-diffusion process on the refractive index profile of the L-GRIN microlens, the average velocity
U and the diffusion coefficient
D, which are also found to vary with the concentration
C and temperature, are important parameters for tunable focusing. For example, the diffusion coefficients between DI water and ethylene glycol are 3.75 × 10
−10 and 1.17 × 10
−9 m
2/s with different mass fractions of 0.025 and 0.95 for ethylene glycol [
24]. In addition, when the temperature varies from 30 to 50 °C, the diffusion coefficient changes from 3.15 × 10
−10 to 6.45 × 10
−10 m
2/s with a fixed mass fraction of 0.8 for the ethylene glycol [
25]. Due to the temperature of liquids usually being stationary during the convection-diffusion process, thediffusion coefficient
D, concentration
C and average velocity
U of liquids are the main influence factors for adjusting the focusing performance of the L-GRIN microlens. It was found by simulations as follows that an adjustable focal length could be achieved under a relatively lower average velocity while the size of the focal spot had to be tuned at a high enough average velocity. Therefore, both the focal length and the focal spot of the output beam can be adjusted by carefully controlling the average velocity of the liquids. Suppose that the DI water and ethylene glycol solution are chosen as the cladding and the core liquids, respectively, and two cases of the average velocity with relative slip and without relative slip between the core and cladding inlet are disscused. The subsequent discussion will be focused on how the adjustment of the output beam will be implemented by adjusting these influence factors.
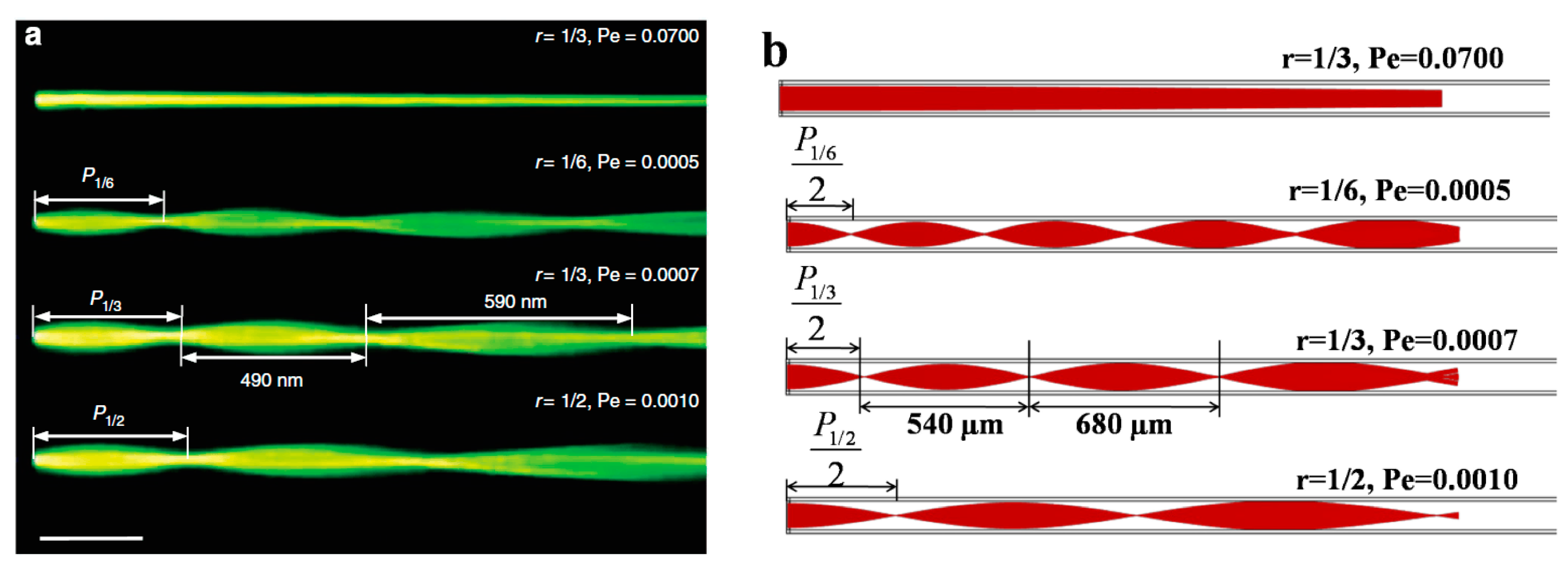
In order to validate our numerical simulation, the comparison between the observed light propagation in Reference [
23] and our simulation results was illustrated in
Figure 2.
Figure 2a shows light propagation in the optofluidic waveguides under different fluidic conditions, and
Figure 2b shows our simulation results at the same fluidic conditions. When driven at a highflow rate of
Qclad = 50 μL·min
−1 (
Pe = 0.07), the light propagates in a straight line and shows no focusing effect. In contrast, at a low flow rate of
Qclad = 0.5 μL·min
−1, the light exhibits curved-ray trajectories and converges repeatedly for different core widths,
r = 1/6, 1/3 and 1/2 (
Pe = 0.0005, 0.0007 and 0.001, respectively) [
23].
Figure 2.
(
a) Observed light propagation under different flow conditions [
23]. At a high flow rate of
Qclad = 50 μL·min
−1, the light is confined in the core due to the step-index distribution. At
Qclad = 0.5 μL·min
−1, the diffusion-induced gradient of the refractive index causes the light to repeatedly merge. With increasing
r, the length of the first section becomes larger, for example
P1/6 = 270 μm,
P1/3 = 300 μm and
P1/2 = 340 μm. The focusing period also increases; for example, the first period for
P1/3 is 300 μm, the second is extended to 490 μm and the third is 590 μm. (Scale bar equals 300 μm.)(
b) Simulated light propagation under the same flow conditions. With increasing r, the length of the first section becomes larger, for example,
P1/6 = 300 μm,
P1/3 = 360 μm and
P1/2 = 410 μm. The focusing period also increases; for example, the first period for
P1/3 is 360 μm, the second is extended to 540 μm and the third is 680 μm.
Figure 2.
(
a) Observed light propagation under different flow conditions [
23]. At a high flow rate of
Qclad = 50 μL·min
−1, the light is confined in the core due to the step-index distribution. At
Qclad = 0.5 μL·min
−1, the diffusion-induced gradient of the refractive index causes the light to repeatedly merge. With increasing
r, the length of the first section becomes larger, for example
P1/6 = 270 μm,
P1/3 = 300 μm and
P1/2 = 340 μm. The focusing period also increases; for example, the first period for
P1/3 is 300 μm, the second is extended to 490 μm and the third is 590 μm. (Scale bar equals 300 μm.)(
b) Simulated light propagation under the same flow conditions. With increasing r, the length of the first section becomes larger, for example,
P1/6 = 300 μm,
P1/3 = 360 μm and
P1/2 = 410 μm. The focusing period also increases; for example, the first period for
P1/3 is 360 μm, the second is extended to 540 μm and the third is 680 μm.
Similarly, the length of the first section increases with the core width and decreases almost linearly with the flow rate of the core fluid in both figures. However, when examining the light propagation pattern in detail, it is found that the self-focusing period is chirped such that the focusing period increases. For instance, as shown in
Figure 2a, the first period for
P1/3 is 300 μm, the second is extended to 490 μm, and the third is 590 μm, owing to the diminishing bidirectional gradient contrast downstream as a result of diffusion [
23]. Furthermore, the first period for
P1/3 is 360 μm, the second is extended to 540 μm, and the third is 680 μm in
Figure 2b. The small difference in focus length maybe due to the difference between two structures, and the change trends are the same. The match between the experimental results in Reference [
23] and our simulation results illustrated that the follow-up simulations could be trusted.