The Five Ws (and one H) of Super-Hydrophobic Surfaces in Medicine

Abstract

Super-hydrophobic surfaces (SHSs) are bio-inspired, artificial microfabricated interfaces, in which a pattern of cylindrical micropillars is modified to incorporate details at the nanoscale. For those systems, the integration of different scales translates into superior properties, including the ability of manipulating biological solutions. The five Ws, five Ws and one H or the six Ws (6W), are questions, whose answers are considered basic in information-gathering. They constitute a formula for getting the complete story on a subject. According to the principle of the six Ws, a report can only be considered complete if it answers these questions starting with an interrogative word: who, why, what, where, when, how. Each question should have a factual answer. In what follows, SHSs and some of the most promising applications thereof are reviewed following the scheme of the 6W. We will show how these surfaces can be integrated into bio-photonic devices for the identification and detection of a single molecule. We will describe how SHSs and nanoporous silicon matrices can be combined to yield devices with the capability of harvesting small molecules, where the cut-off size can be adequately controlled. We will describe how this concept is utilized for obtaining a direct TEM image of a DNA molecule.

1. Introduction

Super-hydrophobic surfaces (SHSs) are bio-inspired, artificial microfabricated interfaces, in which a pattern of cylindrical micropillars is modified to incorporate details at the nanoscale [1,2,3]. For these systems, the integration of different scales translates into superior properties, including a vanishingly small friction coefficient, on account of which biological solutions of medical interest can be manipulated.

The five Ws, five Ws and one H or the six Ws (6W) are questions whose answers are considered basic in information-gathering. They are often mentioned in journalism, research and police investigations. The 6W task seeks to summarize the information essential to understanding a phenomenon by distilling it into the answers to the 6W questions: why, who, what, where and when; where the H stands, instead, for how [4]. In the above description, these five questions are presented in an order that seems logical to the authors; in practice, the approach becomes iterative: it does not matter much where you begin, since answering one question often reveals important aspects of the other questions that you had not yet considered.

In what follows, super-hydrophobic surfaces and some of the most promising applications thereof are reviewed following the scheme of the 6W. The Introduction is dedicated to a discursive articulation of these six theses. The experimental section presents and describes a family of different devices and the nanotechnology methods required for their fabrication. The modeling and theory paragraphs describe the physics of small drops on a surface, providing the mathematical tools for the rational design of those systems. In the Results, some of the most recent biological applications of SHSs are recapitulated, especially pertaining to the early detection of tumors.

Why: A large number of studies confirm that blood contains thousands of intact proteomic molecules coming from the tissues or as products of enzymatic proteolysis in the circulating flux. What has been until only recently considered as a “waste deposit” might reveal itself as an extraordinary mine of data for the evaluation of the health status of tissues or districts of the human body. Single, exclusive markers, or rather, biomarker patterns, integrated with each other, express a high sensitivity and specificity and may be employed to discriminate diseases [5,6]. The major drawback of this approach is the very low abundance of the proteins of study [5,6]. Very rarely, biologists deal with or are able to detect single molecules, and hence, their understanding of molecular events is blurred by a poor experimental resolution. This is the reason why there is an increasing demand for high quality biomolecular sensors. The ability to perform sensing measurements at femto- or atto-molar sample concentrations with single molecule resolution is an outstanding achievement in the field of biosensors. The past decade has seen tremendous progress in the development of micro- and nanoscale sensors with impressive performance. Detection limits down to the single-molecule level have been achieved, with potential applications ranging from the early diagnosis of disease to the fast sequencing of genomes. However, in practical applications, transporting target molecules and particles in extremely dilute solutions to these tiny sensors is a significant challenge that often involves impractical timescales [7]. The physics of diffusion governs the random movement of molecules in a solution and their binding kinetics to the sensor. At ultralow concentrations, it takes an unacceptably long amount of time for a molecule to diffuse to the sensor for detection, which may render the sensor impractical [7,8]. Scientists are now attempting to minimize the time taken for target molecules to bind to such sensors.

Who: Super-hydrophobic surfaces (SHSs) are bio-inspired, nanotechnology artifacts, which feature a reduced friction coefficient, whereby they can be used for a variety of practical applications [1,3,9]. SHSs are typically fabricated using micro- and nano-fabrication techniques, in which a two-dimensional lattice is created by the repetition, or tessellation, of a regular pattern or motif. In doing so, an artificial, periodic pattern is obtained, where the smallest unit of the pattern can be a silicon or polymeric cylindrical micropillar (Figure 1).

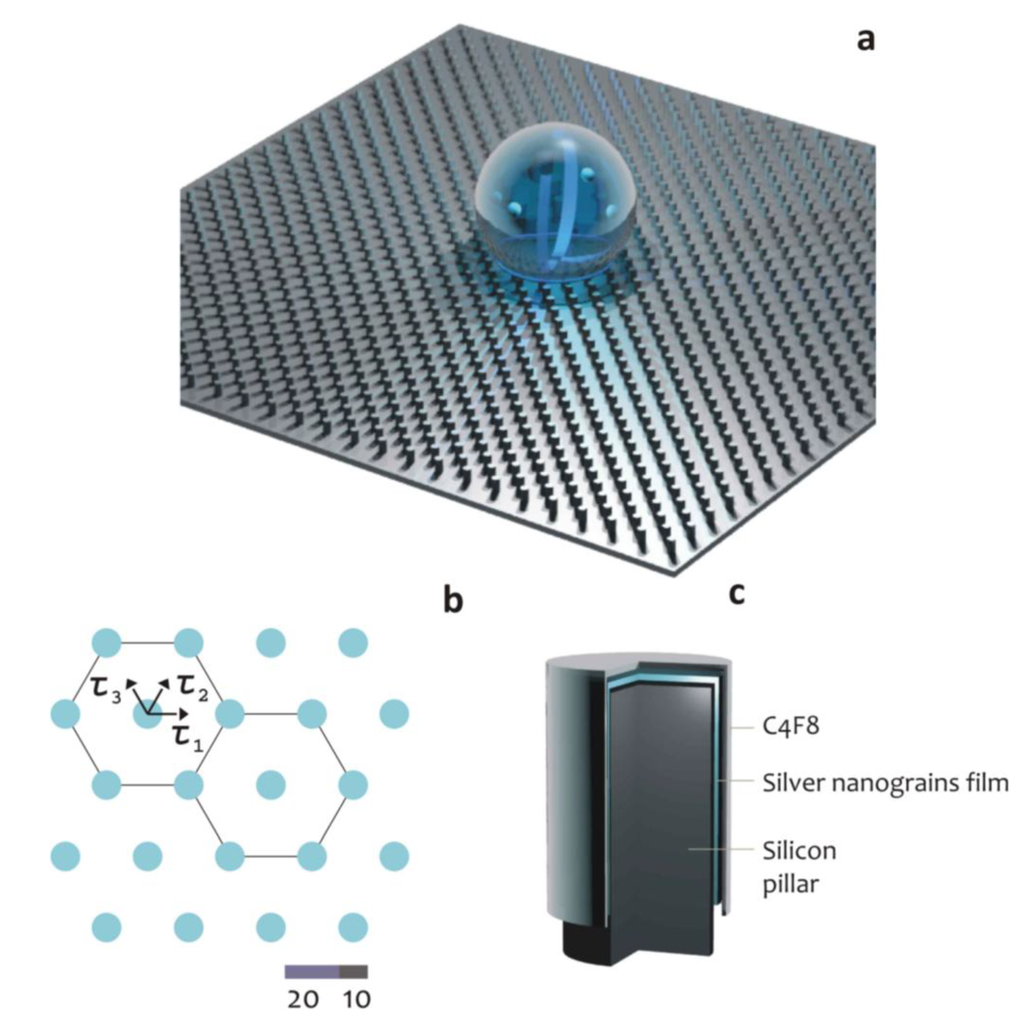
Figure 1. Cartoon representation of a super-hydrophobic surface (a); here, the pattern at the microscale recovers a hexagonal periodic lattice (b); each silicon micropillar is covered by features at the nanoscale that can be, for instance, an array of silver nanograins; the entire device is covered by a Teflon thin film, which assures hydrophobicity (c).

Figure 1. Cartoon representation of a super-hydrophobic surface (a); here, the pattern at the microscale recovers a hexagonal periodic lattice (b); each silicon micropillar is covered by features at the nanoscale that can be, for instance, an array of silver nanograins; the entire device is covered by a Teflon thin film, which assures hydrophobicity (c).

The most practical property of SHSs is a reduced friction coefficient that is responsible for a number of advantages over conventional surfaces, namely: (i) the geometry and positioning of liquid droplets can be easily controlled; (ii) micropatterns can be prefilled with aqueous solutions without the need for surfactants; (iii) droplets can be positioned extremely close to each other on a surface; (iv) super-hydrophobic regions can be used to create patterns to control bio-adhesion; and (v) the discontinuous dewetting effect arising from the extreme difference in contact angle hysteresis between the super-hydrophilic and super-hydrophobic regions can be used to passively dispense aqueous solution into the super-hydrophilic spots without wetting the super-hydrophobic background.

Those advantages, in turn, may be exploited for applications spanning specific areas of the physical, engineering and biological sciences, sometimes bridging traditional disciplines. These applications comprise, but are not restricted to: the pattering of complex geometries with liquids [10,11], the separation of oil from water [12], anti-biofouling coatings [13,14], controlling the adhesion of proteins or bacteria on a surface [15,16,17,18], guiding the aggregation of primary neurons into three-dimensional architectures [19], imaging DNA fibers and gaining exclusive information of the double helix [20] and advances in the very large area of cell microarray technology [21]. Perhaps more important than all this, SHSs can be utilized for efficiently delivering molecules in femto-/atto-molar solutions to a nanoscale plasmonic sensor [7,8,22,23,24], thus bypassing the diffusion limit. This technique involves the integration of plasmonic structures into super-hydrophobic surfaces.

What: Hydrophobic materials repel water; a well-known, natural example of a water repellent material is the lotus leaf: if deposited upon this, a water droplet would assume the form of a sphere without wetting or spreading on the surface [1,2]. Inspired by the lotus effect, we developed super-hydrophobic surfaces that mimic the morphology of the lotus leaf using techniques, such as nano-patterning, polymer coating, plasma etching and the electrochemical assembly of nanoparticles [22,23,24]. We created such a super-hydrophobic surface from arrays of silicon micropillars and optimized the size, periodicity and aspect ratio of those pillars to enable a large contact angle and low-friction forces that were independent of the sample droplet radius. Therefore, we allowed a water droplet containing the molecules of interest to evaporate and slide on the super-hydrophobic surface, leaving very little solution behind. As it evaporated, the solution became increasingly concentrated, until the droplet finally collapsed onto one of the pillars, thus confining the solute to a suspended region of a few square micrometers. In tests with rhodamine 6G molecules as a solute, we found that our silicon pillar surface provided a concentration factor 10,000 times that of a conventional, flat plasmonic substrate [22]. With λ-DNA molecules, we showed that DNA filaments cross-link to form a network that covers several pillars [22]. As a result, this simple “drop and dry” scheme provides the good localization and immobilization of molecules for fluorescent and Raman spectroscopic measurements. We developed this concept even further, as reported in the remainder of the paper. Some of these developments are reported in the Results section.

Where: Although Raman spectroscopy is a very useful tool for detecting and identifying the molecular constituents of a sample, the Raman signal is intrinsically very weak at the few-molecule level, which makes it difficult to extract from any background noise. Strong localization of the molecules during the drying process enhances the Raman spectroscopic signature. To boost the Raman signal further, we integrated a range of plasmonic structures into their super-hydrophobic silicon pillars. These metal structures, presented in Figure 2, and described in the Experimental Section, serve as “hot spots” that intensify the local electric fields and consequently enhance the Raman signal by several orders of magnitude. To put it in a nutshell, we combined these surfaces with bio-photonic devices to obtain an integrated lab-on-a-chip system, where, at the first stage, the SH surface would transport the analytes of interest into a small area, and at the second stage, the biosensors would permit, in that area, the detection of the solute with the resolution of a single molecule.

Figure 2. SEM micrographs of the textures of silicon micropillars (a,b); the top of those pillars can be tailored with random patterns of silver nanoparticles (c,d) or regular arrays of metallic nanodots (e,f) for surface-enhanced Raman scattering (SERS).

Figure 2. SEM micrographs of the textures of silicon micropillars (a,b); the top of those pillars can be tailored with random patterns of silver nanoparticles (c,d) or regular arrays of metallic nanodots (e,f) for surface-enhanced Raman scattering (SERS).

How: Small drops of de-ionized water, containing the moieties at study, should be positioned on the substrate and allowed to evaporate. In sight of a simple balance of forces, the line of contact at the solid interface would recede with time, and thus, the footprint of the drop would also gradually reduce. When the drop gets sufficiently small, a transition to a more stable state occurs, whereby the drop is firmly attached to the substrate, and the scale-down of the area of contact is prevented. This results in the accumulation of a few molecules into a very small region, an increased density and the attainment of the limits of detection.

When: The droplet evaporation time, which takes from a few seconds to several minutes, depending on its size, dramatically shortens the long waiting time of hours or even days for the traditional diffusion process. The transport of a trace inside a slowly evaporating drop on a substrate and the consequent particle deposition is a complex phenomenon that has generated interest for potentials in applications, such as molecular sieves [25], optoelectronic devices [26], drug delivery [27,28] and for the absorption and separation of the low molecular weight content of human plasma [29,30,31]. Despite its complexity, to the first approximation, this mechanism can be regarded (and analyzed) as the superposition of simpler effects. These effects are: (i) the displacement of particles inside an evaporating drop driven by convection and diffusion [32,33]; and (ii) the translocation or capture of a molecule through a nanopore [30,34,35,36].

In brief, the aim of this paper is to expound the contributions that the integration of the super-hydrophobic theme with nano-geometry-based sensors (optical sensors) can possibly offer to clinical medicine, specifically in the discipline of early diagnostics. This is technically viable only if an array of silicon pillars is used like a workable platform, into which micro- or nano-lenses are implanted, and this is described in the rest of paper. That is why we shall mainly focus on artificial, ordered arrays of cylindrical micropillars, disregarding other, still mirable, approaches. This essay is dedicated to the articulation of this specific perspective. It is not a review of the many important contributions that have formed and made scientifically significant the field of super-hydrophobicity.

In the literature, one may find several examples of super-hydrophobic devices created out of plastic, cellulose or other natural (and in-expensive) materials; nevertheless, they are often limited to the still important issue of controlling and driving a droplet in a plane, and they do this either by: (i) changing the curvature/shape of patterns of ink on a flexible paper [37,38]; or (ii) fabricating surfaces with heterogeneous contact angle hysteresis [39]; and, this enables the splitting of the droplet on the surface. The described devices depart from ours in that they do not present any hierarchical nanostructure (nano-lenses) that may manipulate the electromagnetic field around them. The novelty of our approach is represented by the combined use of the super-hydrophobic scheme and nano-optics, which may resolve the issue of detecting biomolecules in an extremely low diluted solution; in this sense, the super-hydrophobic theme is only half of the story.

2. Experimental Section

A large variety of different super-hydrophobic devices is reported in the literature. Those surfaces typically comprise micropillars disposed on the substrate to form a regular hexagonal motif; in some cases, the periodicity of the pillars may be broken to introduce an increased degree of complexity into the geometry of the devices. The pillars are therefore modified to incorporate details at the nanoscale, ranging from bio-photonic devices to nanoporous silicon films. Those extra non-continuous scales would provide the device with additional, sometimes surprising, functions. Moreover, on account of their hierarchical structures bridging different length scales, those devices exhibit an increased hydrophobicity with contact angles as large as nearly 170°. Mathematical modeling and computer simulations can be conveniently used to describe the physics of small drops on a surface; those models, in turn, can be utilized to fabricate the devices on the basis of rational design.

Small drops of DI water containing infinitesimal amounts of analytes are gently positioned upon the surfaces, and the entire process of evaporation is followed over time. The process enables one to concentrate very tiny amounts of agents over micrometric areas. The evaporation process is performed in a clean room to reduce the presence of external contaminants and lasts approximately 30 min. The residual solute may be observed using scanning electron microscope (SEM), transmission electron microscopy (TEM), fluorescent microscopy and Raman spectroscopy techniques.

2.1. SHSs Tailored with Nanosensors

Artificial super-hydrophobic textures comprise a periodic hexagonal lattice of cylindrical silicon (Si) micropillars with a certain diameter and pitch. Nanosized geometries appropriately positioned on the pillars would assure giant surface-enhanced Raman scattering (SERS) enhancement [22,24]. (100) silicon wafers are cleaned with acetone and isopropanol to remove possible contaminants and then etched with a 4% wet hydrofluoric acid (HF) solution. The wafers are then rinsed with DI water and dried with N2. Standard optical lithography techniques are employed to dig out regular arrays of disks within a layer of positive resist that was precedently spin-coated onto clean silicon wafers. Electroless deposition techniques are employed to grow silver nanograins within the holes. Upon removal of the residual resist with acetone, a Bosch reactive ion etching process is utilized, whereby the final structures were obtained in the form of cylindrical pillars with an aspect ratio greater than 2. The electroless grown Ag layer served as a mask during the reactive ion etching (RIE) process, while its characteristic granular structure allowed for the enhancement of the SERS signal. The substrates, as a whole, are then covered with a thin (few nm) film of a Teflon-like (C₄F₈) polymer to assure hydrophobicity. The masks necessary for optical lithography are typically fabricated using standard electron beam lithography methods. Figure 2 reports some examples of the final devices. Electroless deposition is a technique whereby metal ions are reduced as atoms on specific patterned sites of a reducing surface, in our case, a silicon dangling bonding surface, to form nanoparticulates with the desired chemical and structural characteristics. The electroless deposition on a substrate is based on an autocatalytic or a chemical reduction of aqueous metal ions. This process consists of an electron exchange between metal ions and a reducing agent. In this work, Si substrate was used itself as a reducing agent. A fluoridric acid (HF) solution containing silver nitrate (AgNO₃) is used, where Ag was reduced to metal form by the Si substrate oxidation. In particular, the patterned silicon wafer is dipped in a 0.15 M HF solution containing 1 mM silver nitrate for 60 s at a constant temperature T = 313 K. After the growth process, the silicon wafer is rinsed with water and dried under nitrogen flux. The driving force in this process is the difference between redox potentials of the two half-reactions, which depends on solution temperature, concentration and pH. Consequently, these parameters influence the particles size and density. In the deposition process, the kinetics of chemical reaction is some two orders of magnitude faster than diffusion; therefore, a diffusion-limited aggregation model can be utilized to reproduce the results of the process [40].

2.2. SHSs Covered with Nanoporous Silicon Films

In some cases [41], the surface of the silicon pillars is treated to incorporate nanoporous silicon (NPSi) films (Figure 3). NPSi films are prepared upon the pillars through a process of Si anodic dissolution. While simple, untreated Si is intrinsically hydrophilic, and NPSi manifests an apparent contact angle as large as 130°; these micro-/nano-hierarchical structures reveal an increased contact angle approaching 170°, and this may be explained by a dual scale roughness, as reported in [42,43,44,45], and recapitulated in the Theory Section. The major advance of these devices is the simultaneous use of super-hydrophobicity and NPSi films. The nanoporous matrix furnishes to the device the capability of extracting the low molecular weight (LMW) content of a solution, that is a potential source of diagnostic markers for diseases [5,6]. PSi substrates with a pore diameter lower or equal to 10 nm are obtained by Si anodization using an electrolyte mixture of HF, DI water and ethanol (by Sigma-Aldrich, Milan, Italy) (1:1:2, v/v/v). A constant current density of 20 mA/cm² for 5 min at 25 °C is applied. The photoluminescence properties of the PSi substrate are verified using an ultraviolet lamp, in the long wave ultraviolet limit.

Figure 3. Nanoporous silicon devices (a); the silicon micropillars (b) reveal, at smaller scales, pores with an average pore size of 10 nm (c–e).

Figure 3. Nanoporous silicon devices (a); the silicon micropillars (b) reveal, at smaller scales, pores with an average pore size of 10 nm (c–e).

2.3. AG NPs/Nanoporous SH Hybrid Devices

The scheme reported in the former paragraph was developed even further in [46]. Silver nanoparticles were implanted into the super-hydrophobic NPSi film to guarantee superior SERS capabilities (Figure 4). In doing so, multifunctional devices are obtained, revealing different functions. Those functions only arise due to the heterogeneous scales of the system and, namely, the micro, on account of which the substrate is super-hydrophobic, and the nano, which is the typical length scale of the pores and of the silver particles dispersed into the pores. In sight of its hierarchical nature, the device may serve as a biosensor with the ability of: (i) concentrating diluted solutions; (ii) transporting and selecting the biomolecules of interest to the active areas of the device; and (iii) analyzing these molecules with extreme accuracy. Chains of silver nanograins are implanted into the porous matrix using an electroless deposition process, as described in Section 2.1. Silver nanograins are obtained with an average dimension strictly smaller than the pore size.

Figure 4. Micro-textures of nanoporous silicon pillars where electroless silver nanoparticles are infiltrated into the pores. In (a), at a smaller scale, you may observe the micro-pillar covered with the nano-porous silicon film. In (b–e), at larger scale, you can notice the morphology of the nano-porous matrix and of the silver nano-particles infiltrated into the pores.

Figure 4. Micro-textures of nanoporous silicon pillars where electroless silver nanoparticles are infiltrated into the pores. In (a), at a smaller scale, you may observe the micro-pillar covered with the nano-porous silicon film. In (b–e), at larger scale, you can notice the morphology of the nano-porous matrix and of the silver nano-particles infiltrated into the pores.

2.4. TEM Transparent SHSs

The super-hydrophobic concept was utilized in a recent article to obtain a direct image of a DNA molecule [20]. Transmission electron microscopy (TEM) is a technique that allows imaging with intrinsic spatial resolution at the atomic scale. When working with few biomolecules, there are some factors that worsen the final resolution of the obtained images: (i) the poor phase (or absorption) contrast of atomic species constituting the molecule compared to that of the substrate where the molecule is sitting; and (ii) the tendency of the molecule to be rapidly damaged when investigated by a high energy electron beam.

Silicon micropatterned hydrophobic devices allow one to control the deposition of few DNA molecules, which can be suspended, or stretched, between two adjacent pillars. In creating several passing through the holes between the pillars constituting the super-hydrophobic surface (Figure 5), the free passage of the electron beam during TEM measurements (background free imaging) is allowed; in doing so, we circumvent the conventional TEM resolution limitations described above.

Super-hydrophobic (SH) surfaces are designed and microfabricated. These comprise silicon micropillars arranged to form a regular hexagonal motif (A); the devices are therefore modified to incorporate, throughout the substrate, a pattern of holes, B, conveniently aligned with the pillars, which would permit the passage of the electron beam. The process of the fabrication of these devices is basically reduced to: (i) creating Pattern A; (ii) creating Pattern B; and (iii) positioning, as precisely as possible, Pattern A with respect to Pattern B. Pattern A is realized following the methods described in Section 2.1. Pattern B is realized using a deep reactive ion etching (DRIE) process; where the diameter of the holes (6 μm) is sufficiently large to allow practical use in TEM imaging. In the fabrication, conveniently positioned on the substrate, a number of alignment markers are used as a reference for the correct positioning of the holes with respect to the pillars.

Figure 5. Super-hydrophobic surfaces are designed and microfabricated. These comprise silicon micropillars arranged to form a regular hexagonal motif; the devices are therefore modified to incorporate, throughout the substrate, a pattern of holes, conveniently aligned with the pillars, which would permit the passage of the electrons beam. Figure a–f reports the device’s geometry at different magnifications.

Figure 5. Super-hydrophobic surfaces are designed and microfabricated. These comprise silicon micropillars arranged to form a regular hexagonal motif; the devices are therefore modified to incorporate, throughout the substrate, a pattern of holes, conveniently aligned with the pillars, which would permit the passage of the electrons beam. Figure a–f reports the device’s geometry at different magnifications.

2.5. Non-Periodic SHSs

In all of the cited examples, the pattern of the pillars is periodic, that is, the substrate can be obtained as the repetition of a primitive cell, where the cell is the basis for the lattice. The disadvantage of regular arrays of pillars is that the analytes, upon evaporation, would randomly target the substrate, with a lack of precision in positioning the species of interest on specific points of the surface. This limitation can be circumvented on introducing gradients of wettability in the pattern [47]. This is practically done realizing a non-periodic array of micropillars, that is, a distribution, where the pitch, δ, between the pillars is not constant, and it would instead smoothly transition from an external region, where δ is large, to an inner region, where δ is small (Figure 6). By doing so, the hydrophobicity would not be constant over the substrate; rather, some regions would be more hydrophilic than others; on account of this augmented hydrophilicity, a solute, upon evaporation, would preferentially target these hydrophilic regions, which would therefore be the active sites of the devices, and in these sites solely, superior nanosensors can be embedded. The fabrication of these surfaces is the same as that required for regular geometries, as in Section 2.1, except for the fact that the optical masks necessary for the lithographies are generated on the basis of a mathematical model described in [47]. The non-uniform profile of pillars can be obtained using a contraction, which is a mathematical operation that, on a metric space and with respect to a fixed point, would displace the pillars in a fashion that their mutual distance would vary following a certain law. The surface energy of the substrate can be therefore determined and, on deriving that with respect to space, the non-uniform field of forces exerted on the drop during evaporation. This has some similarity with the general theory of relativity, where mass warps space-time to create gravitational fields. Examples of super-hydrophobic devices with a variable pitch are shown in Figure 6.

Figure 6. In the figure are presented devices where gradients of wettability are artificially introduced into the pattern of pillars. This is practically done realizing a non-periodic array of micropillars, that is, a distribution where the pitch, δ, between the pillars is not constant, and it would instead smoothly transition from an external region, where δ is large, to an inner region, where δ is small. Figure a–c shows a non-uniform pattern of pillars with different magnifications and points of view.

Figure 6. In the figure are presented devices where gradients of wettability are artificially introduced into the pattern of pillars. This is practically done realizing a non-periodic array of micropillars, that is, a distribution where the pitch, δ, between the pillars is not constant, and it would instead smoothly transition from an external region, where δ is large, to an inner region, where δ is small. Figure a–c shows a non-uniform pattern of pillars with different magnifications and points of view.

2.6. Rational Design of SHSs

It is well known that the physics of micrometric or sub-millimetric drops is correctly governed by surface tension solely [48]. The angle of contact, θ, at the solid/air/liquid interface indicates the propensity of a droplet of whether wetting or not a surface. Surfaces where θ > 150° are super-hydrophobic. A drop of water, positioned on such surfaces, would maintain a quasi-spherical shape, with a contact angle at the air-solid interface that can be theoretically predicted with excellent accuracy. In the celebrated model of Cassie and Baxter, the wetting behavior of the surface is lumped in the sole parameter, ϕ, that is, the ratio of the solid to the total projected area [49]:

cosθ_c = −1 + ϕ(cosθ + 1)

(1)

at the limit of ϕ going to zero, ϕ→0, θ_c→180°, and the droplet would resemble a perfect sphere. For a periodic hexagonal lattice of cylindrical pillars, where the diameter, d, of the pillars and the distance, δ, between those pillars may be arbitrarily imposed, the fraction, ϕ, can be derived as ϕ = πd²/(d + δ)². If ϕ is small, and thus θ_c is large, the contact line would jump inward from a thread of pillars to another, while the drop evaporates. Therefore, in the first approximation, one would produce structures where the distance between the pillars is large and ϕ is small. Unfortunately, the collateral effect of small ϕ is that a drop would collapse at the early stage of evaporation. Equation (2), below, reveals the minimum radius of a drop before impalement, whereby an irreversible transition to a pinned state occurs. In this situation, no further contact area shrinkage is possible:

(2)

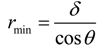
In what follows, a criterion is discussed that would guarantee the best trade-off between sufficiently dense forests of pillars, which prevent the early collapse of the drop and avoid dispersion, and diluted structures, which instead assure a large contact angle. Let the surface be patterned as to reproduce a regular lattice described by d and δ, where the significance of these symbols is given above. If d is fixed, then the system would be determined given the sole δ. The aim here is to determine the optimal δ that would induce large θ, while still retaining the advantages of a small r_min. To do this, we introduce the function, Ψ, which is the superposition of the two non-dimensional contributions Ψ = Ψ₁ + Ψ₂.

Ψ₁ accounts for the effects of the microstructure on the contact line, Ψ₁ = r/R, where R is the initial radius of the drop.

Ψ₂ accounts for the effects of the microstructure upon the smallest radius of contact before collapse:

(3)

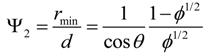
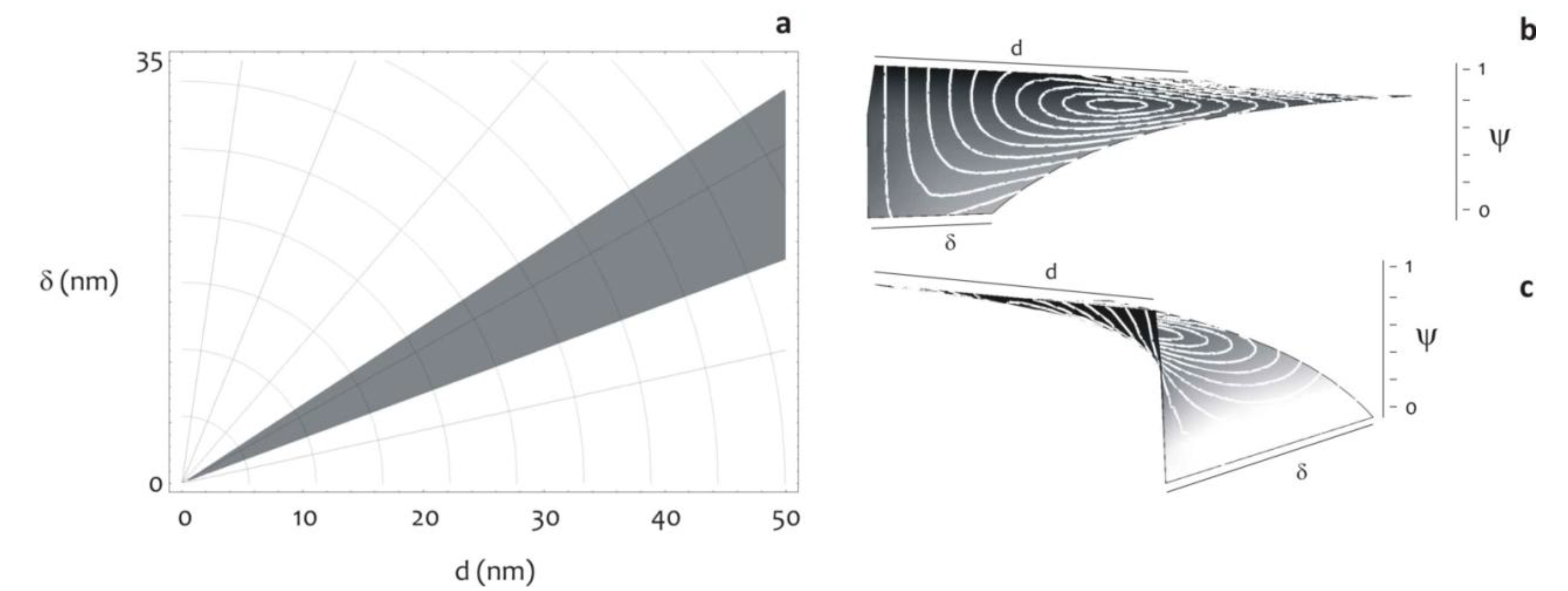
Ψ is not monotonic with respect to δ. A value of δ can be determined where Ψ attains a minimum (Figure 7), and this would the best gap for a fixed d. Figure 7 shows, in the plane d-δ, the area of optimal design according to this criterion.

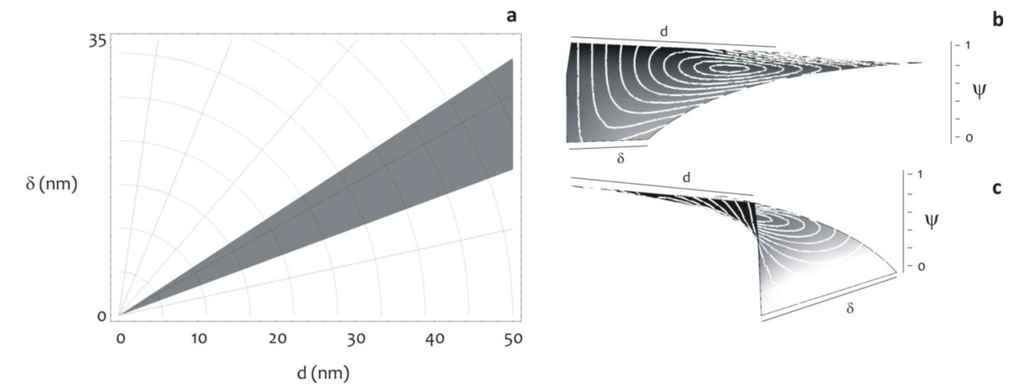
Figure 7. The diagram shows the region of optimal design, that is, the subset of pattern configurations, in terms of d and δ, which guarantee large contact angles, still retaining the advantages of a small radius of collapse (a). This working distance is obtained on minimizing the function, Ψ, as explained in the modeling section (b,c).

Figure 7. The diagram shows the region of optimal design, that is, the subset of pattern configurations, in terms of d and δ, which guarantee large contact angles, still retaining the advantages of a small radius of collapse (a). This working distance is obtained on minimizing the function, Ψ, as explained in the modeling section (b,c).

2.7. Non-Continuum Description of Hierarchical Hydrophobicity

In Section 2.3, we presented devices where the increased hydrophobicity depends on thin nanoporous films. Porous silicon, or nanoporous silicon (NPSi), is a form of Si containing a layer of nanosized pores artificially introduced in its microstructure, thus revealing an increased surface-to-volume ratio. NPSi exhibits certain promising properties, including highly controllable and reproducible pore size and distribution; bio-reactivity; biocompatibility; biodegradability in physiological environment; photo luminescence at room temperature and hydrophobicity [50]. Nevertheless, some NPSi-related phenomena are still not well understood or, at best, their explanation is controversial. This would be the case of the increased hydrophobicity of NPSi films, whereby the observed contact angle of a drop of water settles down to extremely high values, well beyond those predicted by Cassie–Baxter’s classical theories. Considering that those nanoporous surfaces have, on average, a porosity of about p = 0.4, expressed as the fraction of the volume of voids over the total volume, and that the porosity can be, in turn, rephrased in terms of ϕ as ϕ = 1 − p, it follows that for those NPSi films, ϕ = 0.6. Upon using this value in the classical Cassie and Baxter formula Equation (1), a contact angle as large as 95° is predicted, considerably smaller than that revealed by direct experiments, where θ instead approaches 140°. In [42], a new theory has been presented that explains this discrepancy. This theory explores the wettability mechanisms on a randomly patterned surface at a non-continuum level.

Fractals are mathematical objects that are too irregular to be described by conventional geometry. They all retain, to different extents, certain properties that may be reviewed as follows: (i) they reveal details on arbitrarily small scales (fine structure); (ii) they can be generated (and thus described) by short algorithms (perhaps recursively); (iii) they exhibit a fractal dimension, Df, strictly greater than the classical topological dimension. The latter property reserves particular attention, in that it claims that a surface, under a fractal point of view, may have a dimension, Df, even greater than 2, and the more Df is close to 3, the more the fractal set fills the space it is embedded in. On account of this, an NPSi surface, to an extent, depending upon its fractal dimension, would be hierarchical: thus revealing, on different scales, the same self-affine structure. We shall denote, here, with n, the scale factor (that is, the level of detail describing the set at study). Accordingly, the classical Cassie and Baxter expression for the contact angle, θ, may be rephrased in terms of a recursive function in, n [42]:

cosθ_n+1 = −1 + ϕ(cosθ_n + 1)

(4)

Notice that, for n = 1, Equation (4) recapitulates the classical Cassie and Baxter equation. While, the larger n, the more the substrate is hydrophobic. The issue, here, is identifying the correct n. To do this, the surface area magnification factor, σ (that, to a certain measure, is connected to the length of the profile under examination), is deduced according to two different procedures, and from the comparison of these, n would be determined. In the first approach, σ is expressed in terms of the fractals parameters Λ, λ and Df [42]:

(5)

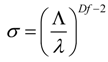
where Λ and λ are the upper and lower limits of the fractal behavior and Df has the meaning explained above. Notice that the parameters in Equation (2) may be deduced experimentally from the Power Spectrum PS, and thus, given an AFM profile, σ would be determined. In the second approach, the definition of σ is used:

(6)

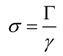
In Equation (6), γ is a length of base (that is, the length of the profile in the continuous limit n = 1), while Г is the fractal, actual length of the profile. On expanding Equation (6), one would obtain:

(7)

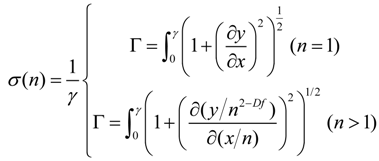
Additionally, on comparing Equations (5) and (7), one would obtain the right n to use in Equation (4).

3. Results

3.1. SEM Verification of the Samples

The devices presented heretofore were verified against the deposition, concentration and detection of a few molecules of Rhodamine 6G (R6G). R6G was used for the evaluation of the devices in that its utilization in biotechnology applications is very well assessed; it is a supplement to fluoresceins, as it offers longer wavelength emission maxima; and it is conveniently and extensively used for standard and non-standard labelling essays. Solutions were prepared containing R6G molecules with a concentration as low as 10⁻¹⁸ M. Evaporation processes of small drops of solution were followed over time until an irreversible transition to a pinning state occurred. Few molecules were conveniently forced to confine into a small area, at the limit, upon a single pillar. Figure 8 shows an array of SEM images of the residual solute of R6G at different magnifications ranging from 150× to 2500×. The initial footprint of the drop measures up to about 1.6 mm, and on average, 1.2 mm, while the solution, at the final stage of the process, sediments in a bounded region sized a few tens of microns or less (Figure 8b–d) and, in some cases, upon one single pillar (Figure 8e). Considering bi-dimensional scale effects solely, the device is capable of concentrating a solution some (1200/40)²~10³ times. More importantly, all the deposits are suspended upon the pillars, the residual R6G is arranged in complex forms or agglomerates that wrap the pillars, connecting them one to the other, without touching the bottom of the substrate.

Figure 8. SEM micrographs showing the concentration ability of super-hydrophobic surfaces (SHSs). At the end of an evaporation process, a few molecules of solute are forced into a micrometric area; in this case, Rhodamine 6G, as it is used as a solute. From a–f, you can notice the residual solute upon evaporation, suspended upon few pillars. In some cases, as in f, the residue links adjacent pillars.

Figure 8. SEM micrographs showing the concentration ability of super-hydrophobic surfaces (SHSs). At the end of an evaporation process, a few molecules of solute are forced into a micrometric area; in this case, Rhodamine 6G, as it is used as a solute. From a–f, you can notice the residual solute upon evaporation, suspended upon few pillars. In some cases, as in f, the residue links adjacent pillars.

3.2. Confocal and SERS Measurements of the Samples

The evaporation sequence of a drop upon a super-hydrophobic surface is reported in (Figure 9a–c), where the volume of the solvent steadily diminishes with the time parameter, t, varying from t = 0 min, in Figure 9a, to t = 30 min, in Figure 9c. This scheme allows one to concentrate a few molecules in a restricted area, as reported in the SEM images above. Fluorescent images in (Figure 9d–f) would prove that the identification of a residue, such as R6G, is correct, and it is not instead constituted by debris or other refuse. The intensity of fluorescence is directly proportional to the quantity of substance deposited on the pillars, and thus, in the central part of the substrate, the amount of R6G is higher and diminishes as we move towards the sides. Notice the high degree of precision with which the intensity of the signal of fluorescence recovers the mass of the solute distributed upon the substrate. Micro-Raman mapping measurements (Figure 9g–i) were performed to further substantiate the method. The mapping analysis was performed by referencing the band centered at 1650 cm⁻¹. In the figures, mapping images in surface mode are overlapped onto the scanning area, and this clearly highlights the variation of intensity as a function of the position within the area of interest. Figure 9g–i shows measurements for an initial concentration of 10⁻¹⁸ M, and in the present case, the Raman signal comes prevalently from the central region of the deposit, as expected.

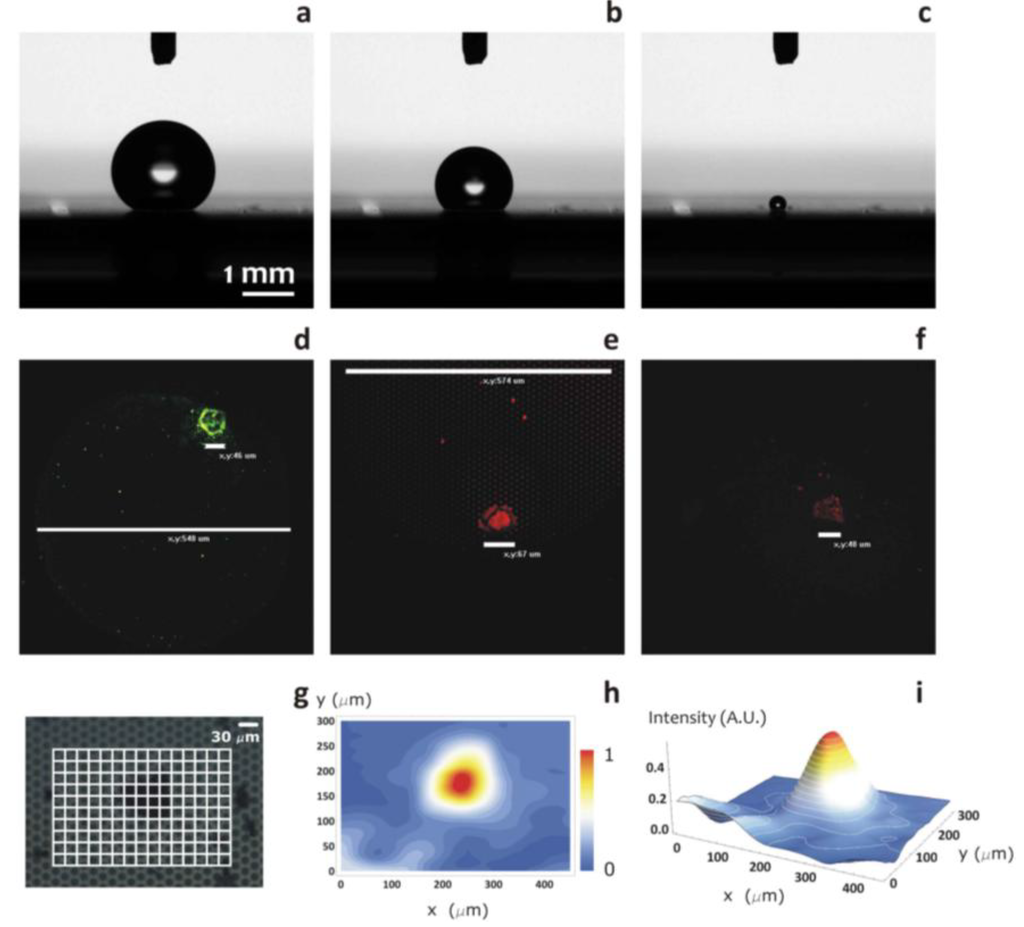
Figure 9. Droplet evaporation scheme showing the volume evolution of a drop on a super-hydrophobic surface over time (a–d). Fluorescent images (d–f) prove that identification of the residue as R6G is correct, and it is not instead constituted by debris or other refuse. The intensity of fluorescence is directly proportional to the quantity of substance deposited on the pillars, and thus, in the central part of the substrate, the amount of Rhodamine 6G (R6G) is higher and diminishes as we move towards the sides. Raman SERS measurements of the samples (g–i).

Figure 9. Droplet evaporation scheme showing the volume evolution of a drop on a super-hydrophobic surface over time (a–d). Fluorescent images (d–f) prove that identification of the residue as R6G is correct, and it is not instead constituted by debris or other refuse. The intensity of fluorescence is directly proportional to the quantity of substance deposited on the pillars, and thus, in the central part of the substrate, the amount of Rhodamine 6G (R6G) is higher and diminishes as we move towards the sides. Raman SERS measurements of the samples (g–i).

3.3. TEM Measurements of DNA fibers

Here, we show the potentials of SHSs in imaging single filaments of DNA using transmission electron microscopy (TEM) techniques. These results have been presented in [20]. The preparation in view of the TEM imaging was obtained by allowing the water to evaporate from the original liquid sample. The super-hydrophobic surface was treated in a way that the adhesion force between it and the water was very low (a friction coefficient of about 0.02), and during the evaporation, pinning of the drop was avoided. As a result, DNA molecules could be deposited, suspended and well tensed between the pillars, and more importantly, several DNA bundles resulted in being suspended in correspondence with the holes Figure 10. The suspended DNA bundles have a well-reproducible diameter, between eight and 200 nm. In Figure 10e, DNA bundles with strong mechanical stability under an electron beam up to 100-keV accelerating energy and beam current in the pA range are shown. This method was used in [20] to image in detail the 10 periods of DNA, where the period measures 2.7 ± 0.2 nm, corresponding to that known for ds λ-DNA in the A conformation.

Figure 10. Super hydrophobic surfaces (a,b) with very low adhesion forces allow one to avoid the pinning of the drop during evaporation. As a result, DNA molecules are deposited, suspended and well tensed between the pillars (a), and more importantly, several DNA bundles resulted in being suspended in correspondence with the holes (c–e).

Figure 10. Super hydrophobic surfaces (a,b) with very low adhesion forces allow one to avoid the pinning of the drop during evaporation. As a result, DNA molecules are deposited, suspended and well tensed between the pillars (a), and more importantly, several DNA bundles resulted in being suspended in correspondence with the holes (c–e).

4. Discussion

Surface plasmons are waves that propagate along the surface of a conductor. By altering the structure of a metal’s surface, the properties of surface plasmons—in particular, their interaction with light—can be tailored, which offers the potential for developing new types of photonic devices. This could lead to miniaturized photonic circuits with length scales that are much smaller than those currently achieved [51]. Surface plasmons and the properties thereof may be directly correlated to Raman scattering. This effect is named after C.V. Raman, who experimentally discovered it in 1928 [52]. When light interacts with matter, it may scatter inelastically from vibrational quantum states. During that process, photons may lose energy to, or gain it from, vibrational excitations. A change in the photon energy must produce a concomitant shift in the frequency of the scattered light. While the Raman effect alone is relatively modest, and thus, it offers an effective, but limited instrument to investigate matter and the properties thereof, it may be artificially incremented by several orders of magnitude (to obtain a substrate-enhanced Raman scattering (SERS) effect) basically in two ways.

An increased Raman signal appears due to a magnification of both incident and Raman-scattered fields, an effect known as electromagnetic enhancement. Moreover, the electronic interaction between molecule and metal can modify the scattering process itself and produce an effectively larger cross-section than would occur by scattering light from the molecule alone, an effect known as electronic or chemical SERS. The total enhancement is a product of the two mechanisms. Here, we shall discuss the metal-radiation interaction mechanism solely.

In the close proximity of metal nanoclusters, field enhancement occurs because of the resonant interaction between the optical fields and surface plasmons in the metal [51,52,53]. In essence, the light from a laser beam excites the surface plasmons, which are collective oscillations of conduction electrons. Those plasmons then radiate a dipolar field. The coherent interaction of the incoming electric field with the dipolar field leads to a redistribution of electric-field intensities in areas around the metal clusters. A molecule nearby or adsorbed on the metal feels an enhanced excitation intensity. Therefore, its Raman-scattered field is enhanced in the same way that the incident laser field is. Indeed, one can liken the metallic clusters to tiny antennas that enhance and transmit the Raman-scattered light. The enhancement depends on the type of metal, its degree of roughness—the sizes and shapes of the clusters that form—and the frequency of the incident light [54,55,56]. In this scenario, the precise and tight control of the morphology of metallic structures at the nanoscale is a major requisite for the design of efficient SERS substrates.

The new revolution in nanoscience, engineering and technology is being driven by our ability to manipulate matter at the molecular, nanoparticle and colloidal level to create designer structures. The discovery and understanding of the fundamental principles of how nanoscale systems of building blocks assemble enables us to nano-engineer new materials, where their physical properties depend intimately on their structure [57]. The organization of individual building blocks into ordered structures is ubiquitous in nature and found at all length scales. Examples include simple and complex crystals in atomic systems, liquid and plastic crystals in molecular materials and super-lattices of nanoparticles and colloids. The formation of atomic materials structures can be rationalized, to the first approximation, from geometric considerations and from a delicate balance of entropy, diffusion, chemical and atomic forces [58,59,60]. Mechanisms that cause nanoparticles to assemble into near-ordered structures are desirable for the correct control of those forces and for the precise organization of these particles into inorganic super-clusters.

Those super-clusters, in turn, may be the constituents (the fundamental building blocks) of efficient SERS substrates, for which one should control as accurately as possible: (i) the size of the features, which should have a characteristic length scale comparable with λ/10 (λ is the electromagnetic wavelength); and (ii) the distance between the elementary nanostructures that, differently from size, should have a characteristic length scale comparable with λ/100. These two length scales are the reason why nanoplasmonics and nanofabrication are tightly connected [55].

While randomly rough surfaces still induce a sensible enhancement in the signal of the electric (E) field [23,61], regular geometries are the best building blocks for advanced optical devices, where a good theoretical control can be achieved for a desired optical response. For certain architectures, this response can be extremely strong, with |E|² enhancement up to six orders of magnitude [54,56,62,63,64,65,66,67]. Recalling that the Raman signal in SERS substrates scales with the fourth power of the electric field, similar geometries would guarantee a Raman increment of the order of 10¹², which is a giant enhancement of the spectroscopy signal, which would be sufficient to reveal, in theory, the signature of a single molecule. With unprecedented applications in fields spanning the physical and biological sciences, including the early detection of cancers or other pathologies, whose evolution in time is related to the release in blood of biomarkers in extremely low abundance ranges.

The fabrication of similar geometries is result that has been achieved. In Figure 2, Figure 4 and Figure 6 and the captions thereof, we report nano-lenses on a pillar surface, where those lenses are either disordered random ensembles of silver nanoparticles in a plane (Figure 2c,d, Figure 6), or ordered arrays of nanoparticles (Figure 2e,f) or networks of metal grains infiltrated in a matrix of nanoporous silicon. In all of the described cases, the size and spacing of the structures is controlled at the nanometer level. Similar nano-geometries were realized using electroless deposition methods, ultra-high resolution Electron Beam Lithography EBL pattering methods or a combination of these, as described in the Experimental Section and, in detail, elsewhere [55,68,69,70,71,72].

Nevertheless, the presented nanomaterials, while they are advanced in the terms of the overall architecture and potential use as nano-lenses, may be ineffective if utilized directly as biosensors, in that the transport of the target species towards the cited sensors, driven by diffusion, would take impractical (unacceptably long) time scales, and this has been scrupulously discussed in the Introduction. Thus, the efficiency of similar sensors is hampered by diffusion.

Recently, a breakthrough strategy has been proposed that delivers the promise to surpass the described limitation, where the adjective, breakthrough, is justified by the fact that a similar strategy relies on a mechanism that is completely different from either plasmonic resonance or diffusion.

Instead, it is based on non-wettable, super-hydrophobic materials.

In this paper, using the original scheme of the five Ws, we reviewed and commented on a new family of devices in which diverse sensitive nanomaterials (that are, silver nanoparticles, nanoporous silicon, ordered arrays of micropillars) and the properties thereof (nanoplasmonics and SERS effects, super-hydrophobicity, nano-filter capabilities) are combined to beat diffusion [22] and use the described nano-lenses more efficiently.

5. Conclusions

Non-invasive analysis in biological fluids is gaining increasing interest in the diagnosis and experimental assessment of diseases. As an example, it is very well understood that malignancies can be identified based on their molecular expression profiles. Exclusive markers extracted from serum, other biological fluids or any sample obtained through minimally invasive techniques can be realistically employed to discriminate cancers or other pathologies. The possibility to realize innovative sensing devices to measure specific analytes without any pain for the patient is a novel frontier in health control. Super-hydrophobic surfaces are biomimetic, microstructured solids with a texture given by a regular hexagonal lattice of micropillars. They deliver great potentials in biotechnology, because they reveal superior properties compared to conventional flat surfaces, including extremely low friction coefficients. On account of this, a millimetric drop would maintain a spherical shape if positioned upon those surfaces. Most importantly, during evaporation, the molecules contained in the drop can be concentrated, localized or transported into specific points of the substrate. These properties may be used for a variety of applications of medical interest. In this work, using the scheme of the 6W, the most promising applications of SHSs are reviewed. On integrating similar substrates with nano-geometrical SERS devices, molecules have been detected in very low abundance ranges, with femto- to zepto-molar sensitivity; DNA fibers have been imaged, thus gaining exclusive information about the double helix; and a few, small Rhodamine molecules have been separated from large albumin proteins using nanoporous silicon as a molecular sieve.