Influence of the Inducer on the Performance of a Miniature High-Speed Centrifugal Pump
Abstract
1. Introduction
2. Simulation Approach and Experimental Validation
2.1. Governing Equations
2.2. Turbulent Model
2.3. Cavitation Model
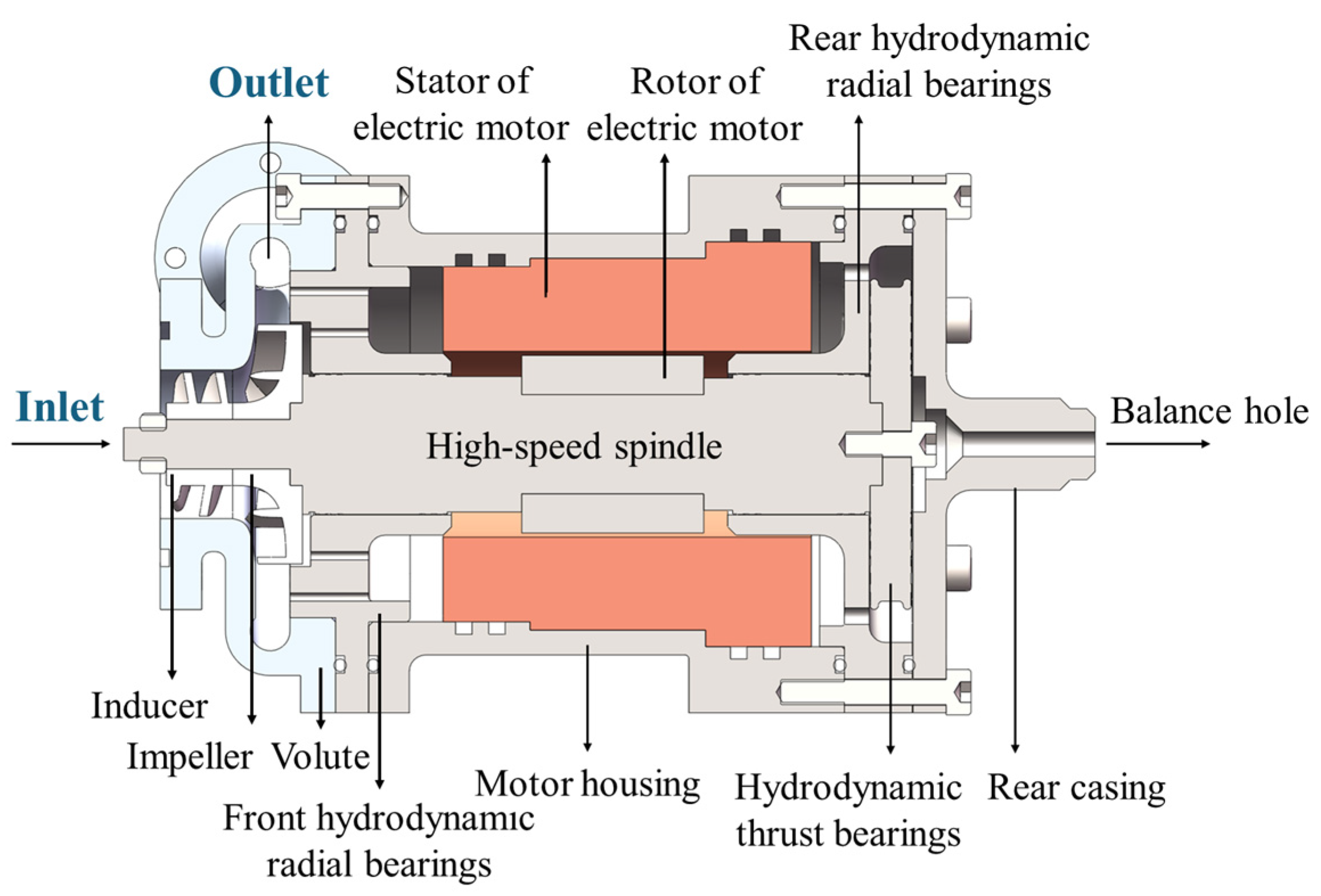
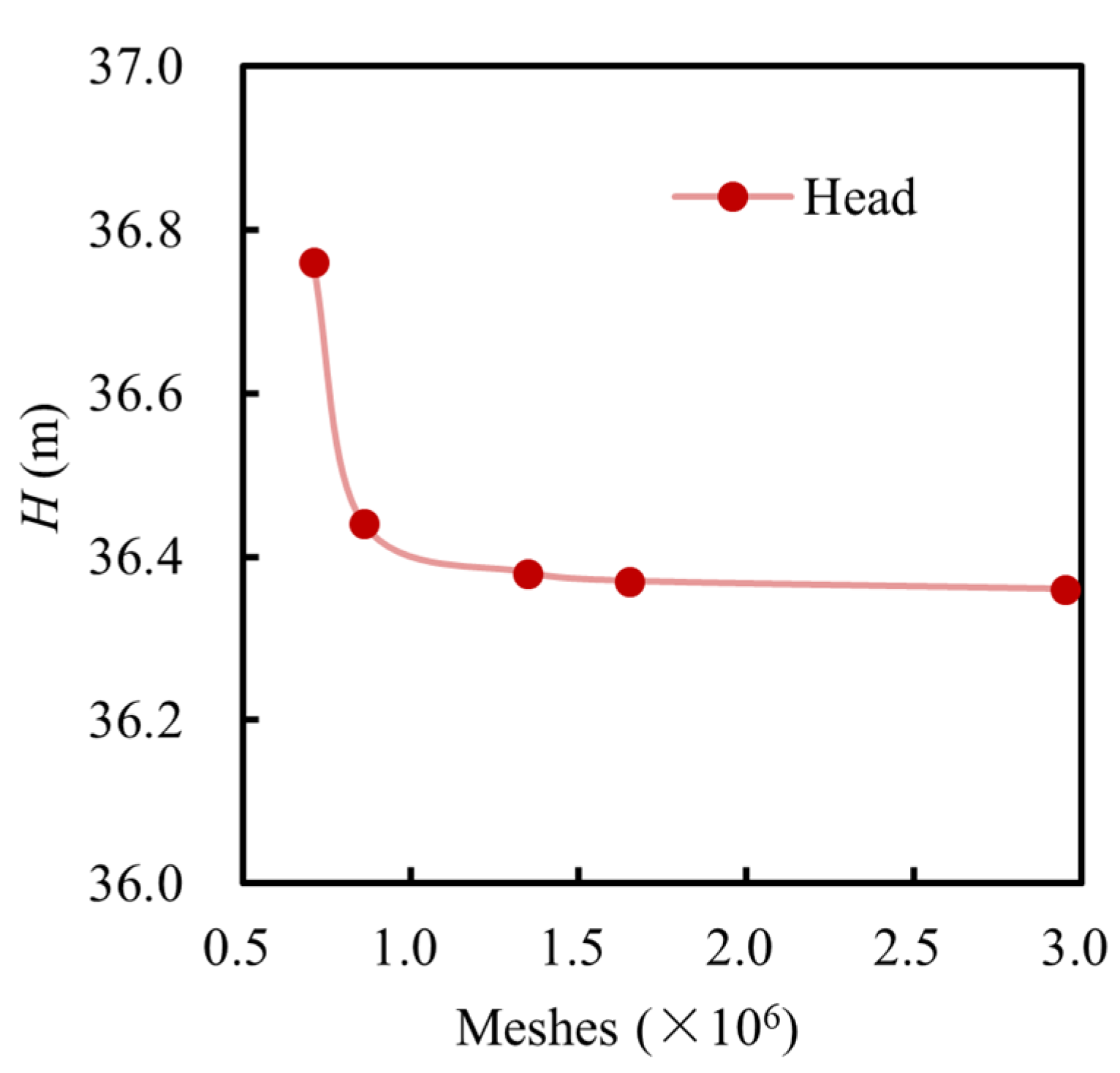
2.4. Computation Domain and Setup
2.5. Experimental Method
3. Analysis of Computational and Experimental Results
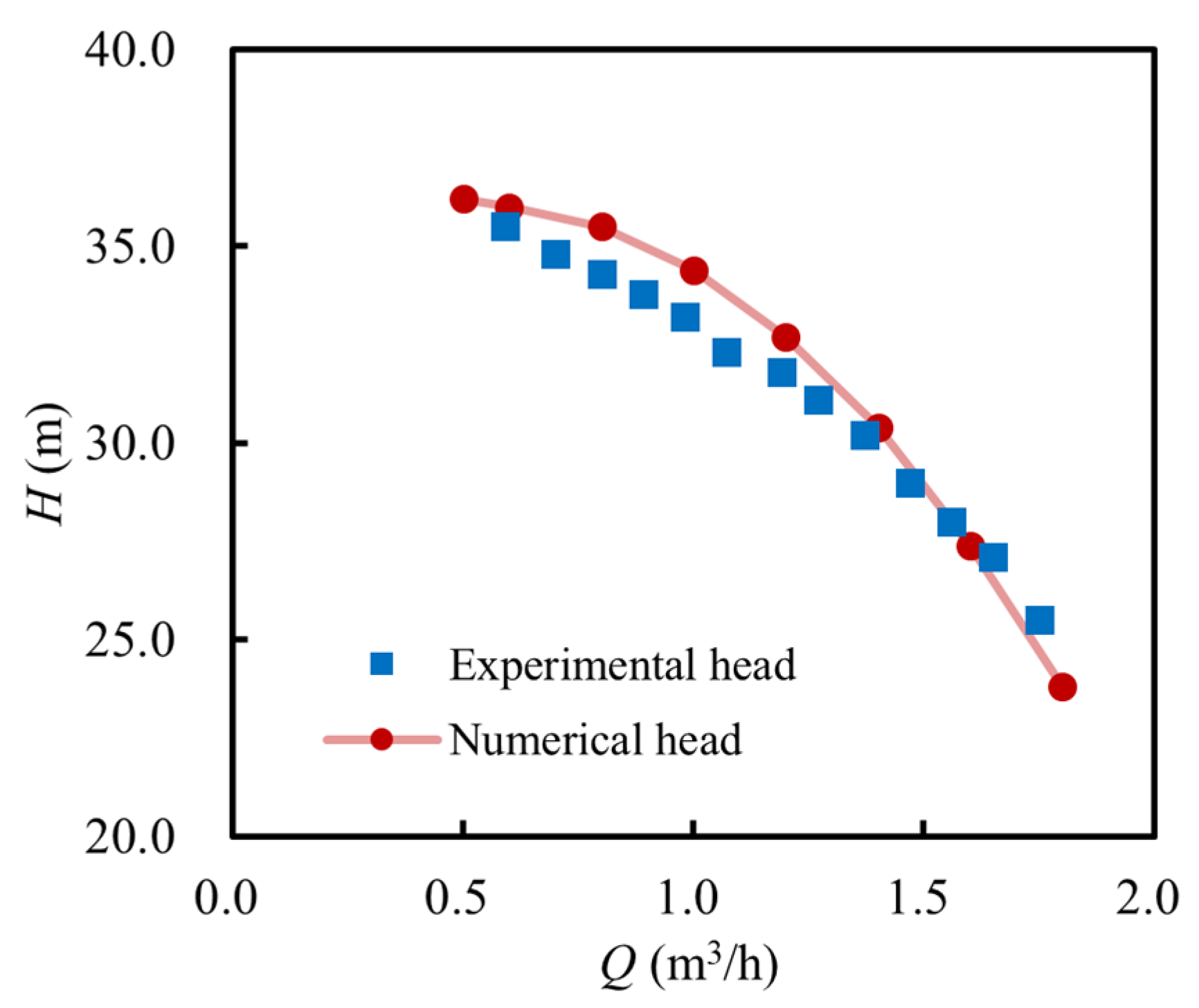
3.1. Validation of Numerical Model
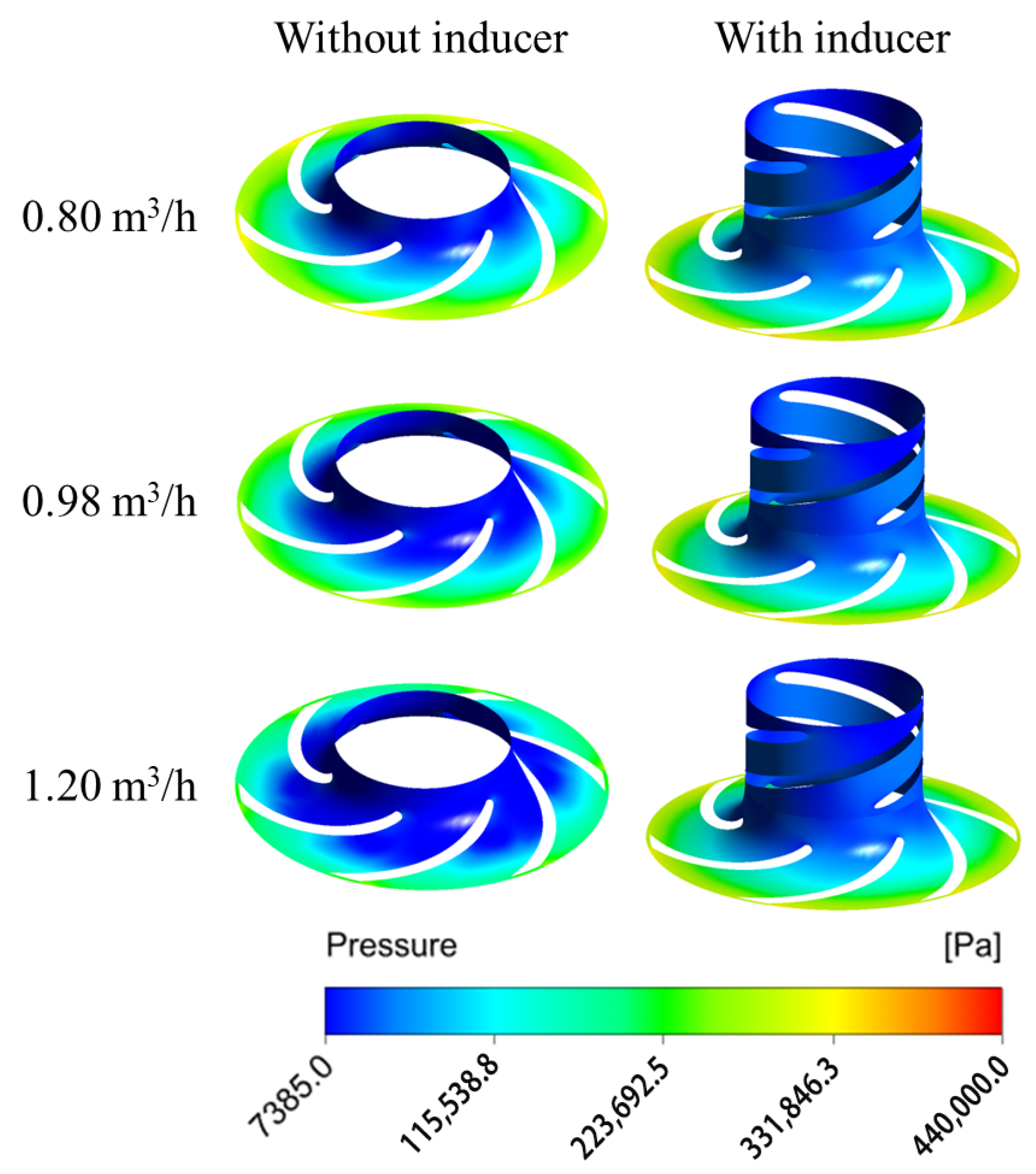
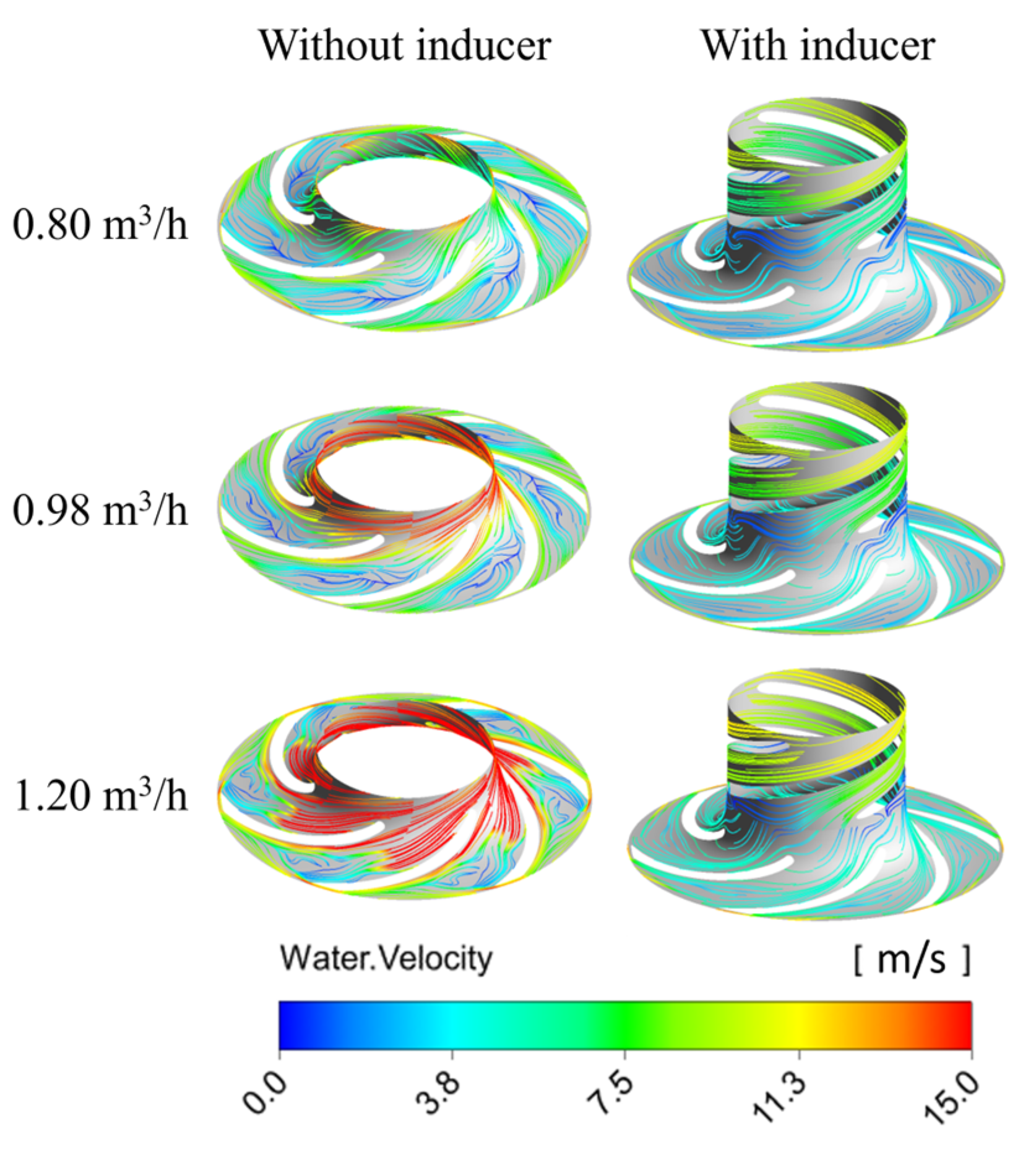
3.2. Effect of the Inducer on Flow Behavior in the MHCP
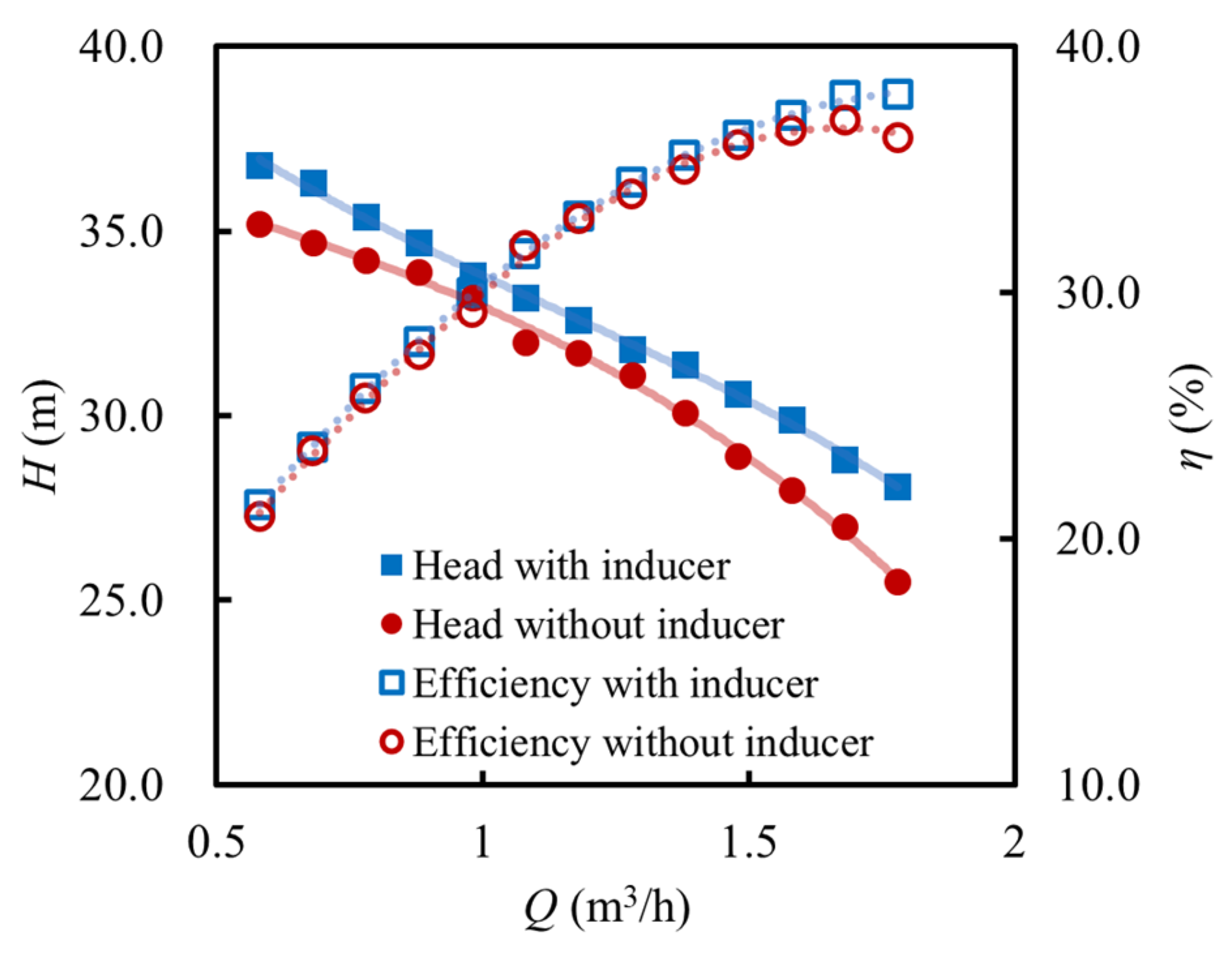
3.3. Effect of the Inducer on the External Performance of the MHCP
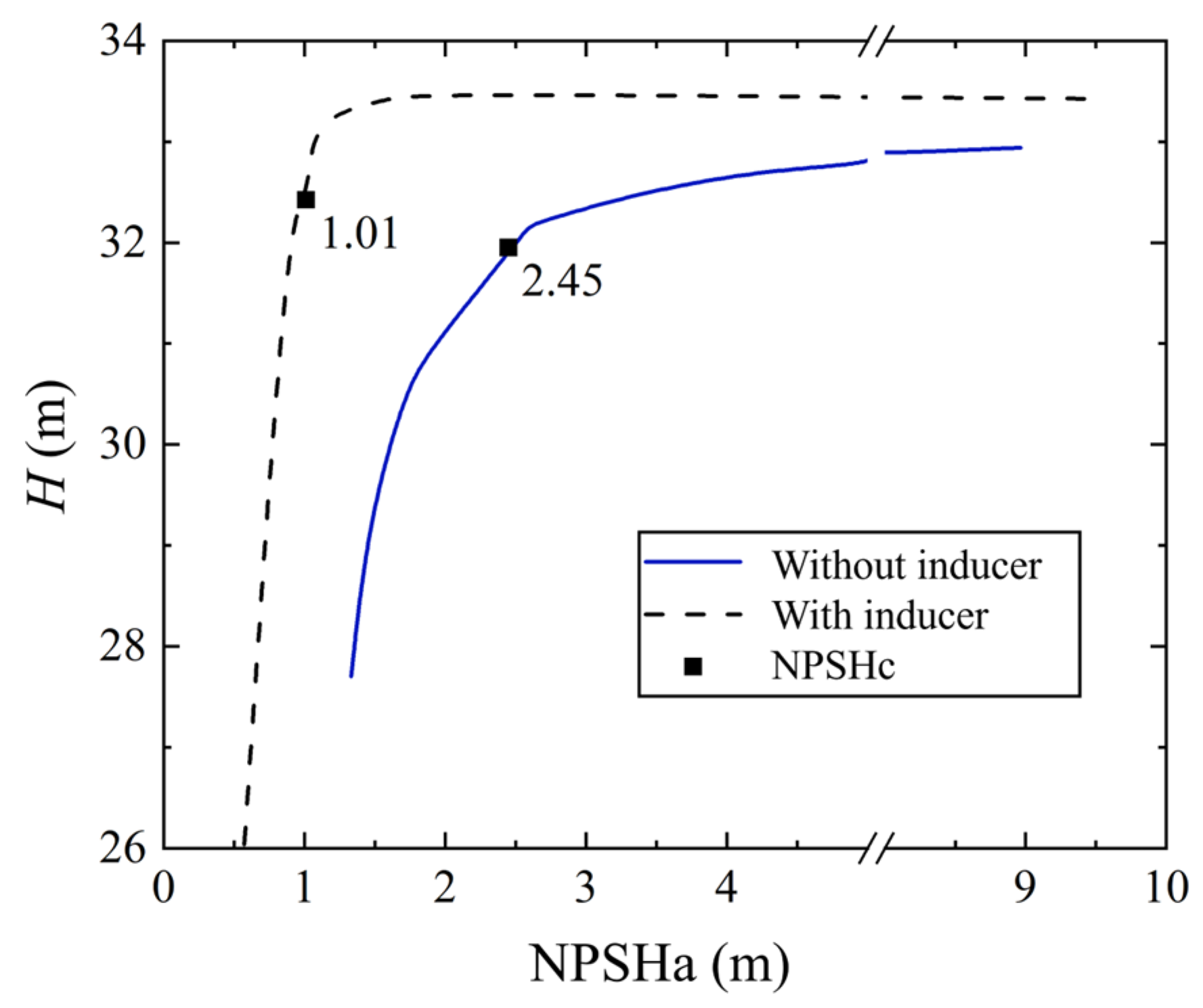
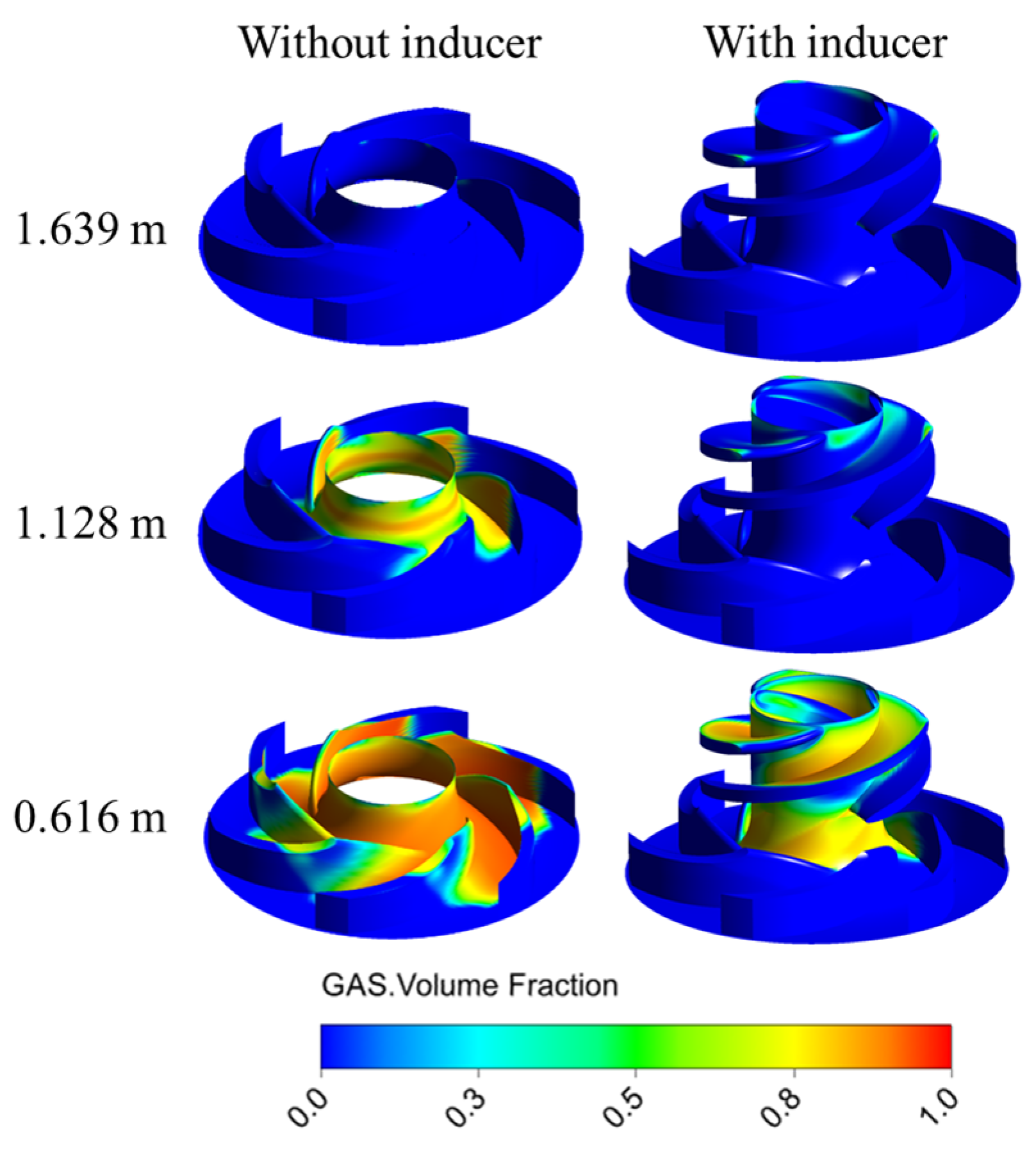
3.4. Analysis of Cavitation Characteristics
4. Conclusions
- (1)
- The numerical model demonstrates good predictive capability for MHCP performance when validated against experimentally obtained hydraulic performance data and flow visualization images. Within the investigated operating range, the addition of an inducer significantly enhances the external performance of the MHCP.
- (2)
- The inducer provides pre-pressurization to the incoming fluid. The relatively high operating speed results in a higher circumferential velocity at the inducer inlet and a reduced inlet flow angle, which allows the main impeller to adopt a smaller blade inlet angle.
- (3)
- The inducer alleviates the local low-pressure zones caused by the vortex cavities generated by the interaction between the tip leakage backflow and the main flow, thereby suppressing cavitation in the non-bladed region.
- (4)
- Once the pump reaches the critical NPSH, the presence of an inducer leads to a more rapid degradation caused by cavitation. This is attributed to the relatively enlarged bladeless region downstream of the inducer’s trailing edge in the MHCP, which intensifies the local pressure drop and accelerates cavitation deterioration in the impeller.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MHCP | Miniature High-Speed Centrifugal Pump |
| NPSHr | Required Net Positive Suction Head |
| UAV | Unmanned Aerial Vehicle |
| NPSHa | Available Net Positive Suction Head |
| NPSHc | Net Positive Suction Head |
References
- Lei, T.; Yang, Z.; Lin, Z.; Zhang, X. State of Art on Energy Management Strategy for Hybrid-Powered Unmanned Aerial Vehicle. Chin. J. Aeronaut. 2019, 32, 1488–1503. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Ji, R.T.; Wang, Y.; Chang, M.; Ma, X.P.; Sha, J.; Mao, D.L. An Improved Energy Management Strategy for the Solar Powered Unmanned Aerial Vehicle at the Extreme Condition. J. Energy Storage 2021, 43, 103114. [Google Scholar] [CrossRef]
- Son, Y.W.; Kang, D.; Kim, J. Passive Battery Thermal Management System for an Unmanned Aerial Vehicle Using a Tetrahedral Lattice Porous Plate. Appl. Therm. Eng. 2023, 225, 120186. [Google Scholar] [CrossRef]
- Sakanova, A.; Tong, C.F.; Nawawi, A.; Simanjorang, R.; Tseng, K.J.; Gupta, A.K. Investigation on Weight Consideration of Liquid Coolant System for Power Electronics Converter in Future Aircraft. Appl. Therm. Eng. 2016, 104, 603–615. [Google Scholar] [CrossRef]
- Wang, B.; Wang, F.; Yang, M.; Bao, Y.; Geng, X.; Shao, S. Investigation on the Two-Phase Loop Cooling System Composed of Maglev Compressor and Liquid Pump for Data Centers. Appl. Therm. Eng. 2023, 218, 119377. [Google Scholar] [CrossRef]
- Baun, D.O.; Köstner, L.; Flack, R.D. Effect of Relative Impeller-to-Volute Position on Hydraulic Efficiency and Static Radial Force Distribution in a Circular Volute Centrifugal Pump. J. Fluids Eng. 2000, 122, 598–605. [Google Scholar] [CrossRef]
- Shi, F.; Tsukamoto, H. Numerical Study of Pressure Fluctuations Caused by Impeller-Diffuser Interaction in a Diffuser Pump Stage. J. Fluids Eng. 2001, 123, 466–474. [Google Scholar] [CrossRef]
- González, J.; Parrondo, J.; Santolaria, C.; Blanco, E. Steady and Unsteady Radial Forces for a Centrifugal Pump With Impeller to Tongue Gap Variation. J. Fluids Eng. 2006, 128, 454–462. [Google Scholar] [CrossRef]
- Barrio, R.; Blanco, E.; Parrondo, J.; González, J.; Fernández, J. The Effect of Impeller Cutback on the Fluid-Dynamic Pulsations and Load at the Blade-Passing Frequency in a Centrifugal Pump. J. Fluids Eng. 2008, 130, 111102. [Google Scholar] [CrossRef]
- Fernández Oro, J.M.; Barrio Perotti, R.; Galdo Vega, M.; González, J. Effect of the Radial Gap Size on the Deterministic Flow in a Centrifugal Pump Due to Impeller-Tongue Interactions. Energy 2023, 278, 127820. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, B.; Lin, X.; Zhou, H.; Chen, S.; Hou, Y.; Xue, R.; Zhang, Z. Numerical and Experimental Investigation of Flow Characteristics in a Fluid Self-Lubricating Centrifugal Pump with R134a Refrigerant. Appl. Sci. 2023, 13, 8062. [Google Scholar] [CrossRef]
- Dehghan, A.A.; Shojaeefard, M.H.; Roshanaei, M. Exploring a New Criterion to Determine the Onset of Cavitation in Centrifugal Pumps from Energy-Saving Standpoint; Experimental and Numerical Investigation. Energy 2024, 293, 130681. [Google Scholar] [CrossRef]
- Zhang, B.; Niu, B.; Zhang, Z.; Chen, S.; Xue, R.; Hou, Y. Application and Challenge of High-Speed Pumps with Low-Temperature Thermosensitive Fluids. Energies 2024, 17, 3732. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Liu, H.; Xiao, Y.; Jiang, L.; Li, M. A Numerical Investigation on Energy Characteristics of Centrifugal Pump for Cavitation Flow Using Entropy Production Theory. Int. J. Heat Mass Transf. 2023, 201, 123591. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Qian, L.; Liu, X.; Yuan, S.; Zhu, B.; Dai, Y. Investigation of Pressure Pulsation Induced by Quasi-Steady Cavitation in a Centrifugal Pump. Phys. Fluids 2023, 35, 25119. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, Y.; Lv, H.; Zhu, Z. Study on External Performance and Internal Flow Characteristics in a Centrifugal Pump under Different Degrees of Cavitation. Phys. Fluids 2023, 35, 14104. [Google Scholar] [CrossRef]
- Yan, L.; Gao, B.; Ni, D.; Zhang, N.; Zhou, W. Numerical Analysis of the Influence of the Non-Uniform Inflow Induced by Streamwise Vortices on the Cavitating Flow around Hydrofoil. Ocean Eng. 2023, 278, 114324. [Google Scholar] [CrossRef]
- Yan, L.; Gao, B.; Ni, D.; Zhang, N.; Zhou, W. Numerical Analysis on the Cavitation Characteristics of a Pump with an Inducer in Non-Uniform Inflow. Ocean Eng. 2022, 256, 111407. [Google Scholar] [CrossRef]
- Parikh, T.; Mansour, M.; Thévenin, D. Investigations on the Effect of Tip Clearance Gap and Inducer on the Transport of Air-Water Two-Phase Flow by Centrifugal Pumps. Chem. Eng. Sci. 2020, 218, 115554. [Google Scholar] [CrossRef]
- Parikh, T.; Mansour, M.; Thévenin, D. Maximizing the Performance of Pump Inducers Using CFD-Based Multi-Objective Optimization. Struct. Multidisc. Optim. 2021, 65, 9. [Google Scholar] [CrossRef]
- Mansour, M.; Wunderlich, B.; Thévenin, D. Effect of Tip Clearance Gap and Inducer on the Transport of Two-Phase Air-Water Flows by Centrifugal Pumps. Exp. Therm. Fluid Sci. 2018, 99, 487–509. [Google Scholar] [CrossRef]
- El Samanody, M.A.; Ghorab, A.; Mostafa, M.A.F. Investigations on the Performance of Centrifugal Pumps in Conjunction with Inducers. Ain Shams Eng. J. 2014, 5, 149–156. [Google Scholar] [CrossRef]
- Zhou, H.; Xue, R.; Liang, Y.; Niu, B.; Chen, S.; Hou, Y. Tip Clearance Influence on the Performance of High-Speed Micro-Pumps. Phys. Fluids 2024, 36, 115129. [Google Scholar] [CrossRef]
- Medvitz, R.B.; Kunz, R.F.; Boger, D.A.; Lindau, J.W.; Yocum, A.M.; Pauley, L.L. Performance Analysis of Cavitating Flow in Centrifugal Pumps Using Multiphase CFD. J. Fluids Eng. 2002, 124, 377–383. [Google Scholar] [CrossRef]
- Hou, Y.; Xue, R. Hydraulic Performance and Flow Characteristics of a High-Speed Centrifugal Pump Based on Multi-Objective Optimization. Fluids 2025, 10, 174. [Google Scholar] [CrossRef]




| Type | Range | Measurement Accuracy |
|---|---|---|
| PT100 (MICROSENSOR, Baoji, China) | −50 °C~250 °C | ±0.5 °C |
| Differential pressure transducer (MICROSENSOR, Baoji, China) | 0~1 MPa | ±0.5% |
| Pressure transducer (MICROSENSOR, Baoji, China) | 0~0.6 MPa | ±0.5% |
| Turbine flowmeter (FIMEET, Hefei, China) | 0.6~6 m3/h | ±0.5% |
| Power meter (QINGZHI, Qingdao, China) | 0~5 kW | ±0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Zeng, X.; Wang, Y. Influence of the Inducer on the Performance of a Miniature High-Speed Centrifugal Pump. Micromachines 2025, 16, 952. https://doi.org/10.3390/mi16080952
Hou Y, Zeng X, Wang Y. Influence of the Inducer on the Performance of a Miniature High-Speed Centrifugal Pump. Micromachines. 2025; 16(8):952. https://doi.org/10.3390/mi16080952
Chicago/Turabian StyleHou, Yifu, Xiaonian Zeng, and Yuchuan Wang. 2025. "Influence of the Inducer on the Performance of a Miniature High-Speed Centrifugal Pump" Micromachines 16, no. 8: 952. https://doi.org/10.3390/mi16080952
APA StyleHou, Y., Zeng, X., & Wang, Y. (2025). Influence of the Inducer on the Performance of a Miniature High-Speed Centrifugal Pump. Micromachines, 16(8), 952. https://doi.org/10.3390/mi16080952







