A Soft Reconfigurable Inverted Climbing Robot Based on Magneto-Elastica-Reinforced Elastomer
Abstract
1. Introduction
- Deformation-controllable magneto-elastica-reinforced elastomer actuators: A magneto-elastica-reinforced elastomer (MERE) is developed through controllable inlay methodology, coupling the discrete-scale magneto-elasticity of spherical magnetic chains with elastomer elasticity. This composite retains the mechanical softness or compliance of elastic solids while exhibiting enhanced ferromagnetic properties and magneto-elastic responsiveness. Furthermore, the deformation of the magnetic-mechanics composite-based actuator can be controlled by modulating the magnetic interactions of magnetic beads.
- Good reconfigurability: Bionic morphology design principles are established to achieve three programmable configurations: linear pattern (inchworm-like crawling), parallel pattern (steering control), and triangular pattern (omnidirectional motion). Robots based on a modular strategy exhibit better adaptability to environments or tasks, and when one module is damaged, we can replace the faulty module instead of the entire robot.
- Multimodal locomotion: Multiple fundamental locomotion modes are demonstrated, including two-anchor crawling, steering-enabled crawling, and omnidirectional movement. Notably, the embedded magnetic spheres generate magnetic adhesion on ferromagnetic surfaces, enabling inverted climbing on curved ferromagnetic substrates. Unlike inverted climbing mechanisms such as capillary adhesion [32], spiny grippers [33], voltage-controlled electroadhesion [34], and vacuum-based systems [35], the proposed method simplifies the process by eliminating the need for complex gait designs, additional adhesion system, and closed-loop feedback.
2. Materials and Methods
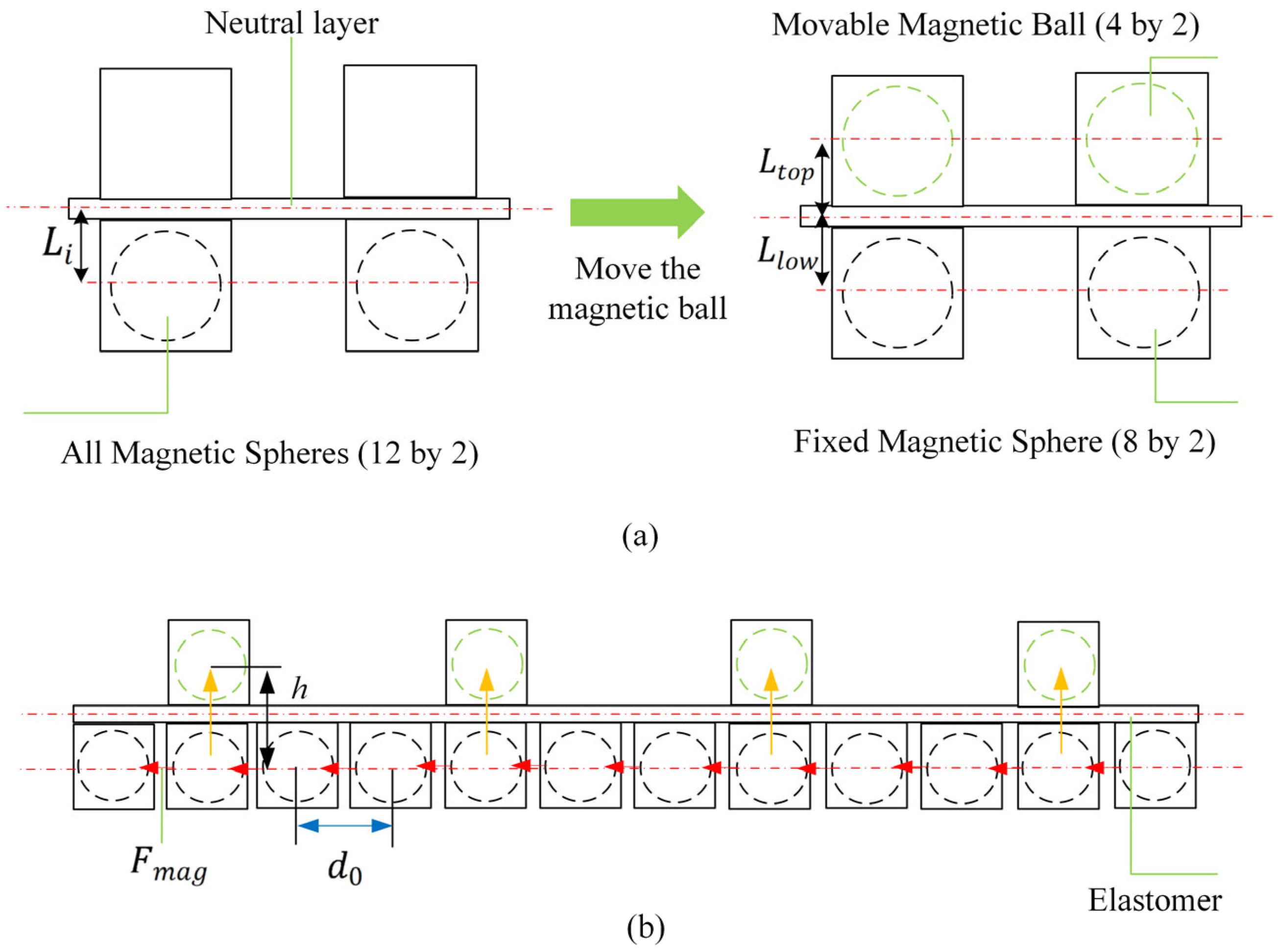
2.1. Basic Concept of Controllable Deformation
2.2. Shape Morphing Mechanism
2.3. Actuation Method
2.4. Multiple Configurations
3. Experimental Research
3.1. Crawling of the Soft Crawler with Linear Pattern
3.2. Crawling of the Soft Crawler with Parallel Two-Unit Pattern
3.3. Omnidirectional Crawling of the Soft Robot with Triangular Pattern
3.3.1. Kinematic Basis for Omnidirectional Crawling
- Unit 1 movement direction: , .
- Unit 2 movement direction: , .
- Unit 3 movement direction: , .
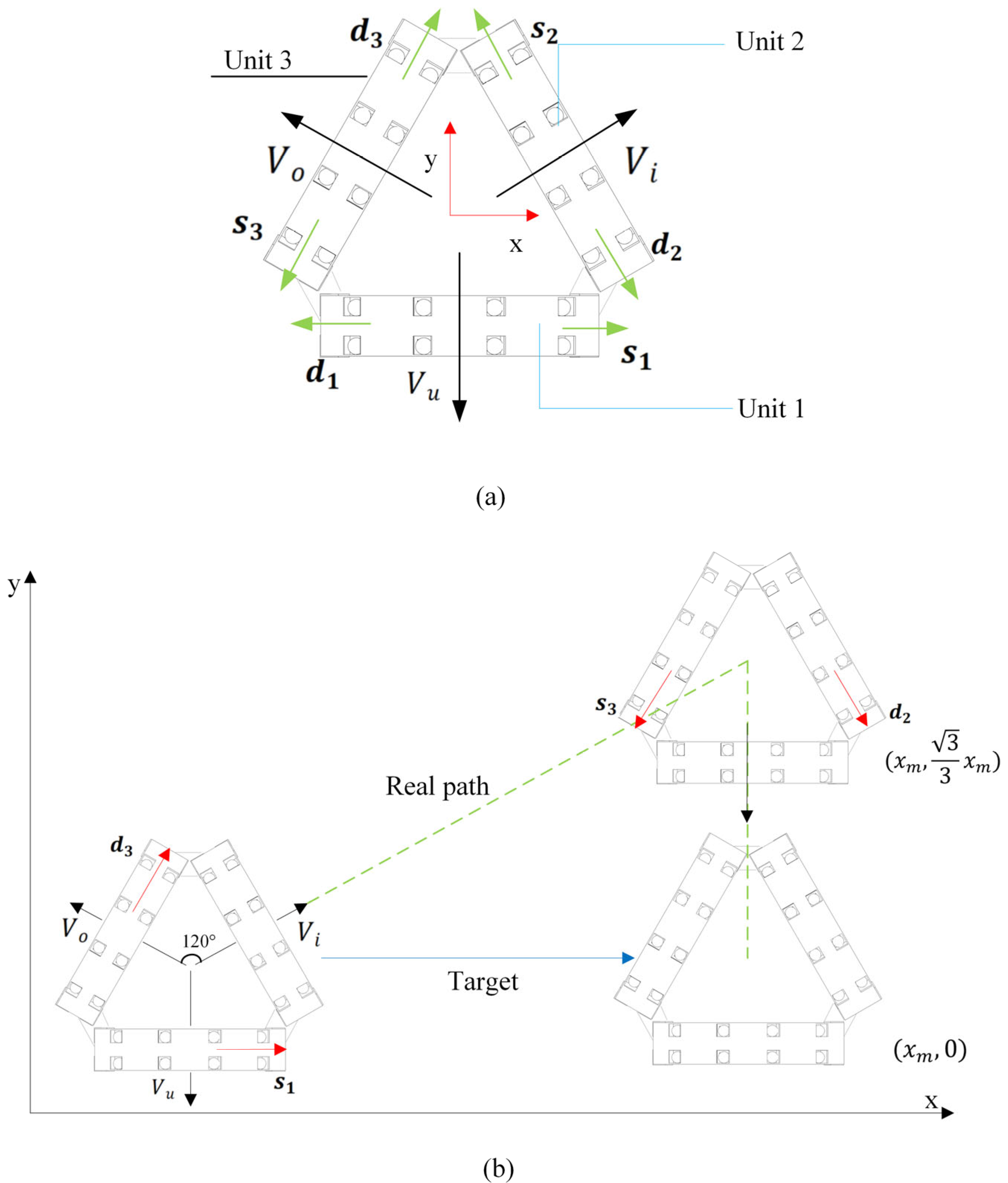
3.3.2. Omnidirectional Motion
- When Unit 2 and Unit 3 cooperate to displace along directions , Unit 1 remains stationary; the robot moves at velocity .
- When Unit 1 and Unit 3 cooperate to displace along directions and , Unit 2 remains stationary; the robot moves at velocity .
- When Unit 1 and Unit 2 cooperate to displace along directions , Unit 3 remains stationary; the robot moves at velocity .
3.4. Inverted Climbing on Ceiling of the Soft Crawler
3.5. Inverted Climbing on Curved Surfaces of the Soft Crawler
3.6. Locomotion Capability Assessment of the Soft Crawler
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qu, J.; Cui, G.; Li, Z.; Fang, S.; Zhang, X.; Liu, A.; Han, M.; Liu, H.; Wang, X.; Wang, X. Advanced flexible sensing technologies for soft robots. Adv. Funct. Mater. 2024, 34, 2401311. [Google Scholar] [CrossRef]
- Hu, F.; Zhang, C. Origami polyhedra-based soft multicellular robots. Soft Robot 2024, 11, 244–259. [Google Scholar] [CrossRef] [PubMed]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef] [PubMed]
- Galloway, K.C.; Becker, K.P.; Phillips, B.; Kirby, J.; Licht, S.; Tchernov, D.; Wood, R.J.; Gruber, D.F. Soft robotic grippers for biological sampling on deep reefs. Soft Robot. 2016, 3, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Kou, Z.; Sefene, E.M.; Mikolajczyk, T. An origami flexiball-inspired soft robotic jellyfish. J. Mar. Sci. Eng. 2023, 11, 714. [Google Scholar] [CrossRef]
- Saeidi, H.; Opfermann, J.D.; Kam, M.; Wei, S.; Leonard, S.; Hsieh, M.H.; Kang, J.U.; Krieger, A. Autonomous robotic laparoscopic surgery for intestinal anastomosis. Sci. Robot. 2022, 7, eabj2908. [Google Scholar] [CrossRef]
- Mirats Tur, J.M.; Garthwaite, W. Robotic devices for water main in-pipe inspection: A survey. J. Field Robot. 2010, 27, 491–508. [Google Scholar] [CrossRef]
- Long, L.; Cao, S.; Rao, F.; Fu, Q.; Leng, Y.; Xu, Q.; Zhang, X. Research and experiment of a novel leak detection robot. Ind. Robot. 2025; in press. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, Q.; Wang, J.; Zhang, B.; Zhong, C.; Zhilenkov, A.A. Exploring embodied intelligence in soft robotics: A review. Biomimetics 2024, 9, 248. [Google Scholar] [CrossRef]
- Ambaye, G.; Boldsaikhan, E.; Krishnan, K. Soft robot design, manufacturing, and operation challenges: A review. J. Manuf. Mater. Process. 2024, 8, 79. [Google Scholar] [CrossRef]
- AboZaid, Y.A.; Aboelrayat, M.T.; Fahim, I.S.; Radwan, A.G. Soft robotic grippers: A review on technologies, materials, and applications. Sens. Actuators A Phys. 2024, 372, 115380. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Mushtaq, R.T.; Wei, Q. Advancements in soft robotics: A comprehensive review on actuation methods, materials, and applications. Polymers 2024, 16, 1087. [Google Scholar] [CrossRef] [PubMed]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic networks for soft robotics that actuate rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Zhang, M.; Li, G.; Yang, X.; Xiao, Y.; Yang, T.; Wong, T.-W.; Li, T. Artificial muscle driven soft hydraulic robot: Electromechanical actuation and simplified modeling. Smart Mater. Struct. 2018, 27, 095016. [Google Scholar] [CrossRef]
- Tatarian, K.; Stower, R.; Rudaz, D.; Chamoux, M.; Kappas, A.; Chetouani, M. How does modality matter? Investigating the synthesis and effects of multi-modal robot behavior on social intelligence. Int. J. Soc. Robot. 2021, 14, 893–911. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef]
- Chi, Y.; Evans, E.E.; Clary, M.R.; Qi, F.; Sun, H.; Cantú, S.N.; Capodanno, C.M.; Tracy, J.B.; Yin, J. Magnetic kirigami dome metasheet with high deformability and stiffness for adaptive dynamic shape-shifting and multimodal manipulation. Sci. Adv. 2024, 10, eadr8421. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Fan, X.; Chen, Q.; Li, M.; Wu, Z.; Tong, D.; Xie, H.; Yang, Z.; Sun, L.; Sitti, M. Machining swarf formation–inspired fabrication of ferrofluidic helical miniature robots with multimodal locomotion capability. Sci. Adv. 2025, 11, eads4411. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, S.; Han, J.; Huang, C.; Yu, H.; Li, D.; Qiu, M.; Cheng, S.; Wu, C.; Cai, M.; et al. Thermal and magnetic dual-responsive catheter-assisted shape memory microrobots for multistage vascular embolization. Research 2024, 7, 0339. [Google Scholar] [CrossRef]
- Hou, C.; Guo, J.; Sun, B.; Chan, K.F.; Song, X.; Zhang, L. Magnetic nanostickers for active control of interface-enhanced selective bioadhesion. Nat. Commun. 2025, 16, 6400. [Google Scholar] [CrossRef]
- Chen, Q.; Feng, H.; Fan, X.; Xie, H.; Sun, L.; Yang, Z. Adaptive Ferrofluidic Robotic System with Passive Component Activation Capabilities. Think. Ski. Creat. 2025, 6, 0300. [Google Scholar] [CrossRef]
- Sun, M.; Hao, B.; Yang, S.; Wang, X.; Majidi, C.; Zhang, L. Exploiting ferrofluidic wetting for miniature soft machines. Nat. Commun. 2022, 13, 7919. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Yue, L.; Yu, L.; Forte, C.T.; Armstrong, C.D.; Zhou, K.; Demoly, F.; Zhao, R.R.; Qi, H.J. Machine learning-enabled forward prediction and inverse design of 4D-printed active plates. Nat. Commun. 2024, 15, 5509. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Nashalian, A.; Ock, I.W.; Popoli, S.; Xu, J.; Yin, J.; Tat, T.; Libanori, A.; Chen, G.; Zhou, Y.; et al. A soft magnetoelastic generator for wind-energy harvesting. Adv. Mater. 2022, 34, 2204238. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Ni, X.; Zhu, B.; Wang, B.; Chen, B. Simulation and optimization of magnetoelastic thin shells. ACM Trans. Graph. 2022, 41, 61. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Y.; Chen, D. Multimodal locomotion control and navigation of a miniature legged robot in challenging terrains. IEEE/ASME Trans. Mechatron. 2021, 26, 1503–1513. [Google Scholar]
- Zhu, H.; Ji, H.; Li, P.; Lai, L. Derivation and experimental validation of multi-parameter performance optimization of magnetic adhesion unit of wall-climbing robot. Actuators 2025, 14, 270. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Zhang, L. Cost analysis of laser-assisted magnetization in microscale permanent magnet fabrication. J. Manuf. Process. 2021, 64, 135–144. [Google Scholar] [CrossRef]
- Baden, T.; Chagas, A.M.; Gage, G.; Marzullo, T.; Prieto-Godino, L.L.; Euler, T. Open labware: 3-D printing your own lab equipment. PLOS Biol. 2015, 13, e1002086. [Google Scholar] [CrossRef]
- Hu, F.; Liu, Y. A magneto-elastica reinforced elastomer makes soft robotic grippers. Sens. Actuators A Phys. 2024, 379, 115977. [Google Scholar] [CrossRef]
- Chen, Y.; Doshi, N.; Wood, R.J. Inverted and inclined climbing using capillary adhesion in a quadrupedal insect-scale robot. IEEE Robot. Autom. Lett. 2020, 5, 4820–4827. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Niu, F.; Li, P.; Li, Y.; Mei, T. A track-type inverted climbing robot with bio-inspired spiny grippers. J. Bionic Eng. 2020, 17, 920–931. [Google Scholar] [CrossRef]
- De Rivaz, S.D.; Goldberg, B.; Doshi, N.; Jayaram, K.; Zhou, J.; Wood, R.J. Inverted and vertical climbing of a quadrupedal microrobot using electroadhesion. Sci. Robot. 2018, 3, eaau3038. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, W.; Huang, Y.; Yin, Y.; Xu, Q. Development of a New Biped Robot with Adaptive Suction Modules for Curved-Surface Climbing. IEEE Robot. Autom. Lett. 2025, 10, 7436–7443. [Google Scholar] [CrossRef]
- Ng, C.S.X.; Tan, M.W.M.; Xu, C.; Yang, Z.; Lee, P.S.; Lum, G.Z. Locomotion of miniature soft robots. Adv. Mater. 2021, 33, 2003558. [Google Scholar] [CrossRef] [PubMed]
- Soon, R.H.; Ren, Z.; Hu, W.; Bozuyuk, U.; Yildiz, E.; Li, M.; Sitti, M. On-demand anchoring of wireless soft miniature robots on soft surfaces. Proc. Natl. Acad. Sci. USA 2022, 119, e2207767119. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Cao, Y.; Sarparast, M.; Yuan, H.; Dong, L.; Tan, X.; Cao, C. Soft crawling robots: Design, actuation, and locomotion. Adv. Mater. Technol. 2020, 5, 1900837. [Google Scholar] [CrossRef]
- Seeja, G.; Doss, A.S.A.; Hency, V.B. A survey on snake robot locomotion. IEEE Access 2022, 10, 112100–112116. [Google Scholar] [CrossRef]
- Liu, J.; Tong, Y.; Liu, J. Review of snake robots in constrained environments. Robot. Auton. Syst. 2021, 141, 103785. [Google Scholar] [CrossRef]
- Li, J.; Li, D.; Wang, C.; Guo, W.; Wang, Z.; Zhang, Z.; Liu, H. Active collision avoidance for teleoperated multi-segment continuum robots toward minimally invasive surgery. Int. J. Robot. Res. 2024, 43, 918–941. [Google Scholar] [CrossRef]
- Feng, M.; Yang, D.; Majidi, C.; Gu, G. High-speed and low-energy actuation for pneumatic soft robots with internal exhaust air recirculation. Adv. Intell. Syst. 2023, 5, 2200257. [Google Scholar] [CrossRef]
- Feng, W.; Sun, L.; Jin, Z.; Chen, L.; Liu, Y.; Xu, H.; Wang, C. A large-strain and ultrahigh energy density dielectric elastomer for fast moving soft robot. Nat. Commun. 2024, 15, 4222. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Zhang, S.; Zhang, W.; Ren, Y. Design and control of a new pneumatic quadruped soft robot based on honeycomb structure. IEEE Access 2024, 12, 98882–98899. [Google Scholar] [CrossRef]
- Kandhari, A.; Wang, Y.; Chiel, H.J.; Quinn, R.D.; Daltorio, K.A. An analysis of peristaltic locomotion for maximizing velocity or minimizing cost of transport of earthworm-like robots. Soft Robot. 2021, 8, 485–505. [Google Scholar] [CrossRef]
- Zhong, S.; Xin, Z.; Hou, Y.; Li, Y.; Huang, H.-W.; Sun, T.; Shi, Q.; Wang, H. Double-Modal Locomotion of a Hydrogel Ultra-Soft Magnetic Miniature Robot with Switchable Forms. Cyborg Bionic Syst. 2024, 5, 0077. [Google Scholar] [CrossRef]
- Li, J.; Zhou, X.; Gui, C.; Yang, M.; Xu, F.; Wang, X. Adaptive climbing and automatic inspection robot for variable curvature walls of industrial storage tank facilities. Autom. Constr. 2025, 172, 106049. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef]







| Parameter | One Unit | Linear Two-Unit | Parallel Two-Unit |
|---|---|---|---|
| Total number of segments () | 3 | 5 | 5 |
| Actuating segments per wave () | 2 | 2 | 2 |
| Bridged segments () | 1 | 1 | 1 |
| Number of waves () | 1 | 1 | 1 |
| Front-anchored slip (mm) | 0.50 | 1.00 | 0.80 |
| Rear-anchored slip (mm) | 2.00 | 3.00 | 2.00 |
| Slip ratio (%) | 68.75 | 75.00 | 82.50 |
| Specific locomotion efficiency () | 0.009 | 0.004 | 0.0038 |
| Predicted actual velocity () | 1.66 | 2.18 | 2.39 |
| Measured velocity () | 1.11 | 1.05 | 1.00 |
| Robot | Actuation | Locomotion Mode | Materials | Cost | |
|---|---|---|---|---|---|
| The presented robot | Rope motor actively and magneto-elastica-driven resilience | Wave crawling | Elastomer | Low | 1.25 |
| Robot in [38] | Dielectric elastomers | Crawling | Dielectric elastomers | Medium | 1.32 |
| Robot in [46] | Magnetron | Scrolling | Hydrogel | Medium | 1.07 |
| Configuration | Locomotion Mode | (BL/s) | |
|---|---|---|---|
| Single unit | Crawling on the ground | 1.11 | 0.0072 |
| Ceiling-based magnetic crawling | 2.17 | 0.0140 | |
| Ceiling-based crawling(curved structures) | 3.40 | 0.0219 | |
| Linear two-unit | Crawling on the ground | 1.05 | 0.0339 |
| Ceiling-based magnetic crawling | 1.28 | 0.0041 | |
| Parallel two-unit | Crawling on the ground | 1.00 | 0.0032 |
| Ground-based turning | 1.11 | 0.0036 | |
| Triangular unit | Crawling on the ground | 1.25 | 0.0081 |
| Robot | Actuation | (BL/s) | Terrain Adaptability |
|---|---|---|---|
| The presented robot | Rope motor method and magneto-elastica-driven resilience |
|
|
| Pneumatic soft crawling robot [38] | Pneumatic | 0.005–0.01 | Ground |
| Small-sized magnetically actuated soft robot [18] | Magnetic | 0.01–0.02 | Ground |
| Ferromagnetic soft robot [48] | Magnetic | 0.006–0.015 | Ferromagnetic surface |
| Shape memory alloy-actuated robot [14] | Thermal | 0.003–0.008 | Ground |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, F.; Zhao, B.; Jiang, W. A Soft Reconfigurable Inverted Climbing Robot Based on Magneto-Elastica-Reinforced Elastomer. Micromachines 2025, 16, 855. https://doi.org/10.3390/mi16080855
Hu F, Zhao B, Jiang W. A Soft Reconfigurable Inverted Climbing Robot Based on Magneto-Elastica-Reinforced Elastomer. Micromachines. 2025; 16(8):855. https://doi.org/10.3390/mi16080855
Chicago/Turabian StyleHu, Fuwen, Bingyu Zhao, and Wenyu Jiang. 2025. "A Soft Reconfigurable Inverted Climbing Robot Based on Magneto-Elastica-Reinforced Elastomer" Micromachines 16, no. 8: 855. https://doi.org/10.3390/mi16080855
APA StyleHu, F., Zhao, B., & Jiang, W. (2025). A Soft Reconfigurable Inverted Climbing Robot Based on Magneto-Elastica-Reinforced Elastomer. Micromachines, 16(8), 855. https://doi.org/10.3390/mi16080855


_Chang.jpg)






