Scattering Characteristics of a Circularly Polarized Bessel Pincer Light-Sheet Beam Interacting with a Chiral Sphere of Arbitrary Size
Abstract
1. Introduction
2. Methods
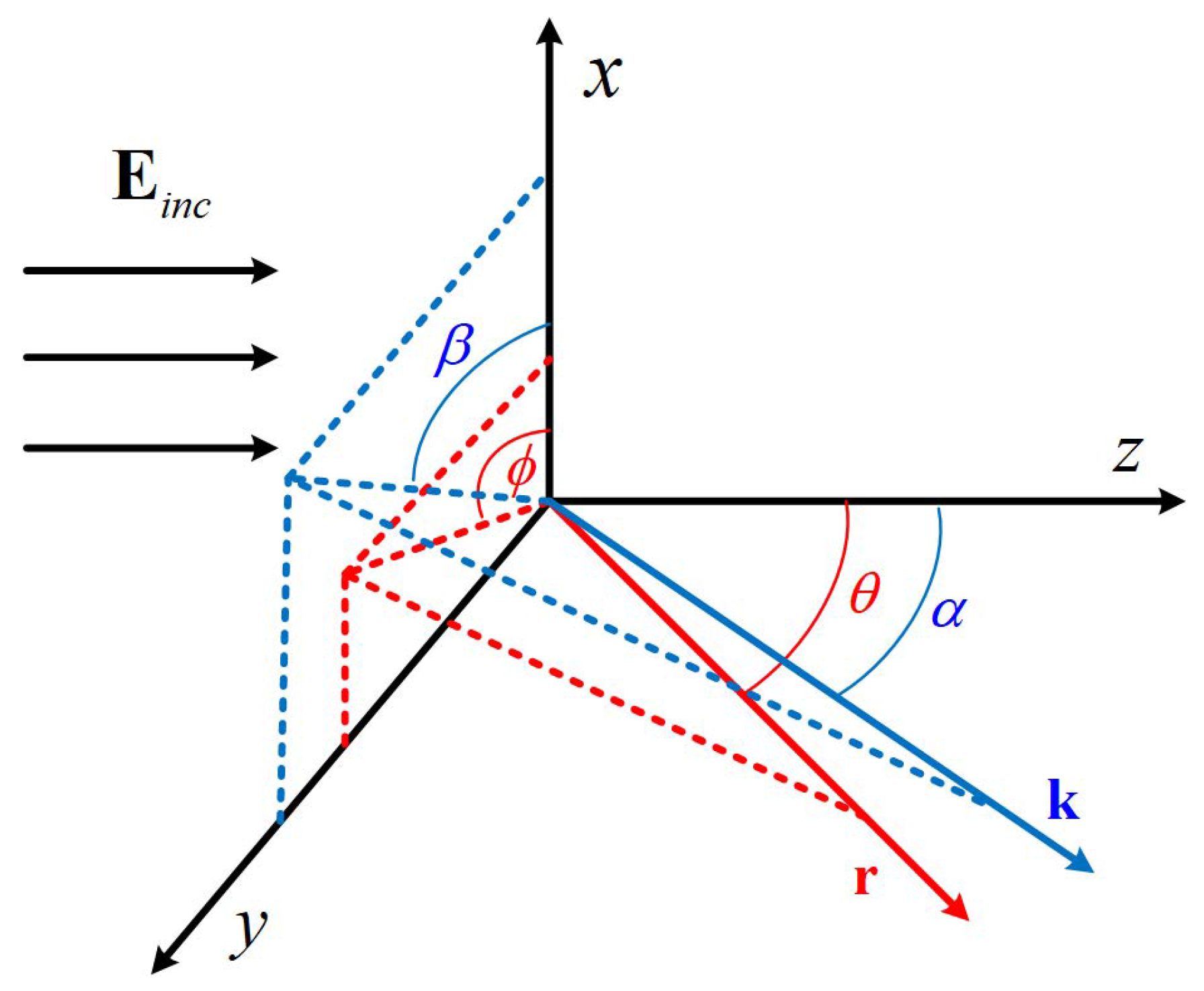
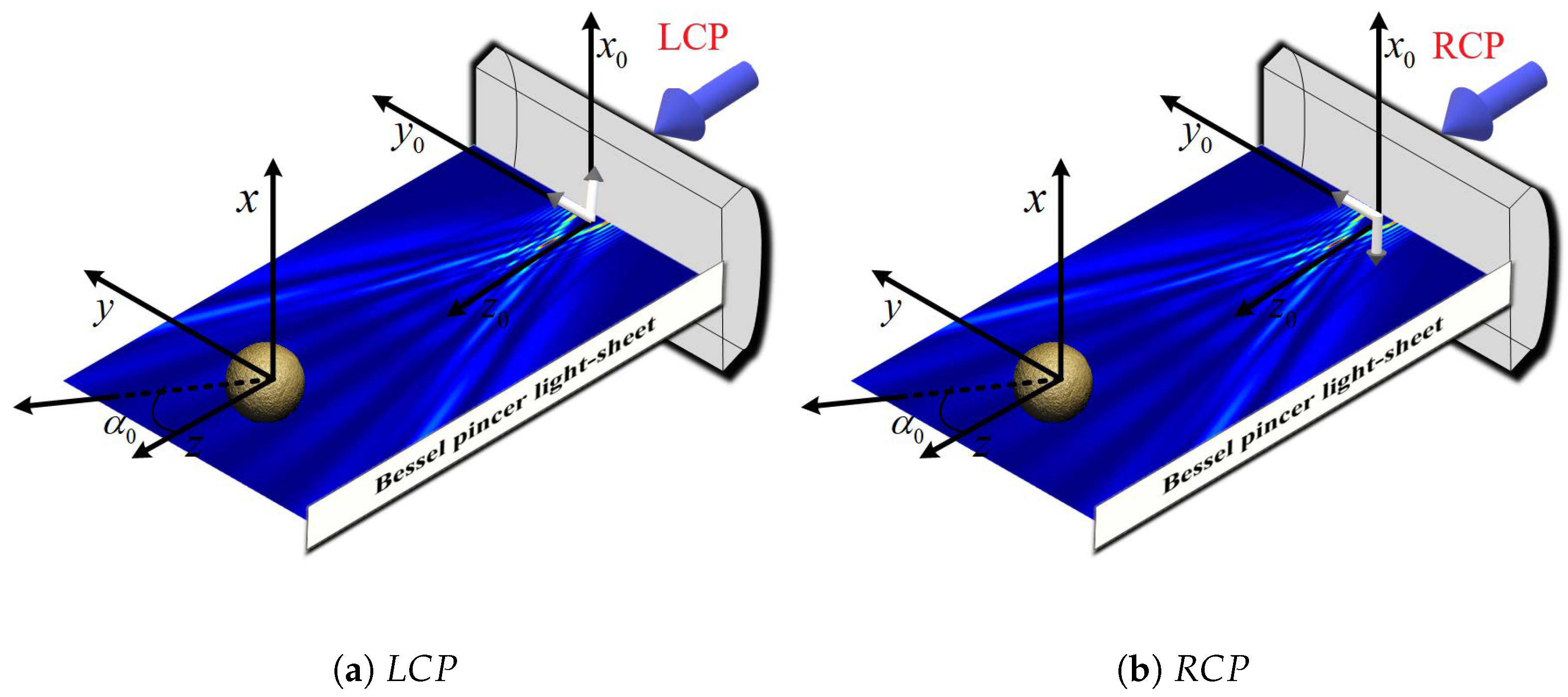
2.1. Angle of Bessel Pincer Light-Sheet Beam
2.2. Scattering of a Bessel Pincer Light-Sheet Beam by a Chiral Sphere
2.3. Far-Field Scattering of a Bessel Pincer Light-Sheet Beam on a Chiral Sphere
3. Results
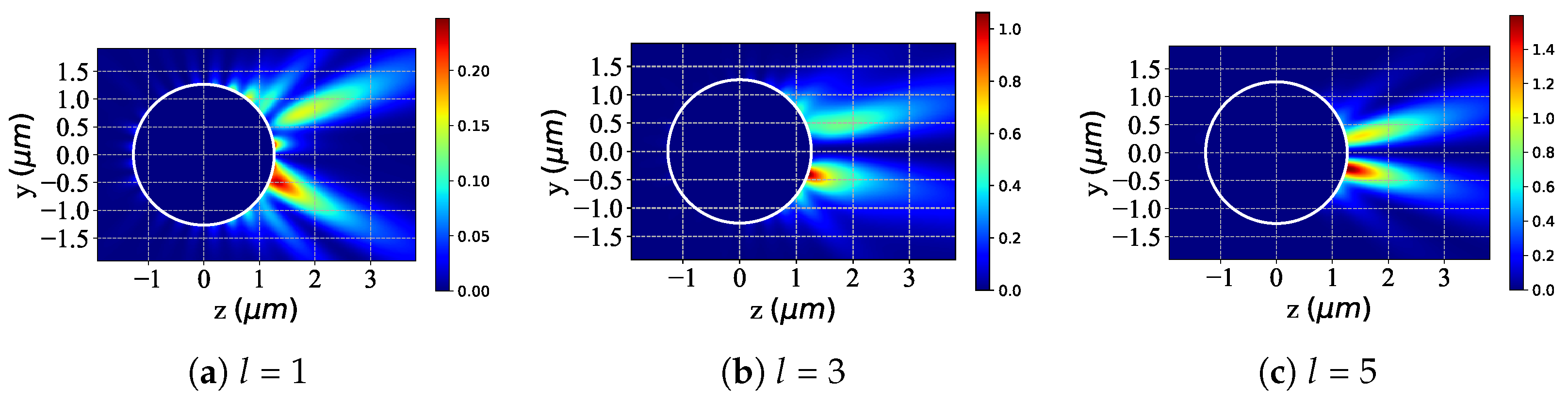
3.1. Scattering Field Distribution of a Chiral Sphere Under the Action of Incident Beam
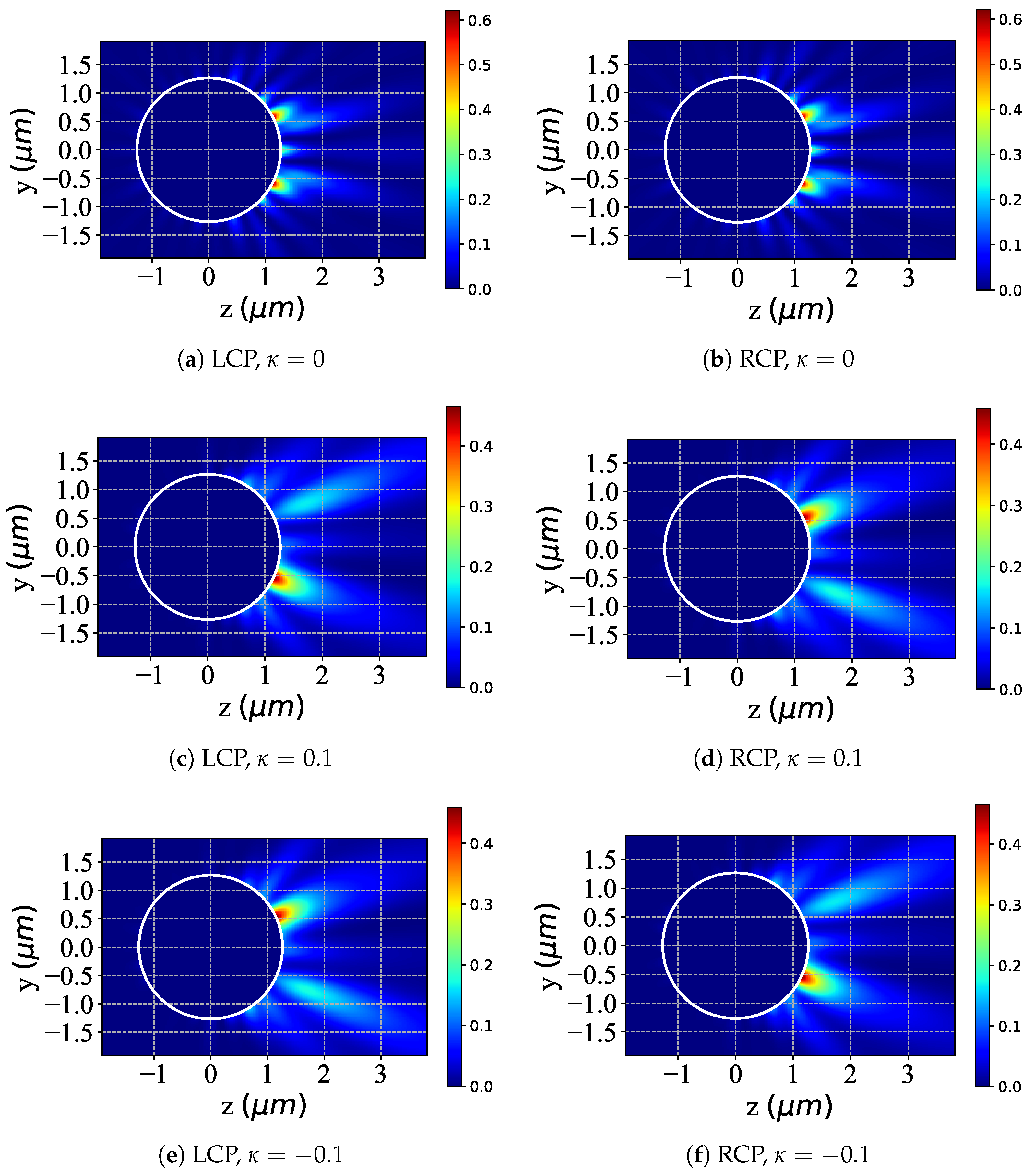
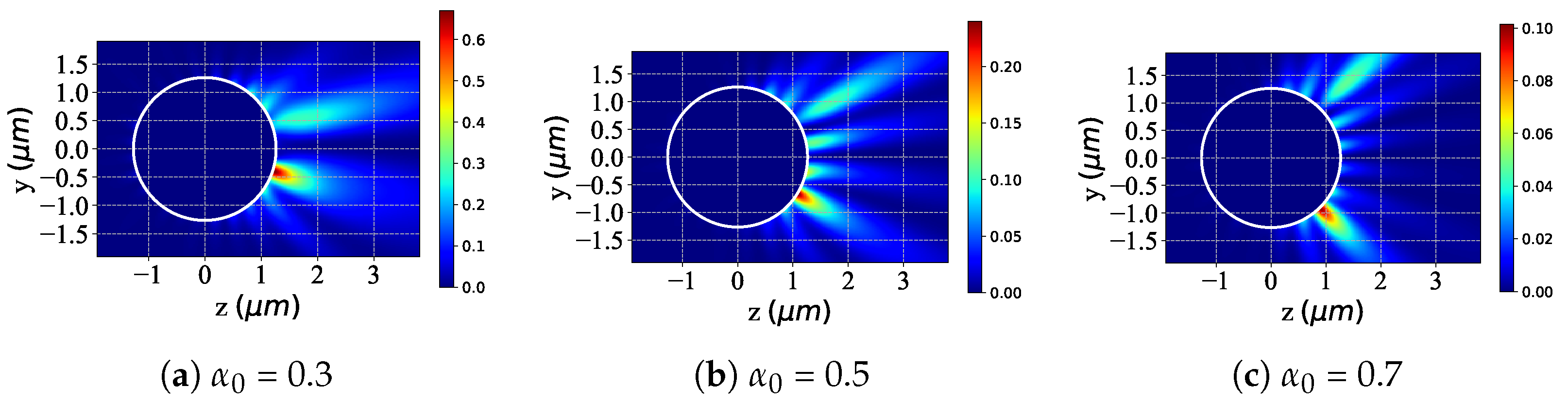
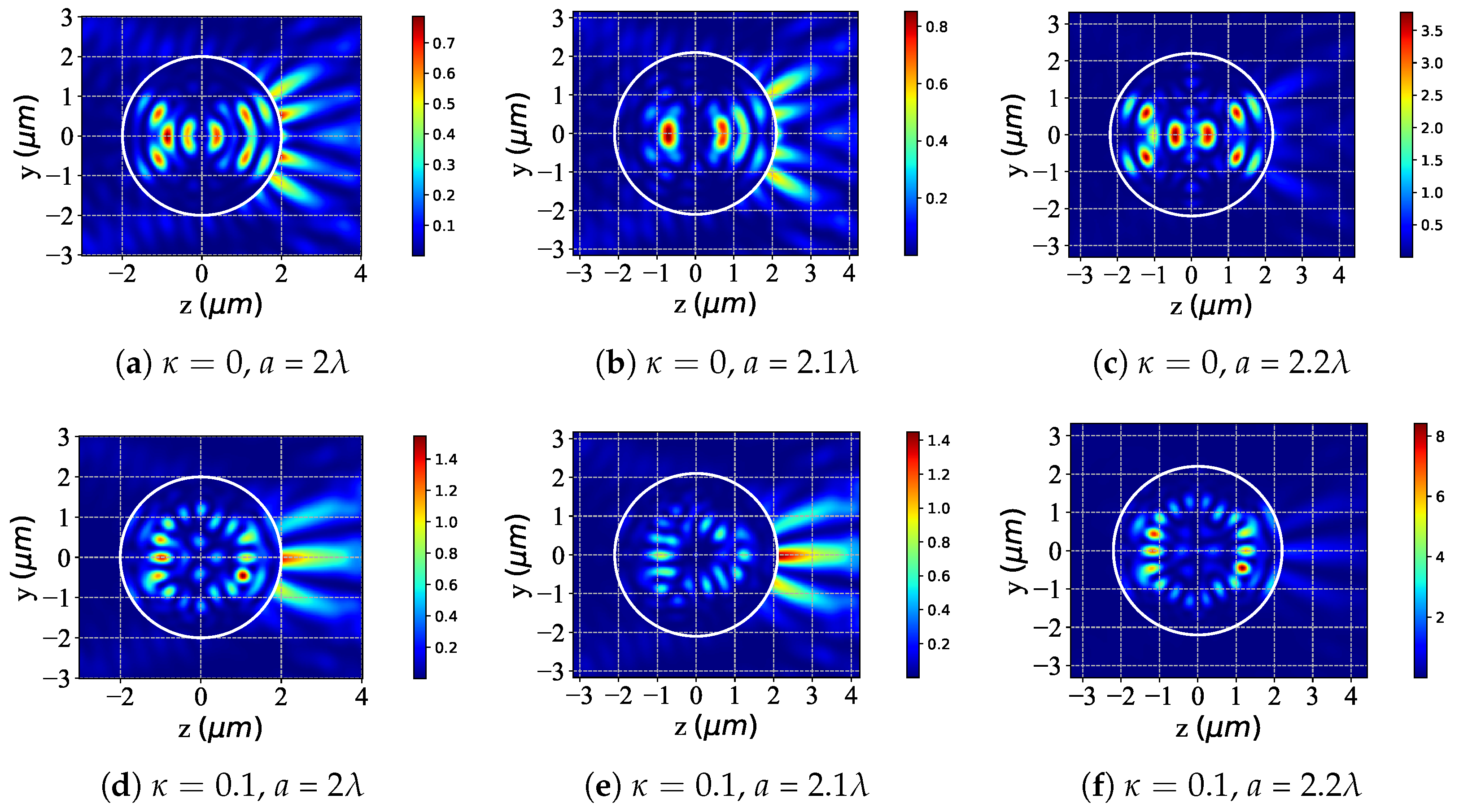
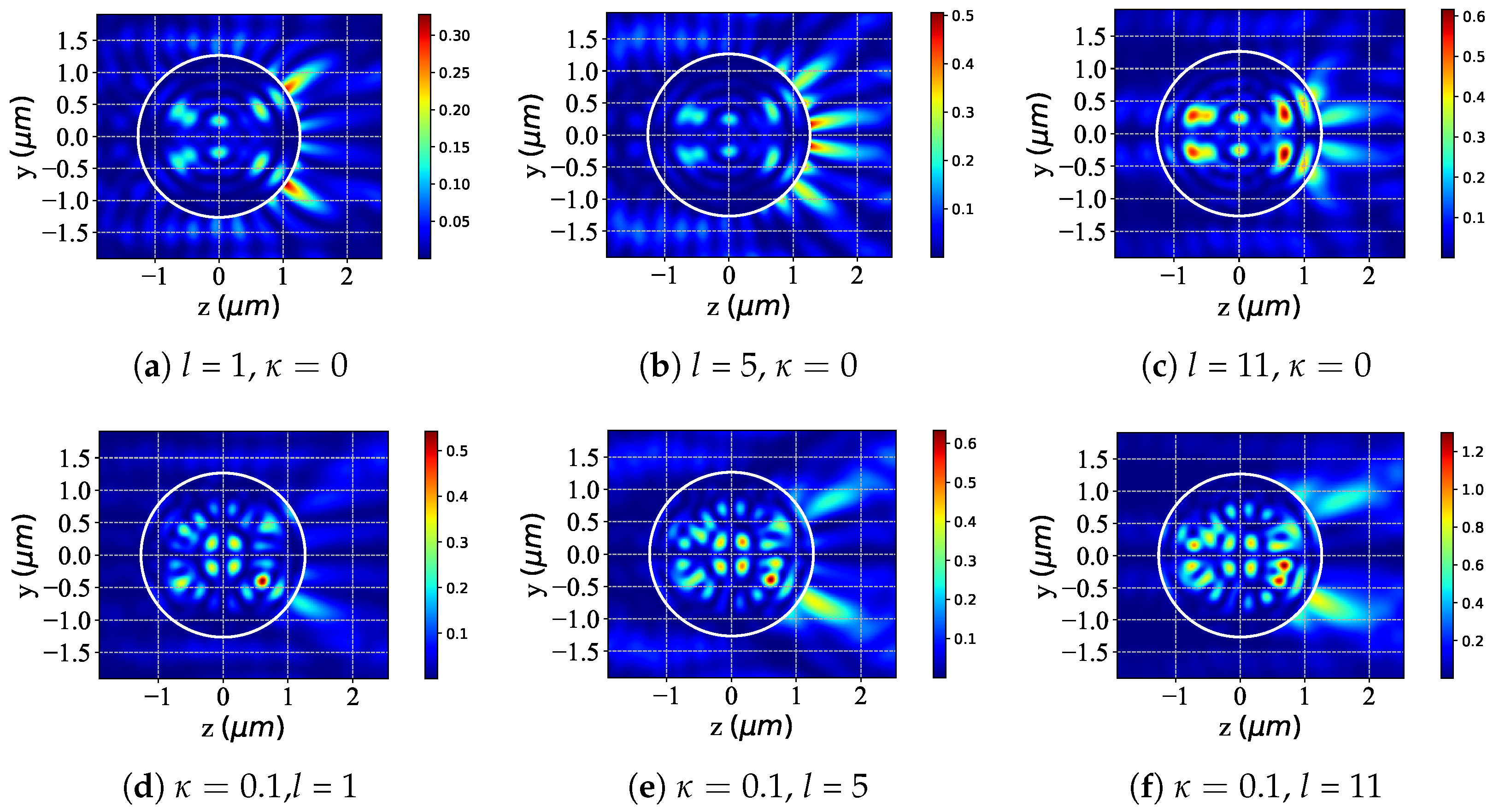
3.2. Near-Surface Field
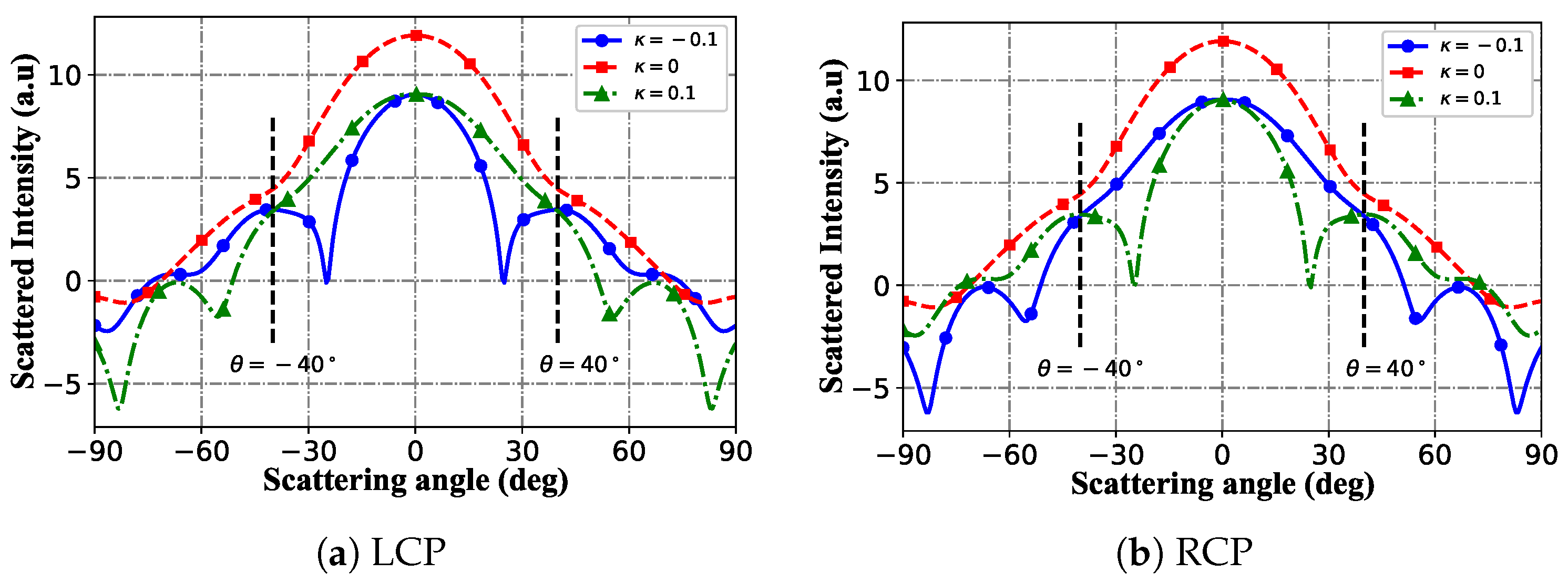
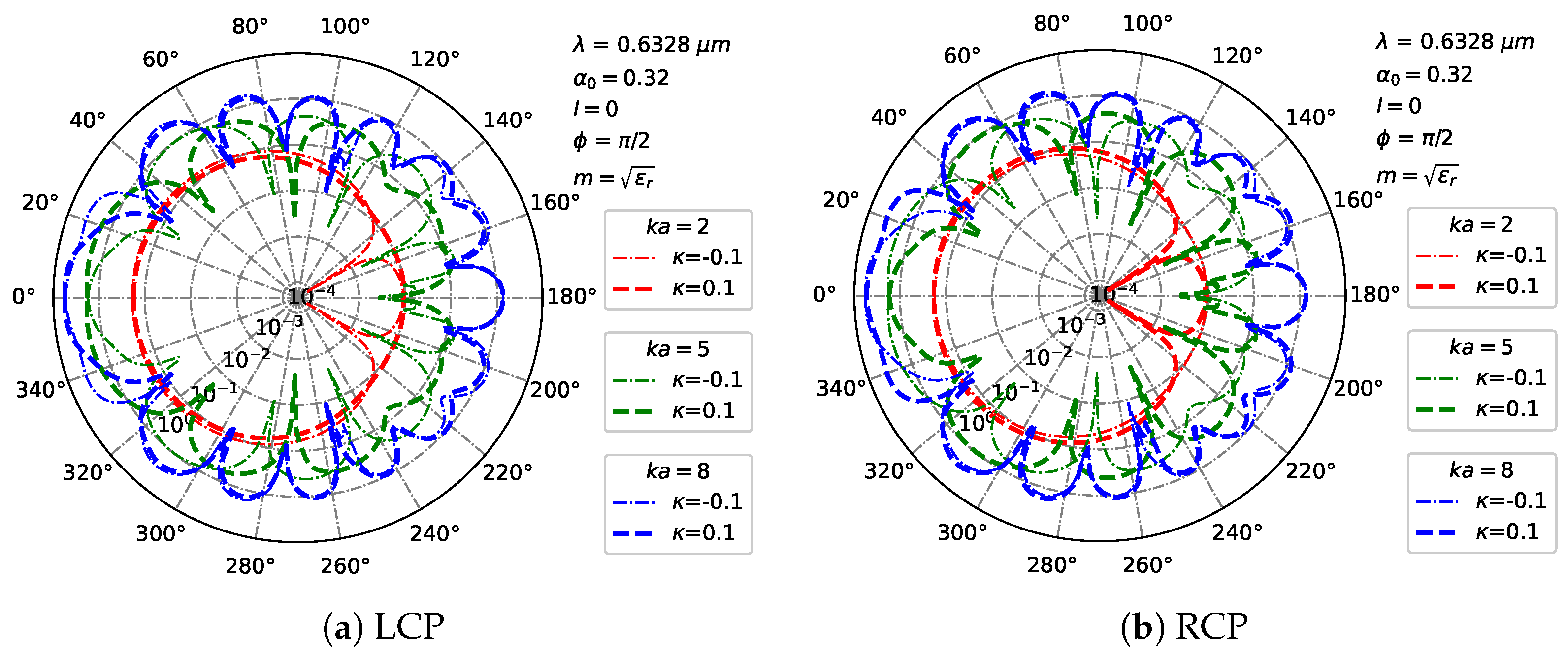
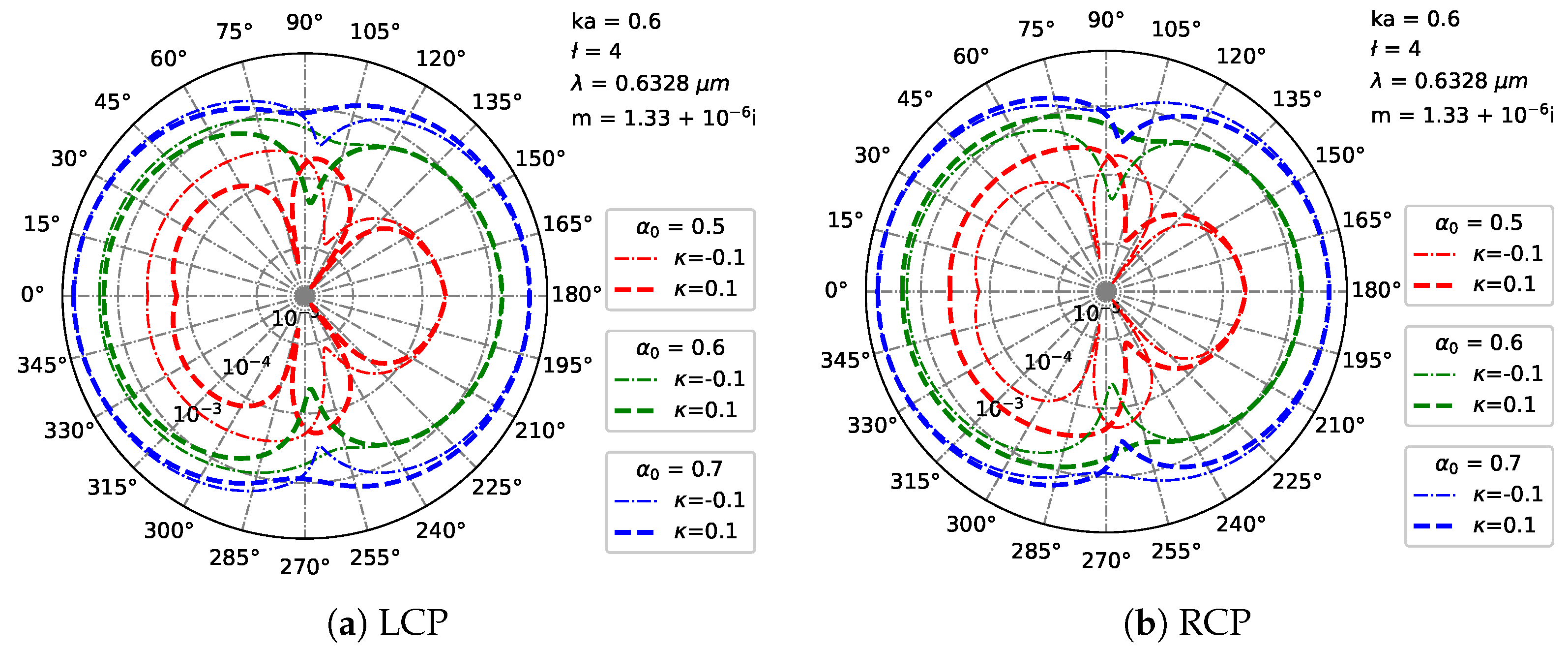
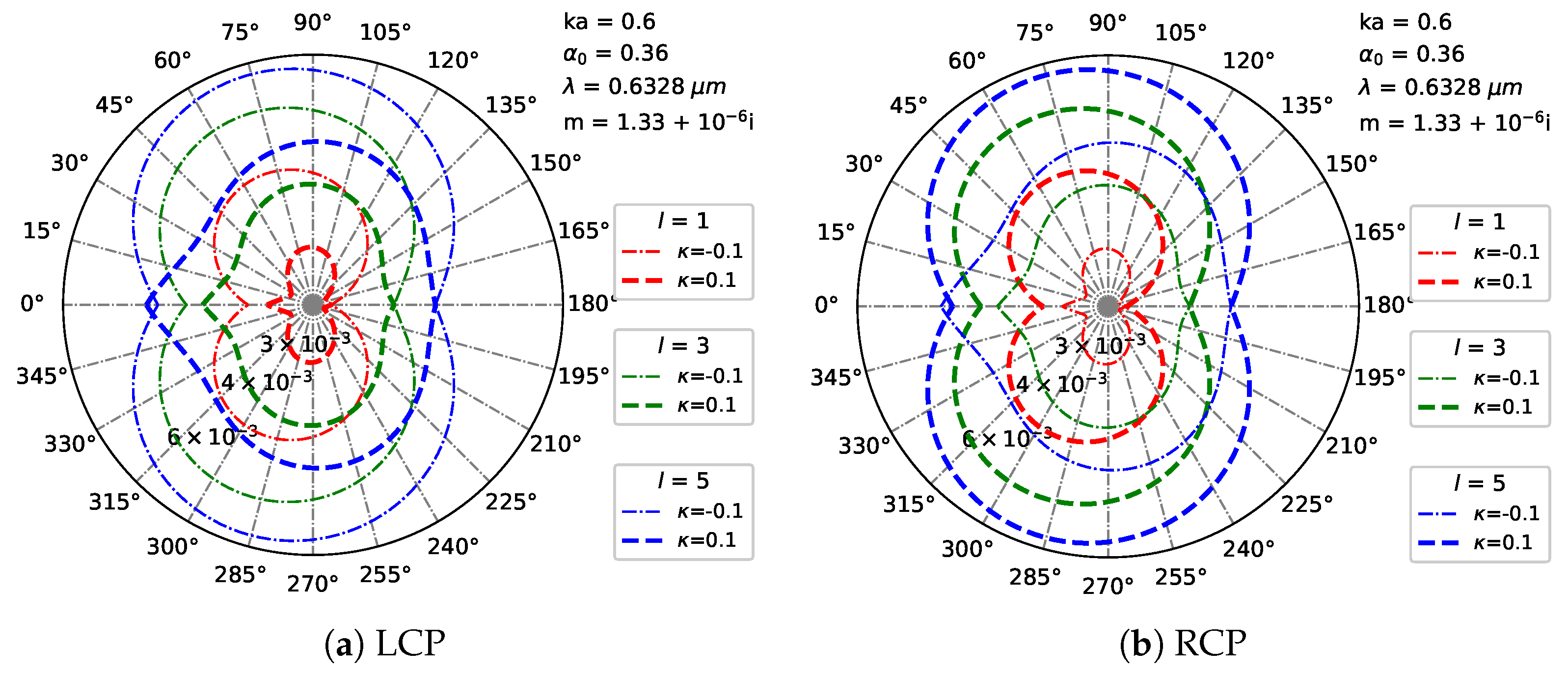
3.3. Far-Region Scattered Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GLMT | Generalized Lorenz–Mie theory |
| VASDM | Vector angular spectrum decomposition method |
| VSWFs | Vector spherical wave functions |
| BSCs | Beam-shape coefficients |
| DDA | Discrete dipole approximation |
| LCP | Left-circularly polarized |
| RCP | Right-circularly polarized |
References
- Guijarro, A.; Yus, M. The Origin of Chirality in the Molecules of Life: A Revision from Awareness to the Current Theories and Perspectives of This Unsolved Problem; Royal Society of Chemistry: London, UK, 2008. [Google Scholar]
- Teng, Y.; Gu, C.; Chen, Z.; Jiang, H.; Xiong, Y.; Liu, D.; Xiao, D. Advances and applications of chiral resolution in pharmaceutical field. Chirality 2022, 34, 1094–1119. [Google Scholar] [CrossRef] [PubMed]
- D’Orazio, G.; Fanali, C.; Asensio-Ramos, M.; Fanali, S. Chiral separations in food analysis. TrAC Trends Anal. Chem. 2017, 96, 151–171. [Google Scholar] [CrossRef]
- Xu, W.; Li, G.; Qu, H.; Zhang, H.; Ma, C.; He, Q.; Cheng, J.; Li, H. Enantioselective separation of agricultural fungicides based on chiral hybrid nanochannel membranes. Chem. Mater. 2024, 36, 1975–1981. [Google Scholar] [CrossRef]
- Wang, F.; Li, X.; Jiang, S.; Han, J.; Wu, J.; Yan, M.; Yao, Z. Enantioselective behaviors of chiral pesticides and enantiomeric signatures in foods and the environment. J. Agric. Food Chem. 2023, 71, 12372–12389. [Google Scholar] [CrossRef] [PubMed]
- Plum, E.; Fedotov, V.; Zheludev, N. Optical activity in extrinsically chiral metamaterial. Appl. Phys. Lett. 2008, 93, 191911. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I.; Fruhnert, M.; Rockstuhl, C. Dual and chiral objects for optical activity in general scattering directions. ACS Photonics 2015, 2, 376–384. [Google Scholar] [CrossRef]
- Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Meta-chirality: Fundamentals, construction and applications. Nanomaterials 2017, 7, 116. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Schäferling, M.; Duan, X.; Giessen, H.; Liu, N. Chiral plasmonics. Sci. Adv. 2017, 3, e1602735. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, A.; Jungmann, R.; Acuna, G.P.; Liu, N. DNA origami route for nanophotonics. ACS Photonics 2018, 5, 1151–1163. [Google Scholar] [CrossRef] [PubMed]
- Gorkunov, M.V.; Antonov, A.A.; Kivshar, Y.S. Metasurfaces with maximum chirality empowered by bound states in the continuum. Phys. Rev. Lett. 2020, 125, 093903. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Cohen, A.E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 2011, 332, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.; Lapthorn, A.; Kelly, S.; Barron, L.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Canaguier-Durand, A.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Mechanical separation of chiral dipoles by chiral light. New J. Phys. 2013, 15, 123037. [Google Scholar] [CrossRef]
- Tkachenko, G.; Brasselet, E. Optofluidic sorting of material chirality by chiral light. Nat. Commun. 2014, 5, 3577. [Google Scholar] [CrossRef] [PubMed]
- Takano, Y.; Takahashi, J.i.; Kaneko, T.; Marumo, K.; Kobayashi, K. Asymmetric synthesis of amino acid precursors in interstellar complex organics by circularly polarized light. Earth Planet. Sci. Lett. 2007, 254, 106–114. [Google Scholar] [CrossRef]
- Rodrigues, S.P.; Lan, S.; Kang, L.; Cui, Y.; Cai, W. Nonlinear imaging and spectroscopy of chiral metamaterials. Adv. Mater. 2014, 26, 6157–6162. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, S.P.; Cui, Y.; Lan, S.; Kang, L.; Cai, W. Metamaterials enable chiral-selective enhancement of two-photon luminescence from quantum emitters. Adv. Mater. 2014, 27, 1124–1130. [Google Scholar] [CrossRef] [PubMed]
- Lakhtakia, A.; Varadan, V.K.; Varadan, V.V. Scattering and absorption characteristics of lossy dielectric, chiral, nonspherical objects. Appl. Opt. 1985, 24, 4146–4154. [Google Scholar] [CrossRef] [PubMed]
- Patti, F.; Saija, R.; Denti, P.; Pellegrini, G.; Biagioni, P.; Iatì, M.A.; Maragò, O.M. Chiral optical tweezers for optically active particles in the T-matrix formalism. Sci. Rep. 2019, 9, 29. [Google Scholar] [CrossRef] [PubMed]
- Worasawate, D.; Mautz, J.R.; Arvas, E. Electromagnetic scattering from an arbitrarily shaped three-dimensional homogeneous chiral body. IEEE Trans. Antennas Propag. 2003, 51, 1077–1084. [Google Scholar] [CrossRef]
- Yuceer, M.; Mautz, J.R.; Arvas, E. Method of moments solution for the radar cross section of a chiral body of revolution. IEEE Trans. Antennas Propag. 2005, 53, 1163–1167. [Google Scholar] [CrossRef]
- Hasanovic, M.; Mei, C.; Mautz, J.R.; Arvas, E. Scattering from 3-D inhomogeneous chiral bodies of arbitrary shape by the method of moments. IEEE Trans. Antennas Propag. 2007, 55, 1817–1825. [Google Scholar] [CrossRef]
- Mei, C. Electromagnetic Scattering from an Arbitrarily Shaped Three Dimensional Inhomogeneous Bianisotropic Body. Ph.D. Dissertation, Syracuse University, Syracuse, NY, USA, 2007. [Google Scholar]
- Demir, V.; Elsherbeni, A.; Worasawate, D.; Arvas, E. A graphical user interface (GUI) for plane-wave scattering from a conducting, dielectric, or chiral sphere. IEEE Antennas Propag. Mag. 2004, 46, 94–99. [Google Scholar] [CrossRef]
- Kuzu, L.; Demir, V.; Elsherbeni, A.; Arvas, E. Electromagnetic scattering from arbitrarily shaped chiral objects using the finite difference frequency domain method. Prog. Electromagn. Res. 2007, 67, 1–24. [Google Scholar] [CrossRef]
- Schneider, A. Circular dichroism and optical rotatory dispersion of scattering suspensions. Chem. Phys. Lett. 1971, 8, 604–608. [Google Scholar] [CrossRef]
- Gordon, D.J. Mie scattering by optically active particles. Biochemistry 1972, 11, 413–420. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F. Light scattering by an optically active sphere. Chem. Phys. Lett. 1974, 29, 458–462. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Hinders, M.; Rhodes, B. Electromagnetic-wave scattering from chiral spheres in chiral media. Il Nuovo C. D 1992, 14, 575–583. [Google Scholar] [CrossRef]
- Cooray, M.; Ciric, I. Wave scattering by a chiral spheroid. JOSA A 1993, 10, 1197–1203. [Google Scholar] [CrossRef]
- Mitri, F. Nonparaxial Bessel and Bessel–Gauss pincers light-sheets. Phys. Lett. A 2017, 381, 171–175. [Google Scholar] [CrossRef]
- Ren, Y.X.; He, H.; Tang, H.; Wong, K.K. Non-diffracting light wave: Fundamentals and biomedical applications. Front. Phys. 2021, 9, 698343. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Hermosa, N.; Belmonte, A.; Torres, J.P. Measuring the translational and rotational velocities of particles in helical motion using structured light. Opt. Express 2014, 22, 16504–16509. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, A.; Prabhakar, S.; Singh, R.P. Entanglement of a quantum optical elliptic vortex. Phys. Lett. A 2011, 375, 1926–1929. [Google Scholar] [CrossRef]
- Mitri, F. Optical trapping of a perfect electromagnetic conductor (PEMC) sphere exhibiting rotary polarization using nonparaxial focused Gaussian single-beam tweezers. Results Opt. 2021, 4, 100089. [Google Scholar] [CrossRef]
- Mitri, F. Cylindrical particle manipulation and negative spinning using a nonparaxial Hermite- Gaussian light-sheet beam. J. Opt. 2016, 18, 105402. [Google Scholar] [CrossRef]
- Mitri, F. Arbitrary scattering of an electromagnetic zero-order Bessel beam by a dielectric sphere. Opt. Lett. 2011, 36, 766–768. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.G. Electromagnetic wave scattering of a high-order Bessel vortex beam by a dielectric sphere. IEEE Trans. Antennas Propag. 2011, 59, 4375–4379. [Google Scholar] [CrossRef]
- Mitri, F.; Li, R.; Guo, L.; Ding, C. Resonance scattering of a dielectric sphere illuminated by electromagnetic Bessel non-diffracting (vortex) beams with arbitrary incidence and selective polarizations. Ann. Phys. 2015, 361, 120–147. [Google Scholar] [CrossRef]
- Mitri, F.; Li, R.; Guo, L.; Ding, C. Optical tractor Bessel polarized beams. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 97–115. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, S.S. Scattering of laser beams and the optical potential well for a homogeneous sphere. JOSA 1983, 73, 303–312. [Google Scholar] [CrossRef]
- Yokota, M.; He, S.; Takenaka, T. Scattering of a HermiteGaussian beam field by a chiral sphere. JOSA A 2001, 18, 1681–1689. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Liao, T.; Zhang, H.; Hui, R. Gaussian beam scattering by a chiral sphere. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1946–1950. [Google Scholar] [CrossRef]
- Shang, Q.c.; Wu, Z.s.; Li, Z.j.; Li, H. Radiation force on a chiral sphere by a Gaussian beam. In Proceedings of the Optics in Health Care and Biomedical Optics IV. SPIE, Beijing, China, 18–20 October 2010; Volume 7845, pp. 425–430. [Google Scholar]
- Zhai, Y.; Zhang, H.; Sun, Y. On-axis Gaussian beam scattering by a chiral cylinder. JOSA A 2012, 29, 2509–2513. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Zhang, H.; Liu, C. Scattering of on-axis Gaussian beam by a chiral spheroid. JOSA A 2012, 29, 2381–2385. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, Y.; Liao, T.; Hui, R. Scattering of an axial Gaussian beam by a conducting spheroid with non-confocal chiral coating. Prog. Electromagn. Res. 2013, 135, 695–712. [Google Scholar] [CrossRef]
- Gouesbet, G. Optical forces exerted by on-axis Bessel beams on Rayleigh particles in the framework of generalized Lorenz-Mie theory. J. Quant. Spectrosc. Radiat. Transf. 2021, 260, 107471. [Google Scholar] [CrossRef]
- Li, T.; Li, X.; Yan, S.; Xu, X.; Wang, S.; Yao, B.; Wang, Z.; Zhu, S. Generation and conversion dynamics of dual Bessel beams with a photonic spin-dependent dielectric metasurface. Phys. Rev. Appl. 2021, 15, 014059. [Google Scholar] [CrossRef]
- Qiu, Z.; Cao, B.; Huang, K.; Zhang, X.; Lu, X. High-dimensional coding/decoding information with braiding period in free-space optical communication link. Optik 2022, 258, 168828. [Google Scholar] [CrossRef]
- Glukhova, S.A.; Yurkin, M.A. Vector Bessel beams: General classification and scattering simulations. Phys. Rev. A 2022, 106, 033508. [Google Scholar] [CrossRef]
- Gouesbet, G.; Lock, J.A.; Han, Y.P.; Wang, J. Efficient computation of arbitrary beam scattering on a sphere: Comments and rebuttal, with a review on the angular spectrum decomposition. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107913. [Google Scholar] [CrossRef]
- Gouesbet, G.; Xu, F.; Han, Y. Expanded description of electromagnetic arbitrary shaped beams in spheroidal coordinates, for use in light scattering theories: A review. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2249–2267. [Google Scholar] [CrossRef]
- Moura, T.; Andrade, U.; Mendes, J.; Rocha, M. Modulating the trapping and manipulation of semiconductor particles using Bessel beam optical tweezers. Opt. Lasers Eng. 2023, 170, 107778. [Google Scholar] [CrossRef]
- Gouesbet, G.; De Angelis, V.S.; Ambrosio, L.A. Optical forces and optical force categorizations exerted on quadrupoles in the framework of generalized Lorenz–Mie theory. J. Quant. Spectrosc. Radiat. Transf. 2023, 298, 108487. [Google Scholar] [CrossRef]
- Qu, T.; Wu, Z.; Mou, Y.; Li, Z. Analysis of scattering of an on-axis zero-order Bessel beam by a chiral sphere. Hongwai Yu Jiguang Gongcheng/Infrared Laser Eng. 2014, 43, 2867–2872. [Google Scholar]
- Li, M.; Yan, S.; Zhang, Y.; Liang, Y.; Zhang, P.; Yao, B. Optical sorting of small chiral particles by tightly focused vector beams. Phys. Rev. A 2019, 99, 033825. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Zhang, Y.; Chen, X.; Yao, B. Optical separation and discrimination of chiral particles by vector beams with orbital angular momentum. Nanoscale Adv. 2021, 3, 6897–6902. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F. Interaction of Bessel pincers light-sheets with an absorptive subwavelength sphere coated by a plasmonic layer. JOSA B 2017, 34, 1471–1477. [Google Scholar] [CrossRef]
- Mitri, F. Nonparaxial fractional Bessel and Bessel–Gauss auto-focusing light-sheet pincers and their higher-order spatial derivatives. J. Opt. 2017, 19, 055602. [Google Scholar] [CrossRef]
- Verveer, P.J.; Swoger, J.; Pampaloni, F.; Greger, K.; Marcello, M.; Stelzer, E.H. High-resolution three-dimensional imaging of large specimens with light sheet–Based microscopy. Nat. Methods 2007, 4, 311–313. [Google Scholar] [CrossRef] [PubMed]
- Keller, P.J.; Schmidt, A.D.; Wittbrodt, J.; Stelzer, E.H. Reconstruction of zebrafish early embryonic development by scanned light sheet microscopy. Science 2008, 322, 1065–1069. [Google Scholar] [CrossRef] [PubMed]
- Santi, P.A. Light sheet fluorescence microscopy: A review. J. Histochem. Cytochem. 2011, 59, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Wei, B.; Wei, Q.; Li, R.; Chen, S.; Song, N. Optical Force of Bessel Pincer Light-Sheets Beam on a Dielectric Sphere of Arbitrary Size. Nanomaterials 2022, 12, 3723. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, R.; Wei, B.; Song, N.; Yang, L.; Sun, H. Scattering of a non-paraxial Bessel pincer light-sheet by a dielectric sphere of arbitrary size. J. Quant. Spectrosc. Radiat. Transf. 2021, 268, 107647. [Google Scholar] [CrossRef]
- Lindell, I.; Sihvola, A.; Tretyakov, S.; Viitanen, A.J. Electromagnetic Waves in Chiral and Bi-Isotropic Media; Artech House: Boston, MA, USA, 1994. [Google Scholar]
- Xu, Y.l. Electromagnetic scattering by an aggregate of spheres. Appl. Opt. 1995, 34, 4573–4588. [Google Scholar] [CrossRef] [PubMed]
- Zangwill, A. Modern Electrodynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Ye, Q.; Lin, H. On deriving the Maxwell stress tensor method for calculating the optical force and torque on an object in harmonic electromagnetic fields. Eur. J. Phys. 2017, 38, 045202. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 2021. [Google Scholar]
- Lorenz, L. XXXVIII. On the identity of the vibrations of light with electrical currents. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1867, 34, 287–301. [Google Scholar] [CrossRef]
- Ren, K.F.; Gouesbet, G.; Gréhan, G. Integral localized approximation in generalized Lorenz–Mie theory. Appl. Opt. 1998, 37, 4218–4225. [Google Scholar] [CrossRef] [PubMed]
- Lakhtakia, A. Beltrami Fields in Chiral Media; World Scientific: Singapore, 1994; Volume 2. [Google Scholar]
- Shang, Q.C.; Wu, Z.S.; Qu, T.; Li, Z.J.; Bai, L.; Gong, L. Analysis of the radiation force and torque exerted on a chiral sphere by a Gaussian beam. Opt. Express 2013, 21, 8677–8688. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wang, N.; Lu, W.; Liu, S.; Lin, Z. Tailoring azimuthal optical force on lossy chiral particles in Bessel beams. Phys. Rev. A 2014, 90, 043850. [Google Scholar] [CrossRef]
- Chen, H.; Lu, W.; Yu, X.; Xue, C.; Liu, S.; Lin, Z. Optical torque on small chiral particles in generic optical fields. Opt. Express 2017, 25, 32867–32878. [Google Scholar] [CrossRef]
- Sarkar, D.; Halas, N. General vector basis function solution of Maxwell’s equations. Phys. Rev. E 1997, 56, 1102. [Google Scholar] [CrossRef]
- Wu, Z.S.; Shang, Q.C.; Li, Z.J. Calculation of electromagnetic scattering by a large chiral sphere. Appl. Opt. 2012, 51, 6661–6668. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, S.; Wei, Q.; Li, R.; Wei, B.; Song, N. Scattering Characteristics of a Circularly Polarized Bessel Pincer Light-Sheet Beam Interacting with a Chiral Sphere of Arbitrary Size. Micromachines 2025, 16, 845. https://doi.org/10.3390/mi16080845
Zhang S, Chen S, Wei Q, Li R, Wei B, Song N. Scattering Characteristics of a Circularly Polarized Bessel Pincer Light-Sheet Beam Interacting with a Chiral Sphere of Arbitrary Size. Micromachines. 2025; 16(8):845. https://doi.org/10.3390/mi16080845
Chicago/Turabian StyleZhang, Shu, Shiguo Chen, Qun Wei, Renxian Li, Bing Wei, and Ningning Song. 2025. "Scattering Characteristics of a Circularly Polarized Bessel Pincer Light-Sheet Beam Interacting with a Chiral Sphere of Arbitrary Size" Micromachines 16, no. 8: 845. https://doi.org/10.3390/mi16080845
APA StyleZhang, S., Chen, S., Wei, Q., Li, R., Wei, B., & Song, N. (2025). Scattering Characteristics of a Circularly Polarized Bessel Pincer Light-Sheet Beam Interacting with a Chiral Sphere of Arbitrary Size. Micromachines, 16(8), 845. https://doi.org/10.3390/mi16080845







