Study on Anisotropic Mechanical Properties of Single-Crystal Silicon at Different Strain Rates
Abstract
1. Introduction
2. Nanoindentation Testing Technology and Sample Pretreatment
2.1. Nanoindentation Testing
2.2. Tensile and Compression Testing
2.3. Test Samples
3. Effects of Different Strain Rates on Mechanical Properties of Single-Crystal Silicon
3.1. Load–Displacement Curve
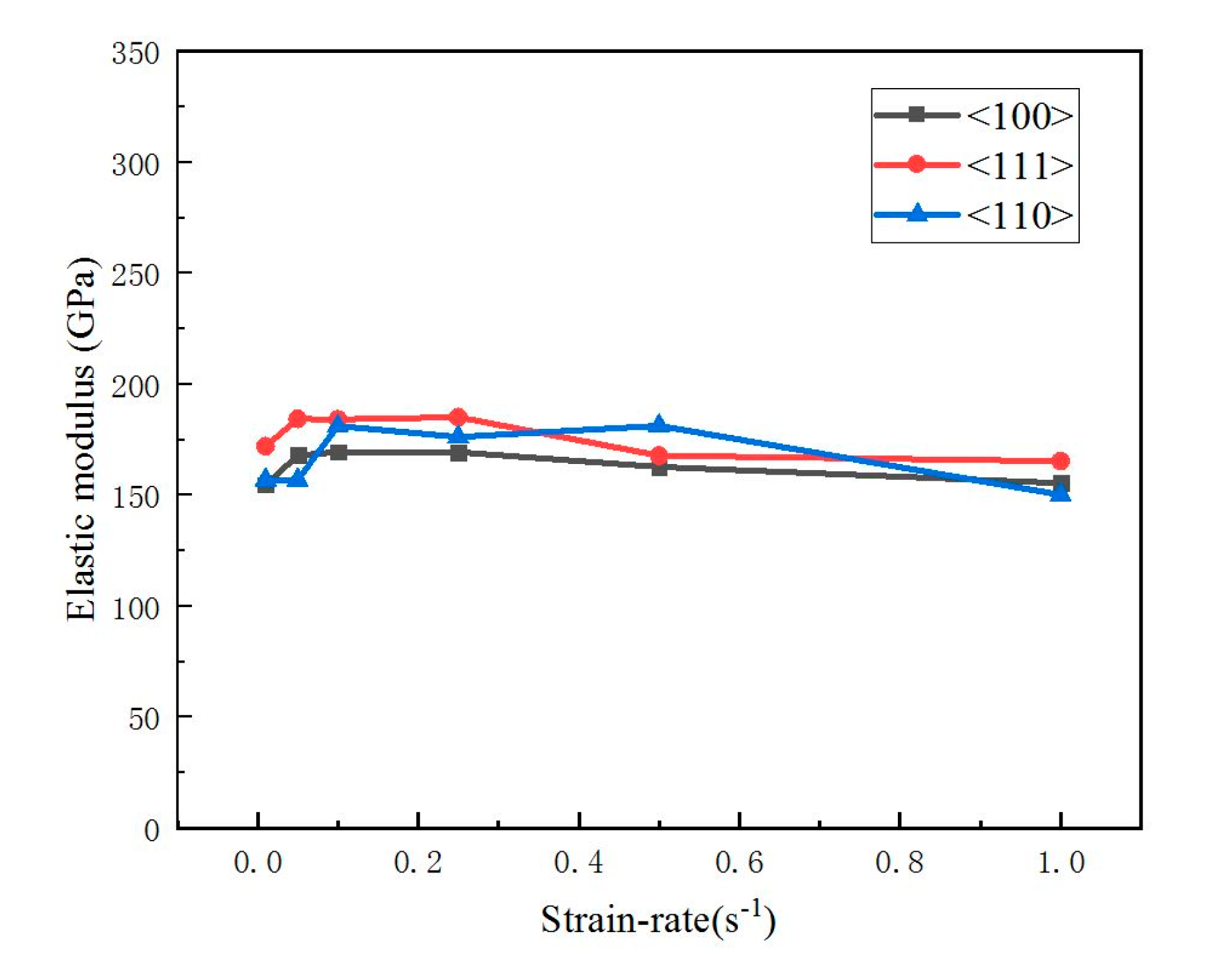
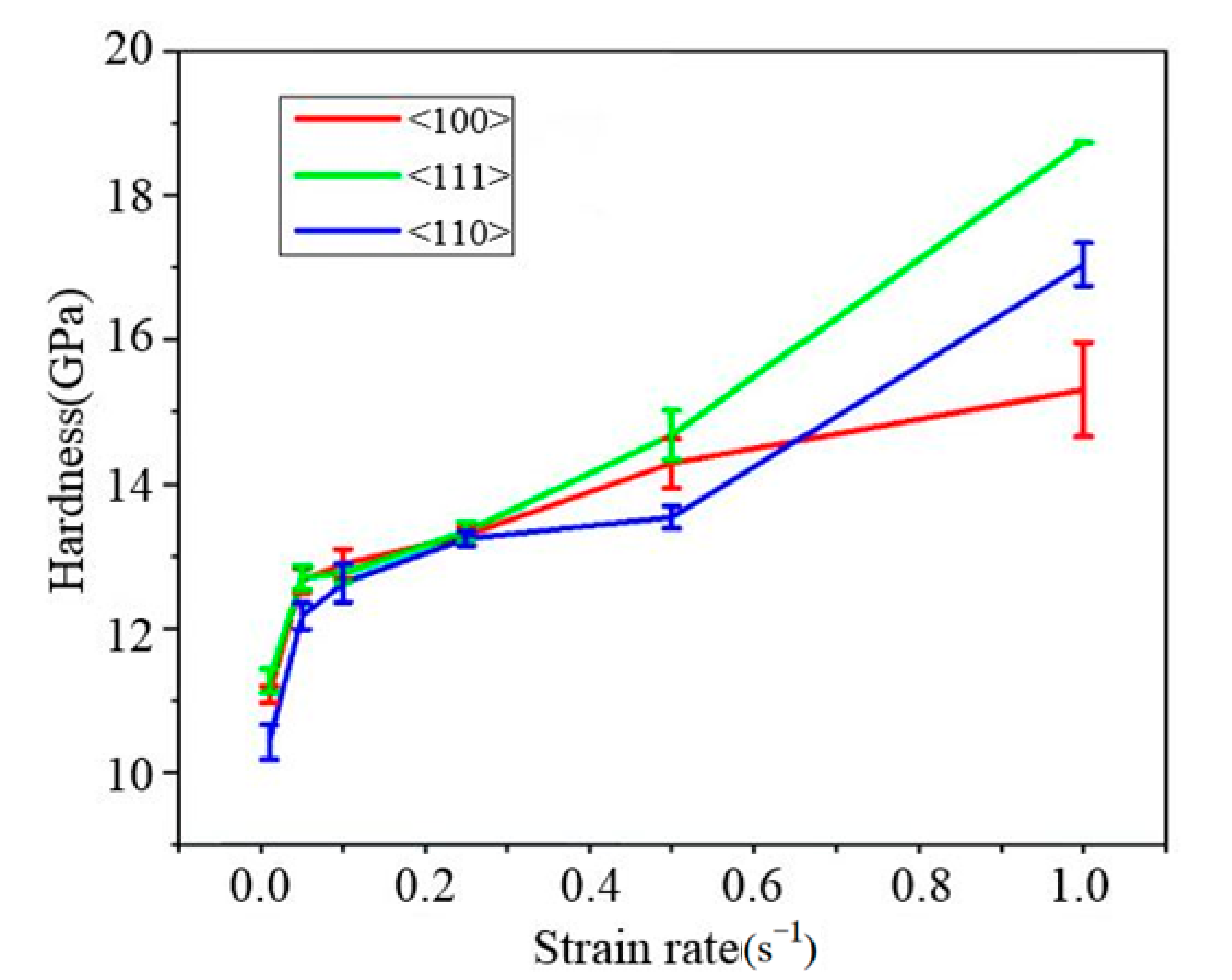
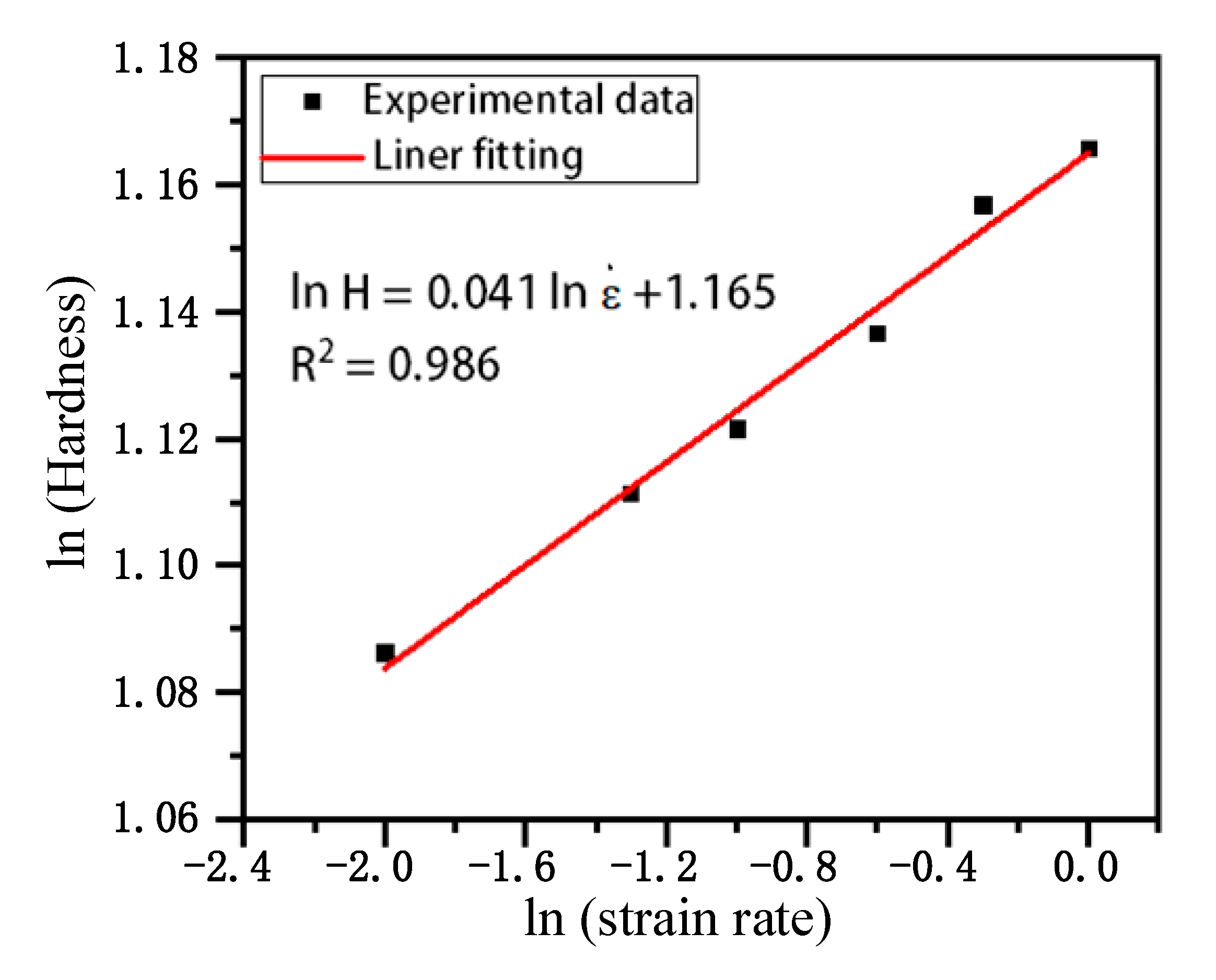
3.2. Elastic Modulus and Hardness
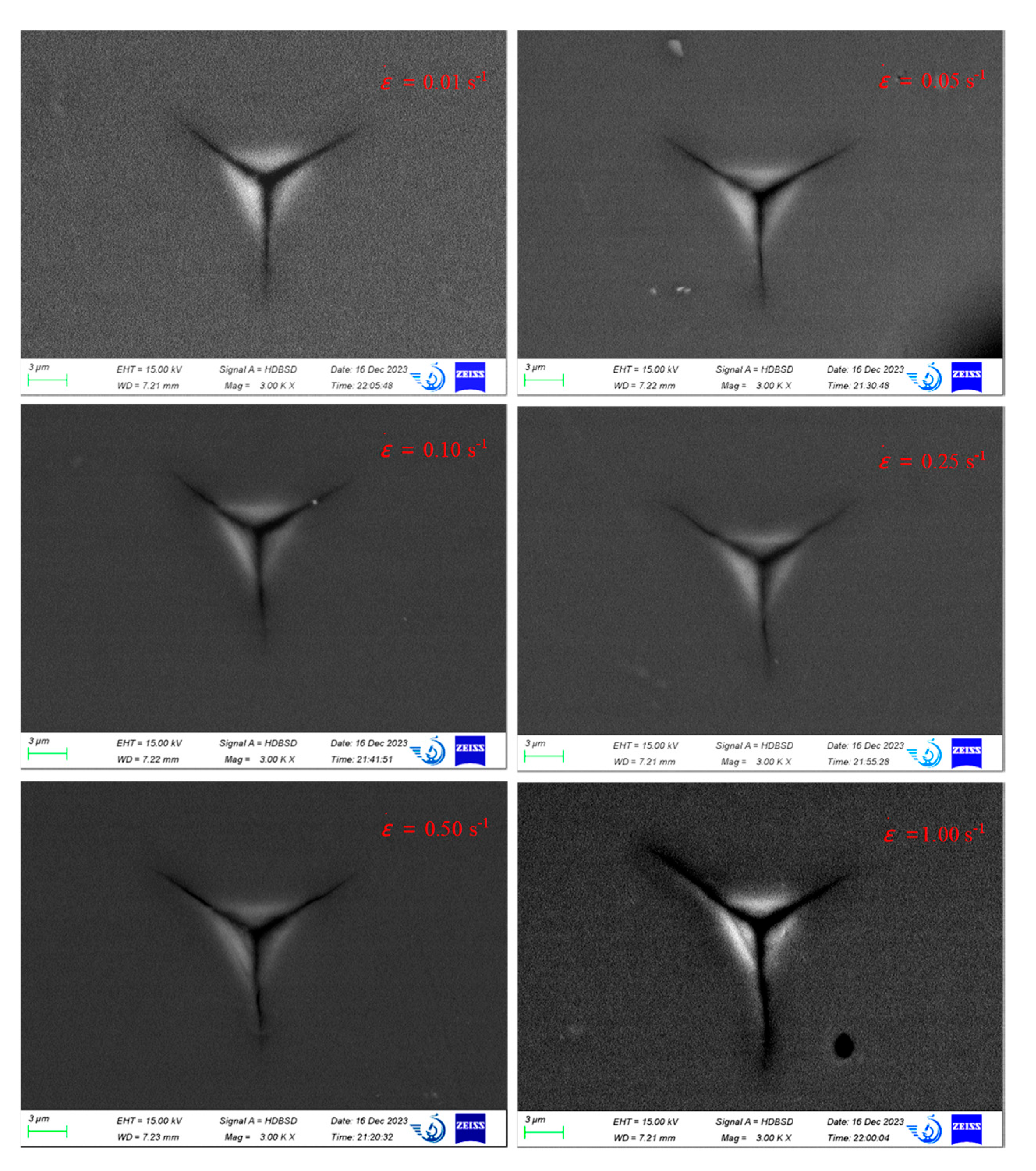
3.3. Study on Anisotropy of Fracture Toughness in Monocrystalline Silicon
- (a)
- Relationship between crack propagation and different strain rates
- (b) Fracture toughness
4. Real Stress–Strain Relationship of Single-Crystal Silicon at Different Strain Rates
5. Results
- (1)
- The indentation load–displacement curve demonstrates that phenomena such as pop-in, pop-out, and elbow can induce phase transformation in single-crystal silicon during testing. The elastic recovery rate of single-crystal silicon at room temperature is approximately 42%.
- (2)
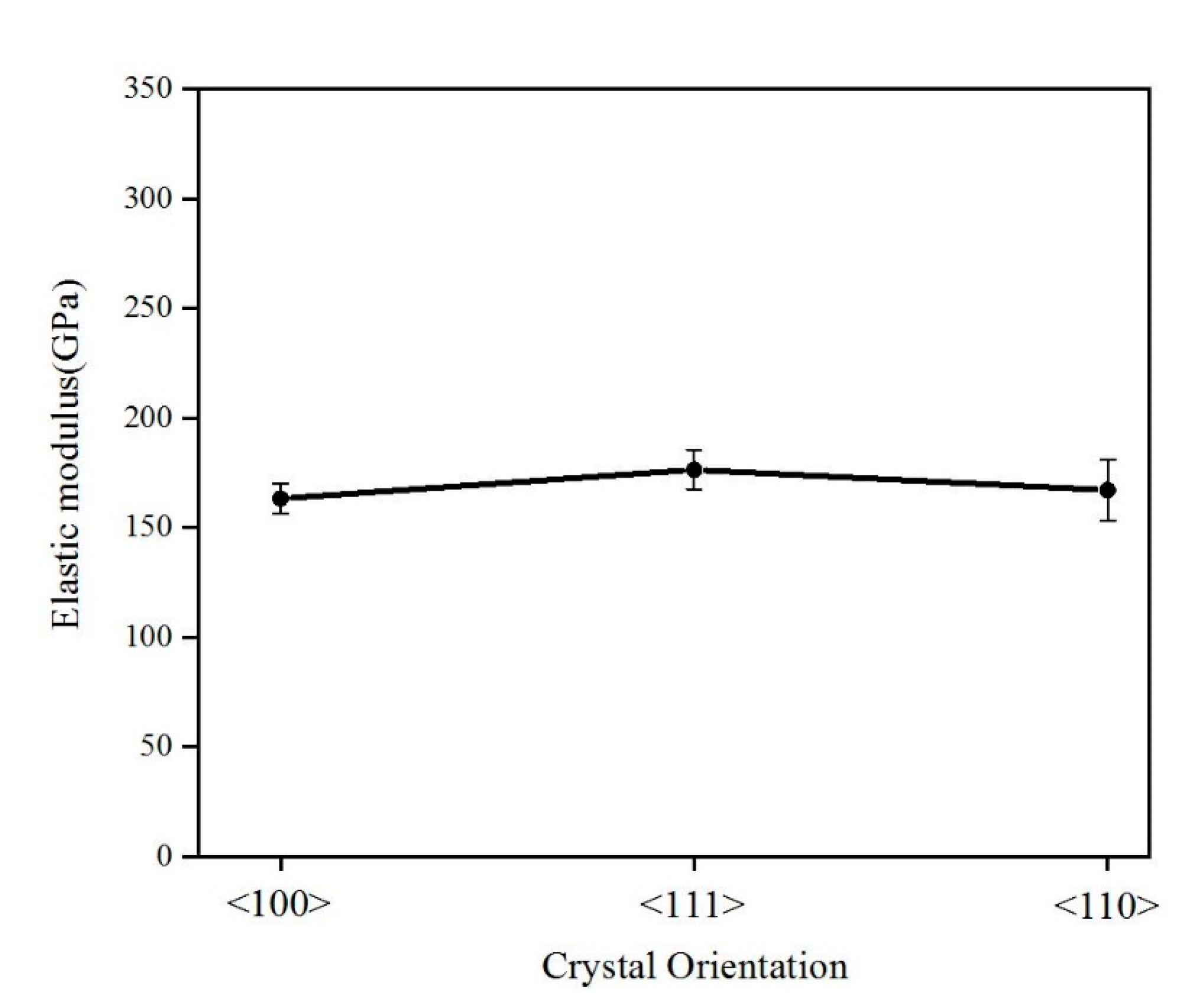
- The elastic modulus of single-crystal silicon demonstrates negligible size effects across varying strain rates. The average elastic moduli for the <100>, <111>, and <110> orientations are recorded as 163.34 GPa, 176.53 GPa, and 167.18 GPa, respectively. Conversely, hardness exhibits a positive correlation with the strain rate, with <111>-oriented silicon displaying notably higher hardness compared with its <100> and <110> counterparts.
- (3)
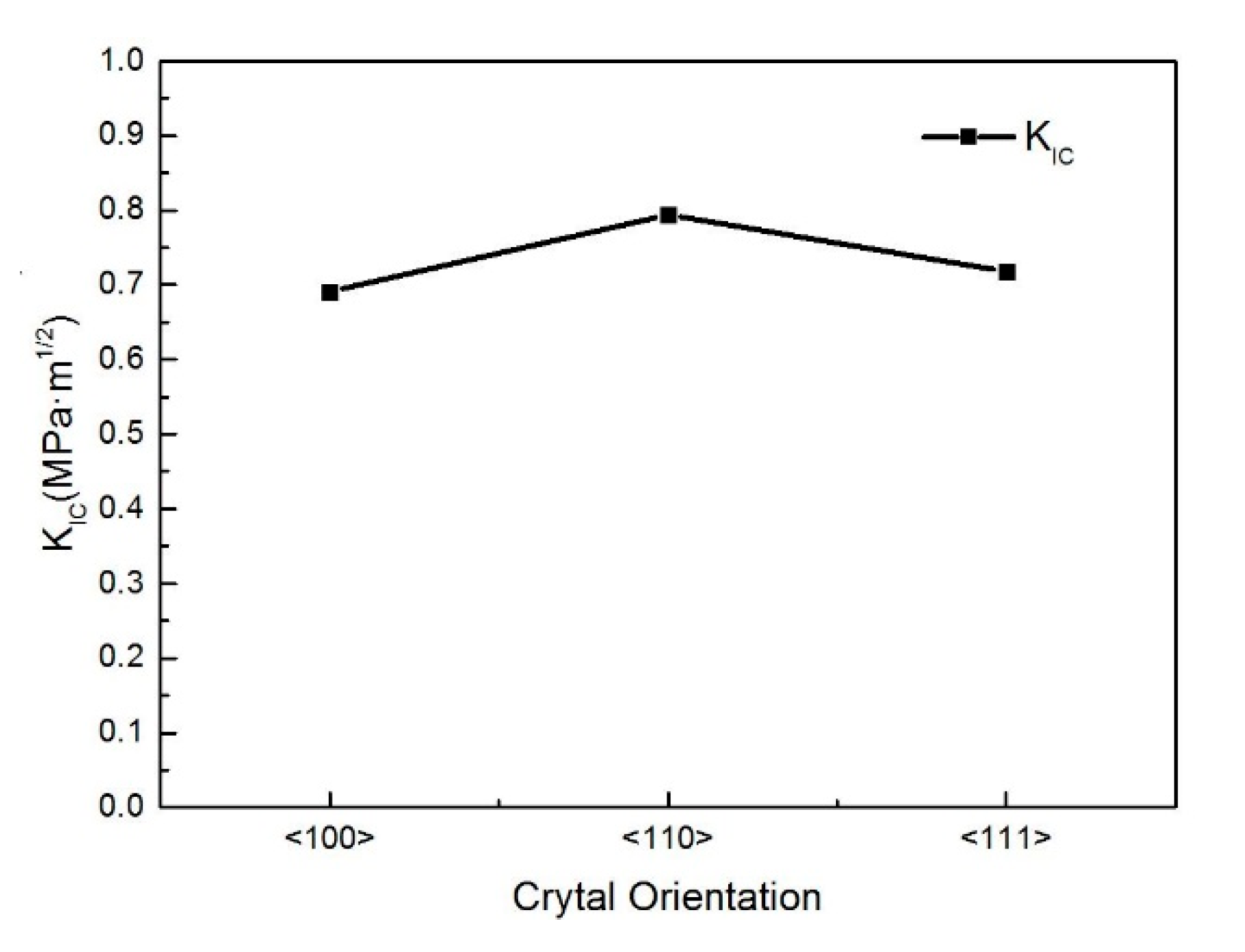
- Room temperature fracture toughness of single-crystal silicon reveals substantial anisotropy; the <100> orientation exhibits the minimum toughness at 0.691 MPa·m1/2, whereas the <110> orientation shows the maximum toughness, 0.797 MPa·m1/2.
- (4)
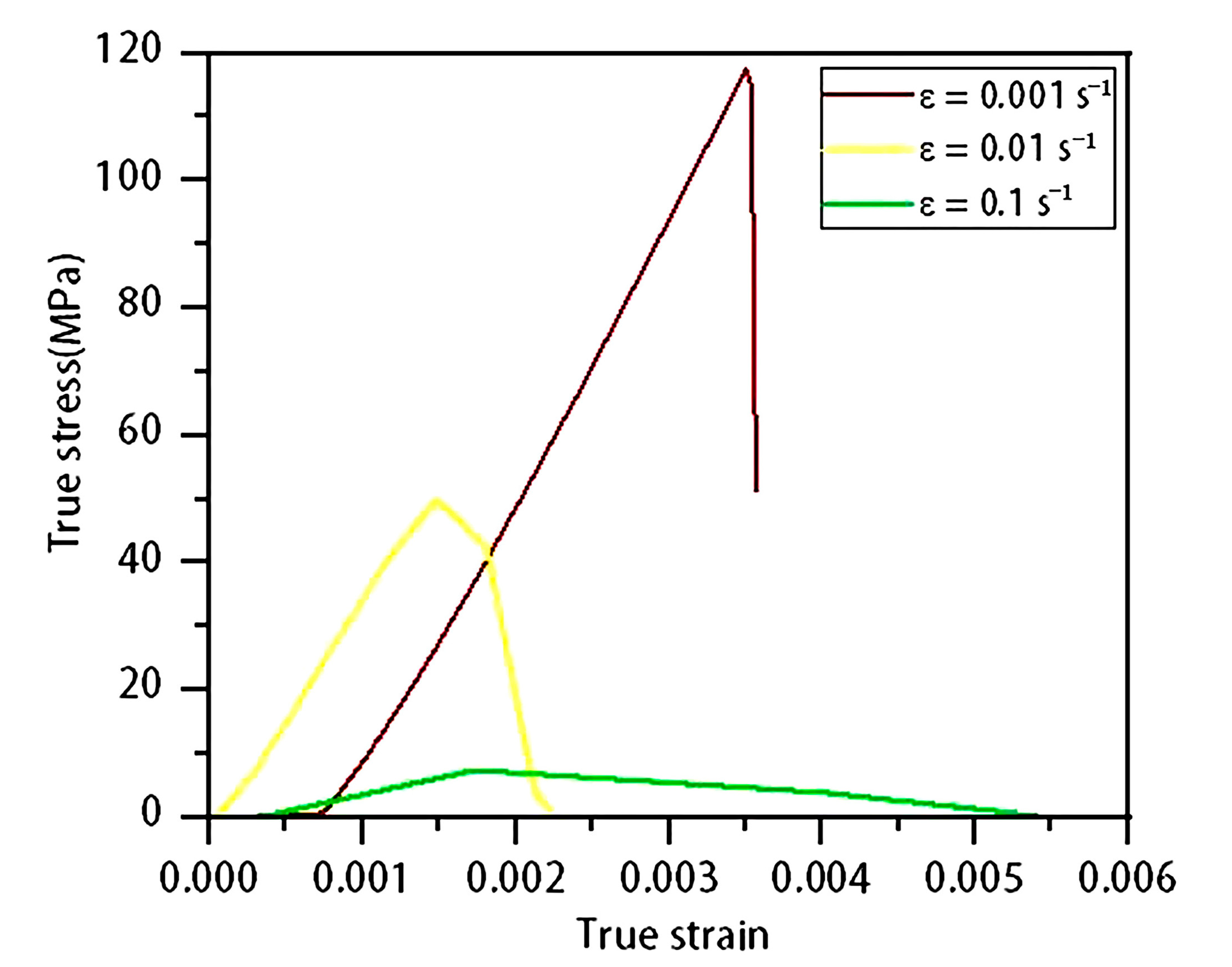
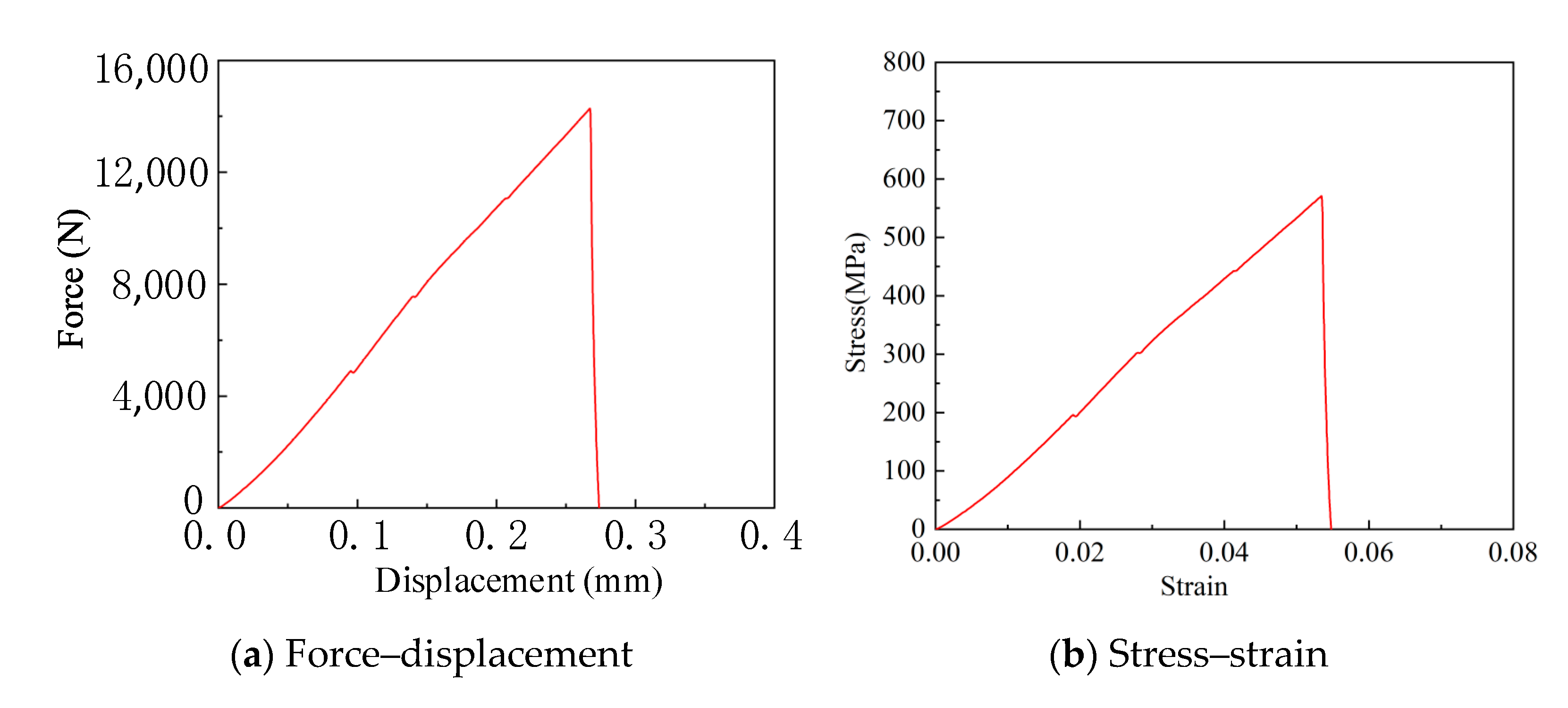
- Both tensile testing and compression testing indicate that single-crystal silicon undergoes fracture under a compressive load of 14,000 N, which translates into a compressive strength of 550 MPa and a static strain of 0.055. Specifically, <100>-oriented silicon exhibits a fracture strength of 117 MPa at a strain rate of 0.001 s−1, which escalates to 550 MPa when the strain rate increases to 0.01 s−1.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arab, A.; Feng, Q. Reliability research on micro-and nano-electromechanical systems: A review. Int. J. Adv. Manuf. Technol. 2014, 74, 1679–1690. [Google Scholar] [CrossRef]
- Marinis, T.F. The future of microelectromechanical systems (MEMS). Strain 2009, 45, 208–220. [Google Scholar] [CrossRef]
- Dastgeer, G.; Nisar, S.; Zulfiqar, M.W.; Eom, J.; Imran, M.; Akbar, K. A review on recent progress and challenges in high-efficiency perovskite solar cells. Nano Energy 2024, 132, 110401. [Google Scholar] [CrossRef]
- Dastgeer, G.; Nisar, S.; Rasheed, A.; Akbar, K.; Chavan, V.D.; Kim, D.-K.; Wabaidur, S.M.; Zulfiqar, M.W.; Eom, J. Atomically engineered, high-speed non-volatile flash memory device exhibiting multibit data storage operations. Nano Energy 2024, 119, 109106. [Google Scholar] [CrossRef]
- Ruffin, P.B. MEMS-based sensor arrays for military applications. Smart Structures and Materials 2002: Smart Electronics, MEMS, and Nanotechnology. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart, San Diego, CA, USA, 11 July 2002; Volume 4700, pp. 111–121. [Google Scholar] [CrossRef]
- Agnello, A.; Dosch, J.; Metz, R.; Sill, R. Acceleration sensing technologies for severe mechanical shock. Sound Vib. 2014, 48, 8–19. [Google Scholar]
- Ghisi, A.; Mariani, S. Effect of imperfections due to material heterogeneity on the offset of polysilicon MEMS structures. Sensors 2019, 19, 3256. [Google Scholar] [CrossRef]
- Namazu, T. Mechanical property measurement of micro/nanoscale materials for MEMS: A review. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 308–324. [Google Scholar] [CrossRef]
- Cook, R.F.; DelRio, F.W.; Boyce, B.L. Predicting strength distributions of MEMS structures using flaw size and spatial density. Microsyst. Nanoeng. 2019, 5, 49. [Google Scholar] [CrossRef]
- Rickhey, F.; Marimuthu, K.P.; Lee, K.; Lee, H. Indentation cracking of monocrystalline silicon considering fracture anisotropy. Theor. Appl. Fract. Mech. 2019, 100, 128–138. [Google Scholar] [CrossRef]
- Huang, J.Y.; E, J.C.; Huang, J.W.; Sun, T.; Fezzaa, K.; Xu, S.L.; Luo, S.N. Dynamic deformation and fracture of single crystal silicon: Fracture modes, damage laws, and anisotropy. Acta Mater. 2016, 114, 136–145. [Google Scholar] [CrossRef]
- Li, L.; Ge, P. Analytical modeling of the stress field in scratching anisotropic single-crystal silicon. Mater. Sci. Semicond. Process. 2022, 152, 107099. [Google Scholar] [CrossRef]
- Hong, Y.; Zhang, N.; Xiong, L. Nanoscale plastic deformation mechanisms of single crystalline silicon under compression, tension and indentation. J. Micromechanics Mol. Phys. 2016, 1, 1640007. [Google Scholar] [CrossRef]
- Schaffar, G.J.K.; Tscharnuter, D.; Maier-Kiener, V. Exploring the high-temperature deformation behavior of monocrystalline silicon-an advanced nanoindentation study. Mater. Des. 2023, 233, 112198. [Google Scholar] [CrossRef]
- Masolin, A.; Bouchard, P.O.; Martini, R.; Bernacki, M. Thermo-mechanical and fracture properties in single-crystal silicon. J. Mater. Sci. 2013, 48, 979–988. [Google Scholar] [CrossRef]
- Boyd, E.J.; Uttamchandani, D. Measurement of the anisotropy of young’s modulus in single-crystal silicon. J. Microelectromechanical Syst. 2011, 21, 243–249. [Google Scholar] [CrossRef]
- Barredo, J.; Parra, V.; Guerrero, I.; Fraile, A.; Hermanns, L. On the mechanical strength of monocrystalline, multicrystalline and quasi-monocrystalline silicon wafers: A four-line bending test study. Prog. Photovolt. Res. Appl. 2014, 22, 1204–1212. [Google Scholar] [CrossRef]
- Tao, H.; Zeng, Q.; Liu, Y.; Zhao, D.; Lu, X. Influence of anisotropy on material removal and deformation mechanism based on nanoscratch tests of monocrystal silicon. Tribol. Int. 2023, 187, 108736. [Google Scholar] [CrossRef]
- Du, X.; Zhao, H.; Zhang, L.; Yang, Y.; Xu, H.; Fu, H.; Li, L. Molecular dynamics investigations of mechanical behaviours in monocrystalline silicon due to nanoindentation at cryogenic temperatures and room temperature. Sci. Rep. 2015, 5, 16275. [Google Scholar] [CrossRef]
- Chung, Y.J.; Lee, G.H.; Beom, H.G. Atomistic insights into the phase transformation of single-crystal silicon during nanoindentation. Nanomaterials 2022, 12, 2071. [Google Scholar] [CrossRef]
- Chai, P.; Li, S.; Li, Y.; Liang, L.; Yin, X. Mechanical behavior investigation of 4H-SiC single crystal at the micro-nano scale. Micromachines 2020, 11, 102. [Google Scholar] [CrossRef]
- Geetha, D.; Pratyank, R.; Kiran, P. Nano-deformation behavior of silicon (100) film studied by depth sensing indentation and nanoscratch technique. Mater. Res. Express 2018, 5, 046407. [Google Scholar] [CrossRef]
- Ma, D.J.; Sun, L.; Wang, L.Z.; Wang, J.L. A new formula for evaluating indentation toughness in ceramics. Exp. Mech. 2018, 58, 177–182. [Google Scholar] [CrossRef]
- Gong, J. Determining indentation toughness by incorporating true hardness into fracture mechanics equations. J. Eur. Ceram. Soc. 1999, 19, 1585–1592. [Google Scholar] [CrossRef]
- Bruns, S.; Johanns, K.E.; Rehman, H.U.R.; Pharr, G.M.; Durst, K. Constitutive modeling of indentation cracking in fused silica. J. Am. Ceram. Soc. 2017, 100, 1928–1940. [Google Scholar] [CrossRef]
- Östlund, F.; Rzepiejewska-Malyska, K.; Leifer, K.; Hale, L.M.; Tang, Y.; Ballarini, R.; Gerberich, W.W.; Michler, J. Brittle-to-ductile transition in uniaxial compression of silicon pillars at room temperature. Adv. Funct. Mater. 2009, 19, 2439–2444. [Google Scholar] [CrossRef]
- Wang, H.; Ramesh, K.T. Dynamic strength and fragmentation of hot-pressed silicon carbide under uniaxial compression. Acta Mater. 2004, 52, 355–367. [Google Scholar] [CrossRef]
- Domnich, V.; Gogotsi, Y.; Dub, S. Effect of phase transformations on the shape of the unloading curve in the nanoindentation of silicon. Appl. Phys. Lett. 2000, 76, 2214–2216. [Google Scholar] [CrossRef]
- Domnich, V.; Aratyn, Y.; Kriven, W.M.; Gogotsi, Y. Temperature dependence of silicon hardness: Experimental evidence of phase transformations. Rev. Adv. Mater. Sci. 2008, 17, 33–41. [Google Scholar]
- Huang, H.; Zhao, H.; Shi, C.; Zhang, L.; Wan, S.; Geng, C. Randomness and statistical laws of indentation-induced pop-out in single crystal silicon. Materials 2013, 6, 1496–1505. [Google Scholar] [CrossRef]
- Sidiropoulos, A.D.; Harea, E.; Konstantinidis, A.A.; Aifantis, E.C. “Pop-in” and “pop-out” effect in monocrystalline silicon. A statistical investigation. J. Mech. Behav. Mater. 2017, 26, 65–71. [Google Scholar] [CrossRef]
- Han, G.; Marimuthu, K.P.; Lee, H. Evaluation of thin film material properties using a deep nanoindentation and ANN. Mater. Des. 2022, 221, 111000. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Zhao, D.; Niu, Y.; Bai, D.; Wang, Y.; Song, M.; Zhao, J.; Wang, S.; Zhu, B.; et al. Effect of temperature on the nanoindentation behavior of monocrystalline silicon by molecular dynamics simulations. Mater. Today Commun. 2024, 40, 110010. [Google Scholar] [CrossRef]
- Sperling, S.O.; Bertens, T.; Hoefnagels, J.P.M.; Broek, K.v.D.; Geers, M. Experimental-numerical analysis of silicon micro-scratching. Int. J. Solids Struct. 2024, 295, 112809. [Google Scholar] [CrossRef]
- Bi, M.; Zhu, J.; Luo, Y.; Cai, H.; Li, X.; Wang, X.; Wei, Y.; Wang, X.; Hu, C.; Hu, J.; et al. Effect of deposition temperature on the surface, structural, and mechanical properties of HfO2 using chemical vapor deposition (CVD). Coatings 2022, 12, 1731. [Google Scholar] [CrossRef]
- Panich, N. Nanoindentation of silicon (100) studied by experimental and finite element method. KMUTT Res. Dev. J. 2004, 27, 273–284. [Google Scholar]
- Stabler, C.; Célarié, F.; Rouxel, T.; Limbach, R.; Wondraczek, L.; Riedel, R.; Ionescu, E. Effect of composition and high-temperature annealing on the local deformation behavior of silicon oxycarbides. J. Eur. Ceram. Soc. 2019, 39, 2287–2296. [Google Scholar] [CrossRef]
- Rocha-Rangel, E. Fracture toughness determinations by means of indentation fracture. In Nanocomposites with Unique Properties and Applications in Medicine and Industry; IntechOpen Limited: London, UK, 2011; pp. 21–38. [Google Scholar] [CrossRef]
- Zhu, X.K.; Joyce, J.A. Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization. Eng. Fract. Mech. 2012, 85, 1–46. [Google Scholar] [CrossRef]
- Gallo, P.; Sumigawa, T.; Kitamura, T. Experimental characterization at nanoscale of single crystal silicon fracture toughness. Fract. Struct. Integr. 2019, 13, 408–415. [Google Scholar] [CrossRef]

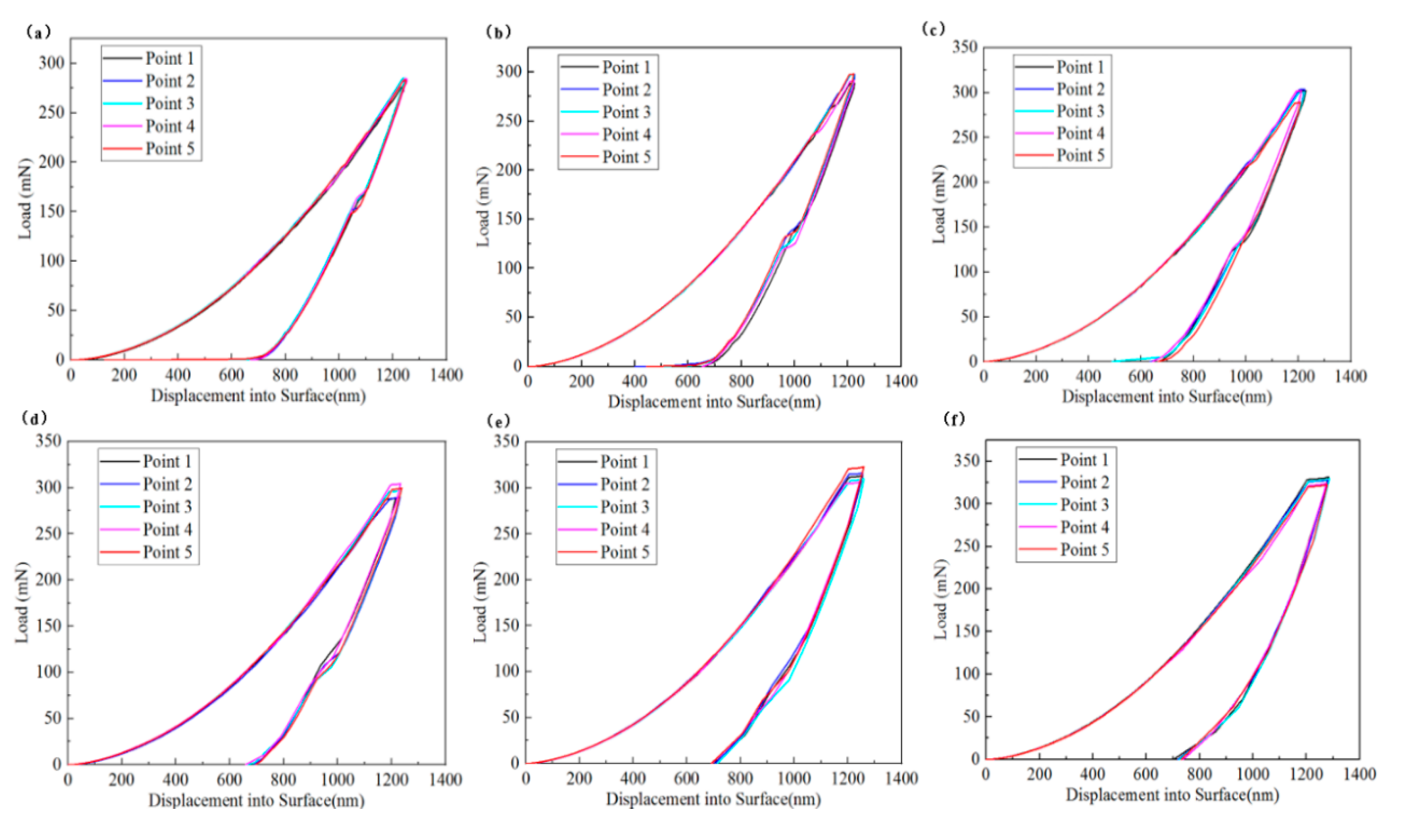
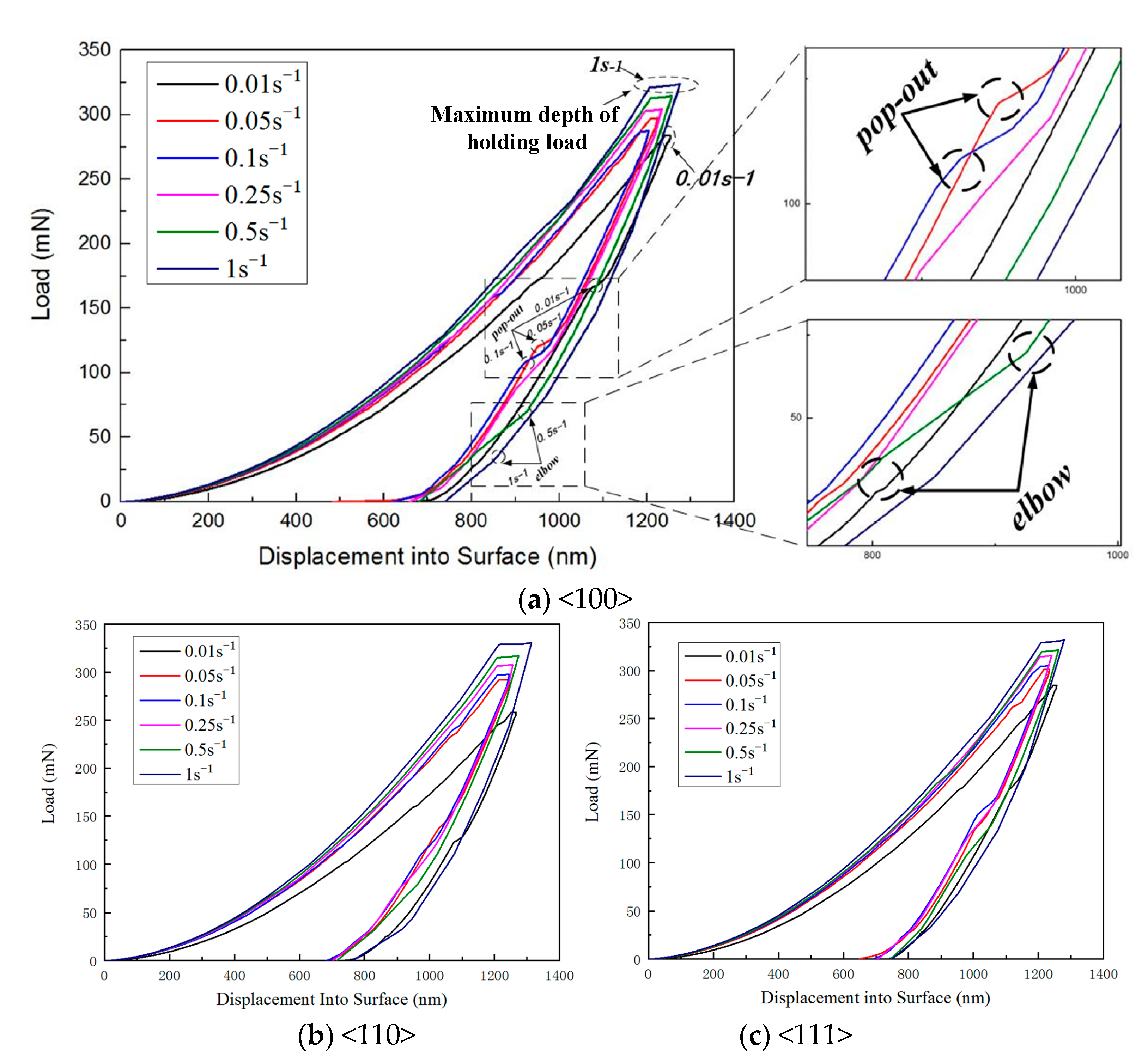
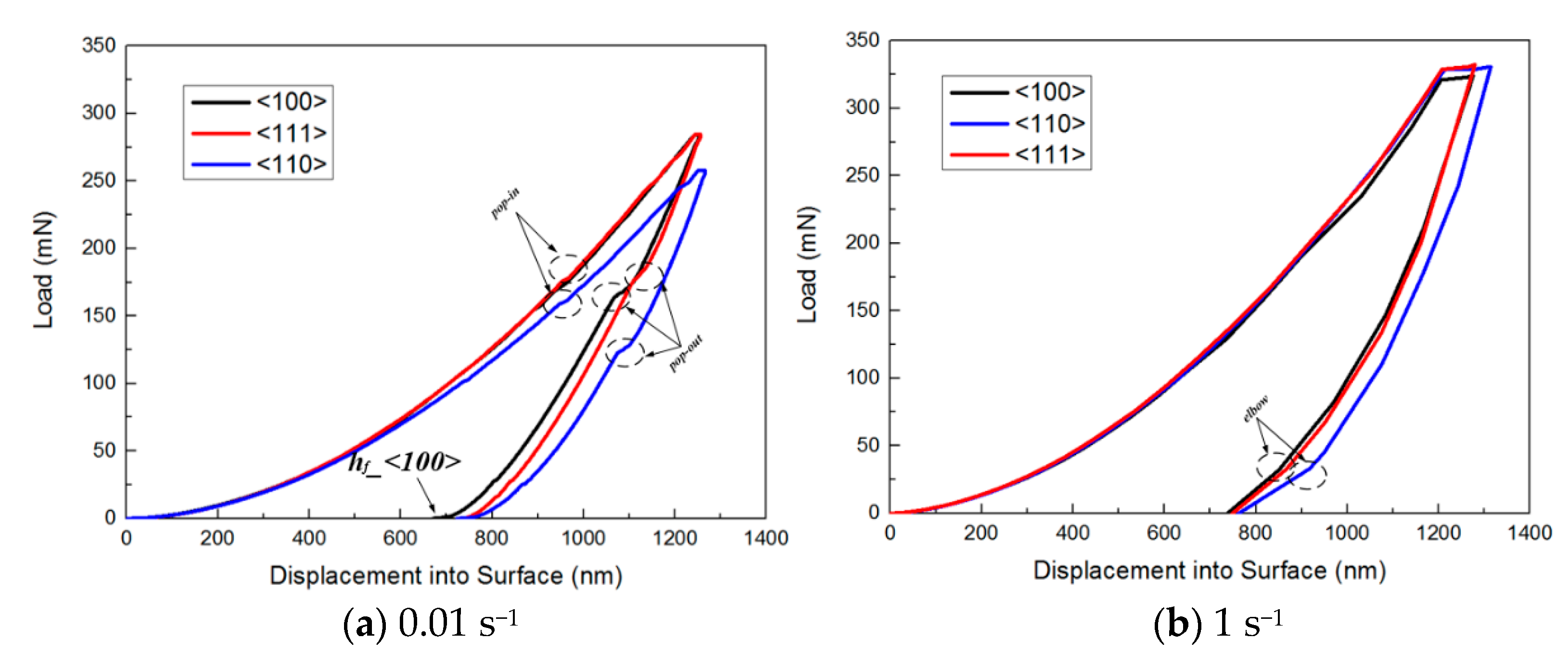
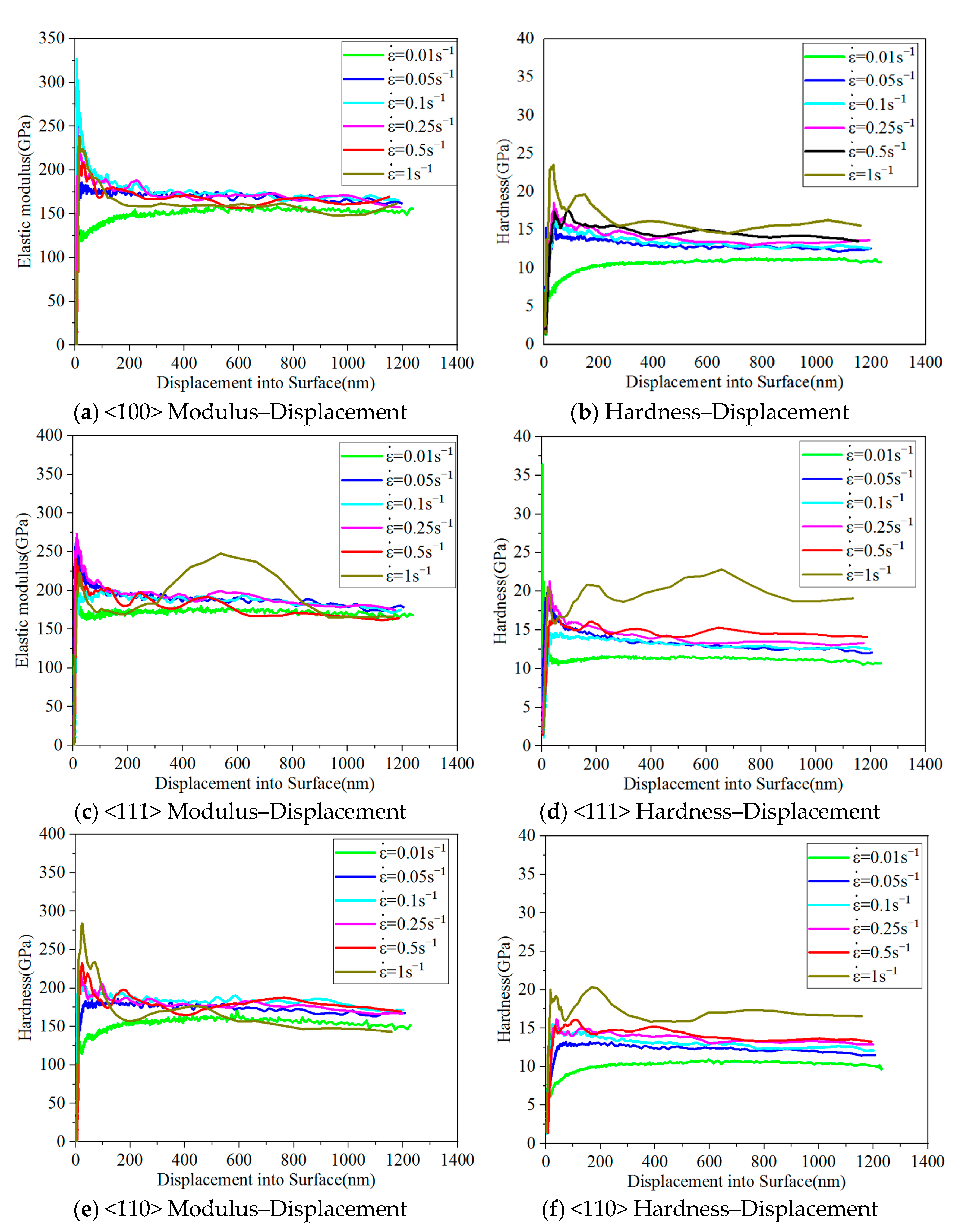
| Strain Rate | Crystallographic Orientation | hmax (nm) | hf (nm) | hmax − hf (nm) | Elasticity of Response Rate |
|---|---|---|---|---|---|
| 0.01 s−1 | <100> | 1252.58 | 671.25 | 581.33 | 46.41% |
| <111> | 1255.40 | 735.84 | 519.56 | 41.38% | |
| <110> | 1266.17 | 724.17 | 542.00 | 42.81% | |
| 1 s−1 | <100> | 1275.43 | 738.33 | 537.10 | 42.10% |
| <111> | 1313.84 | 760.72 | 553.12 | 42.10% | |
| <110> | 1279.76 | 748.22 | 531.54 | 41.53% |
| Crystallographic Orientation | E/H | 0.01 s−1 | 0.05 s−1 | 0.10 s−1 | 0.25 s−1 | 0.50 s−1 | 1.00 s−1 |
|---|---|---|---|---|---|---|---|
| <100> | E (GPa) | 154.81 ± 1.94 | 167.93 ± 3.05 | 169.56 ± 2.53 | 169.48 ± 2.56 | 162.77 ± 3.98 | 155.48 ± 5.98 |
| H (GPa) | 11.08 ± 0.12 | 12.66 ± 0.1 7 | 12.89 ± 0.21 | 13.29 ± 0.12 | 14.29 ± 0.34 | 15.31 ± 0.65 | |
| <111> | E (GPa) | 172.13 ± 2.51 | 184.36 ± 4.11 | 184.17 ± 4.49 | 185.23 ± 5.94 | 167.89 ± 2.30 | 165.38 ± 0.40 |
| H (GPa) | 11.27 ± 0.16 | 12.70 ± 0.16 | 12.76 ± 0.22 | 13.74 ± 0.12 | 14.68 ± 0.34 | 18.73 ± 0.00 | |
| <110> | E (GPa) | 156.97 ± 3.02 | 156.97 ± 3.25 | 181.26 ± 3.70 | 176.25 ± 4.60 | 181.36 ± 4.27 | 150.25 ± 4.49 |
| H (GPa) | 10.43 ± 0.24 | 12.17 ± 0.18 | 12.63 ± 0.27 | 13.24 ± 0.10 | 13.54 ± 0.16 | 17.04 ± 0.30 |
| Crystallographic Orientation | 1 | 2 | 3 | 4 | 5 | Average Value | |
|---|---|---|---|---|---|---|---|
| <100> | C (μm) | 9.452 | 9.162 | 9.358 | 9.185 | 9.263 | 9.284 |
| <110> | C (μm) | 8.452 | 8.261 | 8.781 | 8.755 | 8.805 | 8.611 |
| <111> | C (μm) | 8.858 | 9.441 | 9.265 | 9.453 | 8.256 | 9.054 |
| Crystallographic Orientation | δ | E (Gpa) | H (GPa) | Fmax (mN) | Ca (μm) | KIC (MPa·m1/2) |
|---|---|---|---|---|---|---|
| <100> | 0.016 | 189.438 | 11.486 | 300 | 9.284 | 0.691 |
| <110> | 0.016 | 201.253 | 11.441 | 300 | 8.611 | 0.797 |
| <111> | 0.016 | 192.849 | 11.294 | 300 | 9.054 | 0.718 |
| Strain Rate | 0.01 s−1 | 0.05 s−1 | 0.10 s−1 | 0.25 s−1 | 0.50 s−1 | 1.00 s−1 |
|---|---|---|---|---|---|---|
| α | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 |
| E (Gpa) | 165 | 168 | 171 | 168 | 168 | 177 |
| H (GPa) | 12.2 | 12.9 | 13.2 | 13.7 | 14.4 | 14.7 |
| Fmax (mN)) | 196.2 | 283.3 | 287.5 | 299.8 | 300.8 | 317.4 |
| C1 (μm) | 5.96 | 8.92 | 8.46 | 8.68 | 8.45 | 9.13 |
| C2 (μm) | 5.86 | 8.34 | 8.18 | 7.66 | 7.93 | 9.85 |
| C3 (μm) | 6.58 | 7.13 | 7.94 | 8.69 | 8.90 | 8.07 |
| Ca (μm) | 6.13 | 8.13 | 8.19 | 8.34 | 8.43 | 9.02 |
| KIC (MPa·m1/2) | 0.761 | 0.706 | 0.706 | 0.697 | 0.672 | 0.650 |
| Strain Rate | 0.01 s−1 | 0.05 s−1 | 0.10 s−1 | 0.25 s−1 | 0.50 s−1 | 1.00 s−1 |
|---|---|---|---|---|---|---|
| α | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 | 0.016 |
| E (GPa) | 165 | 168 | 171 | 168 | 168 | 177 |
| H (GPa) | 12.2 | 12.9 | 13.2 | 13.7 | 14.4 | 14.7 |
| Fmax (mN) | 280.4 | 288.6 | 292.6 | 301.1 | 303.9 | 309.8 |
| C1 (μm) | 7.87 | 7.92 | 7.75 | 7.78 | 8.58 | 7.78 |
| C2 (μm) | 6.82 | 6.33 | 8.14 | 7.72 | 7.21 | 10.54 |
| C3 (μm) | 7.47 | 8.23 | 7.88 | 8.47 | 8.78 | 9.43 |
| Ca (μm) | 7.39 | 7.49 | 7.92 | 7.99 | 8.19 | 9.25 |
| KIC (MPa·m1/2) | 0.821 | 0.813 | 0.756 | 0.747 | 0.709 | 0.611 |
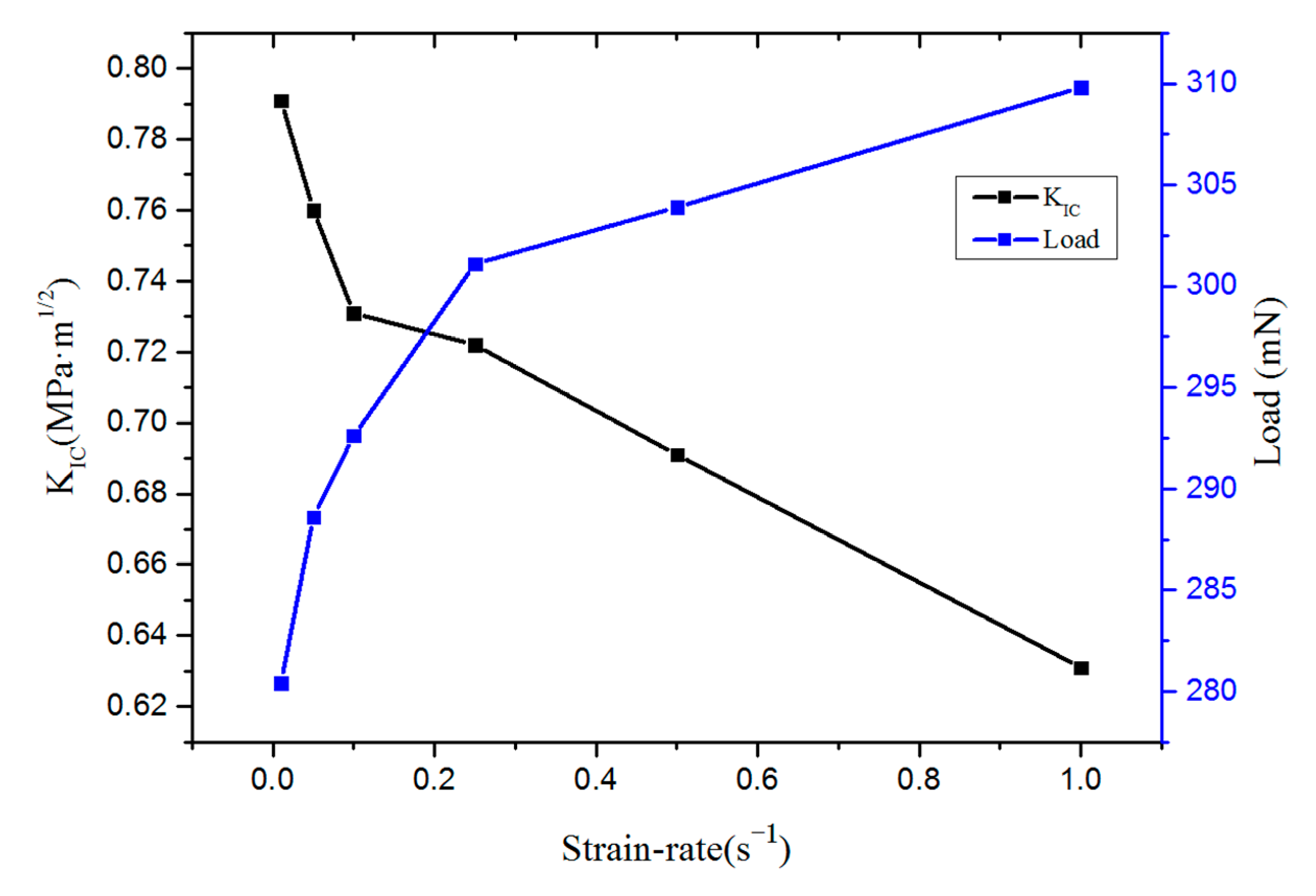
| Strain Rate | 0.01 s−1 | 0.05 s−1 | 0.10 s−1 | 0.25 s−1 | 0.50 s−1 | 1.00 s−1 |
|---|---|---|---|---|---|---|
| Fmax (mN) | 280.4 | 288.6 | 292.6 | 301.1 | 303.9 | 309.8 |
| KIC (MPa·m1/2) | 0.791 | 0.760 | 0.731 | 0.722 | 0.691 | 0.631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Xue, W.; Lou, W.; Liu, M.; Feng, H.; Wang, X.; Li, S.; Wu, S. Study on Anisotropic Mechanical Properties of Single-Crystal Silicon at Different Strain Rates. Micromachines 2025, 16, 744. https://doi.org/10.3390/mi16070744
Tian Z, Xue W, Lou W, Liu M, Feng H, Wang X, Li S, Wu S. Study on Anisotropic Mechanical Properties of Single-Crystal Silicon at Different Strain Rates. Micromachines. 2025; 16(7):744. https://doi.org/10.3390/mi16070744
Chicago/Turabian StyleTian, Zhongwang, Wei Xue, Wenzhong Lou, Min Liu, Hengzhen Feng, Xiaoxia Wang, Shiteng Li, and Shaokuan Wu. 2025. "Study on Anisotropic Mechanical Properties of Single-Crystal Silicon at Different Strain Rates" Micromachines 16, no. 7: 744. https://doi.org/10.3390/mi16070744
APA StyleTian, Z., Xue, W., Lou, W., Liu, M., Feng, H., Wang, X., Li, S., & Wu, S. (2025). Study on Anisotropic Mechanical Properties of Single-Crystal Silicon at Different Strain Rates. Micromachines, 16(7), 744. https://doi.org/10.3390/mi16070744





