Spectrum Fitting Approach for Passive Wireless SAW Sensor Interrogation Using Software-Defined Radio
Abstract
1. Introduction
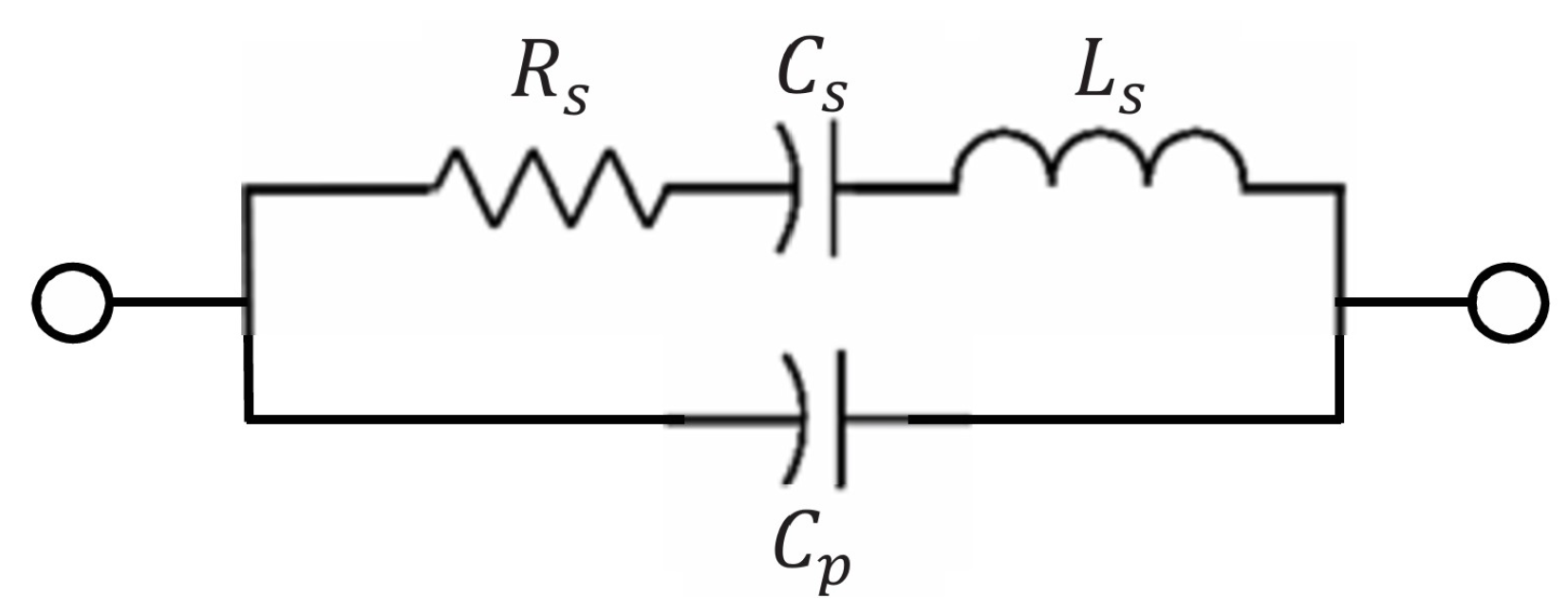
2. Theory and Simulation of the Proposed Method
2.1. Theoretical Analysis
2.2. Measurement Error Simulation
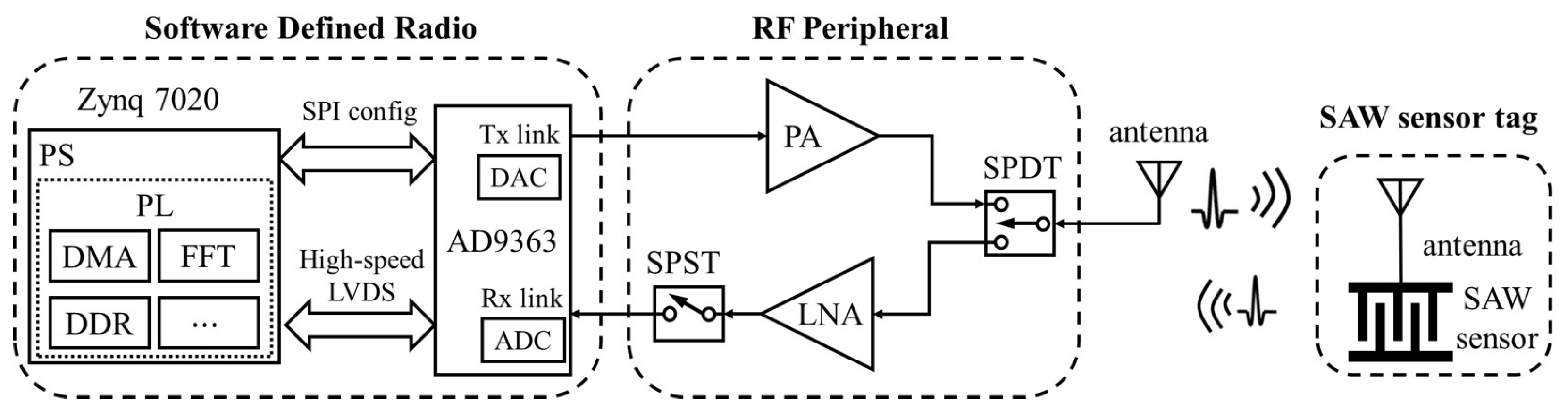
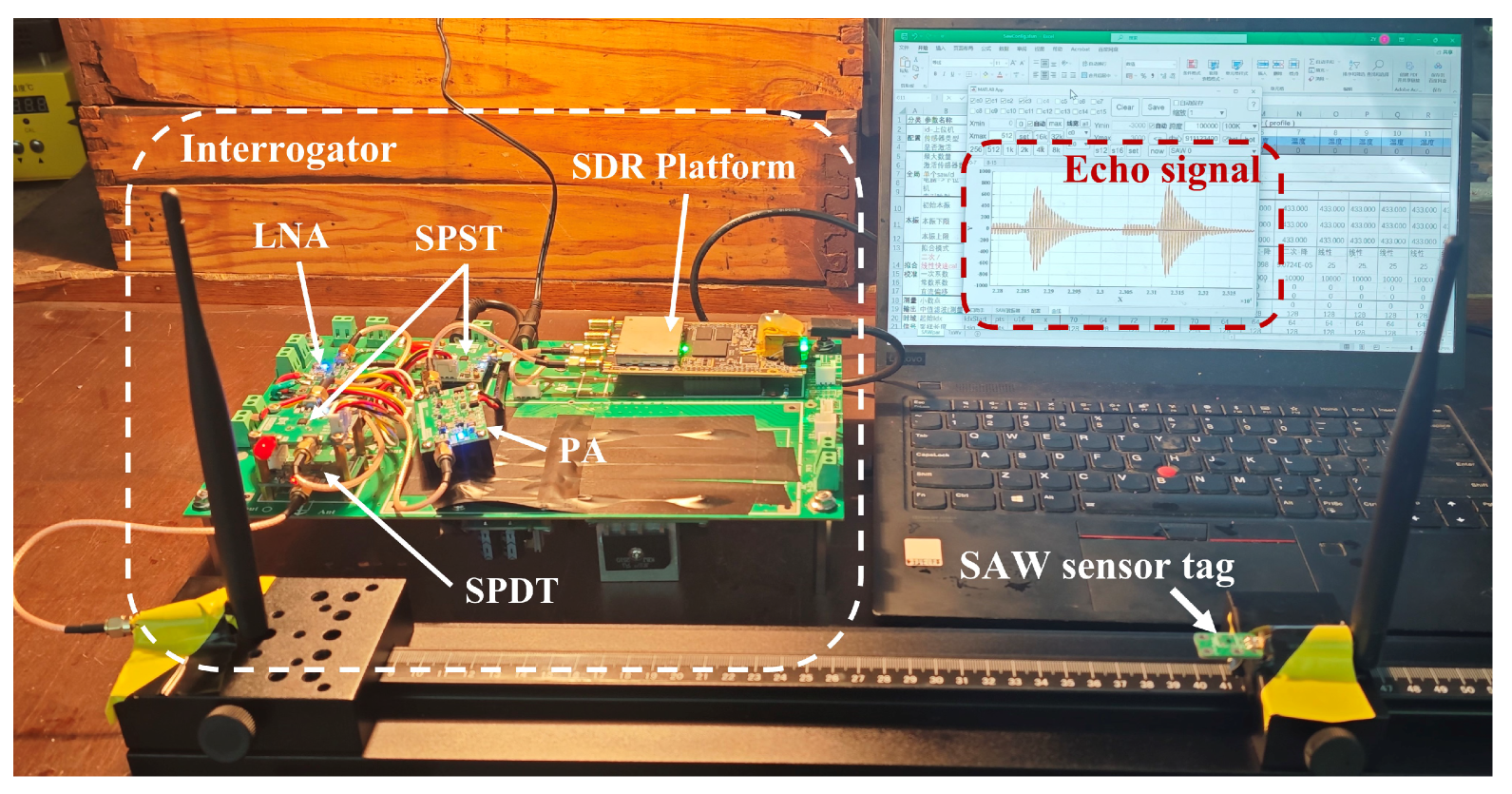
3. Experimental Setup and Results
3.1. Implementation of the SDR Interrogator
3.2. Wireless Measurement of SAW Echo Signals
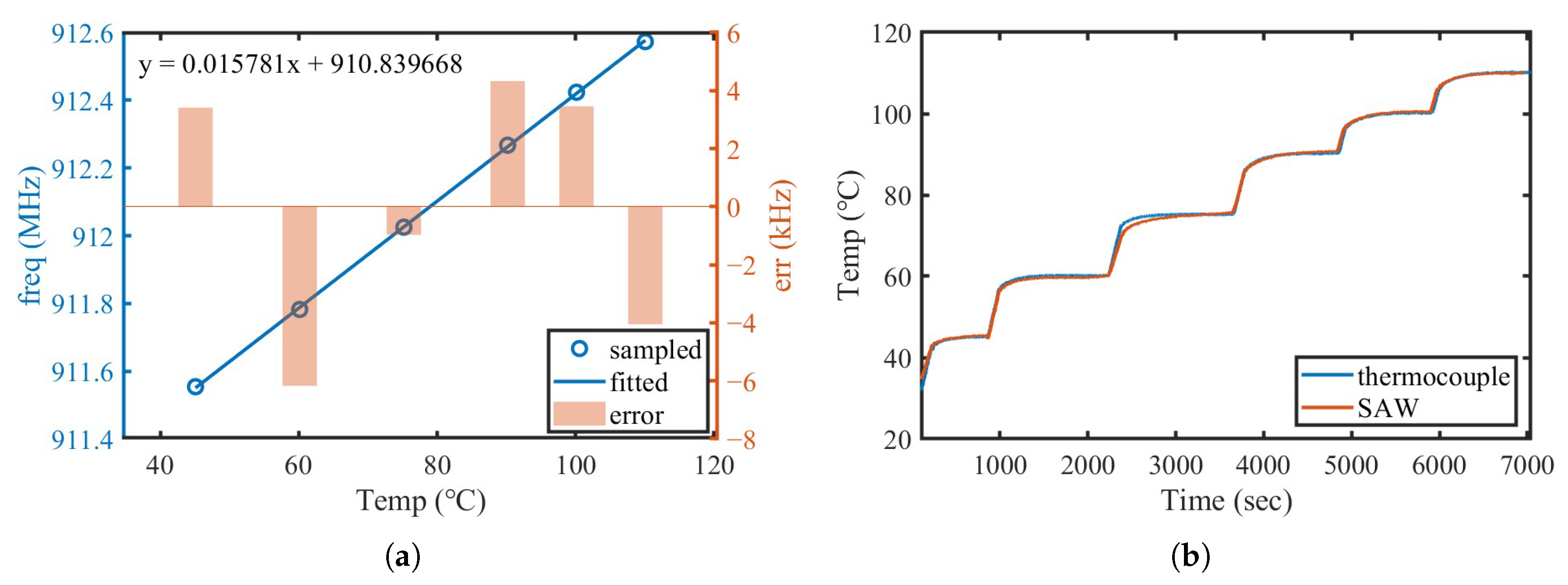
3.3. Frequency Measurement Accuracy
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Y.; Zhang, Y.; Gao, F.; Zhang, J.; Ding, Q.; Dong, S.; Jin, H.; Xuan, W.; Luo, J. High-speed multi-parameter sensing system based on wireless passive SAW tags. Meas. Sci. Technol. 2024, 35, 105101. [Google Scholar] [CrossRef]
- Gao, X.; Cheng, L.; Xue, X.; Zhai, S.; Liang, Y.; Wang, W.; Liu, M.; Zhu, J.; Li, Z. Development of Wireless and Passive SAW Temperature Sensor with Very High Accuracy. Appl. Sci. 2021, 11, 7422. [Google Scholar] [CrossRef]
- Sorokin, A.; Shepeta, A.; Wattimena, M. Wireless SAW passive tag temperature measurement in the collision case. J. Phys. Conf. Ser. 2018, 1008, 012015. [Google Scholar] [CrossRef]
- Kalinin, V.; Lohr, R.; Leigh, A.; Bown, G. Application of Passive SAW Resonant Sensors to Contactless Measurement of the Output Engine Torque in Passenger Cars. In Proceedings of the 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, Switzerland, 29 May–1 June 2007; pp. 499–504. [Google Scholar]
- Gao, F.; Boussaid, F.; Xuan, W.; Tsui, C.Y.; Bermak, A. Dual Transduction Surface Acoustic Wave Gas Sensor for VOC Discrimination. IEEE Electron. Device Lett. 2018, 39, 1920–1923. [Google Scholar] [CrossRef]
- Nicolae, I.; Miu, D.; Viespe, C. Sub-limit detection in SAW sensors by FFT spectral analysis of frequency time instability. Sens. Rev. 2018, 39, 246–251. [Google Scholar] [CrossRef]
- Kent, C.K.; Ramakrishnan, N.; Pratama Kesuma, H. Advancements in One-Port Surface Acoustic Wave (SAW) Resonators for Sensing Applications: A Review. IEEE Sens. J. 2024, 24, 17337–17352. [Google Scholar] [CrossRef]
- Otero, M.J.M.; Malocha, D.C. Wireless 4.74 GHz Harmonically Operated SAWTemperature Sensor. In Proceedings of the 2022 IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Aveiro, Portugal, 12–14 October 2022; pp. 83–86. [Google Scholar]
- Mahdi Jazini, M.; Masoumi, N. Limitations of Fourier Transform Analysis in the Wireless SAW Sensor Systems. In Proceedings of the 2019 Sixth Iranian Conference on Radar and Surveillance Systems, Isfahan, Iran, 4–6 December 2019; pp. 1–5. [Google Scholar]
- Jazini, M.M.; Khoshakhlagh, M.; Masoumi, N. A New Frequency Detection Method Based on FFT in the Application of SAW Resonator Sensor. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018; pp. 232–237. [Google Scholar]
- Humphries, J.R.; Reed, F.K.; Carmichael, C.P.; Fuhr, P.L.; McIntyre, T.J.; Weeks, A.R.; Malocha, D.C. Noise Radar Approach for Interrogating SAW Sensors Using Software Defined Radio. IEEE Sens. J. 2017, 17, 6760–6769. [Google Scholar] [CrossRef]
- Hamsch, M.; Hoffmann, R.; Buff, W.; Binhack, M.; Klett, S. An interrogation unit for passive wireless SAW sensors based on Fourier transform. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 1449–1456. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, V.; Beckley, J.; Makeev, I. High-speed reader for wireless resonant SAW sensors. In Proceedings of the 2012 European Frequency and Time Forum, Gothenburg, Sweden, 23–27 April 2012; pp. 428–435. [Google Scholar]
- Liu, B.; Zhang, C.; Ji, X.; Chen, J.; Han, T. An Improved Performance Frequency Estimation Algorithm for Passive Wireless SAW Resonant Sensors. Sensors 2014, 14, 22261–22273. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, V. Comparison of frequency estimators for interrogation of wireless resonant SAW sensors. In Proceedings of the 2015 Joint Conference of the IEEE International Frequency Control Symposium & the European Frequency and Time Forum, Denver, CO, USA, 12–16 April 2015; pp. 498–503. [Google Scholar]
- Kumar, R.; Mandal, N. SAW Sensor Basics on Material, Antenna, and Applications: A Review. IEEE Sens. J. 2024, 24, 5713–5731. [Google Scholar] [CrossRef]
- Shvetsov, A.S.; Ignatev, N.O.; Merkulov, A.A.; Zhgoon, S.A. Interrogation of SAW-Resonator-Based Vibration Sensor by Low Cost SDR. In Proceedings of the 2024 6th International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 29 February–2 March 2024; pp. 1–6. [Google Scholar]
- Xu, Y.; Amineh, R.K.; Dong, Z.; Li, F.; Kirton, K.; Kohler, M. Software Defined Radio-Based Wireless Sensing System. Sensors 2022, 22, 6455. [Google Scholar] [CrossRef] [PubMed]
- Malocha, D.C.; Humphries, J.R.; Weeks, A.R.; Figueroa, J. SAW passive multi-sensor system: Status and future opportunities. In Proceedings of the 2016 IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–5. [Google Scholar]
- Humphries, J.R.; Malocha, D.C. Software defined radio for passive sensor interrogation. In Proceedings of the 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; pp. 270–273. [Google Scholar]
- Stelzer, A.; Scheiblhofer, S.; Schuster, S.; Brandl, M. Multi reader/multi-tag SAW RFID systems combining tagging, sensing, and ranging for industrial applications. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 18–21 May 2008; pp. 263–272. [Google Scholar]
- Zhou, Y.; Ding, J.; Wang, B.; Gao, F.; Dong, S.; Jin, H. A SAW Wireless Passive Sensing System for Rotating Metal Parts. Sensors 2024, 24, 6703. [Google Scholar] [CrossRef] [PubMed]
- Lurz, F.; Ostertag, T.; Scheiner, B.; Weigel, R.; Koelpin, A. Reader Architectures for Wireless Surface Acoustic Wave Sensors. Sensors 2018, 18, 1734. [Google Scholar] [CrossRef] [PubMed]
- Caldero, P.; Gareis, M.; Vossiek, M. High-Accuracy 3D SAW RFID Tag Localization Using a Multi-Antenna Mobile Robot Based Synthetic Aperture Approach. In Proceedings of the 2020 50th European Microwave Conference (EuMC), Utrecht, The Netherlands, 12–14 January 2021; pp. 698–701. [Google Scholar]
- Zou, Y.; Zhao, Z.; Hu, F.; Cheng, L.; Xue, X.; Wang, W. High-Speed Reader for Contactless Resonant Surface Acoustic Wave Sensors. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]





| FFT Len | Mean () | Stdev. () | 99% Confidence Bound 1 | Span 2 | 3 | 4 | |
|---|---|---|---|---|---|---|---|
| (kHz) | (kHz) | Lower | Upper | (kHz) | |||
| 32,768 | 2.360 | 0.206 | 1.831 | 2.890 | 1.059 | 61 | 0.01 |
| 8192 | 2.589 | 0.343 | 1.706 | 3.472 | 1.766 | 31 | 0.05 |
| 4096 | 2.522 | 0.444 | 1.379 | 3.665 | 2.287 | 21 | 0.07 |
| 2048 | 1.113 | 0.283 | 0.383 | 1.843 | 1.460 | 21 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, Q.; Zhu, G.; Liu, L.; Cao, X.; Ren, T.; Zhou, Y.; Jin, H. Spectrum Fitting Approach for Passive Wireless SAW Sensor Interrogation Using Software-Defined Radio. Micromachines 2025, 16, 656. https://doi.org/10.3390/mi16060656
Wang S, Wang Q, Zhu G, Liu L, Cao X, Ren T, Zhou Y, Jin H. Spectrum Fitting Approach for Passive Wireless SAW Sensor Interrogation Using Software-Defined Radio. Micromachines. 2025; 16(6):656. https://doi.org/10.3390/mi16060656
Chicago/Turabian StyleWang, Shihao, Qi Wang, Guopeng Zhu, Lei Liu, Xinning Cao, Tingxin Ren, Yue Zhou, and Hao Jin. 2025. "Spectrum Fitting Approach for Passive Wireless SAW Sensor Interrogation Using Software-Defined Radio" Micromachines 16, no. 6: 656. https://doi.org/10.3390/mi16060656
APA StyleWang, S., Wang, Q., Zhu, G., Liu, L., Cao, X., Ren, T., Zhou, Y., & Jin, H. (2025). Spectrum Fitting Approach for Passive Wireless SAW Sensor Interrogation Using Software-Defined Radio. Micromachines, 16(6), 656. https://doi.org/10.3390/mi16060656







