Differential Phase Coupler Using Balun-Type Power Divider
Abstract
1. Introduction
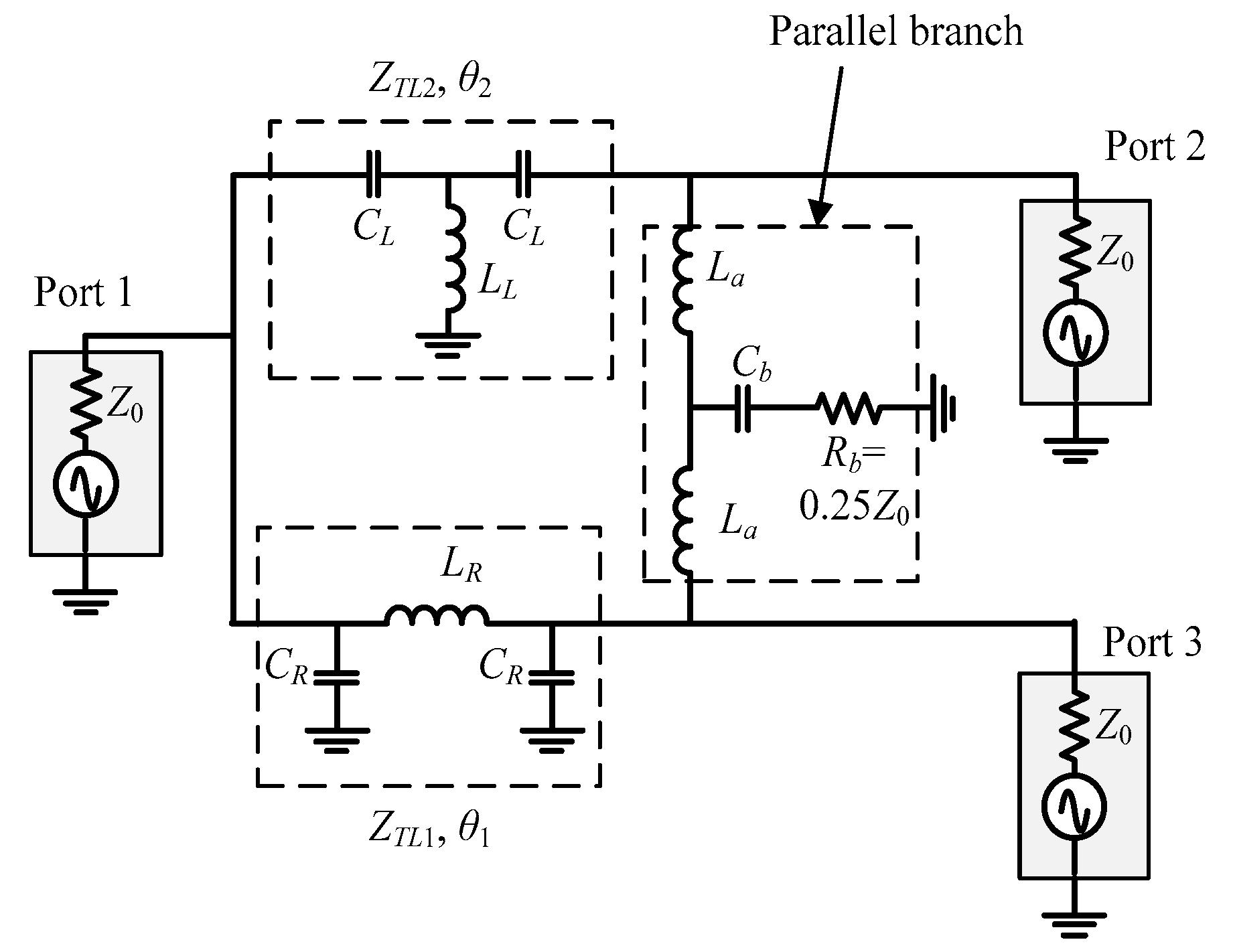
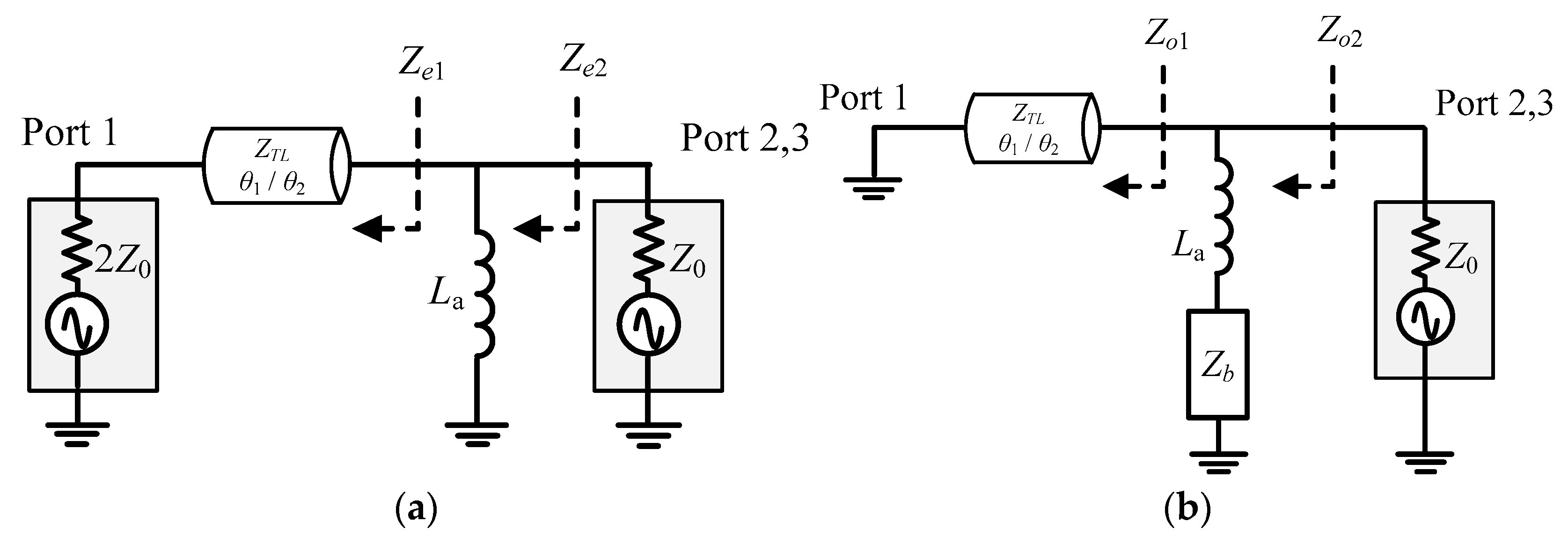
2. Wilkinson-Type Balun with Shorter Length Transmission Lines
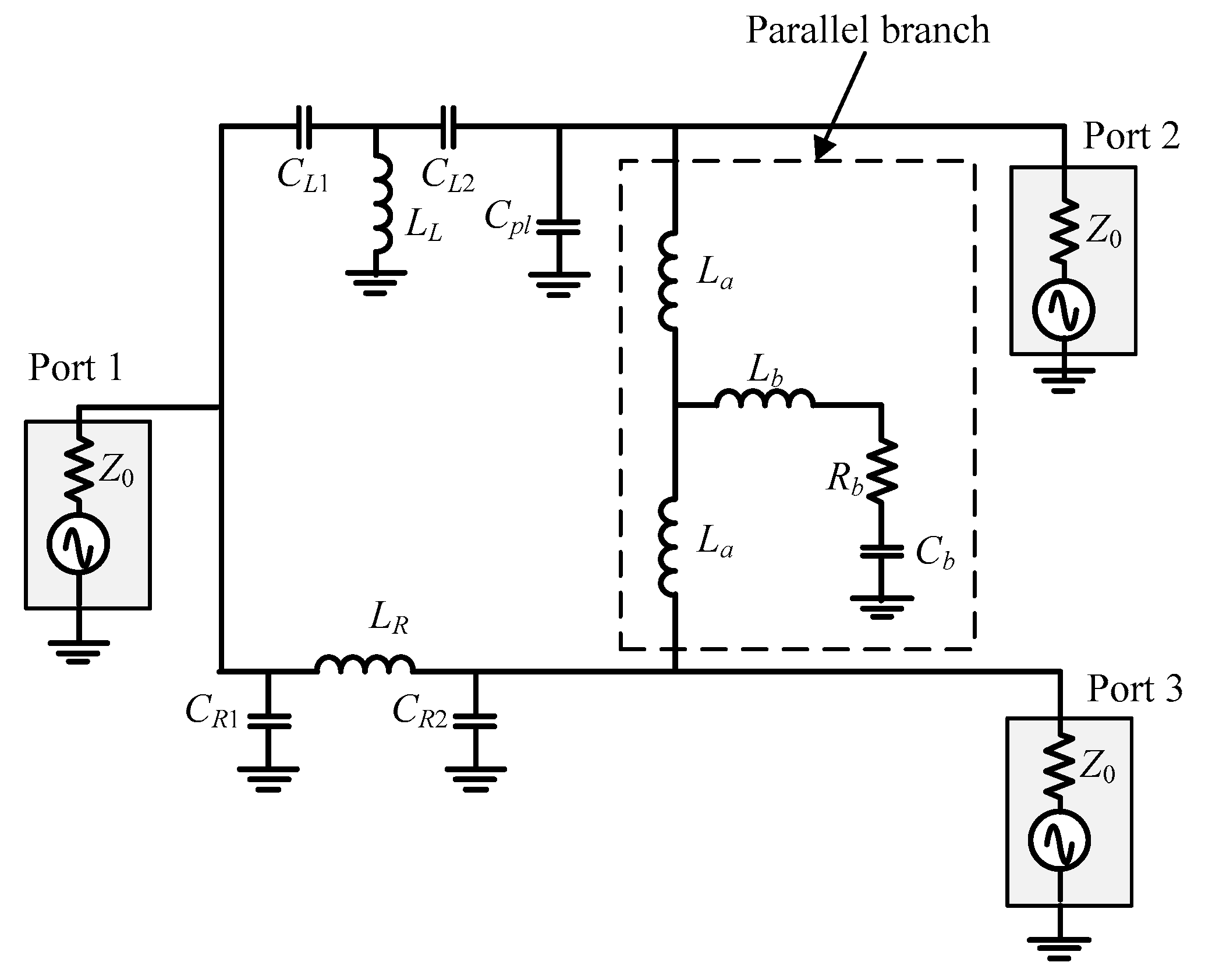
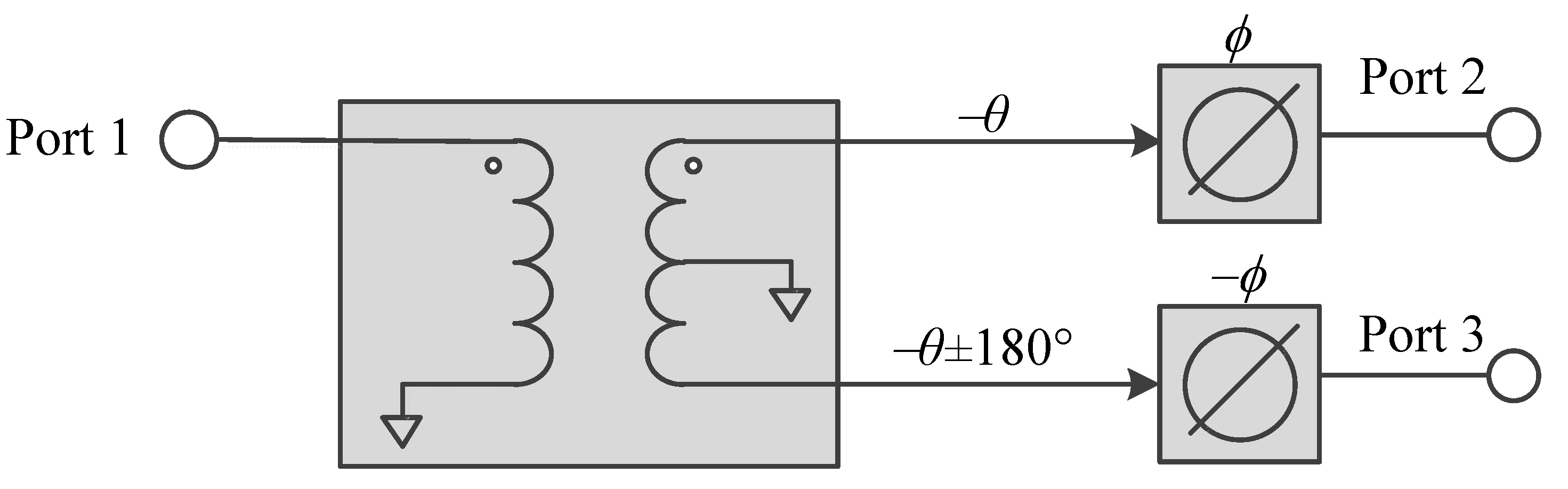
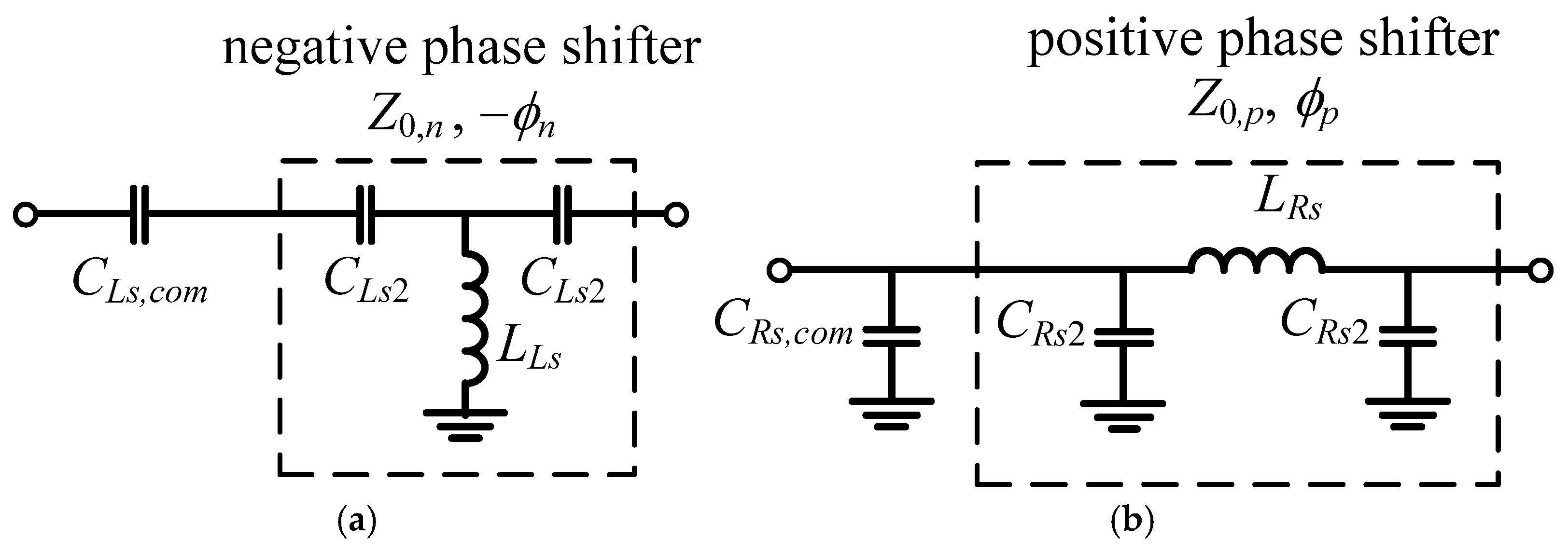
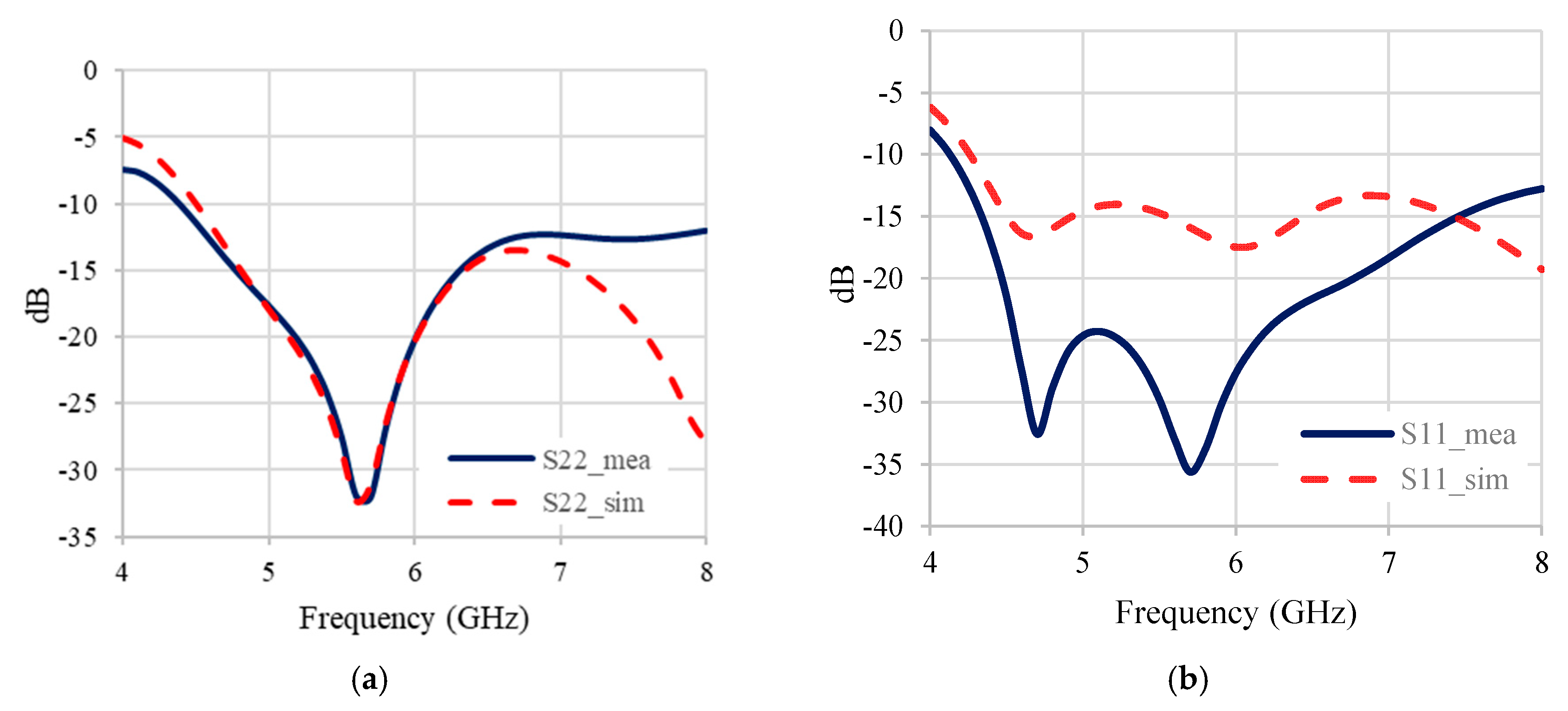
3. Differential Phase Coupler
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, P.; Hong, W.; Zhang, H.; Chen, J.; Tang, H.; Chen, Z. Virtual phase shifter array and its application on Ku band mobile satellite reception. IEEE Trans. Antennas Propag. 2015, 63, 1408–1416. [Google Scholar] [CrossRef]
- Filippi, G.D.; Piotto, L.; Pirbazari, M.M.; Mazzanti, A. D-band RX front-end with a 0°–360° phase shifter based on programmable passive networks in SiGe-BiCMOS. IEEE Trans. Microw. Theory Tech. 2024, 72, 6205–6215. [Google Scholar] [CrossRef]
- Abbasi, M.; Lee, W. A low-loss passive D-band phase shifter for calibration-free, precise phase control. IEEE J. Solid-State Circuits 2024, 59, 1371–1380. [Google Scholar] [CrossRef]
- Lagana, F.; Bibbo, L.; Calcagno, S.; Carlo, D.D.; Pullano, S.A.; Prattico, D.; Angiulli, G. Smart electronic device-based monitoring of SAR and temperature variations in indoor human tissue interaction. Appl. Sci. 2025, 15, 2439. [Google Scholar] [CrossRef]
- Pakasiri, C.; Xu, J.-L.; Wang, S. A 10 GHz Compact Balun with Common Inductor on CMOS Process. Electronics 2023, 12, 468. [Google Scholar] [CrossRef]
- Gong, Y.; Cressler, J.D. A 60-GHz SiGe power amplifier with three-conductor transmission-line-based Wilkinson baluns and asymmetric directional couplers. IEEE Trans. Microw. Theory Tech. 2021, 69, 709–722. [Google Scholar] [CrossRef]
- Hsu, C.-Y.; Chen, C.-Y.; Chuang, H.-R. A 77-GHz CMOS on-chip bandpass filter with balanced and unbalanced outputs. IEEE Electron. Device Lett. 2010, 31, 1205–1207. [Google Scholar] [CrossRef]
- Xiong, W.; Dong, G.; Wang, Y.; Zhu, Z.; Yang, Y. 3-D compact marchand balun design based on through-silicon via technology for monolithic and 3-D integration. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1107–1118. [Google Scholar] [CrossRef]
- Hsu, H.-M.; Huang, J.-S.; Chen, S.-Y.; Lai, S.-H. Design of an on-chip balun with a minimum amplitude imbalance using a symmetric stack layout. IEEE Trans. Microw. Theory Tech. 2010, 58, 814–819. [Google Scholar]
- Cao, J.; Li, Z.; Li, Q.; Wang, Z. A wideband transformer balun with center open stub in CMOS process. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 614–616. [Google Scholar] [CrossRef]
- Hossain, M.S.; Fujishima, M.; Yoshida, T.; Amakawa, S.; Rashid, M.M. Design of CMOS On-Chip Millimeter-Wave Transformer Coupled Balun and Power Divider-Combiner with Optimal Amplitude and Phase Imbalance. In Proceedings of the 2019 1st International Conference on Advances in Science, Engineering and Robotics Technology (ICASERT), Dhaka, Bangladesh, 3–5 May 2019. [Google Scholar]
- Li, S.; Xia, B.; Li, X.; Wang, Y.; Liu, X.; Chen, W. Analysis and design of broadband balance-compensated transformer baluns for silicon-based millimeter-wave circuits. IEEE Trans. Circuits Syst. I Reg. Pap. 2023, 70, 3103–3116. [Google Scholar] [CrossRef]
- Benaouf, T.M.; Hamdoun, A.; Himdi, M.; Lafond, O.; Ammor, H. Hybrid Coupler Used as Tunable Phase Shifter Based on Varactor Diodes. Micromachines 2024, 15, 838. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Lee, G.; Song, J.-I. A lumped-element directional coupler with high isolation for mobile RFID reader. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 382–384. [Google Scholar] [CrossRef]
- Sun, R.; Chen, Q.; Han, R.; Lu, Z. Analysis and design of wideband 90◦microstrip hybrid coupler. IEEE Access 2019, 7, 186409–186416. [Google Scholar] [CrossRef]
- Jafari, E.; Hodiatkashani, F.; Rezaiesarlak, R. A broadband quadrature hybrid using improved wideband Schiffman phase shifter. Prog. Electromagn. Res. C 2009, 11, 229–236. [Google Scholar] [CrossRef]
- Zhang, L.P.; Zhang, H.C.; Shao, C.; He, P.H.; Tang, M.; Mao, J.-F.; Cui, T.J. A broadband 90◦ balun with low-phase-imbalance performance based on periodic slow wave structure. IEEE Trans. Antennas Propag. 2021, 69, 4681–4687. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, J.; Lu, Q.-Y.; Wu, W.; Hong, J. A wideband 90◦ phase shifting element applied in quadrature phase filtering power divider. IEEE Microw. Wirel. Compon. Lett. 2024, 34, 167–170. [Google Scholar] [CrossRef]
- Issakov, V.; Knapp, H.; Bakalski, W.; Wojnowski, M.; Thiede, A.; Simburger, W. Compact on-chip 90◦ and 180◦ splitters/combiners in silicon technology for 24 GHz applications. In Proceedings of the 40th European Microwave Conference, Paris, France, 28–30 September 2010. [Google Scholar]
- Qiu, L.-L.; Zhu, L.; Lyu, Y.-P. Differential phase shifters based on Schiffman type-C and type-F networks with wide phase shift range. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, e22126. [Google Scholar] [CrossRef]
- Nebhen, J.; Ravelo, B. Innovative Microwave Design of Frequency-Independent Passive Phase Shifter with LCL-Network and Bandpass NGD Circuit. Prog. Electromagn. Res. C 2021, 109, 187–203. [Google Scholar] [CrossRef]
- Ravelo, B.; Guerin, M.; Frnda, J.; Sahao, F.E.; Fontgalland, G.; Silva, H.S.; Ngoho, S.; Haddad, F.; Rahajandraibe, W. Design method of constant phase-shifter microwave passive integrated circuit in 130-nm BiCMOS technology with bandpass-type negative group delay. IEEE Accesss 2022, 10, 93084–93103. [Google Scholar] [CrossRef]
- Guerin, M.; Rahajandraibe, W.; Fontgalland, G.; Silva, H.S.; Chan, G.; Wan, F.; Thakur, P.; Thakur, A.; Frnda, J.; Ravelo, B. Theory and original design of resistive-inductive network high-pass negative group delay integrated circuit in 130-nm CMOS technology. IEEE Access 2022, 10, 27147–27161. [Google Scholar] [CrossRef]
- Wan, F.; Gu, T.; Li, B.; Li, B.; Rahajandraibe, W.; Guerin, M.; Lallechere, S.; Ravelo, B. Design and experimentation of inductorless low-pass NGD integrated circuit in 180-nm CMOS technology. IEEE Trans. Comput.-Aided Design Integr. Circuits Syst. 2022, 41, 4965–4974. [Google Scholar] [CrossRef]
- Park, U. A Wilkinson-Type balun using a composite right/left-handed transmission line. J. Inf. Commun. Converg. Eng. 2013, 11, 147–152. [Google Scholar] [CrossRef]
- Caloz, C.; Itoh, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2006. [Google Scholar]





| No. | Q | TL1 | TL2 | Parallel Branch | ||||
|---|---|---|---|---|---|---|---|---|
| LL (nH) (RL) (Ω) | CL (pF) | LR (nH) (RR) (Ω) | CR (pF) | La (nH) (Ra) (Ω) | Cb (pF) | Rb (Ω) | ||
| #1 60°/−120° | ideal | 1.77 | 0.3 | 1.3 | 0.3 | 2.6 | 0.4 | 20 |
| 20 | 1.77 (3.33) | 0.3 | 1.3 (2.5) | 0.3 | 2.6 (5) | 0.4 | 20 | |
| 10 | 1.77 (6.66) | 0.3 | 1.3 (5) | 0.3 | 2.6 (10) | 0.4 | 20 | |
| #2 75°/−105° | ideal | 1.9 | 0.3 | 1.7 | 0.3 | 6.7 | 0.2 | 24 |
| 20 | 1.9 (3.5) | 0.3 | 1.7 (3.3) | 0.3 | 6.7 (12.7) | 0.2 | 24 | |
| 10 | 1.9 (7) | 0.3 | 1.7 (6.6) | 0.3 | 6.7 (25.4) | 0.2 | 24 | |
| #3 90°/−90° | ideal | 1.9 | 0.4 | 1.9 | 0.4 | 0.9 | 0.7 | 12.5 |
| 20 | 1.9 (3.5) | 0.4 | 1.9 (3.5) | 0.4 | 0.9 (1.8) | 0.7 | 12.5 | |
| 10 | 1.9 (7) | 0.4 | 1.9 (7) | 0.4 | 0.9 (3.5) | 0.7 | 12.5 | |
| #4 90°/−90° | 20 | 1.9 (3.5) | 0.38 | 1.9 (3.5) | 0.38 | 14 (26.4) | 0.1 | 11.7 |
| 10 | 1.9 (7) | 0.38 | 1.8 (7) | 0.38 | 15.7 (59) | 0.1 | 33.4 | |
| No. | Q | Fractional Bandwidth (%) | Maximum Phase Deviation (°) |
|---|---|---|---|
| #1 60°/−120° | ideal | 32.84 | 5.31 |
| 20 | 33.58 | 6.35 | |
| 10 | 34.78 | 35.6 | |
| #2 75°/−105° | ideal | 21.14 | 1.99 |
| 20 | 24.39 | 8.12 | |
| 10 | 25.81 | 10.91 | |
| #3 90°/−90° | ideal | 40 | 1.83 |
| 20 | 33.9 | 4.07 | |
| 10 | 1.8 | 1.48 | |
| #4 90°/−90° | 20 | 33.04 | 1.281 |
| 10 | 21.85 | 1.516 |
| References | [15] * | [16] ** | [17] | [18] | [19] | This Work |
|---|---|---|---|---|---|---|
| Process | PCB | PCB | PCB | PCB | CMOS | IPD |
| Type | Power divider and phase shifter | Power divider and phase shifter | Power divider and phase shifter | Combined power divider and phase shifter | Transformer | Balun and phase shifter |
| f0 (GHz) | 3 | 0.65 | 1.75 | 2.5 | 26.5 | 6 |
| S21, S31 (dB) | >−3.5 | −3.2 | >−5 | >−4.68 | −3.5 | >−4.76 |
| |S11|, |S22|, |S33| (dB) | <−16 | −20 | <−15 | <−15 | −19 | <−18 |
| |S23| (dB) | <−20 | −25 | <−55 | <−20 | N/A | <−20 |
| Phase difference deviation (degrees) | <5 | 2 | <3 | <5 | 0.6 | 4.5 |
| Size | 0.239 | 0.047 | N/A *** | 0.35 | 1.4 × 10−4 | 3.6 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakasiri, C.; Chang, C.-Y.; Wang, S. Differential Phase Coupler Using Balun-Type Power Divider. Micromachines 2025, 16, 496. https://doi.org/10.3390/mi16050496
Pakasiri C, Chang C-Y, Wang S. Differential Phase Coupler Using Balun-Type Power Divider. Micromachines. 2025; 16(5):496. https://doi.org/10.3390/mi16050496
Chicago/Turabian StylePakasiri, Chatrpol, Chung-Yu Chang, and Sen Wang. 2025. "Differential Phase Coupler Using Balun-Type Power Divider" Micromachines 16, no. 5: 496. https://doi.org/10.3390/mi16050496
APA StylePakasiri, C., Chang, C.-Y., & Wang, S. (2025). Differential Phase Coupler Using Balun-Type Power Divider. Micromachines, 16(5), 496. https://doi.org/10.3390/mi16050496






