Enhancing Single-Mode Characteristics and Reducing Confinement Loss in Liquid-Core Anti-Resonant Fibers via Selective Filling and Geometrical Optimization
Abstract
1. Introduction
2. Basic Model and Simulation Method
3. Transmission Characteristics
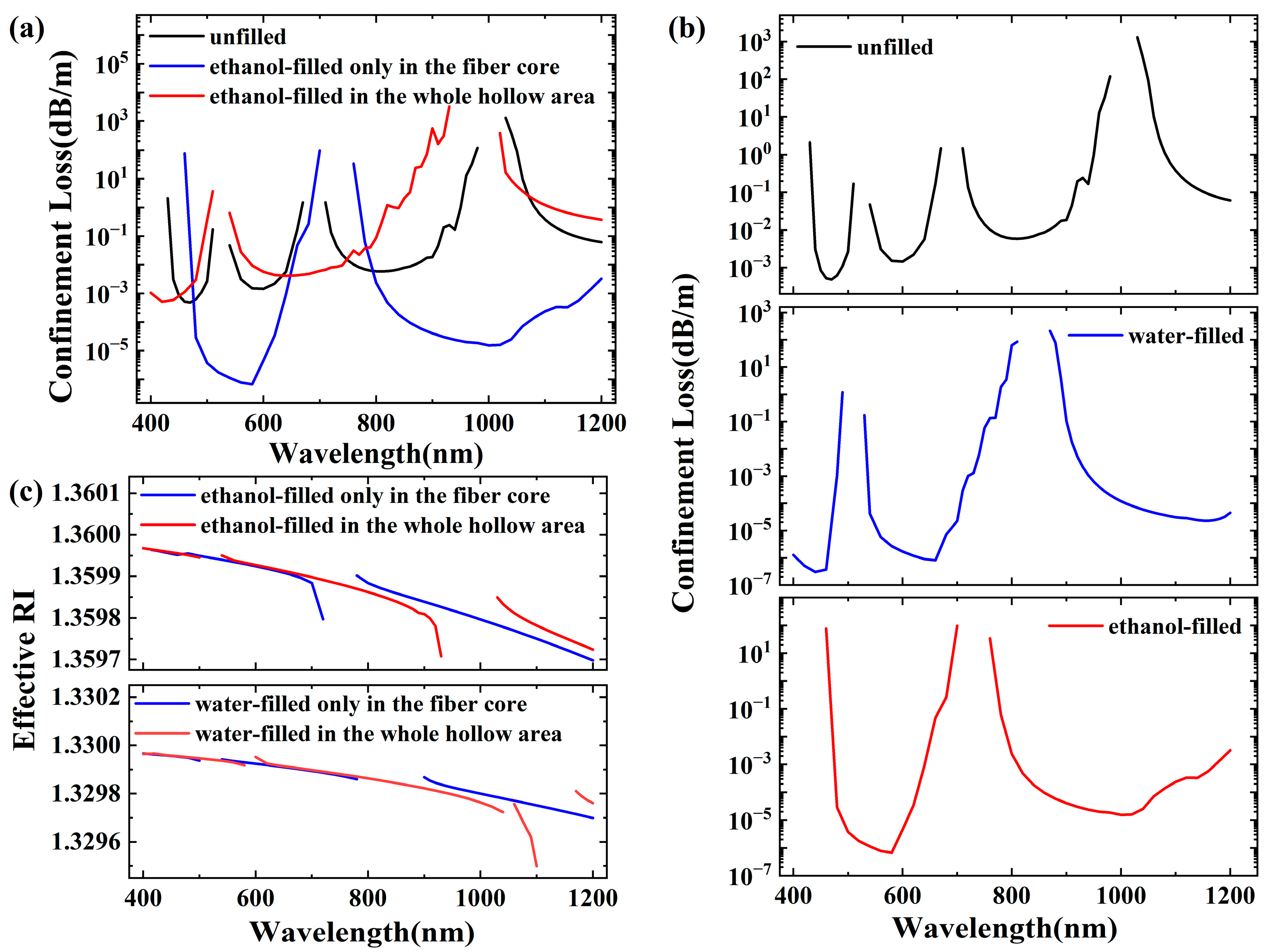
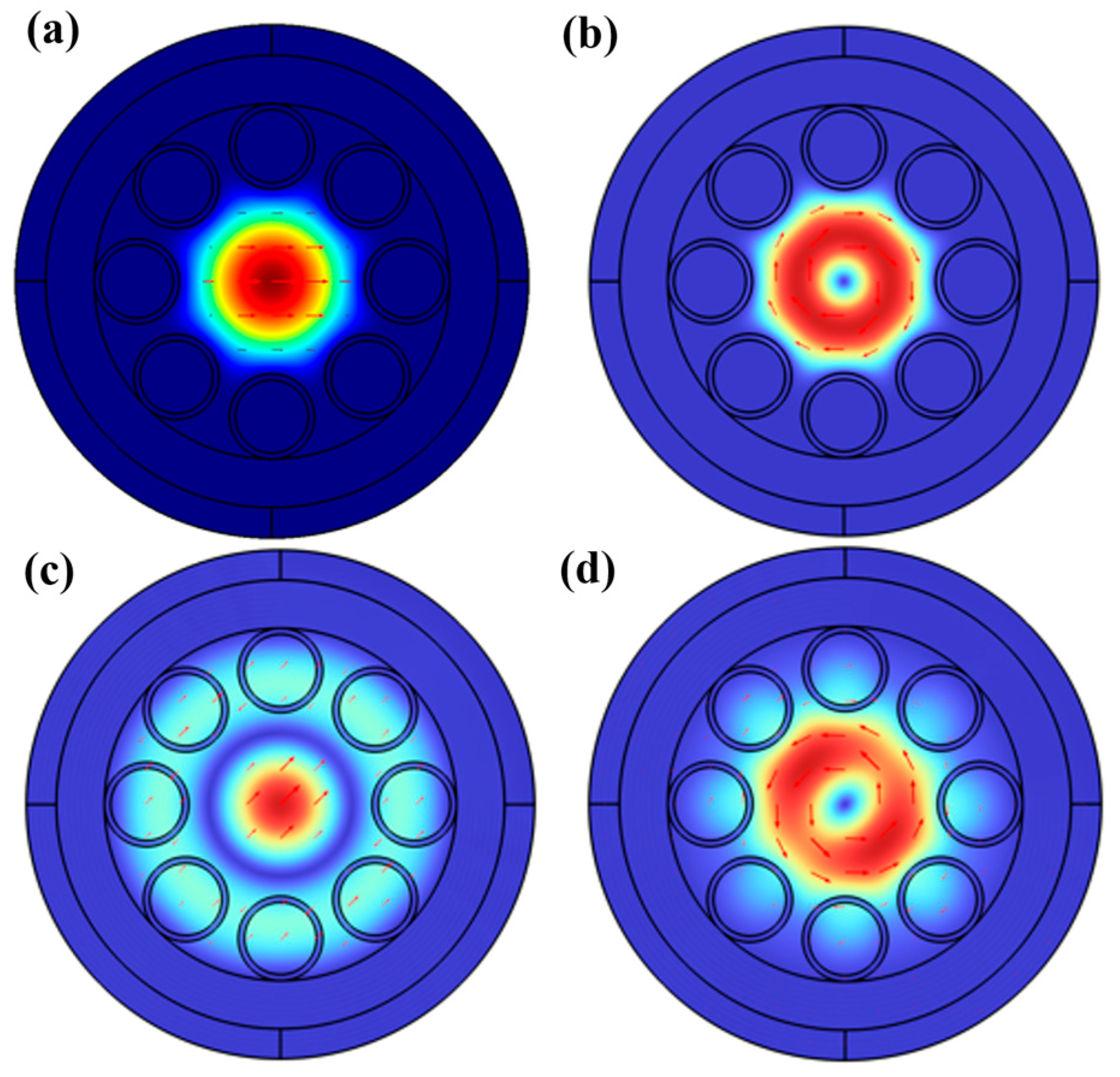
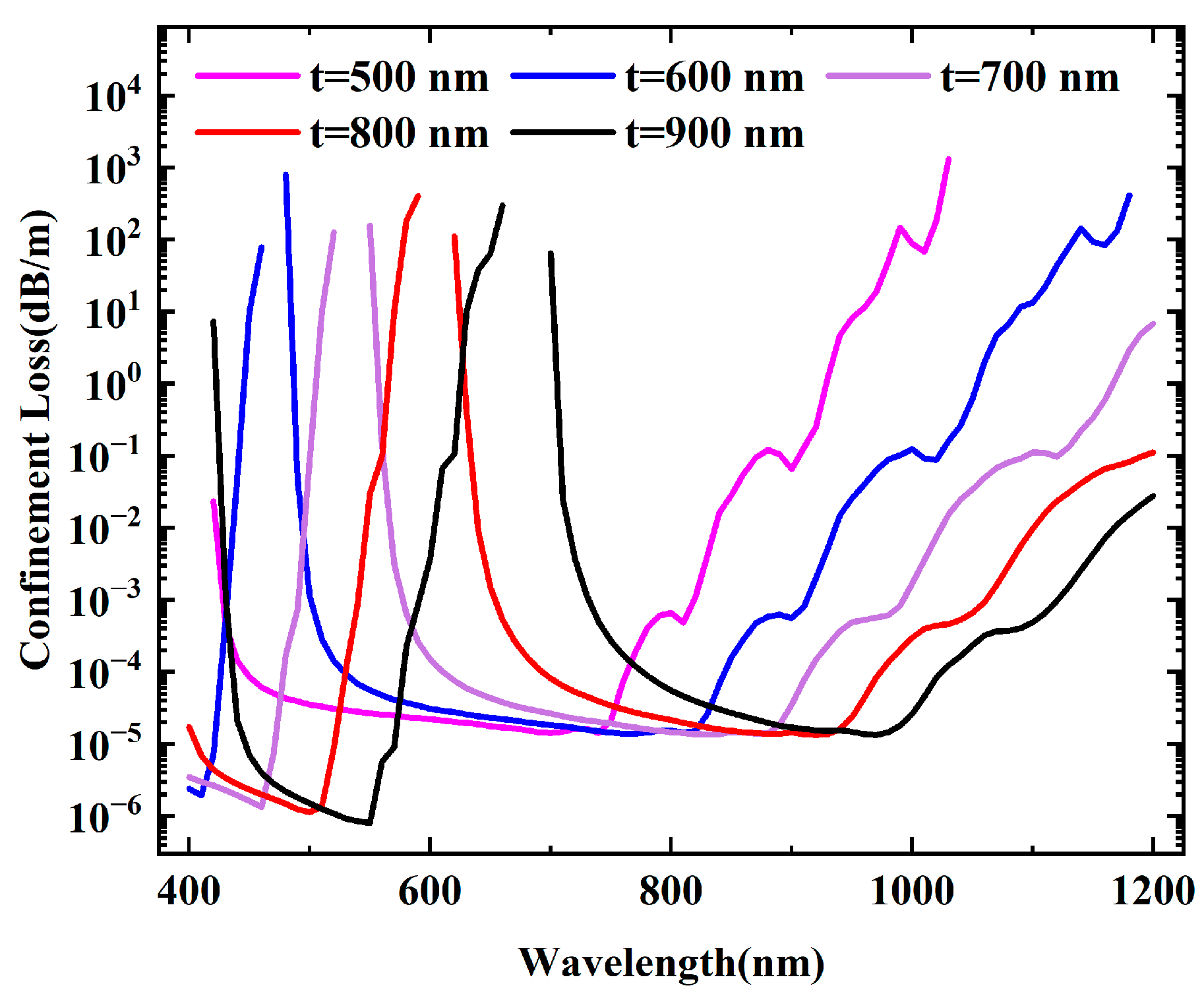
3.1. Confinement Loss and Effective-Mode RI of HE11 Mode
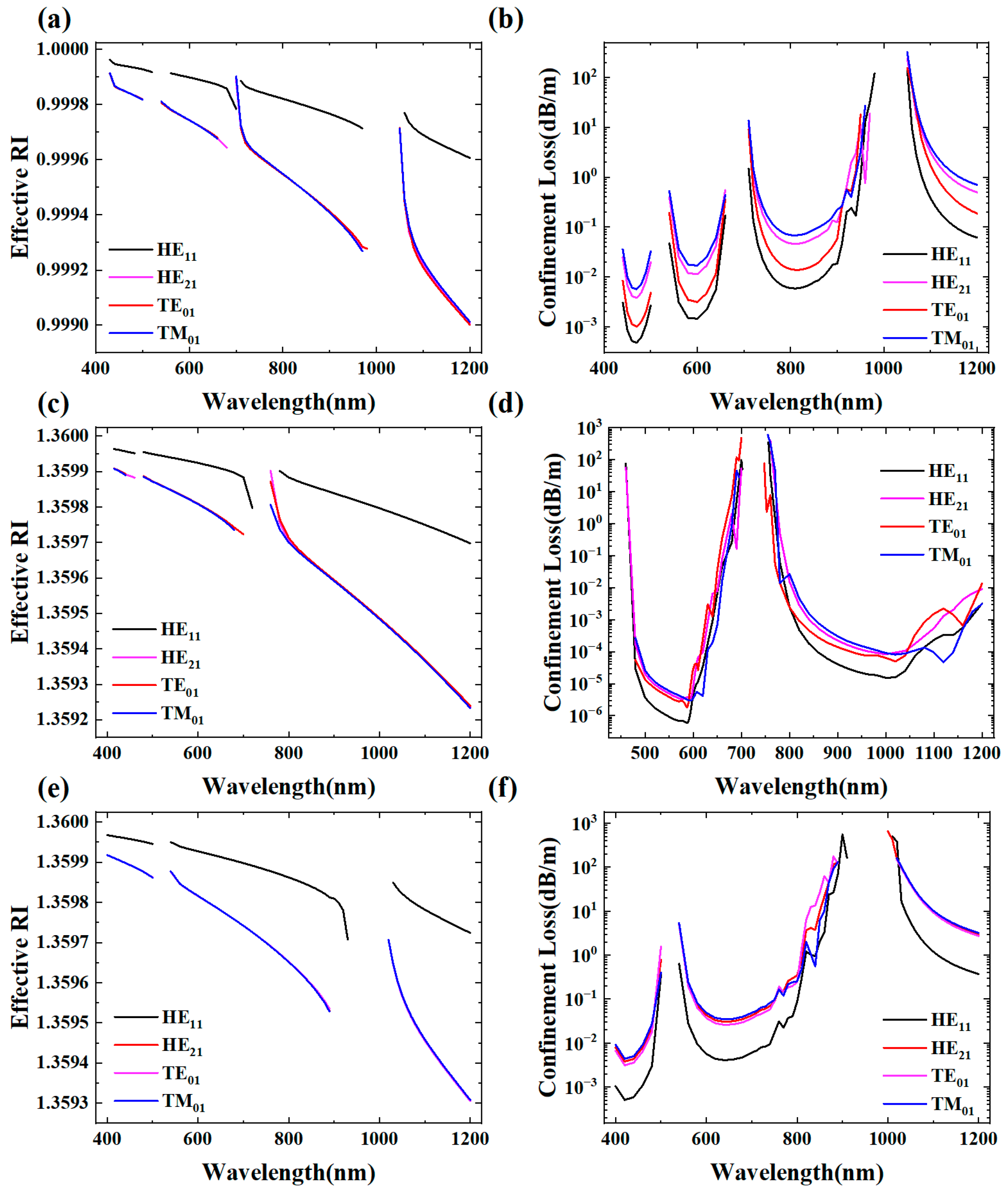
3.2. Confinement Loss and Effective-Mode RI of HE21, TE01, and TM01 Modes
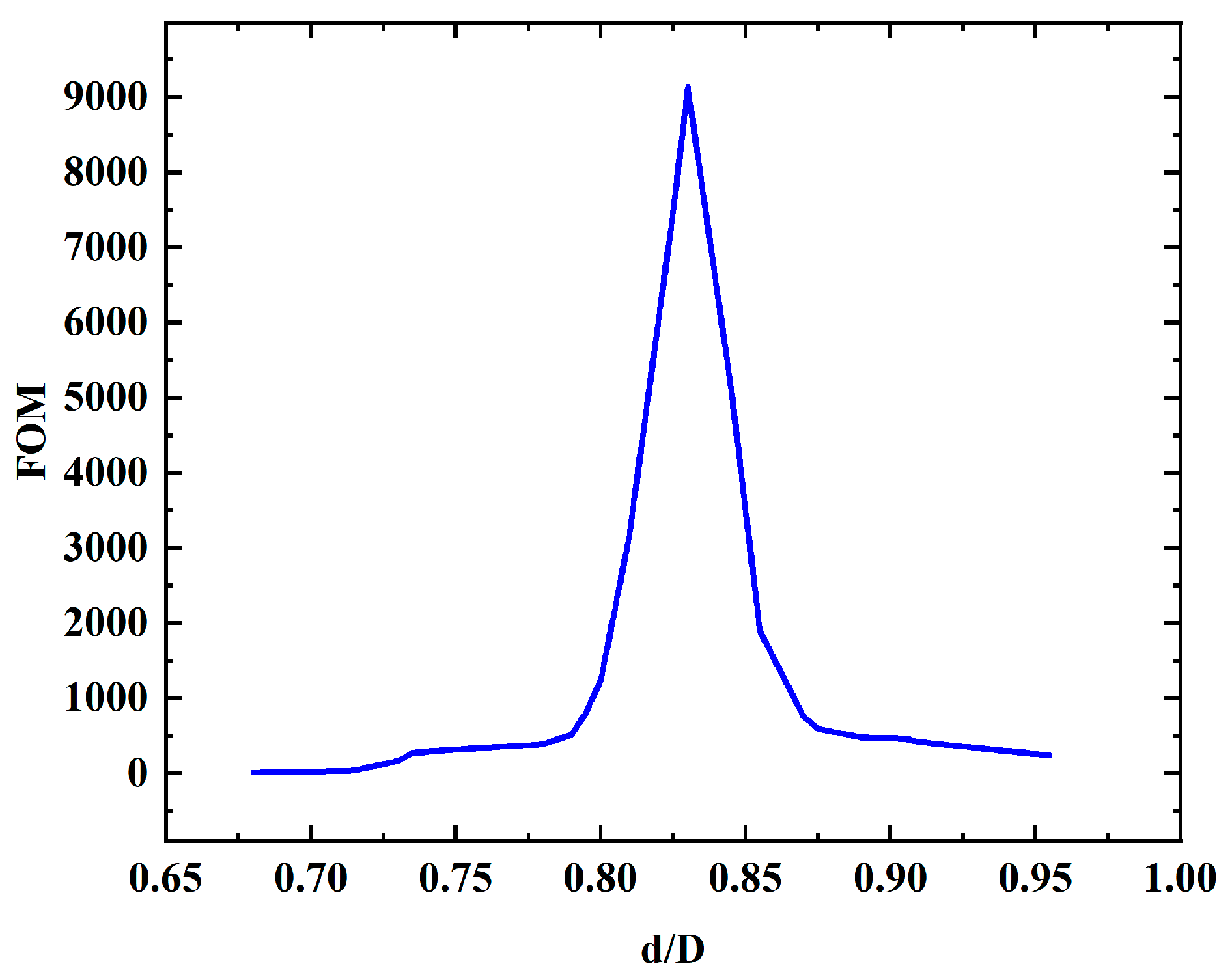
4. Structural Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chemnitz, M.; Junaid, S.; Walther, N.; Scheibinger, R.; Schaarschmidt, K.; Kobelke, J.; Schmidt, M.A. Tailoring soliton fission at telecom wavelengths using composite-liquid-core fibers. Opt. Lett. 2020, 45, 2985–2988. [Google Scholar] [PubMed]
- Junaid, S.; Schaarschmidt, K.; Chemnitz, M.; Chambonneau, M.; Nolte, S.; Schmidt, M.A. Tailoring modulation instabilities and four-wave mixing in dispersion-managed composite liquid-core fibers. Opt. Express 2020, 28, 3097–3106. [Google Scholar] [CrossRef] [PubMed]
- Conti, C.; Schmidt, M.A.; Russell, P.S.J.; Biancalana, F. Highly noninstantaneous solitons in liquid-core photonic crystal fibers. Phys. Rev. Lett. 2010, 105, 263902. [Google Scholar] [CrossRef] [PubMed]
- Crema, A.; Dinelli, E.; Fabbri, E.; Galletti, P.; Greggio, N.; Lastella, V.; Parodi, A.; Pasteris, A.; Pedrizzi, M.; Samori, C. Additives in bioplastics: Chemical characterization, migration in water and effects on photosynthetic organisms. Sci. Total Environ. 2024, 955, 177205. [Google Scholar] [PubMed]
- Chafer, M.; Osorio, J.H.; Amrani, F.; Delahaye, F.; Maurel, M.; Debord, B.; Gerome, F.; Benabid, F. 1-km hollow-core fiber with loss at the silica rayleigh limit in the green spectral region. IEEE Photonics Technol. Lett. 2019, 31, 685–688. [Google Scholar]
- Gu, S.; Wang, X.; Jia, H.; Lian, Z.; Shen, X.; Mai, Y.; Lou, S. Single-ring hollow-core anti-resonant fiber with a record low loss (4.3 dB/km) for high-power laser delivery at 1 μm. Opt. Lett. 2022, 47, 5925–5928. [Google Scholar] [CrossRef] [PubMed]
- Osorio, J.H.; Amrani, F.; Delahaye, F.; Dhaybi, A.; Vasko, K.; Melli, F.; Giovanardi, F.; Vandembroucq, D.; Tessier, G.; Vincetti, L.; et al. Hollow-core fibers with reduced surface roughness and ultralow loss in the short-wavelength range. Nat. Commun. 2023, 14, 1146. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.F.; Feng, W.; Qiao, S.D.; Zhao, Z.X.; Gao, S.F.; Wang, Y.Y. Hollow-core anti-resonant fiber based light-induced thermoelastic spectroscopy for gas sensing. Opt. Express 2022, 30, 18836–18844. [Google Scholar] [PubMed]
- Uebel, P.; Guenendi, M.C.; Frosz, M.H.; Ahmed, G.; Edavalath, N.N.; Menard, J.-M.; Russell, P.S.J. Broadband robustly single-mode hollow-core PCF by resonant filtering of higher-order modes. Opt. Lett. 2016, 41, 1961–1964. [Google Scholar] [PubMed]
- Nissen, M.; Doherty, B.; Hamperl, J.; Kobelke, J.; Weber, K.; Henkel, T.; Schmidt, M.A. UV absorption spectroscopy in water-filled antiresonant hollow core fibers for pharmaceutical detection. Sensors 2018, 18, 478. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.-l.; Ding, W.; Wang, Y.-y.; Gao, S.-f.; Cao, L.; Feng, X.; Wang, P. Characterization of a liquid-filled nodeless anti-resonant fiber for biochemical sensing. Opt. Lett. 2017, 42, 863–866. [Google Scholar] [PubMed]
- Wang, X.; Li, S.; Gao, S.; Wang, Y.; Wang, P.; Ebendorff-Heidepriem, H.; Ruan, Y. Microfluidic raman sensing using a single ring negative curvature hollow core fiber. Biosensors 2021, 11, 430. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.; Liu, S.; Niu, P.; Chen, T. High sensitivity temperature sensor based on polymer-liquid modified anti-resonant reflecting guidance in silica capillary. Heliyon 2023, 9, e13358. [Google Scholar]
- Saitoh, K.; Florous, N.J.; Murao, T.; Koshiba, M. Realistic design of large-hollow-core photonic band-gap fibers with suppressed higher order modes and surface modes. J. Light. Technol. 2007, 25, 2440–2447. [Google Scholar] [CrossRef]
- Goel, C.; Yoo, S. Multimode nested antiresonant hollow core fiber. J. Light. Technol. 2021, 39, 6592–6598. [Google Scholar] [CrossRef]
- Zhu, S.; Pang, F.; Huang, S.; Zou, F.; Dong, Y.; Wang, T. High sensitivity refractive index sensor based on adiabatic tapered optical fiber deposited with nanofilm by ALD. Opt. Express 2015, 23, 13880–13888. [Google Scholar] [PubMed]
- Del Villar, I.; Hernaez, M.; Zamarreno, C.R.; Sanchez, P.; Fernandez-Valdivielso, C.; Arregui, F.J.; Matias, I.R. Design rules for lossy mode resonance based sensors. Appl. Opt. 2012, 51, 4298–4307. [Google Scholar] [PubMed]
- Michieletto, M.; Lyngso, J.K.; Jakobsen, C.; Laegsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef] [PubMed]
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gerome, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Wei, C.; Weiblen, R.J.; Menyuk, C.R.; Hu, J. Negative curvature fibers. Adv. Opt. Photonics 2017, 9, 504–561. [Google Scholar] [CrossRef]
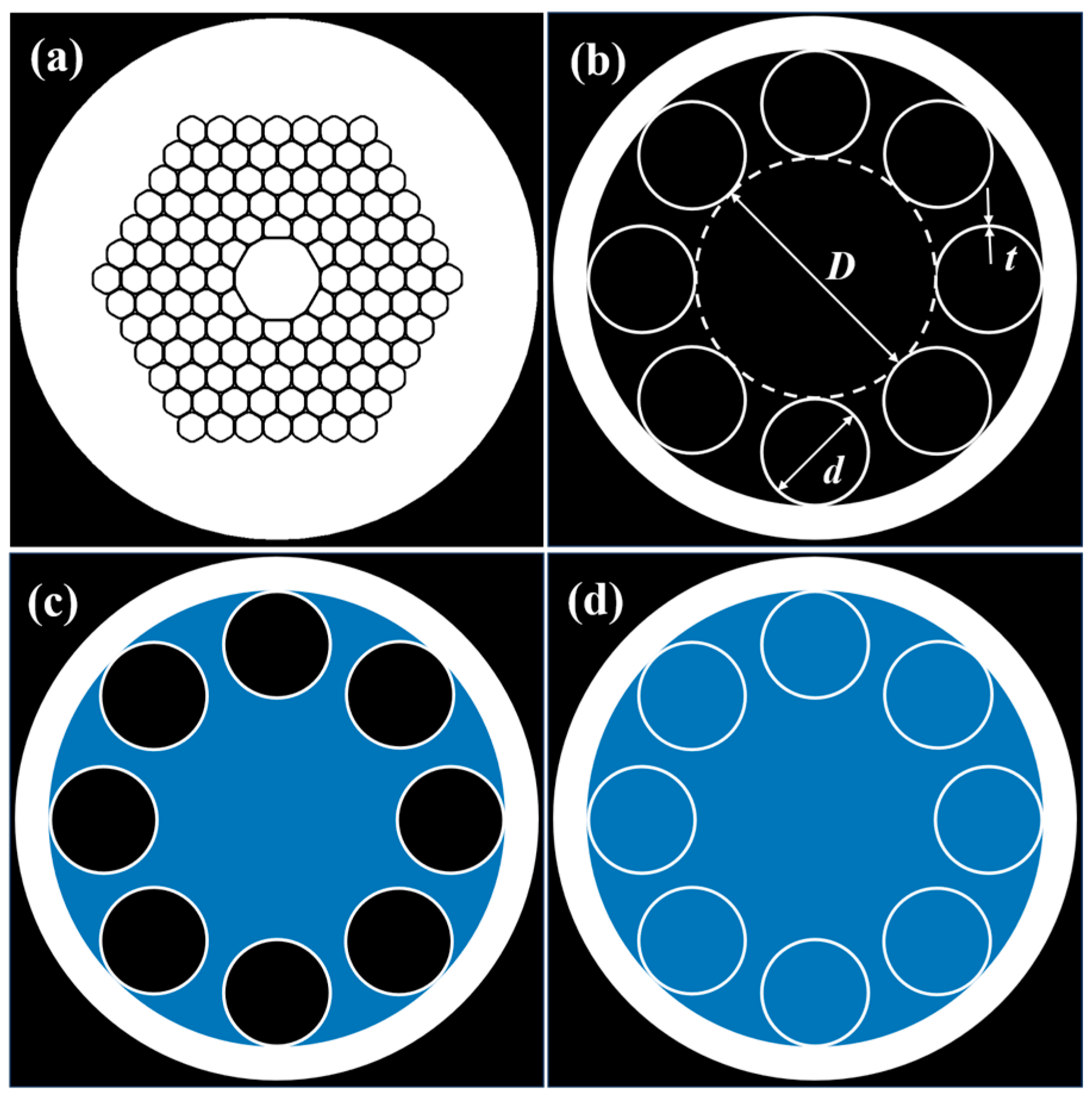


| Core Diameter (D) | Capillary Thickness (t) | Capillary Inner Diameter (d) | Cladding Diameter |
|---|---|---|---|
| 30.5 μm | 1000 nm | 12 μm | 74.5 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Wang, C.; Xiong, C.; Qin, Y.; Zhu, J.; Shen, Y.; Xiao, L. Enhancing Single-Mode Characteristics and Reducing Confinement Loss in Liquid-Core Anti-Resonant Fibers via Selective Filling and Geometrical Optimization. Micromachines 2025, 16, 438. https://doi.org/10.3390/mi16040438
Chen S, Wang C, Xiong C, Qin Y, Zhu J, Shen Y, Xiao L. Enhancing Single-Mode Characteristics and Reducing Confinement Loss in Liquid-Core Anti-Resonant Fibers via Selective Filling and Geometrical Optimization. Micromachines. 2025; 16(4):438. https://doi.org/10.3390/mi16040438
Chicago/Turabian StyleChen, Siyuan, Caoyuan Wang, Cong Xiong, Yu Qin, Jie Zhu, Yichun Shen, and Limin Xiao. 2025. "Enhancing Single-Mode Characteristics and Reducing Confinement Loss in Liquid-Core Anti-Resonant Fibers via Selective Filling and Geometrical Optimization" Micromachines 16, no. 4: 438. https://doi.org/10.3390/mi16040438
APA StyleChen, S., Wang, C., Xiong, C., Qin, Y., Zhu, J., Shen, Y., & Xiao, L. (2025). Enhancing Single-Mode Characteristics and Reducing Confinement Loss in Liquid-Core Anti-Resonant Fibers via Selective Filling and Geometrical Optimization. Micromachines, 16(4), 438. https://doi.org/10.3390/mi16040438





