Using Higher Diffraction Orders to Improve the Accuracy and Robustness of Overlay Measurements
Abstract
1. Introduction
2. Principle
2.1. Resistance of Higher Diffraction Orders to Asymmetric Deformation
2.2. Principle of Multiple Diffraction Order Sharing
2.3. Diffraction Efficiency Enhancement Theory
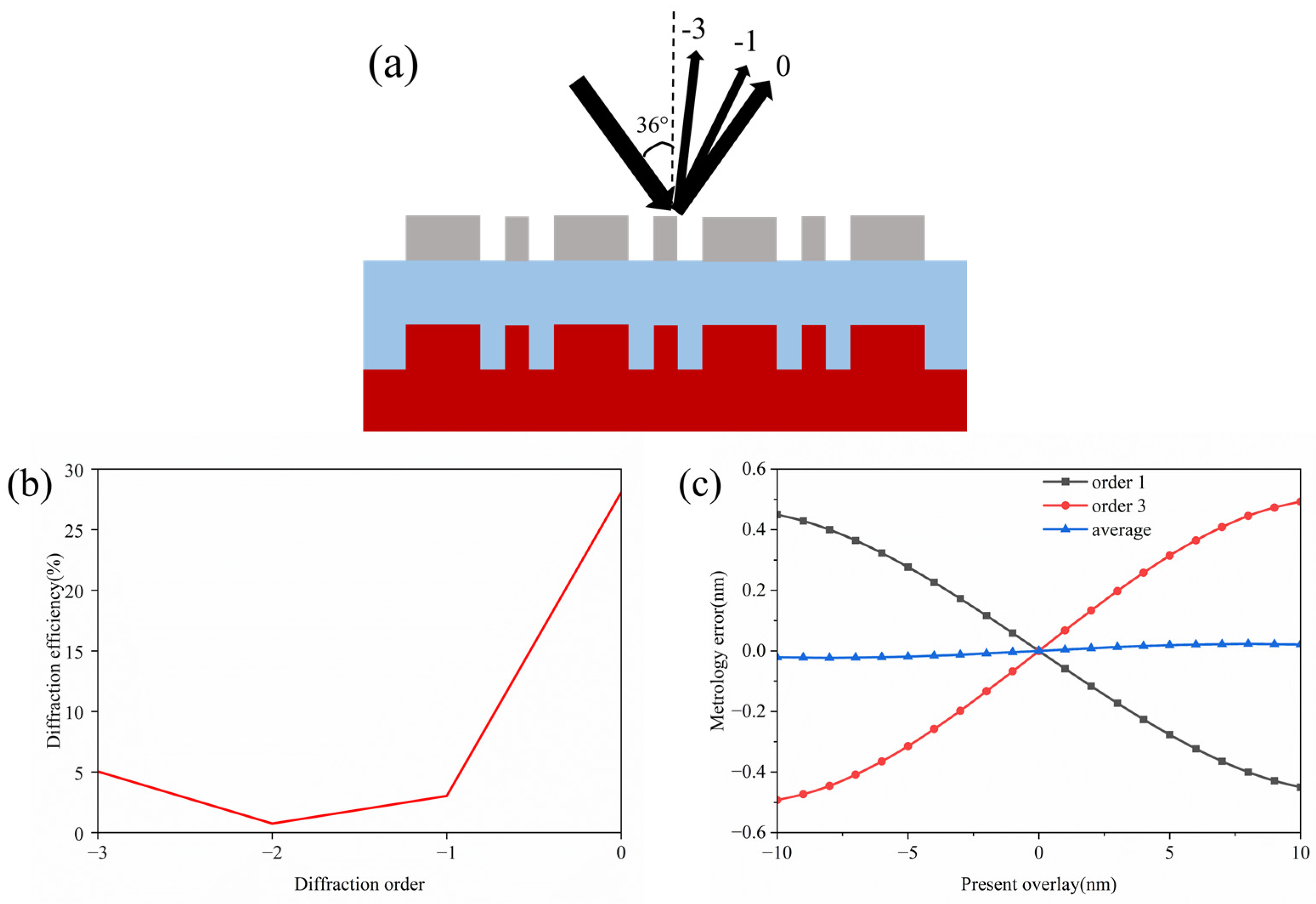
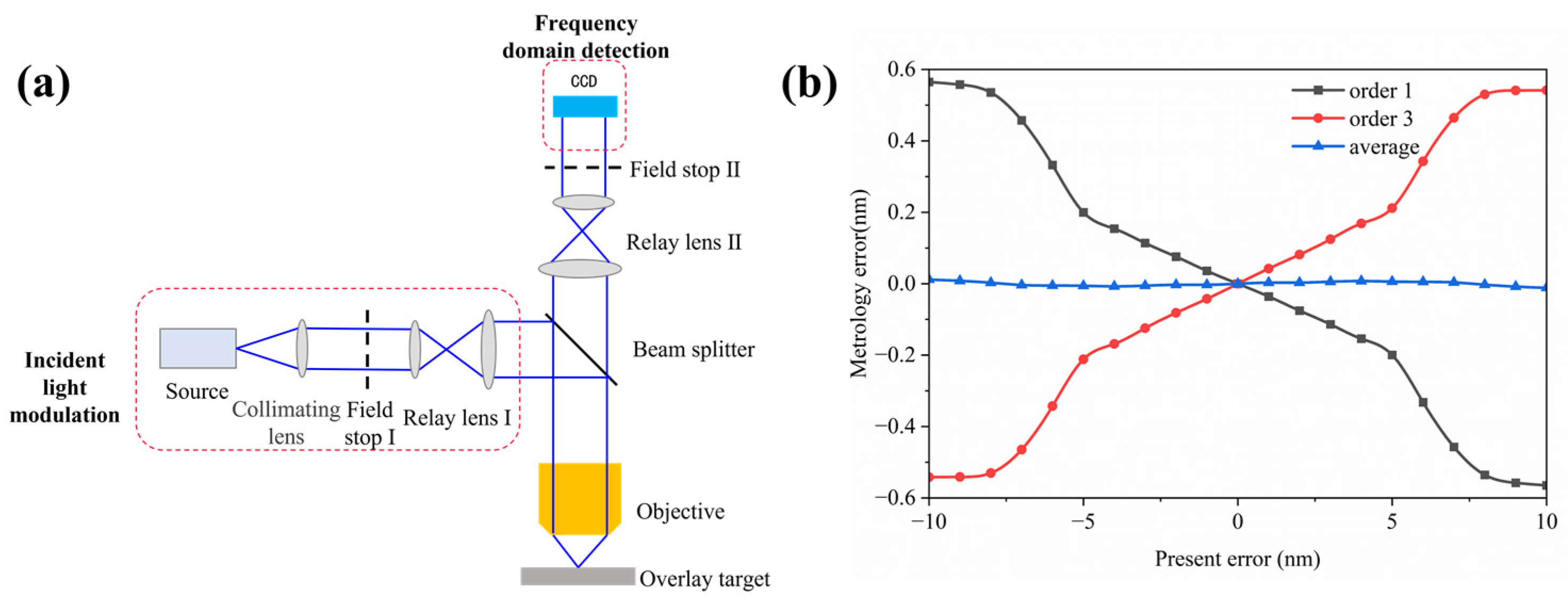
3. Simulation
3.1. RCWA Simulation
3.2. Optical Detection System Simulation
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- den Boef, A.J. Optical wafer metrology sensors for process-robust CD and overlay control in semiconductor device manufacturing. Surf. Topogr. Metrol. Prop. 2016, 4, 023001. [Google Scholar] [CrossRef]
- IEEE. IEEE International Roadmap for Devices and Systems; IEEE: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Bischoff, J.; Brunner, R.; Bauer, J.J.; Haak, U. Light-diffraction-based overlay measurement. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XV, Santa Clara, CA, USA, 26 February–1 March 2001; pp. 222–233. [Google Scholar] [CrossRef]
- Xu, B.; Wu, Q.; Dong, L.; Wei, Y. Selection of DBO measurement wavelength for bottom mark asymmetry based on FDTD method. J. Semicond. 2019, 40, 122403. [Google Scholar] [CrossRef]
- Hsieh, H.-C.; Cheng, J.-M.; Yeh, Y.-C. Optimized wavelength selection for diffraction-based overlay measurement by minimum asymmetry factor variation with finite-difference time-domain simulation. Appl. Opt. 2022, 61, 1389–1397. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.; Hwang, C.; Lee, S.Y.; Jung, W.; Park, J.; Bhattacharyya, K.; den Boef, A.; Mathijssen, S.; Noot, M. Taking the multi-wavelength DBO to the next level of accuracy and robustness. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XXXIV, San Jose, CA, USA, 24–27 February 2020; pp. 222–227. [Google Scholar] [CrossRef]
- Van Schaijk, T.T.; Messinis, C.; Pandey, N.; Koolen, A.; Witte, S.; De Boer, J.F.; Den Boef, A. Diffraction-based overlay metrology from visible to infrared wavelengths using a single sensor. J. Micro/Nanopatterning Mater. Metrol. 2022, 21, 014001. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Ke, C.-M.; Huang, G.-T.; Chen, K.-H.; Smilde, H.-J.H.; Fuchs, A.; Jak, M.; van Schijndel, M.; Bozkurt, M.; van der Schaar, M. On-product overlay enhancement using advanced litho-cluster control based on integrated metrology, ultra-small DBO targets and novel corrections. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XXVII, San Jose, CA, USA, 25–28 February 2013; pp. 28–36. [Google Scholar] [CrossRef]
- Smilde, H.-J.H.; den Boef, A.; Kubis, M.; Jak, M.; van Schijndel, M.; Fuchs, A.; van der Schaar, M.; Meyer, S.; Morgan, S.; Wu, J. Evaluation of a novel ultra small target technology supporting on-product overlay measurements. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XXVI, San Jose, CA, USA, 13–16 February 2012; pp. 431–438. [Google Scholar] [CrossRef]
- Ben-Dov, G.; Tarshish-Shapir, I.; Gready, D.; Ghinovker, M.; Adel, M.; Herzel, E.; Oh, S.; Choi, D.; Han, S.H.; El Kodadi, M. Metrology target design simulations for accurate and robust scatterometry overlay measurements. In Proceedings of the Metrology, Inspection, and Process Control for Microlithography XXX, San Jose, CA, USA, 22–25 February 2016; pp. 1015–1026. [Google Scholar] [CrossRef]
- Lee, J.; Yim, I.; Park, B.S.; Lee, C.; Kwak, M.; Lee, J.; Lee, S.Y.; Hwang, C.; Mummery, J.; Almeida, B.G. Multi-wavelength continuous-bias DBO metrology for improved ADI process-robustness. In Proceedings of the Metrology, Inspection, and Process Control XXXVIII, San Jose, CA, USA, 8 January 2024; pp. 909–913. [Google Scholar] [CrossRef]
- Yang, W.; Lin, N.; Wei, X.; Chen, Y.; Li, S.; Leng, Y.; Shao, J. Improving accuracy and sensitivity of diffraction-based overlay metrology. Chin. Opt. Lett. 2023, 21, 071204. [Google Scholar] [CrossRef]
- Hsieh, H.-C. Improving the cross-layer misalignment measurement accuracy by pattern-center shift induced error calibration. Opt. Lasers Eng. 2022, 155, 107051. [Google Scholar] [CrossRef]
- Du, J.; Dai, F.; Bu, Y.; Wang, X. Calibration method of overlay measurement error caused by asymmetric mark. Appl. Opt. 2018, 57, 9814–9821. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Gu, H.; Jiang, H.; Zhang, C.; Liu, S. Robust overlay metrology with differential Mueller matrix calculus. Opt. Express 2017, 25, 8491–8510. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Wang, Y.; Li, J.; Qi, Y.; Ding, M. Diffraction Efficiency of Enhanced Phase Grating. Acta Opt. Sin. 2021, 41, 1205001. [Google Scholar] [CrossRef]
- Hanmin Yao, S.H.; Xing, T. Optical Projection Lithography for Micro-Nano Fabrication Technology; Beijing University of Technology Press: Beijing, China, 2006. [Google Scholar]
- Moharam, M.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Moharam, M.; Gaylord, T. Rigorous coupled-wave analysis of grating diffraction—E-mode polarization and losses. J. Opt. Soc. Am. 1983, 73, 451–455. [Google Scholar] [CrossRef]
- Moharam, M.; Gaylord, T.K. Three-dimensional vector coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1983, 73, 1105–1112. [Google Scholar] [CrossRef]
- Moharam, M.; Gaylord, T.K. Diffraction analysis of dielectric surface-relief gratings. J. Opt. Soc. Am. 1982, 72, 1385–1392. [Google Scholar] [CrossRef]
- Moharam, M.; Gaylord, T.K. Rigorous coupled-wave analysis of metallic surface-relief gratings. J. Opt. Soc. Am. A 1986, 3, 1780–1787. [Google Scholar] [CrossRef]
- Wei, Y. Advanced Lithography Theory and Applications for Ultra-Large Scale Integration (ULSI) Circuits; Science Press: Beijing, China, 2016. [Google Scholar]

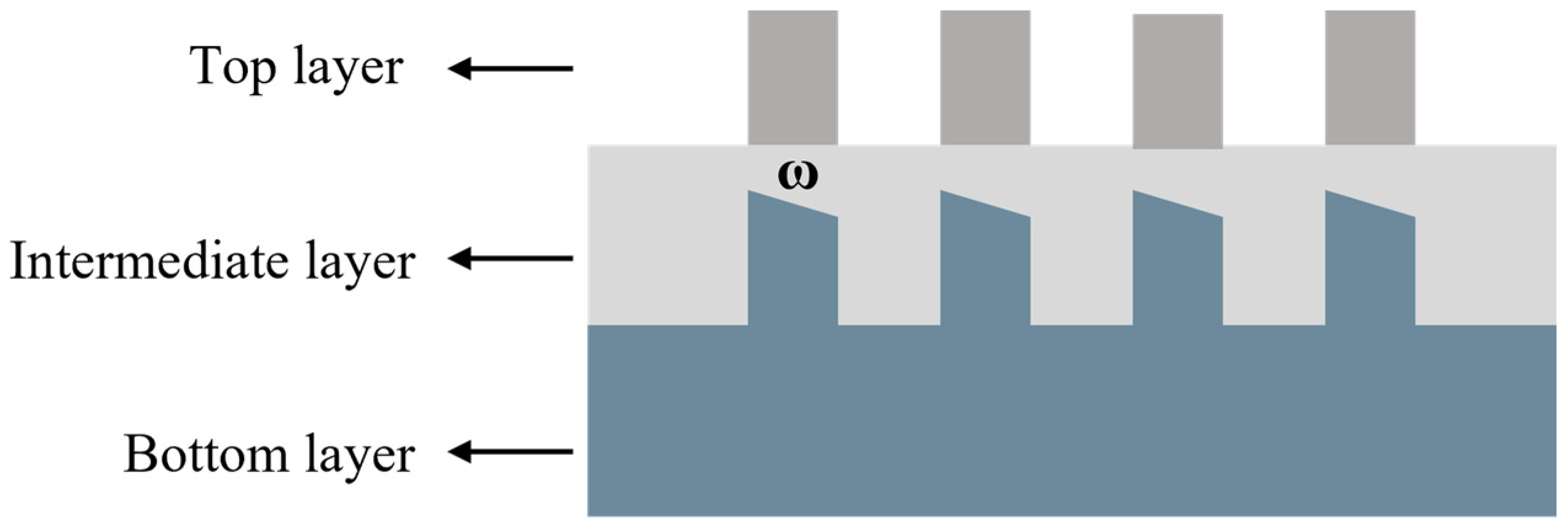


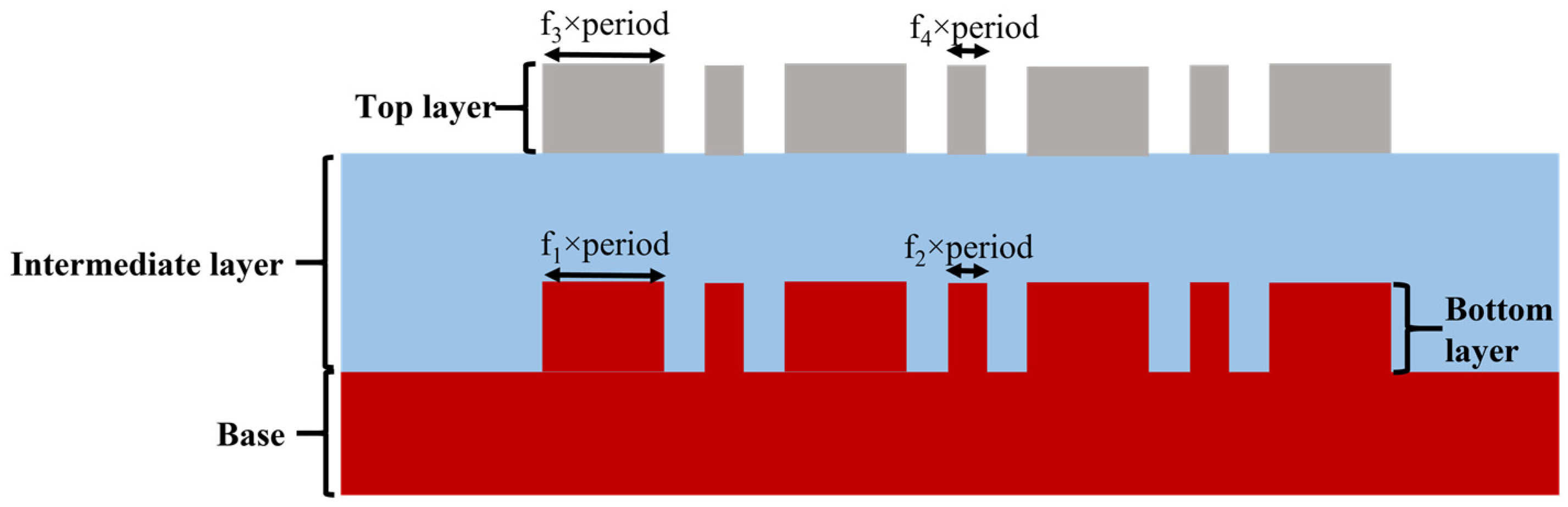


| Layer | Material | Height/nm | Critical Dimension/nm | |
|---|---|---|---|---|
| Bottom layer | Si | 100 | f1 × period (f1 = 0.55) | |
| f2 × period (f2 = 0.15) | ||||
| Intermediate layer | SiO2 | 230 | ||
| Top layer | Photoresist [23] | 100 | f3 × period (f3 = 0.55) | |
| f4 × period (f4 = 0.15) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Tang, Y.; Cheng, X.; Long, Y.; Jiang, J.; He, Y.; Zhao, L. Using Higher Diffraction Orders to Improve the Accuracy and Robustness of Overlay Measurements. Micromachines 2025, 16, 347. https://doi.org/10.3390/mi16030347
Liu S, Tang Y, Cheng X, Long Y, Jiang J, He Y, Zhao L. Using Higher Diffraction Orders to Improve the Accuracy and Robustness of Overlay Measurements. Micromachines. 2025; 16(3):347. https://doi.org/10.3390/mi16030347
Chicago/Turabian StyleLiu, Shaoyu, Yan Tang, Xiaolong Cheng, Yuliang Long, Jinfeng Jiang, Yu He, and Lixin Zhao. 2025. "Using Higher Diffraction Orders to Improve the Accuracy and Robustness of Overlay Measurements" Micromachines 16, no. 3: 347. https://doi.org/10.3390/mi16030347
APA StyleLiu, S., Tang, Y., Cheng, X., Long, Y., Jiang, J., He, Y., & Zhao, L. (2025). Using Higher Diffraction Orders to Improve the Accuracy and Robustness of Overlay Measurements. Micromachines, 16(3), 347. https://doi.org/10.3390/mi16030347






