Vibration Analysis of Al–Al2O3 Micro-Cantilever Sandwich Beams with Porosity in Fluids
Abstract
1. Introduction
2. Theoretical Analysis
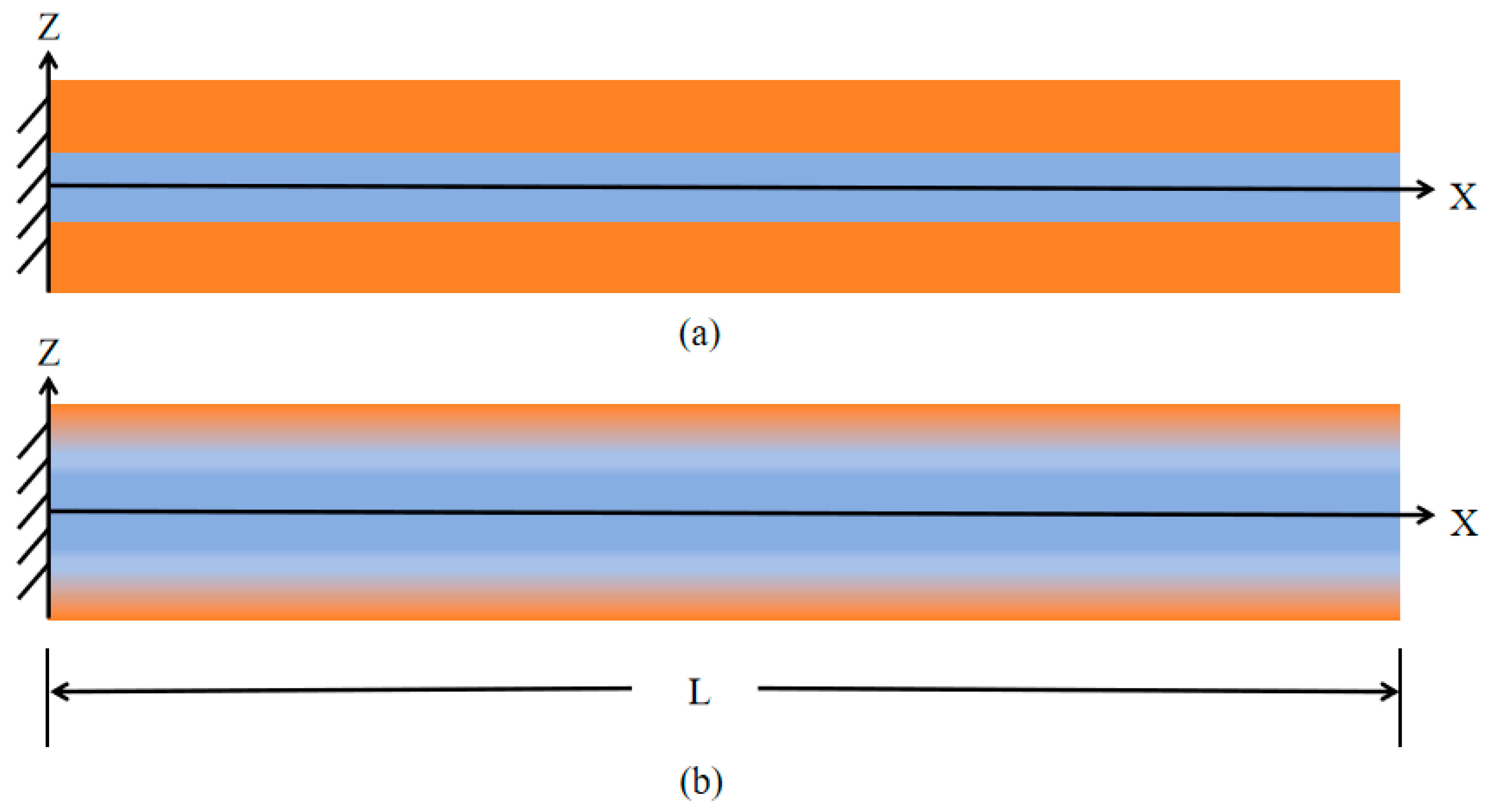
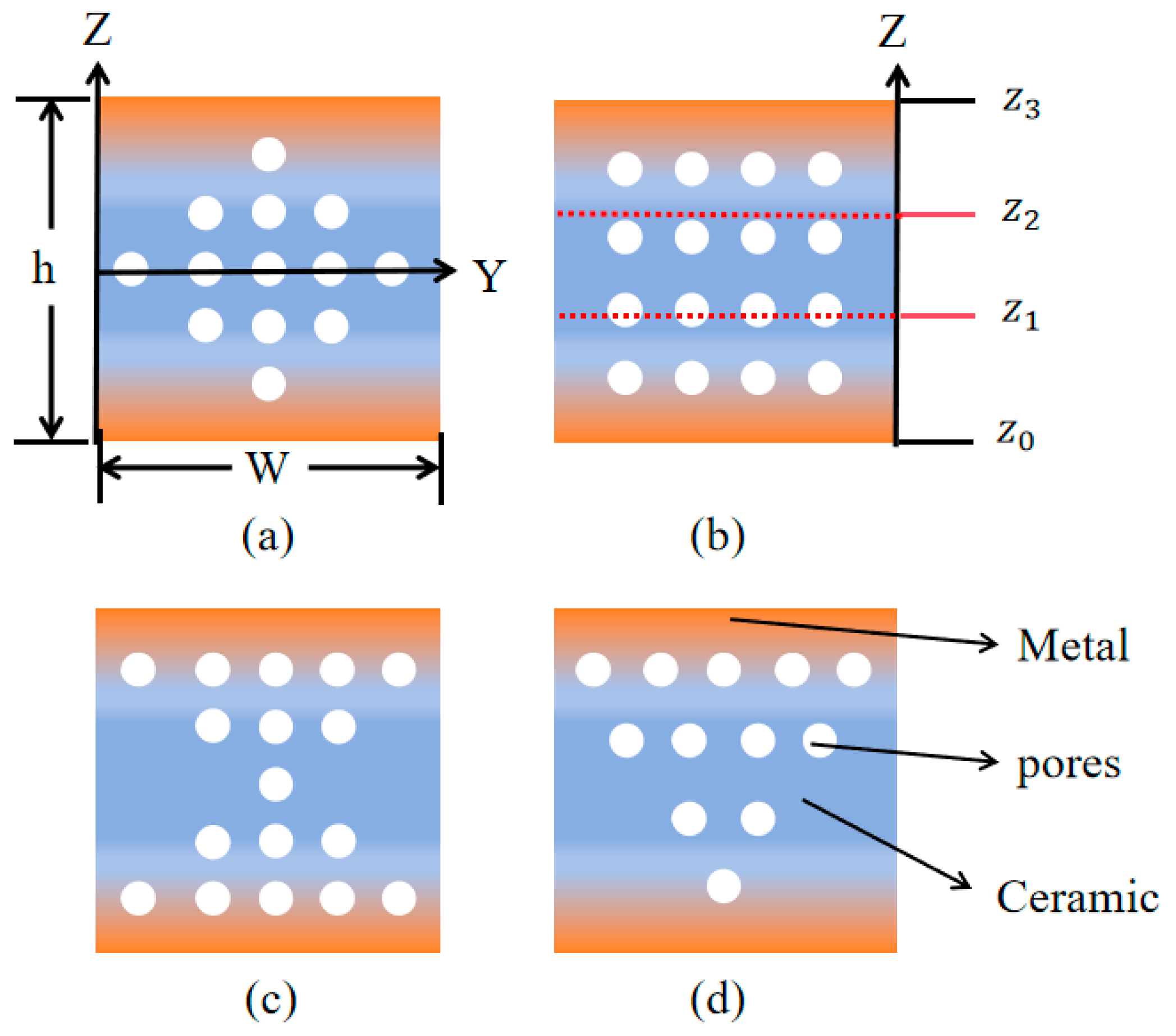
2.1. Power-Law Model of Porous Sandwich Micro-Cantilever Beam
2.2. One-Dimensional Temperature Field
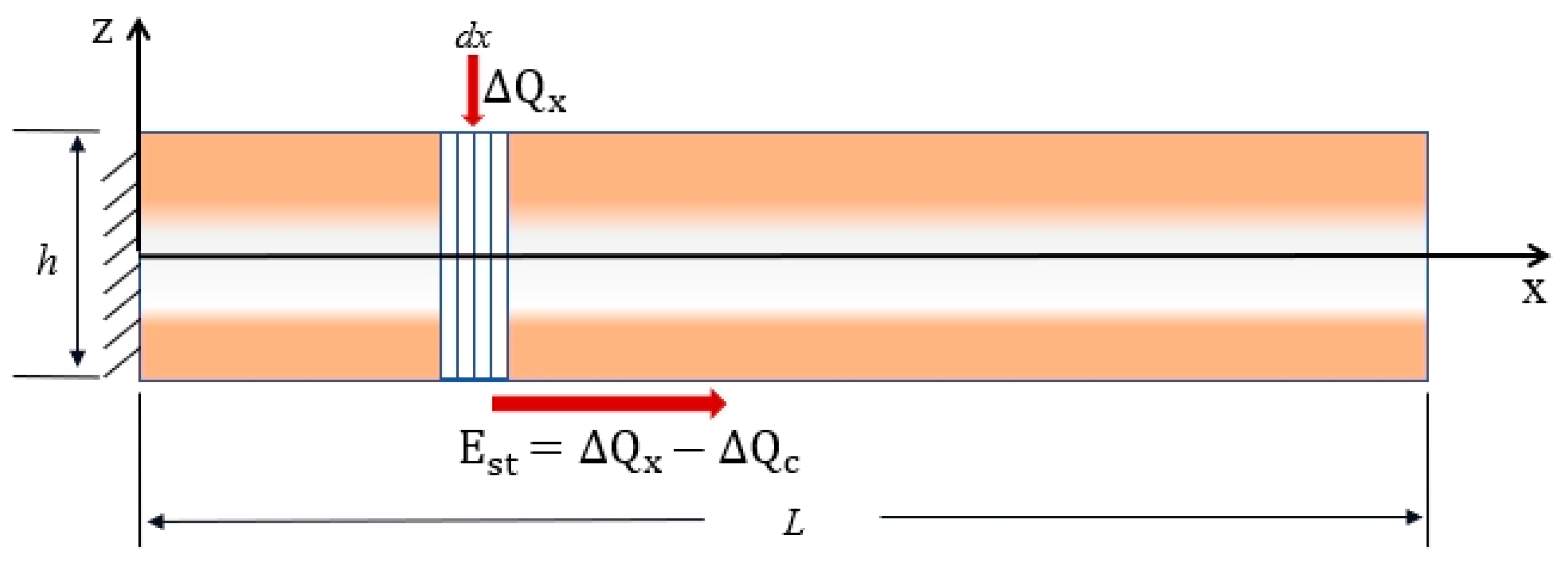
2.3. Analysis of Dynamic Response
2.4. First Order Resonant Frequency
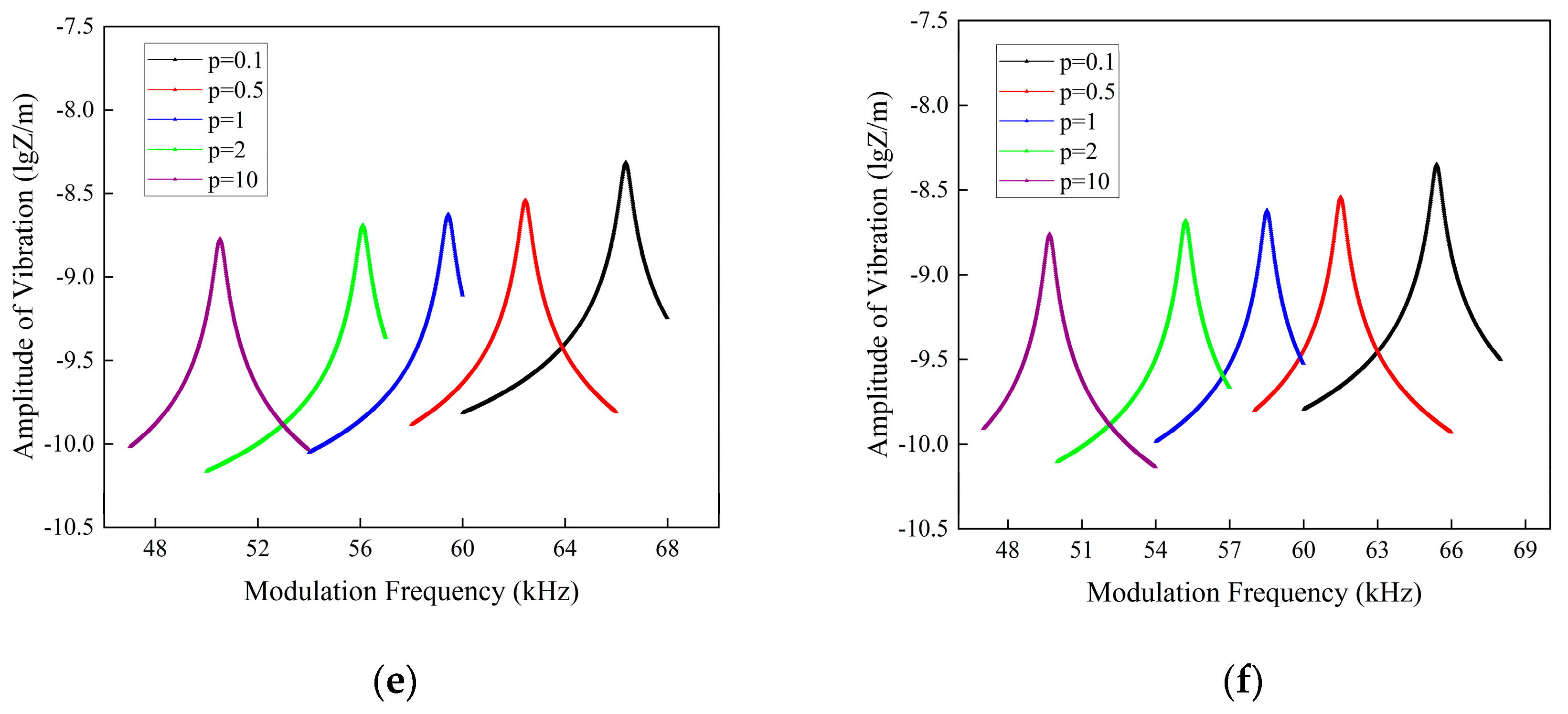
3. Results Analysis
4. Conclusions
- (1)
- The existence of fluid causes the resonance peak of the beam to slow down and the resonance frequency to migrate to lower frequencies. The higher the fluid kinematic viscosity, the more pronounced this phenomenon is;
- (2)
- The impact of pores on the dynamic response to laser loading of the FGM cantilever sandwich beam is low compared to that of the gradient factor p and the fluid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, S.; Liu, X.; Zhou, X.; Liang, X.M.; Gao, D.; Liu, H.; Zhao, G.; Zhang, Q.; Wu, X. Quantification of cell viability and rapid screening anti-cancer drug utilizing nanomechanical fluctuation. Biosens. Bioelectron. 2016, 77, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Karsten, S.L.; Nishida, S.; Kawakatsu, H.; Fujita, H. Application of a new micro-cantilever biosensor resonating at the air-liquid interface for direct insulin detection and continuous monitoring of enzymatic reactions. Lab Chip. 2012, 12, 4115–4119. [Google Scholar] [CrossRef] [PubMed]
- Faegh, S.; Jalili, N.; Sridhar, S.A. Self-sensing piezoelectric micro-cantilever biosensor for detection of ultrasmall adsorbed masses: Theory and experiments. Sensors 2013, 13, 6089–6108. [Google Scholar] [CrossRef]
- Sader, J.E.; Borgani, R.; Gibson, C.T.; Haviland, D.B.; Higgins, M.J.; Kilpatrick, J.I.; Lu, J.; Mulvaney, P.; Shearer, C.J.; Slattery, A.D.; et al. A virtual instrument to standardise the calibration of atomic force microscope cantilevers. Rev. Sci. Instrum. 2016, 87, 093711. [Google Scholar] [CrossRef]
- Chen, L.Q.; Lim, C.W.; Hu, Q.; Ding, H. Asymptotic analysis of a vibrating cantilever with a nonlinear boundary. Science 2009, 52, 1414–1422. (In Chinese) [Google Scholar] [CrossRef]
- Chen, Y.H. Research and prospect of microelectromechanical systems. Electro-Mech. Eng. 2011, 27, 1–7. [Google Scholar]
- Lloyd, D.J. Particle-reinforced aluminum and magnesium matrix composites. Int. Mater. Rev. 1994, 39, 1–23. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J. Strain gradient plasticity: Theory and experiment. Acta Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Stolken, J.S.; Evans, A.G. A micro bend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Guo, S.; Li, Z.; Liu, D. Size-dependent vibration of nickel cantilever micro-beams: Experiment and gradient elasticity. AIP Adv. 2016, 6, 105202. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Lei, J.; Guo, S.; Liu, D.; Wang, L. A standard experimental method for determining the material length scale based on modified couple stress theory. Int. J. Mech. Sci. 2018, 141, 198–205. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.; Tong, P. Couple stress-based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Jung, W.Y.; Park, W.T.; Han, S.C. Bending and vibration analysis of S-FGM microplates embedded in Pasternak elastic medium using the modified couple stress theory. Int. J. Mech. Sci. 2014, 87, 150–162. [Google Scholar] [CrossRef]
- Jani, R.; Reddy, J.N. Experimental validation of the modified couple stresses Timoshenko beam theory for web-core sandwich panels. Compos. Struct. 2014, 111, 130–137. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Modified couple stress theory in orthogonal curvilinear coordinates. Acta Mech. 2019, 230, 851–869. [Google Scholar] [CrossRef]
- Zahra, S.; Sarrami-Foroushani, S.; Azhari, F.; Azhari, M. Application of modified couplestress theory to stability and free vibration analysis of single and multi-layered graphene sheets. Aerosp. Sci. Technol. 2020, 98, 105652. [Google Scholar] [CrossRef]
- Vinh, P.V. Analysis of bi-directional functionally graded sandwich plates via higher-order shear deformation theory and finite element method. J. Sandw. Struct. Mater. 2022, 24, 860–899. [Google Scholar] [CrossRef]
- Jiang, J.; Tang, F.; He, S.; Dong, F.; Liu, S. Vibration Analysis of Porous Cu-Si micro-cantilever Beams in Fluids Based on Modified Couple Stress Theory. Nanomaterials 2024, 14, 1144. [Google Scholar] [CrossRef]
- Jiang, J.; Tang, F.; Gu, S.; He, S.; Dong, F.; Liu, S. Vibration Study of Functionally Graded micro-cantilever Beams in Fluids Based on Modified Couple Stress Theory by Considering the Physical Neutral Plane. Int. J. Struct. Stab. Dyn. 2024, 10, 1142. [Google Scholar] [CrossRef]
- Shi, S.N.; Tang, F.X.; Yu, Y.Q.; Guo, Y.Z.; Dong, F.; Liu, S. Size-dependent vibration analysis of the simply supported functionally graded porous material Al-Al2O3 rectangle microplates based on the modified couple stress theory with innovative consideration of neutral plane and scale distribution. Multidiscip. Model. Mater. Struct. 2024, 20, 229–246. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, Z.; Chen, L.; Yuan, H. Vibration and stability of a spinning functionally graded cylinder in a liquid-filled concentric drum. Phys. Fluids 2023, 35, 047109. [Google Scholar]
- Van Eysden, C.A.; Sader, J.E. Resonant frequencies of a rectangular cantilever beam immersed in a fluid. J. Appl. Phys. 2006, 100, 114916. [Google Scholar] [CrossRef]
- Chen, G.; Thundat, T.; Wachter, E.; Warmack, R.J. Adsorption-induced surface stress and its effects on resonance frequency of micro-cantilevers. J. Appl. Phys. 1995, 77, 3618–3622. [Google Scholar] [CrossRef]




| Material | E/GPa | K/(W/m·K) | C/(J/kg·K) | ||||
|---|---|---|---|---|---|---|---|
| 70 | 0.3 | 2707 | 6.58 | 237 | 2.3 × 10−7 | 880 | |
| 380 | 0.3 | 3800 | 11.00 | 30 | 7.4 × 10−6 | 770 |
| Fluids | ||
|---|---|---|
| air | 1.205 | 1.81 × 10−5 |
| gasoline | 678 | 2.9 × 10−4 |
| water | 998 | 1.01 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, F.; Yuan, X.; He, S.; Jiang, J.; Shi, S.; Li, Y.; Liu, W.; Zhou, Y.; Dong, F.; Liu, S. Vibration Analysis of Al–Al2O3 Micro-Cantilever Sandwich Beams with Porosity in Fluids. Micromachines 2025, 16, 206. https://doi.org/10.3390/mi16020206
Tang F, Yuan X, He S, Jiang J, Shi S, Li Y, Liu W, Zhou Y, Dong F, Liu S. Vibration Analysis of Al–Al2O3 Micro-Cantilever Sandwich Beams with Porosity in Fluids. Micromachines. 2025; 16(2):206. https://doi.org/10.3390/mi16020206
Chicago/Turabian StyleTang, Feixiang, Xiong Yuan, Siyu He, Jize Jiang, Shaonan Shi, Yuhan Li, Wenjin Liu, Yang Zhou, Fang Dong, and Sheng Liu. 2025. "Vibration Analysis of Al–Al2O3 Micro-Cantilever Sandwich Beams with Porosity in Fluids" Micromachines 16, no. 2: 206. https://doi.org/10.3390/mi16020206
APA StyleTang, F., Yuan, X., He, S., Jiang, J., Shi, S., Li, Y., Liu, W., Zhou, Y., Dong, F., & Liu, S. (2025). Vibration Analysis of Al–Al2O3 Micro-Cantilever Sandwich Beams with Porosity in Fluids. Micromachines, 16(2), 206. https://doi.org/10.3390/mi16020206






