Compact SPICE Model for TeraFET Resonant Detectors
Abstract
1. Introduction
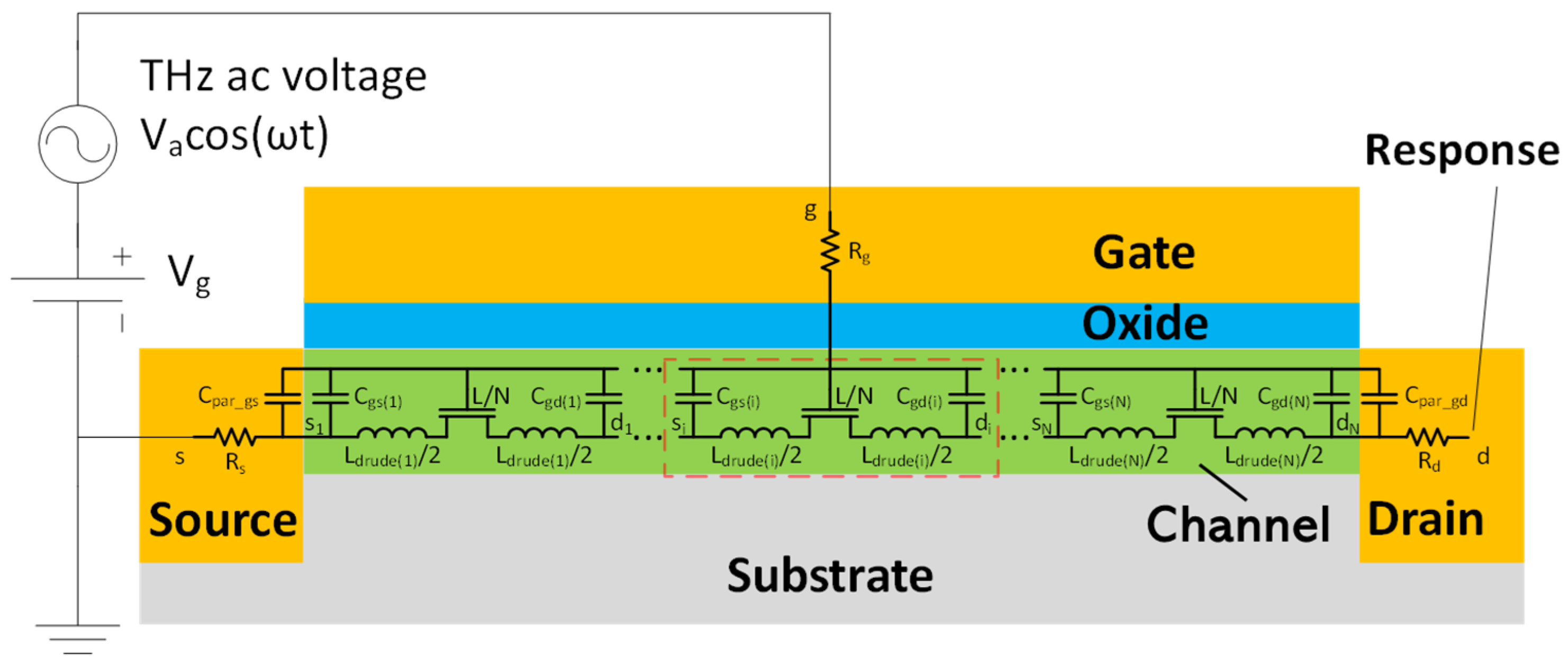
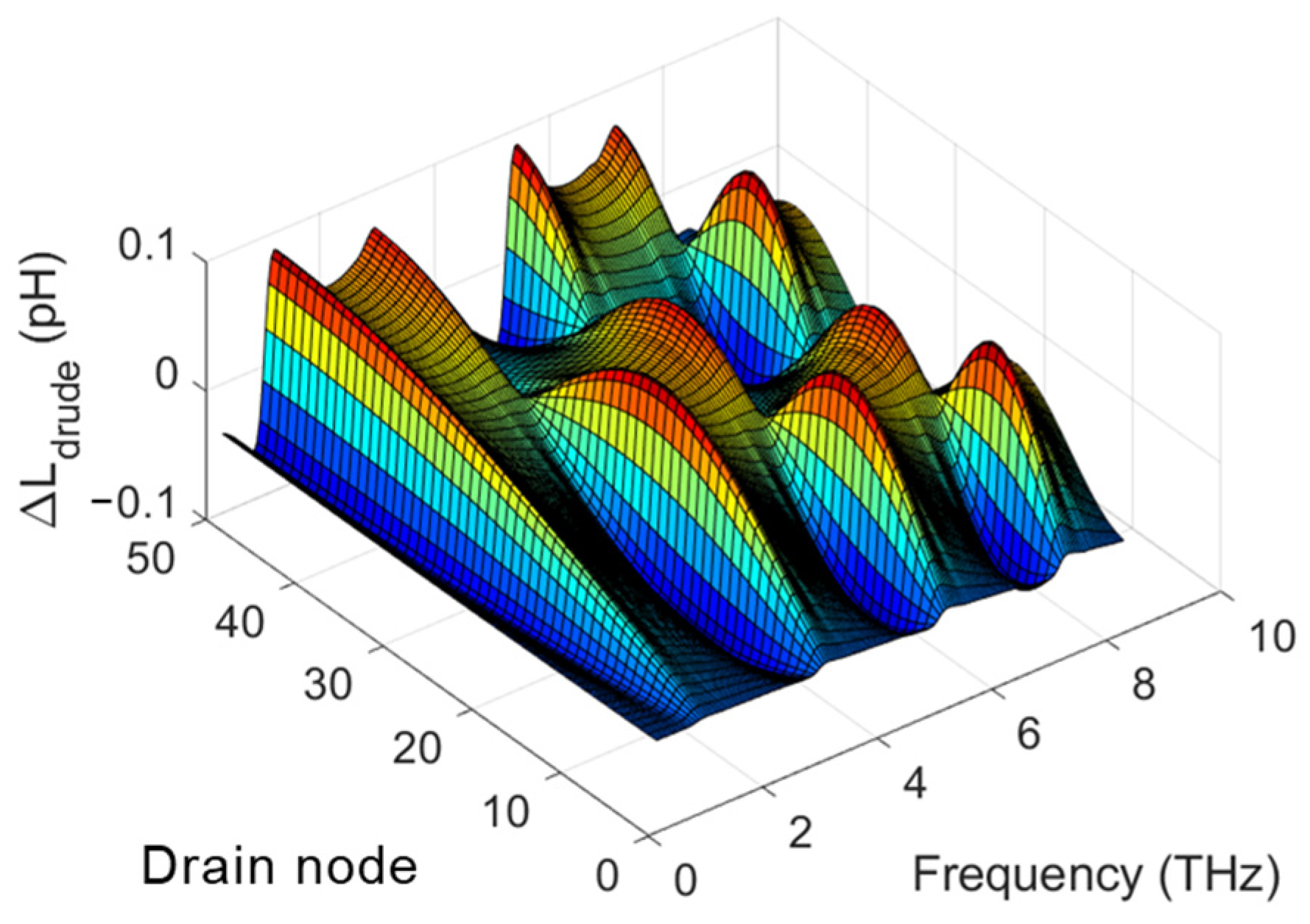
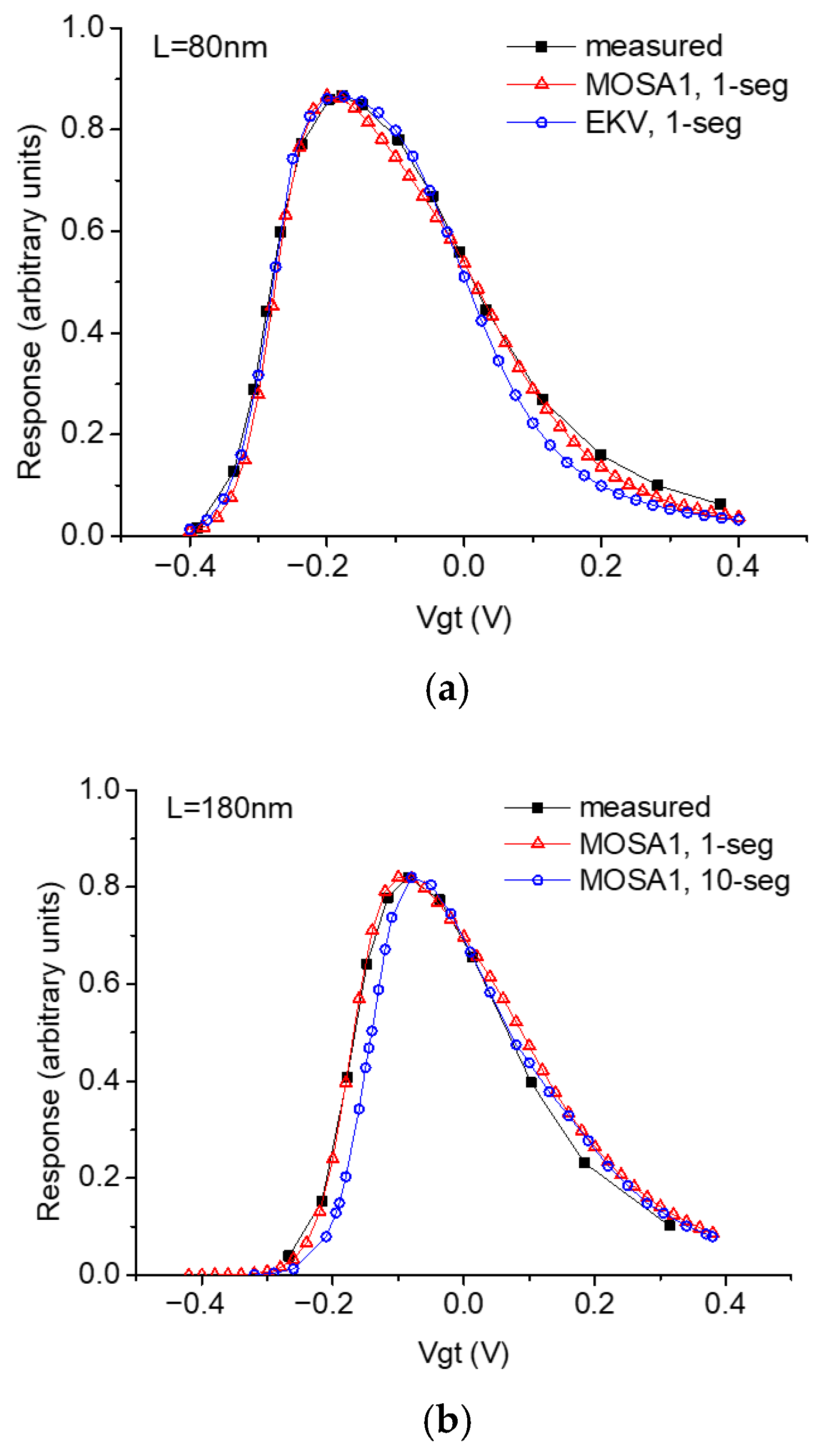
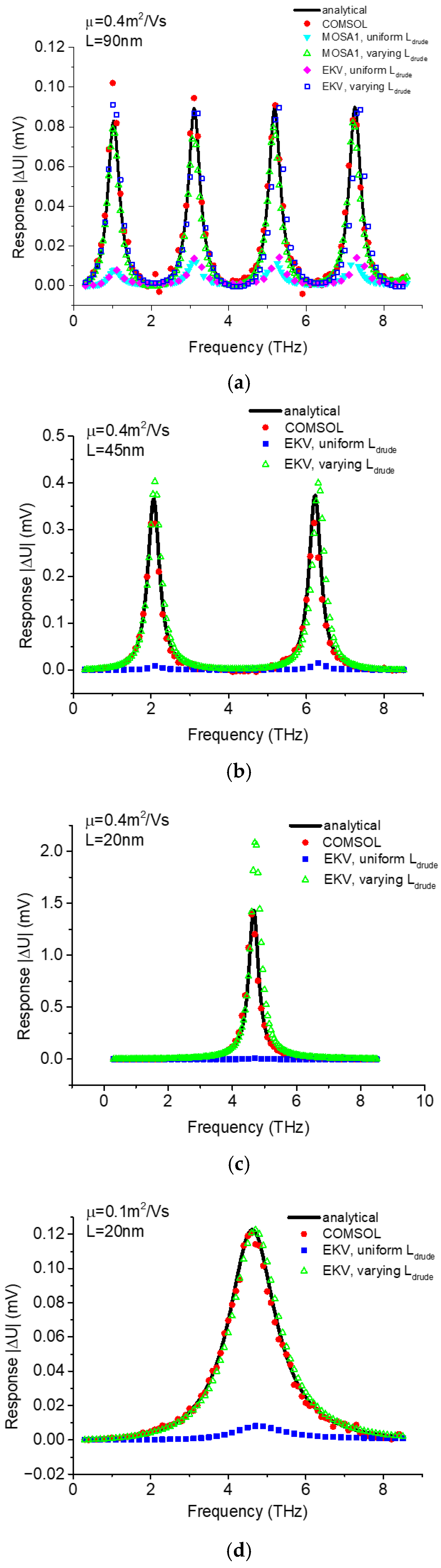
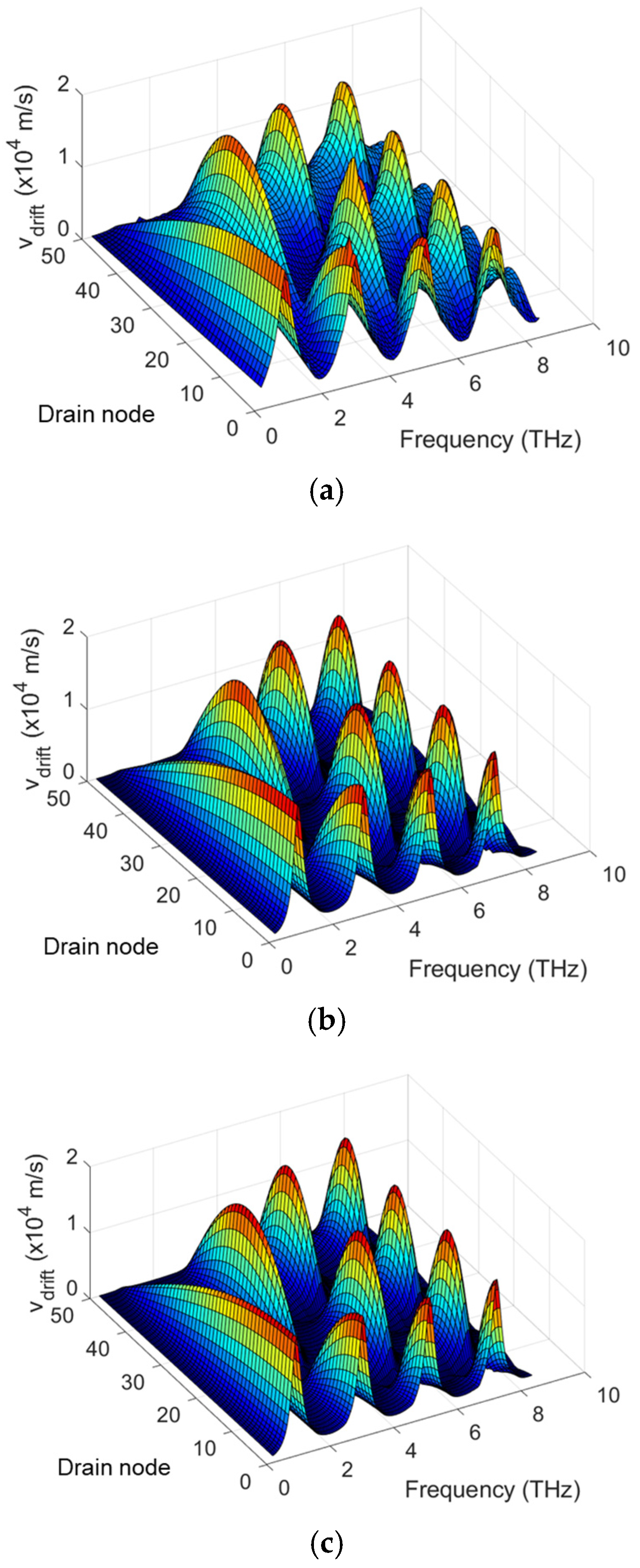
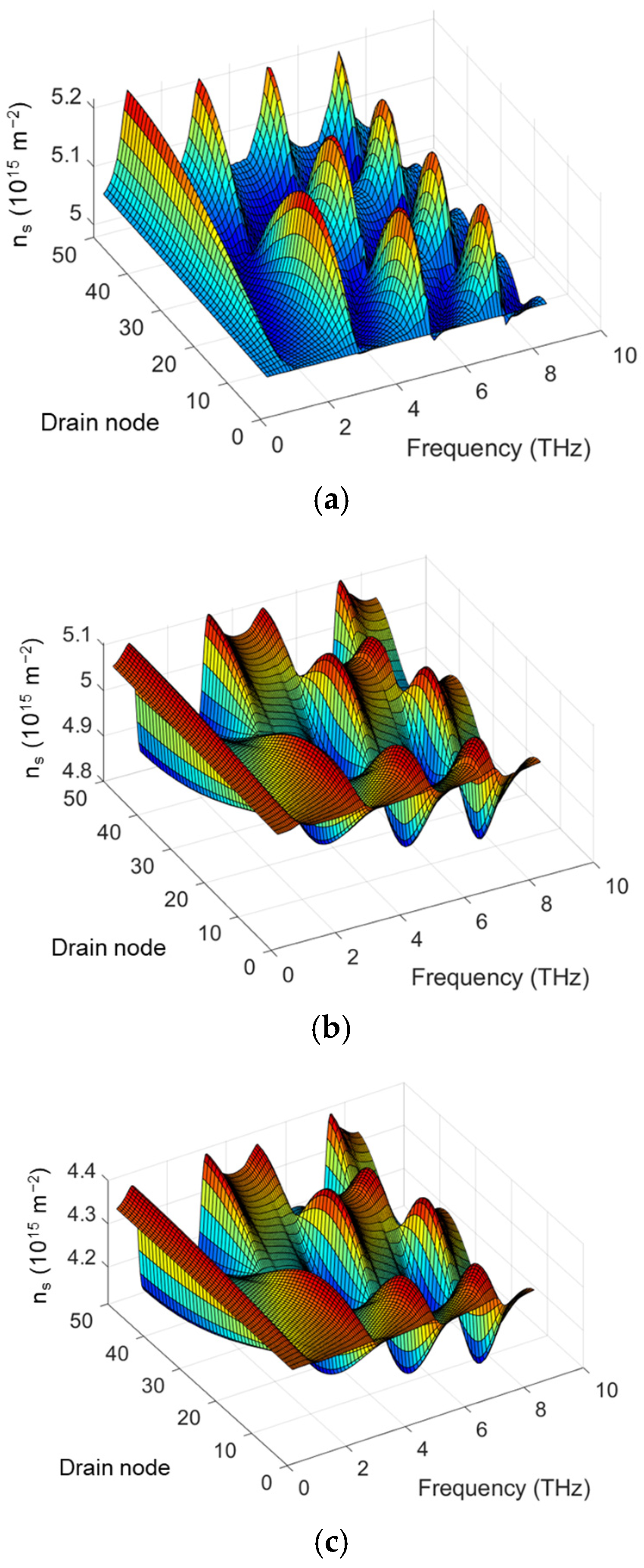
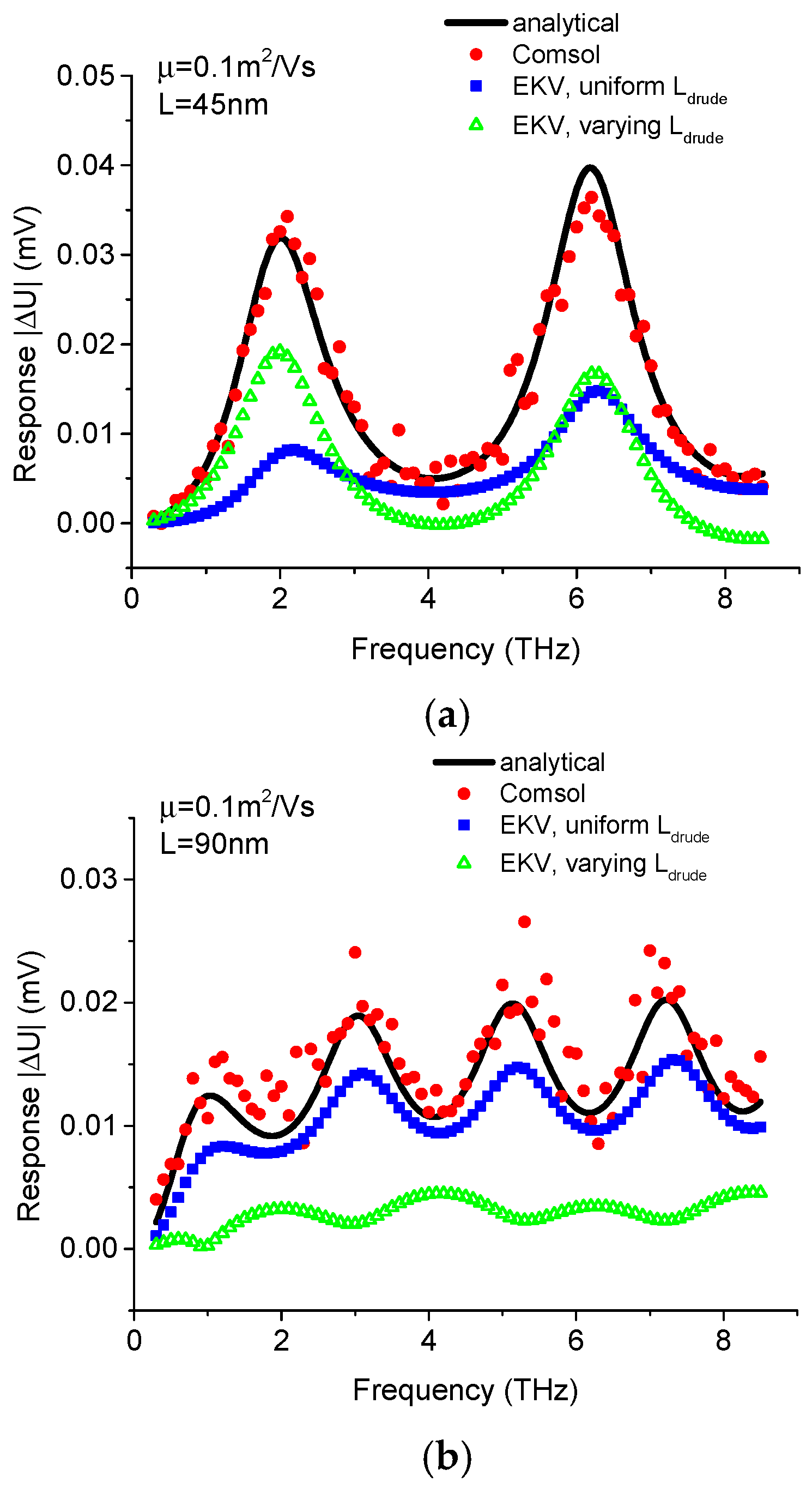
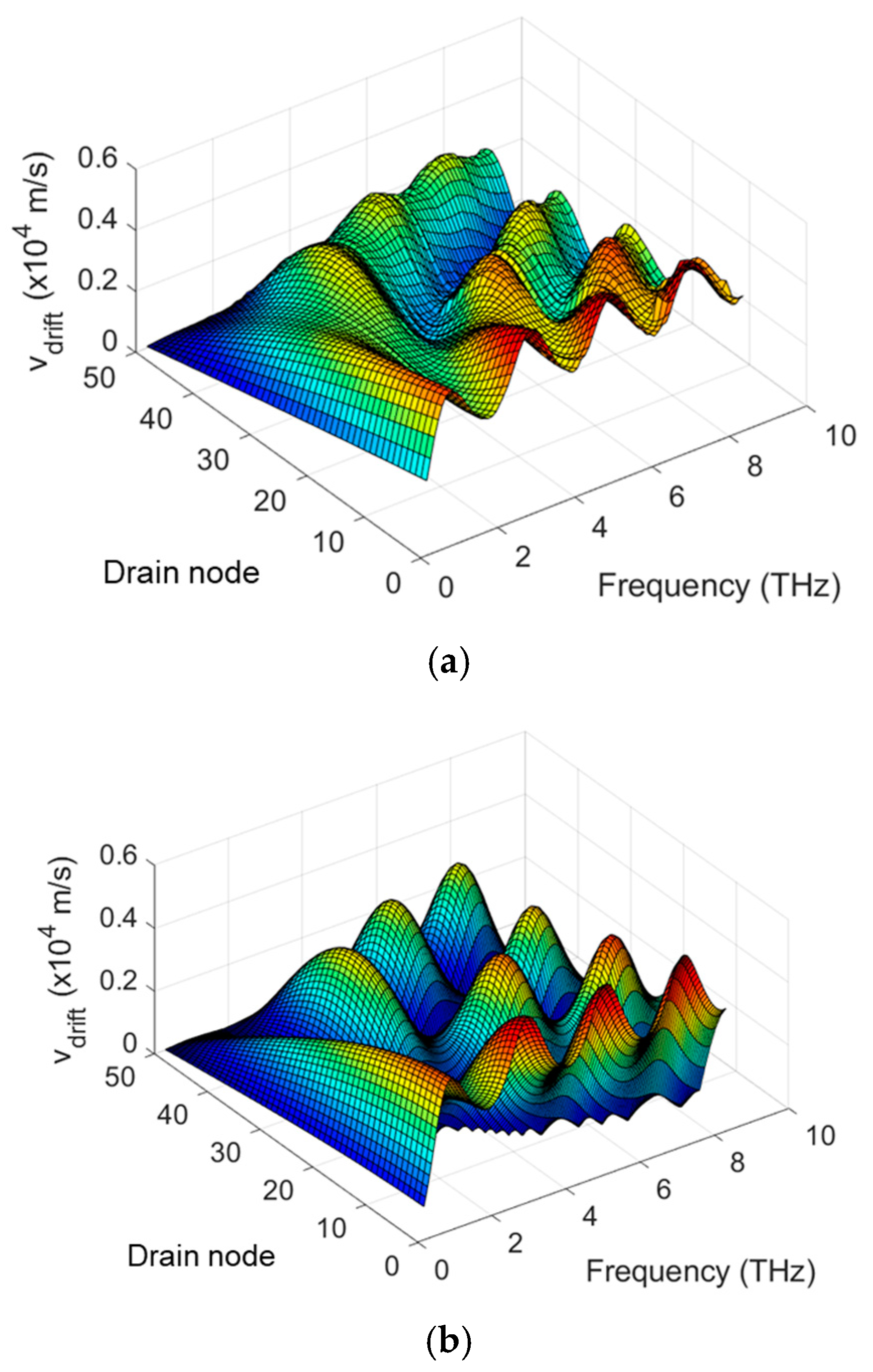
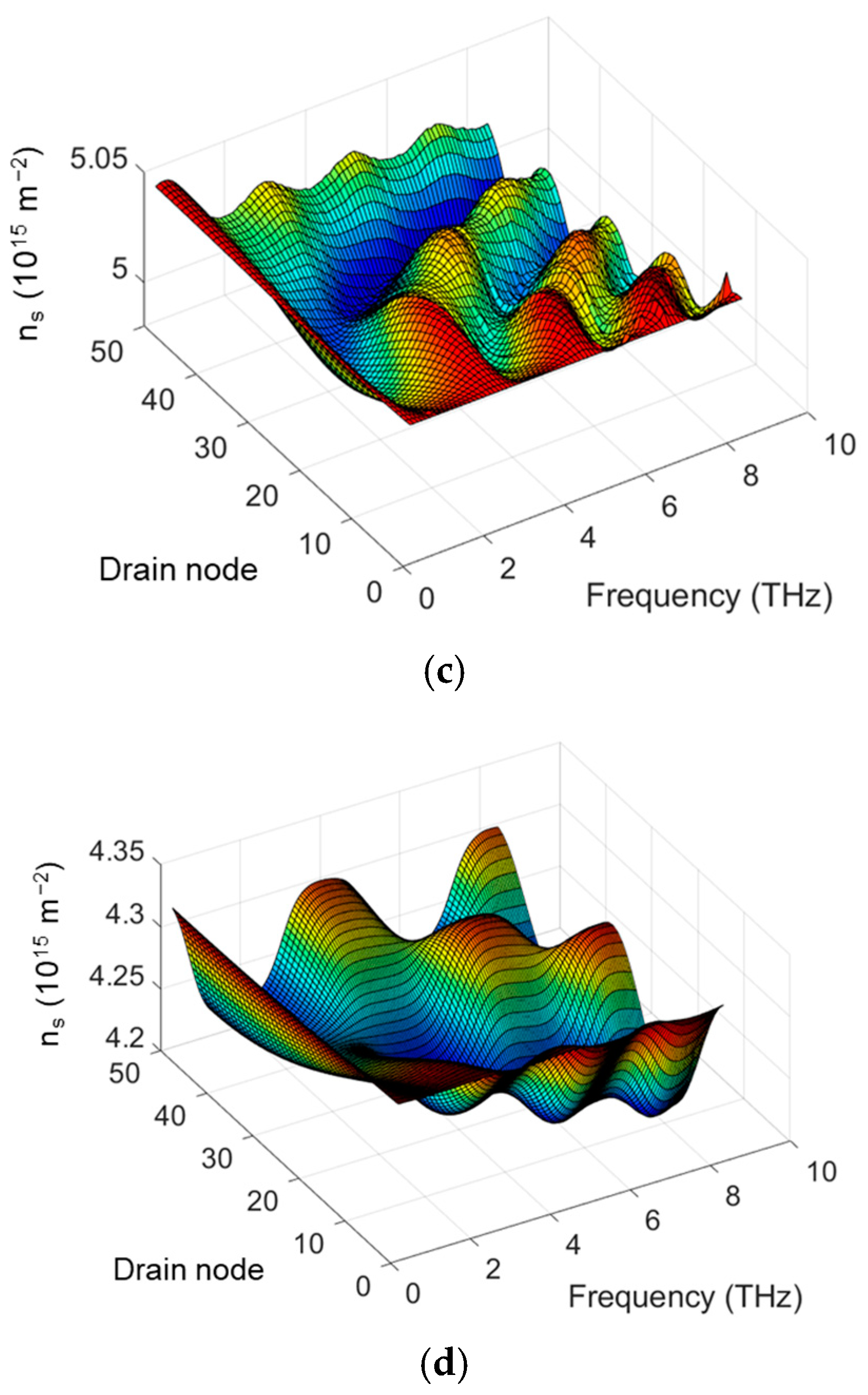
2. TeraFET SPICE Model
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lewis, R.A. A review of terahertz detectors. J. Phys. D Appl. Phys. 2019, 52, 433001. [Google Scholar] [CrossRef]
- Ikamas, K.; Cibiraite, D.; Lisauskas, A.; Bauer, M.; Krozer, V.; Roskos, H.G. Broadband Terahertz Power Detectors Based on 90-nm Silicon CMOS Transistors With Flat Responsivity Up to 2.2 THz. IEEE Electron Device Lett. 2018, 39, 1413–1416. [Google Scholar] [CrossRef]
- Teppe, F.; Knap, W.; Veksler, D.; Shur, M.S.; Dmitriev, A.P.; Kachorovskii, V.Y.; Rumyantsev, S. Room-temperature plasma waves resonant detection of sub-terahertz radiation by nanometer field-effect transistor. Appl. Phys. Lett. 2005, 87, 052107. [Google Scholar] [CrossRef]
- Jain, R.; Zatta, R.; Grzyb, J.; Harame, D.; Pfeiffer, U.R. A terahertz direct detector in 22nm FD-SOI CMOS. In Proceedings of the 2018 13th European Microwave Integrated Circuits Conference (EuMIC), Madrid, Spain, 23–25 September 2018; pp. 25–28. [Google Scholar]
- Pfeiffer, U.; Grzyb, J.; Sherry, H.; Cathelin, A.; Kaiser, A. Toward low-NEP room-temperature THz MOSFET direct detectors in CMOS technology. In Proceedings of the 2013 38th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Mainz, Germany, 1–6 September 2013; pp. 1–2. [Google Scholar]
- Knap, W.; Dyakonov, M.; Coquillat, D.; Teppe, F.; Dyakonova, N.; Łusakowski, J.; Karpierz, K.; Sakowicz, M.; Valusis, G.; Seliuta, D.; et al. Field Effect Transistors for Terahertz Detection: Physics and First Imaging Applications. J. Infrared Millim. Terahertz Waves 2009, 30, 1319–1337. [Google Scholar] [CrossRef]
- Dyakonova, N.; Coquillat, D.; Teppe, F.; Knap, W.; Suszek, J.; Siemion, A.; Sypek, M.; But, D.B.; Sai, P.; Yahniuk, I. Terahertz vision using field effect transistors detectors arrays. In Proceedings of the 2018 22nd International Microwave and Radar Conference (MIKON), Poznan, Poland, 14–17 May 2018; pp. 711–714. [Google Scholar]
- Valusis, G.; Lisauskas, A.; Yuan, H.; Knap, W.; Roskos, H.G. Roadmap of Terahertz Imaging 2021. Sensors 2021, 21, 4092. [Google Scholar] [CrossRef] [PubMed]
- Mittleman, D.M. Twenty years of terahertz imaging [Invited]. Opt Express 2018, 26, 9417–9431. [Google Scholar] [CrossRef] [PubMed]
- Bauer, M.; Venckevičius, R.; Kašalynas, I.; Boppel, S.; Mundt, M.; Minkevičius, L.; Lisauskas, A.; Valušis, G.; Krozer, V.; Roskos, H. Antenna-coupled field-effect transistors for multi-spectral terahertz imaging up to 4.25 THz. Opt. Express 2014, 22, 19235–19241. [Google Scholar] [CrossRef]
- Ojefors, E.; Pfeiffer, U.R.; Lisauskas, A.; Roskos, H.G. A 0.65 THz focal-plane array in a quarter-micron CMOS process technology. IEEE J. Solid-State Circuits 2009, 44, 1968–1976. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Graphene-based plasmonic nano-transceiver for terahertz band communication. In Proceedings of the The 8th European conference on antennas and propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; pp. 492–496. [Google Scholar]
- Wu, K.; Ducournau, G.; Hella, M.M. A 240 GHz receiver with 6 Gb/s data rate based on plasma wave detection in SiGe technology. In Proceedings of the 2019 44th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Paris, France, 1–6 September 2019; pp. 1–2. [Google Scholar]
- Kissinger, D.; Kahmen, G.; Weigel, R. Millimeter-Wave and Terahertz Transceivers in SiGe BiCMOS Technologies. IEEE Trans. Microw. Theory Tech. 2021, 69, 4541–4560. [Google Scholar] [CrossRef]
- Liu, X.; Ytterdal, T.; Shur, M. Plasmonic FET Terahertz Spectrometer. IEEE Access 2020, 8, 56039–56044. [Google Scholar] [CrossRef]
- Gutin, A.; Ytterdal, T.; Kachorovskii, V.; Muraviev, A.; Shur, M. THz SPICE for Modeling Detectors and Nonquadratic Response at Large Input Signal. IEEE Sens. J. 2013, 13, 55–62. [Google Scholar] [CrossRef]
- Liu, X.; Ytterdal, T.; Shur, M. Line of sight THz detector using TeraFET spectrometers. In Proceedings of the 2021 46th International Conference on Infrared, Millimeter and Terahertz Waves (IRMMW-THz), Chengdu, China, 29 August–3 September 2021; pp. 1–2. [Google Scholar]
- Lisauskas, A.; Pfeiffer, U.; Öjefors, E.; Bolìvar, P.H.; Glaab, D.; Roskos, H.G. Rational design of high-responsivity detectors of terahertz radiation based on distributed self-mixing in silicon field-effect transistors. J. Appl. Phys. 2009, 105, 114511. [Google Scholar] [CrossRef]
- Kelanee, y.; Ibrahim, N.; El Zayat, M.; Elnahwy, S. Review on Physics and Modelling of THz Radiation Detection Using Field-effect Transistors. Labyrinth Fayoum J. Sci. Interdiscip. Stud. 2023, 1, 95–106. [Google Scholar] [CrossRef]
- Liu, X.; Dovidenko, K.; Park, J.; Ytterdal, T.; Shur, M.S. Compact Terahertz SPICE Model: Effects of Drude Inductance and Leakage. IEEE Trans. Electron Devices 2018, 65, 5350–5356. [Google Scholar] [CrossRef]
- Fregonese, S.; Cabbia, M.; Yadav, C.; Deng, M.; Panda, S.R.; De Matos, M.; Celi, D.; Chakravorty, A.; Zimmer, T. Analysis of high-frequency measurement of transistors along with electromagnetic and SPICE cosimulation. IEEE Trans. Electron Devices 2020, 67, 4770–4776. [Google Scholar] [CrossRef]
- Liu, X.; Ytterdal, T.; Kachorovskii, V.Y.; Shur, M.S. Compact Terahertz SPICE/ADS Model. IEEE Trans. Electron Devices 2019, 66, 2496–2501. [Google Scholar] [CrossRef]
- Lee, K.; Shur, M.; Fjeldly, T.A.; Ytterdal, T. Semiconductor Device Modeling for VLSI; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog Integr. Circuits Signal Process. 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Dyakonov, M.; Shur, M. Detection, mixing, and frequency multiplication of terahertz radiation by two dimensional electronic fluid. IEEE Trans. Electron Devices 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Mönch, E.; Potashin, S.O.; Lindner, K.; Yahniuk, I.; Golub, L.E.; Kachorovskii, V.Y.; Bel’kov, V.V.; Huber, R.; Watanabe, K.; Taniguchi, T.; et al. Ratchet effect in spatially modulated bilayer graphene: Signature of hydrodynamic transport. Phys. Rev. B 2022, 105, 045404. [Google Scholar] [CrossRef]
- Crabb, J.; Cantos-Roman, X.; Jornet, J.M.; Aizin, G.R. Hydrodynamic theory of the Dyakonov-Shur instability in graphene transistors. arXiv 2021, arXiv:2106.01296. [Google Scholar] [CrossRef]
- Cosme, P.; Terças, H. Hydrodynamical study of terahertz emission in magnetized graphene field-effect transistors. Appl. Phys. Lett. 2021, 118, 131109. [Google Scholar] [CrossRef]
- Fang, L.; Willliam, T.; Adu, K.W.; Terrones, M. Phenomenological Modeling of Confined Phonon States in TMD Quantum Dots. MRS Adv. 2018, 3, 339–344. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Available online: http://www.comsol.com/ (accessed on 3 March 2024).
- Zhang, Y.; Shur, M.S. p-Diamond, Si, GaN, and InGaAs TeraFETs. IEEE Trans. Electron Devices 2020, 67, 4858–4865. [Google Scholar] [CrossRef]
- Zhang, Y.; Shur, M.S. Collision dominated, ballistic, and viscous regimes of terahertz plasmonic detection by graphene. J. Appl. Phys. 2021, 129, 053102. [Google Scholar] [CrossRef]
- Zhang, Y.; Shur, M.S. TeraFET terahertz detectors with spatially non-uniform gate capacitances. Appl. Phys. Lett. 2021, 119, 161104. [Google Scholar] [CrossRef]
- Ibrahim, N.Y.; Rafat, N.H.; Elnahwy, S.E. Modeling of field effect transistor channel as a nonlinear transmission line for terahertz detection. J. Infrared Millim. Terahertz Waves 2013, 34, 606–616. [Google Scholar] [CrossRef]
- Aizin, G.R.; Mikalopas, J.; Shur, M.S. Plasmons in ballistic nanostructures with stubs: Transmission line approach. IEEE Trans. Electron Devices 2018, 66, 126–131. [Google Scholar] [CrossRef]
- Sehmi, H.S.; Langbein, W.; Muljarov, E.A. Optimizing the Drude-Lorentz model for material permittivity: Method, program, and examples for gold, silver, and copper. Phys. Rev. B 2017, 95, 115444. [Google Scholar] [CrossRef]
- Eldlio, M.; Che, F.; Cada, M. Drude-Lorentz Model of Semiconductor Optical Plasmons. In IAENG Transactions on Engineering Technologies; Springer: Dordrecht, The Netherlands, 2014; pp. 41–49. [Google Scholar] [CrossRef]
- Bade, W. Drude-model calculation of dispersion forces. I. General theory. J. Chem. Phys. 1957, 27, 1280–1284. [Google Scholar] [CrossRef]
- Stillman, W.; Guarin, F.; Kachorovskii, V.Y.; Pala, N.; Rumyantsev, S.; Shur, M.; Veksler, D. Nanometer scale complementary silicon MOSFETs as detectors of terahertz and sub-terahertz radiation. In Proceedings of the SENSORS, 2007 IEEE, Atlanta, GA, USA, 28–31 October 2007; pp. 934–937. [Google Scholar]
- Levinshtein, M. Handbook Series on Semiconductor Parameters; World Scientific: Singapore, 1997; Volume 1. [Google Scholar]
- Zhang, Y.; Shur, M. THz detection and amplification using plasmonic field effect transistors driven by DC drain currents. J. Appl. Phys. 2022, 132, 193102. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, Y.; Ytterdal, T.; Shur, M. Compact SPICE Model for TeraFET Resonant Detectors. Micromachines 2025, 16, 152. https://doi.org/10.3390/mi16020152
Liu X, Zhang Y, Ytterdal T, Shur M. Compact SPICE Model for TeraFET Resonant Detectors. Micromachines. 2025; 16(2):152. https://doi.org/10.3390/mi16020152
Chicago/Turabian StyleLiu, Xueqing, Yuhui Zhang, Trond Ytterdal, and Michael Shur. 2025. "Compact SPICE Model for TeraFET Resonant Detectors" Micromachines 16, no. 2: 152. https://doi.org/10.3390/mi16020152
APA StyleLiu, X., Zhang, Y., Ytterdal, T., & Shur, M. (2025). Compact SPICE Model for TeraFET Resonant Detectors. Micromachines, 16(2), 152. https://doi.org/10.3390/mi16020152






