Current–Pressure Dynamics Modeling on an Annular Magnetorheological Valve for an Adaptive Rehabilitation Device for Disabled Individuals
Abstract
1. Introduction
2. Research Method
2.1. Magnetorheological Valve Design
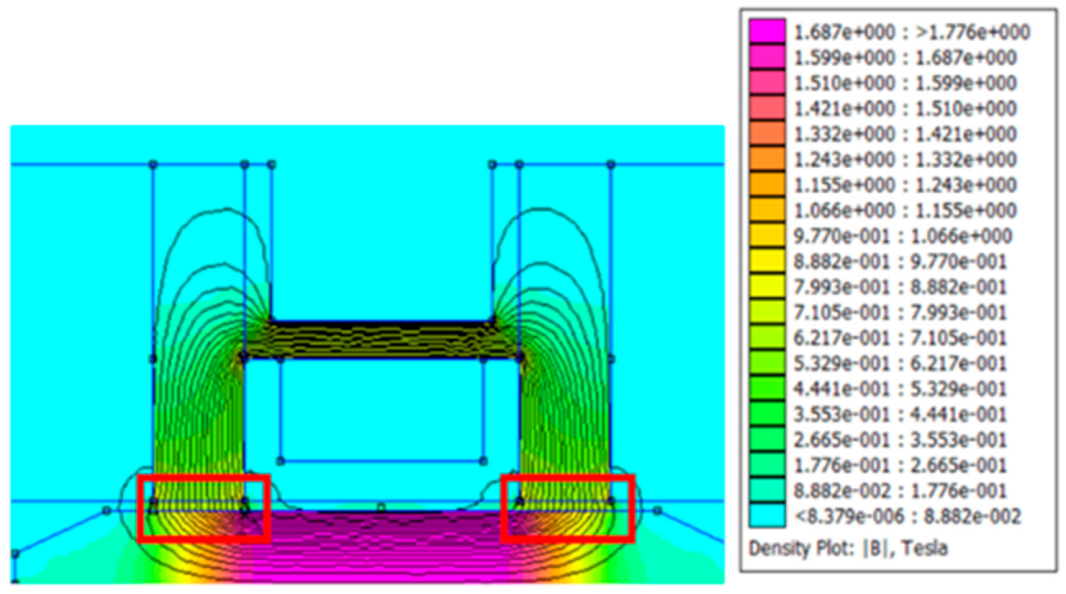
2.2. Magnetic Simulation
3. Experimental Setup and Modeling
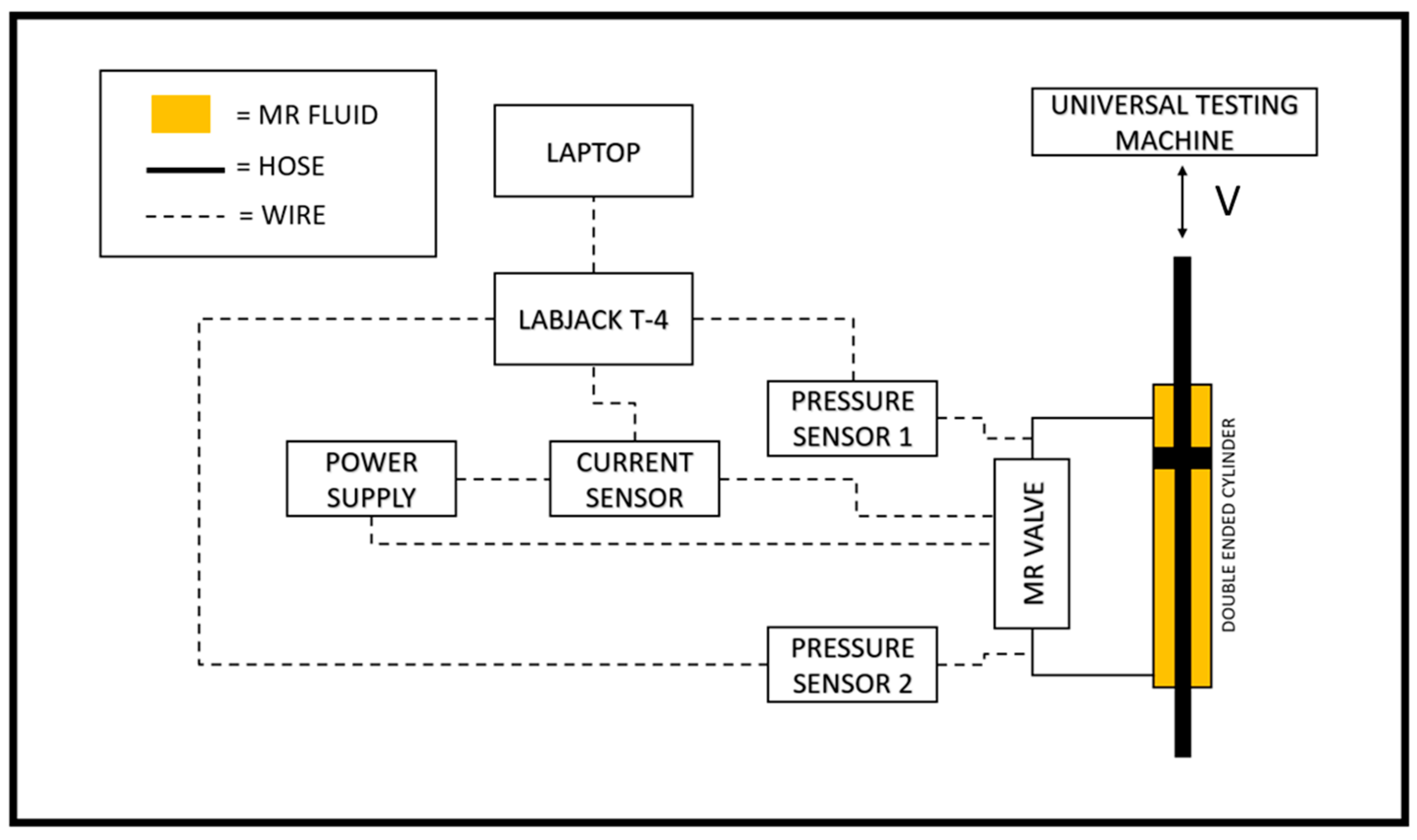
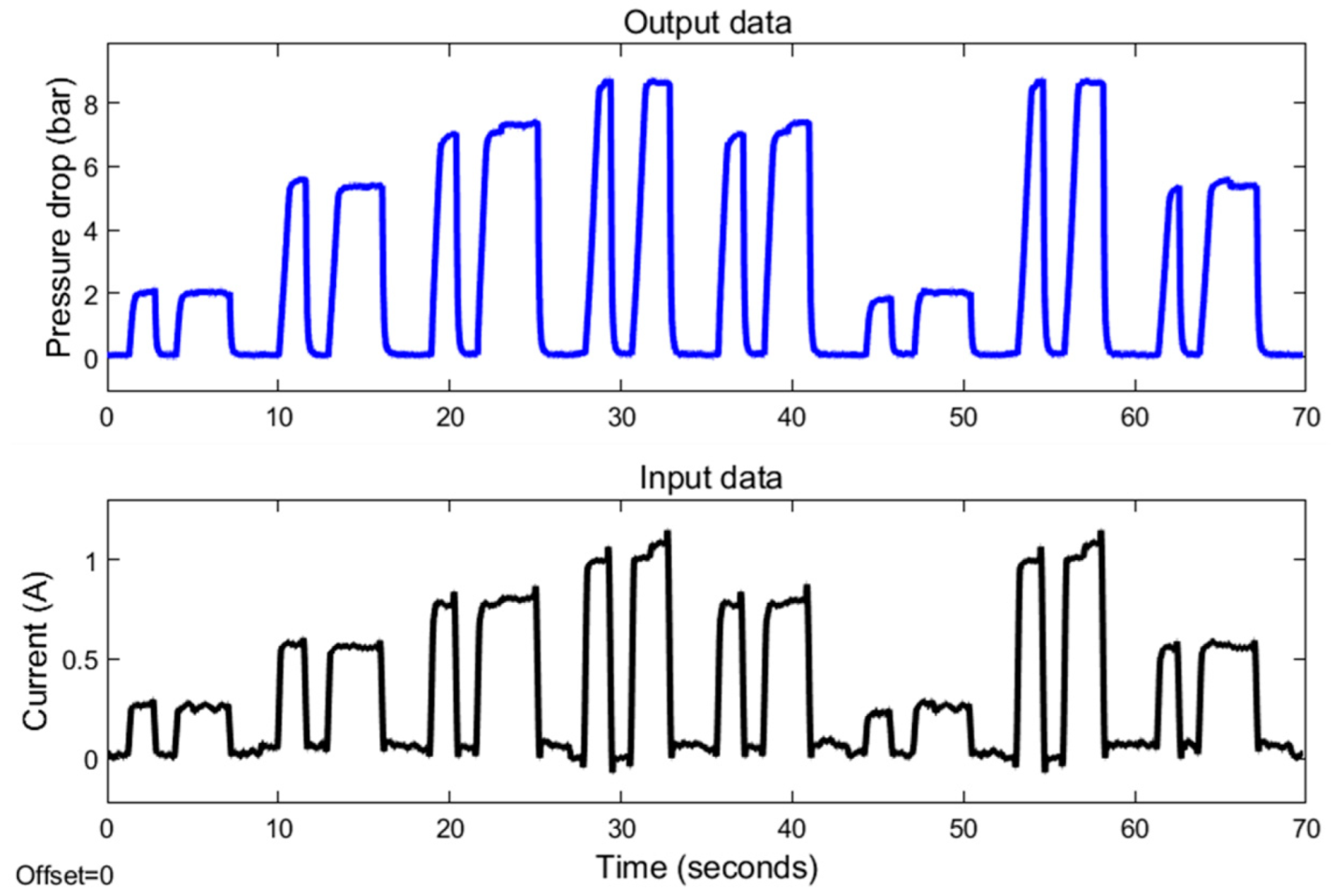
3.1. Experimental Setup
3.2. Linear Black-Box Modeling
- Prepare the experimental data that contain input and output variable relationships. They can be obtained from SISO and MIMO systems, but in the transfer function case, it is recommended to only model the SISO system.
- Analyze the system and define the types of black-box approaches, linear or nonlinear. In this step, it is important to use the correct method so the best result can be obtained easily without too many trials and errors.
- Conduct a modeling process from experimental data with a preferred approach to obtain the best model. In many cases, the modeling process is performed several times to achieve the best and most acceptable results.
- Conduct a validation of the best model performance. Although the best model is achieved, it needs to be validated with the other experimental data in the same systems with different variations to ensure the robustness and sustainability of the best model.
4. Results and Discussion
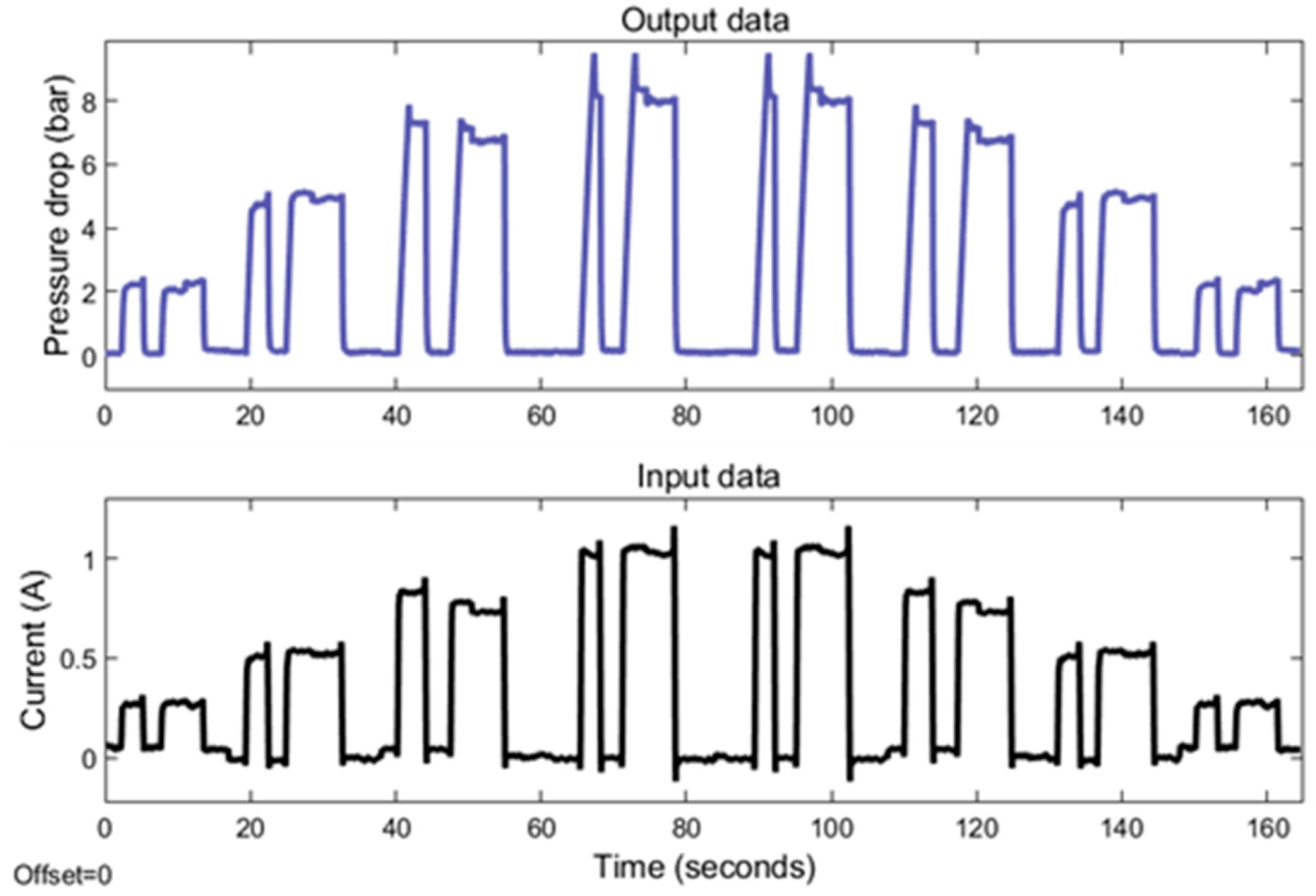
4.1. Experimental Results
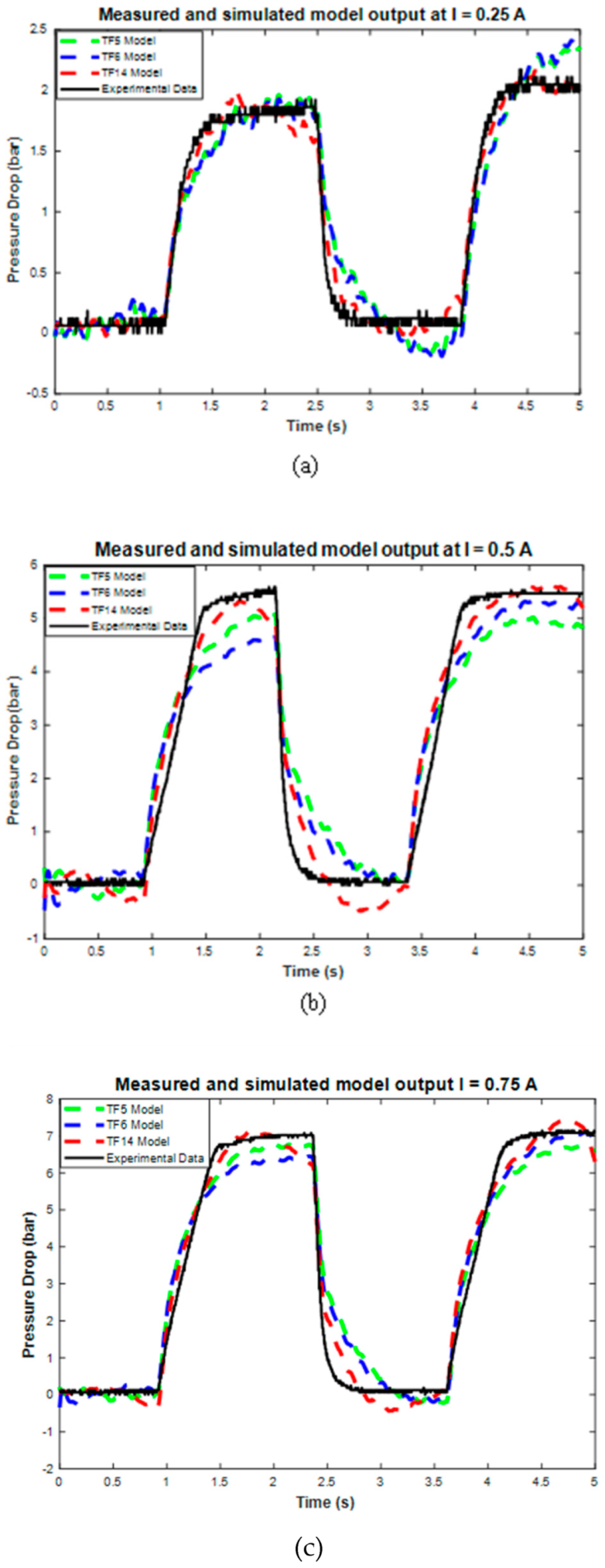
4.2. Modeling Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rabinow, J. The Magnetic Fluid Clutch. Trans. Am. Inst. Electr. Eng. 1948, 67, 1308–1315. [Google Scholar] [CrossRef]
- Imaduddin, F.; Mazlan, S.A.; Ubaidillah; Idris, M.H.; Bahiuddin, I. Characterization and modeling of a new magnetorheological damper with meandering type valve using neuro-fuzzy. J. King Saud Univ. Sci. 2017, 29, 468–477. [Google Scholar] [CrossRef]
- Liu, G.; Gao, F.; Wang, D.; Liao, W.-H. Medical applications of magnetorheological fluid: A systematic review. Smart Mater. Struct. 2022, 31, 043002. [Google Scholar] [CrossRef]
- Fardan, M.F.; Lenggana, B.W.; Ubaidillah, U.; Choi, S.-B.; Susilo, D.D.; Khan, S.Z. Revolutionizing prosthetic design with auxetic metamaterials and structures: A review of mechanical properties and limitations. Micromachines 2023, 14, 1165. [Google Scholar] [CrossRef] [PubMed]
- Strecker, Z.; Jeniš, F.; Kubík, M.; Macháček, O.; Choi, S.-B. Novel Approaches to the Design of an Ultra-Fast Magnetorheological Valve for Semi-Active Control. Materials 2021, 14, 2500. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Zhang, Z.; He, Y.; Li, Z.; Xie, J.; Deng, H. Realization of desired damping characteristics based on an open-loop-controlled magnetorheological damper. J. Vib. Control 2021, 28, 3652–3663. [Google Scholar] [CrossRef]
- Aziz, M.A.; Aminossadati, S.M. State-of-the-art developments of bypass Magnetorheological (MR) dampers: A review. Korea-Australia Rheol. J. 2021, 33, 225–249. [Google Scholar] [CrossRef]
- Li, D.D.; Keogh, D.F.; Huang, K.; Chan, Q.N.; Yuen, A.C.Y.; Menictas, C.; Timchenko, V.; Yeoh, G.H. Modeling the Response of Magnetorheological Fluid Dampers under Seismic Conditions. Appl. Sci. 2019, 9, 4189. [Google Scholar] [CrossRef]
- Abdalaziz, M.; Vatandoost, H.; Sedaghati, R.; Rakheja, S. Development and experimental characterization of a large-capacity magnetorheological damper with annular-radial gap. Smart Mater. Struct. 2022, 31, 115021. [Google Scholar] [CrossRef]
- Abdalaziz, M.; Sedaghati, R.; Vatandoost, H. Development of a new dynamic hysteresis model for magnetorheological dampers with annular-radial gaps considering fluid inertia and compressibility. J. Sound Vib. 2023, 561, 117826. [Google Scholar] [CrossRef]
- Puneet, N.; Kumbhar, S.; Kumar, H.; Gangadharan, K. Analysis of Magneto-rheological Fluid Damper and Linearization of Semi-active Quarter Car Model. NanoWorld J. 2023, 9, S341–S346. [Google Scholar] [CrossRef]
- Yoon, R.; Negash, B.A.; You, W.; Lee, J.; Lee, C.; Lee, K. Bi-exponential model and inverse model of magnetorheological damper for the semi-active suspension of a capsule vehicle. Meas. Control 2022, 56, 558–570. [Google Scholar] [CrossRef]
- Jeyasenthil, R.; Yoon, D.S.; Choi, S.-B. Response time effect of magnetorheological dampers in a semi-active vehicle suspension system: Performance assessment with quantitative feedback theory. Smart Mater. Struct. 2019, 28, 054001. [Google Scholar] [CrossRef]
- Jamadar, M.-E.; Desai, R.M.; Saini, R.S.T.; Kumar, H.; Joladarashi, S. Dynamic Analysis of a Quarter Car Model with Semi-Active Seat Suspension Using a Novel Model for Magneto-Rheological (MR) Damper. J. Vib. Eng. Technol. 2020, 9, 161–176. [Google Scholar] [CrossRef]
- Oh, J.S.; Choi, S.B. Chapter 16—Medical applications of magnetorheological fluid: A review. In Magnetic Materials and Technologies for Medical Applications; Woodhead Publishing Series in Electronic and Optical Materials; Elsevier: Amsterdam, The Netherlands, 2022; pp. 485–500. [Google Scholar] [CrossRef]
- Bai, X.-X.; Shen, S.; Wereley, N.M.; Wang, D.-H. Controllability of magnetorheological shock absorber: I. Insights, modeling and simulation*. Smart Mater. Struct. 2019, 28, 015022. [Google Scholar] [CrossRef]
- Cha, Y.-J.; Agrawal, A.K.; Dyke, S.J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater. Struct. 2012, 22, 015011. [Google Scholar] [CrossRef]
- Stanway, R.; Sproston, J.L.; Stevens, N.G. Non-linear modelling of an electro-rheological vibration damper. J. Electrost. 1987, 20, 167–184. [Google Scholar] [CrossRef]
- Spencer, B.F.; Dyke, S.J.; Sain, M.K.; Carlson, J.D. Phenomenological Model for Magnetorheological Dampers. J. Eng. Mech. 1997, 123, 230–238. [Google Scholar] [CrossRef]
- Lischinsky, P.; Canudas-De-Wit, C.; Morel, G. Friction compensation for an industrial hydraulic robot. IEEE Control. Syst. 1999, 19, 25–32. [Google Scholar] [CrossRef]
- Jiang, Z.; E Christenson, R. A fully dynamic magneto-rheological fluid damper model. Smart Mater. Struct. 2012, 21, 065002. [Google Scholar] [CrossRef]
- Choirunisa, I.; Ubaidillah; Imaduddin, F.; Maharani, E.T.; Priyandoko, G.; Mazlan, S.A. MR Damper Modeling using Gaussian and Generalized Bell of ANFIS Algorithm. Evergreen 2021, 8, 673–685. [Google Scholar] [CrossRef]
- Abdelhamed, M.; Ata, W.G.; Salem, A.M. Nonparametric modeling of magnetorheological damper based on nonlinear black-box technique. J. Phys. Conf. Ser. 2022, 2299, 012008. [Google Scholar] [CrossRef]
- Kostamo, E.; Kostamo, J.; Kajaste, J.; Pietola, M. Magnetorheological valve in servo applications. J. Intell. Mater. Syst. Struct. 2012, 23, 1001–1010. [Google Scholar] [CrossRef]
- Kubík, M.; Válek, J.; Žáček, J.; Jeniš, F.; Borin, D.; Strecker, Z.; Mazůrek, I. Transient response of magnetorheological fluid on rapid change of magnetic field in shear mode. Sci. Rep. 2022, 12, 10612. [Google Scholar] [CrossRef]
- Nasr, A.; Bell, S.; McPhee, J. Optimal design of active-passive shoulder exoskeletons: A computational modeling of human-robot interaction. Multibody Syst. Dyn. 2023, 57, 73–106. [Google Scholar] [CrossRef]
- Calderone, A.; Latella, D.; Bonanno, M.; Quartarone, A.; Mojdehdehbaher, S.; Celesti, A.; Calabrò, R.S. Towards Transforming Neurorehabilitation: The Impact of Artificial Intelligence on Diagnosis and Treatment of Neurological Disorders. Biomedicines 2024, 12, 2415. [Google Scholar] [CrossRef] [PubMed]
- Kabir, R.; Sunny, S.H.; Ahmed, H.U.; Rahman, M.H. Hand Rehabilitation Devices: A Comprehensive Systematic Review. Micromachines 2022, 13, 1033. [Google Scholar] [CrossRef] [PubMed]
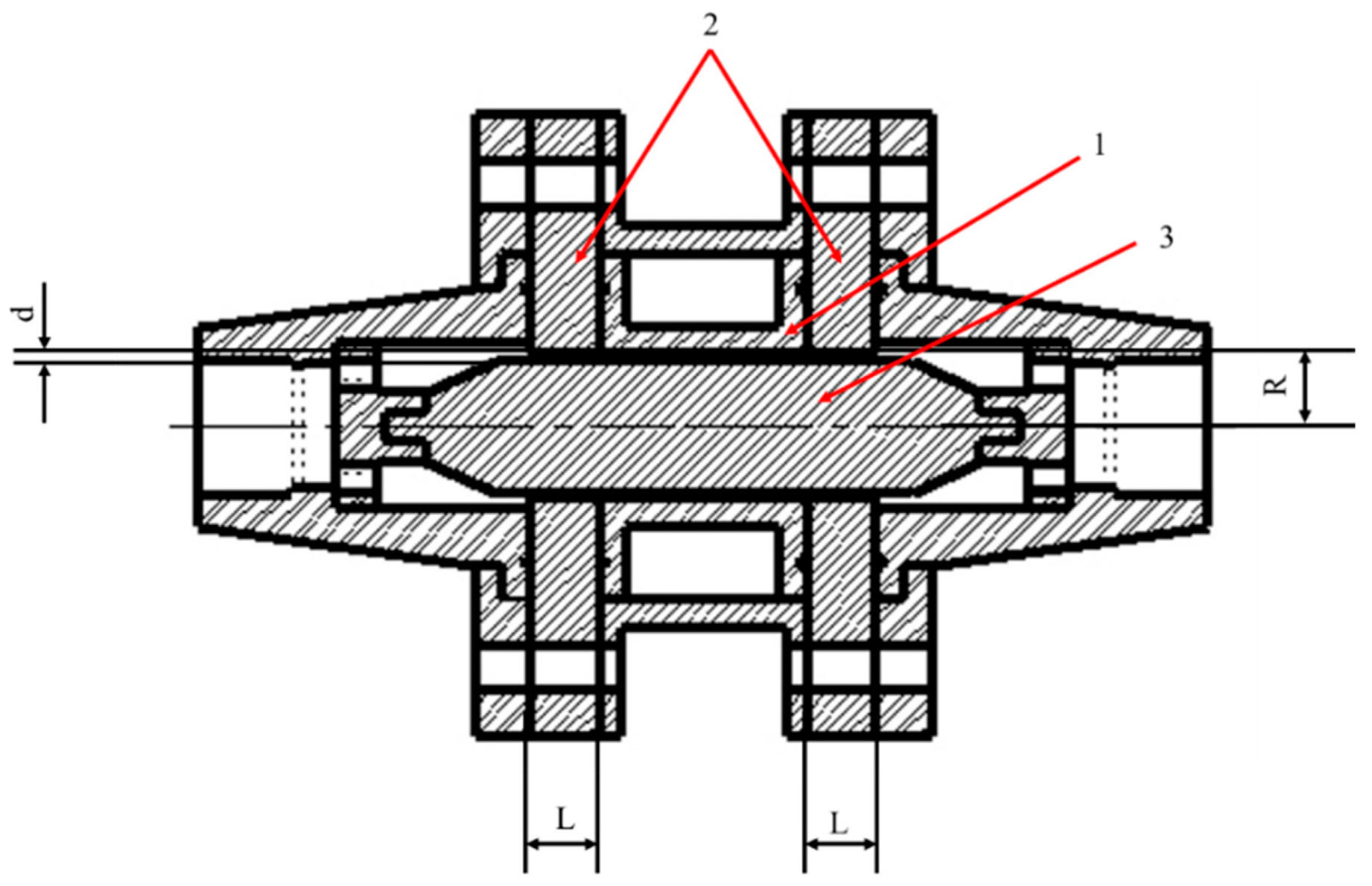





| Components | Dimensions (mm) |
|---|---|
| Magnetization effective length (L) | 10 |
| Annular channel width | 1 |
| Annular channel radius | 19.5 |
| Appearance | Dark Grey Liquid |
|---|---|
| Density (g/m3) | 2.75–2.95 |
| Viscosity (Pa s @40 °C) | 0.106 ± 0.02 |
| Shear Stress (kPa @570 mT) | 68.0 ± 7 |
| Operating Temperature (°C) | −40–140 |
| Flash Point (°C) | >140 |
| Solid Wight Percentage (wt%) | 77–80 |
| Sedimentation Stability (vol%/30 days) | 4.00 |
| Variation | Condition | Current (A) |
|---|---|---|
| 1 | ON–OFF | 0.25 |
| 2 | 0.5 | |
| 3 | 0.75 | |
| 4 | 1.00 |
| Transfer Function | Number of Orders | RMSE (%) | |
|---|---|---|---|
| Poles | Zeros | ||
| 1 | 1 | 0 | 30.445 |
| 2 | 2 | 1 | 30.29 |
| 3 | 3 | 2 | 30.18 |
| 4 | 4 | 3 | 31.035 |
| 5 | 5 | 4 | 30.86 |
| 6 | 6 | 5 | 30.85 |
| 7 | 7 | 6 | 30.73 |
| 8 | 8 | 7 | 30.91 |
| 9 | 9 | 8 | 31.47 |
| 10 | 10 | 9 | 30.75 |
| 11 | 11 | 10 | 31.405 |
| 12 | 12 | 11 | 41.375 |
| 13 | 13 | 12 | 39.46 |
| 14 | 14 | 13 | 82.761 |
| 15 | 15 | 14 | 65.255 |
| Transfer Function | Number of Orders | RMSE (%) | |
|---|---|---|---|
| Poles | Zeros | ||
| 1 | 1 | 0 | 28.53 |
| 2 | 2 | 1 | 29.12 |
| 3 | 3 | 2 | 28.52 |
| 4 | 4 | 3 | 28.88 |
| 5 | 5 | 4 | 28.365 |
| 6 | 6 | 5 | 28.41 |
| 7 | 7 | 6 | 28.79 |
| 8 | 8 | 7 | 28.77 |
| 9 | 9 | 8 | 64.835 |
| 10 | 10 | 9 | 76.7145 |
| 11 | 11 | 10 | 36.43 |
| 12 | 12 | 11 | 33.08 |
| 13 | 13 | 12 | 30.555 |
| 14 | 14 | 13 | 28.48 |
| 15 | 15 | 14 | 145.99 |
| Transfer Function | RMSE of Validation Results (%) |
|---|---|
| TF5 | 20.21 |
| TF6 | 19.77 |
| TF14 | 12.64 |
| Zeros | Poles | ||
|---|---|---|---|
| Notation | Coefficient | Notation | Coefficient |
| A | −41.8 | A | 1 |
| B | 5316.1 | B | 62.2 |
| C | −127,314.3 | C | 5691.3 |
| D | 21,142,462 | D | 247,801.3 |
| E | 143,409,991.3 | E | 6,227,203.6 |
| F | 365,489,941 | F | 22,415,111.8 |
| G | 730,969,627 | G | 60,951,145 |
| H | 1,111,865,214 | H | 103,813,779.8 |
| I | 979,829,670.8 | I | 153,202,135.3 |
| J | 702,601,785.7 | J | 128,318,971.5 |
| K | 205,538,612.5 | K | 87,979,344.5 |
| L | 77,012,779 | L | 26,846,224.5 |
| M | 2,555,603.7 | M | 9,998,137.5 |
| N | 776,563.5 | N | 292,442 |
| 0 | 103,749.2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imaduddin, F.; Arifin, Z.; Ubaidillah; Mahmoud, E.R.I.; Aljabri, A. Current–Pressure Dynamics Modeling on an Annular Magnetorheological Valve for an Adaptive Rehabilitation Device for Disabled Individuals. Micromachines 2025, 16, 144. https://doi.org/10.3390/mi16020144
Imaduddin F, Arifin Z, Ubaidillah, Mahmoud ERI, Aljabri A. Current–Pressure Dynamics Modeling on an Annular Magnetorheological Valve for an Adaptive Rehabilitation Device for Disabled Individuals. Micromachines. 2025; 16(2):144. https://doi.org/10.3390/mi16020144
Chicago/Turabian StyleImaduddin, Fitrian, Zaenal Arifin, Ubaidillah, Essam Rabea Ibrahim Mahmoud, and Abdulrahman Aljabri. 2025. "Current–Pressure Dynamics Modeling on an Annular Magnetorheological Valve for an Adaptive Rehabilitation Device for Disabled Individuals" Micromachines 16, no. 2: 144. https://doi.org/10.3390/mi16020144
APA StyleImaduddin, F., Arifin, Z., Ubaidillah, Mahmoud, E. R. I., & Aljabri, A. (2025). Current–Pressure Dynamics Modeling on an Annular Magnetorheological Valve for an Adaptive Rehabilitation Device for Disabled Individuals. Micromachines, 16(2), 144. https://doi.org/10.3390/mi16020144








