Numerical Simulation and Experimental Verification of Multi-Probe Cryoablation
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Modeling
| Parameter | Description | Unit | Magnitude | Note |
|---|---|---|---|---|
| k | Conductivity of tissue | W/(m·℃) | 0.5 | Liquid Phase |
| 2 | Solid Phase | |||
| c | Specific heat of tissue | J/(kg·℃) | 3600 | Liquid Phase |
| 1800 | Solid Phase | |||
| ρ | Density of tissue | kg/m3 | 1000 | Liquid Phase |
| 998 | Solid Phase | |||
| cb | Specific heat of blood | J/(kg·℃) | 3600 | - |
| wb | Blood perfusion rate | s−1 | 0.0005 | - |
| Qm | Metabolic heat generation | W/m3 | 4200 | - |
| Qlf | Latent heat of phase transition | MJ/m3 | 250 | - |
| Tmu | Upper limit of phase transition | ℃ | −1 | - |
| Tmf | Lower limit of phase transition | ℃ | −8 | - |
| Material | Conductivity | Density | Specific Heat |
|---|---|---|---|
| Nitinol | 21.9 [W/(m*K)] | 4506 [kg/m3] | 522 [J/(kg*K)] |
| PU | 0.18 [W/(m*K)] | 930 [kg/m3] | 1900 [J/(kg*K)] |
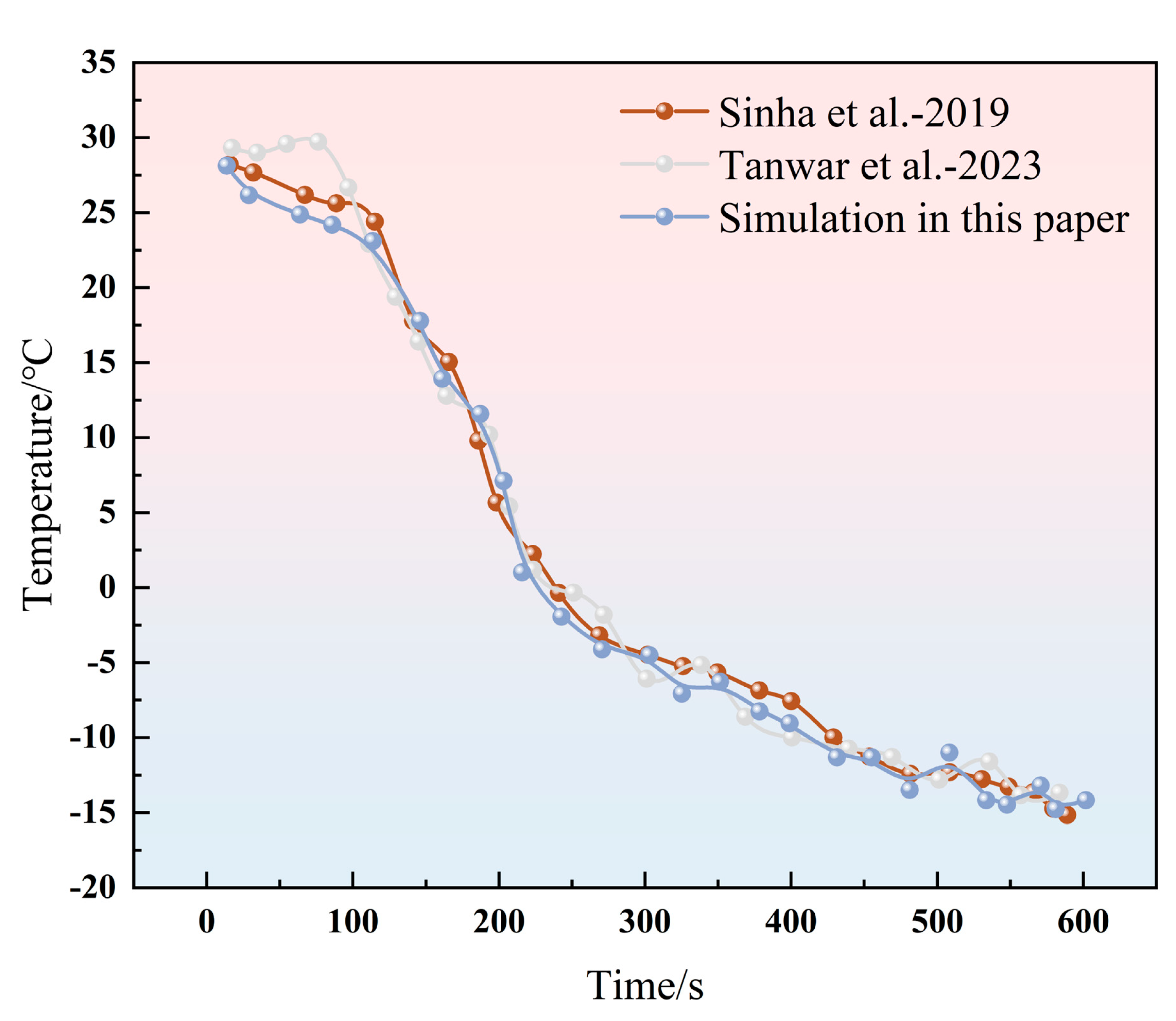
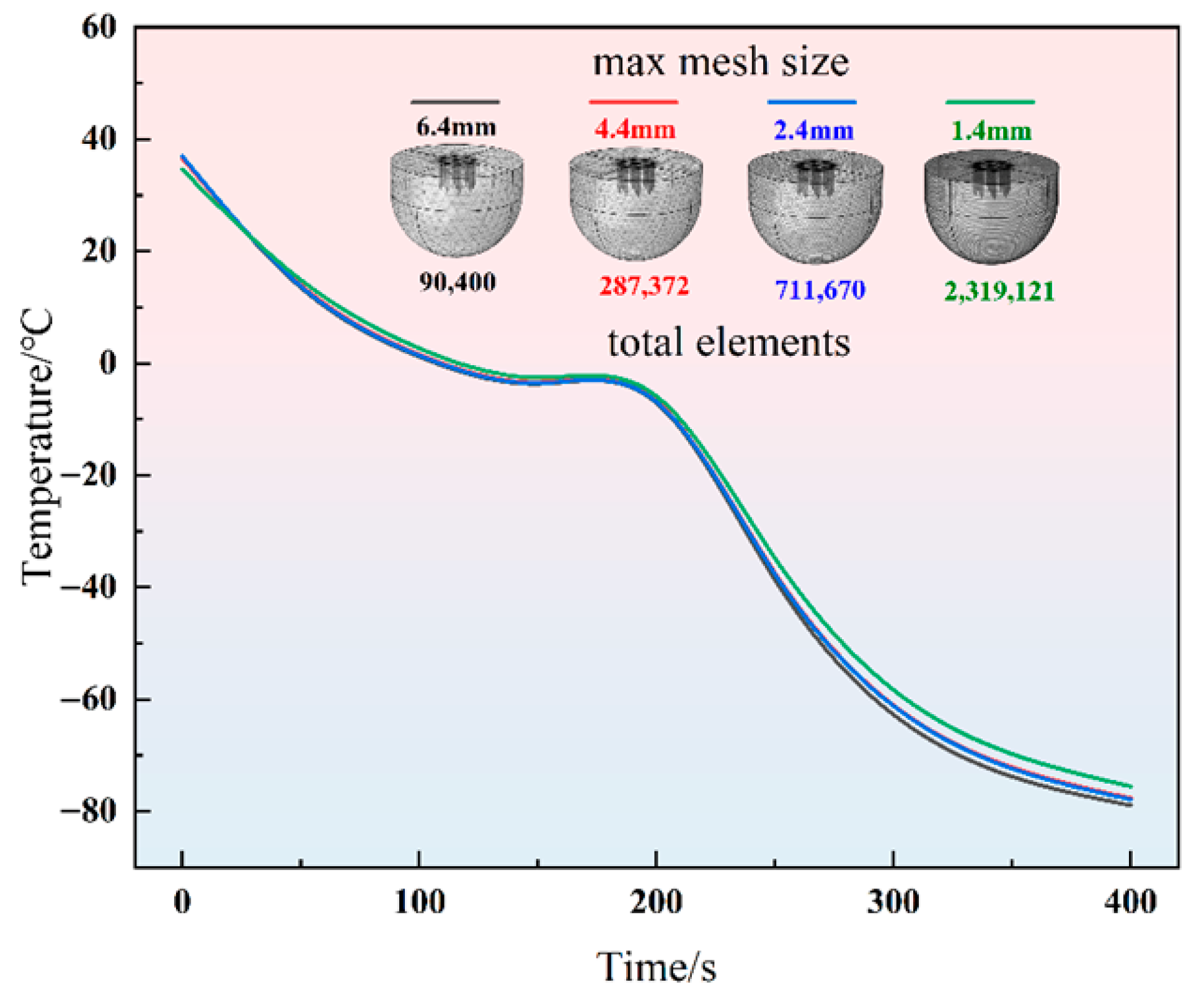
2.2. Numerical Method Verification
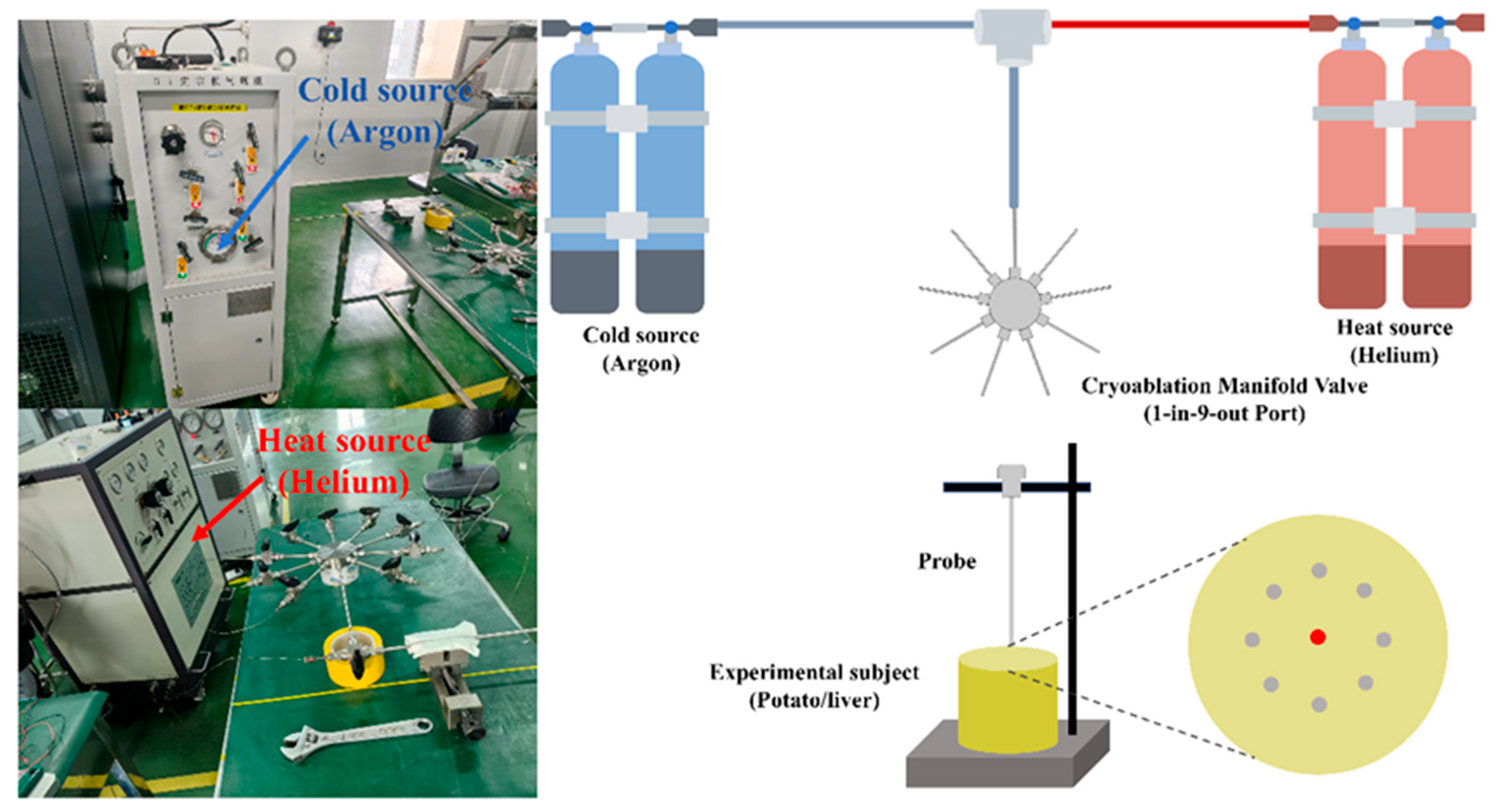
2.3. Experimental Setup
3. Results and Discussion
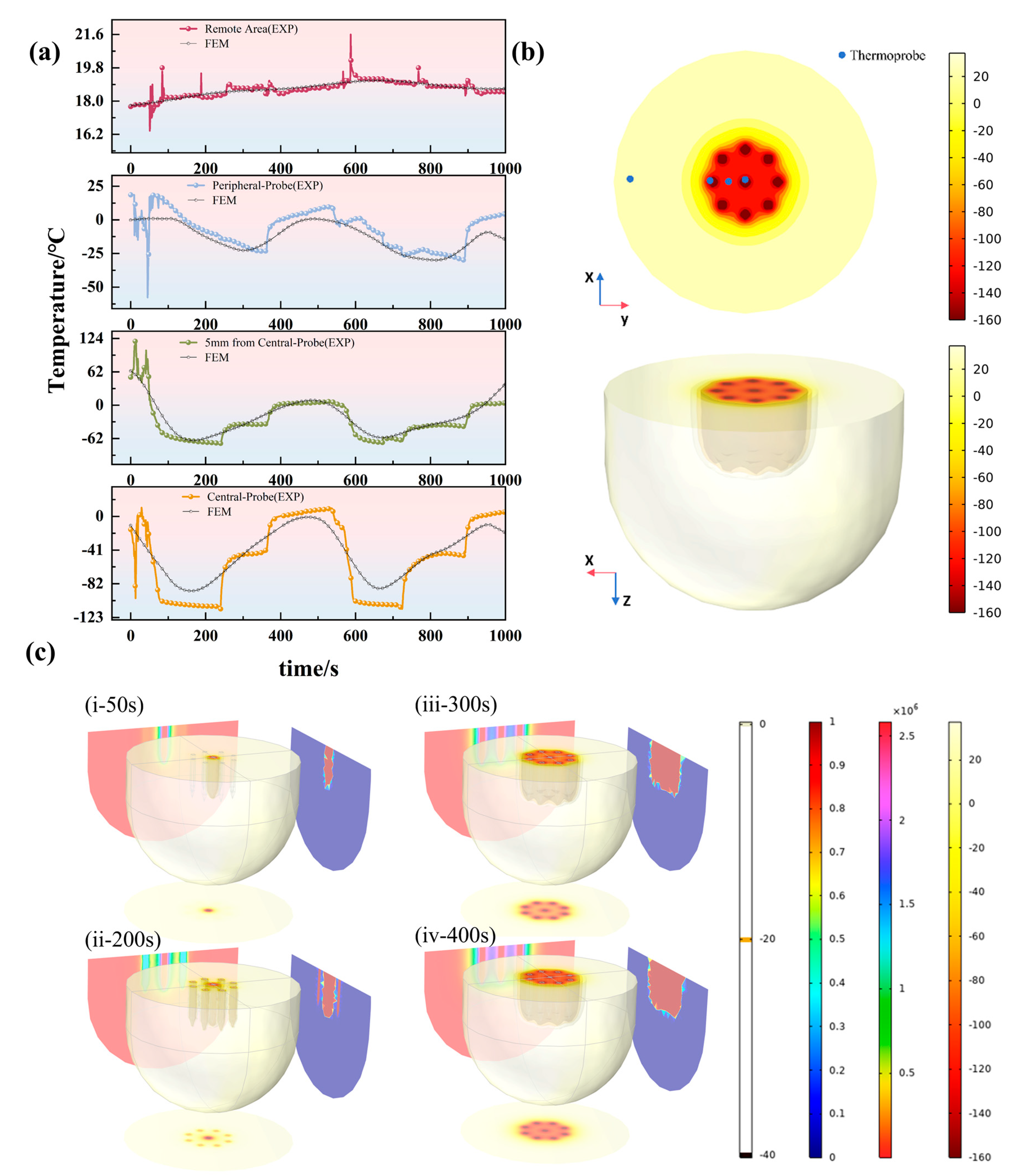
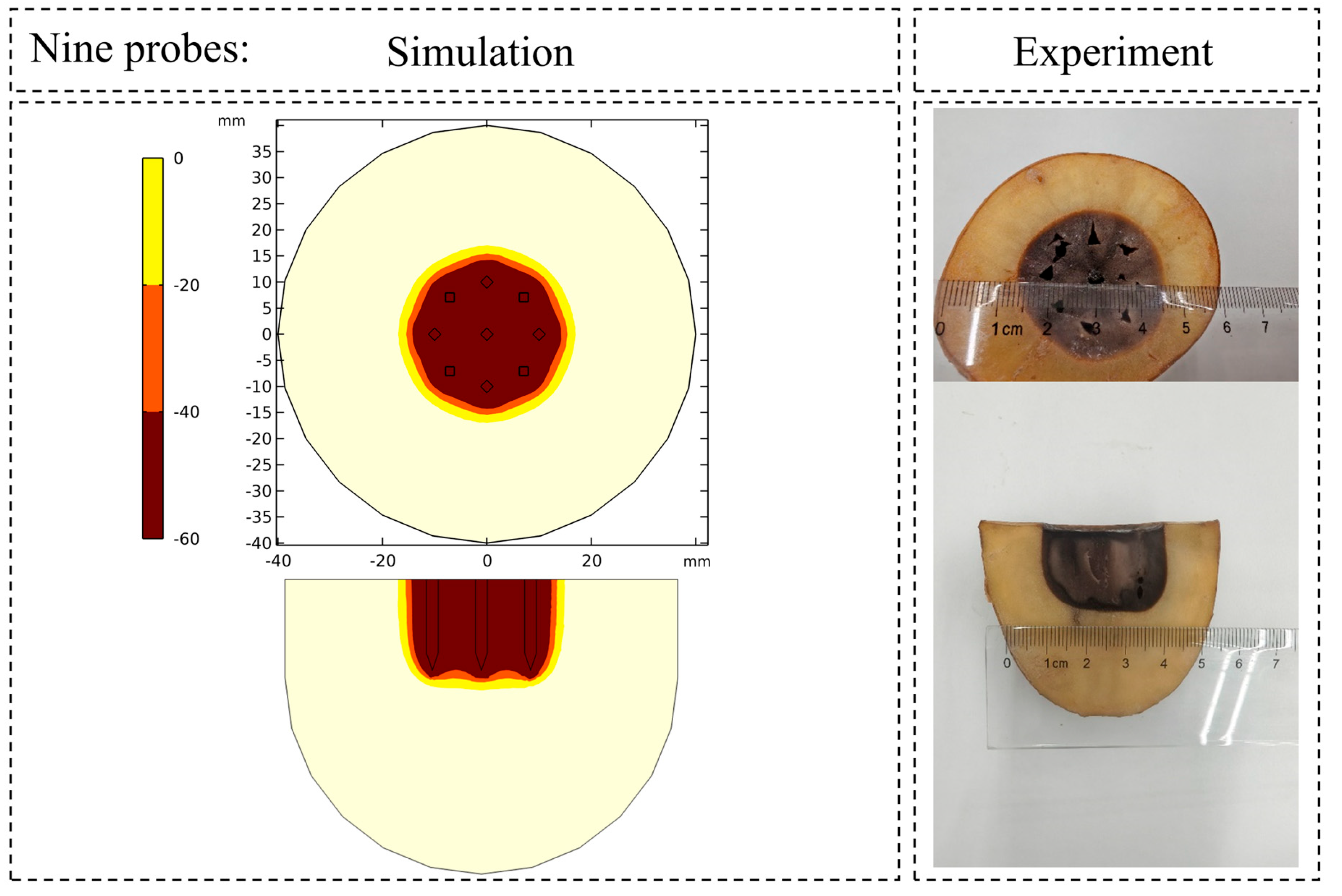
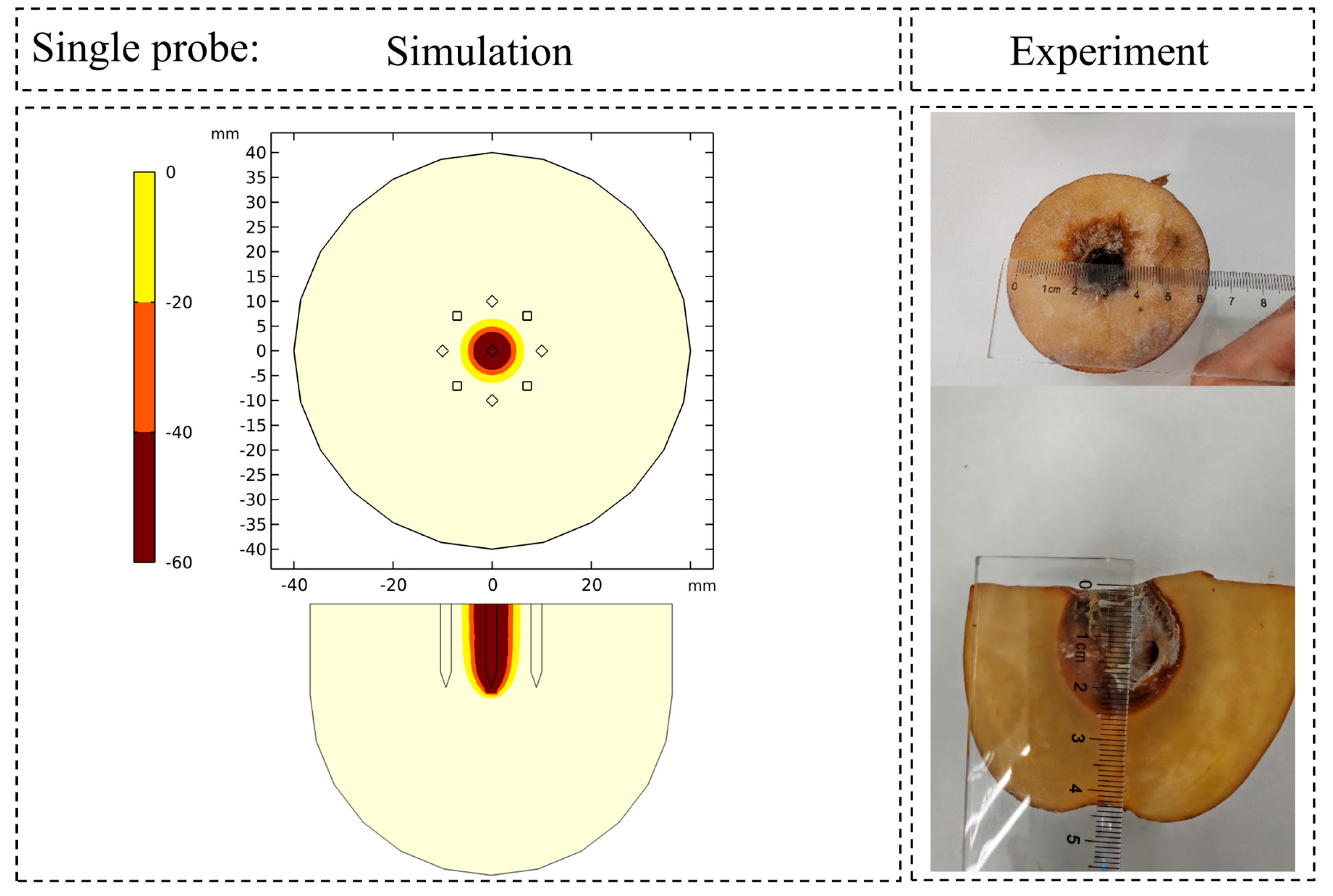
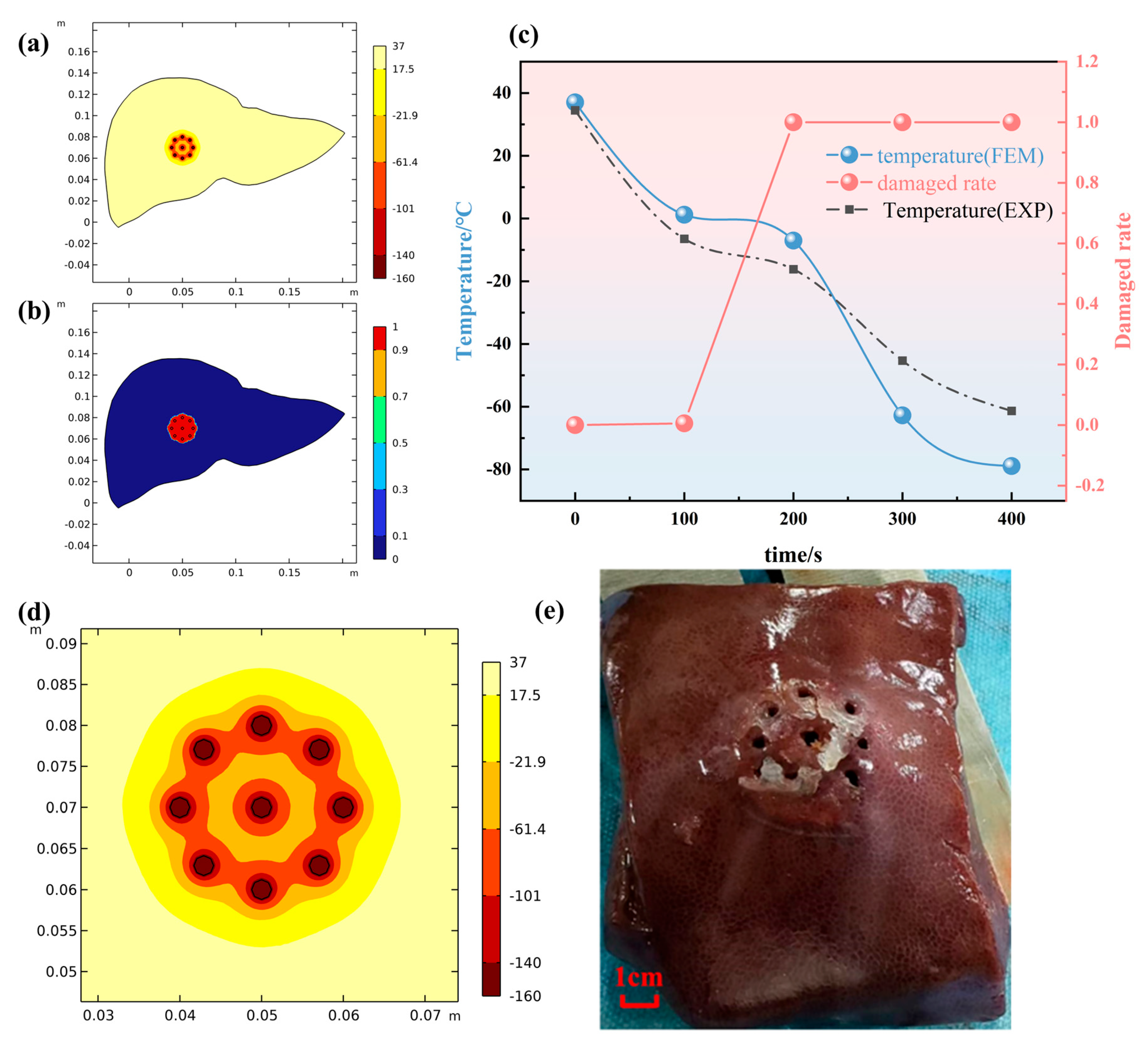
3.1. Thermophysical Validation: Prediction of Ice Ball and Temperature Field
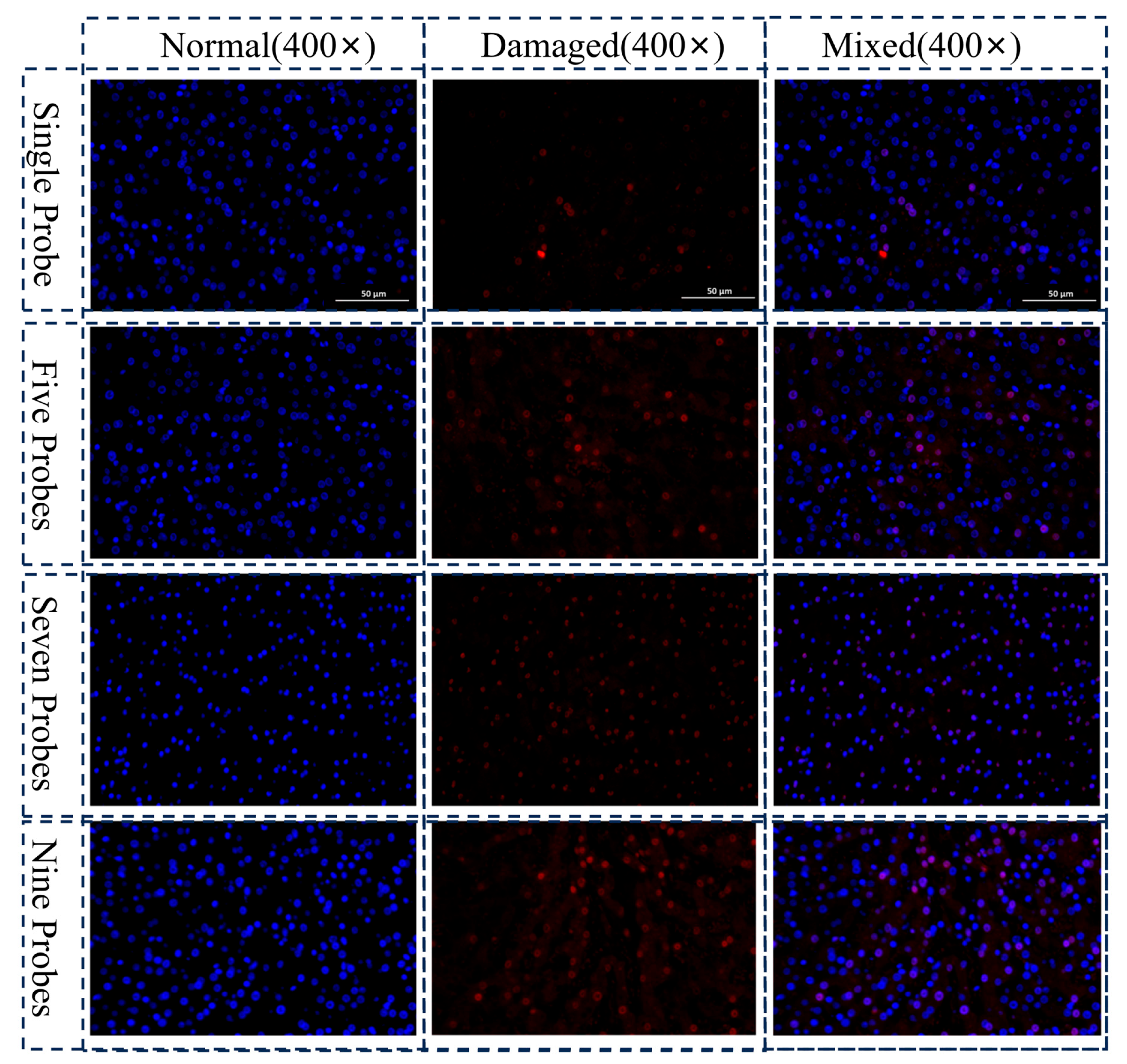
3.2. Biological Damage Assessment
3.3. Limitations and Future Works
- •
- A primary limitation arises from the use of ex vivo porcine liver tissue. While its thermal properties approximate human liver, the critical absence of hemodynamics is not accounted for. In vivo, the “heat sink” effect of major vessels would profoundly alter the ice ball’s shape, consequently resulting in incomplete ablation. This discrepancy poses a foremost clinical challenge that lies beyond the predictive scope of the present model.
- •
- Secondly, the computational model simplifies the liver as a homogeneous, isotropic material, thereby omitting the complex microstructural heterogeneity—including bile ducts, vasculature, and lobular architecture—found in real tissue. This omission of microscale thermophysical variations is a plausible explanation for the mismatch between the simulated lesion boundary and the histologically defined injury zone.
- •
- Thirdly, this study observed a diffuse injury boundary but lacked a quantitative, automated image-analysis protocol to define this transitional zone precisely. The reliance on qualitative and semi-quantitative comparisons thus constrained further analysis of the spatial principles governing its extent.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Y.M.; Paolucci, I.; Brock, K.K.; Odisio, B.C. Image-Guided Ablation for Colorectal Liver Metastasis: Principles, Current Evidence, and the Path Forward. Cancers 2021, 13, 3926. [Google Scholar] [CrossRef]
- Will, M.; Gerlach, T.; Saalfeld, S.; Gutberlet, M.; Düx, D.; Schröer, S.; Hille, G.; Wacker, F.; Hensen, B.; Berg, P. Temperature Simulation of an Ablation Needle for the Prediction of Tissue Necrosis during Liver Ablation. J. Clin. Med. 2024, 13, 5853. [Google Scholar] [CrossRef]
- Kumar, M.; Rai, K.N. Numerical study of cryosurgical treatment of skin cancer. Int. J. Therm. Sci. 2021, 160, 106667. [Google Scholar] [CrossRef]
- Young, J.L.; McCormick, D.W.; Kolla, S.B.; Sountoulides, P.G.; Kaufmann, O.G.; Ortiz-Vanderdys, C.G.; Huynh, V.B.; Kaplan, A.G.; Jain, N.S.; Pick, D.L.; et al. Are multiple cryoprobes additive or synergistic in renal cryotherapy? Urology 2012, 79, 484.e1–484.e6. [Google Scholar] [CrossRef] [PubMed]
- Condino, S.; Cutolo, F.; Cattari, N.; Colangeli, S.; Parchi, P.D.; Piazza, R.; Ruinato, A.D.; Capanna, R.; Ferrari, V. Hybrid Simulation and Planning Platform for Cryosurgery with Microsoft HoloLens. Sensors 2021, 21, 4450. [Google Scholar] [CrossRef]
- Deng, Z.S.; Liu, J. Computerized Planning of Multi-Probe Cryosurgical Treatment for Tumor with Complex Geometry. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition. Volume 2: Biomedical and Biotechnology Engineering, Seattle, WA, USA, 11–15 November 2007; pp. 97–101. [Google Scholar] [CrossRef]
- Rossi, M.R.; Tanaka, D.; Shimada, K.; Rabin, Y. Computerized Planning of Cryosurgery Using Bubble Packing: An Experimental Validation on a Phantom Material. Int. J. Heat Mass Transf. 2008, 51, 5671–5678. [Google Scholar] [CrossRef] [PubMed]
- Giorgi, G.; Avalle, L.; Brignone, M.; Piana, M.; Caviglia, G. An optimisation approach to multiprobe cryosurgery planning. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 885–895. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Zhou, F.; Xu, S.; Wang, Y.; Cheng, L.; Bie, Z.; Li, B.; Li, X.-G. Iceball growth 3D simulation model based on finite element method for hepatic cryoablation planning. BMC Gastroenterol. 2025, 25, 227. [Google Scholar] [CrossRef]
- Rieder, C.; Schwenke, M.; Pätz, T.; Georgii, J.; Ballhausen, H.; Schwen, L.O.; Haase, S.; Preusser, T. Evaluation of a numerical simulation for cryoablation–comparison with bench data, clinical kidney and lung cases. Int. J. Hyperth. 2020, 37, 1268–1278. [Google Scholar] [CrossRef]
- Ramajayam, K.K.; Kumar, A. A novel approach to improve the efficacy of tumour ablation during cryosurgery. Cryobiology 2013, 67, 201–213. [Google Scholar] [CrossRef]
- Kim, C.; O’Rourke, A.P.; Will, J.A.; Mahvi, D.M.; Webster, J.G. Finite-element analysis of hepatic cryoablation around a large blood vessel. IEEE Trans. Biomed. Eng. 2008, 55, 2087–2093. [Google Scholar] [CrossRef]
- Hossain, S.C.; Zhang, X.; Haider, Z.; Hu, P.; Zhao, G. Optimization of prostatic cryosurgery with multi-cryoprobe based on refrigerant flow. J. Therm. Biol. 2018, 76, 58–67. [Google Scholar] [CrossRef]
- Deng, Z.-S.; Liu, J. Numerical simulation of selective freezing of target biological tissues following injection of solutions with specific thermal properties. Cryobiology 2005, 50, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Zhang, H.-F.; Guo, X.-J.; Luo, D.-W.; Gao, D.-Y. Effect of blood flow and metabolism on multidimensional heat transfer during cryosurgery. Med. Eng. Phys. 2007, 29, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Sukumar, S.; Kar, S.P. Numerical investigation of a novel method of laser assisted cryopreservation of biological tissue considering non-fourier heat conduction. Lasers Med. Sci. 2023, 38, 98. [Google Scholar] [CrossRef]
- Tanwar, S.; Famhawite, L.; Verma, P.R. Numerical Simulation of bio-heat transfer for cryoablation of regularly shaped tumours in liver tissue using multiprobes. J. Therm. Biol. 2023, 113, 103531. [Google Scholar] [CrossRef]
- Etheridge, M.L.; Choi, J.; Ramadhyani, S.; Bischof, J.C. Methods for characterizing convective cryoprobe heat transfer in ultrasound gel phantoms. J. Biomech. Eng. 2013, 135, 021002. [Google Scholar] [CrossRef]
- Choi, J.; Bischof, J.C. Review of biomaterial thermal property measurements in the cryogenic regime and their use for prediction of equilibrium and non-equilibrium freezing applications in cryobiology. Cryobiology 2010, 60, 52–70. [Google Scholar] [CrossRef]
- Magalov, Z.; Shitzer, A.; Degani, D. Experimental and Numerical Study of One, Two, and Three Embedded Needle Cryoprobes Simultaneously Operated by High Pressure Argon Gas. ASME J. Heat Transfer. March 2008, 130, 032301. [Google Scholar] [CrossRef]
- Nabaei, M.; Karimi, M. Numerical investigation of the effect of vessel size and distance on the cryosurgery of an adjacent tumor. J. Therm. Biol. 2018, 77, 45–54. [Google Scholar] [CrossRef]
- Mirkhalili, S.M.; Ramazani S A, A.; Nazemidashtarjandi, S. Mathematical study of probe arrangement and nanoparticle injection effects on heat transfer during cryosurgery. Comput. Biol. Med. 2015, 66, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Sinha, V.A.; Ramajayam, K.K.; Kumar, A. A parametric study on the cryosurgery of gel mimicking tissue phantoms. Heat Mass Transf. 2019, 55, 655–667. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Tong, B.; Ni, C.; Fu, G.; Pan, B.; Huang, L. Numerical Simulation and Experimental Verification of Multi-Probe Cryoablation. Micromachines 2025, 16, 1321. https://doi.org/10.3390/mi16121321
Zhang J, Tong B, Ni C, Fu G, Pan B, Huang L. Numerical Simulation and Experimental Verification of Multi-Probe Cryoablation. Micromachines. 2025; 16(12):1321. https://doi.org/10.3390/mi16121321
Chicago/Turabian StyleZhang, Jian, Bei Tong, Changmao Ni, Guoting Fu, Binglei Pan, and Li Huang. 2025. "Numerical Simulation and Experimental Verification of Multi-Probe Cryoablation" Micromachines 16, no. 12: 1321. https://doi.org/10.3390/mi16121321
APA StyleZhang, J., Tong, B., Ni, C., Fu, G., Pan, B., & Huang, L. (2025). Numerical Simulation and Experimental Verification of Multi-Probe Cryoablation. Micromachines, 16(12), 1321. https://doi.org/10.3390/mi16121321